电工学第2章习题答案
《电工学(唐介主编)》第2章习题答案

下一页
上一题
下一题
uC (0) = U0 = R2 IS = (6 × 5)V = 30V
换路后电容经 R3 及 R1 与 R2 的并联电阻放电,响应为零输入 响应.电路可简化为图所示,其中等效电阻设 3×6 R = ( R1 // R2 ) + R3 = ( + 8)Ω = 10Ω 3+ 6 电路的时间常数τ = RC = 10×10×106 s = 104 s iC
uL(0) = R2iL(0) = 12V
.k hd aw .c om
R1
2Ω
i1
R2
3Ω
IS
10 V
案 网
+ uC
S iC
C
+ uL
iL
L
5A
答
稳态值: iC (∞) = 0A uL (∞) = 0V US R1 iL (∞) = + IS = 4A R1 + R2 R1 + R2 i1 (∞) = i L (∞) IS = 1A uC (∞) = R2 i L (∞) = 12V
ww
.k hd aw .c om
i1
S
IS
i2
R3
7Ω
R1
R2
24 A
1.5 Ω
3Ω
+ iL uL L 0.4 H
后
答
课
a
S
R1
+ U S1
6V
b
3Ω
R3
US2 +
3Ω
R2
6Ω
+ iL uL L
1H
6V
返 回
上一页
下一页
2.5.1 图所示电路原已 2.5.1 处于稳态.试用三要素法求 开关 S 闭合后的 uL 和 uR. +
电工学概论习题答案_第二章

2-1. 列出以下节点的电流方程式,并求出x I 。
解:(a) 由KCL 得:1234()()()0x I I I I I +-+-+-+= ∴2341x I I I I I =++-;(b) 由KCL 得:39(5)()0x I ++-+-= ∴7x I A =(c) 由KCL 之推广得:69()0x I ++-= ∴15x I A =(d) 由KCL 得:1(2)(3)40x I +-++-+= ∴0x I =2-2. 列出以下回路的电压方程式,并标出回路循环方向,求出U 。
解:(a) 回路循环方向与I 方向相同,由KVL 得:U+(2S U -)+I R ⋅=0 ∴U = 2S U -I R ⋅(b) 回路循环方向与3I 、4I 方向相同,由KVL 得:44I R ⋅+33I R ⋅+(U -)=0 ∴U = 44I R ⋅+33I R ⋅(c) 回路循环方向为逆时针方向,由KVL 得:U+(9-)+7=0 ∴U = 2V(d) 设回路电流大小为I ,方向为逆时针方向,由KVL 得:2S U +I ⋅4+I ⋅6+(1S U -)+I ⋅3+I ⋅7=0 ∴I = 0.3A因此,U=2S U +I ⋅4 =2-3. 求出下列电路中的电流I 。
解:(a) 由KCL ,流过2Ω电阻的电流大小为(9+I),对2Ω电阻与10V 电压源构成的回路,由KVL ,得:(9)I +⋅2+(10-) =0, 因此,I =-4A ;(b) (2)I -⋅3+6=0; ∴I = 4A;(c) 流过3Ω电阻的电流 1I =93÷=3A流过6Ω电阻的电流 2I =(6+9) ÷6=2.5 A(d) 由KCL ,I + 3-3=0 ∴I =0;2-4. 求出下列电路中的电压U 。
解:(a) (U/10 + U/10) ⨯5 + U = (4-U/10-U/10) ⨯10 ∴U=10V ;(b) 10⨯2 + 10 + U =0 ∴U=-30V(c) 1I =10⨯(64)(46)(64)++++=5A; 2I =10⨯(46)(46)(64)++++=5A; 4⨯1I + U + 6⨯(-2I )=0; ∴U = 10V(d) U + 18⨯393+-=0; ∴U = 02-5. 有50个彩色白炽灯接在24V 的交流电源上,每个白炽灯为60W ,求每个白炽灯的电流及总电流,另外消耗的总功率为多少 答:每个白炽灯上消耗的功率为2U P UI R==,而U =24V ,P =60W , 因此每个白炽灯的电流为P I U ==2.5A ,总电流为I 总=I ⨯ 50=125A 消耗的总功率为P 总=P ⨯ 50=3000W2-6. 在220V 单相交流电源上,接有两台电阻热水器,一台为,一台为3kW ,分别求这两台电热器的电阻。
《电工学》作业答案第二章
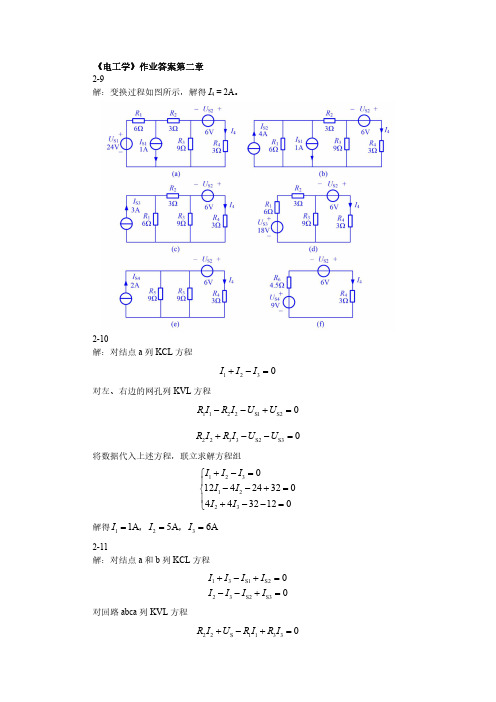
《电工学》作业答案第二章 2-9解:变换过程如图所示,解得I 4 = 2A 。
2-10解:对结点a 列KCL 方程1230I I I对左、右边的网孔列KVL 方程1122S1S20R I R I U U 2233S2S30R I R I U U将数据代入上述方程,联立求解方程组12312230124243204432120I I I I I I I解得1231A 5A 6A I I I ,, 2-11解:对结点a 和b 列KCL 方程13S1S223S2S300I I I I I I I I对回路abca 列KVL 方程22S 11330R I U R I R I将数据代入上述方程,联立求解方程组132321362023022420I I I I I I I解得1232A 1A 2A I I I ,,2-12 解:根据两个结点电路中结点电压方程的一般形式得S1S2S3123a 12312612346V 6V 111111346U U U R R R U R R R 电流I 3可用欧姆定律求得a S333612A 3A 6U U I R2-14解:(a)电路图; (b)电压源U S 单独作用的电路; (c)电流源I S 单独作用的电路电压源U S1单独作用时,将U S2短路,电路如 (b)所示S1123123321232312318A 3.6A 6336333.6A 1.2A 6363.6A 2.4A63U I R R R R R R I I R R R I I R R电压源U S2单独作用时,将U S1短路,电路如图 (c)所示S2213213312131321315A 2A 3362332A 1A3332A 1A33U I R R R R R R I I R R R I I R RU S 和I S 共同作用时111222333 3.61A 2.6A 1.22A 0.8A 2.41A 3.4A I I I I I I I I I 2-16解:(a)I S1单独作用的电路; (b)I S2单独作用的电路; (c)U S 单独作用的电路电流源I S1单独作用时,电路如 (a)所示2S12333A 1.8A 32R I I R R电流源I S2单独作用时,电路如 (b)所示3S22325A 2A 32R I I R R电压源U S2单独作用时,电路如 (c)所示S 2315A 3A 32U I R RI S1、I S1和U S 共同作用时1.823A 6.8A I I I I2-19 解:(a) 求开路电压的电路; (b)求除源电阻的电路; (c) 戴维南等效电路求开路电压的等效电路如 (a)所示。
电工第二章习题及答案

一、选择题1、如图所示,其节点数、支路数、回路数及网孔数分别为(C )。
A、2、5、3、3B、3、6、4、6C、2、4、6、32、如图所示,I=(B )A。
A、2B、7C、5D、63、如图所示,E=(B )V。
A、3B、4C、—4D、—3/4、如图所示电路中,I1和I2的关系为(C )。
A、I1<I2B、I1>I2C、I1=I2D、不确定5、如图所示,求I1和I2的大小。
解:对于左边节点:I1=10+3+5=18A对于右边节点:I2=10+2-5=7A6、基尔霍夫第一定律的依据是(D )A.欧姆定律B.全电流定律C.法拉第定律D.电荷守恒定¥7、理想电压源和理想电流源间(C )A.有等效变换关系B.没有等效变换关系C.有条件下的等效关系D.无法判定8、下列说法错误的是(D )A.在电路节点处,各支路电流参考方向可以任意设定。
B.基尔霍夫电流定律可以扩展应用于任意假定的封闭面。
C.基尔霍夫电压定律应用于任意闭合路径。
D.∑I=0式中各电流的正负号与事先任意假定的各支路电流方向无关9、实际电压源和电流源模型中,其内阻与理想电压源和电流源之间的正确连接关系是(C)A.理想电压源与内阻串联,理想电流源与内阻串联"B.理想电压源与内阻并联,理想电流源与内阻串联C.理想电压源与内阻串联,理想电流源与内阻并联D.理想电压源与内阻并联,理想电流源与内阻并联10、79.下面的叙述正确的是(B )。
A.理想电压源和理想电流源是不能等效变换的B.理想电压源和理想电流源等效变换后内部是不等效的C.理想电压源和理想电流源等效变换后外部是不等效的D.以上说法都不正确二、填空题1、不能用电阻串、并联化简的电路称为__复杂电路_______。
;2、电路中的_____每一分支_______称为支路,____3条或3条以上支路___所汇成的交点称为节点,电路中__________闭合的电路______________都称为回路。
第二章 习题及答案

电工学第二章习题一、填空题1. 两个均为40F μ的电容串联后总电容为 80 F μ,它们并联后的总电容为 20 F μ。
2. 表征正弦交流电振荡幅度的量是它的 最大值 ;表征正弦交流电随时间变化快慢程度的量是 角频率ω ;表征正弦交流电起始位置时的量称为它的 初相 。
三者称为正弦量的 三要素 。
3. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ;电感元件上任一瞬间的电压电流关系可以表示为dtdiLu =L ;电容元件上任一瞬间的电压电流关系可以表示为dtduCi =C 。
由上述三个关系式可得, 电阻 元件为即时元件; 电感 和 电容 元件为动态元件。
4. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 50Ω ,该电路为 容 性电路。
电路中吸收的有功功率为 750W ,吸收的无功功率又为 1000var 。
二、选择题1. 某正弦电压有效值为380V ,频率为50Hz ,计时始数值等于380V ,其瞬时值表达式为( B ) A 、t u 314sin 380=V ;B 、)45314sin(537︒+=t u V ;C 、)90314sin(380︒+=t u V 。
2. 一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P/2,则正弦交流电源电压的最大值为( D ) "A 、;B 、5V ;C 、14V ;D 、10V 。
3. 提高供电电路的功率因数,下列说法正确的是( D )A 、减少了用电设备中无用的无功功率;B 、减少了用电设备的有功功率,提高了电源设备的容量;C 、可以节省电能;D 、可提高电源设备的利用率并减小输电线路中的功率损耗。
4. 已知)90314sin(101︒+=t i A ,︒+=30628sin(102t i )A ,则( C )A 、i1超前i260°;B 、i1滞后i260°;C 、相位差无法判断。
电工学-第二章习题答案
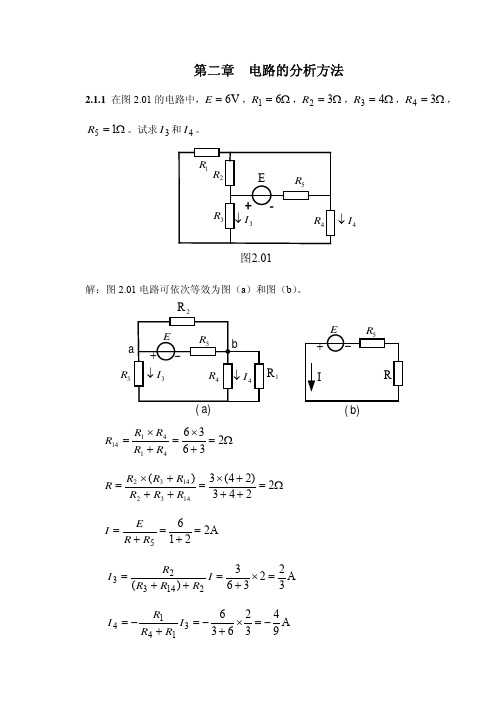
第二章 电路的分析方法2.1.1 在图2.01的电路中,V 6=E ,Ω=61R ,Ω=32R ,Ω=43R ,Ω=34R ,Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解:图2.01电路可依次等效为图(a )和图(b )。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解:根据电压源与电流源的等效变换,图2.12所示电路可依次等效为图(a )和图(b ),由图(b )可求得A 2.15.023=+=I由图(a )可求得:A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中,(1)当将开关S 合在a 点时,求电流1I ,2I 和3I ;(2)当将开关S 合在b 点时,利用(1)的结果,用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解:(1)当将开关S 合在a 点时,图2.19所示电路即为图(a ),用支路电流法可得:=+=+=+12042130423231321I I I I I I I 解得:===A 25A 10A 15321I I I(2)开关S 合在b 点时,利用叠加原理图2.19所示电路可等效为图(a )和图(b ),其中图(a )电路中130V 和120V 两个电压源共同作用时所产生的电流已在(1)中求得,即:A 151=,I A 102=,I A 253=,I由图3(b )可求得:A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则:A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20(a )所示,V 10ab ,,V 124321=====U R R R R E 。
电工第二章习题答案
I1
a
I2
I3
1
R2
d
c
R3
U S2
b 图 2.1 支路电流法
返 返回 回 上 上页 页 下 下页 页
第2章 电路的基本分析方法
2. 支路电流法求解电路的步骤 (1) 选定各支路电流的参考方向;
(2) 根据KCL对n个节点列写n-1节点电流方程; (3) 选定网孔绕行方向,对l-(n-1)个网孔列写 KVL方程; (4) 联立方程求解各支路电流。
R1
a
I 2'
IS
US
U
R2
US
R2
US I2 R1 R2
返 返回 回 上 上页 页 下 下页 页
b
(a) 完整电路
b
(b)电压源单独作用
图 2.3 叠加原理示意图
第2章 电路的基本分析方法
I1
R1
(2)Is单独作用时产生的电流
a
I2
I 1'
R1
a
I 2'
I 1"
R1
a
" I2
US
U
R I1 R2 IS R 1 R 2
1
a
1
U 例2.7电路如图 2.10所示,用戴维 南定理求电压U。 b (1)求开路电压U图 。 解: OC 2.9 戴维南定理求解例 2.4
S
R2
U OC
R2
R0
R0
U OC
I
R3
(1)开路电压
3
S
U 15 S U R 10 7 . 5 V OC 2 R R 10 10 1 2
b 2.8 图 2.8图 例 2.4 图
电工电子学 第二章习题参考答案

( 2 ) S 断 开 时 , A1 的 读 数 为 14.25 A , A2 的 读 数 为 4.75 A ;
iU = 2 ×14.25sin(314t − 36.87D ) A
2.4.7 C)
2.5.1 uo = 100 + 3.74 2 sin(2ωt −175.4D ) + 0.374 2 sin(4ωt −177.7D ) V
2.3.7 ω =1000 rad/s 时 , Z =( 500-j1500) Ω =1581 ∠ − 71.6D Ω 、
i = 10.1 2 sin(1000t + 71.6D ) mA ;
ω =2000 rad/s 时,Z = 500 Ω 、 i = 32 2 sin 2000t mA ;
ω =3000rad/s 时 , Z =( 500+j833.3)= 971.8∠59D Ω 、
2.4.5
•
IU
= 33.15∠15.14D
A
•
、I V
= 13.2∠ − 79.11D
A
•
、I W
= 13.2∠ −199.11D
A,
•
中线电流 I N = 22 A
2.4.6 (1)电流表 A1 的读数为 16.45 A ,电流表 A2 的读数为 9.5 A ;相量
图(略); iU = 2 ×16.45sin(314t − 66.87D ) A
•
I
= 10∠
− 15D
A ,i = 10
2 sin(314t − 15D ) A
2.3.4
(1)iR
=
u R
= 2.2
2 sin 314t
A
iC = 0.69 2 sin(314t + 90D ) A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.0 9 5 5 10
5
0 .6 3 7 10
5
5.7 3 10 ( m )
5
4、计算结果表明,左段伸长5.0955x 10-5m, 右段伸长0.637x 10-5m,全杆伸长5.73 x10-5m。
2-3 图2-36所示三角形支架,杆AB及BC都是 圆截面的。杆AB直径d1=20mm,杆BC直径 d2=40mm,两杆材料均为Q235钢。设重物的 重量G=20kN。问此支架是否安全。
解 选取B为研究对象 1、如图所示,由平衡方程得 ∑Fx=0 G-FBCSin30o=0 ∑Fy=0 FAB-FBCCos30o=0
解得 FBC=G
FA B 3G
2、正应力为
AB
FA B A AB 3 20 10
3
4
110.3M P a [ ] l60 M P a
2
18 2 10 π d
2
3
τ
60M Pa
得 d 14m m 挤压应力 σ p A t d 8 1 0 3 d σ p 2 0 0 M P a 2 1
1
p
p
18 10
3
得 d 1 1m m
挤压应力
p 2A 1 p t2 2 d 18 10
3 3
σp
1
5 10 2 d
σ p 200 M P a
得
d 9mm
综上可知
d 14m m
2- 8 如图2-41所示,齿轮与轴用平键连 接,已知轴直径d=70mm,键的尺寸 b h 20m m 12m m 100m m ,传递的力偶矩 M 2 K N m ;键材料的许用应力 τ
6
25 10
2-7 目 2-40 所 示 销 钉 连 接 、 已 知 F = 18kN.板厚t1 =8mm,t2 =5mm.销钉 与 板 的 材 料 相 同 , 许 用 切 应 力 [τ] = 60MPa.许用挤压应力[σp]=200MPa。 试设计销钉直径d。
解
许用剪应力
τ p 2A1 2 p π 4 d
2-1 试求出图2-34所示各杆1-1,2-2,及3-3截 面上的轴力,并作轴力图。
解b 使用截面法,沿截面1-1将杆分成两段,取 出右段并画出受力图(b)用FN1表示左段对右段 的 作 用 , 由 平 衡 方 程 ∑ Fx=0 , 得FN1=F(拉)
同理,可以计算横截面2-2上的轴力FN2, 由截面2-2右段图(c)的平衡方程∑Fx=0, 得 FN2= F ( 压 ) 同理,可以计算横截面3-3上的轴力FN3, 由截面3-3右段图(d)的平衡方程∑Fx=0, 得FN3= 0
3 2
2 0 0 10
9
4
5.0 9 5 5 10 ( m )
4
5
4 10
右段:
4 10 4 0 10
3 2
L右
F L右
右
EA
右
2 0 0 10
9
4
0.6 3 7 10 ( m )
4
5
1 6 10
左
F左 A左
6 4
4 0 6 .7 8 K N
杆BC的承载极限:
F2 σ
BC
A B C 1 0 0 1 0 3 5 .5 8 1 0
6
4
3 5 5 .8 K N
由
得
FA C FB C F 3 5 5 .8 K N
F 3 5 5 .8 K N
2-6 图2-39所示结构中梁AB的变形及重量 可忽略不计。杆1为钢制圆杆,直径 d1=20mm,E1=200GPa;杆2为铜制圆杆, 直径d2=25mm,E2=100GPa。试问:(1)载 荷F加在何处,才能使梁AB受力后仍保持 水平? (2)若此时F=30kN,求两拉杆内横 截面上的正应力。
解 有平衡方程得
M
A
= 0 , FX = F B 2 F B
FX 2
M
B
= 0, F ( 2 - X ) FA 2 FA =
F(2- X ) 2
由FA引起的变形等于FB引起的变形
FA A EAA A FB B E BA B
即有
F(2- X ) FX 1 .5 1 2 2 π π 9 2 6 9 2 6 200 10 20 10 100 10 25 10 4 4
解:作用在活塞杆截面的工作应力
FN A P π D
2
4 2 π d 4
P
D d
2 2
由强度条件有
P D d
2 2
即
所以 d 2 P D 1 .2 1 0 4 0 0 2 3 8 4 0 m m 6
2 6
50 10
即活塞杆的直径
解 选取C为研究对象 1、如图所示,由平衡方程得 ∑Fx=0 FAC Cos30o-FBCCos30o=0 ∑Fy=0 FAC Sin30o-F+FBCSin30o =0 解得 FAC =FBC=F
2、许用应力为 杆AC的承载极限:
F1 σ A C A A C 1 6 0 1 0 2 1 2 .7 4 1 0
解得X=1.08m,当F=30KN时,
FA 1 3 .8 K N
FB 1 6 .2 K N
正应力
σA
FA AA
1 3.8 1 0 π 4
2
3
4 3 .9 7 M P a
6
20 10
正应力
σ
B
FB AB
1 6.2 1 0 π 4
2
3
3 2 .9 7 M P a
3 6
2
2 8 .5 5 M P a< τ
80M Pa
校
12 100 2
600m m
2
挤压应力
σ
p
Fs A2
5 7 .1 1 0 600 10
3
6
9 5 .1 7 M P a < σ p 2 0 0 M P a
6
400 10
BC
F
BC
2 20 10
3
A BC
4
31.85M P a [ ] l60M P a
6
1600 10
2-4 蒸汽机的汽缸如图2-37所示,汽缸 的 内 径 D = 400mm , 工 作 压 力 P = 1.2MPa。汽缸盖和汽缸用直径为18mm 的螺栓连接。若活塞杆材料的许用应力 为 50MPa , 螺 栓 材 料 的 许 用 应 力 为 40MPa,试求活塞杆的直径及螺栓的个 数。
d 62m m
由强度条件式得
π D P' FN 4 ' 2 π D' nA' n 4
2
'
整理得
n
PD D'
2
2
'
1 .2 1 0 4 0 0
6
2
40 10 18
6
2
1 4 .8
螺栓应至少为16个
2-5 三角形支架ABC如图2-38所示,在C点受到载荷F 的作用。己知,杆AC由两根10号槽钢所组成, [σ]AC=160MPa;杆BC是20a号工字钢所组成, [σ]BC=100MPa。试求最大许可载荷F。
σ
p
80M Pa
2 0 0 M P a ,试校核键的强度。
解 对轴心取矩,由平衡方程得: 力偶
M Fs
d 2
22 0 .0 7
5 7 .1K N
剪切面积为
A b 20 100 2000m m
切应力
Fs A1 5 7 .1 1 0 2000 10
2-2 试求图2-35所示钢杆各段内横截面上的应 力和杆的总变形。钢的弹性模量E=200GPa。
解 1、内力计算 用截面法分别计算左段和右段的内力并作杆 的轴力图(b) 得 F左 =4kN(拉) F右 =4kN(拉)
左段:
L左 F左 L 左 EA 左 4 10 8 0 10
4 10
3
4
1 2 .7 3 M P a
4
2 10
2
右
F右 A右
4 10
3
4
3 .1 8 M P a
4
4
2
10
2、各段变形的计算左、右两段的轴力为F左 F 右 ,横截面面积A左、A右,长度L左,L右均不 相同,变力计算应力分别进行。
3、总变形计算
L L左 L右
解b 使用截面法,沿截面1-1将杆分 成两段,取出右段并画出受力图(b) 用FN1表示左段对右段的作用, 由平衡方程∑Fx=0,得FN1 =F(拉)
同理,可以计算横截面2-2上的轴 力FN2,由截面2-2右段图(c)的平 衡方程Fx=0 ∑,得FN2= F(压)
同理,可以计算横截面3-3上的轴力 FN3,由截面3-3左段图(d)的平衡 方程∑Fx=0,得FN3=F(拉)
