残差值的经验
什么是残差分析如何利用残差分析来检验回归模型的适用性

什么是残差分析如何利用残差分析来检验回归模型的适用性残差分析是统计学中一种常用的方法,用于评估回归模型的适用性。
在回归分析中,我们希望通过建立数学模型来描述自变量与因变量之间的关系。
残差分析则是用来检验模型是否能准确地描述实际数据。
残差(residual)是指观测值与回归方程预测值之间的差异。
回归方程可以表示为:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε,其中Y是因变量,X1、X2、...、Xn是自变量,β0、β1、β2、...、βn是回归系数,ε是误差。
残差计算公式为:残差 = 观测值 - 预测值。
当回归模型适用性良好时,残差应该随机分布在零附近,没有明显的模式或趋势。
接下来,我们将介绍如何利用残差分析来检验回归模型的适用性。
1. 绘制残差图(Residual Plot)残差图是一种展示残差分布的可视化方式。
在横轴上绘制观测值或预测值,纵轴上绘制残差。
如果残差图中的点随机分布在零附近,并且没有明显的模式,则说明回归模型适用性较好。
如果残差图中存在模式或趋势,那么回归模型可能存在问题,需要重新评估模型的可靠性。
2. 检查残差的正态性回归模型通常假设误差项(ε)满足正态分布。
我们可以通过绘制残差的直方图或概率图来检查残差是否服从正态分布。
如果残差近似服从正态分布,则说明回归模型的适用性较好。
3. 检查残差的独立性残差的独立性是指残差之间没有相关性。
我们可以通过绘制残差的自相关图(Autocorrelation Plot)来检验残差是否独立。
如果残差之间没有显示出明显的相关性,则说明回归模型的适用性较好。
4. 检查残差的等方差性等方差性是指残差的方差在自变量的不同取值范围内是恒定的。
我们可以绘制残差的散点图,以观察残差的方差是否与预测值相关。
如果散点图呈现出均匀分布且没有明显的锥形或漏斗形状,则说明回归模型的适用性较好。
总结来说,残差分析是用于检验回归模型适用性的重要方法。
如何做残差分析
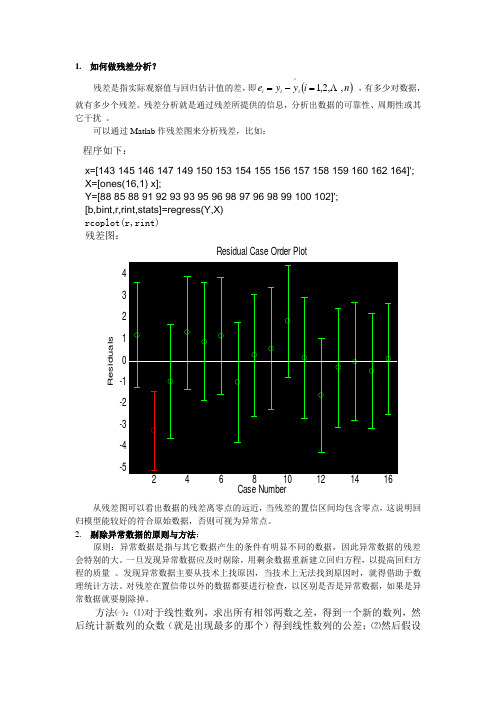
1. 如何做残差分析?残差是指实际观察值与回归估计值的差,即()n i y y e i i i ,,2,1^Λ=-= ,有多少对数据,就有多少个残差。
残差分析就是通过残差所提供的信息,分析出数据的可靠性、周期性或其它干扰 。
可以通过Matlab 作残差图来分析残差,比如: 程序如下:x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; X=[ones(16,1) x];Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';[b,bint,r,rint,stats]=regress(Y,X)rcoplot(r,rint)残差图:-5-4-3-2-11234Residual Case Order PlotR e s i d u a l s Case Number从残差图可以看出数据的残差离零点的远近,当残差的置信区间均包含零点,这说明回归模型能较好的符合原始数据,否则可视为异常点。
2. 剔除异常数据的原则与方法;原则:异常数据是指与其它数据产生的条件有明显不同的数据,因此异常数据的残差会特别的大。
一旦发现异常数据应及时剔除,用剩余数据重新建立回归方程,以提高回归方程的质量 。
发现异常数据主要从技术上找原因,当技术上无法找到原因时,就得借助于数理统计方法。
对残差在置信带以外的数据都要进行检查,以区别是否是异常数据,如果是异常数据就要剔除掉。
方法㈠:⑴对于线性数列,求出所有相邻两数之差,得到一个新的数列,然后统计新数列的众数(就是出现最多的那个)得到线性数列的公差;⑵然后假设第一个数是非异常数字;⑶假设数据不断加公差,看看绝大大多数是不是在原线性数列中,分情况:①若是,则第一个数以及第一个数加公差与原数列相同的元素均为非异常数据,其他则为异常数据;②若不是,则第一个数为异常数列,再假设第2个非异常数据,返回到第⑶步。
残差学习【转载】

残差学习【转载】转⾃:1.定义在回归模型中,假定的期望值为0,⽅差相等且服从正态分布的⼀个随机变量。
但是,若关于的假定不成⽴,此时所做的检验以及估计和预测也许站不住脚。
确定有关的假定是否成⽴的⽅法之⼀是进⾏残差分析(residual analysis).//期望值为0,不是均值为0。
⽅差相等,若以⾃变量为横轴,那么就是残差不会随着⾃变量的增⼤⽽变化。
2.残差普通残差就是使⽤预测值与真实值的差值。
减去残差的均值,⽐上残差的标准差。
百科上是这么说的://这⾥计算⽅差,需要⽤到矩阵的性质吧,我还不太明⽩。
性质3.残差图分析:(a)对所有x值,的⽅差都相同,且描述变量x和y之间的回归模型是合理的,残差图中的所有点落在⼀条⽔平带中间。
(b)对所有的值,的⽅差是不同的,对于较⼤的x值,相应的残差也较⼤,违背了的⽅差相等的假设(c)表明所选的回归模型不合理,应考虑曲线回归或多元回归模型。
标准化残差图如果误差项服从正态分布的这⼀假定成⽴,则标准化残差的分布也服从正态分布。
⼤约有95%的标准化残差在 -2~2 之间。
从图中可以看出,除了箭头所标识的点外,所有的标准化残差都在 -2~2 之间,所以误差项服从正态分布的假定成⽴。
3.R中计算残差普通残差转⾃:> x=c(274, 180, 375, 205, 86, 265, 98, 330, 195, 53, 430, 372, 236, 157, 370)> y=c(162, 120, 223, 131, 67, 169, 81, 192, 116, 55,252, 234, 144, 103, 212)> lm.reg<-lm(y~x)> lm.regCall:lm(formula = y ~ x)Coefficients:(Intercept) x22.59590.5301> plot(x,y)> plot(x,x*0.5301+22.5959)> residuals(lm.reg)12345678-5.83716551.99011421.6250126 -0.2618219 -1.18260615.93353156.4564646 -5.52150249101112131415-9.96104754.30994961.470753214.2152450 -3.6942227 -2.8181046 -6.7246001> length(x)[1] 15> y-predict(lm.reg)12345678-5.83716551.99011421.6250126 -0.2618219 -1.18260615.93353156.4564646 -5.5215024 9101112131415-9.96104754.30994961.470753214.2152450 -3.6942227 -2.8181046 -6.7246001> predict(lm.reg)123456789167.83717118.00989221.37499131.2618268.18261163.0664774.54354197.52150125.96105 10111213141550.69005250.52925219.78476147.69422105.81810218.72460其中,x和y的散点图:标准化误差> rstandard(lm.reg)#使⽤R的函数计算12345678-0.94164790.32358140.2754541 -0.0422737 -0.20464190.95584741.1044435 -0.9081795 9101112131415-1.61211390.77493770.26428162.4037012 -0.5942624 -0.4626949 -1.1352669> ?lm> h=hatvalues(lm.reg)#调⽤帽⼦矩阵的对⾓线元素> h123456780.072115110.086610280.159607710.073727970.193585950.069499580.174780050.1074382891011121314150.078095920.253073440.252152750.155470370.066838690.104239420.15276447> mse=sum((residuals(lm.reg)-mean(residuals(lm.reg)))^2)/13#这⾥为什么要减去两个样本..不明⽩> mse[1] 41.41263> standard_error= residuals(lm.reg)/(sqrt(mse*(1-h)))#⽤公式计算标准化残差> standard_error12345678-0.94164790.32358140.2754541 -0.0422737 -0.20464190.95584741.1044435 -0.9081795 9101112131415-1.61211390.77493770.26428162.4037012 -0.5942624 -0.4626949 -1.1352669通过标准化残差公式计算得到的结果。
高中数学残差计算方法

高中数学残差计算方法残差是指实际观测值与拟合值之间的差异,是统计学中常用的概念。
在高中数学中,残差也是一个重要的概念,它可以帮助我们评估数学模型的拟合程度,进而提高我们的数学分析能力。
本文将介绍高中数学中常用的残差计算方法。
一、线性回归模型的残差计算方法线性回归模型是高中数学中常用的模型之一,它可以用来描述两个变量之间的关系。
在线性回归模型中,残差的计算方法如下:1. 首先,我们需要确定线性回归模型的方程,即y = ax + b,其中y是因变量,x是自变量,a和b是常数。
2. 然后,我们需要计算每个观测值的拟合值,即y' = ax + b。
3. 最后,我们可以通过计算每个观测值的残差来评估模型的拟合程度,即残差 = y - y'。
二、方差分析中的残差计算方法方差分析是一种常用的统计分析方法,它可以用来比较两个或多个样本之间的差异。
在方差分析中,残差的计算方法如下:1. 首先,我们需要确定方差分析的模型,即y = μ + αi + εij,其中y是因变量,μ是总平均数,αi是第i个因子的效应,εij是误差项。
2. 然后,我们需要计算每个观测值的拟合值,即y' = μ + αi。
3. 最后,我们可以通过计算每个观测值的残差来评估模型的拟合程度,即残差 = y - y' - εij。
三、非线性回归模型的残差计算方法非线性回归模型是一种更加复杂的模型,它可以用来描述非线性关系。
在非线性回归模型中,残差的计算方法如下:1. 首先,我们需要确定非线性回归模型的方程,即y = f(x, β),其中y是因变量,x是自变量,β是参数。
2. 然后,我们需要使用最小二乘法来估计参数β。
3. 最后,我们可以通过计算每个观测值的残差来评估模型的拟合程度,即残差 = y - f(x, β)。
总之,残差是高中数学中一个重要的概念,它可以帮助我们评估数学模型的拟合程度,进而提高我们的数学分析能力。
残差分析报告

残差分析报告引言在统计学中,残差是指观测值与模型预测值之间的差异。
残差分析是一种重要的统计工具,用于评估统计模型的拟合程度和模型的假设是否成立。
本报告旨在进行残差分析,以评估模型的合理性并提供有关模型的改进建议。
数据集描述我们使用的数据集包含了100个样本观测值及其对应的预测值。
数据集中的预测值是基于一个线性回归模型得到的,并且我们假设模型满足线性关系假设以及误差项的独立同分布假设。
残差分析方法为了进行残差分析,我们首先计算每个观测值的残差。
残差的计算公式如下:残差 = 观测值 - 预测值接下来,我们将对残差进行如下的常用分析方法:1. 残差的分布图我们首先绘制残差的分布图,以探索残差是否呈现正态分布。
如果残差分布接近正态分布,则说明模型对数据拟合得较好。
2. 残差与预测值的关系图接下来,我们绘制残差与预测值的关系图。
通过这个图可以观察到残差是否随着预测值的变化而有规律地变化。
如果残差与预测值之间存在某种模式,可能表明模型在某个特定范围内表现不佳。
3. 残差与时间的关系图如果数据集有时间变量,我们可以绘制残差与时间的关系图,以观察残差是否随时间呈现某种趋势。
这可以帮助我们检测出可能和时间有关的结构,例如季节性或趋势。
4. 残差与自变量的关系图最后,如果数据集有多个自变量,我们可以绘制残差与每个自变量的关系图,以观察残差是否随自变量的变化而有规律地变化。
这可以帮助我们检测出可能存在的非线性关系或未建模的交互效应。
残差分析结果及建议经过以上的残差分析,我们得出以下结论和建议:1.残差的分布图显示残差近似正态分布,这意味着模型对数据的拟合效果较好,没有明显的偏离。
2.残差与预测值的关系图显示,残差随预测值的增加减小,但总体趋势比较平缓,说明模型在预测值较大的区域仍然可以较好地拟合数据。
3.残差与时间的关系图没有显示出明显的趋势或周期性,表明残差与时间无相关性。
4.残差与自变量的关系图显示,残差随自变量的变化而有规律地变化,可能存在非线性关系或未建模的交互效应。
残差分析--数据分析

(1)以因变量Y的拟合值为横坐标的散点图。 若线性回归关系正确且误差服从正态分布,则 因变量的拟合值与残差向量相互独立。这时残差图 中的点应大致在一个水平的带状区域内,没有任何 明显地趋势,如下图:
还可以用以下坐标做残差图,两种残差图原理 与上一个相同 (2)以自变量观测值为横坐标的散点图。 ( 3 )以观测时间或观测值序号横坐标的散点 图。
因此在实际应用中,从与因变量有线形关系的 自变量集合中,选取一个最优的子集,以建立一个 合理而又简单的回归方程十分重要。
一,穷举法
穷举法就是从与因变量有线性关系的所有可能 自变量的所有子集所拟合的回归方程中,按照一定 的准则选取最优的一个或几个。
下面是sas提供选择的几个穷举法的选取准则
(1) 复相关系数准则
2.3.2 Box-Cox变换
通过残差分析可以发现所给数据的某些特点和模型 假定的一些不足之处,接下来的问题就是要采取相应的 措施改进其不足,以建立更好的回归模型。 一个常用的改进措施就是Box-Cox变换,它通过 对因变量Y做适当变换,使原数据尽可能满足线性回归 模型的条件。
Box-Cox变换对因变量Y做如下变换:
选择,使 SSE ( , Z 达到最小。
其中
( ) ( ) T Z ( ) ( z1( ) , z2 , , z n )
( )
) (Z
( ) T
) ( E X ( X X ) X )Z
T T
1
( )
zi( )
1 n n ( y 1 ) / [ y ] , 0 i i i 1 1 n (ln y )[ y ] n , 0 i i i 1
SSE ( A) SSE ( A, X k ) SSR( X k | A) Fk SSE ( A, X k ) MSE ( A, X k ) (n l 1)
统计残差的计算公式

统计残差的计算公式统计残差是统计学中一个重要的概念,它用于衡量实际观测值与拟合值之间的差异。
在回归分析、方差分析等统计方法中,残差的计算是非常关键的步骤。
本文将介绍统计残差的计算公式,以及如何应用这些公式进行实际计算。
残差的定义。
在统计学中,残差是指实际观测值与拟合值之间的差异。
在回归分析中,拟合值是根据回归方程预测得到的值,而实际观测值是真实的观测结果。
残差可以用来衡量模型的拟合程度,以及检验模型的假设是否成立。
残差的计算公式。
在简单线性回归分析中,残差的计算公式如下:残差 = 实际观测值拟合值。
其中,实际观测值通常用y表示,拟合值通常用ŷ表示。
因此,简单线性回归的残差计算公式可以写为:残差 = y ŷ。
在多元线性回归分析中,残差的计算公式稍有不同。
假设有p个自变量和n个观测值,多元线性回归的残差计算公式可以写为:残差 = y ŷ = y Xβ。
其中,y是n×1的观测值向量,ŷ是n×1的拟合值向量,X是n×(p+1)的设计矩阵,β是(p+1)×1的回归系数向量。
残差可以通过矩阵运算得到,具体计算方法可以参考线性代数的相关知识。
在方差分析中,残差的计算公式也有所不同。
在单因素方差分析中,残差可以通过实际观测值与组内均值之间的差异来计算。
在多因素方差分析中,残差的计算公式更加复杂,需要考虑多个因素之间的交互作用。
残差的应用。
残差在统计学中有着广泛的应用,它可以用来检验回归模型的拟合程度,评估模型的预测能力,以及识别异常值和离群点。
下面将介绍残差在回归分析中的应用。
1. 检验回归模型的拟合程度。
残差可以用来检验回归模型的拟合程度。
如果残差呈现出随机分布、均值接近0、方差稳定的特点,说明模型的拟合程度较好;反之,如果残差呈现出系统性的模式、均值偏离0、方差不稳定的特点,说明模型的拟合程度较差。
2. 评估模型的预测能力。
残差可以用来评估模型的预测能力。
通过比较实际观测值与拟合值之间的差异,可以判断模型的预测能力是否足够准确。
残差的标准误差公式

残差的标准误差公式
残差是统计学中常用的概念,它表示实际观测值与预测值之间的差异。
在回归分析中,残差被用来评估回归模型的拟合程度。
残差的标准误差(standard error of the residual)是衡量残差变异程度的指标,它用来判断回
归模型的精确度。
残差的标准误差公式如下:
SE = √[(Σ(eᵢ²))/(n-p-1)]
其中,SE表示残差的标准误差,eᵢ表示第i个观测值的残差,Σ表示求
和符号,n表示样本容量,p表示模型中的自变量个数。
残差的标准误差公式计算了所有残差平方和的均方根值。
它是残差离散
程度的测量,值越小表示残差的变异程度越小,即回归模型拟合得越好。
在实际应用中,残差的标准误差公式可以用来进行模型的比较和选择。
当比较两个模型时,我们可以计算它们的残差标准误差,并选择较小的那个
作为更好的模型。
此外,残差的标准误差还可以用于构建置信区间和预测区间,帮助我们评估预测结果的置信度。
需要注意的是,残差的标准误差公式假设残差满足正态分布和独立同分
布的条件。
如果残差不满足这些条件,可能会导致标准误差的计算结果不准确。
因此,在使用残差的标准误差时,我们需要注意这些前提条件的合理性。
残差的标准误差公式是衡量回归模型拟合度的重要指标。
它可用于模型
比较、预测精度评估等应用,帮助我们判断回归模型的准确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FLUENT中残差的概念
残差是cell各个face的通量之和,理论上当单元内没有源项使各个面流入的通量也就是对物理量的输运之和应该为零。
最大残差或者RSM残差反映流场与所要模拟流场(只收敛后应该得到的流场,当然收敛后得到的流场与真实流场之间还是存在一定的差距)的鳌头,残差越小越好,由于存在数值精度问题,不可能得到0残差,对于单精度计算一般应该低于初始残差1e-03以下才好,当注意具体情况,看各大个项的收敛情况(比方说连续项不易收敛而能量项容易收敛)。
一般在FLUENT中可以进行进出口流量监控,当残差收敛到一定程度后,还要看进出口流量是否稳定平衡,才可确定收敛与否(翼型计算时要监控升阴力的平衡)。
残差在较高位震荡,需要检查边界条件是否合理,其次检查初始条件是否合理,比如激波的江郎才尽,初始条件的不合适会造成江郎才尽的振荡。
有时流场可能有分离或者回流,这本身是非定常现象,计算时残差会在一定程度上发生振荡,这时如果进出口流量是否达到稳定平衡,也可以认为流场收敛。
另外fluent缺省采用多重网格,在计算后期将多重网格设置为0可以避免一些波长的残差在细网格上发生震荡。
判断计算是否收敛,没有一个通用的方法。
通过残差值的判断的方法,对一些问题或许很有效,但在某些问题中往往会得出错误的结论。
因此,正确的做法是,不公要通过残差值,也要通过监测所有相关变量的完整数据,以及检查流入与流出的物质和能量是否守恒的方法来判断计算是否收敛。
1.监测残差值。
在迭代计算过程中,当各个物理变量的残差值都达到收敛标准时,计算就会发生收敛。
fluent的收敛标准是:除了能量的残差值外,当所有变量的残差值都降到低于10-3时,就认为计算收敛,而能量的残差值的收敛标准为低于10-6。
2.计算结果不再随着迭代的进行发生变化。
有时候,因为收敛标准设置得不合适,物理量的残差值在迭代计算的过程中始终玩法满足收敛标准。
然而,通过在迭代过程中监测某些代表性的流动变量,可能其值已经不再随着迭代的进行发生变化。
此时也可以认为计算收敛。
3.整个系统的质量,动量,能量都守恒。
在Flux Peports对话框中检查流入和流出整个系统的质量,动量,能量是否守恒。
守恒,则计算收敛。
不平衡误差少于0.1%,也可以认为计算是收敛的。
FLUENT不收敛通常的解决方式
1.一般首先是改变初值,尝试不同的初始化,事实上好像初始化很关键,对于收敛。
2.FLUENT的收敛最基础的是网格的质量,计算的时候看怎么样选择CFL数,这个是经验。
3.首先查找网格问题,如果问题复杂比如多相流问题,与模型、边界、初始条件都有关系。
4.边界条件、网格质量。
5.有时初始条件和边界条件严重影响收敛性,我曾经作过一个计算,反反复复,通过修改网格,重新定义初始条件,包括具体的选择的模型,还有老师经常用的方法就是看看哪个因素不收敛,然后寻找和它有关的条件,改变相应参数。
就收敛了。
6.A检查是否哪里误。
比方用mm的unit建构的Mesh.忘了scale...
比方给定的b.c不合理
B从算至发散前几步,看pressure分布,看不出来的话再算几步,看看问题大概出在哪个区域,连
地方都知道的话,应该不难想出问题所在。
C网格,配合第二点作修正,或是认命点就重建个更漂亮的,或是更粗略的来除错...
D再找不出来的话,我会换个solver...
7.我解决的办法是设几个监测点,比如出流或参数变化较大的地方,若这些地方的参数变化很小,就可以认为是收敛了,尽管此时残值曲线还没有降下来。
8.记得好像调节松弛因子也能影响收敛,不过代价是收敛速度。
9.网格有一定的影响,最主要的还是初始和边界条件!。
