空间中的平行关系——数学立体几何
高中数学-立体几何-空间中的平行和垂直关系

高中数学总复习-第七章立体几何-空间中的平行和垂直关系知识结构图】第 3 课空间中的平行关系【考点导读】1.掌握直线和平面平行、两个平面平行的判定定理和性质定理。
2.明确定义与定理的不同,定义是可逆的,既是判定也是性质,而判定定理与性质定理多是不可逆的。
3.要能灵活的对“线线平行” 、“线面平行”和“面面平行”进行转化。
基础练习】1.若a、b为异面直线,直线c∥a,则c与b的位置关系是异面或相交2.给出下列四个命题①垂直于同一直线的两条直线互相平行. ②垂直于同一平面的两个平面互相平行.③若直线l1, l2与同一平面所成的角相等, 则l1,l2互相平行.④若直线l1, l2是异面直线,则与l1,l2都相交的两条直线是异面直线. 其中假.命题的个数是 4 个。
3.对于任意的直线l 与平面a,在平面a内必有直线m,使m与l 垂直。
4. 已知a、b、c 是三条不重合的直线,α、β、r 是三个不重合的平面,下面六个命题:①a∥c,b∥c a∥b;②a∥r,b∥r a∥b;③α∥c,β∥c α∥β;④α∥r,β∥r α∥β;⑤a∥c,α∥c a∥α;⑥a∥r ,α∥r a∥α.其中正确的命题是①④范例导析】例1.如图,在四面体ABCD中,截面EFGH是平行四边形.求证:AB∥平面EFG.证明:∵面EFGH是截面.∴点E,F,G,H分别在BC,BD,DA,AC上.∴ EH 面ABC,GF 面ABD,由已知,EH∥GF.∴ EH∥面ABD.又∵ EH 面BAC,面ABC∩面ABD=AB∴EH∥AB.∴ AB∥面EFG.例2.如图,在正方体ABCD—A1B1C1D1 中,点N在BD上,点M在B1C上,并且CM=DN.求证 :MN ∥平面 AA 1B 1B.分析:“线线平行”、“线面平行”、“面面平行”是可以互相转化的。
本题可以采 用任何一种转化方式。
简证:法 1:把证“线面平行”转化为证“线线平行” 。
即在平面 ABB 1A 1内找一条直线与 MN 平行,如图所示作平行线即可 法 2 :把证“线面平行”转化为证“线线平行” 。
空间中的平行与垂直例题和知识点总结

空间中的平行与垂直例题和知识点总结在立体几何的学习中,空间中的平行与垂直关系是非常重要的内容。
理解和掌握这些关系,对于解决相关的几何问题具有关键作用。
下面我们通过一些例题来深入探讨,并对相关知识点进行总结。
一、平行关系(一)线线平行1、定义:如果两条直线在同一平面内没有公共点,则这两条直线平行。
2、判定定理:如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行。
例 1:在正方体 ABCD A₁B₁C₁D₁中,E,F 分别是 AB,BC 的中点,求证:EF∥A₁C₁。
证明:连接 AC,因为 E,F 分别是 AB,BC 的中点,所以 EF∥AC。
又因为正方体中,AC∥A₁C₁,所以 EF∥A₁C₁。
(二)线面平行1、定义:如果一条直线与一个平面没有公共点,则称这条直线与这个平面平行。
2、判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
例 2:已知四棱锥 P ABCD 的底面是平行四边形,M 是 PC 的中点,求证:PA∥平面 MBD。
证明:连接 AC 交 BD 于 O,连接 MO。
因为四边形 ABCD 是平行四边形,所以 O 是 AC 的中点。
又因为 M 是 PC 的中点,所以MO∥PA。
因为 MO⊂平面 MBD,PA⊄平面 MBD,所以 PA∥平面MBD。
(三)面面平行1、定义:如果两个平面没有公共点,则称这两个平面平行。
2、判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
例 3:在正方体 ABCD A₁B₁C₁D₁中,求证:平面 A₁BD∥平面 B₁D₁C。
证明:因为 A₁B∥D₁C,A₁D∥B₁C,且 A₁B 和 A₁D 是平面A₁BD 内的两条相交直线,D₁C 和 B₁C 是平面 B₁D₁C 内的两条相交直线,所以平面 A₁BD∥平面 B₁D₁C。
二、垂直关系(一)线线垂直1、定义:如果两条直线所成的角为 90°,则这两条直线垂直。
立体几何中的平行问题总结

立体几何中的平行问题总结1. 空间两直线的位置关系(1)相交——有且只有一个公共点;(2)平行——在同一平面内,没有公共点;(3)异面——不在任何一个平面内,没有公共点;2. 平行直线(1)公理4 :平行于同一条直线的两条直线互相平行推理模式:.说明:(1)公理4表述的性质叫做空间平行线的传递性;(2)几何学中,通常用互相平行的直线表示空间里一个确定的方向;(3)如果空间图形的所有点都沿同一个方向移动相同的距离到的位置,则就说图形作了一次平移3. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等4. 直线和平面的位置关系(1)直线在平面内(无数个公共点);(2)直线和平面相交(有且只有一个公共点);(3)直线和平面平行(没有公共点)——用两分法进行两次分类.它们的图形分别可表示为如下,符号分别可表示为,,.5. 线面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.推理模式:.证明:假设直线不平行于平面,∵,∴,若,则和矛盾,若,则和成异面直线,也和矛盾,∴.6. 线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.推理模式:.证明:∵,∴和没有公共点,又∵,∴和没有公共点;和都在内,且没有公共点,∴.7. 平行平面:如果两个平面没有公共点,那么这两个平面互相平行.图形表示:画两个平面平行时,通常把表示这两个平面的平行四边形的相邻两边分别画成平行的.8. 平行平面的判定定理:如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面互相平行.推理模式:,,,,.分析:这个定理从正面证(用定义)比较困难,所以考虑用反证法.启发:(1)如果平面和平面不平行,那么它们的位置关系怎样?(2)如果平面和平面相交,那么交线和平面中的直线与各有怎样的位置关系?(3)相交直线与都与交线平行,这合理吗?为什么?证明:假设,∵,,∴,同理.即在平面内过点有两条直线与平行,与公理4矛盾,∴假设不成立,∴.推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面互相平行.推理模式:.9. 平行平面的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.推理模式:.证明:∵,∴没有公共点,又∵,∴.同理可得面面平行的另一性质:如果两个平面平行,那么其中一个平面内的直线平行于另一个平面.推理模式:.。
高中数学§3.2立体几何中的向量方法(一)——空间向量与平行关系

§3.2立体几何中的向量方法(一)——空间向量与平行关系课时目标 1.理解直线的方向向量与平面的法向量,并能运用它们证明平行问题.2.能用向量语言表述线线,线面,面面的平行关系.1.直线的方向向量直线的方向向量是指和这条直线________或______的向量,一条直线的方向向量有________个.2.平面的法向量直线l⊥α,取直线l的____________a,则向量a叫做平面α的__________.3.空间中平行关系的向量表示(1)线线平行设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2),且a2b2c2≠0,则l∥m ⇔______________⇔__________⇔________________________.(2)线面平行设直线l的方向向量为a=(a1,b1,c1),平面α的法向量为u=(a2,b2,c2),则l∥α⇔________⇔__________⇔________________________.(3)面面平行设平面α,β的法向量分别为u=(a1,b1,c1),v=(a2,b2,c2),则α∥β⇔__________⇔__________⇔________________________.一、选择题1.若n=(2,-3,1)是平面α的一个法向量,则下列向量能作为平面α的一个法向量的是()A.(0,-3,1) B.(2,0,1)C.(-2,-3,1) D.(-2,3,-1)2.若A(-1,0,1),B(1,4,7)在直线l上,则直线l的一个方向向量为()A.(1,2,3) B.(1,3,2)C.(2,1,3) D.(3,2,1)3.已知平面α上的两个向量a=(2,3,1),b=(5,6,4),则平面α的一个法向量为() A.(1,-1,1) B.(2,-1,1)C.(-2,1,1) D.(-1,1,-1)4.从点A(2,-1,7)沿向量a=(8,9,-12)的方向取线段长AB=34,则B点的坐标为() A.(-9,-7,7) B.(18,17,-17)C.(9,7,-7) D.(-14,-19,31)5.在正方体ABCD—A1B1C1D1中,棱长为a,M、N分别为A1B、AC的中点,则MN与平面BB1C1C的位置关系是()A.相交B.平行C.垂直D.不能确定6.已知线段AB的两端点的坐标为A(9,-3,4),B(9,2,1),则与线段AB平行的坐标平面是()A .xOyB .xOzC .yOzD .xOy 或yOz二、填空题7.已知A (1,0,0),B (0,1,0),C (0,0,1),则平面ABC 的单位法向量坐标为________________________.8.已知直线l 的方向向量为(2,m,1),平面α的法向量为⎝⎛⎭⎫1,12,2,且l ∥α,则m =________. 9.如图,在平行六面体ABCD —A 1B 1C 1D 1中,M 、P 、Q 分别为棱AB 、CD 、BC 的中点,若平行六面体的各棱长均相等,则 ①A 1M ∥D 1P ; ②A 1M ∥B 1Q ;③A 1M ∥面DCC 1D 1; ④A 1M ∥面D 1PQB 1.以上结论中正确的是________.(填写正确的序号) 三、解答题10.已知平面α经过三点A (1,2,3),B (2,0,-1),C (3,-2,0),试求平面α的一个法向量. 11.如图所示,在空间图形P —ABCD 中,PC ⊥平面ABCD ,PC =2,在四边形ABCD 中,CD ∥AB ,∠ABC =∠BCD =90°,AB =4,CD =1,点M 在PB 上,且PB =4PM ,∠PBC =30°,求证:CM ∥平面P AD .【能力提升】12.在正方体ABCD—A1B1C1D1中,O是B1D1的中点,求证:B1C∥平面ODC1.13.如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=60°,P A⊥平面ABCD,P A=AC=a,点E在PD上,且PE∶ED=2∶1.在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.平行关系的常用证法(1)证明线线平行只需要证明表示两条直线的向量满足实数倍数关系,如证明AB ∥CD只需证AB →=λCD →.证明线面平行可转化为证直线的方向向量和平面的法向量垂直,然后说明直线在平面外.证面面平行可转化证两面的法向量平行.(2)证明线面平行问题或面面平行问题时也可利用立体几何中的定理转化为线线平行问题,再利用向量进行证明.§3.2 立体几何中的向量方法(一)——空间向量与平行关系知识梳理1.平行 重合 无数 2.方向向量 法向量3.(1)a∥b a =λb a 1a 2=b 1b 2=c 1c 2(a 2b 2c 2≠0)(2)a∥u a·u =0 a 1a 2+b 1b 2+c 1c 2=0(3)u∥v u =k v a 1a 2=b 1b 2=c 1c 2(a 2b 2c 2≠0)作业设计1.D [只要是与向量n 共线且非零的向量都可以作为平面α的法向量.故选D.]2.A [∵AB →=(2,4,6),而与AB →共线的非零向量都可以作为直线l 的方向向量,故选A.]3.C [显然a 与b 不平行,设平面α的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧a·n =0,b·n =0, ∴⎩⎪⎨⎪⎧2x +3y +z =0,5x +6y +4z =0. 令z =1,得x =-2,y =1,∴n =(-2,1,1).]4.B [设B (x ,y ,z ),AB →=(x -2,y +1,z -7) =λ(8,9,-12),λ>0.故x -2=8λ,y +1=9λ,z -7=-12λ, 又(x -2)2+(y +1)2+(z -7)2=342, 得(17λ)2=342,∵λ>0,∴λ=2.∴x =18,y =17,z =-17,即B (18,17,-17).]5.B [可以建立空间直角坐标系,通过平面的法向量AB →和MN →的关系判断.]6.C [AB →=(0,5,-3),AB 与平面yOz 平行.]7.⎝⎛⎭⎫33,33,33或⎝⎛⎭⎫-33,-33,-338.-8解析 ∵l ∥α,∴l 的方向向量与α的法向量垂直.∴(2,m,1)·⎝⎛⎭⎫1,12,2=2+12m +2=0,∴m =-8. 9.①③④解析 ∵A 1M →=AM →-AA 1→=D P →-DD 1→=D 1P →, ∴A 1M ∥D 1P .∵D 1P ⊂面D 1PQB 1,∴A 1M ∥面D 1PQB 1. 又D 1P ⊂面DCC 1D 1,∴A 1M ∥面DCC 1D 1. ∵B 1Q 为平面DCC 1D 1的斜线,∴B 1Q 与D 1P 不平行,∴A 1M 与B 1Q 不平行. 10.解 ∵A (1,2,3),B (2,0,-1),C (3,-2,0),∴AB →=(1,-2,-4),AC →=(2,-4,-3), 设平面α的法向量为n =(x ,y ,z ).依题意,应有n ·AB →=0,n ·AC →=0. 即⎩⎪⎨⎪⎧ x -2y -4z =02x -4y -3z =0,解得⎩⎪⎨⎪⎧x =2y z =0. 令y =1,则x =2.∴平面α的一个法向量为n =(2,1,0).11.证明 建立如图所示的空间直角坐标系Cxyz . 方法一∵∠PBC =30°,PC =2, ∴BC =23,PB =4.于是D (1,0,0),C (0,0,0),A (4,23,0),P (0,0,2). ∵PB =4PM ,∴PM =1,M ⎝⎛⎭⎫0,32,32.∴CM →=⎝⎛⎭⎫0,32,32,DP →=(-1,0,2),DA →=(3,23,0).设CM →=x DP →+y DA →,其中x ,y ∈R .则⎝⎛⎭⎫0,32,32=x (-1,0,2)+y (3,23,0).∴⎩⎨⎧-x +3y =023y =322x =32,解得x =34,y =14.∴CM →=34DP →+14DA →,∴CM →,DP →,DA →共面.∵CM ⊄平面P AD ,∴CM ∥平面P AD .方法二 由方法一可得CM →=⎝⎛⎭⎫0,32,32,DP →=(-1,0,2),DA →=(3,23,0).设平面P AD的法向量为n =(x ,y ,z ),则有,即⎩⎨⎧-x +2z =03x +23y =0.令x =1,解得z =12,y =-32.故n =⎝⎛⎭⎫1,-32,12.又∵CM →·n =⎝⎛⎭⎫0,32,32·⎝⎛⎭⎫1,-32,12=0.∴CM →⊥n ,又CM ⊄平面P AD . ∴CM ∥平面P AD .12.证明 方法一 ∵B 1C →=A 1D →,B 1∉A 1D ,∴B 1C ∥A 1D ,又A 1D ⊂平面ODC 1, ∴B 1C ∥平面ODC 1.方法二 ∵B 1C →=B 1C 1→+B 1B →=B 1O →+OC 1→+D 1O →+OD →=OC 1→+OD →. ∴B 1C →,OC 1→,OD →共面.又B 1C ⊄平面ODC 1,∴B 1C ∥平面ODC 1. 方法三建系如图,设正方体的棱长为1,则可得 B 1(1,1,1),C (0,1,0), O ⎝⎛⎭⎫12,12,1,C 1(0,1,1), B 1C →=(-1,0,-1),OD →=⎝⎛⎭⎫-12,-12,-1,OC 1→=⎝⎛⎭⎫-12,12,0. 设平面ODC 1的法向量为n =(x 0,y 0,z 0),则得⎩⎨⎧-12x 0-12y 0-z 0=0, ①-12x 0+12y 0=0, ②令x 0=1,得y 0=1,z 0=-1,∴n =(1,1,-1). 又B 1C →·n =-1×1+0×1+(-1)×(-1)=0, ∴B 1C →⊥n ,且B 1C ⊄平面ODC 1, ∴B 1C ∥平面ODC 1.13.解 方法一 当F 是棱PC 的中点时,BF ∥平面AEC . ∵BF →=BC →+12CP →=AD →+12(CD →+DP →)=AD →+12(AD →-AC →)+32(AE →-AD →)=32AE →-12AC →. ∴BF →、AE →、AC →共面. 又BF ⊄平面AEC , ∴BF ∥平面AEC . 方法二如图,以A 为坐标原点,直线AD 、AP 分别为y 轴、z 轴,过A 点垂直于平面P AD 的直线为x 轴,建立空间直角坐标系.由题意,知相关各点的坐标分别为A (0,0,0),B ⎝⎛⎭⎫32a ,-12a ,0,C ⎝⎛⎭⎫32a ,12a ,0,D (0,a,0),P (0,0,a ),E ⎝⎛⎭⎫0,23a ,13a . 所以AE →=⎝⎛⎭⎫0,23a ,13a ,AC →=⎝⎛⎭⎫32a ,12a ,0, AP →=(0,0,a ),PC →=⎝⎛⎭⎫32a ,12a ,-a ,BP →=⎝⎛⎭⎫-32a ,12a ,a .设点F 是棱PC 上的点,PF →=λPC →=⎝⎛⎭⎫32aλ,12aλ,-aλ,其中0<λ<1, 则BF →=BP →+PF →=⎝⎛⎭⎫32a λ-1,12a 1+λ,a 1-λ,令BF →=λ1AC →+λ2AE →即⎩⎪⎨⎪⎧λ-1=λ1,1+λ=λ1+43λ2,1-λ=13λ2.解得λ=12,λ1=-12,λ2=32,即λ=12时,BF →=-12AC →+32AE →,即F 是PC 的中点时,BF →、AC →、AE →共面.又BF ⊄平面AEC ,所以当F 是棱PC 的中点时,BF∥平面AEC.。
新高考 核心考点与题型 立体几何 第3讲 空间直线与平面的平行 - 解析
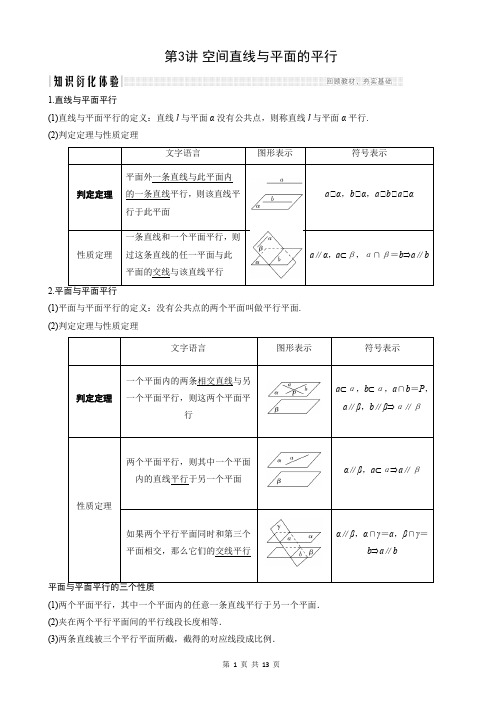
第3讲空间直线与平面的平行1.直线与平面平行(1)直线与平面平行的定义:直线l与平面α没有公共点,则称直线l与平面α平行.(2)判定定理与性质定理2.(1)平面与平面平行的定义:没有公共点的两个平面叫做平行平面.(2)判定定理与性质定理(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(2)夹在两个平行平面间的平行线段长度相等.(3)两条直线被三个平行平面所截,截得的对应线段成比例.[微点提醒] 平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行,即若a ⊄α,a ⊄β,则α⊄β. (2)平行于同一平面的两个平面平行,即若α⊄β,β⊄γ,则α⊄γ. (3)垂直于同一个平面的两条直线平行,即若a ⊄α,b ⊄α,则a ⊄b .考点一 直线与平面平行的判定与性质多维探究角度1 直线与平面平行的判定【例2-1】在如图所示的几何体中,四边形ABCD 是正方形,P A ⊥平面ABCD ,E ,F 分别是线段AD ,PB 的中点,P A =AB =1.证明:EF ∥平面PDC ; 证明 取PC 的中点M ,连接DM ,MF ,∵M ,F 分别是PC ,PB 的中点,∴MF ∥CB ,MF =12CB ,∵E 为DA 的中点,四边形ABCD 为正方形,∴DE ∥CB ,DE =12CB ,∴MF ∥DE ,MF =DE ,∴四边形DEFM 为平行四边形,∴EF ∥DM ,∵EF ⊄平面PDC ,DM ⊂平面PDC ,∴EF ∥平面PDC .规律方法 利用判定定理判定线面平行,关键是找平面内与已知直线平行的直线.常利用三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线.【变式】如图,在直三棱柱ABC A 1B 1C 1中,点M ,N 分别为线段A 1B ,AC 1的中点.求证:MN ∥平面BB 1C 1C .证明:如图,连接A 1C .在直三棱柱ABC A 1B 1C 1中,侧面AA 1C 1C 为平行四边形. 又因为N 为线段AC 1的中点,所以A 1C 与AC 1相交于点N ,即A 1C 经过点N , 且N 为线段A 1C 的中点.因为M 为线段A 1B 的中点,所以MN ∥BC .又因为MN ⊄平面BB 1C 1C ,BC ⊂平面BB 1C 1C ,所以MN ∥平面BB 1C 1C .角度2直线与平面平行性质定理的应用【例2】如图所示,在正方体ABCD-A1B1C1D1中,棱长为2,E,F分别是棱DD1,C1D1的中点.(1)求三棱锥B1-A1BE的体积;(2)试判断直线B1F与平面A1BE是否平行,如果平行,请在平面A1BE上作出与B1F平行的直线,并说明理由.解(1)如图所示,V B1-A1BE =V E-A1B1B=13S△A1B1B· DA=13×12×2×2×2=43.(2)B1F∥平面A1BE.延长A1E交AD延长线于点H,连BH交CD于点G,则BG就是所求直线.证明如下:因为BA1∥平面CDD1C1,平面A1BH∩平面CDD1C1=GE,所以A1B∥GE.又A1B∥CD1,所以GE∥CD1.又E为DD1的中点,则G为CD的中点.故BG∥B1F,BG就是所求直线.规律方法在解决线面、面面平行的判定时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”;而在应用性质定理时,其顺序恰好相反.【变式1】如图,在四棱柱ABCDA1B1C1D1中,E为线段AD上的任意一点(不包括A,D两点),平面CEC1与平面BB1D交于FG.求证:FG∥平面AA1B1B.证明:在四棱柱ABCD A1B1C1D1中,BB1∥CC1,BB1⊂平面BB1D,CC1⊄平面BB1D,所以CC1∥平面BB1D.又CC1⊂平面CEC1,平面CEC1与平面BB1D交于FG,所以CC1∥FG.因为BB1∥CC1,所以BB1∥FG.因为BB1⊂平面AA1B1B,FG⊄平面AA1B1B,所以FG∥平面AA1B1B.【变式2】如图所示,在四棱锥P ABCD-中,//BC平面PAD,12BC AD=,E是PD的中点.(⊄)求证://BC AD;(⊄)求证://CE平面PAB;(⊄)若M是线段CE上一动点,则线段AD上是否存在点N,使//MN平面PAB?说明理由.【分析】(⊄)根据线面平行的性质定理即可证明;(⊄)取PA的中点F,连接EF,BF,利用中位线的性质,平行四边形的性质,以及线面平行的判断定理即可证明;(⊄)取AD中点N,连接CN,EN,根据线面平行的性质定理和判断定理即可证明.【解答】(⊄)在四棱锥P ABCD-中,//BC平面PAD,BC⊂平面ABCD,平面ABCD⋂平面PAD AD=,//BC AD∴,(⊄)取PA的中点F,连接EF,BF,E是PD的中点,//EF AD∴,12EF AD=,又由(⊄)可得//BC AD,12BC AD=,//BC EF∴,BC EF=,∴四边形BCEF是平行四边形,//CE BF∴,CE⊂/平面PAB,BF⊂平面PAB,//CE∴平面PAB.(⊄)取AD中点N,连接CN,EN,E,N分别为PD,AD的中点,//EN PA∴,EN⊂/平面PAB,PA⊂平面PAB,//EN∴平面PAB,又由(⊄)可得//CE平面PAB,CE EN E=,∴平面//CEN平面PAB,M是CE上的动点,AN⊂平面CEN,//MN∴平面PAB,∴线段AD存在点N,使得//MN平面PAB.考点二面面平行的判定与性质典例迁移【例3】(经典母题)如图所示,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:平面EF A1∥平面BCHG.证明:∵E,F分别为AB,AC的中点,∴EF∥BC,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.又G,E分别为A1B1,AB的中点,A1B1綉AB,∴A1G綉EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.又∵A1E∩EF=E,∴平面EF A1∥平面BCHG.【变式1】在本例中,若将条件“E,F,G,H分别是AB,AC,A1B1,A1C1的中点”变为“D1,D分别为B1C1,BC的中点”,求证:平面A1BD1∥平面AC1D.证明如图所示,连接A1C交AC1于点M,⊄四边形A1ACC1是平行四边形,⊄M是A1C的中点,连接MD,⊄D为BC的中点,⊄A1B⊄DM.⊄A1B⊄平面A1BD1,DM⊄平面A1BD1,⊄DM⊄平面A1BD1,又由三棱柱的性质知,D1C1綉BD,⊄四边形BDC1D1为平行四边形,⊄DC1⊄BD1.又DC1⊄平面A1BD1,BD1⊄平面A1BD1,⊄DC1⊄平面A1BD1,又DC1∩DM=D,DC1,DM⊄平面AC1D,因此平面A1BD1⊄平面AC1D.【变式2】如图为一简单组合体,其底面ABCD 为正方形,棱PD 与EC 均垂直于底面ABCD ,2PD EC =,求证:平面//EBC 平面PDA .【分析】推导出//AD BC ,//PD EC ,由此能证明平面//EBC 平面PDA . 【解答】底面ABCD 为正方形,//AD BC ∴,棱PD 与EC 均垂直于底面ABCD ,2PD EC =,//PD EC ∴, ADPD D =,BCEC C =,∴平面//EBC 平面PDA .【例4】如图,已知//αβ,P 是平面α,β外的一点,直线PAB ,PCD 分别与α、β相交于A 、B 和C 、D .(1)求证://AC BD ;(2)已知4PA =,5AB =,3PC =,求PD 的长.【分析】(1)由面面平行的性质即可得证;(2)由平行线的性质即可求解. 【解答】解:(1)证明://αβ,平面PBD AC α=,平面PBD BD β=,//AC BD ∴;(2)由(1)可知,PA PC PB PD =,即4345PD =+,∴274PD =. 规律方法 利用线面平行或面面平行的性质,可以实现与线线平行的转化,尤其在截面图的画法中,常用来确定交线的位置.对于线段长或线段比例问题,常用平行线对应线段成比例或相似三角形来解决.【变式】如图,平面//αβ,线段AB 分别交α,β于M ,N ,线段AD 分别交α,β于C ,D ,线段BF 分别交α,β于F ,E ,若9AM =,11MN =,15NB =,78FMC S ∆=.求END ∆的面积.【分析】利用面面平行的性质得到两个三角形对应边的比,结合面积公式即可得解.【解答】解:平面//αβ,又平面AND ⋂平面MC α=,平面AND ⋂平面ND β=,//MC ND ∴, 同理//EN FM ,又9AM =,11MN =,15NB =,∴926,2015MC AM FM BM ND AN EN BN ====, 又FMC END ∠=∠,所以1sin 92678212015100sin 2FMC ENDFM MC FMCS SEN ND END ∠==⨯=∠,78FMC S ∆=,100END S ∆∴=.故END ∆的面积为:100.方法总结(1)线面平行思考途径 I.转化为直线与平面无公共点;II.转化为线线平行; III.转化为面面平行支持定理 ①; ②; ③配图助记(2)线线平行:思考途径 I.转化为判定共面二直线无交点;II.转化为二直线同与第三条直线平行; III.转化为线面平行; IV.转化为线面垂直; V.转化为面面平行.支持定理①;②;③;④配图助记(3)面面平行:思考途径 I.转化为判定二平面无公共点;II.转化为线面平行; III.转化为线面垂直.////a b b a a ααα⎫⎪⊂⇒⎬⎪⊄⎭////a a αββα⎫⇒⎬⊂⎭//a a a αββαα⊥⎫⎪⊥⇒⎬⎪⊄⎭////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭//a a b b αα⊥⎫⇒⎬⊥⎭////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭//////a b c b a c ⎫⇒⎬⎭αb βa a b αb γβ α aαβaaαbβαa支持定理 ①;②;③配图助记空间平行的判定与性质 基础巩固题组(建议用时:40分钟)一、选择题1.若直线l 不平行于平面α,且l ⊄α,则( ) A.α内的所有直线与l 异面 B.α内不存在与l 平行的直线 C.α与直线l 至少有两个公共点 D.α内的直线与l 都相交解析 因为l ⊄α,直线l 不平行于平面α,所以直线l 只能与平面α相交,于是直线l 与平面α只有一个公共点,所以平面α内不存在与l 平行的直线. 答案 B2.已知直线l ,m ,平面α,β,γ,则下列条件能推出l ∥m 的是( ) A.l ⊂α,m ⊂β,α∥β B.α∥β,α∩γ=l ,β∩γ=m C.l ∥α,m ⊂αD.l ⊂α,α∩β=m解析 选项A 中,直线l ,m 也可能异面;选项B 中,根据面面平行的性质定理,可推出l ∥m ,B 正确;选项C 中,直线l ,m 也可能异面;选项D 中,直线l ,m 也可能相交.故选B. 答案 B3.如图所示的三棱柱ABC -A 1B 1C 1中,过A 1B 1的平面与平面ABC 交于DE ,则DE 与AB 的位置关系是( )A.异面B.平行C.相交D.以上均有可能解析 在三棱柱ABC -A 1B 1C 1中,AB ∥A 1B 1,,////,//a b a b o a b αααβββ⊂⊂⎫⎪=⇒⎬⎪⎭//a a ααββ⊥⎫⇒⎬⊥⎭//////αβαγγβ⎫⇒⎬⎭a β αbOβ aαβ αγ∵AB⊂平面ABC,A1B1⊄平面ABC,∴A1B1∥平面ABC,∵过A1B1的平面与平面ABC交于DE.∴DE∥A1B1,∴DE∥AB.答案B4.设a,b是两条不同的直线,α,β是两个不同的平面,则α∥β的一个充分条件是()A.存在一条直线a,a∥α,a∥βB.存在一条直线a,a⊂α,a∥βC.存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥αD.存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α解析对于选项A,若存在一条直线a,a∥α,a∥β,则α∥β或α与β相交,若α∥β,则存在一条直线a,使得a∥α,a∥β,所以选项A的内容是α∥β的一个必要条件;同理,选项B、C的内容也是α∥β的一个必要条件而不是充分条件;对于选项D,可以通过平移把两条异面直线平移到一个平面中,成为相交直线,则有α∥β,所以选项D的内容是α∥β的一个充分条件.故选D.答案D5.若平面α截三棱锥所得截面为平行四边形,则该三棱锥与平面α平行的棱有()A.0条B.1条C.2条D.1条或2条解析如图所示,四边形EFGH为平行四边形,则EF∥GH.∵EF⊄平面BCD,GH⊂平面BCD,∴EF∥平面BCD.又∵EF⊂平面ACD,平面BCD∩平面ACD=CD,∴EF∥CD.又EF⊂平面EFGH,CD⊄平面EFGH.∴CD∥平面EFGH,同理,AB∥平面EFGH,所以与平面α(面EFGH)平行的棱有2条.答案C二、填空题6.如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上,若EF∥平面AB1C,则EF=________.解析 根据题意,因为EF ∥平面AB 1C ,所以EF ∥AC .又E 是AD 的中点,所以F 是CD 的中点.因为在Rt △DEF 中,DE =DF =1,故EF = 2. 答案27.如图,平面α∥平面β,△ABC ,△A ′B ′C ′分别在α,β内,线段AA ′,BB ′,CC ′共点于O ,O 在α,β之间,若AB =2,AC =1,∠BAC =60°,OA ∶OA ′=3∶2,则△A ′B ′C ′的面积为________.解析 相交直线AA ′,BB ′所在平面和两平行平面α,β相交于AB ,A ′B ′,所以AB ∥A ′B ′.同理BC ∥B ′C ′,CA ∥C ′A ′.所以△ABC 与△A ′B ′C ′的三内角相等,所以△ABC ∽△A ′B ′C ′,A ′B ′AB =OA ′OA =23.S △ABC =12×2×1×32=32, 所以S △A ′B ′C ′=32×⎝⎛⎭⎫232=32×49=239.答案2398.设m ,n 是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题: ①若m ⊂α,n ∥α,则m ∥n ; ②若α∥β,β∥γ,m ⊥α,则m ⊥γ; ③若α∩β=n ,m ∥n ,m ∥α,则m ∥β; ④若m ∥α,n ∥β,m ∥n ,则α∥β.其中是真命题的是________(填上正确命题的序号).解析 ①m ∥n 或m ,n 异面,故①错误;易知②正确;③m ∥β或m ⊂β,故③错误;④α∥β或α与β相交,故④错误. 答案 ② 三、解答题9.已知四棱锥P -ABCD 的底面ABCD 是平行四边形,侧面P AB ⊥平面ABCD ,E 是棱P A 的中点.(1)求证:PC ∥平面BDE ;(2)平面BDE 分此棱锥为两部分,求这两部分的体积比.(1)证明 在平行四边形ABCD 中,连接AC ,设AC ,BD 的交点为O ,则O 是AC 的中点.又E 是P A 的中点,连接EO ,则EO 是△P AC 的中位线,所以PC ∥EO , 又EO ⊂平面EBD ,PC ⊄平面EBD ,所以PC ∥平面EBD .(2)解 设三棱锥E -ABD 的体积为V 1,高为h ,四棱锥P -ABCD 的体积为V , 则三棱锥E -ABD 的体积V 1=13×S △ABD ×h ,因为E 是P A 的中点,所以四棱锥P -ABCD 的高为2h ,所以四棱锥P -ABCD 的体积V =13×S 四边形ABCD ×2h =4×13S △ABD ×h =4V 1,所以(V -V 1)∶V 1=3∶1,所以平面BDE 分此棱锥得到的两部分的体积比为3∶1或1∶3.10.如图,ABCD 与ADEF 均为平行四边形,M ,N ,G 分别是AB ,AD ,EF 的中点.求证:(1)BE ∥平面DMF ; (2)平面BDE ∥平面MNG .证明 (1)连接AE ,则AE 必过DF 与GN 的交点O , 连接MO ,则MO 为△ABE 的中位线,所以BE ∥MO .又BE ⊄平面DMF ,MO ⊂平面DMF , 所以BE ∥平面DMF .(2)因为N ,G 分别为平行四边形ADEF 的边AD ,EF 的中点,所以DE ∥GN , 又DE ⊄平面MNG ,GN ⊂平面MNG , 所以DE ∥平面MNG . 又M 为AB 的中点,所以MN 为△ABD 的中位线,所以BD ∥MN , 又MN ⊂平面MNG ,BD ⊄平面MNG , 所以BD ∥平面MNG ,又DE ,BD ⊂平面BDE ,DE ∩BD =D , 所以平面BDE ∥平面MNG .能力提升题组 (建议用时:20分钟)11.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有()A.4条B.6条C.8条D.12条解析如图,H,G,F,I是相应线段的中点,故符合条件的直线只能出现在平面HGFI中,有FI,FG,GH,HI,HF,GI共6条直线.答案B12.已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是()A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行,则在α内不存在与β平行的直线D.若m,n不平行,则m与n不可能垂直于同一平面解析A项,α,β可能相交,故错误;B项,直线m,n的位置关系不确定,可能相交、平行或异面,故错误;C项,若m⊂α,α∩β=n,m∥n,则m∥β,故错误;D项,假设m,n垂直于同一平面,则必有m∥n与已知m,n不平行矛盾,所以原命题正确,故D项正确.答案D13.在正四棱柱ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,则点Q满足条件________时,有平面D1BQ∥平面P AO.解析如图所示,设Q为CC1的中点,因为P为DD1的中点,所以QB∥P A.连接DB,因为P,O分别是DD1,DB的中点,所以D1B∥PO,又D1B⊄平面P AO,QB⊄平面P AO,PO⊂平面P AO,P A⊂平面P AO,所以D1B∥平面P AO,QB∥平面P AO,又D1B∩QB=B,所以平面D1BQ∥平面P AO.故Q为CC1的中点时,有平面D1BQ∥平面P AO.答案Q为CC1的中点14.已知空间几何体ABCDE中,△BCD与△CDE均是边长为2的等边三角形,△ABC是腰长为3的等腰三角形,平面CDE⊥平面BCD,平面ABC⊥平面BCD.(1)试在平面BCD内作一条直线,使得直线上任意一点F与E的连线EF均与平面ABC平行,并给出证明;(2)求三棱锥E-ABC的体积.解(1)如图所示,取DC的中点N,取BD的中点M,连接MN,则MN即为所求.证明:连接EM,EN,取BC的中点H,连接AH,∵△ABC是腰长为3的等腰三角形,H为BC的中点,∴AH⊥BC,又平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,AH⊂平面ABC,∴AH⊥平面BCD,同理可证EN⊥平面BCD,∴EN∥AH,∵EN⊄平面ABC,AH⊂平面ABC,∴EN∥平面ABC.又M,N分别为BD,DC的中点,∴MN∥BC,∵MN⊄平面ABC,BC⊂平面ABC,∴MN∥平面ABC.又MN∩EN=N,MN⊂平面EMN,EN⊂平面EMN,∴平面EMN∥平面ABC,又EF⊂平面EMN,∴EF∥平面ABC,即直线MN上任意一点F与E的连线EF均与平面ABC平行.(2)连接DH,取CH的中点G,连接NG,则NG∥DH,由(1)可知EN∥平面ABC,∴点E到平面ABC的距离与点N到平面ABC的距离相等,又△BCD是边长为2的等边三角形,∴DH⊥BC,又平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,DH⊂平面BCD,∴DH ⊥平面ABC ,∴NG ⊥平面ABC , 易知DH =3,∴NG =32, 又S △ABC =12·BC ·AH =12×2×32-12=22, ∴V E -ABC =13·S △ABC ·NG =63.。
立体几何复习专题及答案-高中数学

立体几何复习专题姓名: 班级:考点一、空间中的平行关系1.如图,在三棱锥P ABC -中,02,3,90PA PB AB BC ABC ====∠=,平面PAB ⊥平面ABC ,D 、E 分别为AB 、AC 的中点. (1)求证:DE //平面PBC ; (2)求证:AB PE ⊥;(3)求三棱锥B PEC -的体积.2. 如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD △为等边三角形,平面PAC ⊥平面PCD ,PA CD ⊥,2CD =,3AD =,(Ⅰ)设G H ,分别为PB AC ,的中点,求证:GH ∥平面PAD ; (Ⅱ)求证:PA ⊥平面PCD ;3.如图,七面体ABCDEF 的底面是凸四边形ABCD ,其中2AB AD ==,120BAD ∠=︒,AC ,BD 垂直相交于点O ,2OC OA =,棱AE ,CF 均垂直于底面ABCD .(1)证明:直线DE 与平面BCF 不.平行;4.(2014新课标Ⅱ)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(Ⅰ)证明:PB ∥平面AEC ;(Ⅱ)设二面角D AE C --为60°,AP =1,AD =3,求三棱锥E ACD -的体积.考点二、空间中的垂直关系5.如图,在四面体ABCD 中,E ,F 分别是线段AD ,BD 的中点,90ABD BCD ∠=∠=,2EC =,2AB BD ==,直线EC 与平面ABC 所成的角等于30.(1)证明:平面EFC ⊥平面BCD ;6.已知某几何体的直观图和三视图如下图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.(1)求证:BN ⊥平面11C B N ;(2)设M 为AB 中点,在C B 边上求一点P ,使//MP 平面1C NB ,求CBPP 的值.7.(2016全国I )如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF为正方形,2AF FD =,90AFD ∠=,且二面角D AF E --与二面角C BE F --都是60.(I )证明:平面ABEF⊥平面EFDC ;(II )求二面角E BC A --的余弦值.考点三、折叠问题和探究性问题中的位置关系8.如图 1,在直角梯形ABCD 中, //,AB CD AB AD ⊥,且112AB AD CD ===.现以AD 为一边向外作正方形ADEF ,然后沿边AD 将正方形ADEF 翻折,使ADEF 平面与平面ABCD 垂直, M 为ED 的中点,如图 2.(1)求证: //AM 平面BEC ;(2)求证: BC ⊥平面BDE ; .9.如图,在边长为4的正方形ABCD 中,点E,F 分别是AB,BC 的中点,点M 在AD 上,且14AM AD =,将AED,DCF 分别沿DE,DF 折叠,使A,C 点重合于点P ,如图所示2.()1试判断PB 与平面MEF的位置关系,并给出证明;()2求二面角M EF D --的余弦值.10.如图所示,直角梯形ABCD 中,//AD BC ,AD AB ⊥,22AB BC AD ===,四边形EDCF 为矩形,3CF =,平面EDCF ⊥平面ABCD . (1)求证:DF //平面ABE ;(2)求平面ABE 与平面EFB 所成锐二面角的余弦值. (3)在线段DF 上是否存在点P ,使得直线BP 与平面ABE 所成角的正弦值为34,若存在,求出线段BP 的长,若不存在,请说明理由.11.如图1,在边长为4的正方形ABCD中,E是AD的中点,F是CD的中点,现-.将三角形DEF沿EF翻折成如图2所示的五棱锥P ABCFE(1)求证:AC//平面PEF;(2)若平面PEF⊥平面ABCFE,求直线PB与平面PAE所成角的正弦值.12.(2011•浙江)如图,在三棱锥P﹣ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2(1)证明:AP⊥BC;(2)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.13.如图,在直三棱柱111ABC A B C -中,底面ABC 为等边三角形,122CC AC ==.(Ⅰ)求三棱锥11C CB A -的体积;(Ⅱ)在线段1BB 上寻找一点F ,使得1CF AC ⊥,请说明作法和理由.考点四、知空间角求空间角问题14.(2014天津)如图四棱锥P ABCD -的底面ABCD 是平行四边形,2BA BD ==2AD =,5PA PD ==E ,F 分别是棱AD ,PC 的中点.(Ⅰ)证明: EF ∥平面PAB ; (Ⅱ)若二面角P AD B --为60°, (ⅰ)证明:平面PBC ⊥平面ABCD(ⅱ)求直线EF 与平面PBC 所成角的正弦值. PCDBF15.四棱锥P ABCD -中,底面ABCD 为矩形,PA ABCD ⊥平面,E 为PD 的中点.(1)证明://E PB A C 平面;(2)设13AP AD ==,,三棱锥P ABD -的体积34V =,求二面角D -AE -C 的大小16.如图,四棱锥P ABCD -中, PA ⊥底面ABCD ,底面ABCD 是直角梯形,90ADC ∠=︒, //AD BC , AB AC ⊥, 2AB AC ==,点E 在AD 上,且2AE ED =.(Ⅰ)已知点F 在BC 上,且2=CF FB ,求证:平面PEF ⊥平面PAC ;(Ⅱ)当二面角--A PB E 的余弦值为多少时,直线PC 与平面PAB 所成的角为45︒?立体几何专题参考答案1. (1)证明:∵在△ABC 中,D 、E 分别为AB 、AC 的中点,∴DE ∥BC . ∵DE ⊄平面PBC 且BC ⊂平面PBC ,∴DE ∥平面PBC . (2)证明:连接PD .∵PA =PB ,D 为AB 的中点,∴PD ⊥AB .∵DE ∥BC ,BC ⊥AB ,∴DE ⊥AB .又∵PD 、DE 是平面PDE 内的相交直线, ∴AB ⊥平面PDE .∵PE ⊂平面PDE ,∴AB ⊥PE .(3)解:∵PD ⊥AB ,平面PAB ⊥平面ABC ,平面PAB ∩平面ABC =AB ,∴PD ⊥平面ABC ,可得PD 是三棱锥P -BEC 的高. 又∵33,2BECPD S==,1332B PEC P BEC BEC V V S PD --∆∴==⨯=. 2.(I )见解析;(II )见解析;(III )33. (I )证明:连接BD ,易知AC BD H ⋂=,BH DH =,又由BG PG =,故GHPD ,又因为GH ⊄平面PAD ,PD ⊂平面PAD , 所以GH ∥平面PAD .(II )证明:取棱PC 的中点N ,连接DN ,依题意,得DN PC ⊥, 又因为平面PAC ⊥平面PCD ,平面PAC平面PCD PC =,所以DN ⊥平面PAC ,又PA ⊂平面PAC ,故DN PA ⊥, 又已知PA CD ⊥,CD DN D =,所以PA ⊥平面PCD . 3.(1)见解析;(2)23535本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
高中数学-立体几何-空间中的平行和垂直关系

高中数学总复习-第七章立体几何-空间中的平行和垂直关系【知识结构图】第3课空间中的平行关系【考点导读】1.掌握直线和平面平行、两个平面平行的判定定理和性质定理。
2.明确定义与定理的不同,定义是可逆的,既是判定也是性质,而判定定理与性质定理多是不可逆的。
3.要能灵活的对“线线平行”、“线面平行”和“面面平行”进行转化。
【基础练习】1.若ba、为异面直线,直线c∥a,则c与b的位置关系是异面或相交2.给出下列四个命题:①垂直于同一直线的两条直线互相平行. ②垂直于同一平面的两个平面互相平行.③若直线12,l l 与同一平面所成的角相等,则12,l l 互相平行. ④若直线12,l l 是异面直线,则与12,l l 都相交的两条直线是异面直线. 其中假.命题的个数是 4 个。
3.对于任意的直线l 与平面a ,在平面a 内必有直线m ,使m 与l 垂直 。
4. 已知a 、b 、c 是三条不重合的直线,α、β、r 是三个不重合的平面,下面六个命题:①a ∥c ,b ∥c ⇒a ∥b ;②a ∥r ,b ∥r ⇒a ∥b ;③α∥c ,β∥c ⇒α∥β; ④α∥r ,β∥r ⇒α∥β;⑤a ∥c ,α∥c ⇒a ∥α;⑥a ∥r ,α∥r ⇒a ∥α. 其中正确的命题是 ①④ 。
【范例导析】例1.如图,在四面体ABCD 中,截面EFGH 是平行四边形. 求证:AB ∥平面EFG . 证明 :∵面EFGH 是截面.∴点E ,F ,G ,H 分别在BC ,BD ,DA ,AC 上. ∴EH面ABC ,GF面ABD ,由已知,EH ∥GF .∴EH ∥面ABD . 又 ∵EH 面BAC ,面ABC ∩面ABD=AB∴EH ∥AB . ∴AB ∥面EFG .例2. 如图,在正方体ABCD —A 1B 1C 1D 1中,点N 在BD 上,点M 在B 1C 上,并且CM=DN.求证:MN ∥平面AA 1B 1B.分析:“线线平行”、“线面平行”、“面面平行”是可以互相转化的。
立体几何基础平行与垂直的性质与判定

立体几何基础平行与垂直的性质与判定立体几何基础——平行与垂直的性质与判定立体几何是数学中的一个重要分支,它研究的对象是在三维空间内的图形和物体。
在立体几何中,平行和垂直是两个基本概念,它们在判断和解决几何问题时起着重要的作用。
本文将介绍平行与垂直的性质和判定方法,帮助读者更好地理解立体几何的基础知识。
一、平行的性质与判定平行是指在同一平面内,两条直线永不相交的性质。
在立体几何中,我们常用平行性质来推导和证明定理。
以下是一些与平行相关的性质和判定方法。
1. 平行线性质:(1)平行线上的对应角相等:如果两条平行线被一条横截线所交,那么对应的角都是相等的。
(2)平行线上的内错角互补:如果两条平行线被一条横截线所交,那么内错角互补,即相互补充的角和为180度。
(3)平行线上的同旁内角相等:如果两条平行线被一条横截线所交,那么同旁内角相等,即相邻的内角相等。
2. 判定平行线的方法:(1)两条线段平行的充要条件是斜率相等:如果两条线段的斜率相等,那么它们是平行的。
(2)两个向量平行的充要条件是比值相等:如果两个向量的坐标分量比值相等,那么它们是平行的。
(3)两条直线互相垂直的充要条件是斜率乘积为-1:如果两条直线的斜率乘积为-1,那么它们互相垂直。
二、垂直的性质与判定垂直是指两条直线或线段在交点处互相成直角的性质。
垂直的性质在几何证明中经常被用到,下面是关于垂直的一些性质和判定方法。
1. 垂直线性质:(1)垂直线上的对应角互补:如果两条垂直线被一条横截线所交,那么对应的角互补,即相互补充的角和为90度。
(2)垂直线上的内角相等:如果两条垂直线被一条横截线所交,那么内角相等,即相邻的内角相等。
2. 判定垂直线的方法:(1)两条线段垂直的充要条件是斜率乘积为-1:如果两条线段的斜率乘积为-1,那么它们是垂直的。
(2)两个向量垂直的充要条件是内积为0:如果两个向量的内积为0,那么它们是垂直的。
三、平行和垂直在实际中的应用平行和垂直的性质在日常生活和工程实践中有广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【思路】
本题可以转化为证明EE1平行于 平面FCC1内的一条直线或证明平 面A1ADD1与平面FCC1平行.
【解答】
证法一:在直四棱柱ABCD- A1B1C1D1 中 , 取 A1B1 的 中 点 F1 , 连 接 A1D , C1F1 ,
CF1. 因为AB=2CD,且AB∥CD,
所以CD平行且等于A1F1,
∵BC∥AD且BC=1/2AD, 又Q为AD的中点 即BC平行且等于AQ.
M
D
∴四边形BCQA为平行四边形, Q N
C
且N为AC中点,
又∵点M在是棱PC的中点, A
B
∴ MN // PA
………………...…2分
∵ MN⊂平面MQB,PA⊄平面MQB, ...………3分
∴ PA // 平面MBQ.
……………...……4分
【点评】
证明线面平行的方法主要有两种:利 用线面平行的判断定理和面面平行的 性质定理.定理的条件的叙述要完整, 同时也需根据不同特点的题选用不同 方法.关键是找到(或作出)平面内与已 知直线平行的直线,常用平行四边形 的对边平行(如本例)或三角形的中位线 的性质(如变式题),还可以逆用线面平 行的性质先推测出需要的直线.
空间中的平行关系
空间平行例题
空间中的平行关系例题
[2009·山东] 如图所示,在直四棱柱ABCD- A1B1C1D1 中 , 底 面 ABCD 为 等 腰 梯 形 , AB∥CD , AB = 2CD , E 、 E1 、 F 分 别 是 棱 AD、AA1、AB的中点. 证明:直线EE1∥平面FCC1.
2011·丰台一模·立体几何
如图,在四棱锥P-
P
ABCD中,底面ABCD
为直角梯形,AD//BC,Biblioteka ∠ADC=90°,Q为AD
D
的中点,PA=PD,
Q
BC=1/2 AD.若点M是 A 棱PC的中点,求证:PA
// 平面BMQ.(4分)
M
C B
【解答】
连接AC,交BQ于N,
P
连接MN.
……………… 1分
A1F1CD为平行四边形, 所以CF1∥A1D. 又因为E、E1分别是棱AD、AA1的中点, 所以EE1∥A1D, 所以CF1∥EE1,又因为F1C⊂平面FCC1, 所以直线EE1∥平面FCC1.
【解答】
证法二:由已知,DD1∥CC1,所以DD1∥平面FCC1. 又AB∥CD,AB=2CD,所以DC平行且等于AF, 所以四边形AFCD是平行四边形,所以AD∥FC, 所以AD∥平面FCC1. 又AD∩DD1=D, 所以平面A1ADD1 ∥平面FCC1. 因为EE1⊂平面A1ADD1, 所以EE1∥平面FCC1.
