生猪的出售时机数学建模样板
数学建模论文猪的最佳销售时期的数学模型 猪的最佳销售时期的数学模型 猪的最佳销售时期的数学模型 猪的最
数学建模论文课题：猪的最佳销售时期的数学模型问题重述：一般从事猪的商业性饲养和销售总是希望获得利润，因此，饲养某种猪是否获利，怎样获得最大利润，是饲养者必须首先考虑的问题。
如果把饲养技术水平、猪的类型等因素视为不变的，且不考虑市场的需求变化，那么影响获利大小的一个主要因素是如何选择猪的售出时机。
也许有人认为，猪养得越大，售出后获利越大。
其实不然，因为随着猪的生长，单位时间消耗的饲养费用也就越多，但同时其体重增长的速度却不断下降，所以饲养时间太长是不合算的。
试作适当的假设，引入相应的参数，建立猪的最佳销售时机的数学模型。
一、模型假设1、猪的市场价格的变化是连续的，即市场猪肉价格随时间变化的函数可以视为连续函数。
2、饲料市场价格的变化是连续的，即饲料价格随时间变化的函数可以视为连续函数。
3、成本主要由猪苗价格与饲料消耗组成，不考虑其他因素。
4、饲养技术水平、猪的类型等因素视为不变的，且不考虑市场的需求变化。
二、符号说明1、市场猪肉价格为q(t) 元/公斤2、饲料价格为p(t) 元/公斤3、猪苗价格为r 元/公斤4、猪苗重量为m 公斤5、饲养了t 时间后，猪的重量为M(t)公斤6、t 时刻，单位时间增加重量为a(t)公斤7、t 时刻，每消耗1公斤饲料增加的重量为d(t)公斤8、t 时刻，单位时间消耗的饲料为c(t)公斤9、0~t 内消耗饲料的总花费为Z(t)元10、在t 时刻出售可获的利润为Q(t)元三、模型建立1、饲养了t 时间后，猪的重量M(t)的估计由上述符号说明可知：a(t)=c(t)d(t)当时间很短时，即：t~t +⊿t 内增加的重量可由下式表示：M(t~t +⊿t)-M(t )≈a(t) *⊿t= c(t)d(t) *⊿t 即为：()()()dM t c t d t dt =——————————①初值条件：M(0)=m故：0()()()tM t m c s d s ds =+⎰——————————②2、0~t 内消耗饲料的总花费Z(t)的估计当时间很短时，即：t~t +⊿t 内的总花费可由下式表示：Z(t~t +⊿t)-Z(t )≈c(t)p(t) *⊿t 即为：()()()dZ t c t p t dt=——————————③ 初值条件：Z(0)=0故：0()()()t Z t c s p s ds =⎰———————————④3、在t 时刻出售可获利润Q(t)的估计由于：利润=t 时刻售价*猪重量-饲料总花费-猪苗单价*猪苗重量即为：()()*()()*Q t q t M t Z t r m =--——————————⑤ 将②④式代入可得：00()*(())()*()()()()t tQ t m q t r q t c s d s ds c s p s ds =-+-⎰⎰————————————⑥4、在t 时刻出售可获利润Q(t)最大值的估计由⑥式：要求时刻t ，使得Q(t)最大，必须令()0d Q t d t =即： 0()()*[()()]()*[()*()()]0t dQ t dq t m c s d s ds c t q t d t p t dt dt =++-=⎰———————————⑦由⑦式的方程即可解出使Q(t)达到最大的时间,记为T则最大利润为：00()*(())()*()()()()T TQ T m q T r q T c s d s ds c s p s ds =-+-⎰⎰———————————⑧（模型中的函数p(t)、q(t)、c(t)、d(t)均可由统计数据回归得出）四、模型简化与模型求解如果市场猪肉价格与饲料价格取为长期价格水平的平均值(即为常数)，分别为p 元/公斤与q 元/公斤。
姜启源数学建模资料
姜启源数学建模资料简单的优化模型3.1 3.2 3.3 3.4 存贮模型生猪的出售时机森林救火最优价格3.5 血管分支3.6 消费者均衡3.7 冰山运输<i>姜启源数学建模资料</i>静态优化模型现实世界中普遍存在着优化问题静态优化问题指最优解是数不是函数静态优化问题指最优解是数(不是函数不是函数) 建立静态优化模型的关键之一是根据建模目的确定恰当的目标函数求解静态优化模型一般用微分法<i>姜启源数学建模资料</i>问题3.1存贮模型配件厂为装配线生产若干种产品，配件厂为装配线生产若干种产品，轮换产品时因更换设备要付生产准备费，产量大于需求时要付贮存费。
备要付生产准备费，产量大于需求时要付贮存费。
该厂生产能力非常大，即所需数量可在很短时间内产出。
生产能力非常大，即所需数量可在很短时间内产出。
已知某产品日需求量100件，生产准备费5000元，贮存费件生产准备费已知某产品日需求量元每日每件1元试安排该产品的生产计划，每日每件元。
试安排该产品的生产计划，即多少天生产一次(生产周期),每次产量多少，使总费用最小。
),每次产量多少一次(生产周期),每次产量多少，使总费用最小。
不只是回答问题，而且要建立生产周期、要不只是回答问题，而且要建立生产周期、产量与需求量、准备费、贮存费之间的关系。
求需求量、准备费、贮存费之间的关系。
<i>姜启源数学建模资料</i>问题分析与思考日需求100件，准备费5000元，贮存费每日每件元。
件准备费日需求元贮存费每日每件1元每天生产一次，每次每天生产一次，每次100件，无贮存费，准备费件无贮存费，准备费5000元。
元每天费用5000元元每天费用10天生产一次，每次天生产一次，天生产一次每次1000件，贮存费件贮存费900+800+…+100 =4500 准备费5000元，总计元，准备费元总计9500元。
元平均每天费用950元元平均每天费用50天生产一次，每次天生产一次，天生产一次每次5000件，贮存费件贮存费4900+4800+…+100 =*****元，准备费元准备费5000元，总计元总计*****元。
生猪的出售时机数学建模样板
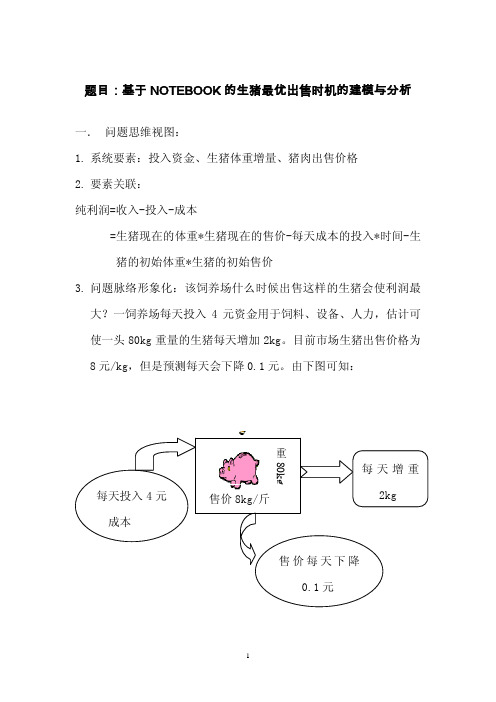
题目：基于NOTEBOOK的生猪最优出售时机的建模与分析 一． 问题思维视图：1.系统要素：投入资金、生猪体重增量、猪肉出售价格2.要素关联：纯利润=收入-投入-成本=生猪现在的体重*生猪现在的售价-每天成本的投入*时间-生猪的初始体重*生猪的初始售价3.问题脉络形象化：该饲养场什么时候出售这样的生猪会使利润最大？一饲养场每天投入4元资金用于饲料、设备、人力，估计可使一头80kg重量的生猪每天增加2kg。
目前市场生猪出售价格为8元/kg，但是预测每天会下降0.1元。
由下图可知：二． 数学刻画：1.给定每天投入4元资金使生猪体重每天增加常数r（=2kg）；生猪出售的市场价格每天降低常数g(=0.1)。
2.给出如下符号列表：符号 t w p C Q R含义 时间 生猪体重单价 t天资金投入纯利润出售收入单位 天 kg 元/kg 元 元 元三． 模型推演：假设r=2，g=0.1，t天后出售，则：生猪体重：w=80+r*t（r=2）; 出售单价：p=8-g*t;出售收入：R=p*w； 资金投入: C=4*t;于是利润为：Q=R-C-8*80.从而得到目标函数(纯利润)：Q(t)=（8-g*t）(80+r*t)-4*t-640 （1）其中，求t（>=0）使Q(t)最大。
这是二次函数最值问题，而且是个现实中的优化问题，故Q(t)的一阶导数为零的t（t>=0）值可使Q（t）取最大值。
先求Q(t)一阶导数：syms t;Q(t)=(8-g*t)*(80+r*t)-4*t-640;y=diff(Q(t),t)y =- r*(g*t-8) - g*(r*t + 80) - 4[g,t,r]=solve('-r*(g*t-80)-g*(r*t+80)=4','g=g','r=r')g =z1t =( 40*z1 + 2)/(z*z1)r =z即： t=(4*r-40*g-2)./(r*g ) (2)在这个模型中：取r=2，g=0.1，则：Q（t）=（8-0.1*t)*(80+2*t)-4*t-640）目标函数MATLAB作图如下：ezplot('(8-0.1*t)*(80+2*t)-4*t-640',[0,20])hold onxlabel('t坐标'); ylabel('Q(t)坐标');从图象可知t=10时，Q（t）max=10。
数学建模课件_生猪的出售时机
t是r的增函数，表1和图3给出它们的关系。
2.设每天生猪体重的增加r=2公斤不变，研 究g变化的影响，由（2）式可得
3 20 g r , g 0 g 0.15 (4)
t是g的减函数，表2和图4给出它们的关系。
可以用相对改变量衡量结果对参数的敏感 程度。t对r的敏感度记作S ( t,r),定义为
Q(t ) p(t ).w(t ) 4t 640 (8)
用微分求解（8）式的极值问题，可知最优 解应满足
p(t ) w(t ) p(t ) w (t ) 4 (9)
（9）式左端是每天利润的增值，右端是每 天投入的资金。于是出售的最佳时机是保 留生猪直到利润的增值等于每天投入的资 金为止。 本例中 p 0.1 , 2是根据估计和预测确 定的，只要它们的变化 不大，上述结论就是 可用的。
按照假设，w 80 rt (r 2)，p 8 gt ( g 0.1). 又知道 R p , C 4t , 再考虑到纯利润扣掉以 当前价格(8元 / 公斤)出售80公斤生猪的收入，有 Q R C 8 80，得到目标函数(纯利润)为
Q(t ) (8 gt )(80 rt ) 4t 640
另外，从敏感性分析知 S (t , r ) 3, ，
所以若1.8 w 2.2 (10 % 以内)， 则结果应为 7 t 13 (30%以内)。
若设p 0.1是最坏的情况，如果这 个(绝对) 值更小，t就应更大。
所以最好的办法是： 过大约一周后重新估计 p, p, w, w, 再作计算。
即生猪价格每天的降低g增加1%，出售时间 提前3%，r和g的微小变化对模型结果的影 响并不算大。 强健性分析（Robustness） 建模过程中假 设了生猪体重的增加和价格的降低都是常 数，由此得到的w和p都是线性函数，这无 疑是对现实情况的简化。更实际的模型应 考虑非线性和不确定性，如记w = w (t), p = p (t) ,则（ r ) r r d r t
数学建模案例之单变量最优化
数学建模案例之单变量最优化生猪的最佳销售时间问题1：一头猪重200磅（1磅=0.454公斤），每天增重5磅，饲养每天需花费45美分。
猪的市场价格为每磅65美分，但每天下降0.01美元，求出售猪的最佳时间。
1．问题分析与假设、符号说明涉及的变量：猪的重量w（磅），饲养时间t≥０（天），t天内饲养猪的化费Q（美元），猪的市场价格p（美元/磅），售出生猪所获得的总收益R（美元），我们最终获得的净收益C（美元）。
涉及的常量：猪的初始重量200（磅），饲养每天的花费0.45（美元），生猪每天的增加重量s（磅），当前的市场价格0.65（美元），生猪价格每天的下降比例系数r。
变量之间的联系：假设1：猪的重量从初始的200（磅）按每天s=5（磅）增加，于是有关系：w（磅）=200（磅）+s（磅/天）×t（天）假设2：当前的市场价格0.65（美元/磅），生猪价格每天的下降比例系数r=0.01，那么出售时生猪的价格为：p（美元/磅）=0.65（美元/磅）- r（美元/磅.天）×t（天）因此，我们有如下关系式：饲养生猪的总的费用为：Q（美元）＝0.45（美元／天）×t（天）售出生猪时获得的总收益为：Ｒ（美元）＝ｐ（美元／磅）×ｗ（磅）最终获得的净收益为：C（美元）＝Ｒ（美元）－Q（美元）当生猪卖出时获得最大净收益的时间即为最佳出售时间，因此原问题转换成数学表述就是求Ｐ达到最大时的时间t≥0，其中P的表达式为：=-=⨯-⨯=-+-C t R t Q t p w t rt st t()()()0.45(0.65)(200)0.452．建立数学模型根据前面的分析，原问题的数学模型如下：max ()..()(0.65)(200)0.45,0C t s t C t rt st t t =-+-≥ （1.1）其中，r ，s 为模型参数，此处取值为s=5，r=0.01。
3．模型求解当s=5，r=0.01时，这是一个单变量t 的函数的最优化问题，而且()C t 是一个连续可微的函数。
生猪的出售时机模型
§2 生猪的出售时机模型［问题的提出］ 一饲养场每天投入4元资金用于饲料、设备、人力，估计可使一头80公斤重的生猪每天增加2公斤．目前生猪出售的市场价格为每公斤8元，但是预测每天会降低0．1元，问该场应该什么时候出售这样的生猪．如果上面的估计和预测有出入，对结果有多大影响．[问题分析及符号约定] 投入资金可使生猪体重随时间增长，但售价(单价)随时间减少，应该存在一个最佳的出售时机，使获得利润最大．这是一个优化问题，根据给出的条件，可作如下的简化假设．每天投入4元资金使生猪体重每天增加常数 (=2公斤)；生猪出售的市场价格每r 天降低常数g(=0．1元)．[模型的建立] 给出以下记号：～时间(天)．～生猪体重(公斤)；单价 (元／t w ~p 公斤)；R-出售的收入(元)；C-t 天投入的资金(元)；Q-纯利润(元)．按照假设，．又知道，再)1.0(8),2(80=-==+=g gt p r rt w t C pw R 4,==考虑到纯利润应扣掉以当前价格(8元／公斤)出售80公斤生猪的收入，有 ，得到目标函数(纯利润)为808⨯--=C R Q其中．求使最大．1.0,2==g r )0(≥t )(t Q [模型的求解] 这是求二次函数最大值问题，用代数或微分法容易得到当时，，即10天后出售，可得最大纯利润20元．1.0,2==g r 20)10(,10==Q t [敏感性分析] 由于模型假设中的参数(生猪每天体重的增加和价格的降低g)是r 估计和预测的，所以应该研究它们有所变化时对模型结果的影响．1．设每天生猪价格的降低元不变，研究变化的影口向，由(2)式可得1.0 g r是的增函数，表1和图3给出它们的关系．t r 2．设每天生猪体重的增加=2公斤不变，研究g 变化的影响，由(2)式可得r是的减函数，表2和图4给出它们的关系． t r可以用相对改变量衡量结果对参数的敏感程度．对的敏感度记作，定义为t r ).(r t S由(3)式，当=2时可算出r 即生猪每天体重增加1％，出售时间推迟3％．r 类似地定义对g 的敏感度，由(4)式，当g=0．1时可算出t ).(g t S即生猪价格每天的降低g 增加1％，出售时间提前3％。
单变量最优化模型的一般方法
总结以上的分析建模的步骤
第二步 选择建模方法 选择解决问题的一般的求解方法 这一步成功需要经验、 这一步成功需要经验、技巧和熟悉相关领域的知识 第三步 推导模型的数学表达式 将第一步中得到的问题重新表达成第二步选定的建模方 法所需要的形式 你可能需要将第一步中的一些变量名改成与第二步所用 的记号一致
提出问题 选择建模方法 推导模型的数学表达式 求解模型 回答问题
列出所有的变量和变量之间的数量关系
全部的变量： 全部的变量： 猪的重量ω 猪的重量ω（磅）； 从现在到猪出售的时间t 从现在到猪出售的时间t（天）； 天内饲养的花费С t天内饲养的花费С（元）； 猪的市场价格Ρ 猪的市场价格Ρ（元）； 售出猪所获得的收益R 售出猪所获得的收益R（元）； 净收益P 净收益P（元）
练习题
A地的一家零售商店甲收到从B地和C地运来的货物。假设x表 地的一家零售商店甲收到从B地和C地运来的货物。假设x 示从B地发来的货物量， 表示从C地发来的货物量。 示从B地发来的货物量，Y表示从C地发来的货物量。 写出该零售商店所收到的单位产品总数的表达式； 写出该零售商店所收到的单位产品总数的表达式； 假设从B 地的运费是每单位0.2元 地运到A 假设从B地A地的运费是每单位0.2元，从C地运到A地的运费 是每单位0.25元 写出到该零售商的总运费的目标函数； 是每单位0.25元。写出到该零售商的总运费的目标函数； 假设该零售商店每月的需求是5000单位的产品 单位的产品， 假设该零售商店每月的需求是5000单位的产品，写出要把 5000单位产品运输到该店的约束条件 5000单位产品运输到该店的约束条件。 单位产品运输到该店的约束条件。 在一个月中， 地运出的货物不超过4000单位 而从C 单位， 在一个月中，从B地运出的货物不超过4000单位，而从C地运 出的货物不超过3000单位 写出模拟这个情况的约束条件。 单位。 出的货物不超过3000单位。写出模拟这个情况的约束条件。 假设，货物量是大于0 的单位量。请结合目标函数和约束条件， 假设，货物量是大于0 的单位量。请结合目标函数和约束条件， 写出满足该店需求的成本最低的数学模型。 写出满足该店需求的成本最低的数学模型。
利用数学模型求解生猪的最佳销售时机问题
ｂ・
由
于红 （９ ０一） 女 ， １７ ， 河北唐 山人 ， 师， 事数 学教 育方面的 讲 从
工作 。
２０ －３３ ０ ９０ －１
安徽 农业科 学
２０ ０ ９盎
Ａ ￡ Ａｔ （ ） ， ０＜０ ） ＜１ 。
个 主要 因素就是 如何选择生猪 的售 出时机 ， 即何时 卖 出获 利
才最 大。可能 会 有人 认 为 ， 养得 越 大 ， 出 后 获 利越 大。 猪 售
其实 不然 ， 精明 的饲 养者 都知道 ， 随着 猪的生 长 ， 位时 间消 单 耗的饲料 费用也会越来 越多 ， 同时其体 重的增 加速 度却 不 但 断下 降 ， 销售 价格 不会 随体 重 的增加 而增 加 ， 以饲 养 时 而 所 间过 长是不合算 的 。下 面就做 出适 当的假设 ， 建立 猪 的最佳 销售 时机 的数 学模 型 。 利用平衡 原理是 建立 微 分方 程模 型 的一 个 常被 选 用 的 且 不考虑市 场需求 ， 即可视 Ｐ ｔ 为常数 Ｐ （， ） 。
‰， 若 （） ｔ 为一 头猪在 ｔ 刻 的重 量 ， 有 （ ）＝ 。 时 则 ０ 。又 设
性 、 论 的明确性 和体 系 的完 整性 ， 结 而且 在 于它 应用 的广 泛
性 。经 济发展 的全球 化 、 计算 机 的迅 猛 发展 ， 学理 论 与 方 数 法 的不 断扩充使得数 学 已经 成 为 当代 高科 技 的一个 重 要组 成部 分 和思想 库 ， 数学 已经成 为 一种 能够 普遍 实施 的技 术 。 应用数学去解 决各类 实际 问题 时 ， 需要 建立数 学模 型 。建 就 立教 学模 型 的过程 ， 把错综 复 杂 的实际 问题 简化 、 象 为 是 抽 合理 的数学 结构 的过 程 。要 通 过 调查 、 集数 据 资料 ， 收 观察 和研究实际对象 的 固有特 征和 内在 规律 ， 抓住 问题 的 主要 矛 盾 ， 立起 反映实 际 问题 的数 量关 系 ， 建 然后 利用 数学 的理 论 和方 法去分折和 解决 问题 。数 学 建模 是联 系 数学 与 实际 问 题 的桥 梁 ， 是数学 在各 个领 域 广泛 应用 的媒介 ， 是数 学科 学 技术转化 的主要途径 ， 数学 建模在科 学技术 发展 中的重要 作 用也越来 越受到数学 界和工程 界的普遍 重视 ， 已成 为现 代 它
生猪的出售时机
2010高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。
如有违反竞赛规则的行为，我们将受到严肃处理。
我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：鄂东职业技术学院参赛队员(打印并签名) ：1. 吴永兵2.3.指导教师或指导教师组负责人(打印并签名)：徐金华日期： 2010 年 7 月 5 日2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：生猪的出售时机摘要这篇论文介绍生猪长大后的出售时机问题。
考察生猪出售的最佳时机，使获得的利益最大。
其中涉及的因素有价格、生长速度，采用预测的方式构建数学模型分析，并对这些因素进行敏感性分析和强健性分析。
关键词：价格变化生长速度敏感性分析强健性分析一、背景介绍某一饲养场每天投入4元资金用于饲料、设备、人力，工作人员估计可使一头80公斤重的生猪每天增加2公斤．目前生猪出售的市场价格为每公斤8元，但是预测每天会降低0．1元，那么该场应该什么时候出售这样的生猪，才能使收益最大．如果上面的估计和预测有出入，对结果有多大影响呢．二、问题分析投入资金可使生猪体重随时间增长，那么是不是投入越多的资金获得的利益越大呢，很显然不是的，大家由背景可知售价(单价)随时间减少，应该存在一个最佳的出售时机，使获得利润最大．这是一个优化问题，根据给出的条件，可作如下的简化假设．三、模型假设每天投入4元资金使生猪体重每天增加常数r (=2公斤)；生猪出售的市场价格每天降低常数g(=0．1元)．四、模型建立给出以下记号：t～时间(天)．w～生猪体重(公斤)；~p单价 (元／公斤)；R-出售的收入(元)；C-t天投入的资金(元)；Q-纯利润(元)．按照假设，)1.0rrtgtw．又知道tp=g=，再考虑,=R4Cpw2),8((80===-+到纯利润应扣掉以当前价格(8元／公斤)出售80公斤生猪的收入，有80R8⨯=CQ，--得到目标函数(纯利润)为其中1.0t使)(≥,2=r．求)0=gQ最大．(t五、模型求解这是求一个二次函数最大值问题，用代数或微分法容易得到当1.0,10=t，即10天后出售，可得最大纯利润20元．(=Q,2==gr时，20)10六、敏感性分析由于模型假设中的参数(生猪每天体重的增加r和价格的降低g)是估计和预测的，所以应该研究它们有所变化时对模型结果的影响．1．设每天生猪价格的降低1.0g元不变，研究r变化的影口向，由(2)式可得t是r的增函数，表1和图3给出它们的关系．2．设每天生猪体重的增加r=2公斤不变，研究g变化的影响，由(2)式可得t是r的减函数，表2和图4给出它们的关系．可以用相对改变量衡量结果对参数的敏感程度．t 对r 的敏感度记作).(r t S ，定义为由(3)式，当r =2时可算出即生猪每天体重r 增加1％，出售时间推迟3％． 类似地定义t 对g 的敏感度).(g t S ，由(4)式，当g=0．1时可算出即生猪价格每天的降低g 增加1％，出售时间提前3％。
数学建模论文-肥猪最佳销售时机问题
数学建模论文肥猪的最佳销售时机作者:摘要：人们通过对猪的饲养和销售，总希望获阿得最大收益。
因此建立与此相关的数学模型来求解最大收益与最佳销售时间就有着重要的实际意义。
对于收入部分，由于市场价格受多种不确定因素的影响且变化较大，我们假设价格保持不变，所以收入正比于猪的体重；猪的体重与时间的关系可以用Gompertz模型来模拟。
对于成本部分，认为由饲料成本和猪仔价格组成。
通过对饲料消耗量和体重的实际数据的分析，发现线性拟合的效果较理想，由此利用该关系确定饲料的消耗。
至此问题转化为建立猪的生长模型和饲料消耗模型。
对于最优化模型，我们从两个方面进行了考虑，一是总利润的最大值，二是日均利润最大值。
通过以上分析，较好地解决了肥猪最佳销售时机问题，对养殖户有一定参考意义。
肥猪的最佳销售时机关键词：数学建模；肥猪最佳销售时机；饲料消耗模型；Gompertz模型问题的叙述与分析：一般从事猪的饲养和销售总希望获得利润，因此饲养某种猪是否获利，怎样获得最大利润，是饲养者必须考虑的问题。
如果把饲养技术水平，猪的性质等因素看成不变的，且不考虑市场的需求变化，那么影响获利大小的一个主要因素是如何选择猪的售出时机，即何时把猪卖出获利最大。
也许有人认为，猪养的越大，售出后获利愈大，其实不然，因为随着猪的生长，单位时间消耗的饲养费用也就愈多，但同时其体重的增长速度却不断下降，所以饲养时间过长是不合算的。
考虑某个品种猪的最佳销售时机的数学模型。
要求猪的最佳销售时机，目标是寻求最大利润的取得，由此实际上需要找出收入和支出分别是什么，受什么影响。
为了简化问题，我们只考虑一头猪的利润，并且做了一系列的理想化的假设，比如生猪价格固定等，所以收入与猪的体重成正比，而成本则由固定成本（如猪仔价格，防疫费用）和变化成本（主要是饲料的消耗）组成，最终问题转化成建立猪的生长模型和饲料消耗模型。
通过查阅大量相关资料，我们选择了用Gompertz模型来模拟猪的生长情况，而对于后者，我们对实际原始数据进行了分析，建立了较理想的模型。
关于生猪出售时机的优化模型
故纯利润＝出售收入一 投入资金 原收入
即 口： — 一０１， Ｒ Ｃ ８×２可得纯利润为 Ｑ （ 一ｔ８＋ｔ ６一０ １ ＝１ ｇ）０ ｒ 一ｔ８×２ ２ （ ）
（） ６
即生猪每天体重增加 ， 出售时间便推迟 １ ％。 ， ４
该 实 际 问题 转 化 为求 ， ０ （ ）使 Ｑ（ ） ｆ 大 ，即 利 用 微 分 法 求 二 ）最
优化问题是人们在 工程 技术、 经济管理和科学研究等领域中最常遇到的
一
量ｒ 和价 格的降低 量ｇ 的变化 ， ） 对模型结果的影响 ， 以及模型的结果对两个因 素的敏感程度。 （） １ 设价 格 的降低 ｇ ｏ 元保持不 变， ＝． １ 分析ｒ 的变化对结 果的影 响， 由
类问题。 如 厂家需 根据生产成本和市场需求等 因素确定产品价格， 商家需
即Ｒ＝ｐ Ｃ ｔ ｗ， ＝６
ｔ 的减 函数 ， 反应了两者之 间的关系。 是ｇ 表２
我们使用相对改变量进一步衡量结果对 参数的敏感程度， 对ｒ ｔ 的敏感度
记 做 ） ，定 义为
） 而ｔｔ ｄ ：Ｄ ／ ｔ ｒ
（） ５ 由 （ ａ ） 式 ， 当 ｒ２ ： 时 得 帅
（） ２ 式可得
ｆ：
皇
、
，
， １１ ≥ ．７ －
（） ３
ｔ 的增函数， 反应了两者之间的关系。 是ｒ 表１
１ ２ １３ １ ４ ． ． ．
１５ ．
１６ ．
１７ ．
１８ ．
１９ ．
１６ １ ｌ ． ｌ ． ． ７ ６．５ Ｏ Ｏ ３ ３
１ ．５ ６２
１ 问 题 分 析 、
１ ６ ｌ １ ｌ ． ８．３ ６ ４ ５ Ｏ ３ ６ ２． １４ ０ ４． ｌ ２． ４ ０Ｏ １ ． ７ ． ．８ ５ ．３ Ｏ．３ ０ １ １ ．４ ０ １ ０ １ ０．７ ０ １ Ｏ １ ． ０ ０ ２ ． ２ ．５ ．６ １ ．８ ．９ Ｏ ２ ． １ ０ ２ ５
生猪出售时机的数学模型
的增加值 r 为常数，r=1 公斤/天，于是
w(t) w(0) rt
(2.3.2)
3. 模型建立和求解
所以在 t 天之后出售生猪的收入
R(t) p(t)w(t) p(0)w(0) rp(0) gw(0)t grt2
于是在 t 天之后出售生猪比现在出售多赚的纯利润 为：
Q(t) R(t) C(t) p(0)w(0)
注意 t 是 g 的减函数： t rp(0) c 1 w(0) . 为 2r g 2r
了使 t>0，g 应该满足 rp(0) gw(0) c 0 . 所以
S(t, g) c rp(0) rp(0) gw(0) c
(2.3.14)
代入具体数值，可算出 S(t, g) 5.5.
4. 灵敏度分析
解释成：如果 r 增加 1%，则 t 变化的百分比是 1%的 S(t,r)倍. 如果 S(t,r)很小，则 t 对 r 不灵敏；反之，则 t 对 r 灵敏，r 的微小变化会带来 t 的较大的变化.
4. 灵敏度分析
在实 践中，由 (2. 3. 7)式定义 的灵敏度 需要数值计 算得到列表的结果（见表 2.3）.
3. 模型建立和求解
模型假设：
（1）农场每天投入的资金 c 为常数，c=3.2 元，
即
C(t) ct
（2）现在生猪出售的市场价格为 p(0)=12 元/公
斤，价格每天的降低值 g 为常数，g=0.08 元/公斤/天，
于是
p(t) p(0) gt
(2.3.1)
（3）现在生猪的体重为 w(0)=90 公斤，体重每天
5. 强健性分析
本案例中， p(t) g ， w(t) r 是根据估计或预 测确定的，灵敏度分析说明，只要它们在未来不长的 一段时间内变化不太大，由于假设它们是常数而导致 的最佳出售时机的误差就不会太大，所以可以认为我 们的模型是强健的.
生猪出售时机的数学模型[推荐]
![生猪出售时机的数学模型[推荐]](https://img.taocdn.com/s3/m/eb20171e443610661ed9ad51f01dc281e53a5663.png)
生猪出售时机的数学模型[推荐]猪肉是国人最喜爱的一种肉类产品，也是世界上最消费的肉类之一。
对于养殖户来说，合理的出售时间很重要，可以使得收益最大化，同时也可以保证市场的供需平衡。
在本文中，我们将建立一个数学模型来预测生猪出售的最佳时间，以帮助养殖户做出更加准确的决策。
1. 市场需求变化趋势首先，我们需要了解市场需求的变化趋势。
因为市场需求的变化会直接影响到生猪价格的波动。
一般来说，猪肉的需求与季节、人口、经济因素等紧密相关。
下面就以一些常见因素为例，简单分析需求趋势的变化规律。
（1）季节性需求猪肉是我国重要的春节离不开的食品，季节性需求是猪肉价格波动的重要因素。
春节前各地的销售市场都会陆续大幅增加猪肉品种的销售，销售量的提高占据了市场的主要推动力量。
过年过节，猪肉是各个家庭的必备品，所以春节前后不仅销量大增，而且价格也会慢慢上升。
（2）人口增长和改变的消费习惯随着我国人口增长和生活习惯、消费观念的改变，猪肉消费的需求也发生了很大的变化。
由于人口数量不断增长，猪肉的总需求量也在不断提升，所以在这种市场背景下，生猪的价格会保持较为长期的上升趋势。
（3）经济因素人们消费能力与市场经济环境密切相关，市场经济催生了人们消费需求的增长，生猪价格一般也会随着市场经济的发展而稳步提高。
2. 生猪价格波动规律了解到市场需求的变化趋势后，我们需要在此基础上分析生猪价格波动的规律。
生猪价格的波动可以分为短期和长期两种趋势，短期波动受季节和政策等因素的影响比较大，而长期波动则受到供需关系等因素的影响比较大。
（1）短期波动规律短期波动受到季节和政策等因素的影响，波动幅度相对较小。
一般在春节、端午节、中秋节等节假日前期，生猪价格仍会有所上升。
而在政府宏观调控政策出现较大变动时，也会对生猪价格产生影响。
长期波动受到供需关系等因素的影响。
由于生猪属于周期性消费品，所以在市场需求增长的时期，生猪价格总体上呈现上升趋势。
但是随着养殖场数量的增加和技术的不断发展，生猪生产能力不断提高，当供大于求时，猪肉价格也会出现下跌现象。
数学模型12
V=ad/(b+d) =7.83d/(75.60+d)
五. 建模问题与数学问题的处理 问题的叙述：原始、粗糙、不规范。 问题的假设：问题的研实际情况差异不大或结 论可信。 问题的答案：不确定、不封闭。
六. 建模过程流程
均匀、匀速地撤出。 教室门口的时间。
3.忽略列队的时间和第一个人到达 4. 人体厚度相同w
继续讨论
1. T=(nd+L)/v, v增, 则T减; d增, 则 T增. 增 减 增 增 2. 多行行进 3.令d=0, 则有 则有T=L/v, 疏散时间与人数无关 疏散时间与人数无关! 令 假设中忽略了人体的厚度!! 假设中忽略了人体的厚度 4.考虑厚度的影响 T=(n(d+w)+L)/v, 考虑厚度的影响 若v→v*,d=0, 则 T* = (nw+L)/v* 最短 合理吗？ 合理吗？
假设
1.出售前，猪每天增重相同。 1.出售前，猪每天增重相同。 出售前 2.猪的售价每天降低的数量相同 2.猪的售价每天降低的数量相同 3.用于猪饲料的花费每天不变 3.用于猪饲料的花费每天不变 4.猪在饲养和出售期间内不再有其他的花 4.猪在饲养和出售期间内不再有其他的花 费
变量和参量：
猪的重量w(t)(磅), 售价 饲养时间 t(天),猪的重量 天 猪的重量 磅 售价p(t)美元 美元 售猪所获得的总收益R(t)(美元 ， 美元)， 售猪所获得的总收益 美元 t 天内饲料的总花费 天内饲料的总花费C(t)(美元 ， 美元)， 美元 最终获得的净收益P(t)(美元 。 美元)。 最终获得的净收益 美元 美元/磅 售价日减少量 美元 美元)， 猪的现价 p0(美元 磅),售价日减少量 r(美元 ， 美元 猪的初重w 磅 ， 猪的初重 0(磅)，猪的日增重量 g(磅)， 磅， 美元)。 每天饲料的花费 k(美元 。 美元
数学建模引例1-程序
猪的最佳销售一、猪的最佳销售时机问题： 1、问题的提出：对于猪的商业性饲养和销售，人们总是希望获得最大的利润，在市场需求不变的情况下，如果我们不考虑猪的饲养技术、水平，猪的类型等因素的影响，那么影响销售利润的主要因素，就是销售时机问题，由于随着猪的生长，单位时间消耗的饲养费用逐渐增多，而猪的体重增长却逐渐变慢，因此对猪的饲养时间过长是不合算的。
假定一头猪在开始饲养时的重量为x 0，在饲养后任意时刻t 的重量为x (t )，对于某一品种的猪，它的最大重量假定为X 0，猪的最小出售体重为x s ，相应的饲养时间为t s 。
一头猪从开始饲养到时刻t 所需的费用为y (t )，同时我们假定反映猪体重变化速度的参数为α，猪在达到最大体重后，单位时间的饲养费为y ，反映饲养费用变化大小的参数为λ，请根据上面的假设，建立起猪的最佳销售时机的数学模型，并用下面所给的数据验证你的模型。
假设X 0=200（kg ），x s =75（kg ），α=0.5（kg/天），猪的市场销售价设为c =6元/kg ，γ=1.5（元/天），λ=1（元/天），x 0=5kg 。
2、问题分析：由于猪在进行饲养时已具有一定的体重，而其体重的增加随饲养时间的延长逐渐减慢，因此由Logistic 模型可得)1(0X x dt dx -=α；又由于猪的体重增加，单位时间消耗的饲养费用就越多，达到最大体重后，饲养费用为常数γ，所以有)1(0X x dt dy --=λγ，因此，得到微分方程：⎪⎪⎪⎩⎪⎪⎪⎨⎧==--=-=0)0()0()1()1(000y x x X x dt dy X x dt dx λγα 求解可得：⎪⎪⎩⎪⎪⎨⎧---=--=--)1)(()()()(0000000t X t X e x X t t y e x X X t x αααλγ （1） 养猪能否获利，主要看猪从出生到t s 时，如果出售是否可以获利，因此，获利的充要条件为：)(00s s t y c x c x +≥ （2）其中c 0为仔猪的价格。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
题目：基于NOTEBOOK的生猪最优出售时机的建模与分析 一． 问题思维视图：
1.系统要素：投入资金、生猪体重增量、猪肉出售价格
2.要素关联：
纯利润=收入-投入-成本
=生猪现在的体重*生猪现在的售价-每天成本的投入*时间-生
猪的初始体重*生猪的初始售价
3.问题脉络形象化：该饲养场什么时候出售这样的生猪会使利润最
大？一饲养场每天投入4元资金用于饲料、设备、人力，估计可使一头80kg重量的生猪每天增加2kg。
目前市场生猪出售价格为8元/kg，但是预测每天会下降0.1元。
由下图可知：
二． 数学刻画：
1.给定每天投入4元资金使生猪体重每天增加常数r（=2kg）；生猪出售的市场价格每天降低常数g(=0.1)。
2.给出如下符号列表：
符号 t w p C Q R
含义 时
间 生猪
体重
单价 t天资金
投入
纯利润出售收入
单位 天 kg 元/kg 元 元 元
三． 模型推演：
假设r=2，g=0.1，t天后出售，则：
生猪体重：w=80+r*t（r=2）; 出售单价：p=8-g*t;
出售收入：R=p*w； 资金投入: C=4*t;
于是利润为：Q=R-C-8*80.
从而得到目标函数(纯利润)：
Q(t)=（8-g*t）(80+r*t)-4*t-640 （1）
其中，求t（>=0）使Q(t)最大。
这是二次函数最值问题，而且是个现实中的优化问题，故Q(t)的一阶导数为零的t（t>=0）值可使Q（t）取最大值。
先求Q(t)一阶导数：
syms t;
Q(t)=(8-g*t)*(80+r*t)-4*t-640;
y=diff(Q(t),t)
y =- r*(g*t-8) - g*(r*t + 80) - 4
[g,t,r]=solve('-r*(g*t-80)-g*(r*t+80)=4','g=g','r=r')
g =z1
t =( 40*z1 + 2)/(z*z1)
r =z
即： t=(4*r-40*g-2)./(r*g ) (2)
在这个模型中：取r=2，g=0.1，则：
Q（t）=（8-0.1*t)*(80+2*t)-4*t-640）
目标函数MATLAB作图如下：
ezplot('(8-0.1*t)*(80+2*t)-4*t-640',[0,20])
hold on
xlabel('t坐标'); ylabel('Q(t)坐标');
从图象可知t=10时，Q（t）max=10。
即10天后出售，可得最大利润
为20元。
四． 超参数：
1.设每天生猪的降低g=0.1元不变，研究r变化的影响，由（2）式
可得：
t=（40*r-60）./r, r>=1.5 （3）MATLAB作图如下：
ezplot('(40*r-60)./r',[1.5,3])
hold on
xlabel('r坐标');ylabel('t坐标');
2.设生猪体重的增加r=2kg不变，研究g变化的影响，由（2）可知： t=（3-20*g）./g, 0 <=g<=0.15 (4) 作如下：
MATLAB图
ezplot('(3-20*g)./g',[0.06,0.15])
hold on
xlabel('g坐标');ylabel('t坐标');
由上述2个关系图可知：r是t的增函数，t是g的减函数。
于是可
以用相对变量衡量结果对参数的敏感程度。
t对r的敏感度记作S（t，
r），定义为：
s(t,r)=(Δt./t)./( Δr./r)
≈(dt./dr)*(r./t) (5)
由（3）式，当r=2时 s(t,r)≈60./(40*r-60) （6）
即生猪每天的体重r增加1%，出售时间推迟3%。
类似定义t对g的敏感度S（t，g），由（4）式，当g=0.1时可以出：
s(t,g)= (Δt./t)./( Δg./g)
≈(dt./dg)*(g./t)=-3./(3-20)=3 (7)
即生猪价格每天的降低g 增加1%，出售时间提前3%。
五． 超模型：
研究r，g 不是常数时对模型的影响：
综上可知，出售的最佳时机是保留生猪直到每天利润的增值等于每天的费用时为止。
由于本案例:S （t，r）=3，如果1.8≤w'≤2.2(10%),则7≤t ≤13（30%）建议一周后（t=7）重新评估p,p',w,w',再做计算。
六． 评注：
总而言之，这个案例短期内还是有很大的研究价值。
由于在本案例中：当t=10天时，它就能使利润最大化。
也就是说短期内生猪体重增量和市场价格变动不会出现巨大的波动，从而就不会使模型的估计值与实际情况偏差很大。
但是当t 取值很大时，这个案例就会有很大的弊
端。
因为生猪的出售价格就可能受外来同类产品的冲击，各种替代产品的影响，各种节日的影响等等，这些都将会使估算利润出现很大偏差。