华师大版-数学-八年级上册-《定理与证明》名师教案
新华东师大版八年级数学上册《13章 全等三角形 13.1 命题、定理与证明 定理与证明》优质课教案_1

八年级数学导学案 课 题全等三角形及其判定条件 课 型 新授课 编 号 主 编组长审核 领导审核班 级 小 组 姓 名【学习目标】1、掌握两个三角形全等的条件(对应边相等,对应角相等)。
2、能找出对应边、对应角。
【自学指导】预习课本59页“全等三角形的判定条件”第1,2,3自然段,,完成下列问题:1.能够 的两个三角形叫做全等三角形。
2.全等三角形的对应边 ,对应角 。
3.两个三角形中,六个元素指的是 和【自学检测】1. 如图,点O 是平行四边形ABCD 的对角线的交点,△AOB 绕O 旋转180º,可以与△___________重合,这说明△AOB ≌△___________.这两个三角形的对应边是AO 与__________,OB 与__________,BA 与__________;对应角是∠AOB 与________,∠OBA 与_________,∠BAO 与___________.(第1题) (第2题) 第3题2、如图,AE 是平行四边形ABCD 的高,将△ABE 沿AD 方向平移,使点A 与点D 重合,点E 与点F 重合,则△ABE ≌_________, ∠F =_________3、如图,点D 是等腰直角三角形ABC 内一点,AB =AC ,将△ABD 绕点A 逆时针旋转90°,点D 与点E 重合,则△ABD ≌_________, AD =_________, BD =_________.【合作探究】1、在两个三角形中只有一组角对应相等,则这两个三角形一定全等吗?若不一定,请举反例并画图。
2、在两个三角形中只有一组边对应相等,则这两个三角形一定全等吗?若不一定,请举反例并画图。
3、如果两个三角形有三组对应相等的元素(边或角)有几种情况,分别是:【知识梳理】1.能够完全重合的两个三角形是全等三角形,相互重合的顶点是对应顶点,相互重合的边是对应边,相互重合的角是对应角。
八年级数学上册第13章全等三角形13.1命题定理与证明13.1.2定理与证明教案新版华东师大版word版本

2.命题有哪几类?各是什么?
3.一个命题都可以写成什么形式?哪一步分是题设?哪一步分是结论?
前一节课 我们讲过,要 证明一个命题是假命题,只要举 出 一个反例就行了.这节课,我们将探究怎样证明一个命题是真命题.
面向全体学生提出相关的问题。明确要研究,探索的问题是什么,怎样去研究和讨论。.
留给学生一定的思考和回顾知识的时 间。
为学生创设表现才华的平台。
一.知识:
(一 )定理
用逻辑推理的方法证明它们是正确的命题叫做定理.
(二)证明
根据条 件,定义以及定理等,经过推理论证,来判断一个命题是否正确,这样的推理过程叫做证明.
(三)命题,公理和定理的区别与联系
学生讨 论
二应用:
问题1.看下面的命题ห้องสมุดไป่ตู้不是真命题?
教学反思
定理与证明
教学目标
知识与技能
了解命题、定理的含义;理解证明的必要性.
过程与方法
结合实例让学生意识到证明的必要性,培养学生说理有据,有条理地表达自己想法的良好意识.
情感态度与价值观
初步感受定理化方法对数学发展和人类文明的价值.
教学重点
知道什么是定理
教学难点
理解证明的必要性.
教学内容与过程
教法学法设计
请看下 面的问题:
一条直线截两条平 行直线所得的同位角相等;
问题2.三角形三边的垂直平分线的交点都在三角形的内部是不是真 命题?
解答:不是
问题3.直角三角形的两个锐角互余是不是真命题?
解答:是,请 你证明.
课后小结:定理,证 明.
课后练习:见教材58页
课后作业:复印给学生
创设良好的问题情境,激活学生的求知欲,促使学生 为问题的解决形成一个合适的思维意向,收到最佳的教学效益。使学生在问题情境中,通过观察、操作、思考交流和运用,逐步形成良 好的数学思维习惯,发展数学应用意识,感受学习数学的乐趣。
八年级数学上册 13.1 命题、定理与证明 13.1.2 定理与证明教案 (新版)华东师大版
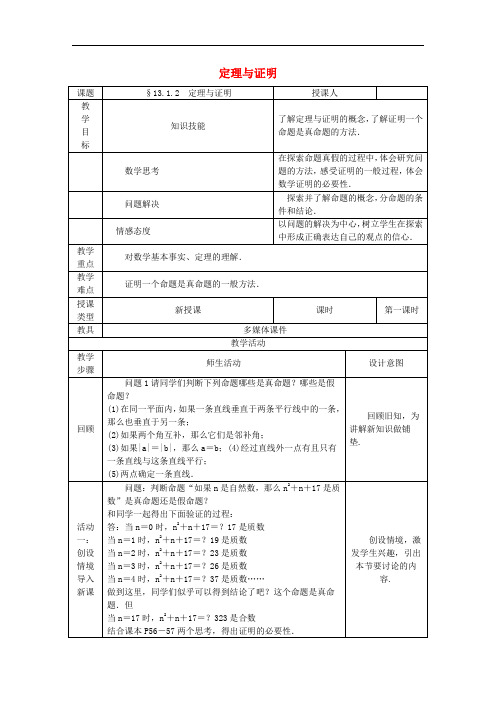
1.要求学生注意定理也是命题注意它的两个组成部分:条件和结论.
2.能证明一个较简单的命题是真命题.
【拓展提升】
[厦门中考]A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权.比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队(有且只有两个队)出线.小组赛结束后,如果A队没有全胜,那么A队的积分至少要几分才能保证一定出线?请说明理由.
例如图13-1-,有下列三个条件:
图13-1-
①DE∥BC:②∠1=∠2;③∠B=∠C.
(1)若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成几个命题,请你都写出来;
(2)请你就其中的一个真命题给出推理过程.
解:(1)一共能组成2个命题,它们是:题设:①②,结论:③;题设:①③,结论:②;
②[讲授效果反思]
A.重点□B.难点□C.易错点□
举反例说明一个命题是假命题是一个难点,教学时要帮助学困生,关注他们在这方面的不足.证明过程的书写是一个较为长期的训练过程,不期望一节课上学生就能很好地掌握.
③[师生互动反思]
学生根据定理的内容画出相应的图形会有较大的困难,师生共同完成.
④[习题反思]
教学
重点
对数学基本事实、定理的理解.
教学
难点
证明一个命题是真命题的一般方法.
授课
类型
新授课
课时
第一课时
教具
多媒体课件
教学活动
教学
步骤
师生活动
设计意图
回顾
问题1请同学们判断下列命题哪些是真命题?哪些是假命题?
华东师大版数学八年级上册-13.1 命题、定理与证明 (第一课时)教案

13.1命题、定理与证明(第一课时)一、学前导入:同学们,“猫是有四条腿的动物”这个判断对吗? “有四条腿的动物是猫”这个判断对吗? 今天我们将学习像这样判断一件事情的语句。
二、课前训练:试判断下列句子是否正确.(1)如果两个角是对顶角,那么这两个角相等;( )(2)两直线平行,同位角相等; ( )(3)同旁内角相等,两直线平行; ( )(4)平行四边形的对角线相等; ( )(5)直角都相等. ( )(6)三角形的内角和等于180°. ( )(7)等腰三角形的两个底角相等 . ( )三、新知导入:1、什么叫命题?_______________________________________________________________________________________________________________________I、点拨提示:(1)错误的命题也是命题。
如:“3<2”是一个命题(2)命题必须是对某种事情作出判断,如问句,几何的作法等就不是命题。
II、巩固练习:判断下列语句是不是命题?是用“√”,不是用“×表示。
1)长度相等的两条线段是相等的线段吗?()2)两条直线相交,有且只有一个交点()3)不相等的两个角不是对顶角()4)一个平角的度数是180度()5)相等的两个角是对顶角()6)取线段AB的中点C()7)画两条相等的线段()2、命题的结构:在数学中,许多命题是由______________________两部分组成的。
______________是_____________,______________是由______________________,这种命题常可写成______________________的形式,“如果”开始的部分是______,“那么”开始的部分是_______.I、例题展示:例:把命题“在一个三角形中,等角对等边”改写成:“如果…那么…”的形式,并分别指出命题的条件和结论。
定理与证明-华东师大版八年级数学上册教案

定理与证明-华东师大版八年级数学上册教案一、教学目标1.了解定理与证明的基本概念和方法;2.能够正确运用定理和相关知识进行数学问题的证明;3.提高数学思维和解决问题的能力。
二、教学重难点1.定理的理解和运用;2.证明的方法与技巧;3.证明过程中思维的拓展。
三、教学内容1.定义:定理是一种真实的、重要的数学命题,需要经过证明才能成立;2.定理的分类:数形结合、解析几何、代数方程、数论等;3.定理的证明方法:直接证明、间接证明、归谬法等;4.基本定理的讲解和运用:比如射影定理、等腰三角形定理、余弦定理等;5.综合运用定理和公式解决实际问题。
四、教学过程1. 导入(5分钟)请学生们回忆上节课学过的定理和证明方法,并举例说明其运用。
2. 讲解定理与证明的基本概念和方法(20分钟)1.讲解定理的定义和分类,举例说明;2.讲解证明的基本方法和技巧,如直接证明、间接证明、归谬法等;3.举例说明定理的证明过程,并让学生模仿练习。
3. 讲解基本定理并运用于实际问题的解决(20分钟)1.介绍常见的基本定理,如射影定理、等腰三角形定理、余弦定理等;2.利用定理解决实际问题的案例分析,并让学生进行练习。
4. 合作探究与案例演示(20分钟)将学生分组,让他们自行查找和收集相关定理和证明的例题,进行合作探究;然后让其中一小组进行案例演示,展示其探究和归纳分析的结果。
5. 课堂小结(5分钟)1.对今天的教学内容进行回顾;2.强调掌握定理和证明的基本方法和技巧;3.提醒学生关注几何图形和代数方程的联系。
五、课后作业1.完成课堂练习题;2.完成课后练习题;3.查找和阅读相关数学文献,了解更多有关定理和证明的知识。
六、教学反思通过本次教学,学生们了解了数学中定理和证明的基本概念和方法,并掌握了一些基本定理的运用和证明。
在教学设计中,我采取了多种教学方法和形式,如讲解、案例分析、小组讨论等,注重培养学生的思维能力和团队合作意识。
但是还需注意,在小组讨论和案例演示环节中,需关注每个小组的参与度和发言机会,让每个学生都能学有所获,提高教学效果。
华师大版八年级数学上册《定理与证明》优质课课件

• 15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年7月2021/7/292021/7/292021/7/297/29/2021
• 16、提出一个问题往往比解决一个更重要。因为解决问题也许仅是一个数学上或实验上的技能而已,而提出新的问题,却需要有创造性的想像力,而且标志着科学的真正进步。2021/7/292021/7/29July 29, 2021
(两直线平行,同位角相等)
∵ ∠3=∠1 ( 对顶角相等 )
∴∠1=∠2 ( 等量代换 )
命题证明的步骤: 1.根据题意,画出图形; 2.根据题设、结论,结合图形,写出
已知、求证; 3.经过分析,找出由已知推出求证的
途径,写出证明过程.
根据下列命题,画出图形,并结合 图形写出已知、求证(不写证明过程): 1)垂直于同一直线的两直线平行; 2)内错角相等,两直线平行; 3)一个角的平分线上的点到这个角的两边
OE平分∠AOB, OF平分∠BOC
求证:OE⊥OF
E
B
证明:∵OE平分∠AOB,
12 F
∴∠1=
OF平分∠BOC
1
2∠AOB,
∠2= 1
2
A ∠BOC
O
C
又∠AOB、∠BOC互为邻补角
∵ ∠AOB+∠BOC=180° ∴∠1+∠2= 1 (∠AOB+∠BOC)=90° ∴ OE⊥OF 2
如何判断一个命题是假命题?
• 17、儿童是中心,教育的措施便围绕他们而组织起来。2021/7/292021/7/292021/7/292021/7/29
• 2、Our destiny offers not only the cup of despair, but the chalice of opportunity. (Richard Nixon, American President )命运给予我们的不是失望之酒,而是机会之杯。二〇二一年六月十七日2021年6月17日星期四 • 3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。10:516.17.202110:516.17.202110:5110:51:196.17.202110:516.17.2021 • 4、All that you do, do with your might; things done by halves are never done right. ----R.H. Stoddard, American poet做一切事都应尽力而为,半途而废永远不行6.17.20216.17.202110:5110:5110:51:1910:51:19 • 5、You have to believe in yourself. That's the secret of success. ----Charles Chaplin人必须相信自己,这是成功的秘诀。-Thursday, June 17, 2021June 21Thursday, June 17, 20216/17/2021
[配套K12]八年级数学上册 13.1 命题、定理与证明 第2课时 定理与证明教案 (新版)华东师大版
![[配套K12]八年级数学上册 13.1 命题、定理与证明 第2课时 定理与证明教案 (新版)华东师大版](https://img.taocdn.com/s3/m/3ab3d0364a7302768e99397a.png)
13.1 命题、定理与证明第二课时定理与证明教学目标1.知识与技能:了解命题、公理、定理的含义;理解证明的必要性.2.过程与方法:结合实例让学生意识到证明的必要性,培养学生说理有据,有条理地表达自己想法的良好意识.3.情感、态度与价值观:初步感受公理化方法对数学发展和人类文明的价值.重点与难点1.重点:知道什么是公理,什么是定理2.难点:理解证明的必要性.教学过程一、复习引入教师讲解:前一节课我们讲过,要证明一个命题是假命题,只要举出一个反例就行了.这节课,我们将探究怎样证明一个命题是真命题.二、探究新知(一)公理教师讲解:数学中有些命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理.我们已经知道下列命题是真命题:两点确定一条直线;两点之间、线段最短;过一点有且只有一条直线与已知直线垂直;过直线外一点有且只有一条直线与这条直线平行;两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.在本书中我们将这些真命题均作为公理.(二)定理教师引导学生通过举反例来说明下面两题中归纳出的结论是错误的.从而说明证明的重要性.1、教师讲解:请大家看下面的例子:当n=1时,(n2-5n+5)2=1;当n=2时,(n2-5n+5)2=1;当n=3时,(n2-5n+5)2=1.我们能不能就此下这样的结论:对于任意的正整数(n2-5n+5)2的值都是1呢?实际上我们的猜测是错误的,因为当n=5时,(n2-5n+5)2=25.2、教师再提出一个问题让学生回答:如果a=b,那么a2=b2.由此我们猜想:当a>b时,a2> b2.这个命题是真命题吗?[答案:不正确,因为3>-5,但3 2<(-5)2]教师总结:在前面的学习过程中,我们用观察、验证、归纳、类比等方法,发现了很多几何图形的性质.但由前面两题我们又知道,这些方法得到的结论有时不具有一般性.也就是说,由这些方法得到的命题可能是真命题,也可能是假命题.教师讲解:数学中有些命题可以从公理出发用逻辑推理的方法证明它们是正确的,并且可以进一步作为推断其他命题真假的依据,这样的真命题叫做定理.(三)例题与证明例如,有了“三角形的内角和等于180°”这条定理后,我们还可以证明刻画直角三角形的两个锐角之间的数量关系的命题:直角三角形的两个锐角互余.教师板书证明过程.教师讲解:此命题可以用来作为判断其他命题真假的依据,因此我们把它也作为定理.定理的作用不仅在于它揭示了客观事物的本质属性,而且可以作为进一步确认其他命题真假的依据.三、随堂练习课本P58练习第1、2题.四、课时总结1、在长期实践中总结出来为真命题的命题叫做公理.2、用逻辑推理的方法证明它们是正确的命题叫做定理五、布置作业课本P58 习题13.1 3。
华东师大版八年级上册数学教学设计《定理与证明》

华东师大版八年级上册数学教学设计《定理与证明》一. 教材分析华东师大版八年级上册数学教材在《定理与证明》这一章节中,主要向学生介绍定理与证明的概念、方法和过程。
本章内容是学生继学习几何初步知识后,进一步深化对几何图形性质和规律的理解,培养学生逻辑思维和论证能力。
本章的主要内容包括定理的定义、定理的证明、公理化体系等。
通过本章的学习,使学生掌握定理与证明的基本概念和方法,提高学生分析问题和解决问题的能力。
二. 学情分析学生在学习本章内容前,已经掌握了基本的几何知识,具备一定的逻辑思维能力。
但部分学生对抽象的逻辑论证过程可能存在理解上的困难,因此,在教学过程中需要关注这部分学生的学习情况,加强对其逻辑思维和论证能力的培养。
同时,学生对于新知识的学习兴趣和积极性较高,可以通过引导和激励,激发学生学习本章内容的兴趣。
三. 教学目标1.知识与技能:使学生掌握定理与证明的基本概念和方法,学会阅读和理解几何论证过程。
2.过程与方法:培养学生逻辑思维和论证能力,提高学生分析问题和解决问题的能力。
3.情感态度与价值观:激发学生学习几何的兴趣,培养学生的抽象思维和创新意识。
四. 教学重难点1.教学重点:定理与证明的基本概念和方法,几何论证过程的阅读和理解。
2.教学难点:定理证明的逻辑推理过程,学生逻辑思维和论证能力的培养。
五. 教学方法1.引导法:通过问题引导,激发学生思考,培养学生逻辑思维和论证能力。
2.案例分析法:分析典型几何论证案例,使学生掌握定理与证明的方法。
3.小组合作学习法:引导学生进行合作交流,共同探讨几何论证问题,提高学生分析问题和解决问题的能力。
六. 教学准备1.教学课件:制作多媒体课件,帮助学生直观地理解定理与证明的概念和方法。
2.教学案例:准备一些典型的几何论证案例,用于分析和讲解。
3.练习题:设计一些有关定理与证明的练习题,巩固所学知识。
七. 教学过程1.导入(5分钟)通过复习几何基本知识,引导学生思考几何论证的过程,引出本章内容——定理与证明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
13.1 命题、定理与证明
第二课时定理与证明
教学目标
1.知识与技能:了解命题、公理、定理的含义;理解证明的必要性.
2.过程与方法:结合实例让学生意识到证明的必要性,培养学生说理有据,有条理地表达自己想法的良好意识.
3.情感、态度与价值观:初步感受公理化方法对数学发展和人类文明的价值.
重点与难点
1.重点:知道什么是公理,什么是定理
2.难点:理解证明的必要性.
教学过程
一、复习引入
教师讲解:前一节课我们讲过,要证明一个命题是假命题,只要举出一个反例就行了.这节课,我们将探究怎样证明一个命题是真命题.
二、探究新知
(一)公理教师讲解:数学中有些命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理.
我们已经知道下列命题是真命题:
两点确定一条直线;
两点之间、线段最短;
过一点有且只有一条直线与已知直线垂直;
过直线外一点有且只有一条直线与这条直线平行;
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
在本书中我们将这些真命题均作为公理.
(二)定理教师引导学生通过举反例来说明下面两题中归纳出的结论是错误的.从而说明证明的重要性.
1、教师讲解:请大家看下面的例子:
当n=1时,(n2-5n+5)2=1;
当n=2时,(n2-5n+5)2=1;
当n=3时,(n2-5n+5)2=1.
我们能不能就此下这样的结论:对于任意的正整数(n2-5n+5)2的值都是1呢?
实际上我们的猜测是错误的,因为当n=5时,(n2-5n+5)2=25.
2、教师再提出一个问题让学生回答:如果a=b,那么a2=b2.由此我们猜想:当a>b时,a2>b2.这个命题是真命题吗?
[答案:不正确,因为3>-5,但3 2<(-5)2]
教师总结:在前面的学习过程中,我们用观察、验证、归纳、类比等方法,发现了很多几何图形的性质.但由前面两题我们又知道,这些方法得到的结论有时不具有一般性.也就是说,由这些方法得到的命题可能是真命题,也可能是假命题.
教师讲解:数学中有些命题可以从公理出发用逻辑推理的方法证明它们是正确的,并且可以进一步作为推断其他命题真假的依据,这样的真命题叫做定理.
(三)例题与证明
例如,有了“三角形的内角和等于180°”这条定理后,我们还可以证明刻画直角三角形的两个锐角之间的数量关系的命题:直角三角形的两个锐角互余.
教师板书证明过程.
教师讲解:此命题可以用来作为判断其他命题真假的依据,因此我们把它也作为定理.
定理的作用不仅在于它揭示了客观事物的本质属性,而且可以作为进一步确认其他命题真假的依据.
三、随堂练习
课本P58练习第1、2题.
四、课时总结
1、在长期实践中总结出来为真命题的命题叫做公理.
2、用逻辑推理的方法证明它们是正确的命题叫做定理
五、布置作业
课本P58 习题13.1 3。
