棱台体体积计算公式及拟柱体的计算
棱柱、p棱锥、棱台、圆柱、圆锥、圆台的计算

棱柱、棱锥、棱台、圆柱、圆锥、圆台的计算一、空间几何体的表面积问题1:有一只蚂蚁从圆柱的下底面圆周上一点A出发,沿着圆柱侧面爬行一周,到达上底面圆周上一点B(线段AB是圆柱的一条母线),问蚂蚁爬行的最短路线是多长?平面展开图:沿着多面体的某些棱将它们展开成平面图形,这个平面图形叫做该几何体的平面展开图。
(一)棱柱、棱锥、棱台的侧面积1、直棱柱:侧棱和底面垂直的棱柱叫做直棱柱。
其侧面展开图是一个矩形。
正棱柱:底面为正多边形的直棱柱叫做正棱柱。
◆S直棱柱侧=ch其中c为棱柱的底面周长,h直棱柱的高。
2、正棱锥定义:如果一个棱锥的底面是正多边形,并且顶点在底面的正投影是底面中心,这样的棱锥叫做正棱锥。
性质:(1)正棱锥的侧棱长相等。
(2)侧棱和底面所成的角相等。
棱锥的侧面展开图是由各个侧面组成的。
◆S=ch´(其中c为棱锥底面周长,h’为侧面等腰三角形底边上的高——斜高)正棱锥侧3、正棱台定义:正棱锥被平行于底面的平面所截,截面与底面之间的部分叫做正棱台。
侧面展开图是由各个侧面组成的。
S正棱台侧=(c +c’)h’(其中c,c’为棱台上下底面的周长,h’为各个等腰梯形的高,即棱台的斜高)。
(二)、圆柱、圆锥、圆台的侧面积把圆柱、圆锥、圆台的侧面沿着它们的一条母线剪开后展在平面上,展开图的面积就是它们的侧面积。
1、圆柱的侧面积◆如果圆柱底面半径是r,周长是c,侧面母线长是l,那么它的侧面积是2、圆锥的侧面积◆如果圆锥底面半径是r,周长是c,侧面母线长是l,那么它的侧面积是3、圆台的侧面积◆如果圆台的上、下面半径是周长分别是侧面母线长是,那么它的侧面积是二、柱锥台的体积公式长方体的体积公式是什么?如:某长方体的长宽高分别是7cm,5cm,4cm,其体积为多少,即为多少个正方体?1、祖暅原理两等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等。
2、柱体的体积公式3、锥体的体积公式4、台体的体积计算公式◆柱体,锥体,台体之间的关系:5、球体的体积公式与表面积公式(1)利用祖暅原理可得(2)利用极限的思想推导出球的表面积公式:S球面=4πR2【典型例题】例1. 有一根长为5 cm,底面半径为1 cm的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为多少厘米?(精确到0.1 cm)解:由题意知:BC=5 cm,AB=8,点A与点C就是铁丝的起止位置,故线段AC的长度即为铁丝的最短长度。
棱台基础体积计算公式

棱台基础体积计算公式棱台这玩意儿,在数学的世界里就像是一个藏着神秘宝藏的小盒子,等着咱们去揭开它的秘密。
而棱台基础体积的计算公式,就是打开这个小盒子的关键钥匙。
先来说说棱台是啥。
想象一下,咱有一个大棱锥,然后像切蛋糕一样,从上面切下一块,剩下的部分就是棱台啦。
比如说,建筑工地上的那些有棱有角的水泥墩子,很多就长得像棱台。
那棱台的体积到底咋算呢?公式是 V = 1/3×h×(S₁ + S₂ +√(S₁×S₂)) 。
这里的 V 就是体积,h 是棱台的高,S₁和 S₂分别是棱台上底和下底的面积。
我记得有一次,我去参观一个正在修建的水塔。
那个水塔的底座就是一个棱台形状的。
工程师们正在热火朝天地计算着各种数据,其中就包括这个棱台底座的体积。
我凑过去看,他们拿着图纸,上面标着各种尺寸,嘴里还念叨着:“这上底面积是多少,下底面积是多少,高又是多少。
”然后就开始按照公式一顿算。
我在旁边看着,心里也跟着默默算起来。
咱们来具体拆解一下这个公式哈。
先看 h ,这个高就是从棱台上底的中心点垂直往下到下底的距离。
可别量错了,不然算出来的体积可就差得十万八千里啦。
再说说 S₁和 S₂,也就是上底和下底的面积。
如果上底和下底都是正方形或者长方形,那面积就很好算,长乘以宽就行。
但要是碰上那种不规则的形状,比如梯形,就得费点心思啦。
咱们举个例子,假如有一个棱台,上底是一个边长为2 米的正方形,下底是一个边长为 4 米的正方形,棱台的高是 3 米。
那先算上底面积S₁ = 2×2 = 4 平方米,下底面积 S₂ = 4×4 = 16 平方米。
然后把这些数字代入公式,V = 1/3×3×(4 + 16 + √(4×16)) ,算出来就是 28 立方米。
在实际生活中,棱台的体积计算可重要啦。
像修建水坝、建造金字塔模型,甚至是做一个独特的花坛,都可能用到这个公式。
高中数学 立体几何的柱,锥,台,球的公式
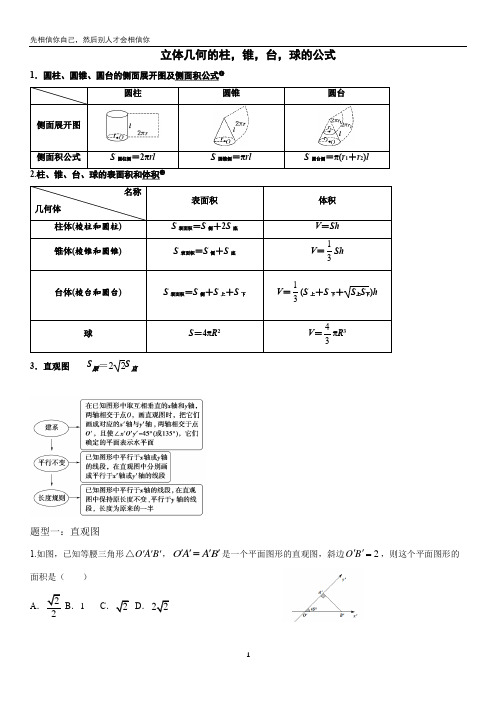
立体几何的柱,锥,台,球的公式1.圆柱、圆锥、圆台的侧面展开图及侧面积公式❶圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=2πrlS 圆锥侧=πrlS 圆台侧=π(r 1+r 2)l2.柱、锥、台、球的表面积和体积❷名称几何体表面积 体积 柱体(棱柱和圆柱) S 表面积=S 侧+2S 底 V =Sh 锥体(棱锥和圆锥)S 表面积=S 侧+S 底V =13Sh 台体(棱台和圆台) S 表面积=S 侧+S 上+S 下 V =13(S 上+S 下+S 上S 下)h 球S =4πR 2V =43πR 3 3.直观图 S 原=22S 直题型一:直观图1.如图,已知等腰三角形O A B '''△,OA AB ''''=是一个平面图形的直观图,斜边2O B ''=,则这个平面图形的面积是( ) A .22B .1C .2D .222.一个梯形的直观图是一个如图所示的等腰梯形,且1A B ''=,3O C ''=,2O A ''=,则原梯形的面积为( )A .22B .42C .8D .43.如图所示为水平放置的正方形ABCO ,在平面直角坐标系xOy 中点B 的坐标为(2,2),用斜二测画法画出它的直观图A ′B ′C ′O ′,则四边形A ′B ′C ′O ′的面积为___________.4.如图所示,是三角形ABC 的直观图,则三角形ABC 的面积S △ABC =_______;(请用数字填写)5.如图,正方形O ′A ′B ′C ′的边长为1,它是一个水平放置的平面图形的直观图,则原图形的周长为( ) A .4 B .6C .8D .222+6.正三角形ABC 的边长为2 cm ,如图,△A’B’C’为其水平放置的直观图,则△A’B’C’的周长为( ) A .8 cmB .6 cmC .(2 +√6)cmD .(2 + 2√3)cm7.用斜二测画法画出水平放置的△ABC 的直观图如图所示,已知A’C’ = 3,B’C’ = 2,则△ABC 中AB 边上的中线长为_________.8.(多空题)在如图所示的直观图中,四边形O ′A ′B ′C ′为菱形且边长为2 cm ,则在平面直角坐标系中原四边形OABC 为________(填具体形状),其面积为________ cm 2.9.已知用斜二测画法得到的某水平放置的平面图形的直观图是如图所示的等腰直角△O B C ''',其中1O B ''=,则原平面图形中最大边长为( ) A .2B .22C .3D .2310.如图,△A ′B ′C ′表示水平放置的△ABC 根据斜二测画法得到的直观图,A B ''在x '轴上,B ′C ′与x '轴垂直,且2B C ''=,则△ABC 的边AB 上的高为( )A .2B .22C .4D .4211.如图所示,△A ′B ′C ′表示水平放置的△ABC 在斜二测画法下的直观图,A ′B ′在x ′轴上,B ′C ′与x ′轴垂直,且B ′C ′=3,则△ABC 的边AB 上的高为( ) A .6√2 B .3√3 C .3√2 D .3题型二棱柱、棱锥、棱台的表面积和体积1.正三棱锥的所有棱长均为a ,则该三棱锥的表面积为( ) A .33a 2B .23a 2C .3a 2D .4a 22.已知正四棱锥的底面边长是2,侧棱长是5,则该正四棱锥的表面积为( ) A .3B .12C .8D .433.已知高为3的棱柱ABC -A 1B 1C 1的底面是边长为1的正三角形,如图,则三棱锥B -AB 1C 的体积为( ) A .41 B .21 C .63 D .43 4.将一个棱长为a 的正方体,切成27个全等的小正方体,则表面积增加了( ) A .26aB .212aC .218aD.224a5.将一个正方体截去四个角后得到一个正四面体,这个正四面体的体积是正方体体积的( )A .21 B .31 C .61 D .41 6.如图所示,在三棱台ABC - A 1B 1C 1中,A 1B 1:AB = 1:2,则三棱锥B - A 1B 1C 1与三棱锥A 1 - ABC 的体积比为( ) A .1:2 B .1:3 C .1:2D .1:47.在底面半径为1的圆锥中,若该圆锥侧面展开图的面积是2π,则该圆锥的体积为( )A .B .C .D .8.已知球A 与球B 的体积之比为8:27,则球A 与球B 的半径之比为( ) A .:B .4:9C .2:3D .3:29.球的一个截面面积为49πcm 2,球心到球截面距离为24cm ,则球的表面积是 . 10.用一个平面截半径为25cm 的球,截面面积是49πcm 2,则球心到截面的距离是 . 11.已知一个长方体的三个面的面积分别是2,3,6,则这个长方体的体积为_________。
棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积

例2、有一堆相同规格的六角螺帽毛坯共重5.8kg.已知底面 六边形的边长是12mm,高是10mm,内孔直径是10mm,那么约有 毛坯多少个?(铁的比重是7.8g/cm3)
O P N
分析:六角螺帽毛坯的体积是一个正六棱柱的体积与一个圆 柱的体积的差.
数学是上帝描述自然的符号
O P
长方体体积公式是计算其他几何体体积的基础. (2)柱、锥、台体积的计算公式及它们之间的联系
数学是上帝描述自然的符号
锥体截面性质
平行于底面的截面与底面相似,且
S1
S截 S底
h 1 2 S 小棱锥侧 ( ) = h S 原棱锥侧
S
当平行于底面的截面过棱锥高 S中截 的中点时,这个截面常被称为 中截面,思考: S底
——这两个棱柱的体积怎么求?
数学是上帝描述自然的符号
长方体的体积
D1 C1
A1 D
A
d
B1
c
C
V长 方 体 = abc 或 V = S底h
S
a
B
b
d= a+ b+ c
2
2
2
2
数学是上帝描述自然的符号
1、柱体的体积
等底等高柱体 的体积相等吗?
数学是上帝描述自然的符号
等底等高柱体的体积相等
h
S
底
h
解:如图,AC为高,BC为底面的边 心距,则AC=146.6,BC=115.2,
底面周长 c=4×230.4.
1 S侧面积 c AB 2
1 2 2 42 3 0 . 4 1 1 5 . 2 1 4 6 . 6 2
2 8 5 9 1 6 .2 (m ).
柱、锥、台体、圆的面积与体积公式

柱、锥、台体、圆的面积与体积公式(一)圆柱、圆锥、圆台的侧面积将侧面沿母线展开在平面上,则其侧面展开图的面积即为侧面面积。
1、圆柱的侧面展开图——矩形圆柱的侧面积2,,,S cl rl r l cπ==圆柱侧其中为底面半径为母线长为底面周长2、圆锥的侧面展开图——扇形圆锥的侧面积1,,,2S cl rl r l cπ==圆锥侧其中为底面半径为母线长为底面周长3、圆台的侧面展开图——扇环圆台的侧面积(二)直棱柱、正棱锥、正棱台的侧面积把侧面沿一条侧棱展开在一个平面上,则侧面展开图的面积就是侧面的面积。
1、柱的侧面展开图——矩形直棱柱的侧面积2、锥的侧面展开图——多个共点三角形正棱锥的侧面积3、正棱台的侧面展开图——多个等腰梯形正棱台的侧面积说明:这个公式实际上是柱体、锥体和台体的侧面积公式的统一形式①即锥体的侧面积公式;②c'=c 时即柱体的侧面积公式;(三)棱柱和圆柱的体积,V Sh h =柱体其中S 为柱体的底面积,为柱体的高斜棱柱的体积=直截面的面积×侧棱长(四)棱锥和圆锥的体积1,3V Sh h =锥体其中S 为锥体的底面积,为锥体的高(五)棱台和圆台的体积说明:这个公式实际上是柱、锥、台体的体积公式的统一形式:①0S =上时即为锥体的体积公式;②S 上=S 下时即为柱体的体积公式。
(六)球的表面积和体积公式(一)简单的组合几何体的表面积和体积——割补法的应用割——把不规则的组合几何体分割为若干个规则的几何体;补——把不规则的几何体通过添补一个或若干个几何体构造出一个规则的新几何体,如正四面体可以补成一个正方体,如图:BCC 1四、考点与典型例题考点一 几何体的侧面展开图例1. 有一根长为5cm ,底面半径为1cm 的圆柱形铁管,用一段铁丝在铁管上缠绕4圈,并使铁丝的两个端点落在圆柱的同一母线的两端A 、D,则铁丝的最短长度为多少厘米?DCBA 解:展开后使其成一线段AC cm =考点二 求几何体的面积例2. 设计一个正四棱锥形的冷水塔顶,高是0.85m ,底面的边长是1.5m ,制造这种塔顶需要多少平方米铁板?(保留两位有效数字)ESO解:)m (40.313.15.1214S 2=⨯⨯⨯=⇒答:略。
1.3.1 柱体、椎体、台体的体积

上底扩大
上底缩小
V = Sh
S′ = S
S为底面面积, 为底面面积, 为底面面积 h为锥体高 为锥体高
S′ = 0 1 1 V = Sh V = (S′ + S′S + S)h 3 3 S为底面面积, 为底面面积, 为底面面积 S分别为上、下底面 分别为上、 分别为上 h为柱体高 为柱体高 面积, 面积,h 为台体高
4 3 5 3 4 5 4 3 5 3 5 4
V = 12π
V = 16π
48 V= π 5
典型例题
有一堆规格相同的铁制( 例3 有一堆规格相同的铁制(铁的密度是 7.8 g / cm 3 )六角螺帽共重 六角螺帽共重5.8kg,已知底面是正六边 , 边长为12mm,内孔直径为 形,边长为 ,内孔直径为10mm,高为 ,高为10mm, , 问这堆螺帽大约有多少个( 问这堆螺帽大约有多少个( π 取3.14)? )? 解:六角螺帽的体积是六棱柱 的体积与圆柱体积之差, 的体积与圆柱体积之差,即: 3 10 2 2 V= ×12 × 6 ×10 − 3.14 × ( ) ×10 4 2 ≈ 2956(mm3 )
1.3.1 柱体、椎体、台体的体积 柱体、椎体、
长方体的体积
V = Sh
圆柱的体积
V = Sh
一般柱体的体积 V柱体 = Sh
圆柱的体积
圆锥的体积
1 V = Sh 3
V = Sh
棱柱的体积
棱锥的体积
1 V = Sh 3 1 = Sh 3
V = Sh
所以锥体的体积为 V锥体
台体的体积 以四棱台为例
x
h
S'ห้องสมุดไป่ตู้
h
棱台计算体积公式

棱台计算体积公式棱台是一个几何体,由一个上底、一个下底和四个三角形侧面组成。
它的特点是上底和下底平行,并且四个三角形侧面都是等腰三角形。
计算棱台的体积是数学中的一个基本问题,下面将介绍棱台计算体积的公式和具体步骤。
棱台的体积可以通过以下公式来计算:体积 = (上底面积 + 下底面积 + 上底与下底面积的平方根乘以上底与下底的边长之差) × 高÷ 3其中,上底面积是指上底的面积,下底面积是指下底的面积,高是指棱台的高度。
这个公式适用于任意形状的棱台,只要知道上底、下底和高就可以计算出体积。
下面通过一个具体的例子来演示如何计算一个棱台的体积。
假设有一个棱台,它的上底面积是5平方厘米,下底面积是10平方厘米,上底与下底的边长之差是3厘米,高是8厘米。
我们可以使用上面的公式来计算它的体积。
计算上底与下底面积的平方根乘以上底与下底的边长之差。
根据给定的数据,上底与下底的边长之差是3厘米,上底与下底面积的平方根乘以上底与下底的边长之差就是√(5+10) × 3 = √15 × 3 = 3√15厘米。
然后,将上底面积、下底面积和上底与下底面积的平方根乘以上底与下底的边长之差相加。
根据给定的数据,上底面积是5平方厘米,下底面积是10平方厘米,上底与下底面积的平方根乘以上底与下底的边长之差是3√15厘米。
将它们相加得到5 + 10 + 3√15 = 15 + 3√15厘米。
将上面的结果乘以高,再除以3。
根据给定的数据,高是8厘米。
将15 + 3√15乘以8,再除以3,得到(15 + 3√15) × 8 ÷ 3 = (120 + 24√15) ÷ 3 ≈ 40 + 8√15厘米。
所以,这个棱台的体积约为40 + 8√15立方厘米。
通过上面的例子,我们可以看到,计算棱台的体积并不复杂,只需要知道上底、下底和高,就可以使用公式来计算。
同时,我们还可以发现,棱台的体积与上底和下底的面积、上底与下底面积的平方根乘以上底与下底的边长之差以及高都有关系,因此在计算时需要将这些因素都考虑进去。
棱台通用体积公式

棱台通用体积公式
棱台的体积公式是指一种几何图形棱台的体积计算公式。
棱台是一个由一个底面和与其平行的多个侧面组成的多面体,其侧面可以是三角形或四边形。
通过使用棱台的体积公式,可以快速准确地计算出棱台的体积。
通用的棱台体积公式为:V = (1/3) * h * (A1 + A2 + sqrt(A1 * A2))
其中,V表示棱台的体积,h表示棱台的高,A1和A2分别表示棱台的两个底面的面积。
这个公式适用于所有的棱台,不论其底面是三角形还是四边形,只需要输入底面面积和高即可计算出体积。
需要注意的是,这个公式中的A1和A2必须是底面的面积,而不是侧面的面积。
如果出现侧面的面积,需要将其替换为底面的面积。
棱台是一个常见的几何图形,在数学和物理中都有广泛的应用。
通过掌握棱台的体积公式,可以更好地理解和应用这个几何图形。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
棱台体体积计算公式:
V=(1/3)H(S上+S下+√[S上×S下])H是高,S上和S下分别是上下底面的面积拟柱体的计算实例:
1.按下图计算基坑的挖方量
解:由拟柱体公式得:
上口面积
上口面积
坑底面积
中间截面积
代入上列基坑挖方量计算公式得:
或用公式
2.某建筑外墙采用毛石基础,其断面尺寸如下图所示,地基为粘土,已知
土的可松性系数,。
试计算每100m长基槽的挖方量;若留下回填土后,余土要求全部运走,计算预留填土量及弃土量。
解:基槽开挖截面积按梯形计算,即:
每100m长基槽的挖方量:
基础所占的体积:
预留填方量(按原土计算):
弃土量(按松散体积计算):
3.上节例题的基础上算出该场地平整的总挖方量和填方量
解:土方量计算(-为挖方,+为填方):
方格(9)与方格(6)全是挖方,其挖方量为:
方格(9)
方格(6)
方格(1)与方格(4)全是填方,其填方量为:
方格(1)
方格(4)
方格(2)、(3)、(5)、(7)、(8)均为部分挖方部分填方,用近似公式计算,其挖填方量分别为:
方格(2)
方格(3)
方格(5)
方格(7)
方格(8)
总挖方量:
总填方量:
两者相比较,填方比挖方多4m3,基本平衡。
4.某建筑场地地形图和方格网(边长a=20.0m)布置如图所示。
土壤为二类
土,场地地面泄水坡度,。
试确定场地设计标高(不考虑土的可松性影响,余土加宽边坡),计算各方格挖、填土方工程量。
解:1) 计算场地设计标高
2) 根据泄水坡度计算各方格角点的设计标高
以场地中心点(几何中心o)为,由式得各角点设计标高为:
其余各角点设计标高均可求出,详见图2.12。
3) 计算各角点的施工高度
得各角点的施工高度(以“+”为填方,“-”为挖方):
各角点施工高度见图2.12。
4) 确定“零线”,即挖、填方的分界线
确定零点的位置,将相邻边线上的零点相连,即为“零线” 。
如1-5线上:
,即零点距角点1的距离为0.67m。
5) 计算各方格土方工程量(以“+”为填方,“-”为挖方)
①全填或全挖方格:
(+)
(+)
(+)
(-)
②三填一挖或三挖一填方格,由式(2.13):
(+)
(-)
(-)
(+)
(+)
(-)
将计算出的各方格土方工程量按挖、填方分别相加,得场地土方工程量总计:
挖方:503.92m3
填方:504.26m3
挖方、填方基本平衡。
扇形面积公式同弧长公式系?
2006年11月03日星期五 20:28扇=(lR)/2 (l为扇形弧长)
S扇=(n/360)πR^2 (n为圆心角的度数)
S扇=(lR)/2 (l为扇形弧长)
弧长等于弧所对的圆心角乘以乘以半径长再除以180
就是l=nπr/180°
巧记公式
○王文镕
L=、S扇形=这两个公式是圆中计算弧长和扇形面积的基本公式,从形式上看,它们有相同的地方,也有不同点,如果只靠死记硬背,时间一长,很容易遗忘或者混淆。
如果我们掌握知识的来源,搞清推导过程,这两个公式就能牢牢、准确地记住了。
首先来看弧长的计算公式L=的推导过程:
因为360°的圆心角所对的弧长就是圆周长C=2πR(R为圆的半径)
所以1°的圆心角所对的弧长是2πR,即。
这样n°的圆心角所对的弧长的计算公式是L=2πR=。
再来看扇形面积的计算公式S扇形=的推导过程:
因为圆心角为360°的扇形面积就是圆面积S=πR2,
所以圆心角为1°的扇形面积是πR2,
这样圆心角为n°的扇形面积的计算公式是S扇形=πR2。
搞清楚推导过程,下面我们不妨再把这两个公式放到一起,加以比较,找一找它们的相同点及不同点。
L=2πR, S扇形=πR2
我们可以看到,这两个公式都分别是由两部分组成的,前一部分,由推导过程可知:n°的圆心角所
对的弧长是圆周长的倍,圆心角为n°的扇形面积是圆面积的倍,所以这两个公式的前一部分是相同的,都是;而后一部分也有它们的规律:因为n°的圆心角所对的弧长是圆周长的一部分,所以弧长的计算公式的后一部分为圆周长的计算公式:2πR,而圆心角为n°的扇形面积是圆面积的一部分,所以扇形面积计算公式的后一部分是圆面积的计算公式πR2。
这样,这两个公式在掌握了它们的推导过程后,又通过对比,找出它们的异同点,记忆起来就不会感到困难了。
(王文镕《中国中学生报》)。
