0-1规划的隐枚举法
例析0-1整数规划及隐枚举法的应用

例析0-1整数规划及隐枚举法的应用自主招生近年来成为各大高校又一招纳人才的举措,面试在自主招生中扮演着越来越重要的角色,考生面试的成绩不容忽视。
因此如何确定面试专家的分配方案,使录取工作真正公平合理的进行,是各大高校积极考虑的问题。
本文通过采用0-1整数规划及隐枚举法建立相关模型,较好地解决了这一问题。
1 预备知识简介1.1 线性规划[1]在人们的生产实践中,经常会遇到如何利用现有资源来安排生产,以取得最大经济效益的问题。
此类问题构成了运筹学的一个重要分支——数学规划,而线性规划则是数学规划的一个重要分支。
若在线性规划模型中,变量限制为整数,则为整数线性规划。
0-1整数规划是整数规划中的特殊情形,它的变量仅取0或1。
合理地引用0-1规划能够容易且高效率地求解相关问题。
1.2 隐枚举法[2]隐枚举法是Balas E在1965年提出的,是求解0-1规划问题的一种有效方法。
它只检查一部分变量组合,在这过程中根据已有信息自动舍弃许多不可能成为最优解的组合,求得最优解,从而大大减少了工作量。
隐枚举法只需比较目标函数在小部分组合点上的取值大小,就能求得最优解和最优值。
2 问题描述与建模2.1 问题描述某高校采用通过专家面试的方式进行自主招生,经过初选合格进入面试的考生有N人,拟聘请老师M人进行面试。
每位学生要分别接收“面试组”每位老师的单独面试,每个面试组由4名老师组成。
已知要求面试不同考生的“面试组”成员不能完全相同。
试求在考生数N已知的条件下,聘请老师数M至少应为多大,才能做到任两位学生的“面试组”都没有两位面试老师相同。
2.2 数学建模该问题是一个单目标规划问题,解决的是满足一定约束条件要求,计算在给出一定的学生人数下,所需要教师的最少人数。
根据实际情况分析,一般面试学生的个数要远大于教师的个数。
因为教师人数较少,容易进行分组(即按照约束条件将教师每4人分成一组),满足约束条件的情况下,所能组合的最大组数目即可面试学生的最大人数[3~4]。
01规划问题深入剖析

x4 3
x4=y04+2y14
代入原问题,得到:
Max Z= 3 y01+6y11+12y21 + 4y02+8y12+16y22 + 5 y03+10y13 + 6 y04+12y14
改进过滤性条件Z 5
循 (X2,X1,X3) 环 3 (0,1,0) 4 (0,1,1)
(0’)
s.t. s.t. s.t s.t s.t 满 Z 0’ 1 .2 .3 .4 足 值 3 no 8 0 2 1 1 ye 8 s
改进过滤性条件Z 8 (0’’)
循 (X2,X1,X3) 环 5 (1,0,0) 6 (1,0,1) 7 (1,1,0) 8 (1,1,1) s.t. s.t. s.t s.t s.t 满 Z 0’’ 1 .2 .3 .4 足 值 -2 no 3 no 1 no 6 no
5
指派问题(分配问题) (Assignment Problem)
例5-11 有一份中文说明书,需 翻译成英、日、德、俄四种文字, 分别记作E、J、G、R,现有甲、 乙、丙、丁四人,他们将中文说 明书翻译成英、日、德、俄四种 文字所需时间如下,问应该如何 分配工作,使所需总时间最少?
任务 人员 甲 乙 丙
4 0-1规划的解法
0-1 规划在线性整数规划中具有重要地位。
定理:任何整数规划都可以化成0-1规划。
一般地说,可把整数x变成(k+1)个0-1变量公 式为:x=y0+2y1+22y2+….2kyk 若x上界为U,则对0<x<U,要求k满足2k+1 U+1.
解 0—1 规划的隐枚举法

(5)解 0—1 规划的隐枚举法解 0—1 规划的隐枚举法有其独特的工作程序,具体过程如下。
a.模型转化为求极小的问题b.变量替换。
极小问题模型的目标函数中所有变量系数为负的0—1变量,可利用变量替换x k=1-x'k (x'k是引入的新的0—1变量),将目标函数中所有变量系数化为正数。
c.目标函数中变量按系数大小排列,约束条件中变量排列顺序也相应调整。
d.按目标函数值由小到大的顺序依次排列可能的解,并予以可行性检验。
e.发现求极小问题的最优解并停止。
f.转化为原问题的最优解。
例4 用隐枚举法求解下列0—1规划问题Max Z=3x1+2x2-5x3-2x4+3x5x+x2+x3+2x4 +x5≤417x1 +3x3-4x4+3x5≤811x1-6x2 +3x4 +5x5≥3x=0, 1, j=1, 2, 3, 4, 5.j解:①转化为求极小的问题Min Z=-3x1-2x2+5x3+2x4-3x5-x1 -x2-x3-2x4 -x5≥-4-7x1 -3x3+4x4-3x5≥-811x1 -6x2 +3x4 +5x5≥3x=0, 1, j=1, 2, 3, 4, 5.j②令x'1=1-x1, x'2=1-x2, x'5=1-x5, 带入极小问题模型中,得Min Z=3 x'1+2 x'2+5x3+2x4+3 x'5-8x'+x'2-x3-2x4 +x'5≥-117x'1 -3x3+4x4+3x'5≥2-11x'1 +6x'2 +3x4-5x'5≥-7x=0, 1, j= 3, 4; x'j =0, 1, j= 1, 2, 5.j③目标函数中变量按系数大小排列,约束条件中变量排列顺序也相应调整,得Min Z=5x3+3 x'1+3 x'5+2 x'2+2x4-8-x3+x'1 +x'5+x'2-2x4 ≥-1 ①-3x3+ 7x'1 +3x'5 +4x4≥2②-11x'1 -5x'5+6x'2 +3x4≥-7 ③x=0, 1, j= 3, 4; x'j =0, 1, j= 1, 2, 5.j④按目标函数值由小到大的顺序排列可能的解,并予以可行性检验。
0-1规划介绍
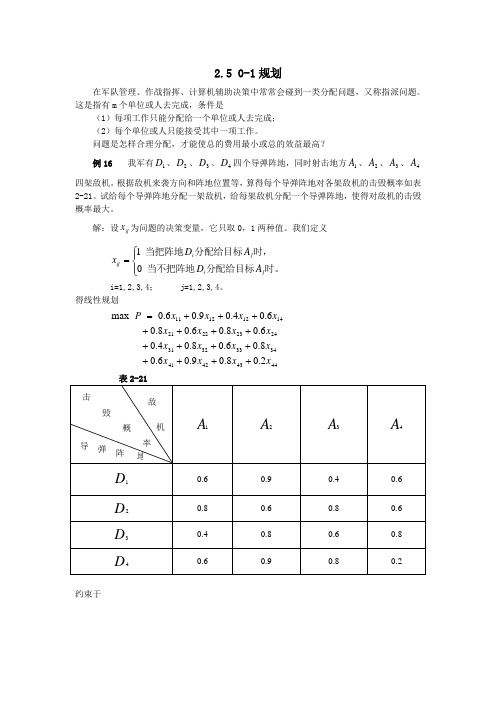
2.5 0-1规划在军队管理、作战指挥、计算机辅助决策中常常会碰到一类分配问题,又称指派问题。
这是指有m 个单位或人去完成,条件是(1)每项工作只能分配给一个单位或人去完成; (2)每个单位或人只能接受其中一项工作。
问题是怎样合理分配,才能使总的费用最小或总的效益最高?例16我军有1D 、2D 、3D 、4D 四个导弹阵地,同时射击地方1A 、2A 、3A 、4A 四架敌机。
根据敌机来袭方向和阵地位置等,算得每个导弹阵地对各架敌机的击毁概率如表2-21。
试给每个导弹阵地分配一架敌机,给每架敌机分配一个导弹阵地,使得对敌机的击毁概率最大。
解:设ij x 为问题的决策变量,它只取0,1两种值。
我们定义⎪⎩⎪⎨⎧=时。
分配给目标当不把阵地时,分配给目标当把阵地j i j i ij A D A D x 01i=1,2,3,4;j=1,2,3,4。
得线性规划444342413433323124232221141212112.08.09.06.08.06.08.04.06.08.06.08.06.04.09.06.0max x x x x x x x x x x x x x x x x P +++++++++++++++=表2-21 A 1A 2A 3A 4D 10.6 0.9 0.4 0.6 D 20.8 0.6 0.8 0.6 D 30.4 0.8 0.6 0.8 D 40.60.90.80.2约束于敌机 击毁概率 导 弹阵地⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧====+++=+++=++=+++=+++=+++=+++=+++4,3,2,1,4,3,2,1,,1,0111111114434241443332313423222124131211144434241343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ij + 由于这个规划的决策变量只能取0,1两个值,故这种规划我们也称之为0-1规划。
0-1规划1

0-1型整数线性规划0-1型整数线性规划是一类变量仅取0或1的特殊的整数规划;一般描述如下⎩⎨⎧===10),,1(..min 或取n i A t s f i x bx cx 其中),,(,)(,),,(),,,(111'=='==⨯m n m ij n n b b a A x x c c b x c 。
此时的决策变量称为0-1变量或二进制变量。
在实际问题中,如果引进0-1变量,就可以把各种需要分别讨论的线性(或非线性)规划问题统一在一个问题中讨论。
13.6.2 求解0-1线性规划的隐牧举法分枝定界法就是一种解整数规划的隐牧举法,0-1规划可以通过增加限定10≤≤i x 的整数规划来求解。
对于n 个变量的0-1规划,如果使用穷举法,则需要检查2n 个取值组合,这显然不是聪明的办法。
这里所说的隐牧举法,是根据0-1规划的特点,设计的一些方法,只检查变量组合的一部分,而不是全部。
值得说明的是,对于有些问题(例如一部分变量是0-1变量的混合线性规划)隐牧举法有时是不适用的,还得使用穷举法。
隐牧举法原理与算法步骤:(ⅰ)记∞=f f 0,将n 个决策变量构成的x 的2n 个取值组合按二进制(或某种顺序)排列;(ⅱ)按上述顺序对x 的取值首先检验0f f cx ≤=是否成立,若不成立则放弃该取值的x ,按次序换(ⅰ)中下一x 的取值重复上述过程;若成立,则转下一步;(ⅲ)对x 逐一检验b x A ≤中的m 个条件是否满足,一旦某一条件不满足便停止检验后面的条件,而放弃这一x 的取值,按次序换(ⅰ)中下一x 的取值执行(ⅱ),若m 个条件全满足,则转下一步;(ⅳ)记),,min(00f f f = 按次序换(ⅰ)中下一x 的取值,执行(ⅱ); (ⅴ)最后一组满足b x cx A f f ≤≤=和0的x 即为最优解。
求解0-1型整数线性规划的MATLAB 程序Ⅰ、转换十进制数为二进制数的程序如下是枚举和隐枚举程序中要调用的把十进制数转换为二进制数的程序。
0-1规划中并行隐枚举法的实现方式

I PLEM ENTI M NG APPRoACH FoR PARALLEL I PLI T M CI ENUM ERATI oN N 1 PROGRAM M D I 0. G
Z n n e g Ya
( eat etfC m ue Si c n e nl y C nrl hn o lU i rt,W h n私 0 7 , ue, hn ) Dp r n o p t c nea dTc o g , et i N r nv sy u a m o r e h o a C a ma ei D 9 H biC ia
An d,t ee i s mei r v me t d n t ei l i e u r t n O t ep o lm ih i h r e a c mp t g c n b 6v d b a all h r s o mp o e n ma eo h mp i t n me ai ,S r b e wh c s a d t s r l o u i a e s 1e y p r l c o h o i n e
mea in meh d i h e t y t o v t r t t o st e b s s l ei o wa o .Ac o dn ec aa trs co aa ll o u i g tc l s le bg a d c mp e r be a t c r ig t t h r c eit f r l mp t ,i al ov i n o l xp o lmsf s. oh i p ec n A t o o ii g t ep allc mp t g wi h mp i i e u r t n i p e e t d i i p p rt e o v h r b e me t n d a o e me d c mb n n h a l o u i t t e i l t n me ai s r s n e t s a e r s le t e p o l m n i e b v . h r e n h c o n h o o
关于求解0_1型整数规划的若干问题

0 前言化问题,可知最优解的目标函数一定不小于 5。
为此,在求最优解之前先增加一个约束条件,即过滤0- 1 型整数规划是整数规划的特例,其数学模型的目 条件:3x - 2x +5x !5##⊙ 标函数、约束条件与线性规划相同,不同的是其变量只能1 2 3 过滤条件的作用是:在检验一个解是否为可行解之取 0 和 1,分别表示两种截然相反的结果。
0- 1 型整数规前,先看目标函数是否不小于 5,若小于 5,则肯定不是最 划应用很广,如土木工程系统的最优工程配置问题,城建优解,其可行性无须再检验而直接被淘汰,可以大大减少规划中的居民点、给水点、加油站和商业网点的最优布局计算工作量。
问题,均可应用 0- 1 型整数规划求得最优解。
有了过滤条件,就可以列表计算。
对解集中的解逐个检0- 1 型整数规划的数学模型如下:验,先检验过滤条件,若不符合则直接淘汰该解;若符合条 目标函数:件⊙,再按①~④顺序检验每一个约束条件,当某一个约 束条件不满足时即行淘汰,其右边的约束条件再无检验 约束条件:的必要。
这样,计算工作量可大为减少。
本例中有 3 个变量,共有 23=8 个解需要检验,通过计 算求得的最优解为: .本例以 为初始可行解,通过建立过滤条1 求解 0- 1 型整数规划三种通用的方法 件,只计算了 18 次就找到了最优解,而用穷举法需要计算1.1 穷举法40 次,技术工作量大大减少了。
如在求解过程发现更好的 由于 0- 1 型整数规划的变量个数有限且取值非 0 即可行解及时更换过滤条件 ,计算工作量还可进一步减少。
1,所以不难将解的集合找出来,再检验每个解的可行性, 1.2.2 对隐枚法法 I 的评价 凡符合全部约束条件者均为可行解,通过比较目标函数 对隐枚举法 I 来说其数学模型无须转化为标准型,减的值便可找到最优解,这个解法称为穷举法。
当变量和约 少了人工处理的工作量,但它需要检验的方案较多,而且 束条件很多时,其工作量是非常大的。
运筹学 第三章 0-1规划

例2 求解0-1规划
编号
max z 3 x1 2 x2 5 x3
s.t. x1 2 x2 x3 2
①
x1 4 x2 x3 2 x1 2 x2 3
② ③
4x2 x3 6
④
xi 0 or 1, i 1,2,3
算法过程:1. 先找出一个可行解,比如(1,0,0).相应
cnn
称为指派问题 的效益矩阵。
?
定理:将指派问题的效益矩阵的行(列)分别减去该行(列) 的最小元素,得到的新指派问题和原问题的最优解相同. 意义:根据定理,对指派问题可以化简,使 最优值呢? 得其效益矩阵中每一行至少有一个0元素.
这种简化对于求解有何帮助?
任务 A
B
C
D
人员
甲
2
15
13
4
乙
10
在海淀区,由A6,A7中至少选一个. 假设选用Ai点,设备投资估计为bi元,每年获利估计ci元, 但是总投资额不超过B元。问应该选择哪几个点可以使年 利润最大?
➢分析问题
如图,如何确定选择哪些点?有多少种可能?
试一试
枚举 法
A7
A6
海淀区
共有多少情形?
A5 A4
西城区 专门的解法研究 ——隐枚举法.
安排n个人完成n项工作,使总效率最高的问题称为指 派问题或者分派问题(Assignment problem).
例 甲、乙、丙、丁四人去完成A、B、C、D四项工作. 要求每个人只能完成一项工作,每个工作只能一人完成,
他们所需费用如下表,应如何安排工作,使所需总费用最
少?
任务 A
B
C
D
人员
甲
2
10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013-2014(2)专业课程实践论文题目:0-1规划的隐枚举法
一、算法理论 0—1规划在整数规划中占有重要地位,一方面因为许多实际问题,例如指派问题、选地问题、送货问题都可归结为此类规划,另一方面任何有界变量的整数规划都与0—1规划等价,用0—1规划方法还可以把多种非线性规划问题表示成整数规划问题,所以不少人致力于这个方向的研究。
求解0—1规划的常用方法是分枝定界法,对各种特殊问题还有一些特殊方法。
线性模型中,当变量的取值只能是“0”或“1”时,称之为“0-1规划问题”。
有种极其简单的解法,就是将变量取值为0或1的所有组合列出,然后分别代入目标函数,选出其中能使目标函数最优化的组合,即为最优解。
但是真的这样会做很多无用功,浪费大量资源,所以,需要改进方法。
本文主要介绍隐枚举法的应用原理,意在剖析其“隐”在何处。
从而帮助读者更好地应用这种方法。
和线性规划问题一样,首先需要将模型标准化。
标准化对0-1规划问题提出四点要求:
1.目标函数为最小优化
2.目标函数中变量的系数都为正
3.在目标函数中,变量按系数值从小到大排列,则约束函数中,变量的排列次序也做相应改变。
4.所有变量均为0或1
0-1线性规划的基本形式是
1
min n
j j
j Z c x ==∑
011,2,,..1,2,,j ij j j x j m s t a x b i n ==⋅⋅⋅⎧⎪⎨≤=⋅⋅⋅⎪⎩∑或
function [intx,intf] = ZeroOneprog(c,A,b,x0)
%目标函数系数向量,c
%不等式约束矩阵,A
%不等式约束右端向量,b
%初始整数可行解,x0
%目标函数取最小值时的自变量值,intx
%目标函数的最小值,intf
sz = size(A);
if sz(2) < 3
[intx,intf] = Allprog(c,A,b); %穷举法
else
[intx,intf] = Implicitprog(c,A,b,x0); %隐枚举法end
function [intx,intf] = Allprog(c,A,b)
sz_A = size(A);
rw = sz_A(1);
col = sz_A(2);
minf = inf;
for i=0:(2^(col)-1) %枚举空间
x1 = myDec2Bin(i,col); %十进制转化为二进制if A*x1 >= b %是否满足约束条件
f_tmp = c*x1;
if f_tmp < minf
minf = f_tmp;
intx = x1;
intf = minf;
else
continue;
end
else
continue;
end
end
function [intx,intf] = Implicitprog(c,A,b,x0)%隐枚举法
sz_A = size(A);
rw = sz_A(1);
col = sz_A(2);
minf = c*x0;
A = [A;-c];
b = [b;-minf]; %增加了一个限制分量
for i=0:(2^(col)-1)
x1 = myDec2Bin(i,col);
if A*x1 >= b
f_tmp = c*x1;
if f_tmp < minf
minf = f_tmp;
b(rw+1,1) = -minf; %隐枚举法与穷举法的区别在于此句 intx = x1;
intf = minf;
else
continue;
end
else
continue;
end
end
function y = myDec2Bin(x,n) %十进制转化为二进制
str = dec2bin(x,n);
for j=1:n
y(j) = str2num(str(j));
end
y = transpose(y);
四、算法实现
例1.求解下面0-1规划
()⎪⎩⎪⎨⎧=≥++++≥++++++++=105224287453232min 5
4321543215432154321或,x ,x ,x ,x x x x x x x x x x x x ,s.t.x x x x x x f
解:在MATLAB 命令框在输入下列命令:
>> c=[1 2 3 1 1];
>> A=[2 3 5 4 7;1 1 4 2 2];
>> b=[8;5];
>> x0=[1;1;1;1;1];
>> [intx,intf]=ZeroOneprog(c,A,b,x0) 所得结果如下:
123
1231231213
123max 3252244..346,,01
z x x x x x x x x x s t x x x x x x x =-++-≤⎧⎪++≤⎪⎪+≤⎨⎪+≤⎪⎪⎩为或 解:在MATLAB 命令框在输入下列命令: >> c=[-3,2,-5];
>> A=[-1,-2,1;-1,-4,-1;-1,-1,0;-4,0,-1]; >> b=[-2;-4;-3;-6];
>> x0=[1;0;0];
>> [intx,intf]=ZeroOneprog(c,A,b,x0)
1234
12341234124min 3721648..535
01,1,2,3,4j z x x x x x x x x x x x x s t x x x x j =+-+-+-≥⎧⎪-++≥⎪⎨++≥⎪⎪==⎩
或 解:在MATLAB 命令框在输入下列命令: >> c=[3,7,-1,1];
A=[2,-1,1,-1;1,-1,6,4;5,3,0,1]; b=[1;8;5];
>> x0=[1;1;1;1];
>> [intx,intf]=ZeroOneprog(c,A,b,x0)
123
123123123max 62323352..24
01,1,2,3j z x x x x x x x x x s t x x x x j =++++≤⎧⎪-+≥⎪⎨++≤⎪⎪==⎩
或
解:在MATLAB 命令框在输入下列命令: >> c=[-6,-2,-3];
A=[-1,-2,-1;3,-5,1;-2,-1,-1];
b=[-3;2;-4];
x0=[1;0;0];
[intx,intf]=ZeroOneprog(c,A,b,x0)。
