勒让德多项式资料
勒让德多项式

边( z − z0 )的各次幂的系数均为零 ]来确定。
一、勒让德方程的级数解
2
− 2x l (l + 1) p(x ) = , q(x ) = , 2 2 − 1− x 1 x ∞
令
∞ ∞
(1 − x )y′′ − 2 xy′ + l (l + 1)y = 0
y = ∑ ck x
k =0 k
§14.1 勒让德多项式
(11)
( ( − 1) (4 − 0 )! − 1) (4 − 2)! 2 P2 (x ) = 2 x + 2 x0 2 0!(2 − 0 )!(2 − 0 )! 2 1!(2 − 1)!(2 − 2)!
1 2 = (3x − 1) 2
→ 无穷级数
三、本征值问题
§14.1 勒让德多项式
总之,本征值问题 1 − x 2 y ′′ − 2 xy ′ + l (l + 1) y = 0, l (l + 1) − 常数 (8) y x = ±1 → 有限,
(
)
本征值 : l (l + 1), l = 0,1,2,...
本征函数:
n
y0 ( x ) = c0 + c2 x + ... + cl x , l = 2n
( 2l )! cl = l 2 2 (l !)
记上述l次多项式y0 ( x )或y1 (x )为Pl ( x ),
称之为l阶Legendre多项式。
四、勒让德多项式
l 2
§14.1 勒让德多项式
l -勒让德多项式 , l = 2n l 2 其中 = 2 l − 1 , l = 2n + 1 2 1 − x 2 y ′′ − 2 xy ′ + l (l + 1) y = 0, l (l + 1) − 常数 (8 ) 于是: y x = ±1 → 有限 ,
数学物理方程课件第六章勒让德多项式

2 (2n)!
2n n!
2n n! 2n n!2n 1 2n 153
2 (2n)!
2n 1!
2 2n 1
数学物理方程与特殊函数
第6章勒让德多项式
性质2 递推公式
(n 1)Pn1 (x) (2n 1)xPn (x) nPn1 (x) 0
Pn1 (x) Pn1 (x) 2n 1Pn (x)
n0
Cn
2n 1 2
1 1
x Pn (x)dx
C0
1 2
1
1 x P0 (x)dx
1 2
1
x dx
1
1 2
C2n1 0
C2n
4n 1 2
1 1
x
P2n
(x)dx
4n
1
1 0
xP2n
( x)dx
4n 1
22n 2n!
1 d2n 0 x dx2n
(x2 1)2n dx
4n 1 22n 2n !
数学物理方程与特殊函数
第6章勒让德多项式
三 勒让德多项式
y APn (x) BQn (x)
Pn
(x)
M
(1)m
m0
2n 2m!
2n m!(n m)!(n
2m)!
xn2m
Pn
1 2n n!
dn dx n
(x2
1)n
当n为偶数时M
n 2
当n为奇数时 M
n 1 2
P0 (x) 1
P1(x) x
2)(n 1)(n 4!
3)
x4
]
c 1 c0
y2
a1[ x
(n
1)(n 3!
2)
勒让德(legendre)多项式及其性质

勒让德(legendre)多项式及其性质一.勒让德多项式勒让德多项式是由勒让德方程的通解推导出来的,所以我们首先引入勒让德方程,以及勒让德方程的幂级数解,勒让德方程的表达式如下:其中为非负实数(1.1)它的幂级数解如下:(1.2)其中:(1.3)(1.4)由达朗贝尔判别法可知,当不为整数时,这两个级数的收敛半径为1,在(1.3)式和(1.4)式中,与可以任意取值,它们起着任意常数的作用,显然,在区间(-1,1)内和都是方程(1.1)的解,所以(1.2)是(1.1)的通解。
上面(1.3)和(1.4)幂级数当时级数收敛,此外级数是发散的。
并且,我们发现,当取非负整数时,和中有一个便退化为次多项式,它就是方程(1.1)在闭区间[-1,1]上的有界解。
此时,适当的选定这个多项式的最高次幂系数,所得的多项式称为阶勒让德多项式或第一类勒让德函数,记作,下面我们来推导勒让德多项式的表达式。
1 当为正偶数时退化为次多项式。
为求得的表达式,在中我们通过来表示其它各项的系数。
为此,将系数递推关系式改写成下列形式:(1.5)在(1.5)式中取,得:(1.6)习惯上取为(1.7)于是有:(1.8)在(1.5)式中取,并利用之值得:(1.9)一般地,我们有()(1.10)我们将这些系数带入(1.3)中,并把此时的记作,可得:(1.11)这就是当为正偶数时勒让德多项式。
2 当为正奇数时退化为次多项式,我们把记作,同理可得:(1.12)把(1.11)和(1.12)写成统一的形式,得(1.13)其中表示的整数部分由上述讨论可知,当为非负整数时,和中有一个是阶勒让德多项式,而另一个是无穷级数,记作,称为第二类勒让德函数,此时方程(1.1)通解为:(1.14)特别当时,由(1.11)和(1.12)式得:它们的图形如下:二.勒让德多项式的性质首先介绍一下勒让德多项式的母函数:试将函数(1.15)展开成的幂级数(1.16)可以证明级数展开式中的系数恰好是勒让德多项式,最终得到(1.17)因此称为勒让德多项式的母函数。
legendre正交多项式的定义

legendre正交多项式的定义
勒让德正交多项式(Legendre Orthogonal Polynomials)是一类有限多项式,可用于详细描述不同空间机械变换过程中函数的变化情况。
它们是18th 世纪法国数学家兼物理学家Adrien-Marie Legendre所提出的一组多项式,他把它们命名为“set of world polynomials”。
它们和其他多项式,例如伯努利多项式有很多共性:如果我们把函数拆分成若干个断开的t点,他们都可以用简洁易懂的表达式来描述它们之间的变化。
Legendre正交多项式的定义是:它们是按照一定程序构成的一组正交多项式,用来表示一组函数值,使其具有正交性质。
它们都能满足下列条件:
1、有限值:在给定的连续函数序列中,勒让德正交多项式具有使其有限值的性质;
2、正交性:每一个多项式与任意一个多项式都可以构成正交(Orthogonal)关系,即互不相关;
3、定义域:它们的定义域是一个有限范围内的数值;
4、等号绝对值:它们在[-1,+1] 上具有相同的等号绝对值;
5、有限偏导:它们有限次地可以偏导;
6、可微性:它们是可微的;
8、变换性:他们具有变换性,可以通过使用标准变换来改变它们的大小;
总之,勒让德正交多项式是一组特定的,同时具有上述特性的有限多项式,可以通过它们来详细描述函数的变化情况及它们在空间机械变换历程中的变化趋势。
勒让德多项式
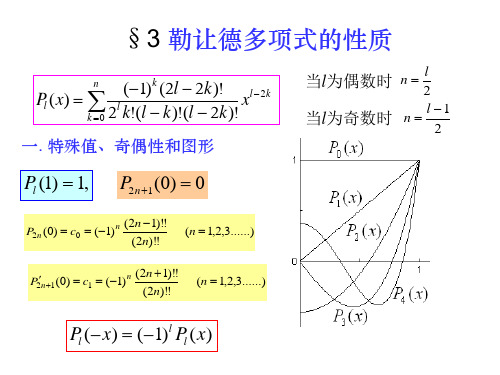
(1) k (2l 2k )! l 2 k Pl ( x) l x k 0 2 k!(l k )!(l 2k )!
n
一. 特殊值、奇偶性和图形
l 2 l 1 n 当l为奇数时 2
当l为偶数时 n
Pl (1) 1,
P2 n (0) c0 (1) n
六. 勒让德多项式的正交性、完备性与模
0, lk 2 1 Pl ( x)Pk ( x)dx Nl2 , l k 2l 1
1
勒让德多项式完备性 若f(x)是定义在[-1,1]区间上任意一个平方可积的函数,
那么
f ( x) cl Pl ( x)
l 0
(l 1) P l 1 ( x) lP l 1 ( x) (2l 1) xP l ( x)
2. P l ( x) P l 1 ( x) 2 xP l ( x) P l 1 ( x)
3. 4.
P l 1 ( x) xP l ( x) (l 1) P( x) Pl 1 ( x) P l 1 ( x) 2l 1P l ( x)
1 1 2rx r xr
2
r Pl ( x)
l l 0 2
(l 1) P l 1 ( x) lP l 1 ( x) (2l 1) xP l ( x)
1 2rx r 2
(1 2rx r ) lr l 1Pl ( x)
l 0
( x r ) r l Pl ( x) (1 2rx r 2 ) lr l 1Pl ( x)
证
2 l
1 dl 2 l Pl ( x) l ( x 1 ) 2 l! dx l
勒让德多项式

从而得到
1
ห้องสมุดไป่ตู้
Θ
sin θ
d dΘ (sin θ ) + n( n + 1) sin 2 θ = m 2 dθ dθ
( 6. 4 )
( 6. 5 )
1 d 2Φ + m2 = 0 2 Φ dϕ
(2 勒让德多项式的一些性 质; )
有关的定解问题。 (3 会用勒让德多项式求解 有关的定解问题。 )
§6.1
勒让德方程的引出
u xx + u yy + uzz = 0
在第四章中, 域内的迪利克雷问题: 在第四章中,我们用格 林函数法解决了球形区 域内的迪利克雷问题:
{
球函数
z
θ
●
拉普拉斯方程 第一类边界条件
数学物理方法
第六章 勒让德多项式 ( Legendre polynomials )
勒让德( 勒让德(1752~1833) ~ ) Legendre . Adrien-Marie 阿德利昂·玛利 埃 勒让德 公元1752─公元1833 为法国数学家, 勒让德( 1752─公元1833) 阿德利昂 玛利·埃·勒让德(公元1752─公元1833)为法国数学家,生于 玛利 巴黎,卒于巴黎。 1770年毕业于马扎兰学院 1775年任巴黎军事学院数学 年毕业于马扎兰学院。 巴黎,卒于巴黎。约1770年毕业于马扎兰学院。1775年任巴黎军事学院数学 教授。1782年以 关於阻尼介质中的弹道研究》获柏林科学院奖金, 年以《 教授。1782年以《关於阻尼介质中的弹道研究》获柏林科学院奖金,次年当 选为巴黎科学院院士。1787年成为伦敦皇家学会会员 年成为伦敦皇家学会会员。 选为巴黎科学院院士。1787年成为伦敦皇家学会会员。 曾与拉格朗日( )、拉普拉斯 拉普拉斯( 勒让德 (Legendre) 曾与拉格朗日(Lagrange)、拉普拉斯(Laplace) 并列为法国数学界的“ 世纪末19世纪初法国数学的复兴, 并列为法国数学界的“三 L ”,为18世纪末19世纪初法国数学的复兴,做出了 , 18世纪末19世纪初法国数学的复兴 卓越的贡献。 卓越的贡献。
n阶勒让德多项式
n阶勒让德多项式
n阶勒让德多项式,即费马以及17世纪数学家阶勒让德发明的多项式,是一类可以累加次方系数形成多项式的代数结构,其格式通常为: p(x) = anxn + an-1xn-1 + an-2xn-2 +…+ a1x + a0,其中n为次方,an为系数。
它是多元多项式中最为简单和最引人注目的
代数结构之一,可以用来求解多项式等级,数学研究和科学模型。
费马在16. 和 17. 世纪,把多项式用来描述它发现的定理,但是他的定理中只有阶勒让
德多项式作为一种类型的多元多项式。
以后,哥白尼,除了把它用作几何定理的数学工具,也尝试用来求解力学模型,机械和重力计算等。
最后,阶勒让德多项式发展成为具有一系
列应用的重要数学结构,帮助我们解决一系列数学和科学的问题。
阶勒让德多项式可以用来解决非常复杂的问题。
它的精确性可以解决复杂的微分方程,并
用来模拟科学问题,如建模,反应,预测和决策。
有诸多的科学应用,如气体和液体的物理,数值计算,天气预报,航空飞行路径规划,传送原理等。
阶勒让德多项式在数学中也
有重要作用。
它可以用来解决数学中多元多项式的问题,包括拟合数据点,最小二乘法,
求导数和斐波那契数列等。
此外,阶勒让德多项式还可以用于绘图,带来更多精彩可视化效果,其动态图式可使数学
变得更容易理解。
因此,阶勒让德多项式在数学及其相关领域中应用大大改善,提升了可
视化和数学解决问题的效率。
通过阶勒让德多项式的应用,我们已经实现了解决许多复杂问题的能力,同时也为科学发
展做出了贡献,我们可以期望它会继续发展,带来更多的突破和发现。
勒让德多项式是区间什么的正交函数
勒让德多项式是一类具有重要性质的正交函数,它们在数学和工程领域中有着广泛的应用。
本文将介绍勒让德多项式的定义、性质、正交关系以及其在实际问题中的应用。
一、勒让德多项式的定义勒让德多项式是勒让德微分方程的解,该微分方程形式如下:\[ (1-x^2)y''-2xy'+n(n+1)y=0 \]其中n为非负整数。
根据其定义,勒让德多项式可以通过勒让德微分方程的解出来。
勒让德多项式的具体形式可以表示为:\[ P_n(x)= \frac{1}{2^n n!} \frac{d^n}{dx^n}(x^2-1)^n \]其中n为非负整数,P_n(x)表示第n阶的勒让德多项式。
二、勒让德多项式的性质勒让德多项式具有许多重要的性质,例如:1. 勒让德多项式是正交的,即对于不同的n和m,有以下正交性质成立:\[ \int_{-1}^{1}P_n(x)P_m(x)dx=0, \quad(n\neq m) \]2. 勒让德多项式满足勒让德微分方程,这也是它的定义所在。
3. 勒让德多项式具有递推关系,即通过递推关系可以方便地计算高阶的勒让德多项式。
三、勒让德多项式的正交关系及应用勒让德多项式的正交性质在数学和工程领域中有着重要的应用。
在数学分析中,勒让德多项式的正交性质可以用来进行函数的展开和逼近,例如在傅立叶级数、泰勒级数及函数的插值逼近中。
在数值计算和数值分析中,勒让德多项式的正交特性也被广泛应用,例如在数值积分方法中,通过勒让德多项式的正交性质可以得到高效的数值积分算法。
勒让德多项式还具有广泛的物理应用,例如在量子力学中,勒让德多项式常常用来描述原子轨道的形状。
在实际问题中,勒让德多项式的正交性质为我们提供了一种简便而有效的数学工具,通过利用勒让德多项式的正交性质,我们可以更加方便地解决各种数学和工程问题。
勒让德多项式作为一类重要的正交函数,在数学和工程领域中具有着广泛的应用。
通过深入研究勒让德多项式的定义、性质、正交关系及其应用,我们可以更好地理解和运用这一类特殊的函数,从而为解决各种实际问题提供更加有效的数学工具。
勒让德多项式归一化
勒让德多项式归一化(原创版)目录1.勒让德多项式的基本概念2.勒让德多项式归一化的定义3.勒让德多项式归一化的方法4.勒让德多项式归一化的应用正文1.勒让德多项式的基本概念勒让德多项式(Legendre polynomial)是一种特殊的多项式,用于描述球坐标系中的函数。
在数学、物理和工程领域中,勒让德多项式被广泛应用。
勒让德多项式的基本形式为:Pn(x) = Rn(x) / Rn(1),其中 Rn(x) 是勒让德多项式的 n 阶导数,Rn(1) 是勒让德多项式在 x=1 处的值。
2.勒让德多项式归一化的定义勒让德多项式归一化是指将勒让德多项式进行标准化处理,使得它在某个区间内具有特定的性质,如归一化常数、正交性等。
勒让德多项式归一化的目的是为了将复杂的函数表示为简单的多项式形式,从而方便进行求解和分析。
3.勒让德多项式归一化的方法常见的勒让德多项式归一化方法有以下几种:(1)直接积分法:通过对勒让德多项式进行积分,可以得到其归一化后的形式。
这种方法适用于较简单的勒让德多项式。
(2)正交化方法:通过对勒让德多项式进行正交化处理,使得它们满足正交条件。
正交化方法包括:格拉米 - 施密特正交化、勒让德正交化等。
这种方法适用于较复杂的勒让德多项式。
(3)单位化方法:通过对勒让德多项式进行单位化处理,使得它们满足归一化条件。
单位化方法通常用于具有特定边界条件的问题。
4.勒让德多项式归一化的应用勒让德多项式归一化在许多领域具有广泛的应用,如:(1)在数值分析中,勒让德多项式归一化可用于求解微分方程、插值和逼近问题。
(2)在物理学中,勒让德多项式归一化可用于描述原子、分子和凝聚态系统的波函数。
(3)在工程领域中,勒让德多项式归一化可用于优化控制系统、信号处理和数据压缩等问题。
第六章_勒让德多项式
6.1 勒让德方程的引出
引入参数 n n 1 分解整理得
d 2R dR 2 r 2r n n 1 R 0 2 dr dr
欧拉型方程
1 d d 1 d 2 sin d sin 2 2 n n 1 0 sin d
引入参数 分解可得两个常微分方程
" 0
d d sin sin n n 1 sin 2 0 d d
§1 勒让德方程的引出
第一个方程与自然周期条件 2 结合,构成本征值问题
d 2 dR R d d R d 2 r dr r 2 sin d sin d r 2 sin 2 d 2 0 2 r dr
用
r 遍乘各项并移项整理,即得 R
2
1 d 2 dR 1 d d 1 d 2 r dr sin d sin d sin 2 d 2 R dr
k n 1 2
这两个多项式可以统一写成
(2n 2k )! Pn ( x) (1) n x n2 k , n 0,1, 2, 2 k !(n k )!(n 2k )! k 0
k n 2
n 阶勒让德多项式
6. 3 勒让德多项式
0~4阶Legendre多项式为
(2k 2 l )(2k 4 l ) (l )(l 1)(l 2k 1) a2 k a0 (2k )!
6. 2
勒让德方程的求解
(1 l )(l 2) a3 a1 3! (3 l )(l 4) (3 l )(1 l )(l 2)(l 4) a5 a3 a1 54 5!
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其中本征值λ 对应于原方程中的n(n+1)。
部分实例
下表列出了头11阶(n从0到10)勒让德多项式的表达式:
n
1
2
3
4
5
6
7
8
9
1
头6阶(n从0到5)勒让德多项式的曲线如下图所示:
向量和
拉普拉斯方程(与和对称轴的夹角无关)。
若设为对称轴,为观测者位置向量和轴的夹角,则势函数的解可表示为:
其中和由具体边界条件确定
递推关系
相邻的三个勒让德多项式具有三项递推关系式:
另外,考虑微分后还有以下递推关系:
其中最后一个式子在计算勒让德多项式的积分中较为有用。
移位勒让德多项式
移位勒让德多项式的正交区间定义在[0,1]上,即:
其显式表达式为:
相应的罗德里格公式为:
下表列出了头4阶移位勒让德多项式:
n
0 1
1 2x ? 1
2 6x2 ? 6x + 1
3 20x3 ? 30x2 + 12x ? 1
0 1
1
2x ? 1
2
6x2 ? 6x + 1
3
20x3 ? 30x2 +
12x ? 1
0 1
1 2x ? 1
2 6x2 ? 6x + 1
3 20x3 ? 30x2 + 12x ? 1。
