第2讲 分段函数及函数的单调性
(完整版)分段函数及函数的性质知识梳理

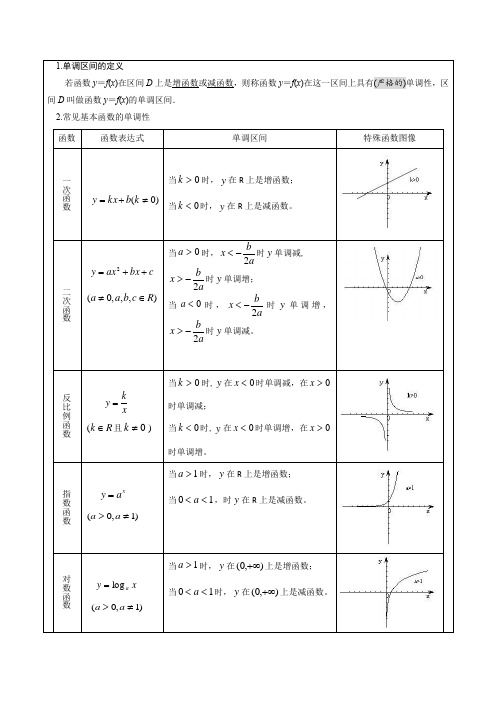
分段函数及函数的性质分段函数概念 在自变量的不同取值范围内,有不同的对应法则,需要用不同的解析式来表示的函数叫做分段表示的函数,简称分段函数.定义域 分段函数的定义域是自变量的各个不同取值范围的并集 函数值 求分段函数的函数值()0f x 时,应该首先判断0x 所属的取值范围,然后再把0x 代入到相应的解析式中进行计算.注意 分段函数在整个定义域上仍然是一个函数,而不是几个函数,只不过这个函数在定义域的不同范围内有不同的对应法则,需要用相应的解析式来表示.分段函数的作图 因为分段函数在自变量的不同取值范围内,有着不同的对应法则,所以作分段函数的图像时,需要在同一个直角坐标系中,要依次作出自变量的各个不同的取值范围内相应的图像,从而得到函数的图像. 例1 设函数()221,0,,0.x x y f x x x -⎧⎪==⎨>⎪⎩„(1)求函数的定义域; (2)求()()()2,0,1f f f -的值.(3)作出函数图像.1.设函数 ()221,20,1,0 3.x x y f x x x +-<⎧⎪==⎨-<<⎪⎩„(1)求函数的定义域; (2)求()()()2,0,1f f f -的值. (3)作出函数图像.2.设函数()41,20,1,0 3.x x f x x --<⎧=⎨-<<⎩„(1)求函数的定义域; (2)求()2(0)(1)f f f -,,; (3)作出函数图像.3 .()⎩⎨⎧>-≤+=,0,2,0,12x x x x x f 若()2f f ⎡⎤⎣⎦= . 4.已知⎩⎨⎧<+≥-=)6()2()6(5)(x x f x x x f ,则f(3)为( ) A 2 B 3 C 4 D 5函数的性质 1 单调性概念 函数值随着自变量的增大而增大(或减小)的性质叫做函数的单调性.1 即对于任意的()12,,x x a b ∈,当12x x <时,都有()()12f x f x <成立.这时把函数()f x叫做区间(),a b 内的增函数,区间(),a b 叫做函数()f x 的增区间.2 即对于任意的()12,,x x a b ∈,当12x x <时,都有()()12f x f x >成立.这时函数()f x 叫做区间(),a b 内的减函数,区间(),a b 叫做函数()f x 的减区间.3 如果函数()f x 在区间(),a b 内是增函数(或减函数),那么,就称函数()f x 在区间(),a b 内具有单调性,区间(),a b 叫做函数()f x 的单调区间.例 判断函数42y x =-的单调性1. 已知函数f ( x )=x 2+ax +b ,且对任意的实数x 都有f (1+x )=f (1-x ) 成立。
高三数学总复习优质课件 函数 导数及其应用 第2节 函数的单调性与最值

(B)(1,+∞)
(C)(-∞,1)
(D)(0,+∞)
解析:因为f(x)是R上的减函数且f(2a-1)<f(a),所以2a-1>a,所以a>1,故
选B.
4.若函数f(x)=(m-2)x+b在R上是减函数,则f(m)与f(2)的大小关系是
( A )
(A)f(m)>f(2)
(B)f(m)<f(2)
在这一区间具有(严格的)单调性, 区间D 叫做函数y=f(x)的单调区间.
2.函数的最值
前提
条件
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足
(3)对于任意的 x∈I,
(1)对于任意的x∈I,都有 f(x)≤M ; 都有 f(x)≥M
;
(2)存在x ∈I,使得 f(x0)=M _
(4)存在x ∈I,使得
所以(2a+2b)x+c=0,所以 c=0,a=-b,
所以二次函数图象的对称轴方程为 x= .
因为 f(x)在区间[2m,m+1]上不单调,所以 2m< <m+1,所以- <m< .
答案:(- , )
[对点训练3] 若函数f(x)=2|x-a|+3在区间[1,+∞)上不单调,则a的取值范
是增函数;如果y=f(u)和u=g(x)的单调性相反,那么y=f(g(x))是减函数.在
应用这一结论时,必须注意:函数u=g(x)的值域必须是y=f(u)的单调区间的
子集;
(3)两个增(减)函数的和仍为增(减)函数;一个增(减)函数与一个减(增)函
微课《分段函数的单调性》ppt课件

(2)相邻两段函数中,自变量取值小 的一段函数的最小值(或下边界)大 于等于自变量取值大的一段函数的最 大值(或上边界)。
例题分析
a , x1 例若函数f(x) 是R上的增函数, a ) x2, x1 ( 4 2 求实数a的取值范围。 变式:把次题中的增函数改为减函数,求a的范围。
x
分段函数的单调性
分段函数的单调性规律:
1.分段函数在其定义域内是增函数必 须满足的条件:
(1)每一段都是增函数; (2)相邻两段函数中,自变量取值小 的一段函数的最大值(或上边界)小 于等于自变量取值大的一段函数的最 小值(或下边界)。
分段函数的单调性规律:
2.分段函数在其定义域内是减函数必 须满足的条件: (1)每一段都是减函数;
巩固练习
(a 2)x-2a(x 1) (1)已知f(x) 是R上的增函数, x(x 1) log a 求实数a的取值范围。 Nhomakorabea(x 0)
x
a (2)已知f(x) 是R上的减函数, (a -3)x 4 a(x 0) 求实数a的取值范围。
专题2.2 函数的单调性与最值(重难点突破)(解析版)

专题2.2 函数的单调性与最值(重难点突破)(理科)一、考纲要求1.理解函数的单调性、最大(小)值及其几何意义.2.会运用基本初等函数的图象分析函数的性质.3.培养学生数学抽象、逻辑推理、直观想象能力。
二、考情分析三、考点梳理【基础知识梳理】1、函数的单调性(1)单调函数的定义增函数减函数定义一般地,设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2当x1<x2时,都有f(x1)<f(x2),那么就说函数f(x)在区间D上是增函数当x1<x2时,都有f(x1)>f(x2),那么就说函数f(x)在区间D上是减函数图象描述1/ 112 / 11自左向右看图象是上升的自左向右看图象是下降的(2)单调区间的定义如果函数y =f (x )在区间D 上是增函数或减函数,那么就说函数y =f (x )在这一区间具有(严格的)单调性,区间D 叫做y =f (x )的单调区间. 2、函数的最值前提设函数()y f x =的定义域为I ,如果存在实数M 满足 条件(1)对于任意的x I ∈,都有()f x M ≤;(2)存在0x I ∈,使得()0f x M =(3)对于任意的x I ∈,都有()f x M ≥;(4)存在0x I ∈,使得()0f x M =结论 M 为最大值 M 为最小值注意:(1)函数的值域一定存在,而函数的最值不一定存在;(2)若函数的最值存在,则一定是值域中的元素;若函数的值域是开区间,则函数无最值,若函数的值域是闭区间,则闭区间的端点值就是函数的最值. 【知识拓展】1、函数单调性的常用结论(1)若()(),f x g x 均为区间A 上的增(减)函数,则()()f x g x +也是区间A 上的增(减)函数; (2)若0k >,则()kf x 与()f x 的单调性相同;若0k <,则()kf x 与()f x 的单调性相反; (3)函数()()()0y f x f x =>在公共定义域内与()y f x =-,1()y f x =的单调性相反; (4)函数()()()0y f x f x =≥在公共定义域内与()y f x =(5)奇函数在其关于原点对称的区间上单调性相同,偶函数在其关于原点对称的区间上单调性相反; (6)一些重要函数的单调性: ①1y x x =+的单调性:在(],1-∞-和[)1,+∞上单调递增,在()1,0-和()0,1上单调递减; ②b y ax x=+(0a >,0b >)的单调性:在,b a ⎛-∞-⎝和,b a ⎫+∞⎪⎪⎭上单调递增,在,0b a ⎛⎫ ⎪ ⎪⎝⎭和b a ⎛ ⎝3 / 11上单调递减.四、题型分析(一) 判断函数的单调性 1.判断函数单调性的方法:(1)定义法,步骤为:取值,作差,变形,定号,判断.利用此方法证明抽象函数的单调性时,应根据所给抽象关系式的特点,对1x 或2x 进行适当变形,进而比较出()1f x 与()2f x 的大小.(2)利用复合函数关系,若两个简单函数的单调性相同,则这两个函数的复合函数为增函数;若两个简单函数的单调性相反,则这两个函数的复合函数为减函数,简称“同增异减”.(3)图象法:从左往右看,图象逐渐上升,则单调递增;图象逐渐下降,则单调递减. (4)导数法:利用导函数的正负判断函数的单调性.(5)利用已知函数的单调性,即转化为已知函数的和、差或复合函数,判断函数的单调性.2.在利用函数的单调性写出函数的单调区间时,首先应注意函数的单调区间应是函数定义域的子集或真子集,求函数的单调区间必须先确定函数的定义域;其次需掌握一次函数、二次函数等基本初等函数的单调区间.例1.(2020·安徽省池州一中模拟)下列四个函数中,在x ∈(0,+∞)上为增函数的是( )A .f (x )=3-xB .f (x )=x 2-3xC .f (x )=-1x +1D .f (x )=-|x |【答案】C【解析】当x >0时,f (x )=3-x 为减函数;当x ∈⎝⎛⎭⎫0,32时,f (x )=x 2-3x 为减函数, 当x ∈⎝⎛⎭⎫32,+∞时,f (x )=x 2-3x 为增函数;当x ∈(0,+∞)时,f (x )=-1x +1为增函数; 当x ∈(0,+∞)时,f (x )=-|x |为减函数.【变式训练1】.(2020届陕西省咸阳市高三第一次模拟)函数cos 4y x ππ⎛⎫=-⎪⎝⎭的单调递增区间是( )A .132,244k k ⎡⎤-+⎢⎥⎣⎦()k ∈Z B .372,244k k ⎡⎤++⎢⎥⎣⎦()k ∈Z C .312,244k k ⎡⎤-+⎢⎥⎣⎦()k ∈Z D .152,244k k ⎡⎤++⎢⎥⎣⎦()k ∈Z4 / 11【答案】C【解析】令()224k x k k Z πππππ-≤-≤∈,解得()312244k x k k Z -≤≤+∈, 因此,函数cos 4y x ππ⎛⎫=-⎪⎝⎭的单调递增区间是()312,244k k k Z ⎡⎤-+∈⎢⎥⎣⎦,故选C 。
函数单调性判断方法
,0上是减函数。
C .(-∞,-1]D .[1,+∞)[小结](1)单调区间是定义域的子集,故求单调区间时应树立“定义域优先”的原则.(2)单调区间只能用区间表示,不能用集合或不等式表示;如有多个单调区间应分开写,不能用并集符号“∪”连接,也不能用“或”连接.(3)函数的单调性是函数在某个区间上的“整体”性质,所以不能仅仅根据某个区间内的两个特殊变量x 1,x 2对应的函数值的大小就判断函数在该区间的单调性,必须保证这两个变量是区间内的任意两个自变量.题型二、分段函数单调性判断及应用使用情景:分段函数的单调性问题解题模板:第一步 通过观察分析,决定如何对自变量进行分类;第二步 根据常见函数的单调性,分别计算每段函数的单调性;第三步 满足函数在整个区间上是增函数(或减函数),即左段的函数的最大值(或最小值)小于等于右段函数的最小值(或最大值);第四步 得出结论.【例1】 已知函数()[)()232,0,32,,0x x f x x a a x ⎧∈+∞⎪=⎨+-+∈-∞⎪⎩在区间(),-∞+∞上是增函数,则常数a 的取值范围是 ( ) A .()1,2 B .(][),12,-∞+∞ C .[]1,2 D .()(),12,-∞+∞+∞+∞ D(2,) (1,)【变式练习3】已知函数223,1()lg(1),1x x f x xx x ⎧+-≥⎪=⎨⎪+<⎩,则((3))f f -= ,()f x 的最小值是[小结] 1、最值问题使用情景:分段函数的最值问题解题模板:第一步 通过观察分析,决定如何对自变量进行分类;第二步 根据常见函数的最值,分别计算每段函数的最值;第三步 满足函数在整个区间上的最值,即比较每段函数的最值大小,谁最大谁是最大值,谁最小谁是最小值;第四步 得出结论.2、单调性问题其一是分段函数在每一个区间上的增函数(或减函数)与整体函数相同;其二是满足函数在整个区间上是增函数(或减函数),即左段的函数的最大值(或最小值)小于等于右段函数的最小值(或最大值).题型三、抽象函数的单调性【例1】已知奇函数()f x 的定义域为[]2,2-,且在[]2,0-内递减,求满足:2(1)(1)0f m f m -+-<的实数m 的取值范围.【例2】定义在上的偶函数满足:,在区间与上分别递增和递减,则不等式的解集为 .【变式练习1】设奇函数()f x 在区间[1,1]-上是增函数,且(1)1f -=-.当[1,1]x ∈-时,函数2()21f x t at ≤-+,对一切[1,1]a ∈-恒成立,则实数t 的取值范围为( )A.22t -≤≤B.2t ≤-或2t ≥C.0t ≤或2t ≥D.2t ≤-或2t ≥或0t =【变式练习2】已知f (x )是定义在R 上的偶函数,且在区间(-∞,0)上单调递增.若实数a 足1(2)(2)a f f ->-,则a 的取值范围是______[小结]不等式中的数形结合问题,在解题时既要想形又要以形助数,常见的“以形助数”的方法有: (1)借助数轴,运用数轴的有关概念,解决与绝对值有关的问题,解决数集的交、并、补运算非常有效. (2)借助函数图象性质,利用函数图象分析问题和解决问题是数形结合的基本方法,需注意的问题是准确把握代数式的几何意义实现“数”向“形”的转化.题型四、函数单调性判断方法(性质)的应用函数单调性的性质:(1)若f (x ),g (x )均为区间A 上的增(减)函数,则f (x )+g (x )也是区间A 上的增(减)函数,更进一步,即增+增=增,增-减=增,减+减=减,减-增=减;(2)若k >0,则kf (x )与f (x )单调性相同;若k <0,则kf (x )与f (x )单调性相反; (3)在公共定义域内,函数y =f (x )(f (x )≠0)与y =-f (x ),y =1f (x )单调性相反;(4)在公共定义域内,函数y =f (x )(f (x )≥0)与y =f (x )单调性相同;(5)奇函数在其关于原点对称的区间上单调性相同,偶函数在其关于原点对称的区间上单调性相反. 【常见判断方法】方法一 定义法使用情景:一般函数类型解题模板:第一步 取值定大小:设任意,且; 第二步 作差:;第三步 变形(合并同类项、通分、分解因式、配方等); 第四步 定符号; 第五步 得出结论. 【例1】 判断并证明:21()1f x x =+在(,0)-∞上的单调性.12,x x D ∈12x x <12()()f x f x -x 的取值范围是( )A .(8,+∞)B .(8,9]C .[8,9]D .(0,8)[方法技巧]用单调性求解与抽象函数有关不等式的策略(1)在求解与抽象函数有关的不等式时,往往是利用函数的单调性将“f ”符号脱掉,使其转化为具体的不等式求解.此时应特别注意函数的定义域.(2)有时,在不等式一边没有符号“f ”时,需转化为含符号“f ”的形式.如若已知f (a )=0,f (x -b )<0,则f (x -b )<f (a ).应用(三) 求参数的取值范围[例5] (1)如果函数f (x )=ax 2+2x -3在区间(-∞,4)上是单调递增的,则实数a 的取值范围是( ) A.⎝⎛⎭⎫-14,+∞ B.⎣⎡⎭⎫-14,+∞ C.⎣⎡⎭⎫-14,0 D.⎣⎡⎦⎤-14,0(2)设函数f (x )=⎩⎪⎨⎪⎧-x 2+4x ,x ≤4,log 2x ,x >4.若函数y =f (x )在区间(a ,a +1)上单调递增,则实数a 的取值范围是( )A .(-∞,1]B .[1,4]C .[4,+∞)D .(-∞,1]∪[4,+∞)[易错提醒](1)若函数在区间[a ,b ]上单调,则该函数在此区间的任意子区间上也是单调的.(2)对于分段函数的单调性,除注意各段的单调性外,还要注意衔接点的取值.【变式练习3】1.函数f (x )=|x -2|x 的单调减区间是( )A .[1,2]B .[-1,0]C .[0,2]D .[2,+∞)2.已知函数y =f (x )是R 上的偶函数,当x 1,x 2∈(0,+∞),x 1≠x 2时,都有(x 1-x 2)·[f (x 1)-f (x 2)]<0.设a =ln 1π,b =(ln π)2,c =ln π,则( ) A .f (a )>f (b )>f (c )B .f (b )>f (a )>f (c )C .f (c )>f (a )>f (b )D .f (c )>f (b )>f (a )3.定义在R 上的奇函数y =f (x )在(0,+∞)上单调递增,且f ⎝⎛⎭⎫12=0,则满足f log 19x >0的x 的集合为________.随堂检测1.已知f (x )=⎩⎪⎨⎪⎧(2-a )x +1,x <1,a x ,x ≥1,满足对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2>0成立,那么a 的取值范围是________.2.讨论函数f (x )=x +a x(a >0)的单调性.。
第02课函数的单调性与最大(小)值(课件)

【典例】(多选)下列函数在(0,+∞)上单调递增的是( )
A.y=ex-e-x
B.y=|x2-2x|
C.y=x+cos x
D.y= x2+x-2
【解析】∵y=ex 与 y=-e-x 为 R 上的增函数,∴y=ex-e-x 为 R 上的增函数,故 A 正确; 由 y=|x2-2x|的图象知,故 B 不正确;对于选项 C,y′=1-sin x≥0,∴y=x+cos x 在 R 上为增函数,故 C 正确; y= x2+x-2的定义域为(-∞,-2]∪[1,+∞),故 D 不正确.
【典例】已知二次函数 f(x)=x2-2x+3, 当 x∈[t,t+1]时,求 f(x)的最小值 g(t).
【解析】①当 t>1 时,f(x)在[t,t+1]上是增函数, 所以当 x=t 时,f(x)取得最小值,此时 g(t)=f(t)=t2-2t+3. ②当 t≤1≤t+1,即 0≤t≤1 时,f(x)在[t,t+1]上先递减后递增, 故当 x=1 时,f(x)取得最小值,此时 g(t)=f(1)=2. ③当 t+1<1,即 t<0 时,f(x)在[t,t+1]上是减函数,所以当 x=t+1 时,f(x)取得最小值,
函数 f(x)= x-1在其定义域内是增函数.
【解析】函数 f(x)= x-1的定义域是[1,+∞),
设∀x1,x2∈[1,+∞),且 x1<x2,则 f(x2)-f(x1)= x2-1- x1-1
=
x2-1- x1-1 x2-1+ x2-1+ x1-1
x1-1=
x2-x12-+x1x1-1.
因为 x1,x2∈[1,+∞),且 x1<x2,所以 x2-1+ x1-1>0,x2-x1>0.
第2讲分段函数及函数的单调性

第二讲分段函数及函数的单调性一.分段函数若函数在其定义域内,对于定义域内的不同取值区间,有着不同的对应关系,这样的函数通常叫做分段函数.分段函数无论分成几段,都是一个函数,不要误解为是“由几个函数组成”.求分段函数的函数值,如果自变量的范围不确定,要分类讨论.常见的命题类型有:(1)分段函数的函数求值问题;(2)分段函数的自变量求值问题;(3)分段函数与函数性质、方程、不等式问题.二.函数的单调性1.单调性的定义增函数减函数一般地,设函数f(x)的定义域为I :如果对于定义域I 内某个区间D 上的任意两个自变量的值x1, x2定义当 x1<x2 时,都有 f(x1)<f(x2),那么就说函数f(x) 在区间 D 上是当 x1<x2 时,都有f(x1 )>f(x2) ,那么就说函数f(x) 在区间 D 上是___________ ________图象描述自左向右看图象是 __________ 自左向右看图象是_________单调区间的定义如果函数 y= f(x)在区间 D 上是增函数或减函数,那么就说函数y= f(x)在这一区间具有(严格的 )_______ ,区间 D 叫做函数 y= f(x) 的___________.2.函数的最值前提设函数 y=f(x)的定义域为 I,如果存在实数M 满足条件①对于任意的 x∈ I,都有 f(x)≤M ;①对于任意 x∈ I ,都有 f(x)≥M;②存在 x0∈ I ,使得 f(x0)= M ②存在 x0∈I ,使得 f(x0)= M结论M 为函数 y= f(x)的最大值M 为函数 y= f(x)的最小值三.题型详解题型一分段函数的函数求值(域)问题1.已知函数 f(x)= log 2x , x>0 ,1 的值是 ________.x 则 f f 3 + 1,x ≤ 0, 422. 若函数 ??(??) = ?? + 1, ??≤1=( ) lg??, ??> ,则 ??(??(10))1 A . lg101B .2C . 1D .03.设定义在 N 上的函数 f ( x )满足 f ( n ) = n 13 (n 2000), f [ f ( n 18)] (n 2000), 试求 f ( 2002)的值 .1, x>1,4.设函数 f(x)= x则 f(f(2)) = ________,函数 f(x)的值域是________.- x - 2, x ≤ 1,题型二 分段函数的自变量求值问题1x 2, x ∈ [0,+∞ ,1.已知 f(x)= π,若 f(a)= 1,则 a =________.2|sin x|, x ∈ - , 022x- 2,x ≤0, 且 f(a)=- 2,则 f(7 - a)= ()2.已知函数f(x)=- log 3x , x>0 ,3 57A .-log37B .- 4C .- 4D .- 4a -1 x +1, x ≤ 1, 3.已知函数f(x)=a x - 1, x>1,若 f(1)= 1,则 f(3)=________.2题型三 分段函数与函数性质、方程、不等式问题.x 2+ 2ax , x ≥ 2,1.已知函数f(x)=2 x + 1, x<2,若 f(f(1))>3 a 2,则 a 的取值范围是________.2.已知函数 f( x )=x 2 ( x 2),则 f ( lg30 -lg3 )=___________________ ; 2 ( x 2), 不等式 xf ( x - 1)< 10 的解集是 ___________________.题型四 .常见函数的单调性一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、正弦函数、余弦函数、正切函数的单调性、单调区间。
第二章 2·2函数的单调性与最值

1.函数单调性的定义增函数减函数定义设函数y=f(x)的定义域为A,区间M⊆A,如果取区间M中任意两个值x1,x2,改变量Δx=x2-x1>0,则当Δy=f(x2)-f(x1)>0时,就称函数y=f(x)在区间M上是增函数Δy=f(x2)-f(x1)<0时,就称函数y=f(x)在区间M上是减函数图象自左向右看图象是上升的自左向右看图象是下降的2.如果一个函数在某个区间M上是增函数或是减函数,就说这个函数在这个区间M上具有单调性,区间M 称为单调区间.3.函数的最值前提设函数y=f(x)的定义域为I,如果存在实数M满足条件(1)对于任意的x∈I,都有f(x)≤M;(2)存在x0∈I,使得f(x0)=M.(3)对于任意的x∈I,都有f(x)≥M;(4)存在x0∈I,使得f(x0)=M.结论M为最大值M为最小值【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)在增函数与减函数的定义中,可以把“任意两个自变量”改为“存在两个自变量”.(×)(2)对于函数f(x),x∈D,若x1,x2∈D且(x1-x2)·[f(x1)-f(x2)]>0,则函数f(x)在D上是增函数.(√)(3)函数y =f (x )在[1,+∞)上是增函数,则函数的单调递增区间是[1,+∞).( × ) (4)函数y =1x 的单调递减区间是(-∞,0)∪(0,+∞).( × )(5)所有的单调函数都有最值.( × )(6)对于函数y =f (x ),若f (1)<f (3),则f (x )为增函数.( × )1.(2014·北京)下列函数中,在区间(0,+∞)上为增函数的是( ) A .y =x +1 B .y =(x -1)2 C .y =2-x D .y =log 0.5(x +1) 答案 A解析 A 项,函数y =x +1在[-1,+∞)上为增函数,所以函数在(0,+∞)上为增函数,故正确;B 项,函数y =(x -1)2在(-∞,1)上为减函数,在[1,+∞)上为增函数,故错误;C 项,函数y =2-x =(12)x 在R上为减函数,故错误;D 项,函数y =log 0.5(x +1)在(-1,+∞)上为减函数,故错误. 2.若函数f (x )=|2x +a |的单调递增区间是[3,+∞),则a 的值为( ) A .-2 B .2 C .-6 D .6 答案 C解析 由图象易知函数f (x )=|2x +a |的单调增区间是[-a 2,+∞),令-a2=3,∴a =-6.3.若函数y =ax 与y =-bx 在(0,+∞)上都是减函数,则y =ax 2+bx 在(0,+∞)上是( )A .增函数B .减函数C .先增后减D .先减后增答案 B解析 由y =ax 在(0,+∞)上是减函数,知a <0; 由y =-bx 在(0,+∞)上是减函数,知b <0.∴y =ax 2+bx 的对称轴x =-b2a<0, 又∵y =ax 2+bx 的开口向下,∴y =ax 2+bx 在(0,+∞)上是减函数.故选B. 4.(教材改编)已知函数f (x )=2x -1,x ∈[2,6],则f (x )的最大值为________,最小值为________. 答案 2 25解析 可判断函数f (x )=2x -1在[2,6]上为减函数,所以f (x )max =f (2)=2,f (x )min =f (6)=25.5.(教材改编)已知函数f (x )=x 2-2ax -3在区间[1,2]上具有单调性,则实数a 的取值范围为________________________________________________________________________. 答案 (-∞,1]∪[2,+∞)解析 函数f (x )=x 2-2ax -3的图象开口向上,对称轴为直线x =a ,画出草图如图所示.由图象可知函数在(-∞,a ]和[a ,+∞)上都具有单调性,因此要使函数f (x )在区间[1,2]上具有单调性,只需a ≤1或a ≥2,从而a ∈(-∞,1]∪[2,+∞).题型一 确定函数的单调性(区间)命题点1 给出具体解析式的函数的单调性例1 (1)下列函数中,在区间(0,+∞)上为增函数的是( ) A .y =ln(x +2) B .y =-x +1 C .y =(12)x D .y =x +1x(2)函数f (x )=log 12(x 2-4)的单调递增区间是( )A .(0,+∞)B .(-∞,0)C .(2,+∞)D .(-∞,-2)(3)y =-x 2+2|x |+3的单调增区间为________. 答案 (1)A (2)D (3)(-∞,-1],[0,1] 解析 (1)y =ln(x +2)的增区间为(-2,+∞), ∴在区间(0,+∞)上为增函数.(2)因为y =log 12t 在定义域上是减函数,所以求原函数的单调递增区间,即求函数t =x 2-4的单调递减区间,结合函数的定义域,可知所求区间为(-∞,-2).(3)由题意知,当x ≥0时,y =-x 2+2x +3=-(x -1)2+4;当x <0时,y =-x 2-2x +3=-(x +1)2+4, 二次函数的图象如图.由图象可知,函数y =-x 2+2|x |+3在(-∞,-1],[0,1]上是增函数. 命题点2 解析式含参函数的单调性例2 试讨论函数f (x )=axx -1(a ≠0)在(-1,1)上的单调性.解 设-1<x 1<x 2<1, f (x )=a ⎝⎛⎭⎪⎫x -1+1x -1=a ⎝⎛⎭⎫1+1x -1,f (x 1)-f (x 2)=a ⎝⎛⎭⎫1+1x 1-1-a ⎝⎛⎭⎫1+1x 2-1=a (x 2-x 1)(x 1-1)(x 2-1),由于-1<x 1<x 2<1,所以x 2-x 1>0,x 1-1<0,x 2-1<0, 故当a >0时,f (x 1)-f (x 2)>0,即f (x 1)>f (x 2), 函数f (x )在(-1,1)上递减;当a <0时,f (x 1)-f (x 2)<0,即f (x 1)<f (x 2), 函数f (x )在(-1,1)上递增.综上,当a >0时,f (x )在(-1,1)上单调递减;当a <0时,f (x )在(-1,1)上单调递增. 引申探究若本题中的函数变为f (x )=axx 2-1 (a >0),则f (x )在(-1,1)上的单调性如何?解 设-1<x 1<x 2<1, 则f (x 1)-f (x 2)=ax 1x 21-1-ax 2x 22-1 =ax 1x 22-ax 1-ax 2x 21+ax 2(x 21-1)(x 22-1)=a (x 2-x 1)(x 1x 2+1)(x 21-1)(x 22-1) ∵-1<x 1<x 2<1,∴x 2-x 1>0,x 1x 2+1>0,(x 21-1)(x 22-1)>0. 又∵a >0,∴f (x 1)-f (x 2)>0, ∴函数在(-1,1)上为减函数.思维升华 确定函数单调性的方法:(1)定义法和导数法,证明函数单调性只能用定义法和导数法;(2)复合函数法,复合函数单调性的规律是“同增异减”;(3)图象法,图象不连续的单调区间不能用“∪”连接.已知a >0,函数f (x )=x +ax(x >0),证明:函数f (x )在(0,a ]上是减函数,在[a ,+∞)上是增函数.证明 方法一 任意取x 1>x 2>0,则 f (x 1)-f (x 2)=⎝⎛⎭⎫x 1+a x 1-⎝⎛⎭⎫x 2+a x 2=(x 1-x 2)+⎝⎛⎭⎫a x 1-a x 2=(x 1-x 2)+a (x 2-x 1)x 1x 2=(x 1-x 2)⎝⎛⎭⎫1-a x 1x 2.当a ≥x 1>x 2>0时,x 1-x 2>0,1-ax 1x 2<0,有f (x 1)-f (x 2)<0,即f (x 1)<f (x 2),此时,函数f (x )=x +ax (a >0)在(0,a ]上为减函数;当x 1>x 2≥a 时,x 1-x 2>0,1-ax 1x 2>0, 有f (x 1)-f (x 2)>0,即f (x 1)>f (x 2),此时,函数f (x )=x +ax(a >0)在[a ,+∞)上为增函数;综上可知,函数f (x )=x +ax (a >0)在(0,a ]上为减函数,在[a ,+∞)上为增函数.方法二 f ′(x )=1-a x 2,令f ′(x )>0,则1-ax2>0,解得x >a 或x <-a (舍).令f ′(x )<0,则1-ax 2<0,解得-a <x <a .∵x >0,∴0<x <a .故f (x )在(0,a ]上为减函数,在[a ,+∞)上为增函数.题型二 函数的最值例3 已知函数f (x )=x 2+2x +ax ,x ∈[1,+∞),a ∈(-∞,1].(1)当a =12时,求函数f (x )的最小值;(2)若对任意x ∈[1,+∞),f (x )>0恒成立,试求实数a 的取值范围. 解 (1)当a =12时,f (x )=x +12x +2在[1,+∞)上为增函数,f (x )min =f (1)=72.(2)f (x )=x +ax+2,x ∈[1,+∞).①当a ≤0时,f (x )在[1,+∞)内为增函数. 最小值为f (1)=a +3.要使f (x )>0在x ∈[1,+∞)上恒成立,只需a +3>0,即a >-3,所以-3<a ≤0. ②当0<a ≤1时,f (x )在[1,+∞)上为增函数, f (x )min =f (1)=a +3.所以a +3>0,a >-3,所以0<a ≤1.综上所述,f (x )在[1,+∞)上恒大于零时,a 的取值范围是(-3,1]. 思维升华 求函数最值的常用方法(1)单调性法:先确定函数的单调性,再由单调性求最值;(2)图象法:先作出函数的图象,再观察其最高点、最低点,求出最值;(3)换元法:对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求最值.(1)函数f (x )=⎩⎪⎨⎪⎧1x ,x ≥1,-x 2+2,x <1的最大值为________.(2)已知函数f (x )=1a -1x (a >0,x >0),若f (x )在⎣⎡⎦⎤12,2上的值域为[12,2],则a =________. 答案 (1)2 (2)25解析 (1)当x ≥1时,函数f (x )=1x 为减函数,所以f (x )在x =1处取得最大值,为f (1)=1;当x <1时,易知函数f (x )=-x 2+2在x =0处取得最大值,为f (0)=2. 故函数f (x )的最大值为2.(2)由反比例函数的性质知函数f (x )=1a -1x (a >0,x >0)在⎣⎡⎦⎤12,2上单调递增, 所以⎩⎪⎨⎪⎧f ⎝⎛⎭⎫12=12,f (2)=2,即⎩⎨⎧1a -2=12,1a -12=2,解得a =25.题型三 函数单调性的应用 命题点1 比较大小 例4 已知函数f (x )=log 2x +11-x,若x 1∈(1,2),x 2∈(2,+∞),则( ) A .f (x 1)<0,f (x 2)<0 B .f (x 1)<0,f (x 2)>0 C .f (x 1)>0,f (x 2)<0 D .f (x 1)>0,f (x 2)>0 答案 B解析 ∵函数f (x )=log 2x +11-x 在(1,+∞)上为增函数,且f (2)=0,∴当x 1∈(1,2)时,f (x 1)<f (2)=0, 当x 2∈(2,+∞)时,f (x 2)>f (2)=0, 即f (x 1)<0,f (x 2)>0.命题点2 解不等式例5 已知函数f (x )为R 上的减函数,则满足f ⎝⎛⎭⎫⎪⎪⎪⎪1x <f (1)的实数x 的取值范围是( ) A .(-1,1) B .(0,1) C .(-1,0)∪(0,1) D .(-∞,-1)∪(1,+∞)答案 C解析 由f (x )为R 上的减函数且f ⎝⎛⎭⎫⎪⎪⎪⎪1x <f (1),得⎩⎪⎨⎪⎧⎪⎪⎪⎪1x >1,x ≠0,即⎩⎪⎨⎪⎧|x |<1,x ≠0.∴-1<x <0或0<x <1.命题点3 求参数范围例6 (1)如果函数f (x )=ax 2+2x -3在区间(-∞,4)上是单调递增的,则实数a 的取值范围是( ) A .a >-14 B .a ≥-14C .-14≤a <0D .-14≤a ≤0(2)已知f (x )=⎩⎪⎨⎪⎧(2-a )x +1,x <1,a x ,x ≥1,满足对任意x 1≠x 2,都有f (x 1)-f (x 2)x 1-x 2>0成立,那么a 的取值范围是________.答案 (1)D (2)[32,2)解析 (1)当a =0时,f (x )=2x -3,在定义域R 上是单调递增的,故在(-∞,4)上单调递增; 当a ≠0时,二次函数f (x )的对称轴为x =-1a ,因为f (x )在(-∞,4)上单调递增, 所以a <0,且-1a ≥4,解得-14≤a <0.综合上述得-14≤a ≤0.(2)由已知条件得f (x )为增函数, ∴⎩⎪⎨⎪⎧2-a >0,a >1,(2-a )×1+1≤a ,解得32≤a <2,∴a 的取值范围是[32,2).思维升华 函数单调性应用问题的常见类型及解题策略(1)比较大小.比较函数值的大小,应将自变量转化到同一个单调区间内,然后利用函数的单调性解决. (2)解不等式.在求解与抽象函数有关的不等式时,往往是利用函数的单调性将“f ”符号脱掉,使其转化为具体的不等式求解.此时应特别注意函数的定义域. (3)利用单调性求参数.①视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数; ②需注意若函数在区间[a ,b ]上是单调的,则该函数在此区间的任意子集上也是单调的; ③分段函数的单调性,除注意各段的单调性外,还要注意衔接点的取值.(1)f (x )是定义在(0,+∞)上的单调增函数,满足f (xy )=f (x )+f (y ),f (3)=1,当f (x )+f (x -8)≤2时,x 的取值范围是( ) A .(8,+∞) B .(8,9]C .[8,9]D .(0,8)(2)若f (x )=-x 2+2ax 与g (x )=ax +1在区间[1,2]上都是减函数,则a 的取值范围是( )A .(-1,0)∪(0,1)B .(-1,0)∪(0,1]C .(0,1)D .(0,1]答案 (1)B (2)D解析 (1)2=1+1=f (3)+f (3)=f (9),由f (x )+f (x -8)≤2,可得f [x (x -8)]≤f (9),因为f (x )是定义在(0,+∞)上的增函数,所以有⎩⎪⎨⎪⎧x >0,x -8>0,x (x -8)≤9,解得8<x ≤9.(2)由f (x )=-x 2+2ax 在[1,2]上是减函数可得[1,2]⊆[a ,+∞),∴a ≤1. ∵y =1x +1在(-1,+∞)上为减函数,∴由g (x )=ax +1在[1,2]上是减函数可得a >0,故0<a ≤1.1.确定抽象函数单调性解函数不等式典例 (12分)函数f (x )对任意的m 、n ∈R ,都有f (m +n )=f (m )+f (n )-1,并且x >0时,恒有f (x )>1. (1)求证:f (x )在R 上是增函数; (2)若f (3)=4,解不等式f (a 2+a -5)<2.思维点拨 (1)对于抽象函数的单调性的证明,只能用定义.应该构造出f (x 2)-f (x 1)并与0比较大小.(2)将函数不等式中的抽象函数符号“f ”运用单调性“去掉”是本题的切入点.要构造出f (M )<f (N )的形式. 规范解答(1)证明 设x 1,x 2∈R ,且x 1<x 2,∴x 2-x 1>0, ∵当x >0时,f (x )>1,∴f (x 2-x 1)>1.[2分] f (x 2)=f [(x 2-x 1)+x 1]=f (x 2-x 1)+f (x 1)-1,[4分] ∴f (x 2)-f (x 1)=f (x 2-x 1)-1>0⇒f (x 1)<f (x 2), ∴f (x )在R 上为增函数.[6分](2)解 ∵m ,n ∈R ,不妨设m =n =1, ∴f (1+1)=f (1)+f (1)-1⇒f (2)=2f (1)-1,[8分] f (3)=4⇒f (2+1)=4⇒f (2)+f (1)-1=4⇒3f (1)-2=4, ∴f (1)=2,∴f (a 2+a -5)<2=f (1),[10分] ∵f (x )在R 上为增函数,∴a 2+a -5<1⇒-3<a <2,即a ∈(-3,2).[12分]解函数不等式问题的一般步骤:第一步:(定性)确定函数f (x )在给定区间上的单调性; 第二步:(转化)将函数不等式转化为f (M )<f (N )的形式;第三步:(去f )运用函数的单调性“去掉”函数的抽象符号“f ”,转化成一般的不等式或不等式组; 第四步:(求解)解不等式或不等式组确定解集;第五步:(反思)反思回顾.查看关键点,易错点及解题规范.温馨提醒 本题对函数的单调性的判断是一个关键点.不会运用条件x >0时,f (x )>1,构造不出f (x 2)-f (x 1)=f (x 2-x 1)-1的形式,便找不到问题的突破口.第二个关键应该是将不等式化为f (M )<f (N )的形式.解决此类问题的易错点:忽视了M 、N 的取值范围,即忽视了f (x )所在的单调区间的约束.[方法与技巧]1.利用定义证明或判断函数单调性的步骤 (1)取值;(2)作差;(3)定量;(4)判断.2.确定函数单调性有四种常用方法:定义法、导数法、复合函数法、图象法,也可利用单调函数的和差确定单调性.3.求函数最值的常用求法:单调性法、图象法、换元法. [失误与防范]1.分段函数单调性不仅要考虑各段的单调性,还要注意衔接点.2.函数在两个不同的区间上单调性相同,一般要分开写,用“,”或“和”连接,不要用“∪”.A 组 专项基础训练 (时间:35分钟)一、选择题1.下列四个函数中,在区间(0,1)上是减函数的是( ) A .y =log 2xB .y =x 13C .y =-⎝⎛⎭⎫12xD .y =1x 答案 D解析 y =log 2x 在(0,+∞)上为增函数;y =x 13在(0,+∞)上是增函数;y =⎝⎛⎭⎫12x 在(0,+∞)上是减函数,y =-⎝⎛⎭⎫12x 在(0,+∞)上是增函数;y =1x 在(0,+∞)上是减函数,故y =1x 在(0,1)上是减函数.故选D. 2.已知函数y =log 2(ax -1)在(1,2)上单调递增,则实数a 的取值范围是( ) A .(0,1]B .[1,2]C .[1,+∞)D .[2,+∞) 答案 C解析 要使y =log 2(ax -1)在(1,2)上单调递增,则a >0且a -1≥0,∴a ≥1.3.已知函数y =f (x )的图象关于x =1对称,且在(1,+∞)上单调递增,设a =f ⎝⎛⎭⎫-12,b =f (2),c =f (3),则a ,b ,c 的大小关系为( ) A .c <b <a B .b <a <c C .b <c <a D .a <b <c 答案 B解析 ∵函数图象关于x =1对称,∴a =f ⎝⎛⎭⎫-12=f ⎝⎛⎭⎫52,又y =f (x )在(1,+∞)上单调递增, ∴f (2)<f ⎝⎛⎭⎫52<f (3),即b <a <c .4.若函数f (x )=x 2-2x +m 在 [3,+∞)上的最小值为1,则实数m 的值为( ) A .-3 B .-2 C .-1 D .1 答案 B解析 ∵f (x )=(x -1)2+m -1在[3,+∞)上为单调增函数,且f (x )在[3,+∞)上的最小值为1, ∴f (3)=1,即22+m -1=1,m =-2.5.已知函数f (x )=2ax 2+4(a -3)x +5在区间(-∞,3)上是减函数,则a 的取值范围是( ) A .(0,34) B .(0,34]C .[0,34)D .[0,34]答案 D解析 当a =0时,f (x )=-12x +5,在(-∞,3)上是减函数, 当a ≠0时,由⎩⎪⎨⎪⎧a >0,-4(a -3)4a ≥3,得0<a ≤34,综上a 的取值范围是0≤a ≤34.二、填空题6.已知函数f (x )=x 2-2x -3,则该函数的单调增区间为________. 答案 [3,+∞)解析 设t =x 2-2x -3,由t ≥0,即x 2-2x -3≥0, 解得x ≤-1或x ≥3.所以函数的定义域为(-∞,-1]∪[3,+∞).因为函数t =x 2-2x -3的图象的对称轴为x =1,所以函数在(-∞,-1]上单调递减,在[3,+∞)上单调递增.又因为y =t 在[0,+∞)上单调递增,所以函数f (x )的增区间为[3,+∞).7.已知函数f (x )=⎩⎪⎨⎪⎧ x 2+12a -2,x ≤1,a x -a ,x >1,若f (x )在(0,+∞)上单调递增,则实数a 的取值范围为________.答案 (1,2]解析 由题意,得12+12a -2≤0,则a ≤2,又a x -a 是增函数,故a >1,所以a 的取值范围为1<a ≤2. 8.函数f (x )=⎝⎛⎭⎫13x -log 2(x +2)在区间[-1,1]上的最大值为________.答案 3解析 由于y =⎝⎛⎭⎫13x 在R 上递减,y =log 2(x +2)在[-1,1]上递增,所以f (x )在[-1,1]上单调递减,故f (x )在[-1,1]上的最大值为f (-1)=3.三、解答题9.已知f (x )=x x -a(x ≠a ). (1)若a =-2,试证明f (x )在(-∞,-2)内单调递增;(2)若a >0且f (x )在(1,+∞)上单调递减,求a 的取值范围.(1)证明 任设x 1<x 2<-2,则f (x 1)-f (x 2)=x 1x 1+2-x 2x 2+2 =2(x 1-x 2)(x 1+2)(x 2+2). ∵(x 1+2)(x 2+2)>0,x 1-x 2<0,∴f (x 1)<f (x 2),∴f (x )在(-∞,-2)上单调递增.(2)解 任设1<x 1<x 2,则f (x 1)-f (x 2)=x 1x 1-a -x 2x 2-a =a (x 2-x 1)(x 1-a )(x 2-a ). ∵a >0,x 2-x 1>0,∴要使f (x 1)-f (x 2)>0,只需(x 1-a )(x 2-a )>0在(1,+∞)上恒成立,∴a ≤1.综上所述,a 的取值范围是(0,1].10.设函数y =f (x )是定义在(0,+∞)上的函数,并且满足下面三个条件:①对任意正数x ,y ,都有f (xy )=f (x )+f (y );②当x >1时,f (x )<0;③f (3)=-1.(1)求f (1),f (19)的值; (2)如果不等式f (x )+f (2-x )<2成立,求x 的取值范围.解 (1)令x =y =1易得f (1)=0.而f (9)=f (3)+f (3)=-1-1=-2,且f (9)+f ⎝⎛⎭⎫19=f (1)=0,故f ⎝⎛⎭⎫19=2. (2)设0<x 1<x 2,则x 2x 1>1,f ⎝⎛⎭⎫x 2x 1<0, 由f (xy )=f (x )+f (y )得f (x 2)=f ⎝⎛⎭⎫x 1·x 2x 1=f (x 1)+f ⎝⎛⎭⎫x 2x 1<f (x 1), 所以f (x )是减函数.由条件①及(1)的结果得:f [x (2-x )]<f ⎝⎛⎭⎫19,其中0<x <2,由函数f (x )在R 上单调递减,可得⎩⎪⎨⎪⎧ x (2-x )>19,0<x <2,由此解得x 的取值范围是⎝⎛⎭⎫1-223,1+223. B 组 专项能力提升(时间:20分钟)11.函数f (x )=|x -2|x 的单调减区间是( )A .[1,2]B .[-1,0]C .[0,2]D .[2,+∞) 答案 A解析 由于f (x )=|x -2|x =⎩⎪⎨⎪⎧x 2-2x ,x ≥2,-x 2+2x ,x <2. 结合图象可知函数的单调减区间是[1,2].12.定义新运算:当a ≥b 时,a b =a ;当a <b 时,ab =b 2,则函数f (x )=(1x )x -(2x ),x ∈[-2,2]的最大值等于( )A .-1B .1C .6D .12答案 C解析 由已知,得当-2≤x ≤1时,f (x )=x -2,当1<x ≤2时,f (x )=x 3-2.∵f (x )=x -2,f (x )=x 3-2在定义域内都为增函数.∴f (x )的最大值为f (2)=23-2=6.13.(2015·山东)定义运算“⊗”:x ⊗y =x 2-y 2xy (x ,y ∈R ,xy ≠0),当x >0,y >0时,x ⊗y +(2y )⊗x 的最小值为________.答案 2解析 由题意,得x ⊗y +(2y )⊗x =x 2-y 2xy +(2y )2-x 22yx =x 2+2y 22xy ≥2x 2·2y 22xy=2,当且仅当x =2y 时取等号. 14.已知函数f (x )=lg(x +a x-2),其中a 是大于0的常数. (1)求函数f (x )的定义域;(2)当a ∈(1,4)时,求函数f (x )在[2,+∞)上的最小值;(3)若对任意x ∈[2,+∞)恒有f (x )>0,试确定a 的取值范围.解 (1)由x +a x -2>0,得x 2-2x +a x>0, 当a >1时,x 2-2x +a >0恒成立,定义域为(0,+∞),当a =1时,定义域为{x |x >0且x ≠1}, 当0<a <1时,定义域为{x |0<x <1-1-a 或x >1+1-a }.(2)设g (x )=x +a x-2,当a ∈(1,4),x ∈[2,+∞)时, g ′(x )=1-a x 2=x 2-a x2>0恒成立, 所以g (x )=x +a x-2在[2,+∞)上是增函数. 所以f (x )=lg ⎝⎛⎭⎫x +a x -2在[2,+∞)上是增函数. 所以f (x )=lg ⎝⎛⎭⎫x +a x -2在[2,+∞)上的最小值为f (2)=lg a 2. (3)对任意x ∈[2,+∞)恒有f (x )>0,即x +a x-2>1对x ∈[2,+∞)恒成立. 所以a >3x -x 2,令h (x )=3x -x 2,而h (x )=3x -x 2=-⎝⎛⎭⎫x -322+94在x ∈[2,+∞)上是减函数, 所以h (x )max =h (2)=2,所以a >2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二讲 分段函数及函数的单调性
一.分段函数
若函数在其定义域内,对于定义域内的不同取值区间,有着不同的对应关系,这样的函数通常叫做分段函数.
分段函数无论分成几段,都是一个函数,不要误解为是“由几个函数组成”.求分段函数的函数值,如果自变量的范围不确定,要分类讨论.
常见的命题类型有:
(1)分段函数的函数求值问题;
(2)分段函数的自变量求值问题;
(3)分段函数与函数性质、方程、不等式问题.
二.函数的单调性
1.单调性的定义
自左向右看图象是__________
自左向右看图象是_________
如果函数y =f (x )在区间D 上是增函数或减函数,那么就说函数y =f (x )在这一区间具有(严格的)_______,区间D 叫做函数y =f (x )的___________.
2.函数的最值
题型一分段函数的函数求值(域)问题
1.已知函数f (x )=⎩⎪⎨⎪⎧
log 2x ,x >0,3x +1,x ≤0,则f ⎝⎛⎭⎫f ⎝⎛⎭⎫14的值是________. 2. 若函数f(x)={x 2+1,x ≤1lgx,x >1
,则f(f(10))=( ) A .lg101 B .2 C .1 D .0
3.设定义在N 上的函数f (x )满足f (n )=⎩
⎨⎧-+)]18([13n f f n ),2000(),2000(>≤n n 试求f (2002)的值.
4.设函数f (x )=⎩⎪⎨⎪⎧
1x , x >1,-x -2,x ≤1,
则f (f (2))=________,函数f (x )的值域是________.
题型二 分段函数的自变量求值问题 1.已知f (x )=⎩⎨⎧ x 12,x ∈[0,+∞),|sin x |,x ∈⎝⎛⎭⎫-π2,0,若f (a )=12,则a =________. 2.已知函数f (x )=⎩⎪⎨⎪⎧ 2x -2,x ≤0,-log 3x ,x >0,且f (a )=-2,则f (7-a )=( ) A .-log 37 B .-34 C .-54 D .-74
3.已知函数f (x )=⎩⎪⎨⎪⎧ (a -1)x +1,x ≤1,a x -1,x >1,
若f (1)=12,则f (3)=________. 题型三 分段函数与函数性质、方程、不等式问题.
1.已知函数f (x )=⎩⎪⎨⎪⎧
x 2+2ax ,x ≥2,2x +1,x <2,若f (f (1))>3a 2,则a 的取值范围是________. 2.已知函数f (x )=⎩⎨⎧<-≥-),
2(2),2(2x x x 则f (lg30-lg3)=___________________; 不等式xf (x -1)<10的解集是___________________.
题型四.常见函数的单调性
一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、正弦函数、余弦函数、正切函数的单调性、单调区间。
题型五.判定函数的调性
1.f(x)图像 如图所示,请写出f(x)
的单调区间
2.判断下列函数的单调性
(1)y =x +
x
1(x>0);(对勾函数) (2) 设函数f (x )=b x a x ++(a >b >0),求f (x )的单调区间,并证明f (x )在其单调区间上的单调性.(真分数的性质)
(3) 讨论函数f (x )=1
2-x ax (a >0)在x ∈(-1,1)上的单调性.(分类讨论) (4) 指出函数y =log 3(x 2+2x -3)的单调区间,指出函数y =⎝ ⎛⎭⎪⎫
13-223+1x x 的单调区间。
题型六 函数单调性的简单应用
1.函数f (x )=⎩⎪⎨⎪⎧ 1x ,x ≥1,-x 2+2,x <1
的最大值为________. 2.已知函数f (x )的图象关于直线x =1对称,当x 2>x 1>1时,[f (x 2)-f (x 1)](x 2-x 1)<0恒成立,
设a =f ⎝⎛⎭
⎫-12,b =f (2),c =f (e),则a ,b ,c 的大小关系是_______________. 3.已知函数f (x )为R 上的减函数,则满足f(x-2)<f (1)的实数x 的取值区间是_____________.
4. 已知函数f (x )=⎩⎪⎨⎪⎧
(a -2)x -1,x ≤1,log a x ,x >1,若f (x )在R 上单调递增,则实数a 的取值区间为________.
函数单调性的应用
(1)求函数值域、最值;
(2)比较大小;
比较函数值的大小,应将自变量转化到同一个单调区间内,然后利用函数的单调性解决.
(3)解不等式
在求解与抽象函数有关的不等式时,往往是利用函数的单调性将“f ”符号脱掉,使其转化为具体的不等式求解.此时应特别注意函数的定义域.
(4)利用单调性求参数
视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数.
[提醒] ①若函数在区间[a ,b ]上单调,则该函数在此区间的任意子区间上也是单调的;②分段函数的单调性,除注意各段的单调性外,还要注意衔接点的取值.。
