自动控制原理__第二章习题答案
自动控制原理-第2章习题解答精选全文完整版

第2章 控制系统的数学模型习题及解答2-1 已知质量-弹簧系统如题2-1图所示,图中标明了质量和弹簧的弹性系数。
当外力F (t )作用时,系统产生运动,如果在不计摩擦的情况下,以质量m 2的位移y (t )为输出,外力F (t )为输入,试列写系统的运动方程。
解: 设 质量m 1的位移量为x (t ),根据牛顿第二定律有y k y x k dt yd m 21222-)(−= ①)(1221y x k F dtxd m −−= ②①式可以写作y k k x k dtyd m )(211222+−= ③由①式也可以得到y k dtyd m y x k 22221)(+=− ④③式两端同时求二阶导数,可得2221221442)(dty d k k dt x d k dt yd m +−= ⑤将②、③式代入⑤式中,整理可得F m k y m k k dty d m k m k m m dt y d m 1112122122121442)(=−++++ 2-2 求题2-2图中由质量-弹簧-阻尼器组成的机械系统,建立系统的运动方程。
其中,x (t )为基底相对于惯性空间的位移,y (t )为质量相对于惯性空间的位移。
z (t )= y (t )- x (t )为基底和质量之间的相对位移,z (t )由记录得到, x (t )和z (t )分别为输入量和输出量。
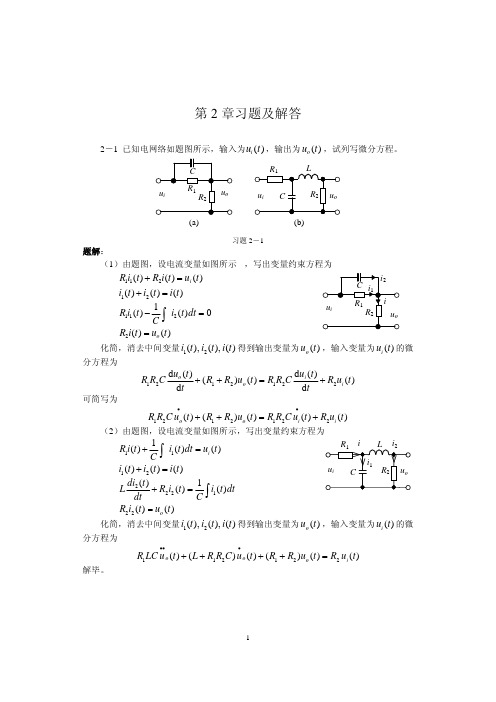
解:应用牛顿第二定律可得dtt dz f kz dt y d m )(22−−= 将z (t )= y (t )- x (t )代入上式,整理可得2222dtx d m kz dt dz f dt z d m −=++题2-2图题2-1图解:(a )引入中间变量u c (t)表示电容器两端的电压。
根据基尔霍夫电流定律有o c c u R u R dt du C2111=+ 根据基尔霍夫电压定律有o i c u u u −=联立消去中间变量,可得描述输入量u i (t )和输出量u o (t )之间关系的微分方程为i i o o u R dt du C u R R R R dt du C121211+=++ (b )引入回路电流i (t )和电容器两端的电压u c (t)作为中间变量,根据基尔霍夫电压定律有i o u u i R =+1 另有电容元件的元件约束关系方程dtdu Ci c =和i R u u o c 2−=联立求解,消去中间变量可得i i o o u R dt du C u R R R R dt du C121211+=++(c )设电容器C 2两端的电压为u c 2(t),根据基尔霍夫电流定律有dtduC u u R dt u u d C c o i o i 2211)(1)(=−+− ①求导可得22221221)(1)(dtu d C dt u u d R dt u u d C c o i o i =−+− ② 另有输出支路电压方程o c c u u dtdu C R =+2222 等式两边求导有dtdu dt du dt u d C R oc c =+222222 ③将①、②代入③式,整理可得i ii ooo u C R dt du C R C R C R dt u d C R u C R dt du C R C R C R C R dt u d C R 2121221121221212122112121122+++=++++2-4 试求题2-4图所示有源RC 电路的微分方程,其中u i (t )为输入量,u o (t )为输出量。
自动控制原理_王万良(课后答案2
第2章习题2.1 列写如图题2.1所示电路中以电源电压U 作为输入,电容1C ,2C 上的电压1c U 和2c U 作为输出的状态空间表达式。
图题2.1答案:X L R LL M C R M C M C R M C C X ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−−−−+−=211321321100)(& X y ⎥⎦⎤⎢⎣⎡=010001其中)(3221311C C C C C C R M ++=2.2 如图题2.2所示为RLC 网络,有电压源s e 及电流源s i 两个输入量。
设选取状态变量23121,,C C L u x u x i x ===;输出量为y 。
建立该网络动态方程,并写出其向量-矩阵形式(提示:先列写节点a ,b 的电流方程及回路电势平衡方程)。
图题2.2*答案:⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡−+⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡−−+−=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡s s e i C L L R C C L L L RR 0001100100111x x x 12121321&&&U 3+-se[]111−−−=R y ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x +[]⎥⎦⎤⎢⎣⎡s s e i R 11 2.3 列写图题2.3所示RLC 网络的微分方程。
其中,r u 为输入变量,c u 为输出变量图题2.3答案:r c cc u u dt du RC dtu d LC =++22 2.4 列写图题2.4所示RLC 网络的微分方程,其中r u 为输入变量,c u 为输出变量。
图题2.4答案:r c cc uu dt du R L dtu d LC =++22 2.5 图题2.5所示为一弹簧—质量—阻尼器系统,列写外力)(t F 与质量块位移)(t y 之间)(t图题2.5答案:)()()()(22t f t ky dt t dy f dtt y d m =++ 2.6 列写图题2.6所示电路的微分方程,并确定系统的传递函数,其中r u 为输入变量,cu 为输出变量。
自动控制原理第二章习题解答
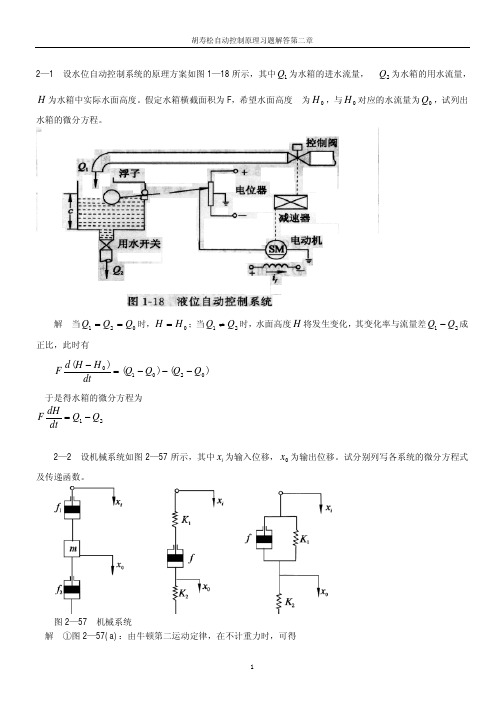
Z1 + Z2
R1 T1s +
1
+
1 C2
s
(T2
s
+
1)
R1C2 s + (T1s + 1)(T2 s + 1)
(b)以 K1 和 f1 之间取辅助点 A,并设 A 点位移为 x ,方向朝下;根据力的平衡原则,可列出如下原始方程:
K 2 (xi − x0 ) + f 2 (x&i − x&0 ) = f1 (x&0 − x&) (1)
+
C1C2
R
d 2u0 dt 2
整理得:
C1C2
R
d 2u0 dt 2
+
(C2
+
2C1 )
du0 dt
+ u0 R
=
C1C2 R
d 2ui dt 2
+ ui R
+
2C1
dui dt
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式的模态。
(1) 2x&(t) + x(t) = t;
所以:
f1 f2 s2 + ( f1 + f2 )s +1
X 0 (s) =
f1 f2s2 + ( f1K2 + K1 f2 )s + K1K2
= K1K2
K 1
K2
X i (s) f1 f2s2 + ( f1K2 + K1 f1 + K1 f2 )s + K1K2
f1 f2 s2 + ( f1 + f2 )s +1+ f1
自动控制原理C作业(第二章)答案
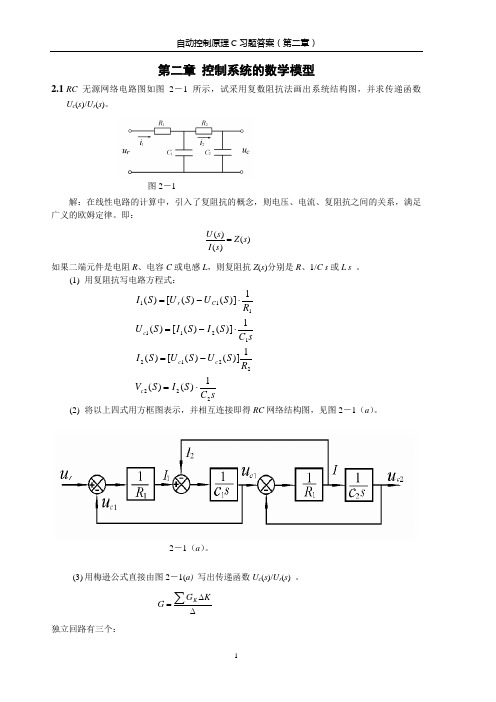
4 3
0.1
图 3-1 二阶控制系统的单位阶跃响应
解 在单位阶跃作用下响应的稳态值为 3,故此系统的增益不是 1,而是 3。系统模型为
(s)
s2
3
2 n
2n s
2 n
然后由响应的 p % 、 t p 及相应公式,即可换算出 、 n 。
p%
c(t p ) c() c()
4
3
3
33%
t p 0.1(s)
P1 G1G2
1 1
P2 G2G4
2 1
因此,传递函数为
C(s) P11 P2 2
R(s)
G2G1 G4G2 1 G1G2G3
3
自动控制原理 C 习题答案(第二章)
2.4 用梅森公式求系统传递函数。
R(S)
-
_
+ G1(s)
- _
G2(s)
+ C(S)
+
图 2-4 解: 单独回路 5 个,即
L1
1 R
1 C1S
1 R1C1S
11
1
L2
R2
C2S
R2C2 S
L3
1 C1S
1 R2
1 R2C1S
回路相互不接触的情况只有 L1 和 L2 两个回路。则
L12
L1L2
1 R1C1R2C2S 2
由上式可写出特征式为:
1
( L1
L2
L3 )
L1 L2
1
1 R1C1S
1 R2C2 S
1 R2C1S
1 R1C1R2C2S 2
益 K1 和速度反馈系数 Kt 。同时,确定在此 K1 和 Kt 数值下系统的延迟时间、上升时间和调节时间。
自动控制原理第二章习题答案详解
习题习题2-1 列写如图所示系统的微分方程习题2-1附图习题2-2 试建立如图所示有源RC网络的动态方程习题2-2附图习题2-3 求如图所示电路的传递函数, 并指明有哪些典型环节组成(a)(b)(c)习题2-3附图习题2-4 简化如图所示方块图, 并求出系统传递函数习题2-4附图习题2-5 绘制如下方块图的等效信号流图, 并求传递函数图(a)图(b)习题2-5附图习题2-6 系统微分方程组如下, 试建立对应信号流图, 并求传递函数。
),(d )(d )(),(d )(d ),()()()(),()(),(d )(d )(),()()(54435553422311121t y tt y T t x k t x k tt x t y k t x t x t x t x k t x t x k tt x t x t y t r t x +==--==+=-=τ习题2-7 利用梅逊公式直接求传递函数。
习题2-7附图习题2-8 求如图所示闭环传递函数, 并求(b)中)(s H x 的表达式, 使其与(a)等效。
图(a )图(b)习题2-8附图习题2-9 求如下各图的传递函数(a)(b)(c)习题2-9附图习题2-10 已知某些系统信号流图如图所示, 求对应方块图(a )(b)(c)(d)习题2-10附图习题答案习题2-1答案:解:设外加转矩M 为输入量,转角θ为输出量,转动惯量J 代表惯性负载,根据牛顿定律可得:θθθ1122d d d d k t f M tJ --=式中,1,1,k f 分别为粘性阻尼系数和扭转弹性系数,整理得:M k t f tJ =++θθθ1122d d d d习题2-2答案:解: 设r u 为输入量,c u 为输出量,,,,21i i i 为中间变量,根据运算放大器原理可得:1221d d R u i R u i t u c i r c c ===消去中间变量可得: r c c u R Ru t u C R 122d d -=+ 习题2-3答案: 解: (a)11111111221212211121121120++=+++=+++=+++=Ts Ts s R R R C R s C R R sC R sC R sC sC R R sC R u u i β其中:221121,R R R C R T +==β, 一阶微分环节,惯性环节.(b)21121212111221122011//1R R s C R R R s C R R R sC R R R sC R R u u i+++=++=+= 11111111212121221121111++=+∙++∙+=+++=Ts Ts s C R R R R s C R R R R R R s C R R s C R αα其中 α=+=21211,R R R T C R , 一阶微分环节,惯性环节.(c)s C R s C R s C R s C R s C R sC R R sC sC R u u i 21221122112211220)1)(1()1)(1(1//11+++++=+++= 由微分环节,二阶振荡环节组成。
孙亮版《自动控制原理》课后习题答案
t
F ( s ) = F1 ( s) + F2 ( s ) =
− s Aω ⋅ (1 + e ω ) 2 2 s +ω
π
(c) 由于信号 f (t ) 为周期信号,第一周期的信号如图所示, 其拉氏变换为
F1 ( s ) =
M 2 M −ηTs M −Ts M − e + e = (1 − 2e −ηTs + e −Ts ) s s s s F (s) = 1 ⋅ F1 ( s ) 1 − e −Ts
• •
忽略二次以上各项有
F ( x, i ) = F0 ( x0 , i0 ) + F x ( x, i ) x = x0 ⋅ ( x − x0 ) + F i ( x, i ) x = x0 ⋅ (i − i0 )
i =i0 i =i0
令
ΔF = F ( x, i ) − F0 ( x0 , i0 ) K x = F x ( x , i ) x = x0
→ F2 ( s ) = −
t0 f3(t)
f2(t)
1 1 −t 0 s 1 −t0 s 1 − e − t0 s (1 + t0 s ) F ( s ) = F1 ( s ) + F2 ( s ) + F3 ( s ) = 2 − 2 ⋅ e − t0 ⋅ ⋅ e = s s s s2 (b) 由于信号 f (t ) 可以分解为信号的组合如图所示, f(t) f1(t) f2(t) A Aω f1 (t ) = A sin ωt → F1 ( s ) = 2 2 s +ω 0 π π − s Aω π ω → F2 ( s ) = 2 ⋅e f 2 (t ) = sin ωt ⋅1(t − ) 2 ω s +ω ω
自动控制原理课后习题答案第二章

解:由图可得
联立上式消去中间变量U1与U2,可得:
2-8某位置随动系统原理方块图如图2-7所示。已知电位器最大工作角度,功率放大级放大系数为K3,要求:
(1) 分别求出电位器传递系数K0、第一级与第二级放大器得比例系数K1与K2;
(2) 画出系统结构图;
(3) 简化结构图,求系统传递函数。
证明:(a)根据复阻抗概念可得:
即 取A、B两点进行受力分析,可得:
整理可得:
经比较可以瞧出,电网络(a)与机械系统(b)两者参数得相似关系为
2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指出各方程式得模态。
(1)
(2)
2-7由运算放大器组成得控制系统模拟电路如图2-6所示,试求闭环传递函数Uc(s)/Ur(s)。
2-10试简化图2-9中得系统结构图,并求传递函数C(s)/R(s )与C(s)/N(s)。
图2-9 题2-10系统结构图
分析:分别假定R(s)=0与N(s)=0,画出各自得结构图,然后对系统结构图进行等效ቤተ መጻሕፍቲ ባይዱ换,将其化成最简单得形式,从而求解系统得传递函数。
解:(a)令N(s)=0,简化结构图如图所示:
可求出:
令R(s)=0,简化结构图如图所示:
所以:
(b)令N(s)=0,简化结构图如下图所示:
所以:
令R(s)=0,简化结构图如下图所示:
2-12 试用梅逊增益公式求图2-8中各系统信号流图得传递函 数C(s)/R(s)。
图2-11 题2-12系统信号流图
解:
(a)存在三个回路:
存在两条前向通路:
所以:
(3)简化后可得系统得传递函数为
自控原理习题解答(第二章)

[答2 ( 31 ) 1 ) ] (t) x(t) (t) Tx T sx(s) x (s) 1 1 1 T x (s) 1 T s 1 s T 1 t 1 T 1 1 T x ( t ) L x (s) L e 1 s T T
答2 4(c)
e y (s) e x (s) C2 1 1 I(s) R 1 R2 C1s C 2s R 2 C 1 C 2 s 2 C 1s 1 R 2 C1 C 2 s C1 2 (R1 R 2 )C1C 2 s C 2 s C1s (R1 R 2 )C1C 2 s C 2 C1 R 2 C1 C 2 s C1 (R1 R 2 )C1C 2 s C 2 C1 (R1 R 2 )C1C 2 s C 2 C1 R 2 C1 C 2 C1 s K d Td s C 2 C1 C 2 C1 K (R1 R 2 )C1C 2 s (R1 R 2 )C1C 2 s Td s 1 T s 1 1 1 C 2 C1 C 2 C1 为实际微分环节 惯性环节 1 I(s) (R 2 ) C 2s
X(s) G1 G1 H3 H2 H1
-
Y(s) G2
G3
G4 X(s)
G1
-
-
G2 H3
-
Y(s) G3 G4
-
H2
G4 H3
1 2e 2t e t cos 3t 3s2 2s 8 8 A s 1 2 s(s 2)(s 2s 4) s 0 2 4 3s2 2s 8 B (s 2) 2 2 s(s 2)(s 2s 4) s 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1试建立如图 所示电路的动态微分方程。
解:输入u i 输出u ou 1=u i -u oi 2=C du 1 dt )- R 2(u i -u o )=R 1u 0-CR 1R 2( du i dt dt du oC + - -i u o R 1R 2 i 1 i i 2u 1i 1=i-i 2 u o i= R 2u 1 i 1= R 1 = u i -u o R 1 dt d (u i -u o ) =C C d (u i -u o ) dtu o - R 2 = u i -u o R 1 CR 1R 2 du o dt du idt +R 1u o +R 2u 0=CR 1R 2 +R 2u i(a)i=i 1+i 2 i 2=C du 1dt u o i 1= R 2 u 1-u o = L R 2 du o dt R1i= (u i -u 1) (b)C+-iu o R 1R 2i 1 ii 2Lu 1 = R 1 u i -u 1 u o +C R 2 du 1 dtu 1=u o + L R 2 du odt du o dt R 1R 2 L du o dt + CL R 2 d 2u o dt 2 = - - u i R 1 u o R 1 u o R 2 +C )u o R 1R 2 L du o dt ) CL R 2 d 2u o dt 2 = + +( u i R 1 1 R 11 R 2+(C+ 解:2-2 求下列函数的拉氏变换。
(1)t t t f 4cos 4sin )(+=(2)te t tf 43)(+= (3)tte t f --=1)( (4)t e t t f 22)1()(-= 解:(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s s+42+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t 解:L [t 3+e 4t ]= 3!s 41s-4+ 6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:解:2-3求下列函数的拉氏反变换。
(1))3)(2(1)(+++=s s s s F (2) )2()1()(2++=s s ss F (3) )1(152)(22++-=s s s s s F (4) )2)(34(2)(2++++=s s s s s FA 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解:A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-(2) F(s)=s (s+1)2(s+2)F(s)=-2e -2t -te -t +2e -t解:= A 2s+1s+2+ A 3+ A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0解:= s +A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=j-5j-1=-A 1+jA 2 A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解:=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34A 2= +3e 212-4+f(t)=-t 32e -3t-t e -t 1= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)]t t t f sin 5cos 1)(-+=2-4 解下列微分方程 6)(6)(5)(22=++t y dt t dy dtt y d 初始条件:2)0()0(==yy A 1=1y(t)=1+5e -2t -4e -3tA 2=5 A 3=-4Y(s)=6+2s 2+12s s(s 2+5s+6)解:s 2Y(s)-sy(0)-y'(0)+5sY(s)-5y(0)+6Y(s)= 6ss 2Y (s )-2s-2+5sY (s )-10+6Y (s )= 6s= A 1s+2s+3+ A 3s + A 22-5试画题图所示电路的动态结构图,并求传递函数。
(1)+解:( U r (s)U c (s)=1R 11+(+sC)R21R 1+sC)R 2=R 2+R 1R 2sC R 1+R 2+R 1R 2sC(2)+C+--u ru c R 1R 2Lu 1i 2i 1iI(s)U r (s)_1R 1U 1(s)解:I 1(s)-I 2(s)L 1=-R 2 /Ls L 2=-/LCs 2L 3=-1/sCR 1L 3Δ1=1L 1 L 3=R 2/LCR 1s 21CsU 1(s)U c (s)-1LsR 2R 2I 1(s)U c (s)L 1L 2P 1=R 2/LCR 1s 2U =R 1CLs 2+(R 1R 2C+L)s+R 1+R 2r (s)U c (s)R 22-6用运算放大器组成的有源电网络如图所示,试采用复数阻抗法写出它们的 传递函数。
解:电路等效为:U U IR 1O R 3SCR 2R 21SC ·+1+=-U -O=R 3+SC R 2R 2+1-∞△++CR 1R2R3u i u oR 1+R 3+R 2R 3CS =-R 1(R 2SC+1)R 2R 3=-( + )R 1(R 2SC+1)R 11R 1R 2=-( +R 3)(R 2SC+1)=R 21R3R 2SC ++R 1-2-8设有一个初始条件为零的系统,当其输入端作用一个脉冲函数δ(t)时,它的输出响应c(t)如图所示。
试求系统的传递函数。
c(t)tTδ解:c(t)=K (t-T)K T t-T C(s)=K (1-e )Ts 2-TS C(s)=G(s)2-9 若某系统在阶跃输入作用r(t)=1(t)时,系统在零初始条件下的输出响应为:t t e e t c --+-=21)(,试求系统的传递函数。
解:G(s)=C(s)/R(s)=(s+1)(s+2)(s 2+4s+2)C(s)=(s+1)(s+2)(s 2+4s+2)脉冲响应:2s +2=1+1s +1-c(t)=δ(t)+2e -2t -e -t2-10 已知系统的微分方程组的拉氏变换式,试画出系统的动态结构图并求传递函数)()(s R s C 。
)()]()()[()()()(87111s C s G s G s G s G s R s X --= )]()()()[()(36122s X s G s X s G s X -=)()]()()([)(3523s G s G s C s X s X -= )()()(34s X s G s C =解:X 1(s)=R(s)G 1(s)-G 1(s)[G 7(s)-G 8(s)]C(s)X 2(s)=G 2(s)[X 1(s)-G 6(s)X 3(s)]X 3(s)=G 3(s)[X 2(s)-C(s)G 5(s)]G 1G 2G 3G 5---C(s)-R(s)G 4G 6G 8G 7={R(s)-C(s)[G 7(s)-G 8(s)]}G 1(s)C(s)[G 7(s)-G 8(s)]G 6(s)X 3(s)X 1(s)X 2(s)C (s)G 5(s)X 3(s)G 1G 2G 5-C(s)-R(s)G 7-G 8G 1+G 3G 2G 63G 4G 1G 2G 3G 5---C(s)-R(s)G 4G 6G8G 7G -C(s)R(s)G 7-G 81+G 3G 2G 6 +G 3G 4G 51G 2G 3G 4C 1+G 3G 2G 6 +G 3G 4G 5+G 1G 2G 3G 4(G 7 -G 8)G 1G 2G 3G 4R (s )(s )=2-11 已知控制系统结构图如图所示,试分别用结构图等效变换和梅逊公式求系统传递函数)()(s R s C 。
解:(a)解:(b)求系统的传递函数R (s )C (s )=1+G 1G 2H +G 1G 4HG 1G 2+G 2G 3+G 1G 2G 3G 4 H L 1=-G 1G L 2=-G 1G 4H P 1=G 1G 2Δ1 =1P 2=G 3G 2Δ=1+G 1G 4H+G 1G 2H Δ2=1+G 1G 4H(c)C(s)R(s)1+G 1G 2+G 1H 1–G 3H 1G 1G 2(1–G 3H 1)=H_G 1+C(s)R(s)G 2(d)解: (1)_G 1+C(s)R(s)G 2HG 2C(s)1+G 2H 1(G 1+G 2 )R(s)=(2)L 1L 1=-G 2H P 1=G 1Δ1 =1P 2=G 2Δ2 =1C(s)1+G 2H1(G 1+G 2 )R(s)= -_G 1+C(s)R(s)G 2G 3G 4(e)解: (1)_C(s)R(s)G 1+G 2G 3-G 4C(s)=R(s)1+(G 1+G 2)(G 3-G 4)(G 1+G 2)L 1L 2L 3L 4L 2=G 1G 4L 3=-G 2G 3L 4=G 2G 4(2)L 1=-G 1G 3P 1=G 1Δ1=1P 2=G 2Δ2=11+G 1G 3+G 2G 3–G 1G 4-G 2G 4=(G 1+G 2)C(s)R(s)_G 1+C(s)R(s)G 2(f)G _C(s)R(s)G 11-G 22C(s)G =R(s)1+1-G21G 1G 21+G 1G 2–G 2G 1(1–G 2)=解: (1)(2)L 1L 1=-G 1G 2L 2L 2=G 2P 1=G 1Δ1=1-G 2Δ=1+G 1G 2-G 2C(s)R(s)1+G 1G 2–G 2G 1(1–G 2)=2-12求图所示系统的传递函数)()(s R s C ,)()(s D s C 。
解:(a)D (s )C (s )C R (s )(s )L 1=G 2H 2L 2=-G 1G 2H 3Δ1P 1=G 1G 21-G 2H 2+G 1G 2H 3G 2G 1=R (s )C (s )L 1=G 2H2L 2=-G 1G 2H 3P 1=G 2Δ1=1P 2=-G 1G 2H 1Δ2=11-G 2H 2+G 1G 2H 3G 2(1-G 1H 1 )=D (s )C (s )(b)求:(C D s )(s )C R (s )(s )解:L 1=-G 1G 2L 2=-G 1G 2H Δ1=1P 1=G 1G 21+G 1G 2H+G 1G 2G 1G 2=R (s )C (s )P 1=G n G 2Δ1=1P 2=1Δ2=1+G 1G 2HD (s )C (s )1+G 1G 2+G 1G 2H=1+G n G 2+G 1G 2H2-13求图所示系统的传递函数)()(s R s C ,)()(s R s E 。
