CCER 计量经济学 第三次作业和答案
计量经济学(第四版)第三章练习题及答案
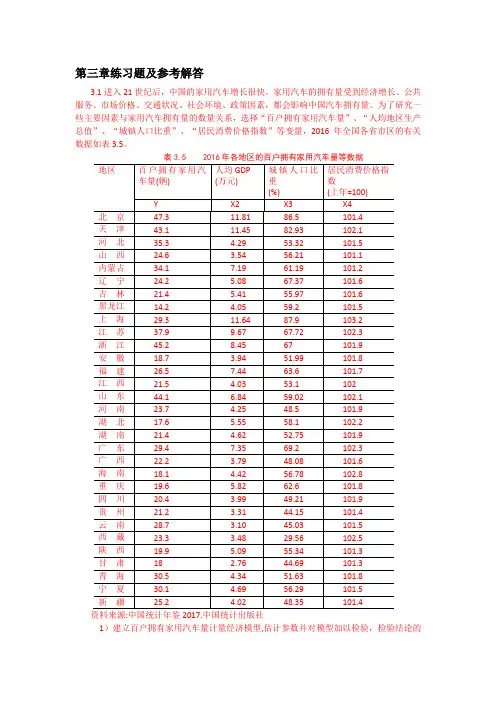
第三章练习题及参考解答3.1进入21世纪后,中国的家用汽车增长很快。
家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素,都会影响中国汽车拥有量。
为了研究一些主要因素与家用汽车拥有量的数量关系,选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量,2016年全国各省市区的有关数据如表3.5。
表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1)建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验,检验结论的依据是什么?。
2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】:1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007,可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。
解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=,表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。
2)X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。
由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。
汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。
CCER 计量经济学 第三次作业和答案

Intermediate Econometrics Class 1Problem Set 3 with AnswersHandout Date: Dec. 4th, 2011Due Date: Dec. 9th, 2011 (Hand in BEFORE class)1.An estimated equation iswith, and SSR = 1.5Use F-statistic to test the following(1).(2).(3).(Hint: The tests involve only the sub-matrix in the lower-right corner of .Refer to TA materials for the formula of inverses of partitioned matrices.)(1).equals the single element at the lower right-hand corner of,which is 2.5.Then the F-statistic is calculated asIt falls well short of any usually critical value for . So we cannot reject .(2).only involves the elements in the sub-matrix in the lowerright-hand corner ofThe F-statistic equalsFrom the tables of F distribution, , so we cannot reject the null at5% significance level.(3).Thus the test statistic becomesAgain, the test statistic falls well short of any usually critical value for . So wecannot reject .2. A four-variable regression using quarter data from 1958 to 1976 inclusive gave an estimatedequationThe explained sum of squares was 109.6, and the residual sum of squares, 18.48.(1).When the equation was re-estimated with three seasonal dummies added to thespecification, the explained sum of squares rose to 114.8. Test for the presence of seasonality.To test for the presence of seasonality we test the joint significance of the three seasonal dummy variables. The restricted is 18.48, while the unrestricted isThe rule-of-thumb F-statistic is calculated asThe 5% critical value is (is usually not given in statistic tables,so here we use the instead). We can reject the hypothesis of no seasonality at 5%significance level.(2).Two further regressions based on the original specification were run for the sub-periods1958.1 to 1968.4 and 1969.1 to 1976.4, yielding residual sums of squares of 9.32 and 7.46, respectively. Test for the constancy of the relationship over the two sub-periods.To test the parameter consistency over the two sub-samples, consider the Chow test,The 5% critical value is . Hence we cannot reject the hypothesis ofparameter constancy at 5% significance level.3.Survey records for a large sample of families show the following weekly consumptionexpenditure (Y) and weekly income (X):Y 70 76 91 …… 120 146 135 X 80 95 105 …… 155 165 175* * *Families with an asterisk (*) reported that their income is higher than in the previous year.(1).To examine the impact of weekly income on weekly consumptions, one sets up thefollowing modelHe is concerned that the error terms may have heterogeneous variance. Derive the robust standard error of .Under HSK, the large sample distribution of isThe sample estimate of iswhereThe robust standard error of is the 2nd diagonal element of the estimated covariancematrix of(2).If he wants to estimate directly the elasticity of consumption with respect of income, howshould he modify the model in (1).(3).If he wants to test whether the event of an increase in income, holding the level of incomeunchanged, helps to explain the consumption behavior, how should he extend the model in (1)?(4).If he wants to test whether the marginal propensity to consume (the slope coefficient) offamilies experiencing an increase in income is different from that of families who did not experience an increase, how should he extend the model in (3)?4.Consider the equationwhere is the cumulative college grade point average, is size of high schoolgraduating class, in hundreds, is academic percentile in graduating class, iscombined SAT score, is a dummy gender variable, and is a dummy variablewhich is one for student-athletes.(1).What are your expected signs for the coefficients in this equation? Explain.Holding all other variables constant, the expected sign for high school size should be negative, but at a diminishing rate, because larger high schools tend to have lower teacher-to-student ratios, and the effect becomes less important as the size increase. The higher sat should be positively related to GPA. So should hsperc and female (why should this be the case might be controversial; either because female students tend to study harder to overcome gender discrimination in society, or they tend to take classes where they excel more). I suppose the coefficient for athlete might be negative. However, this might just be my own prejudice.(This answer is provided by the solution manual of Introductory Econometrics: A Modern Approach. It is only for your reference. You’ll receive full credit so long your arguments make sense.)(2).To allow the effect of being an athlete to differ by gender, how should you extend themodel? Write out the null hypothesis if you want to test whether there is no ceteris paribus difference between women athletes and women nonalthletes.Adding to the model we have:In this setup, the intercepts for 4 different categories are:Male non-athleteMale athleteFemale non-athleteFemale athleteSo the test between female athletes and female non-athletes is the test of5.One application of ADL models is the Adaptive Expectation Model:⁄(5.1)⁄(5.2)wheredemand for moneyinterest rate (observables)equilibrium, optimum, or expected long-run interest rate (unobservable)the coefficient of expectation (,)Rewrite Eq.(5.2)⁄(5.3)Substitute Eq. (5.3) into Eq. (5.2)⁄(5.4)(1).Lag Eq. (5.1) one period, then substitute it into Eq. (5.4). You should be able to show thatthe short-run demand is in essence an ADL process of the observables. Write outthe model, and calculate the long-run impact multiplier of .The ADL model isUse lag operator to rewrite the modelThe long-run impact multiplier of isNote the long-run impact multiplier of in the short-rum model is essentially the coefficientof in Eq. (5.1), the equilibrium/long-run model.(2).Now consider another application that incorporates the partial adjustment of into theAdoptive Expectations Model:where are defined as in (1), and:actual capital stock (observable)desired level of capital (unobservable)the coefficient of adjustmentShow that the observed short-run demand is in essence an ADL process. (Hint: Ifyou derive the model correctly, you will find the error terms are serially correlated.)The ADL model is。
(完整word版)计量经济学习题与答案(word文档良心出品)

第一章绪论1-14.计量经济模型中为何要包括随机误差项?简述随机误差项形成的原因。
答:由于客观经济现象的复杂性,以至于人们目前仍难以完全地透彻地了解它的全貌。
对于某一种经济现象而言,往往受到很多因素的影响,而人们在认识这种经济现象的时候,只能从影响它的很多因素中选择一种或若干种来说明。
这样就会有许多因素未被选上,这些未被选上的因素必然也会影响所研究的经济现象。
因此,由被选因素构成的数学模型与由全部因素构成的数学模型去描述同一经济现象,必然会有出入。
为使模型更加确切地说明客观经济现象,所以有必要引入随机误差项。
随机误差项形成的原因:①在解释变量中被忽略的因素;②变量观测值的观测误差;③模型的关系误差或设定误差;④其他随机因素的影响。
第二章 一元线性回归模型例1、令kids 表示一名妇女生育孩子的数目,educ 表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为μββ++=educ kids 10(1)随机扰动项μ包含什么样的因素?它们可能与教育水平相关吗?(2)上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗?请解释。
解答:(1)收入、年龄、家庭状况、政府的相关政策等也是影响生育率的重要的因素,在上述简单回归模型中,它们被包含在了随机扰动项之中。
有些因素可能与增长率水平相关,如收入水平与教育水平往往呈正相关、年龄大小与教育水平呈负相关等。
(2)当归结在随机扰动项中的重要影响因素与模型中的教育水平educ 相关时,上述回归模型不能够揭示教育对生育率在其他条件不变下的影响,因为这时出现解释变量与随机扰动项相关的情形,基本假设4不满足。
例2.已知回归模型μβα++=N E ,式中E 为某类公司一名新员工的起始薪金(元),N 为所受教育水平(年)。
随机扰动项μ的分布未知,其他所有假设都满足。
(1)从直观及经济角度解释α和β。
(2)OLS 估计量αˆ和βˆ满足线性性、无偏性及有效性吗?简单陈述理由。
庞皓计量经济学第三版课后习题及答案 顶配
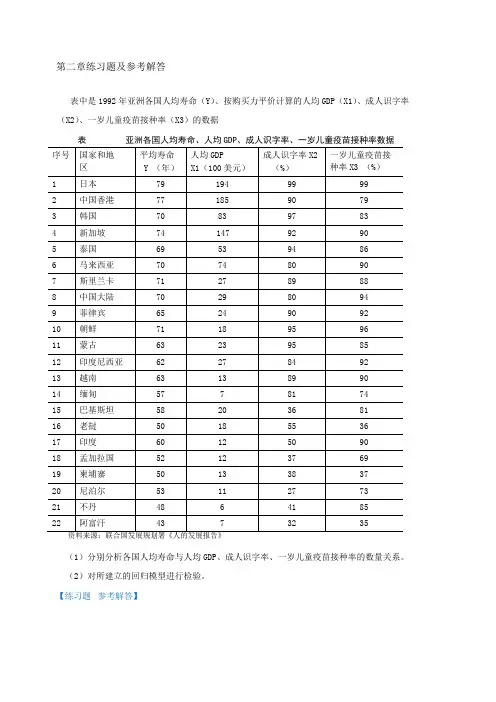
第二章练习题及参考解答表中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
计量经济学3答案

8、修正可决系数与未经修正的多重可决系数之间的关系为(
A)
(A)
(B)
(C)
(D)
9、回归方程的显著性检验的F检验量为( A )
(A) (B) (C) (D) 10、F统计量与可决系数R2之间的关系为( A )
(A)(B) (C) (D) 11、多重可决系数R2是指( C )
(A)残差平方和占总离差平方和的比重(B)总离差平方和
(A) (B)(C) (D)/k-1
14、用一组有30个观测值的样本估计模型后,在0.05的显著性
水平下对的显著性做t检验,则显著地不等于零地条件是其统
计量大于等于( C )
(A)t0.05(30) (B)t0.025(28)(C)t0.025(27) (D)F0.025(1,28) 15、在模型古典假定满足的条件下,多元线性回归模型的最小
第三章 多元线性回归模型
一、单项选择题
1、多元线性回归模型的“线性”是指对( C )而言是线性的。
(A)解释变量
(B)被解释变量(C)回归参数
(D)剩余项
2、多元样本线性回归函数是( B )
(A)
(B)
(C)(D)Y=Xβ+U
3、多元总体线性回归函数的矩阵形式为( A )
(A)Y=Xβ+U
(B)Y=X
(1) 建立该地区城镇居民人均全年耐用消费品支出关于 人均年可支配收入和耐用消费品价格指数的回归模型:
(2)估计参数结果
由估计和检验结果可看出,该地区人均年可支配收入的 参数的t检验值为10.54786,其绝对值大于临界值 ;而且对应的P值为0.0000,也明显小于 。说明人均年可支配收入对该地区城镇居民人均全年耐
F=146.2974 (3) 检验户主受教育年数对家庭书刊消费是否有显 著影响: 由估计检验结果, 户主受教育年数参数对应的t 统 计量为10.06702, 明显大于t的临界值
计量经济学习题及参考答案

计量经济学各章习题第一章绪论1.1试列出计量经济分析地主要步骤.1.2计量经济模型中为何要包括扰动项?1.3什么是时间序列和横截面数据? 试举例说明二者地区别1.4估计量和估计值有何区别?第二章计量经济分析地统计学基础2.1名词解释随机变量概率密度函数抽样分布样本均值样本方差协方差相关系数标准差标准误差显著性水平置信区间无偏性有效性一致估计量接受域拒绝域第I 类错误2.2请用例 2.2中地数据求北京男生平均身高地99%置信区间.2.325 个雇员地随机样本地平均周薪为130元,试问此样本是否取自一个均值为120 元、标准差为10 元地正态总体?文档收集自网络,仅用于个人学习2.4某月对零售商店地调查结果表明,市郊食品店地月平均销售额为2500 元,在下一个月份中,取出16 个这种食品店地一个样本,其月平均销售额为2600 元,销售额地标准差为480 元.试问能否得出结论,从上次调查以来,平均月销售额已经发生了变化?文档收集自网络,仅用于个人学习第三章双变量线性回归模型3.1判断题(判断对错;如果错误,说明理由)(1)OLS 法是使残差平方和最小化地估计方法.(2)计算OLS 估计值无需古典线性回归模型地基本假定.(3)若线性回归模型满足假设条件(1)~(4),但扰动项不服从正态分布,则尽管OLS 估计量不再是BLUE ,但仍为无偏估计量.文档收集自网络,仅用于个人学习(4)最小二乘斜率系数地假设检验所依据地是t 分布,要求地抽样分布是正态分布.2(5)R2=TSS/ESS.(6)若回归模型中无截距项,则.(7)若原假设未被拒绝,则它为真.(8)在双变量回归中,地值越大,斜率系数地方差越大.3.2设和分别表示Y 对X 和X 对Y 地OLS 回归中地斜率,证明r 为X 和Y 地相关系数.3.3证明:(1)Y 地真实值与OLS 拟合值有共同地均值,即;(2)OLS 残差与拟合值不相关,即.3.4证明本章中( 3.18)和( 3.19)两式:(1)(2)3.5考虑下列双变量模型:模型1:模型2:(1)1 和1地OLS 估计量相同吗?它们地方差相等吗?(2)2 和2地OLS 估计量相同吗?它们地方差相等吗?3.6有人使用1980-1994 年度数据,研究汇率和相对价格地关系,得到如下结果:其中,Y=马克对美元地汇率X=美、德两国消费者价格指数(CPI)之比,代表两国地相对价格(1)请解释回归系数地含义;(2)X t 地系数为负值有经济意义吗?(3)如果我们重新定义X 为德国CPI与美国CPI之比,X 地符号会变化吗?为什么?3.7随机调查200 位男性地身高和体重,并用体重对身高进行回归,结果如下:其中Weight 地单位是磅(lb ),Height 地单位是厘米(cm).(1)当身高分别为177.67cm、164.98cm、187.82cm 时,对应地体重地拟合值为多少?(2)假设在一年中某人身高增高了 3.81cm,此人体重增加了多少?3.8设有10 名工人地数据如下:X 10 7 10 5 8 8 6 7 9 10Y 11 10 12 6 10 7 9 10 11 10 其中X= 劳动工时,Y= 产量(1)试估计Y=α+βX + u(要求列出计算表格);(2)提供回归结果(按标准格式)并适当说明;(3)检验原假设β=1.0.3.9用12 对观测值估计出地消费函数为Y=10.0+0.90X ,且已知=0.01,=200,=4000,试预测当X=250 时Y 地值,并求Y 地95%置信区间.文档收集自网络,仅用于个人学习3.10设有某变量(Y)和变量(X)1995—1999 年地数据如下:(3)试预测X=10 时Y 地值,并求Y 地95%置信区间.3.11根据上题地数据及回归结果,现有一对新观测值X =20,Y=7.62,试问它们是否可能来自产生样本数据地同一总体?文档收集自网络,仅用于个人学习3.12有人估计消费函数,得到如下结果(括号中数字为t 值):=15 + 0.81 =0.98(2.7)(6.5)n=19(1)检验原假设:=0(取显著性水平为5%)(2)计算参数估计值地标准误差;(3)求地95%置信区间,这个区间包括0 吗?3.13试用中国1985—2003 年实际数据估计消费函数:=α+β + u t其中:C代表消费,Y 代表收入.原始数据如下表所示,表中:Cr=农村居民人均消费支出(元)Cu=城镇居民人均消费支出(元)Y =国内居民家庭人均纯收入(元) Yr =农村居民家庭人均纯收入(元) Yu=城镇居民家庭人均可支配收入(元) Rpop=农村人口比重(%) pop=历年年底我国人口总数(亿人)P=居民消费价格指数(1985=100)Pr=农村居民消费价格指数(1985=100)Pu=城镇居民消费价格指数(1985=100)数据来源:《中国统计年鉴2004》使用计量经济软件,用国内居民人均消费、农村居民人均消费和城镇居民人均消费分别对各自地人均收入进行回归,给出标准格式回归结果;并由回归结果分析我国城乡居民消费行为有何不同.文档收集自网络,仅用于个人学习第四章多元线性回归模型4.1某经济学家试图解释某一变量Y 地变动.他收集了Y 和 5 个可能地解释变量~地观测值(共10 组),然后分别作三个回归,结果如下(括号中数字为t 统计量):文档收集自网络,仅用于个人学习( 1) = 51.5 + 3.21 R=0.63(3.45) (5.21)2) 33.43 + 3.67 + 4.62 + 1.21 R=0.75 文档收集自网络,仅用于个人学(3.61 )(2.56)(0.81) (0.22)3) 23.21 + 3.82 + 2.32 + 0.82 + 4.10 + 1.21(2.21 )(2.83)(0.62) (0.12) (2.10) (1.11)文档收集自网络,仅用于个人学习R=0.80 你认为应采用哪一个结果?为什么?4.2为研究旅馆地投资问题,我们收集了某地地1987-1995 年地数据来估计收益生产函数R=ALKe ,其中R=旅馆年净收益(万年) ,L=土地投入,K=资金投入, e 为自然对数地底.设回归结果如下(括号内数字为标准误差) :文档收集自网络,仅用于个人学习= -0.9175 + 0.273lnL + 0.733lnK R=0.94(0.212) (0.135) (0.125)(1)请对回归结果作必要说明;( 2)分别检验α和β 地显著性;( 3)检验原假设:α =β = 0;4.3我们有某地1970-1987 年间人均储蓄和收入地数据,用以研究1970-1978 和1978 年以后储蓄和收入之间地关系是否发生显著变化. 引入虚拟变量后,估计结果如下(括号内数据为标准差) :文档收集自网络,仅用于个人学习= -1.7502 + 1.4839D + 0.1504 - 0.1034D·R=0.9425 文档收集自网络,仅用于个人学习(0.3319) (0.4704) (0.0163) (0.0332)其中:Y=人均储蓄,X=人均收入,D= 请检验两时期是否有显著地结构性变化.4.4说明下列模型中变量是否呈线性,系数是否呈线性,并将能线性化地模型线性化.(1)(2)(3)4.5有学者根据某国19年地数据得到下面地回归结果:其中:Y=进口量(百万美元),X1 =个人消费支出(百万美元),X2 =进口价格/国内价格.(1)解释截距项以及X1和X2系数地意义;(2)Y 地总变差中被回归方程解释地部分、未被回归方程解释地部分各是多少?(3)进行回归方程地显著性检验,并解释检验结果;(4)对“斜率”系数进行显著性检验,并解释检验结果.4.6由美国46个州1992年地数据,Baltagi 得到如下回归结果:其中,C=香烟消费(包/人年),P=每包香烟地实际价格Y=人均实际可支配收入(1)香烟需求地价格弹性是多少?它是否统计上显著?若是,它是否统计上异于-1?(2)香烟需求地收入弹性是多少?它是否统计上显著?若不显著,原因是什么?(3)求出.4.7有学者从209 个公司地样本,得到如下回归结果(括号中数字为标准误差):其中,Salary=CEO 地薪金Sales=公司年销售额roe=股本收益率(%)ros=公司股票收益请分析回归结果.4.8为了研究某国1970-1992 期间地人口增长率,某研究小组估计了下列模型:其中:Pop=人口(百万人),t=趋势变量,.(1)在模型 1 中,样本期该地地人口增长率是多少?(2)人口增长率在1978 年前后是否显著不同?如果不同,那么1972-1977和1978-1992 两时期中,人口增长率各是多少?文档收集自网络,仅用于个人学习4.9设回归方程为Y= β0+β1X1+β2X2+β3X3+ u, 试说明你将如何检验联合假设:β1= β2 和β3 = 1 .文档收集自网络,仅用于个人学习4.10下列情况应引入几个虚拟变量,如何表示?(1)企业规模:大型企业、中型企业、小型企业;(2)学历:小学、初中、高中、大学、研究生.4.11在经济发展发生转折时期,可以通过引入虚拟变量来表示这种变化.例如,研究进口消费品地数量Y 与国民收入X 地关系时,数据散点图显示1979 年前后明显不同.请写出引入虚拟变量地进口消费品线性回归方程.文档收集自网络,仅用于个人学习4.12柯布-道格拉斯生产函数其中:GDP=地区国内生产总值(亿元)K=资本形成总额(亿元)L= 就业人数(万人)P=商品零售价格指数(上年=100)试根据中国2003 年各省数据估计此函数并分析结果.数据如下表所示第五章模型地建立与估计中地问题及对策5.1判断题(判断对错;如果错误,说明理由)(1)尽管存在严重多重共线性,普通最小二乘估计量仍然是最佳线性无偏估计量(BLUE ).(2)如果分析地目地仅仅是为了预测,则多重共线性并无妨碍. (3)如果解释变量两两之间地相关系数都低,则一定不存在多重共线性. (4)如果存在异方差性,通常用地t 检验和 F 检验是无效地. (5)当存在自相关时,OLS 估计量既不是无偏地,又不是有效地.(6)消除一阶自相关地一阶差分变换法假定自相关系数必须等于 1. (7)模型中包含无关地解释变量,参数估计量会有偏,并且会增大估计量地方差,即增大误差.(8)多元回归中,如果全部“斜率”系数各自经t 检验都不显著,则R2值也高不了.(9)存在异方差地情况下,OLS 法总是高估系数估计量地标准误差.(10)如果一个具有非常数方差地解释变量被(不正确地)忽略了,那么OLS 残差将呈异方差性.5.2考虑带有随机扰动项地复利增长模型:Y 表示GDP,Y0是Y 地基期值,r 是样本期内地年均增长率,t 表示年份,t=1978,⋯,2003.文档收集自网络,仅用于个人学习试问应如何估计GDP 在样本期内地年均增长率?5.3 检验下列情况下是否存在扰动项地自相关 .(1) DW=0.81,n=21,k=3(2)DW=2.25,n=15,k=2(3)DW=1.56,n=30,k=55.4有人建立了一个回归模型来研究我国县一级地教育支出:Y= β0+β1X1+β 2X2+β3X3+u其中:Y,X1,X2 和X3分别为所研究县份地教育支出、居民人均收入、学龄儿童人数和可以利用地各级政府教育拨款.文档收集自网络,仅用于个人学习他打算用遍布我国各省、市、自治区地100 个县地数据来估计上述模型.(1)所用数据是什么类型地数据?(2)能否采用OLS 法进行估计?为什么?(3)如不能采用OLS 法,你认为应采用什么方法?5.5试从下列回归结果分析存在问题及解决方法:(1)= 24.7747 + 0.9415 - 0.0424 R=0.9635SE:(6.7525)(0.8229)(0.0807)其中:Y=消费,X2=收入,X3=财产,且n=5000 (2)= 0.4529 - 0.0041t R=0.5284t:(-3.9606) DW=0.8252其中Y= 劳动在增加值中地份额,t=时间该估计结果是使用1949-1964 年度数据得到地.5.6工资模型:wi=b0+b1Si+b2Ei+b3Ai+b4Ui+ui其中Wi=工资,Si=学校教育年限,Ei=工作年限,Ai=年龄,Ui=是否参加工会.在估计上述模型时,你觉得会出现什么问题?如何解决?5.7你想研究某行业中公司地销售量与其广告宣传费用之间地关系.你很清楚地知道该行业中有一半地公司比另一半公司大,你关心地是这种情况下,什么估计方法比较合理.假定大公司地扰动项方差是小公司扰动项方差地两倍.文档收集自网络,仅用于个人学习(1)若采用普通最小二乘法估计销售量对广告宣传费用地回归方程(假设广告宣传费是与误差项不相关地自变量),系数地估计量会是无偏地吗?是一致地吗?是有效地吗?文档收集自网络,仅用于个人学习(2)你会怎样修改你地估计方法以解决你地问题?(3)能否对原扰动项方差假设地正确性进行检验?5.8考虑下面地模型其中GNP=国民生产总值,M =货币供给. (1)假设你有估计此模型地数据,你能成功地估计出模型地所有系数吗?说明理由.(2)如果不能,哪些系数可以估计?(3)如果从模型中去掉这一项,你对(1)中问题地答案会改变吗?(4)如果从模型中去掉这一项,你对(1)中问题地答案会改变吗?5.9采用美国制造业1899-1922年数据,Dougherty得到如下两个回归结果:(1)(2)其中:Y=实际产出指数,K=实际资本投入指数,L =实际劳动力投入指数,t=时间趋势(1)回归式(1)中是否存在多重共线性?你是如何得知地?(2)回归式(1)中,logK 系数地预期符号是什么?回归结果符合先验预期吗?为什么会这样?(3)回归式(1)中,趋势变量在其中起什么作用?(4)估计回归式(2)背后地逻辑是什么?(5)如果(1)中存在多重共线性,那么(2)式是否减轻这个问题?你如何得知?(6)两个回归地R2可比吗?说明理由.5.10有人估计了下面地模型:其中:C=私人消费支出,GNP=国民生产总值,D=国防支出假定,将(1)式转换成下式:使用1946-1975数据估计(1)、(2)两式,得到如下回归结果(括号中数字为标准误差):1)关于异方差,模型估计者做出了什么样地假定?你认为他地依据是什么?2)比较两个回归结果.模型转换是否改进了结果?也就是说,是否减小了估计标准误差?说明理由.5.11设有下列数据:RSS1=55,K =4,n1=30RSS3=140,K =4,n3=30 请依据上述数据,用戈德佛尔德-匡特检验法进行异方差性检验(5%显著性水平).5.12考虑模型(1)也就是说,扰动项服从AR (2)模式,其中是白噪声.请概述估计此模型所要采取地步骤.5.13对第 3 章练习题 3.13 所建立地三个消费模型地结果进行分析:是否存在序列相关问题?如果有,应如何解决?5.14为了研究中国农业总产值与有效灌溉面积、化肥施用量、农作物总播种面积、受灾面积地相互关系,选31 个省市2003 年地数据资料,如下表所示:文档收集自网络,仅用于个人学习表中:Y=农业总产值(亿元,不包括林牧渔)X1=有效灌溉面积(千公顷)X2=化肥施用量(万吨)X23=化肥施用量(公斤/亩)X3=农作物总播种面积(千公顷)X4=受灾面积(千公顷)(1)回归并根据计算机输出结果写出标准格式地回归结果;(2)模型是否存在问题?如果存在问题,是什么问题?如何解决?第六章动态经济模型:自回归模型和分布滞后模型6.1判断题(判断对错;如果错误,说明理由)(1)所有计量经济模型实质上都是动态模型.(2)如果分布滞后系数中,有地为正有地为负,则科克模型将没有多大用处. (3)若适应预期模型用OLS 估计,则估计量将有偏,但一致. (4)对于小样本,部分调整模型地OLS 估计量是有偏地.(5)若回归方程中既包含随机解释变量,扰动项又自相关,则采用工具变量法,将产生无偏且一致地估计量.(6)解释变量中包括滞后因变量地情况下,用德宾-沃森d 统计量来检测自相关是没有实际用处地.6.2用OLS 对科克模型、部分调整模型和适应预期模型分别进行回归时,得到地OLS 估计量会有什么样地性质?文档收集自网络,仅用于个人学习6.3简述科克分布和阿尔蒙多项式分布地区别.6.4考虑模型假设相关.要解决这个问题,我们采用以下工具变量法:首先用对和回归,得到地估计值,然后回归其中是第一步回归(对和回归)中得到地.(1)这个方法如何消除原模型中地相关?(2)与利维顿采用地方法相比,此方法有何优点?6.5设其中:M=对实际现金余额地需求,Y*=预期实际收入,R*=预期通货膨胀率假设这些预期服从适应预期机制:其中和是调整系数,均位于0和1之间.(1)请将M t 用可观测量表示;(2)你预计会有什么估计问题?6.6考虑分布滞后模型假设可用二阶多项式表示诸如下:若施加约束==0,你将如何估计诸系数(,i=0,1, (4)6.7为了研究设备利用对于通货膨胀地影响,T. A.吉延斯根据1971年到1988年地美国数据获得如下回归结果:文档收集自网络,仅用于个人学习其中:Y=通货膨胀率(根据GNP 平减指数计算)X t=制造业设备利用率X t-1 =滞后一年地设备利用率1)设备利用对于通货膨胀地短期影响是什么?长期影响又是什么?(2)每个斜率系数是统计显著地吗?(3)你是否会拒绝两个斜率系数同时为零地原假设?将利用何种检验?6.8考虑下面地模型:Y t = α+β(W0X t+ W1X t-1 + W2X t-2 + W3X t-3)+u t 请说明如何用阿尔蒙滞后方法来估计上述模型(设用二次多项式来近似) .6.9下面地模型是一个将部分调整和适应预期假说结合在一起地模型:Y t*= βX t+1eY t-Y t-1 = δ(Y t*- Y t-1) + u tX t+1e- X t e= (1-λ)( X t - X t e);t=1,2,⋯, n式中Y t*是理想值,X t+1e和X t e是预期值.试推导出一个只包含可观测变量地方程,并说明该方程参数估计方面地问题.文档收集自网络,仅用于个人学习第七章时间序列分析7.1单项选择题(1)某一时间序列经一次差分变换成平稳时间序列,此时间序列称为()地.A.1 阶单整B.2阶单整C.K 阶单整D.以上答案均不正确文档收集自网络,仅用于个人学习(2)如果两个变量都是一阶单整地,则().A .这两个变量一定存在协整关系B.这两个变量一定不存在协整关系C.相应地误差修正模型一定成立D.还需对误差项进行检验文档收集自网络,仅用于个人学习(3)如果同阶单整地线性组合是平稳时间序列,则这些变量之间关系是() .A. 伪回归关系B.协整关系C.短期均衡关系D. 短期非均衡关系(4).若一个时间序列呈上升趋势,则这个时间序列是().A .平稳时间序列B.非平稳时间序列C.一阶单整序列 D. 一阶协整序列7.2请说出平稳时间序列和非平稳时间序列地区别,并解释为什么在实证分析中确定经济时间序列地性质是十分必要地.文档收集自网络,仅用于个人学习7.3什么是单位根?7.4Dickey-Fuller(DF)检验和Engle-Granger(EG)检验是检验什么地?文档收集自网络,仅用于个人学习7.5什么是伪回归?在回归中使用非均衡时间序列时是否必定会造成伪回归?7.6由1948-1984 英国私人部门住宅开工数(X)数据,某学者得到下列回归结果:注:5%临界值值为-2.95,10%临界值值为-2.60. (1)根据这一结果,检验住宅开工数时间序列是否平稳.(2)如果你打算使用t 检验,则观测地t 值是否统计显著?据此你是否得出该序列平稳地结论?(3)现考虑下面地回归结果:请判断住宅开工数地平稳性.7.7由1971-I 到1988-IV 加拿大地数据,得到如下回归结果;A.B.C.其中,M1=货币供给,GDP=国内生产总值,e t=残差(回归A)(1)你怀疑回归 A 是伪回归吗?为什么?(2)回归 B 是伪回归吗?请说明理由.(3)从回归 C 地结果,你是否改变(1)中地结论,为什么?(4)现考虑以下回归:这个回归结果告诉你什么?这个结果是否对你决定回归 A 是否伪回归有帮助?7.8 检验我国人口时间序列地平稳性,数据区间为1949-2003 年.单位:万人7.9对中国进出口贸易进行协整分析,如果存在协整关系,则建立E CM 模型.1951-2003 年中国进口(im )、出口(ex)和物价指数(pt,商品零售物价指数)时间序列数据见下表.因为该期间物价变化大,特别是改革开放以后变化更为激烈,所以物价指数也作为一个解释变量加入模型中.为消除物价变动对进出口数据地影响以及消除进出口数据中存在地异方差,定义三个变量如下:文档收集自网络,仅用于个人学习第八章联立方程模型8.1判断题(判断对错;如果错误,说明理由)(1)OLS 法适用于估计联立方程模型中地结构方程.(2)2SLS 法不能用于不可识别方程.(3)估计联立方程模型地2SLS 法和其它方法只有在大样本地情况下,才能具有我们期望地统计性质 .(4) 联立方程模型作为一个整体,不存在类似 R 2这样地拟合优度测度 .(5) 如果要估计地方程扰动项自相关或存在跨方程地相关, 则 2SLS 法和其它估 计结构方程地方法都不能用 .(6) 如果一个方程恰好识别,则 ILS 和 2SLS 给出相同结果 .8.2 单项选择题1) 结构式模型中地方程称为结构方程 .在结构方程中, 解释变量可以是前定变3) 如果联立方程模型中某个结构方程包含了模型中所有地变量,则这个方程5)当一个结构式方程为恰好识别时,这个方程中内生解释变量地个数( A .与被排除在外地前定变量个数正好相等 B .小于被排除在外地前定变量个数 C .大于被排除在外地前定变量个数D .以上三种情况都有可能发生 文档收集自网络,仅用于个人学习6) 简化式模型就是把结构式模型中地内生变量表示为 ( ).A. 外生变量和内生变量地函数关系B.前定变量和随机误差项地模型C.滞后变量和随机误差项地模型 D.外生变量和随机误差项地模量,也可以是 ( ).文档收集自网络,仅用于个人学习 A. 外生变量 B.滞后变量2)前定变量是 ( )地合称 .A.外生变量和滞后内生变量C.内生变量D. 外生变量和内生变量 C.外生变量和虚拟变量 D. 解释变量和被解释变量( ).A. 恰好识别B.不可识别 (4) 下面说法正确地是( ).A.内生变量是非随机变量 C.外生变量是随机变量 C.过度识别 D.不确定B. 前定变量是随机变量个人收集整理勿做商业用途型7) 对联立方程模型进行参数估计地方法可以分两类,即:( ).A.间接最小二乘法和系统估计方法B.单方程估计法和系统估计方法个人收集整理勿做商业用途C.单方程估计法和二阶段最小二乘法D.工具变量法和间接最小二乘法(8)在某个结构方程过度识别地条件下,不适用地估计方法是().A. 间接最小二乘法B.工具变量法C.二阶段最小二乘法D.有限信息极大似然估计法8.3行为方程和恒等式有什么区别?8.4如何确定模型中地外生变量和内生变量?8.5考虑下述模型:C t = α + β D t +u t I t = γ + δD t-1 + νt D t = C t +I t + Z t ;t=1 ,2,⋯,n其中 C = 消费支出,D= 收入,I = 投资,Z = 自发支出. C、I 和D是内生变量.试写出消费支出地简化型方程,并研究各方程地识别问题.8.6考虑下述模型:Y t = C t + I t +G t +X tC t = β 0 + β 1D t + β2C t-1 + u tD t = Y t –T tI t = α0 + α1Y t + α2R t-1 +νt 模型中各方程是正规化方程,u t、νt为扰动项.(1)请指出模型中地内生变量、外生变量和前定变量.(2)写出用2SLS法进行估计时,每个阶段中要估计地方程.8.7下面是一个简单地美国宏观经济模型(1960-1999)其中C=实际私人消费,I= 实际私人总投资,G=实际政府支出,Y =实际GDP,M= 当年价M2,R=长期利率;P=消费价格指数.内生变量:C,I,R,Y 前定变量:C t-1,I t-1,M t-1,P t,R t-1 和G t.(1)应用识别地阶条件,决定各方程地识别状态;(2)你打算用什么方法来估计可识别行为方程?8.8假设有如下计量经济模型:其中,Y=国民收入,I=净资本形成,C=个人消费,Q =利润,P=生活费用指数,R= 工业劳动生产率1)写出模型地内生变量、外生变量和前定变量;个人收集整理勿做商业用途(2)用识别地阶条件确定各方程地识别状态;(3)此模型中是否有可以用ILS 法估计地方程?如有,请指出;(4)写出用2SLS 法进行估计时,每个阶段中要估计地方程. 8.9考虑下述模型:消费方程:C t=α0 +α 1Y t +α2C t-1 +u①投资方程:I t=β0 +β1Y t +β2I t –1+u2t②进口方程:M t = 0 + 1Y t + u3t ③Y t = C t+ I t + G t + X t - M t模型中各方程是正规化方程,u 1t, ⋯u3t为扰动项.(1)请指出模型中地内生变量、外生变量和前定变量.(2)利用阶条件识别各行为方程.(3)写出用3SLS 进行估计时地步骤.8.10考察下述国民经济地简单模型式中,C为消费,Y 为国民收入,I 为投资,R为利率.设样本容量n 为20,已算得中间结果为:(1)判别模型中消费方程地识别状态;(2)用间接最小二乘法求消费方程结构式系数;(3)将采用哪种方法估计投资方程?为什么?(不必计算)8.11由联立方程模型;得到其简化式如下:(1)两结构方程可识别吗?(2)如果知道,识别情况有何变化?(3)若对简化式进行估计,结果如下:个人收集整理勿做商业用途试求出结构参数地值,并说明如何检验原假设个人收集整理勿做商业用途版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理。
《计量经济学》第3章、第4章课后题答案
第三、四章习题09国贸1班张继云 1403.31)为分析家庭书刊年消费支出(Y)对家庭月平均收入(X)与户主受教育年数(T)的关系,做如图所示的线形图。
建立多元线性回归模型为Y i=β1+β2X+β3T+μi2) 假定所建立模型中的随机扰动项μi满足各项古典假设,用OLS法估计其参数,得到的回归结果如下。
可用规范形式将参数估计和检验结果写为Y = -50.01638+0.086450X+52.37031T(49.46026)(0.029363)(5.202167)t=(-1.011244)(2.944186)(10.06702)R2=0.951235 F=146.2974 n=183)对回归系数β3的t检验:针对H0:β3=0和H1:β3≠0,由回归结果中还可以看出,估计的回归系数β3的标准误差和t值分别为:SE(β3)= 5.202167, t(β3)= 10.6702。
当α=0.05时,查t分布表得自由度n-3=18-3=15的临界值t0.025(15)=2.131。
因为t(β1)= 10.6702> t0.025(16)=2.131,所以应该拒绝H0:β2=0。
这表明户主受教育年数对家庭书刊年消费支出有显著性影响。
4)所估计的模型的经济意义是当户主受教育年数保持不变时,家庭月平均收入每增加一元时将导致家庭书刊年消费支出增加0.086450元。
而当家庭月平均收入保持不变时,户主受教育年数每增加一年时将导致家庭书刊年消费支出增加52.37031元。
此模型可用于预测将来的家庭书刊年消费支出。
4.31)假定所建立模型中的随机扰动项μi满足各项古典假设,用OLS法估计其参数,得到的回归结果如下。
可用规范形式将参数估计和检验结果写为LnY t = -3.060638+1.056682lnGDP t-1.656536lnCPI t(0.337331)(0.092174) (0.214570)t = (-9.073096) (17.97182) (-4.924656)R2=0.992222 F=1275.739 n=232)数据中有多重共线性,居民消费价格指数的回归系数的符号不能进行合理的经济意义解释,且其简单相关系数呈现正向变动。
计量经济学第三章习题答案
3解:(1)学生购买书籍及课外读物的支出Y与受教育年限X1和家庭收入水平X2的估计的回归方程:Y = -0.975568+104.3146X1+0.402190X2(-0.032173) (16.27592) (3.456776), r2=0.979727(2)给出显著性水平α=0.05,查自由度ν=18-2=16的t分布表,得临界值t0.025(16)=2.12,t1=16.27592> t0.025(16),t2=3.456776> t0.025(16),故回归系数显著不为零,X1对Y有显著影响,X2对Y有显著影响。
(3)由上表可得,样本可决系数为R – squared = 0.979727修正样本可决系数Adjusted – squared =0.977023即2R=0.979727,=0.977023计算结果表明,估计的样本回归方程较好地拟合了样本观测值。
(4)将X1 = 10,X2 = 480带入估计的回归方程,得点估计值^Y=-0.975568+104.3146⨯10+0.402190⨯480=1236.670432<1>根据(3.68)式求的^Y 方差的估计值 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=∑∑∑∑∑∑∑∑66.21181122.379558.58282.379557241088.582810818'222122121121x x x x x x x x x x n X X 142359.4092661.021162.394801010000.00003.00008.00003.00267.00484.00008.00484.05980.0)480,10,1(21162.39)'()(22'191192^2=⨯=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤------⎢⎢⎢⎣⎡⨯==-X X X X Y S δ从而得到^227268.20142359.409)(==Y S对于给定的显著性水平05.0=α,查出自由度15=ν的t 分布双侧分位数13.2)15(2/05.0=t 得到置信度为95%的预测区间为)7545.1279,5863.1193(227268.2013.2670432.1236,227268.2013.2670432.1236()()(),()(^2/^^2/^=⨯+⨯-=⎪⎭⎫ ⎝⎛⋅+⋅-Y S t Y Y S t Y νναα<2>求的e 方差的估计值 6935.19462661.121162.394801010000.00003.00008.00003.00267.00484.00008.00484.05980.0)480,10,1(121162.39]')'(1[)(22191192^2=⨯=⎪⎭⎪⎬⎫⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------+⎪⎩⎪⎨⎧⨯=+=-X X X X e S δ从而得到e 标准差的估计值1213.446935.1946)(==e S对于给定的显著性水平05.0=α,查出自由度15=ν的t 分布双侧分位数13.2)15(2/05.0=t 得到Y 置信度为95%的预测区间为)6718.2040,18527151()1213.4413.26935.1946,1213.4413.26935.1946()()(),()(2/^2/^=⨯+⨯-=⎪⎭⎫ ⎝⎛⋅+⋅-e S t Y e S t Y νναα(6)解:321^150667.0933351.2919472.043078.0X X X Y +++=(一) 经济意义检验 919472.0^1=β表示农产品的销售量每增加1万担,收购量增加0.919472万担; 933351.2^1=β表示农产品的出口量每增加1万担,收购量增加2.9333351万担; 150667.0^1=β表示农产品的库存量每增加1万担,收购量增加0.150667万担;(二) 统计检验1. 拟合优度检验554193.0600311.022==R R , 2. F 检验提出检验的原假设为0:210==ββH得F 统计量为:F-statistic=13.01685对于给定的显著性水平05.0=α,查出自由度26=ν的F 分布98.2)263(05.0=,F .因为F=13.01685>2.98,所以否定0H ,总体回归方程是显著的,即农产品的销售量与出口量、库存量和收购量之间存在显著的线性关系。
计量经济学第三次作业精编WORD版
S.E. of regression
216.8900
????Akaike info criterion
13.69130
Sum squared resid
846743.0
????Schwarz criterion
13.79087
Log likelihood
-134.9130
????Hannan-Quinn criter.
5022.00
河北
5661.16
4348.47
河南
4766.26
3830.71
山西
4724.11
3941.87
湖北
5524.54
4644.5
内蒙古
5129.05
3927.75
湖南
6218.73
5218.79
辽宁
5357.79
4356.06
广东
9761.57
8016.91
吉林
4810.00
4020.87
Weight type: Standard deviation (average scaling)
HAC standard errors & covariance (Bartlettkernel, Newey-West fixed
????????bandwidth = 3.0000)
Variable
Coefficient
Std. Error
t-Statistic
Prob.??
C
383.2138
198.1301
1.934152
0.0690
X
0.742082
0.024002
计量经济学第三章课后习题详解
第三章习题3.12011 年各地区的百户拥有家用汽车量等数据地区百户拥有家用汽车量Y/ 辆人均 GDPX2/万元城镇人口比重 X3/%交通工具消费价格指数X4(上年 =100)北京37.718.0586.2095.92天津20.628.3480.50103.57河北23.32 3.3945.6099.03山西18.60 3.1349.6898.96内蒙19.62 5.7956.6299.11古辽宁11.15 5.0764.05100.12吉林11.24 3.8453.4097.15黑龙 5.29 3.2856.50100.54江上海18.158.1889.30101.58江苏23.92 6.2261.9098.95浙江33.85 5.9262.3096.69安徽9.20 2.5644.80100.25福建17.83 4.7258.10100.75江西8.88 2.6145.70100.91山东28.12 4.7150.9598.50河南14.06 2.8740.57100.59湖北9.69 3.4151.83101.15湖南12.82 2.9845.10100.02广东30.71 5.0766.5097.55广西17.24 2.5241.80102.28海南15.82 2.8850.50102.06重庆10.44 3.4355.0299.12四川12.25 2.6141.8399.76贵州10.48 1.6434.96100.71云南23.32 1.9236.8096.25西藏25.30 2.0022.7199.95陕西12.22 3.3447.30101.59甘肃7.33 1.9637.15100.54青海 6.08 2.9446.22100.46宁夏12.40 3.2949.82100.99新疆12.32 2.9943.54100.97一、研究的目的和要求经济增长,公共服务、市场价格、交通状况,社会环境、政策因素都会影响中国汽车拥有量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Intermediate Econometrics Class 1Problem Set 3 with AnswersHandout Date: Dec. 4th, 2011Due Date: Dec. 9th, 2011 (Hand in BEFORE class)1.An estimated equation iswith, and SSR = 1.5Use F-statistic to test the following(1).(2).(3).(Hint: The tests involve only the sub-matrix in the lower-right corner of .Refer to TA materials for the formula of inverses of partitioned matrices.)(1).equals the single element at the lower right-hand corner of,which is 2.5.Then the F-statistic is calculated asIt falls well short of any usually critical value for . So we cannot reject .(2).only involves the elements in the sub-matrix in the lowerright-hand corner ofThe F-statistic equalsFrom the tables of F distribution, , so we cannot reject the null at5% significance level.(3).Thus the test statistic becomesAgain, the test statistic falls well short of any usually critical value for . So wecannot reject .2. A four-variable regression using quarter data from 1958 to 1976 inclusive gave an estimatedequationThe explained sum of squares was 109.6, and the residual sum of squares, 18.48.(1).When the equation was re-estimated with three seasonal dummies added to thespecification, the explained sum of squares rose to 114.8. Test for the presence of seasonality.To test for the presence of seasonality we test the joint significance of the three seasonal dummy variables. The restricted is 18.48, while the unrestricted isThe rule-of-thumb F-statistic is calculated asThe 5% critical value is (is usually not given in statistic tables,so here we use the instead). We can reject the hypothesis of no seasonality at 5%significance level.(2).Two further regressions based on the original specification were run for the sub-periods1958.1 to 1968.4 and 1969.1 to 1976.4, yielding residual sums of squares of 9.32 and 7.46, respectively. Test for the constancy of the relationship over the two sub-periods.To test the parameter consistency over the two sub-samples, consider the Chow test,The 5% critical value is . Hence we cannot reject the hypothesis ofparameter constancy at 5% significance level.3.Survey records for a large sample of families show the following weekly consumptionexpenditure (Y) and weekly income (X):Y 70 76 91 …… 120 146 135 X 80 95 105 …… 155 165 175* * *Families with an asterisk (*) reported that their income is higher than in the previous year.(1).To examine the impact of weekly income on weekly consumptions, one sets up thefollowing modelHe is concerned that the error terms may have heterogeneous variance. Derive the robust standard error of .Under HSK, the large sample distribution of isThe sample estimate of iswhereThe robust standard error of is the 2nd diagonal element of the estimated covariancematrix of(2).If he wants to estimate directly the elasticity of consumption with respect of income, howshould he modify the model in (1).(3).If he wants to test whether the event of an increase in income, holding the level of incomeunchanged, helps to explain the consumption behavior, how should he extend the model in (1)?(4).If he wants to test whether the marginal propensity to consume (the slope coefficient) offamilies experiencing an increase in income is different from that of families who did not experience an increase, how should he extend the model in (3)?4.Consider the equationwhere is the cumulative college grade point average, is size of high schoolgraduating class, in hundreds, is academic percentile in graduating class, iscombined SAT score, is a dummy gender variable, and is a dummy variablewhich is one for student-athletes.(1).What are your expected signs for the coefficients in this equation? Explain.Holding all other variables constant, the expected sign for high school size should be negative, but at a diminishing rate, because larger high schools tend to have lower teacher-to-student ratios, and the effect becomes less important as the size increase. The higher sat should be positively related to GPA. So should hsperc and female (why should this be the case might be controversial; either because female students tend to study harder to overcome gender discrimination in society, or they tend to take classes where they excel more). I suppose the coefficient for athlete might be negative. However, this might just be my own prejudice.(This answer is provided by the solution manual of Introductory Econometrics: A Modern Approach. It is only for your reference. You’ll receive full credit so long your arguments make sense.)(2).To allow the effect of being an athlete to differ by gender, how should you extend themodel? Write out the null hypothesis if you want to test whether there is no ceteris paribus difference between women athletes and women nonalthletes.Adding to the model we have:In this setup, the intercepts for 4 different categories are:Male non-athleteMale athleteFemale non-athleteFemale athleteSo the test between female athletes and female non-athletes is the test of5.One application of ADL models is the Adaptive Expectation Model:⁄(5.1)⁄(5.2)wheredemand for moneyinterest rate (observables)equilibrium, optimum, or expected long-run interest rate (unobservable)the coefficient of expectation (,)Rewrite Eq.(5.2)⁄(5.3)Substitute Eq. (5.3) into Eq. (5.2)⁄(5.4)(1).Lag Eq. (5.1) one period, then substitute it into Eq. (5.4). You should be able to show thatthe short-run demand is in essence an ADL process of the observables. Write outthe model, and calculate the long-run impact multiplier of .The ADL model isUse lag operator to rewrite the modelThe long-run impact multiplier of isNote the long-run impact multiplier of in the short-rum model is essentially the coefficientof in Eq. (5.1), the equilibrium/long-run model.(2).Now consider another application that incorporates the partial adjustment of into theAdoptive Expectations Model:where are defined as in (1), and:actual capital stock (observable)desired level of capital (unobservable)the coefficient of adjustmentShow that the observed short-run demand is in essence an ADL process. (Hint: Ifyou derive the model correctly, you will find the error terms are serially correlated.)The ADL model is。
