二次函数中的存在性问题(答案)(可编辑修改word版)
二次函数的存在性问题(面积)及答案

图12-2xCOy ABD 11二次函数的存在性问题(面积问题)1、[08云南双柏]已知:抛物线y =ax 2+bx +c 与x 轴交于A 、B 两点,与y 轴交于点C ,其中点B 在x 轴的正半轴上,点C 在y 轴的正半轴上,线段OB 、OC 的长(OB <OC )是方程x 2-10x +16=0的两个根,且抛物线的对称轴是直线x =-2. (1)求A 、B 、C 三点的坐标;(2)求此抛物线的表达式;(3)求△ABC 的面积; (4)若点E 是线段AB 上的一个动点(与点A 、点B 不重合),过点E 作EF ∥AC 交BC 于点F ,连接CE , 设AE 的长为m ,△CEF 的面积为S ,求S 与m 之间的函数关系式,并写出自变量m 的取值范围;(5)在(4)的基础上试说明S 是否存在最大值,若存在,请求出S 的最大值,并求出此时点E 的坐标, 判断此时△BCE 的形状;若不存在,请说明理由.2、 [09湖南益阳]阅读材料:如图12-1,过△ABC 的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算PABCAB 98SS =三角形面积的新方法:ah S ABC 21=∆,即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题:如图12-2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ∆; (3)是否存在一点P ,使PABCAB98S S =若存在,求出P 点的坐标;若不存在,请说明理由.图13、[09吉林长春]如图,在直角坐标系中,矩形ABCD 的边AD 在y 轴正半轴上,点A 、C 的坐标分别 为(0,1)(2,4).点P 从点A 出发,沿A →B →C 以每秒1个单位的速度运动,到点C 停止;点Q 在x 轴上,横坐标为点P 的横、纵坐标之和.抛物线c bx x y ++-=241经过A 、C 两点.过点P 作x 轴的垂线, 垂足为M ,交抛物线于点R .设点P 的运动时间为t (秒),△PQR 的面积为S (平方单位).(1)求抛物线对应的函数关系式.(2分) (2)分别求t=1和t=4时,点Q 的坐标.(3分)(3)当0<t ≤5时,求S 与t 之间的函数关系式,并直接写出S 的最大值.(5分)4、(07云南昆明)如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB 。
二次函数存在性问题专题复习(全面典型含答案)

中考数学专题复习——存在性问题存在性问题是指判断满足某种条件的事物是否存在的问题,这类问题的知识覆盖面较广,综合性较强,题意构思非常精巧,解题方法灵活,对学生分析问题和解决问题的能力要求较高,是近几年来包括深圳在内各地中考的“热点”。
这类题目解法的一般思路是:假设存在→推理论证→得出结论。
若能导出合理的结果,就做出“存在”的判断,导出矛盾,就做出不存在的判断。
以下为几种典型的二次函数中出现的存在性问题,讲解后希望各位考生在以后的考试中如果遇到此类型时能够很顺畅的把过程写下来。
一、二次函数中相似三角形的存在性问题1.(2011枣庄10分)如图,在平面直角坐标系xoy 中,把抛物线2y x =向左平移1个单位,再向下平移4个单位,得到抛物线2()y x h k =-+.所得抛物线与x 轴交于A ,B 两点(点A 在点B 的左边),与y 轴交于点C ,顶点为D. (1)写出h k 、的值;(2)判断△ACD 的形状,并说明理由;(3)在线段AC 上是否存在点M ,使△AOM ∽△ABC ?若存在,求出点M 的坐标;若不存在,说明理由.2.(2011临沂13分)如图,已知抛物线经过A (﹣2,0),B (﹣3,3)及原点O ,顶点为C . (1)求抛物线的解析式;(2)若点D 在抛物线上,点E 在抛物线的对称轴上,且A 、O 、D 、E 为顶点的四边形是平行四边形,求点D 的坐标;(3)P 是抛物线上的第一象限内的动点,过点P 作PM ⊥x 轴,垂足为M ,是否存在点P ,使得以P 、M 、A 为顶点的三角形△BOC 相似?若存在,求出点P 的坐标;若不存在,请说明理由.二、二次函数中面积的存在性问题3. (2011日照10分)如图,抛物线()20y ax bx a >=+与双曲线ky x=相交于点A ,B .已知点B 的坐标为(-2,-2),点A 在第一象限内,且tan ∠AOX 错误!未找到引用源。
中考数学 二次函数存在性问题 与参考答案
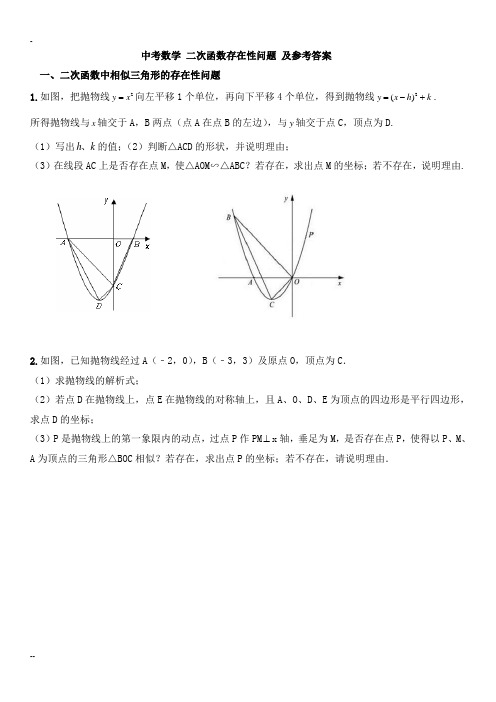
中考数学二次函数存在性问题及参考答案一、二次函数中相似三角形的存在性问题1.如图,把抛物线2=向左平移1个单位,再向下平移4个单位,得到抛物线2y x=-+.y x h k()所得抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.(1)写出h k、的值;(2)判断△ACD的形状,并说明理由;(3)在线段AC上是否存在点M,使△AOM∽△ABC?若存在,求出点M的坐标;若不存在,说明理由.2.如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.(1)求抛物线的解析式;(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.二、二次函数中面积的存在性问题3.如图,抛物线()20y ax bx a >=+与双曲线ky x=相交于点A ,B .已知点B 的坐标为(-2,-2),点A 在第一象限内,且tan ∠AOX =4.过点A 作直线AC ∥x 轴,交抛物线于另一点C . (1)求双曲线和抛物线的解析式; (2)计算△ABC 的面积;(3)在抛物线上是否存在点D ,使△ABD 的面积等于△ABC 的面积.若存在,请你写出点D 的坐标;若不存在,请你说明理由.4.如图,抛物线y =ax 2+c (a >0)经过梯形ABCD 的四个顶点,梯形的底AD 在x 轴上, 其中A (-2,0),B (-1, -3). (1)求抛物线的解析式;(3分)(2)点M 为y 轴上任意一点,当点M 到A 、B 两点的距离之和为最小时,求此时点M 的坐标;(2分) (3)在第(2)问的结论下,抛物线上的点P 使S △PAD =4S △ABM 成立,求点P 的坐标.(4分) (4)在抛物线的BD 段上是否存在点Q 使三角形BDQ 的面积最大,若有,求出点Q 的坐标,若没有,请说明理由。
二次函数中的存在性问题

⼆次函数中的存在性问题⼆次函数中的存在性问题存在性问题是指判断满⾜某种条件的事物是否存在的问题,这类问题的知识覆盖⾯较⼴,综合性较强,题意构思⾮常精巧,解题⽅法灵活,对学⽣分析问题和解决问题的能⼒要求较⾼,是近⼏年来各地中考的“热点”。
这类题⽬解法的⼀般思路是:假设存在→推理论证→得出结论。
若能导出合理的结果,就做出“存在”的判断,导出⽭盾,就做出“不存在”的判断。
以下⼏篇内容为⼏种典型的⼆次函数中出现的存在性问题,希望⼤家在以后的学习中如果遇到此类型时能够轻松解决。
⼀、特殊三⾓形的存在性问题(⼀)⼆次函数中的等腰三⾓形存在性问题如果△ABC是等腰三⾓形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.因此,解等腰三⾓形的存在性问题时,通常要进⾏分类讨论。
这类问题有⼏何法和代数法两种⽅法,我们要根据具体情况灵活选择简便的⽅法。
⼏何法⼀般分三步:分类、画图、计算.代数法⼀般也分三步:罗列三边长,分类列⽅程,解⽅程并检验.(⼆)⼆次函数中的直⾓三⾓形存在性问题如果△ABC是直⾓三⾓形,那么存在①∠A为直⾓,②∠B为直⾓,③∠C为直⾓三种情况.因此,解直⾓三⾓形的存在性问题时,通常要进⾏分类讨论。
这类问题有⼏何法和代数法两种⽅法,我们要根据具体情况灵活选择简便的⽅法。
⼏何法⼀般分三步:分类、画图、计算.代数法⼀般也分三步:罗列三边长,分类列⽅程,解⽅程并检验.(三)⼆次函数中的等腰直⾓三⾓形存在性问题在解决等腰直⾓三⾓形存在性问题时,往往要⽤到⼏何和代数相结合的⽅法,设出点的坐标后,利⽤等腰直⾓三⾓形的⼏何性质及函数关系式列⽅程求解,最常⽤到的有:①两直⾓边相等,直⾓边与斜边的⽐为1:√2;②斜边中线垂直于斜边,且等于斜边的⼀半。
③直⾓顶点处构造三垂直,得到全等三⾓形,利⽤对应边的等量关系求解。
二次函数的存在性问题(Word版解析+答案)

中考压轴题解析二次函数的存在性问题【典例分析】【考点 1】二次函数与相似三角形问题例1】已知抛物线y ax2 bx 3与 x轴分别交于A( 3,0),B(1,0)两点,与 y轴交于点 C.2)点 F 是线段 AD 上一个动点.1AD .2ABC 相似?若相似,求出点 F 的坐标;若不相似,请说明理由.变式1-1】如图,抛物线y ax2 2x c经过A( 1,0),B两点,且与y轴交于点C(0,3) ,抛物线与直线y x 1交于A,E 两点.(1)求抛物线的解析式;(2)坐标轴上是否存在一点Q,使得AQE是以AE为底边的等腰三角形?若存在,请直接写出点Q 的坐标;若不存在,说明理由.(3)P点在x轴上且位于点B 的左侧,若以P,B,C为顶点的三角形与ABE相似,求点P的坐AF①如图 1,设k ,当 k 为何值时,CFAD1)求抛物线的表达式及顶点 D 的坐标;标.1【变式1-2】如图,已知抛物线y m(x 2)(x m)(m > 0)与 x 轴相交于点 A,B,与 y轴相交于点 C,且点 A 在点 B 的左侧 .( 1)若抛物线过点( 2, 2),求抛物线的解析式;(2)在( 1)的条件下,抛物线的对称轴上是否存在一点H ,使 AH+CH 的值最小,若存在,求出点 H 的坐标;若不存在,请说明理由;(3)在第四象限内,抛物线上是否存在点M ,使得以点 A,B,M 为顶点的三角形与△ACB 相似?若存在,求出 m 的值;若不存在,请说明理由 .考点 2】二次函数与直角三角形问题BC交于点D,连接AC 、AD ,求VACD的面积;3 点E为直线BC上的任意一点,过点E作x轴的垂线与抛物线交于点F ,问是否存在点E使VDEF 为直角三角形?若存在,求出点E 坐标,若不存在,请说明理由.例2】如图,抛物线y ax2bx c a 0的顶点坐标为2, 1 ,图象与y 轴交于点C 0,3 ,与x轴2 设抛物线对称轴与直线【变式2-1】如图,经过x 轴上A( 1,0), B(3,0)两点的抛物线y m(x 1)2 4m (m 0)交y 轴于点C ,设抛物线的顶点为D ,若以DB 为直径的⊙ G 经过点C ,求解下列问题:1)用含m的代数式表示出C,D 的坐标;2)求抛物线的解析式;3)能否在抛物线上找到一点Q,使△BDQ 为直角三角形?如能,求出Q点的坐标,若不能,请说明理由。
(完整word版)二次函数专题训练(正方形的存在性问题)含答案

二次函数专题训练(正方形的存在性)1.如图,已知抛物线y=x 2+bx+c 的图象经过点 A ( l , 0), B(﹣ 3,0),与 y 轴交于点C,抛物线的极点为 D ,对称轴与x 轴订交于点E,连结 BD .( 1)求抛物线的分析式.( 2)若点 P 在直线 BD 上,当 PE=PC 时,求点P 的坐标.( 3)在( 2)的条件下,作PF⊥ x 轴于 F,点 M 为 x 轴上一动点,N 为直线 PF 上一动点, G 为抛物线上一动点,当以点F, N ,G,M 四点为极点的四边形为正方形时,求点M 的坐标.2.如图,抛物线y= ﹣x2+bx+c 与 x 轴交于点 A 和点 B,与 y 轴交于点C,点 B 坐标为( 6,0),点 C 坐标为( 0, 6),点 D 是抛物线的极点,过点 D 作 x 轴的垂线,垂足为E,连结 BD .( 1)求抛物线的分析式及点 D 的坐标;( 2)点 F 是抛物线上的动点,当∠FBA= ∠ BDE 时,求点 F 的坐标;( 3)若点 M 是抛物线上的动点,过点M 作 MN ∥x 轴与抛物线交于点N ,点 P 在 x 轴上,点 Q 在座标平面内,以线段MN 为对角线作正方形MPNQ ,请写出点Q 的坐标.3.如图,已知抛物线y=ax2 +bx﹣ 3 过点 A (﹣ 1, 0), B( 3,0),点 M 、 N 为抛物线上的动点,过点M 作MD ∥ y 轴,交直线 BC 于点 D ,交 x 轴于点 E.过点 N 作 NF ⊥ x 轴,垂足为点 F( 1)求二次函数 y=ax2+bx ﹣ 3 的表达式;( 2)若 M 点是抛物线上对称轴右边的点,且四边形MNFE 为正方形,求该正方形的面积;( 3)若 M 点是抛物线上对称轴左边的点,且∠DMN=90°, MD=MN ,请直接写出点M 的横坐标.4.(2015 贵州省毕节地域) 如图,抛物线y=x 2+bx+c 与 x 轴交于 A (﹣ 1,0), B( 3, 0)两点,极点M 关于 x 轴的对称点是M′.( 1)求抛物线的分析式;( 2)若直线AM′与此抛物线的另一个交点为C,求△ CAB 的面积;( 3)能否存在过A, B 两点的抛物线,其极点P 对于 x 轴的对称点为Q,使得四边形APBQ 为正方形?若存在,求出此抛物线的分析式;若不存在,请说明原因.5. (2016 辽宁省铁岭市 ) .如图,抛物线y= ﹣x2+bx+c 与 x 轴交于点 A ,点 B,与 y 轴交于点C,点 B 坐标为( 6,0),点 C 坐标为( 0,6),点 D 是抛物线的极点,过点 D 作 x 轴的垂线,垂足为E,连结 BD .( 1)求抛物线的分析式及点 D 的坐标;( 2)点 F 是抛物线上的动点,当∠FBA= ∠ BDE 时,求点 F 的坐标;( 3)若点 M 是抛物线上的动点,过点M作MN∥ x轴与抛物线交于点N ,点 P 在 x 轴上,点 Q 在平面内,以线段 MN 为对角线作正方形MPNQ ,请直接写出点Q 的坐标.二次函数专题训练(正方形的存在性)6.(2016 广东省茂名市 ) .如图,抛物线 y=﹣ x2+bx+c 经过 A (﹣ 1, 0), B(3,0)两点,且与 y 轴交于点 C,点 D 是抛物线的极点,抛物线的对称轴DE 交 x 轴于点 E,连结 BD .(1)求经过 A ,B ,C 三点的抛物线的函数表达式;(2)点 P 是线段 BD 上一点,当 PE=PC 时,求点 P 的坐标;( 3)在( 2)的条件下,过点P 作 PF⊥x 轴于点 F, G 为抛物线上一动点,M 为 x 轴上一动点, N 为直线PF 上一动点,当以F、 M 、 G 为极点的四边形是正方形时,恳求出点M 的坐标.二次函数专题训练(正方形的存在性问题)参照答案1.如图,已知抛物线 y=x 2+bx+c 的图象经过点 A ( l , 0), B(﹣ 3,0),与 y 轴交于点 C,抛物线的极点为D ,对称轴与 x 轴订交于点 E,连结 BD .( 1)求抛物线的分析式.( 2)若点 P 在直线 BD 上,当 PE=PC 时,求点P 的坐标.( 3)在( 2)的条件下,作PF⊥ x 轴于 F,点 M 为 x 轴上一动点,N 为直线 PF 上一动点, G 为抛物线上一动点,当以点F, N ,G,M 四点为极点的四边形为正方形时,求点M 的坐标.【解答】解:( 1)∵抛物线y=x2+bx+c 的图象经过点 A ( 1, 0), B(﹣ 3,0),∴,∴,∴抛物线的分析式为y=x2+2x ﹣ 3;( 2)由( 1)知,抛物线的分析式为y=x 2+2x ﹣ 3;∴C( 0,﹣ 3),抛物线的极点 D(﹣ 1,﹣ 4),∴E(﹣ 1, 0),设直线 BD 的分析式为y=mx+n ,∴,∴,∴直线BD 的分析式为y= ﹣ 2x ﹣6,设点 P( a,﹣ 2a﹣ 6),∵ C( 0,﹣ 3), E(﹣ 1, 0),依据勾股定理得,PE2=( a+1)2+(﹣ 2a﹣ 6)2,22 2PC =a +(﹣ 2a﹣ 6+3 ),∵PC=PE,∴( a+1)2+(﹣ 2a﹣ 6)2 =a2+(﹣ 2a﹣ 6+3 )2,∴a=﹣ 2,∴ y= ﹣ 2×(﹣ 2)﹣ 6=﹣ 2,∴P(﹣ 2,﹣ 2),(3)如图,作 PF⊥ x 轴于 F,∴ F(﹣ 2, 0),设 M ( d, 0),∴ G( d, d2+2d ﹣ 3), N(﹣ 2, d2+2d﹣ 3),∵以点 F, N ,G, M 四点为极点的四边形为正方形,必有FM=MG ,∴|d+2|=|d2+2d ﹣ 3|,∴ d= 或 d= ,∴点 M 的坐标为(, 0),(, 0),(, 0),(, 0).2.如图,抛物线y= ﹣x2+bx+c 与 x 轴交于点 A 和点 B,与 y 轴交于点C,点 B 坐标为( 6,0),点 C 坐标为( 0, 6),点 D 是抛物线的极点,过点 D 作 x 轴的垂线,垂足为E,连结 BD .( 1)求抛物线的分析式及点 D 的坐标;( 2)点 F 是抛物线上的动点,当∠FBA= ∠ BDE 时,求点 F 的坐标;( 3)若点 M 是抛物线上的动点,过点M 作 MN ∥ x 轴与抛物线交于点N,点 P 在 x 轴上,点Q 在座标平面内,以线段MN 为对角线作正方形MPNQ ,请写出点Q 的坐标.【解答】解:( 1)把 B 、C 两点坐标代入抛物线分析式可得,解得,∴抛物线分析式为y=﹣x2+2x+6 ,∵ y= ﹣x2+2x+6= ﹣(x﹣2)2+8,∴ D(2,8);( 2)如图 1,过 F 作 FG⊥ x 轴于点 G,设 F( x,﹣x2+2x+6 ),则 FG=|﹣x2+2x+6| ,∵∠ FBA= ∠BDE ,∠ FGB= ∠ BED=90°,∴△ FBG ∽△ BDE ,∴=,∵ B(6,0),D(2,8),∴ E( 2,0), BE=4 ,DE=8 , OB=6 ,∴ BG=6 ﹣ x,∴=,当点 F 在 x 轴上方时,有=,解得x=﹣1或x=6(舍去),此时F点的坐标为(﹣1,);当点 F 在 x 轴下方时,有=﹣,解得x=﹣3或x=6(舍去),此时F 点坐标为(﹣ 3,﹣);综上可知 F 点的坐标为(﹣1,)或(﹣3,﹣);( 3)如图 2,设对角线MN 、 PQ 交于点 O′,∵点 M 、 N 对于抛物线对称轴对称,且四边形MPNQ 为正方形,∴点 P 为抛物线对称轴与x 轴的交点,点Q 在抛物线的对称轴上,设Q(2, 2n),则 M 坐标为( 2﹣ n,n),∵点 M 在抛物线 y= ﹣ x2+2x+6 的图象上,∴ n=﹣(2﹣n)2+2(2﹣n)+6,解得n=﹣1+或n=﹣1﹣,∴知足条件的点Q 有两个,其坐标分别为(2,﹣ 2+2)或(2,﹣2﹣2).3.如图,已知抛物线y=ax2 +bx﹣ 3 过点 A (﹣ 1, 0), B( 3,0),点 M 、 N 为抛物线上的动点,过点M 作MD ∥ y 轴,交直线 BC 于点 D ,交 x 轴于点 E.过点 N 作 NF ⊥ x 轴,垂足为点 F( 1)求二次函数 y=ax2+bx ﹣ 3 的表达式;( 2)若 M 点是抛物线上对称轴右边的点,且四边形MNFE 为正方形,求该正方形的面积;( 3)若 M 点是抛物线上对称轴左边的点,且∠DMN=90°, MD=MN ,请直接写出点M 的横坐标.【解答】解:( 1)把 A (﹣ 1, 0),B ( 3, 0)代入 y=ax 2+bx ﹣ 3,得:,解得,故该抛物线分析式为:y=x 2﹣2x﹣ 3;(2)由( 1)知,抛物线分析式为: y=x 2﹣2x﹣ 3=( x﹣ 1)2﹣ 4,∴该抛物线的对称轴是 x=1 ,极点坐标为( 1,﹣ 4).如图,设点 M 坐标为( m, m2﹣2m﹣ 3),此中 m> 1,∴ME=| ﹣ m2+2m+3|,∵M 、 N 对于 x=1 对称,且点 M 在对称轴右边,∴点 N 的横坐标为 2﹣ m,∴MN=2m ﹣ 2,∵四边形MNFE 为正方形,∴ME=MN ,∴|﹣ m2+2m+3|=2m ﹣ 2,分两种状况:①当﹣ m2+2m+3=2m ﹣ 2 时,解得: m1= 、 m2=﹣(不切合题意,舍去),当 m= 时,正方形的面积为( 2 ﹣2)2=24 ﹣ 8 ;②当﹣ m2 3 4=2﹣(不切合题意,舍去),+2m+3=2 ﹣ 2m 时,解得: m =2+ , m当 m=2+ 时,正方形的面积为[2 (2+ )﹣ 2]2=24+8 ;综上所述,正方形的面积为24+8 或 24﹣ 8 .( 3)设 BC 所在直线分析式为y=px+q ,把点 B (3, 0)、C( 0,﹣ 3)代入表达式,得:,解得:,∴直线 BC 的函数表达式为y=x﹣ 3,设点 M 的坐标为( t, t2﹣ 2t﹣ 3),此中 t <1,则点 N( 2﹣ t, t2﹣2t﹣ 3),点 D ( t, t﹣ 3),∴MN=2 ﹣ t﹣t=2 ﹣2t, MD=|t 2﹣ 2t﹣ 3﹣ t+3|=|t2﹣3t|.∵ MD=MN ,∴ |t2﹣ 3t|=2﹣ 2t,分两种状况:①当 t2﹣ 3t=2﹣ 2t 时,解得 t 1=﹣ 1, t2=2 (不切合题意,舍去).二次函数专题训练(正方形的存在性)②当 3t﹣ t2=2﹣ 2t 时,解得3 2(不切合题意,舍去).t = , t =综上所述,点 M 的横坐标为﹣ 1 或.4.(2015 贵州省毕节地域 ) 如图,抛物线 y=x 2+bx+c 与 x 轴交于 A (﹣ 1,0), B( 3, 0)两点,极点M 关于 x 轴的对称点是M′.( 1)求抛物线的分析式;( 2)若直线AM′与此抛物线的另一个交点为C,求△ CAB 的面积;( 3)能否存在过A, B 两点的抛物线,其极点P 对于 x 轴的对称点为Q,使得四边形APBQ 为正方形?若存在,求出此抛物线的分析式;若不存在,请说明原因.剖析:(1)依据待定系数法,可得函数分析式;( 2)依据轴对称,可得M′的坐标,依据待定系数法,可得AM′的分析式,依据解方程组,可得B点坐标,依据三角形的面积公式,可得答案;( 3)依据正方形的性质,可得P、 Q 点坐标,依据待定系数法,可得函数分析式.解答:解:( 1)将 A 、 B 点坐标代入函数分析式,得,解得,抛物线的分析式y=x 2﹣ 2x﹣ 3;( 2)将抛物线的分析式化为极点式,得 y= ( x﹣1)2﹣ 4, M点的坐标为( 1,﹣ 4), M′点的坐标为( 1, 4),设AM′的分析式为 y=kx+b ,将 A 、M′点的坐标代入,得,解得,AM′的分析式为y=2x+2 ,联立 AM′与抛物线,得,解得,C点坐标为( 5,12). S△ABC = ×4×12=24;( 3)存在过 A ,B 两点的抛物线,其极点P 对于 x 轴的对称点为Q,使得四边形APBQ 为正方形,由 ABPQ 是正方形, A (﹣ 1, 0) B ( 3, 0),得P( 1,﹣ 2), Q( 1, 2),或 P(1, 2), Q( 1,﹣ 2),将 A 点坐标代入函数分析式,得a(﹣ 1﹣ 1)2﹣ 2=0 ,解得 a=,抛物线的分析式为y=(x﹣1)2﹣2,②当 P( 1, 2)时,设抛物线的分析式为 y=a( x﹣ 1)2+2,将 A点坐标代入函数分析式,得 a(﹣ 1﹣ 1)2+2=0 ,解得 a=﹣,抛物线的分析式为y=﹣(x﹣1)2+2,综上所述: y=(x﹣1)2﹣2或y=﹣(x﹣1)2+2,使得四边形APBQ 为正方形.5. (2016 辽宁省铁岭市 ) .如图,抛物线y= ﹣x2+bx+c 与 x 轴交于点 A ,点 B,与 y 轴交于点C,点 B坐标为( 6,0),点 C 坐标为( 0,6),点 D 是抛物线的极点,过点 D 作 x 轴的垂线,垂足为E,连结 BD .( 1)求抛物线的分析式及点 D 的坐标;( 2)点 F 是抛物线上的动点,当∠ FBA=∠ BDE时,求点 F 的坐标;( 3)若点 M 是抛物线上的动点,过点M作MN∥ x轴与抛物线交于点N ,点 P 在 x 轴上,点 Q 在平面内,以线段 MN 为对角线作正方形MPNQ ,请直接写出点Q 的坐标.剖析( 1)由点 B 、C 的坐标利用待定系数法即可求出抛物线的分析式,再利用配方法将抛物线分析式变形成极点式即可得出结论;( 2)设线段 BF 与 y 轴交点为点 F′,设点 F′的坐标为( 0, m),由相像三角形的判断及性质可得出点F′的坐标,依据点B、F′的坐标利用待定系数法可求出直线BF 的分析式,联立直线BF 和抛物线的分析式成方程组,解方程组即可求出点 F 的坐标;( 3)设对角线 MN 、 PQ 交于点 O′,如图 2 所示.依据抛物线的对称性联合正方形的性质可得出点P、 Q 的地点,设出点Q 的坐标为( 2, 2n),由正方形的性质可得出点M 的坐标为(2﹣n, n).由点 M 在抛物线图象上,即可得出对于n 的一元二次方程,解方程可求出n 值,代入点Q 的坐标即可得出结论.解答解:( 1)将点 B ( 6,0)、 C( 0, 6)代入 y=﹣x2+bx+c 中,得:,解得:,∴ 抛物线的分析式为y= ﹣x2+2x+6 .∵ y= ﹣x2+2x+6= ﹣(x﹣2)2+8,∴点 D 的坐标为( 2, 8).(2)设线段 BF 与 y 轴交点为点 F′,设点 F′的坐标为( 0,m),如图 1 所示.∵∠ F′BO=∠ FBA= ∠ BDE ,∠ F′OB=∠ BED=90°,∴△ F′BO∽△ BDE ,∴.∵点 B (6, 0),点 D( 2, 8),11∴点 E( 2, 0),BE=6 ﹣ 4=4 , DE=8 ﹣ 0=8 ,OB=6 ,∴OF′=?OB=3,∴点 F′(0, 3)或( 0,﹣ 3).设直线 BF 的分析式为y=kx±3,则有 0=6k+3 或 0=6k﹣ 3,解得: k= ﹣或k=,∴直线 BF 的分析式为y=﹣x+3 或 y=x﹣ 3.联立直线 BF 与抛物线的分析式得:① 或② ,解方程组①得:或(舍去),∴ 点F的坐标为(﹣1,);解方程组②得:或(舍去),∴ 点F的坐标为(﹣3,﹣).综上可知:点 F 的坐标为(﹣ 1,)或(﹣ 3,﹣).( 3)设对角线 MN 、 PQ 交于点 O′,如图 2 所示.∵点 M 、 N 对于抛物线对称轴对称,且四边形MPNQ 为正方形,∴点 P 为抛物线对称轴与x 轴的交点,点 Q 在抛物线对称轴上,设点 Q 的坐标为(2, 2n),则点 M 的坐标为( 2 ﹣ n, n).∵点 M 在抛物线 y= ﹣x2+2x+6 的图象上,∴ n=﹣+2( 2﹣ n) +6,即 n2+2n ﹣ 16=0,解得: n1= ﹣ 1 , n2 =﹣﹣1.∴点 Q 的坐标为(2,﹣ 1)或( 2,﹣﹣ 1).6. (2016 广东省茂名市 ) 】.如图,抛物线 y= ﹣ x2 +bx+c 经过 A (﹣ 1,0), B( 3,0)两点,且与 y 轴交于点 C,点 D 是抛物线的极点,抛物线的对称轴DE 交 x 轴于点 E,连结 BD .(1)求经过 A ,B ,C 三点的抛物线的函数表达式;(2)点 P 是线段 BD 上一点,当 PE=PC 时,求点 P 的坐标;( 3)在( 2)的条件下,过点P 作 PF⊥x 轴于点 F, G 为抛物线上一动点,M 为 x 轴上一动点, N 为直线PF 上一动点,当以F、 M 、 G 为极点的四边形是正方形时,恳求出点M 的坐标.剖析( 1)利用待定系数法求出过A, B,C 三点的抛物线的函数表达式;12( 2)连结 PC、PE,利用公式求出极点 D 的坐标,利用待定系数法求出直线BD 的分析式,设出点P 的坐标为( x,﹣ 2x+6 ),利用勾股定理表示出PC2和 PE2,依据题意列出方程,解方程求出x 的值,计算求出点 P 的坐标;(3)设点 M 的坐标为( a, 0),表示出点 G 的坐标,依据正方形的性质列出方程,解方程即可.解答解:( 1)∵抛物线 y= ﹣x2+bx+c 经过 A (﹣ 1, 0), B ( 3, 0)两点,∴,解得,,∴ 经过A,B,C三点的抛物线的函数表达式为y= ﹣ x2+2x+3 ;( 2)如图 1,连结 PC、PE, x= ﹣=﹣=1,当x=1 时, y=4 ,∴点 D 的坐标为( 1, 4),设直线 BD 的分析式为: y=mx+n ,则,解得,,∴ 直线BD的分析式为y= ﹣ 2x+6,设点 P 的坐标为( x,﹣ 2x+6),则PC2=x 2+(3+2x ﹣ 6)2,PE2=( x﹣ 1)2+(﹣ 2x+6 )2,∵PC=PE,∴x2+(3+2x ﹣6)2=(x﹣1)2+(﹣2x+6 )2,解得, x=2,则 y= ﹣2×2+6=2 ,∴点 P 的坐标为( 2, 2);(3)设点 M 的坐标为( a, 0),则点 G 的坐标为( a,﹣ a2 +2a+3),∵以 F、M 、 G 为极点的四边形是正方形,∴ FM=MG ,即 |2﹣ a|=|﹣ a2 +2a+3|,当 2﹣ a=﹣ a2+2a+3 时,整理得,a2﹣ 3a﹣1=0 ,解得, a=,当2﹣ a=﹣(﹣ a2+2a+3)时,整理得, a2﹣ a﹣5=0 ,解得, a= ,∴当以 F、M 、G 为极点的四边形是正方形时,点 M 的坐标为(,0),(,0),(,0),(, 0).13。
二次函数中的存在性问题(等腰三角形)答案

学习必备 欢迎下载1、(福建龙岩)解:( 1)抛物线的对称轴x5a 52a 2y( 2) A( 3,0)B(5,4)C (0,4)CMB把点 A 坐标代入 yax 2 5ax 4 中,解得 a1 A1N6Q151P 3 xy2 4Kxx66P 共有 3 个.以下分三类情形探索. P 2 ( 3)存在符合条件的点设抛物线对称轴与 x 轴交于 N ,与 CB 交于 M .P 1过点 B 作 BQx 轴于 Q ,易得 BQ4, AQ8, AN 5.5 , BM52① 以 AB 为腰且顶角为角A 的△PAB 有 1 个: △P 1AB .AB 2 AQ 2 BQ 2 82 4280在 Rt △ ANP 1 中, P NAP 2 AN 2AB 2 AN 280 (5.5) 21995 , 199222② AB 为腰且顶角为角B 的△PAB 有 1 个: △P 2AB .在 Rt △ BMP 2 中, MP 22BM 2AB 2BM 28025295 P 25 8 295BP 2422 ,2③以 AB 为底,顶角为角P 的 △PAB 有 1 个,即 △P 3AB .画 AB 的垂直平分线交抛物线对称轴于 P 3 ,此时平分线必过等腰△ABC 的顶点 C .过点P 3 作 P 3 K 垂直 y 轴,垂足为 K ,显然 Rt △ PCK 3 ∽ Rt △ BAQ .P 3KBQ 1CKAQ .2Q P 3K 2.5CK5于是 OK1P 3 (2.5, 1)2、 [07 年云南省] 解:( 1)∵抛物线经过点A(1, 0) 、 B(5 , 0)∴ y a(x 1)(x 5) .又∵抛物线经过点 C(0 , 5) ∴5a 5 , a 1 .∴抛物线的解析式为y ( x 1)(x 5)x 2 6x 5 .( 2)∵ E 点在抛物线上,∴ m = 42–4× 6+5 = - 3.∵直线 y = kx+b 过点 C ( 0, 5)、 E ( 4, –3),b5,解得 k = -2, b = 5.∴4k b 3.学习必备欢迎下载设直线 y=- 2x+5 与 x 轴的交点为 D,当 y=0 时, - 2x+5=0 ,解得 x= 5.∴ D 点的坐标为(5,0).22∴ S=S△BDC + S△BDE= 1(55)5+1(55) 3 =10.2222( 3)∵抛物线的顶点P0(3 ,4) 既在抛物线的对称轴上又在抛物线上,∴点 P0 (3 , 4) 为所求满足条件的点.( 4)除P0点外,在抛物线上还存在其它的点P 使得△ ABP 为等腰三角形.理由如下:∵AP0BP02242 2 5 4 ,∴分别以 A 、 B 为圆心半径长为 4 画圆,分别与抛物线交于点B 、1、2、3、A、 4 、 5 、 6 ,P P P P P P除去 B 、 A 两个点外,其余 6 个点为满足条件的点.(说明:只说出P 点个数但未简要说明理由的不给分)3、 [08 广东梅州 ]解:(1)DC∥ AB,AD =DC =CB,∠ DAB=∠ CBA,∠ DAB=2∠∠ CDB=∠ CBD=∠ DBA ,DBA ,∠DAB+∠ DBA =90 ,∠DAB =60,∠DBA=30 , AB=4,DC=AD=2 ,Rt AOD , OA=1, OD= 3 ,.A( - 1, 0), D( 0, 3 ),C(2, 3 ).( 2)根据抛物线和等腰梯形的对称性知,满足条件的抛物线必过点A(- 1,0), B( 3, 0),故可设所求为y =a(x+1)(x-3)将点 D(0, 3 )的坐标代入上式得, a =3.3所求抛物线的解析式为y =3( x1)( x3).················7分3其对称轴 L 为直线x =1.·····································8 分( 3)PDB 为等腰三角形,有以下三种情况:①因直线 L 与 DB 不平行, DB 的垂直平分线与L 仅有一个交点P1,P1D =P1B,P1DB 为等腰三角形;······································9分②因为以 D 为圆心,DB 为半径的圆与直线L 有两个交点 P2、P3,DB =DP2,DB =DP 3, P2DB, P3DB 为等腰三角形;③与②同理, L 上也有两个点 P4、 P5,使得 BD=BP4, BD =BP5.···········10 分由于以上各点互不重合,所以在直线L 上,使PDB 为等腰三角形的点 P 有 5 个.学习必备 欢迎下载4、 [08 浙江温州 ]解:( 1)QA Rt , AB6, AC8 , BC 10.Q 点D 为 AB 中点,BD1AB 3.2Q DHBA 90o , BB . △ BHD ∽△ BAC ,DH BD DHBDgAC3 12AC,BC 108.BC5(2)Q QR ∥ AB ,QRCA 90o .RQ QC y 10 xAQ CC , △ RQC ∽△ ABC ,,ABBC6,10D P3 x即 y 关于 x 的函数关系式为:y6.1 M5B2( 3)存在,分三种情况:H Q①当 PQPR 时,过点 P 作 PM QR 于 M ,则 QMRM .Q 12 90o ,C2 90o ,1C .cos 1cosC8 4 ,10 5 AQM 4 13 x 6418D25,x.QP,1255B5H5②当 PQRQ 时,3 x 6 12 , x 6 .A55③当 PR QR 时,则 R 为 PQ 中垂线上的点,于是点R 为 EC 的中点,DRECPERCQE PR1 1 QR BA BCCRCEAC 2 . Q tan CCR,HQ24CA3 x66 1518155.综上所述,当x 为或 6 或时, △ PQR 为等腰三角形.2, x52825、( 09 重庆).解:( 1)由已知,得 C (3,0) , D (2,2) ,Q ADE 90°CDBBCD ,AEAD gtan ADE 2 tan BCD1 1.22E(0,1) . ··············································(1 分)设过点 E 、 D 、 C 的抛物线的解析式为 y ax 2 bxc( a 0) .将点 E 的坐标代入,得 c 1 .4a 2b 1,将 c 1 和点 D 、C 的坐标分别代入,得················(2 分)9a 3b 1 0.5a5 x 2 13 x解这个方程组,得6 , 故抛物线的解析式为 y1. ··(3 分)136 6b6(2) EF 2GO 成立. ·······································(4 分)Q 点 M 在该抛物线上,且它的横坐标为6 ,5点 M 的纵坐标为12. ······································(5 分)5y设 DM 的解析式为y kxb 1 (k 0) , F M将点 D 、M 的坐标分别代入,得A DB2k b 1 , k 1 , E26b 1 12 解得2k .b 1.x553O G K C1DM 的解析式为 x 3. ·······························(6 分)y2F (0,3) , EF2 . ········································(7 分)过点 D 作DK ⊥OC 于点 K ,则DA DK .Q ADK FDG 90°,FDA GDK . 又 Q FAD GKD 90°, △DAF ≌△ DKG . KG AF 1. GO 1. ····································( 8 分)EF 2GO .( 3) Q 点 P 在 AB 上, G(10), , C(3,0) ,则设 P(12), .PG 2 (t 1)222, PC 2 (3 t )2 22,GC 2.①若 PGPC ,则 (t1)2 22 (3 t) 2 22 ,解得 t 2 . P(2,2) ,此时点 Q 与点 P 重合. Q (2,2) . ············(9 分)② 若 PGGC ,则22 ,解得t 1,, ,此时GP ⊥ x 轴.1) 22P(1 2)(tGP 与该抛物线在第一象限内的交点Q 的横坐标为1,点 Q 的纵坐标为 7.7. ·····························(10 分),3Q 1 3③若 PC GC ,则 (3t) 2 22 22 ,解得 t 3 , P(3,2) ,此时 PC GC2, △PCG 是等腰直角三角形.过点 Q 作 QH ⊥ x 轴于点 H ,则 QHGH ,设 QHh ,yQ(Q)AD(P)Q (h1, h) .PB (P)QE5(h 1)213(h 1) 1 h .676x解得 h 12 (舍去).OGH C, h 2512 7Q, . ····················( 12 分)5 5综上所述,存在三个满足条件的点Q ,即Q(2,2) 或Q7 或 Q 12 7 ., ,1 3 5 51⋯⋯2分6(沈阳) 24.解:( 1)符合条件的等腰△OMP 只有 1 个 . 点 P 的坐标为( , 4)2( 2)符合条件的等腰△ OMP 有 4个. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3 分如图①,在△ 1 中, 1= = 4,OPMOP OM7在 Rt △ OBP 1中, BO = 2,2227215BP 1= OP 1- OB =4-(2)= 2∴ 1(- 7, 15 ) ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5 分P 2 2在 Rt △ OMP 2中, OP 2= OM = 4,∴ P 2( 0, 4) 在△ OMP 3中, MP 3= OP 3,∴点3在 的垂直平分线上,∵=4,∴ 3(2, 4)P OMOMP在 Rt △ OMP 中, OM = MP = 4,∴ P ( 4, 4)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 9 分444( 3)若 M ( 5,0),则符合条件的等腰三角形有 7 个 . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分点 P 的位置如图②所示。
二次函数存在性问题及解答

初中数学二次函数存在性问题总复习试题及解答1.(10广东深圳)如图,抛物线y =ax 2+c (a >0)经过梯形ABCD 的四个顶点,梯形的底AD 在x 轴上,其中A (-2,0),B (-1, -3). (1)求抛物线的解析式;(2)点M 为y 轴上任意一点,当点M 到A 、B 两点的距离之和为最小时,求此时点M 的坐标;(3)在第(2)问的结论下,抛物线上的点P 使S △P AD =4S △ABM 成立,求点P 的坐标.答案:(1)、因为点A 、B 均在抛物线上,故点A 、B 的坐标适合抛物线方程∴403a c a c +=⎧⎨+=-⎩ 解之得:14a c =⎧⎨=-⎩;故24y x =-为所求 (2)如图2,连接BD ,交y 轴于点M ,则点M 就是所求作的点 设BD 的解析式为y kxb =+,则有203k b k b +=⎧⎨-+=-⎩,12k b =⎧⎨=-⎩,故BD 的解析式为2y x =-;令0,x =则2y =-,故(0,2)M -(3)、如图3,连接AM ,BC 交y 轴于点N ,由(2)知,OM=OA=OD=2,90AMB ∠=︒ 易知BN=MN=1,易求AM BM ==122ABMS=⨯=;设2(,4)P x x -, 依题意有:214422AD x -=⨯,即:2144422x ⨯-=⨯解之得:x =±,0x =,故 符合条件的P点有三个:123((0,4)P P P --图22. (10北京)在平面直角坐标系xOy 中,抛物线y = -41-m x 2+45mx +m 2-3m +与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上。
(1) 求点B 的坐标;(2) 点P 在线段OA 上,从O 点出发向点运动,过P 点作x 轴的 垂线,与直线OB 交于点E 。
延长PE 到点D 。
使得ED =PE 。
以PD 为斜边在PD 右侧作等腰直角三角形PCD (当P 点运动 时,C 点、D 点也随之运动) 当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求 OP 的长;若P 点从O 点出发向A 点作匀速运动,速度为每秒1一点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止 运动,P 点也同时停止运动)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数中的存在性问题姓名1.已知抛物线y=﹣x2+ x﹣3 与x 轴交于A,B 两点,与y 轴交于点C.在直线CA 上方的抛物线上是否存在一点D,使得△ACD 的面积最大?若存在,求出点D 的坐标;若不存在,请说明理由.2.已知y=ax2+bx+c(a≠0)图象与直线y=kx+4 相交于A(1,m),B(4,8)两点,与x 轴交于原点及点C.(1)求直线和抛物线解析式;(2)在x 轴上方的抛物线上是否存在点D,使S△OCD=2S△OAB?如果存在,求出点D 坐标,如果不存在,说明理由.3.已知直线y=x﹣3 与x 轴交于点A,与y 轴交于点C,抛物线y=﹣x2+mx+n 经过点A 和点C.(1)求此抛物线的解析式;(2)在直线CA 上方的抛物线上是否存在点D,使得△ACD 的面积最大?若存在,求出点D 的坐标;若不存在,说明理由.4.在平面直角坐标系xOy 中,抛物线y=﹣x2+bx+c 与x 轴交于A、B 两点(点A 在点B 的左侧),过点A 的直线y=kx+1 交抛物线于点C(2,3).(1)求直线AC 及抛物线的解析式;(2)若直线y=kx+1 与抛物线的对称轴交于点E,以点E 为中心将直线y=kx+1 顺时针旋转90°得到直线l,设直线l 与y 轴的交点为P,求△APE 的面积;(3)若G 为抛物线上一点,是否存在x 轴上的点F,使以B、E、F、G 为顶点的四边形为平行四边形?若存在,直接写出点F 的坐标;若不存在,请说明理由.5.如图,在平面直角坐标系中,抛物线交x 轴于A,B 两点(A 在B 的左侧),交y 轴于点C.(1)求直线BC 的解析式;(2)求抛物线的顶点及对称轴;(3)若点Q 是抛物线对称轴上的一动点,线段AQ+CQ 是否存在最小值?若存在,求出点Q 的坐标;若不存在,说明理由;(4)若点P 是直线BC 上方的一个动点,△PBC 的面积是否存在最大值?若存在,求出点P 的坐标及此时△PBC 的面积;若不存在,说明理由.解得:x=1 或 x=4,∴B (1,0),A (4,0),令 x=0,得到 y=﹣3,即 C (0,﹣3),设直线 AC 解析式为 y=kx+b ,将 A 与 C 坐标代入得:, 解得:k=,b=﹣3,∴直线 AC 解析式为 y=x ﹣3,设平行于直线 AC ,且与抛物线只有一个交点的直线方程为 y=x+m ,此时直线与抛物线交于点 D ,使得△ACD 的面积最大,与二次函数解析式联立消去 y 得:﹣x 2+x ﹣3= x+m , 整理得:3x 2﹣12x+4m+12=0,∴△=144﹣12(4m+12)=0,解得:m=0,∴此时直线方程为 y=x ,点 D 坐标为(2,).2.(2008•宁波校级自主招生)已知 y=ax 2+bx+c (a ≠0)图象与直线 y=kx+4 相交于 A (1,m ),B (4,8)两点,与 x 轴交于原点及点 C .(1) 求直线和抛物线解析式;(2) 在 x 轴上方的抛物线上是否存在点 D ,使 S △OCD =2S △OAB ?如果存在,求出点 D 坐标,如果不存在,说明理由.解答: 解:(1)∵直线 y=kx+4 过 A (1,m ),B (4,8)两点,∴ ,解得 ,∴y=x+4,1. 已知抛物线 y=﹣ x 2+ x ﹣3 与 x 轴交于 A ,B 两点,2. 与 y 轴交于点 C .在直线 CA 上方的抛物线上是否存在3. 一点 D ,使得△ACD 的面积最大?若存在,求出点 D4. 的坐标;若不存在,请说明理由.解答: 解:对于抛物线 y=﹣x 2+x ﹣3, 令 y=0,得到﹣ x 2+x ﹣3=0,和点 C .(1) 求此抛物线的解析式;(2) 在直线 CA 上方的抛物线上是否存在点 D ,使得△ACD 的面积最大?若存在,求出点 D 的坐标;若不存在,说明理由.解答: 解:(1)把 x=0 代入 y= x ﹣3 得 y=﹣3,则 C 点坐标为(0,﹣3),把 O 、A 、B 三点坐标代入抛物线解析式,得 , ,∴y=﹣x 2+6x ;(2)存在.设 D 点纵坐标为 h (h >0),由 O (0,0),A (1,5),B (4,8),可知 S △OAB =6,∴S △OCD =2S △OAB =12, ×6×h=12,解得 h=4,由﹣x 2+6x=4,得 x=3±, ∴D (3+,4)或(3﹣,4).3.(2014 春•昌平区期末)已知直线 y=x ﹣3 与 x 轴交于点 A ,与 y 轴交于点 C ,抛物线 y=﹣x 2+mx+n 经过点 A 把 y=0 代入 y=x ﹣3 得x ﹣3=0,解得 x=4,则 A 点坐标为(4,0),把 A (4,0),C (0,﹣3)代入 y=﹣x 2+mx+n 得 ,解得 ,所以二次函数解析式为 y=﹣x 2+x ﹣3;(2)存在. 过 D 点作直线 AC 的平行线 y=kx+b ,当直线 y=kx+b 与抛物线只有一个公共点时,点 D 到 AC 的距离最大,此时△ACD 的面积最大,∵直线 AC 的解析式为 y=x ﹣3,∴k= ,即 y=x+b ,由直线 y=x+b 和抛物线 y=﹣x 2+ x ﹣3 组成方程组得 ,消去 y 得到3x 2﹣12x+4b+12=0,∴△=122﹣4×3×(4b+12)=0,解得b=0,∴3x2﹣12x+12=0,解得x1=x2=2,把x=2,b=0 代入y=x+b 得y=,∴D 点坐标为(2,).4.(2010•孝感模拟)在平面直角坐标系xOy 中,抛物线y=﹣x2+bx+c 与x 轴交于A、B 两点(点A 在点B 的左侧),过点A 的直线y=kx+1 交抛物线于点C(2,3).(1)求直线AC 及抛物线的解析式;(2)若直线y=kx+1 与抛物线的对称轴交于点E,以点E 为中心将直线y=kx+1 顺时针旋转90°得到直线l,设直线l 与y 轴的交点为P,求△APE 的面积;(3)若G 为抛物线上一点,是否存在x 轴上的点F,使以B、E、F、G 为顶点的四边形为平行四边形?若存在,直接写出点F 的坐标;若不存在,请说明理由.解答:解:(1)∵点C(2,3)在直线y=kx+1 上,∴2k+1=3.解得k=1.∴直线AC 的解析式为y=x+1.∵点A 在x 轴上,∴A(﹣1,0).∵抛物线y=﹣x2+bx+c 过点A、C,∴解得∴抛物线的解析式为y=﹣x2+2x+3.(2)由y=﹣x2+2x+3=﹣(x﹣1)2+4,可得抛物线的对称轴为x=1,B(3,0).∴E(1,2).根据题意,知点A 旋转到点B 处,直线l 过点B、E.设直线l 的解析式为y=mx+n.将B、E 的坐标代入y=mx+n 中,联立可得m=﹣1,n=3.∴直线l 的解析式为y=﹣x+3.∴P(0,3).过点E 作ED⊥x 轴于点D.∴S△PAE=S△PAB﹣S△EAB= AB•PO﹣AB•ED= ×4×(3﹣2)=2.(3)存在,点F 的坐标分别为(3﹣,0),(3+,0),(﹣1﹣,0)(﹣1+,0).5.(2013 秋•红安县校级月考)如图,在平面直角坐标系中,抛物线交x 轴于A,B 两点(A 在B 的左侧),交y 轴于点C.(1)求直线BC 的解析式;(2)求抛物线的顶点及对称轴;(3)若点Q 是抛物线对称轴上的一动点,线段AQ+CQ 是否存在最小值?若存在,求出点Q 的坐标;若不存在,说明理由;(4)若点P 是直线BC 上方的一个动点,△PBC 的面积是否存在最大值?若存在,求出点P 的坐标及此时△PBC 的面积;若不存在,说明理由.考点:二次函数综合题.专题:压轴题.分析:(1)令y=0,解关于x 的一元二次方程求出点B 的坐标,令x=0 求出点C 的坐标,设直线BC 的解析式为y=kx+b,然后利用待定系数法求一次函数解析式解答即可;(2)把二次函数解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;(3)根据轴对称确定最短路线问题,直线BC 与对称轴的交点即为使线段AQ+CQ 最小的点Q,然后利用直线解析式求解即可;(4)过点P 作PD∥y 轴与BC 相交于点D,根据抛物线解析式与直线BC 的解析式表示出PD,再根据S△PBC=S△PCD+S△PBD 列式整理,然后利用二次函数最值问题解答.解答:解:(1)令y=0,则﹣x2+x+2=0,整理得,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,所以,点B 的坐标为(3,0),令x=0,则y=2,所以,点C 的坐标为(0,2),设直线BC 的解析式为y=kx+b,则,解得,所以,直线BC 的解析式为y=﹣x+2;(2)∵y=﹣x2+ x+2,=﹣(x2﹣2x+1)+2+ ,=﹣(x﹣1)2+ ,∴顶点坐标为(1,),对称轴为直线x=1;(3)由轴对称确定最短路线问题,直线BC 与对称轴的交点即为使线段AQ+CQ 最小的点,x=1 时,y=﹣×1+2=,所以,存在Q(1,),使线段AQ+CQ 最小;(4)如图,过点P 作PD∥y 轴与BC 相交于点D,则PD=(﹣x2+x+2)﹣(﹣x+2)=﹣x2+2x,所以,S△PBC=S△PCD+S△PBD,=×(﹣x2+2x)×3,=﹣x2+3x,=﹣(x﹣)2+ ,所以,当x=时,△PBC 的面积最大为,此时,y=﹣×()2+ ×+2= ,所以,存在P(,),使S △PBC 最大= .点评:本题是二次函数综合题型,主要利用了抛物线与x 轴的交点坐标的求解,待定系数法求一次函数解析式,二次函数的顶点坐标与对称轴的求法,轴对称确定最短路线问题,二次函数的最值问题.。
