(完整版)二次函数中的存在性问题(答案)

合集下载

二次函数的存在性问题(面积)及答案

图12-2xCOy ABD 11二次函数的存在性问题(面积问题)1、[08云南双柏]已知：抛物线y ＝ax 2＋bx ＋c 与x 轴交于A 、B 两点，与y 轴交于点C ，其中点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，线段OB 、OC 的长（OB <OC ）是方程x 2－10x ＋16＝0的两个根，且抛物线的对称轴是直线x ＝－2．（1）求A 、B 、C 三点的坐标；（2）求此抛物线的表达式；（3）求△ABC 的面积；（4）若点E 是线段AB 上的一个动点（与点A 、点B 不重合），过点E 作EF ∥AC 交BC 于点F ，连接CE ，设AE 的长为m ，△CEF 的面积为S ，求S 与m 之间的函数关系式，并写出自变量m 的取值范围；（5）在（4）的基础上试说明S 是否存在最大值，若存在，请求出S 的最大值，并求出此时点E 的坐标，判断此时△BCE 的形状；若不存在，请说明理由．2、 [09湖南益阳]阅读材料：如图12-1，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a )，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算PABCAB 98SS =三角形面积的新方法：ah S ABC 21=∆，即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题：如图12-2，抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0)，交y 轴于点B .(1)求抛物线和直线AB 的解析式；(2)点P 是抛物线(在第一象限内)上的一个动点，连结PA ，PB ，当P 点运动到顶点C 时，求△CAB 的铅垂高CD 及CAB S ∆； (3)是否存在一点P ，使PABCAB98S S =若存在，求出P 点的坐标；若不存在，请说明理由.图13、[09吉林长春]如图，在直角坐标系中，矩形ABCD 的边AD 在y 轴正半轴上，点A 、C 的坐标分别为（0，1）（2，4）．点P 从点A 出发，沿A →B →C 以每秒1个单位的速度运动，到点C 停止；点Q 在x 轴上，横坐标为点P 的横、纵坐标之和．抛物线c bx x y ++-=241经过A 、C 两点．过点P 作x 轴的垂线，垂足为M ，交抛物线于点R ．设点P 的运动时间为t （秒），△PQR 的面积为S （平方单位）．（1）求抛物线对应的函数关系式．（2分）（2）分别求t=1和t=4时，点Q 的坐标．（3分）（3）当0＜t ≤5时，求S 与t 之间的函数关系式，并直接写出S 的最大值．（5分）4、（07云南昆明）如图，在直角坐标系中，点A 的坐标为（－2，0），连结OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB 。

二次函数存在性问题

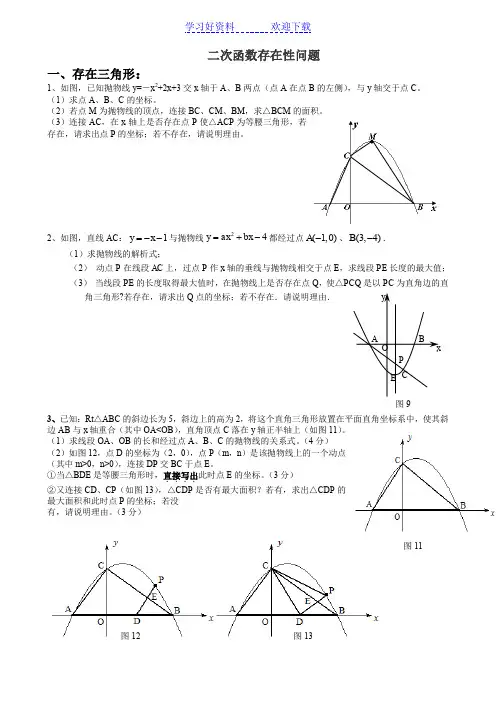
二次函数存在性问题一、存在三角形：1、如图，已知抛物线y=－x 2+2x+3交x 轴于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C 。

（1）求点A 、B 、C 的坐标。

（2）若点M 为抛物线的顶点，连接BC 、CM 、BM ，求△BCM 的面积。

（3）连接AC ，在x 轴上是否存在点P 使△ACP 为等腰三角形，若存在，请求出点P 的坐标；若不存在，请说明理由。

2、如图，直线AC ：1y x =--与抛物线24y ax bx =+-都经过点(1,0)A -、(3,4)B -．（1）求抛物线的解析式；（2）动点P 在线段AC 上，过点P 作x 轴的垂线与抛物线相交于点E ，求线段PE 长度的最大值；（3）当线段PE 的长度取得最大值时，在抛物线上是否存在点Q ，使△PCQ 是以PC 为直角边的直角三角形?若存在，请求出Q 点的坐标；若不存在．请说明理由．3、已知：Rt △ABC 的斜边长为5，斜边上的高为2，将这个直角三角形放置在平面直角坐标系中，使其斜边AB 与x 轴重合（其中OA<OB ），直角顶点C 落在y 轴正半轴上（如图11）。

（1）求线段OA 、OB 的长和经过点A 、B 、C 的抛物线的关系式。

（4分）（2）如图12，点D 的坐标为（2，0），点P （m ，n ）是该抛物线上的一个动点（其中m >0，n >0），连接DP 交BC 于点E 。

①当△BDE 是等腰三角形时，直接写出．．．．此时点E 的坐标。

（3分） ②又连接CD 、CP （如图13），△CDP 是否有最大面积？若有，求出△CDP 的最大面积和此时点P 的坐标；若没有，请说明理由。

（3分）图11A B O C 图9 yx P E 图12 图13二、存在四边形：1、如图，已知抛物线)0(2≠++=a c bx ax y 的顶点坐标为Q ()1,2-，且与y 轴交于点C ()3,0，与x 轴交于A 、B 两点（点A 在点B 的右侧），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD ∥y 轴，交AC 于点D ．（1）求该抛物线的函数关系式；（2）当△ADP 是直角三角形时，求点P 的坐标；（3）在问题（2）的结论下，若点E 在x 轴上，点F 在抛物线上，问是否存在以A 、P 、E 、F 为顶点的平行四边形？若存在，求点F 的坐标；若不存在，请说明理由．2、在平面直角坐标系中，已知抛物线经过A )0,4(-，B )4,0(-，C )0,2(三点．（1）求抛物线的解析式；（2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．（3）若点P 是抛物线上的动点，点Q 是直线x y -=上的动点，判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标．3、如图，在平面直角坐标系中CDA Rt AOB Rt ∆≅∆,且)2,0(),0,1(B A -抛物线22-+=ax ax y 经过点C 。

二次函数中的存在性问题(答案)(可编辑修改word版)

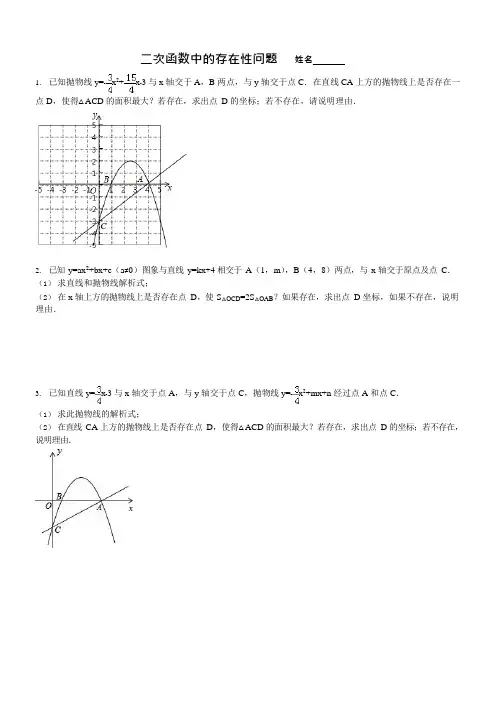
二次函数中的存在性问题姓名1.已知抛物线y=﹣x2+ x﹣3 与x 轴交于A，B 两点，与y 轴交于点C．在直线CA 上方的抛物线上是否存在一点D，使得△ACD 的面积最大？若存在，求出点D 的坐标；若不存在，请说明理由．2.已知y=ax2+bx+c（a≠0）图象与直线y=kx+4 相交于A（1，m），B（4，8）两点，与x 轴交于原点及点C．（1）求直线和抛物线解析式；（2）在x 轴上方的抛物线上是否存在点D，使S△OCD=2S△OAB？如果存在，求出点D 坐标，如果不存在，说明理由．3.已知直线y=x﹣3 与x 轴交于点A，与y 轴交于点C，抛物线y=﹣x2+mx+n 经过点A 和点C．（1）求此抛物线的解析式；（2）在直线CA 上方的抛物线上是否存在点D，使得△ACD 的面积最大？若存在，求出点D 的坐标；若不存在，说明理由．4.在平面直角坐标系xOy 中，抛物线y=﹣x2+bx+c 与x 轴交于A、B 两点（点A 在点B 的左侧），过点A 的直线y=kx+1 交抛物线于点C（2，3）．（1）求直线AC 及抛物线的解析式；（2）若直线y=kx+1 与抛物线的对称轴交于点E，以点E 为中心将直线y=kx+1 顺时针旋转90°得到直线l，设直线l 与y 轴的交点为P，求△APE 的面积；（3）若G 为抛物线上一点，是否存在x 轴上的点F，使以B、E、F、G 为顶点的四边形为平行四边形？若存在，直接写出点F 的坐标；若不存在，请说明理由．5.如图，在平面直角坐标系中，抛物线交x 轴于A，B 两点（A 在B 的左侧），交y 轴于点C．（1）求直线BC 的解析式；（2）求抛物线的顶点及对称轴；（3）若点Q 是抛物线对称轴上的一动点，线段AQ+CQ 是否存在最小值？若存在，求出点Q 的坐标；若不存在，说明理由；（4）若点P 是直线BC 上方的一个动点，△PBC 的面积是否存在最大值？若存在，求出点P 的坐标及此时△PBC 的面积；若不存在，说明理由．解得：x=1 或 x=4，∴B （1，0），A （4，0），令 x=0，得到 y=﹣3，即 C （0，﹣3），设直线 AC 解析式为 y=kx+b ，将 A 与 C 坐标代入得：，解得：k=，b=﹣3，∴直线 AC 解析式为 y=x ﹣3，设平行于直线 AC ，且与抛物线只有一个交点的直线方程为 y=x+m ，此时直线与抛物线交于点 D ，使得△ACD 的面积最大，与二次函数解析式联立消去 y 得：﹣x 2+x ﹣3= x+m ，整理得：3x 2﹣12x+4m+12=0，∴△=144﹣12（4m+12）=0，解得：m=0，∴此时直线方程为 y=x ，点 D 坐标为（2，）．2．（2008•宁波校级自主招生）已知 y=ax 2+bx+c （a ≠0）图象与直线 y=kx+4 相交于 A （1，m ），B （4，8）两点，与 x 轴交于原点及点 C ．（1）求直线和抛物线解析式；（2）在 x 轴上方的抛物线上是否存在点 D ，使 S △OCD =2S △OAB ？如果存在，求出点 D 坐标，如果不存在，说明理由．解答：解：（1）∵直线 y=kx+4 过 A （1，m ），B （4，8）两点，∴ ，解得，∴y=x+4，1. 已知抛物线 y=﹣ x 2+ x ﹣3 与 x 轴交于 A ，B 两点，2. 与 y 轴交于点 C ．在直线 CA 上方的抛物线上是否存在3. 一点 D ，使得△ACD 的面积最大？若存在，求出点 D4. 的坐标；若不存在，请说明理由．解答：解：对于抛物线 y=﹣x 2+x ﹣3，令 y=0，得到﹣ x 2+x ﹣3=0，和点 C ．（1）求此抛物线的解析式；（2）在直线 CA 上方的抛物线上是否存在点 D ，使得△ACD 的面积最大？若存在，求出点 D 的坐标；若不存在，说明理由．解答：解：（1）把 x=0 代入 y= x ﹣3 得 y=﹣3，则 C 点坐标为（0，﹣3），把 O 、A 、B 三点坐标代入抛物线解析式，得，，∴y=﹣x 2+6x ；（2）存在．设 D 点纵坐标为 h （h ＞0），由 O （0，0），A （1，5），B （4，8），可知 S △OAB =6，∴S △OCD =2S △OAB =12， ×6×h=12，解得 h=4，由﹣x 2+6x=4，得 x=3±， ∴D （3+，4）或（3﹣，4）．3．（2014 春•昌平区期末）已知直线 y=x ﹣3 与 x 轴交于点 A ，与 y 轴交于点 C ，抛物线 y=﹣x 2+mx+n 经过点 A 把 y=0 代入 y=x ﹣3 得x ﹣3=0，解得 x=4，则 A 点坐标为（4，0），把 A （4，0），C （0，﹣3）代入 y=﹣x 2+mx+n 得，解得，所以二次函数解析式为 y=﹣x 2+x ﹣3；（2）存在．过 D 点作直线 AC 的平行线 y=kx+b ，当直线 y=kx+b 与抛物线只有一个公共点时，点 D 到 AC 的距离最大，此时△ACD 的面积最大，∵直线 AC 的解析式为 y=x ﹣3，∴k= ，即 y=x+b ，由直线 y=x+b 和抛物线 y=﹣x 2+ x ﹣3 组成方程组得，消去 y 得到3x 2﹣12x+4b+12=0，∴△=122﹣4×3×（4b+12）=0，解得b=0，∴3x2﹣12x+12=0，解得x1=x2=2，把x=2，b=0 代入y=x+b 得y=，∴D 点坐标为（2，）．4．（2010•孝感模拟）在平面直角坐标系xOy 中，抛物线y=﹣x2+bx+c 与x 轴交于A、B 两点（点A 在点B 的左侧），过点A 的直线y=kx+1 交抛物线于点C（2，3）．（1）求直线AC 及抛物线的解析式；（2）若直线y=kx+1 与抛物线的对称轴交于点E，以点E 为中心将直线y=kx+1 顺时针旋转90°得到直线l，设直线l 与y 轴的交点为P，求△APE 的面积；（3）若G 为抛物线上一点，是否存在x 轴上的点F，使以B、E、F、G 为顶点的四边形为平行四边形？若存在，直接写出点F 的坐标；若不存在，请说明理由．解答：解：（1）∵点C（2，3）在直线y=kx+1 上，∴2k+1=3．解得k=1．∴直线AC 的解析式为y=x+1．∵点A 在x 轴上，∴A（﹣1，0）．∵抛物线y=﹣x2+bx+c 过点A、C，∴解得∴抛物线的解析式为y=﹣x2+2x+3．（2）由y=﹣x2+2x+3=﹣（x﹣1）2+4，可得抛物线的对称轴为x=1，B（3，0）．∴E（1，2）．根据题意，知点A 旋转到点B 处，直线l 过点B、E．设直线l 的解析式为y=mx+n．将B、E 的坐标代入y=mx+n 中，联立可得m=﹣1，n=3．∴直线l 的解析式为y=﹣x+3．∴P（0，3）．过点E 作ED⊥x 轴于点D．∴S△PAE=S△PAB﹣S△EAB= AB•PO﹣AB•ED= ×4×（3﹣2）=2．（3）存在，点F 的坐标分别为（3﹣，0），（3+，0），（﹣1﹣，0）（﹣1+，0）．5．（2013 秋•红安县校级月考）如图，在平面直角坐标系中，抛物线交x 轴于A，B 两点（A 在B 的左侧），交y 轴于点C．（1）求直线BC 的解析式；（2）求抛物线的顶点及对称轴；（3）若点Q 是抛物线对称轴上的一动点，线段AQ+CQ 是否存在最小值？若存在，求出点Q 的坐标；若不存在，说明理由；（4）若点P 是直线BC 上方的一个动点，△PBC 的面积是否存在最大值？若存在，求出点P 的坐标及此时△PBC 的面积；若不存在，说明理由．考点：二次函数综合题．专题：压轴题．分析：（1）令y=0，解关于x 的一元二次方程求出点B 的坐标，令x=0 求出点C 的坐标，设直线BC 的解析式为y=kx+b，然后利用待定系数法求一次函数解析式解答即可；（2）把二次函数解析式整理成顶点式形式，然后写出顶点坐标与对称轴即可；（3）根据轴对称确定最短路线问题，直线BC 与对称轴的交点即为使线段AQ+CQ 最小的点Q，然后利用直线解析式求解即可；（4）过点P 作PD∥y 轴与BC 相交于点D，根据抛物线解析式与直线BC 的解析式表示出PD，再根据S△PBC=S△PCD+S△PBD 列式整理，然后利用二次函数最值问题解答．解答：解：（1）令y=0，则﹣x2+x+2=0，整理得，x2﹣2x﹣3=0，解得x1=﹣1，x2=3，所以，点B 的坐标为（3，0），令x=0，则y=2，所以，点C 的坐标为（0，2），设直线BC 的解析式为y=kx+b，则，解得，所以，直线BC 的解析式为y=﹣x+2；（2）∵y=﹣x2+ x+2，=﹣（x2﹣2x+1）+2+ ，=﹣（x﹣1）2+ ，∴顶点坐标为（1，），对称轴为直线x=1；（3）由轴对称确定最短路线问题，直线BC 与对称轴的交点即为使线段AQ+CQ 最小的点，x=1 时，y=﹣×1+2=，所以，存在Q（1，），使线段AQ+CQ 最小；（4）如图，过点P 作PD∥y 轴与BC 相交于点D，则PD=（﹣x2+x+2）﹣（﹣x+2）=﹣x2+2x，所以，S△PBC=S△PCD+S△PBD，=×（﹣x2+2x）×3，=﹣x2+3x，=﹣（x﹣）2+ ，所以，当x=时，△PBC 的面积最大为，此时，y=﹣×（）2+ ×+2= ，所以，存在P（，），使S △PBC 最大= ．点评：本题是二次函数综合题型，主要利用了抛物线与x 轴的交点坐标的求解，待定系数法求一次函数解析式，二次函数的顶点坐标与对称轴的求法，轴对称确定最短路线问题，二次函数的最值问题．。

二次函数的存在性问题(Word版解析+答案)

中考压轴题解析二次函数的存在性问题【典例分析】【考点 1】二次函数与相似三角形问题例1】已知抛物线y ax2 bx 3与 x轴分别交于A( 3,0)，B(1,0)两点，与 y轴交于点 C．2)点 F 是线段 AD 上一个动点．1AD .2ABC 相似？若相似，求出点 F 的坐标；若不相似，请说明理由．变式1-1】如图，抛物线y ax2 2x c经过A( 1,0)，B两点，且与y轴交于点C(0,3) ，抛物线与直线y x 1交于A，E 两点．(1)求抛物线的解析式；(2)坐标轴上是否存在一点Q，使得AQE是以AE为底边的等腰三角形？若存在，请直接写出点Q 的坐标；若不存在，说明理由．(3)P点在x轴上且位于点B 的左侧，若以P，B，C为顶点的三角形与ABE相似，求点P的坐AF①如图 1，设k ，当 k 为何值时，CFAD1)求抛物线的表达式及顶点 D 的坐标；标．1【变式1-2】如图，已知抛物线y m（x 2）（x m）（m > 0）与 x 轴相交于点 A，B，与 y轴相交于点 C，且点 A 在点 B 的左侧 .（ 1）若抛物线过点（ 2， 2），求抛物线的解析式；（2）在（ 1）的条件下，抛物线的对称轴上是否存在一点H ，使 AH+CH 的值最小，若存在，求出点 H 的坐标；若不存在，请说明理由；（3）在第四象限内，抛物线上是否存在点M ，使得以点 A，B，M 为顶点的三角形与△ACB 相似？若存在，求出 m 的值；若不存在，请说明理由 .考点 2】二次函数与直角三角形问题BC交于点D，连接AC 、AD ，求VACD的面积；3 点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F ，问是否存在点E使VDEF 为直角三角形？若存在，求出点E 坐标，若不存在，请说明理由．例2】如图，抛物线y ax2bx c a 0的顶点坐标为2, 1 ，图象与y 轴交于点C 0,3 ，与x轴2 设抛物线对称轴与直线【变式2-1】如图，经过x 轴上A（ 1，0）， B（3，0）两点的抛物线y m（x 1）2 4m （m 0）交y 轴于点C ，设抛物线的顶点为D ，若以DB 为直径的⊙ G 经过点C ，求解下列问题：1）用含m的代数式表示出C，D 的坐标；2）求抛物线的解析式；3）能否在抛物线上找到一点Q，使△BDQ 为直角三角形？如能，求出Q点的坐标，若不能，请说明理由。

二次函数中的存在性问题作业及答案

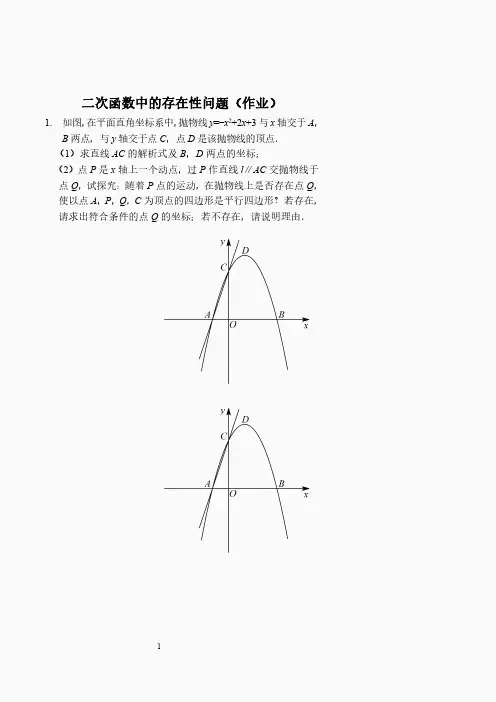
二次函数中的存在性问题（作业）1.如图，在平面直角坐标系中，抛物线y=-x2+2x+3与x轴交于A，B两点，与y轴交于点C，点D是该抛物线的顶点．（1）求直线AC的解析式及B，D两点的坐标；（2）点P是x轴上一个动点，过P作直线l∥AC交抛物线于点Q，试探究：随着P点的运动，在抛物线上是否存在点Q，使以点A，P，Q，C为顶点的四边形是平行四边形？若存在，请求出符合条件的点Q的坐标；若不存在，请说明理由．2.如图，已知二次函数1(2)(1320)48y x x =+-的图象过点A (-4，3)，B (4，4)，交x 轴于C 、D 两点．（1）求证：△ACB 是直角三角形；（2）若点P 是x 轴上方抛物线上的一个动点，设点P 的横坐标为m ，过点P 作PH ⊥x 轴于点H ，是否存在以P 、H 、D 为顶点的三角形与△ABC 相似？若存在，求出m 的值；若不存在，请说明理由．3.如图，在平面直角坐标系中，直线3342y x =-与抛物线2543412+--=x x y 交于A 、B 两点，点A 在x 轴上．若点P 是直线AB 上方抛物线上的一动点（不与点A 、B 重合），设点P 的横坐标为m ，连接PA ，以PA 为边作图示一侧的正方形APFG ．随着点P 的运动，正方形的大小、位置也随之改变．当顶点F 或G 恰好落在y 轴上时，请写出对应的点P 的坐标．4.在平面直角坐标系中，抛物线23y ax bx =++与x 轴的两个交点分别为A (-3，0)，B (1，0)，过顶点C 作CH ⊥x 轴于点H ．（1）直接填写：a =，b =，顶点C 的坐标为；（2）若点P 是x 轴上方抛物线上的一动点（点P 与顶点C 不重合），PQ ⊥AC 于点Q ，当△PCQ 与△ACH 相似时，求点P 的坐标．【参考答案】1．解：（1）由抛物线解析式y=-x2+2x+3可得：A(-1，0)，B(3，0)，C(0，3)，D(1，4)，再由A、C两点坐标，可得直线AC的解析式为：y=3x+3（2）由题意可得：PQ∥AC且PQ=AC，①如图1，当点Q在点P上方时，过点Q作QE⊥x轴于点E，可证△PEQ≌△AOC∴QE=OC=3故令y=-x2+2x+3=3，解得：x1=0(舍去)，x2=2故Q1(2，3)②如图2，当点Q 在点P 下方时，同①过点Q 作QE ⊥x 轴于点E ，可证△PEQ ≌△AOC∴QE =OC =3故令y =-x 2+2x +3=-3，解得：1=1+7x ，2=17x -故2(1+73)Q -，，3(173)Q --，综上，Q 点的坐标为Q 1(2，3)、2(1+73)Q -，，3(173)Q --，2．(1)证明：由抛物线的表达式1(2)(1320)48y x x =+-，可得：C (-2，0)，D 20(0)13，，如图1，过点A 、B 分别作x 轴的垂线，垂足为E 、F ，则AE =3，EC =2，CF =6，BF =4∵12AE EC CF BF ==且∠AEC =∠BFC =90°∴△AEC ∽△CFB∴∠ACE =∠CBF∴∠ACE +∠BCF =∠CBF +∠BCF =90°∴∠ACB =90°即△ACB 是直角三角形（2）由题意得：1(,(2)(1320))48P m m m +-，(,0)H m 在Rt △ACB 中，由（1）可知：12AC CB =，故△PHD 也是直角边的比为1:2的直角三角形，①如图2，当点P 在第二象限抛物线上，即m ＜-2时，∴1(2)(1320)48PH m m =+-，201=(2013)1313DH m m =--i ）12PH DH =解得：150=13m -ii ）2PH DH =解得：2122=13m -②如图3，当点P 在第一象限抛物线上，即m ＞2013时，∴1(2)(1320)48PH m m =+-，201=(1320)1313DH m m =--i ）12PH DH =解得：32=13m -（舍去）ii ）2PH DH =解得：470=13m 综上，50=13m -，122=13m -或70=13m 时满足条件. 3.解：由23342135442y x y x x ⎧=-⎪⎪⎨⎪=--+⎪⎩可得，A (-8,152-),B (2,0).则－8＜m ＜2.1当G 点在y 轴上时，此时，如图1过点A 作CD ∥y 轴，过点P ，G 分别作x 轴的平行线交CD 于D 、C 两点∵PA AG PAD AGC D C =⎧⎪∠=∠⎨⎪∠=∠⎩∴△PAD ≌△AGC∴AD =CG =2，则点P 在y =2这条直线上由2135=2442x x --+可求得，1231731722x x +==－－－，.∴P 1(3172+－，2),P 2(3172－－，2)2当F 点在y 轴上时，此时，如图2过点A 作AH ∥y 轴，过点P 作x 轴的平行线，交AH 于H 点,交y 轴于点E .此时△PAH ≌△FPE∴EP =AH =m ，即P （m ，m ）P 在抛物线上，将P （m ，m ）代入抛物线解析式可得由2135442m m m --+=可求得，1278978922m m +==－－－，.又∵-8＜m ＜2，∴只取17892m +=－∴P 3(789789,22++－－)综上所述：P 1(3172+－，2)，P 2(3172－－，2)，P 3(789789,22++－－).备注：图1对应P 24.解：（1）由A （-3，0）、B （1，0）可知，a =-1，b =-2，顶点C 的坐标为（-1，4）；抛物线解析式：223y x x =--+（2）①若点P 在对称轴右侧，如图1.此时∠QCP ＞∠ACH ,所以只可能是∠QCP =∠HAC ，即△PCQ ∽△CAH .过点Q 作DE ∥y 轴，分别过点C 、点P 作x 轴的平行线交DE 于D 点,E 点.则△CDQ ∽△QEP ，又∵∠DQC =∠HCA ，∠D =∠AHC =90°，∴△CDQ ∽△QEP ∽△AHC .∴12CD AH DQ HC ==.设CD =m ，则DQ =2m,又∵△AHC ∽△CQP ，∴12CQ AH QP HC ==.又∵△CDQ ∽△QEP ，∴12CD DQ CQ QE EP QP ===则QE =2m ，EP =4m .由C （-1，4）可得P （-1+3m ，4-4m ）代入抛物线解析式可得，2441+321+33m m m -=--+（-）（-）解得m 1=0（舍去），m 2=49代入P 点坐标可得P (12039，)2若点P 在对称轴左侧,如图2.此时∠QCP ＜∠HAC ,所以只可能是∠QCP =∠HCA ，即△PCQ ∽△ACH .过点P 作PF ∥y 轴，过点Q 作x 轴的平行线交PF 于点F ,交CH 于点G .则△PFQ ∽△QGC ∽△AHC ∽△PQC .∴12PF QG PQ AH FQ GC QC HC ====.设PF =n ，则FQ =QG =2n ,GC =4n .由C 点坐标可知，P （－1－4n ，4－3n ），代入抛物线解析式可得，243142143n n n =+－－（－－）－（－－）解得n 1=0（舍去），n 2=316代入P 点坐标可得P (755416－，)综上所述，满足条件的点P 坐标为(12039，)或(755416－，)．。

二次函数中存在性问题(等腰三角形存在性问题)

二次函数中的存在性问题 (等腰三角形 )[07 福建龙岩 ]如图，抛物线y ax 2 5ax 4 经过 △ ABC 的三个极点，y已知 BC ∥ x 轴，点 A 在 x 轴上，点 C 在 y 轴上，且 ACBC ．CB（1）求抛物线的对称轴；1（2）写出 A ， B ， C 三点的坐标并求抛物线的分析式；A（3）研究：若点P 是抛物线对称轴上且在x 轴下方的动点，1 x能否存在 △ PAB 是等腰三角形．若存在，求出全部切合条件的点 P 坐标；不存在，请说明原因．解：（ 1）抛物线的对称轴 x 5a 52a2y（2） A( 3，0)B(5，4)C (0，4)CＭB把点 A 坐标代入 yax 25ax 4 中，解得 a1A1Ｎ6Ｑx151P 3x 2Ｋyx 466P 共有 3 个．以下分三类情况研究．P 2（3）存在切合条件的点设抛物线对称轴与 x 轴交于 N ，与 CB 交于 M ．P 1过点 B 作 BQx 轴于 Q ，易得 BQ4 ， AQ 8 ， AN5.5 ， BM52① 以 AB 为腰且顶角为角A 的 △ PAB 有 1 个： △ P 1AB ．AB 2 AQ 2 BQ 2 82 4280在 Rt △ ANP 中， PNAP 2 AN 2AB 2 AN 280(5.5) 2199 P 1 5 ，199111222② AB 为腰且顶角为角B 的 △PAB 有 1 个： △ P 2 AB ．在 Rt △ BMP 2 中， MP 2 22AB22252955 8295BP 2BMBM 802P 2 2 ，42③以 AB 为底，顶角为角P 的 △ PAB 有 1 个，即 △ P 3 AB ．画 AB 的垂直均分线交抛物线对称轴于P 3 ，此时均分线必过等腰 △ ABC 的极点 C ．过点 3 作P 3 K 垂直y 轴，垂足为 K，明显Rt △ 3∽ Rt △ BAQ ．P 3KBQ 1．PPCKCKAQ2Q P 3 KCK 5 于是 OK1P 3， 1)[07 广西河池 ]如图，已知抛物线y 2 x24x 2的图象与 x 轴交于 A，B 两点，与 y 轴交于点 C，抛物33线的对称轴与 x 轴交于点 D．点 M 从 O 点出发，以每秒 1 个单位长度yP的速度向 B 运动，过 M 作 x 轴的垂线，交抛物线于点P，交 BC 于 Q．C（1）求点 B 和点 C 的坐标；Q（2）设当点 M 运动了 x（秒）时，四边形OBPC 的面积为 S，求 S 与 x 的函数关系式，并指出自变量x 的取值范围．B xA（3）在线段 BC 上能否存在点Q，使得△ DBQ 成为以 BQ 为一腰的ODM等腰三角形？若存在，求出点Q 的坐标，若不存在，说明原因．（1）把 x =0 代入y 2 x2 4 x2得点 C 的坐标为 C（ 0， 2）33把 y =0 代入y2x24x 2 得点B的坐标为B（3，0）3 3（2）连接 OP，设点 P 的坐标为 P（ x， y）四边形 OBPC =S△OPC+S△OPB=12x13y = x3 2 x24x 2= x23x 3S22233∵点 M 运动到 B 点上停止，∴0≤ x ≤ 32∴ S x33（ 0≤ x ≤ 3 ）24（3）存在． BC= OB2OC2=13①若 BQ = DQ∵ BQ = DQ ，BD = 2∴ BM = 1∴ OM = 3 1 = 2∴ tan OBC QM OC2∴ QM =2因此 Q 的坐标为 Q （ 2，2）．BM OB333②若 BQ=BD=2∵ △ BQM ∽△ BCO，∴BQ QM BM==BO BC CO∴2QM∴ QM =4 13 13=213∵ BQ= BM∴2=BM BC OB133∴ BM = 613∴ OM =3613··························11 分1313因此 Q 的坐标为 Q （3613， 4 13）···························12 分1313[07 年云南省 ]已知：如图，抛物线y ax2bx c 经过 A (1, 0) 、 B (5 , 0) 、 C (0 , 5) 三点．（1）求抛物线的函数关系式；y（2）若过点 C 的直线y kx b 与抛物线订交于点E（4，m），C恳求出△ CBE 的面积 S的值；（3）在抛物线上求一点P0使得△ABP0为等腰三角形并1A–O B x 1写出 P0点的坐标；E（4）除（ 3）中所求的P0点外，在抛物线上能否还存在其他的点P 使得△ ABP 为等腰三角形？若存在，请求出一共有几个知足条件的点P（要求简要说明原因，但不证明）；若不存在这样的点P ，请说明原因．解：（ 1）∵抛物线经过点A(1, 0)、 B(5 , 0)∴ y a(x 1)(x5) ．又∵抛物线经过点 C(0 , 5)∴ 5a 5 ， a 1 ．∴抛物线的分析式为y( x1)(x5)x2 6 x 5 ．（ 2）∵ E 点在抛物线上，∴ m = 42–4× 6+5 = - 3．∵直线 y = kx+b 过点 C（0， 5）、E（ 4，–3），∴ b 5,解得 k = - 2，b = 5．4k b 3.设直线 y=- 2x+5 与 x 轴的交点为 D ，当 y=0 时， - 2x+5=0 ，解得 x=5．∴D 点的坐标为（5，0）．22∴ S=S BDC + S BDE=1(5515 3 =10．)5+(5)△△2222（3）∵抛物线的极点P0(3 ,4)既在抛物线的对称轴上又在抛物线上，∴点 P0 (3 , 4) 为所求知足条件的点．（4）除P0点外，在抛物线上还存在其他的点P 使得△ ABP 为等腰三角形．原因以下：∵ AP0BP02242254，∴分别以 A 、 B 为圆心半径长为 4 画圆，分别与抛物线交于点 B 、P1、P2、P3、 A 、P4、P5、P6，除掉 B 、 A 两个点外，其他 6 个点为知足条件的点．（说明：只说出P 点个数但未简要说明原因的不给分）[07 山东威海 ]如图①，在平面直角坐标系中，点 A 的坐标为 (12)，，点 B 的坐标为 (31)，，二次函数yx 2的图象记为抛物线 l 1 ．（ 1）平移抛物线 l 1 ，使平移后的抛物线过点 A ，但可是点 B ，写出平移后的一个抛物线的函数表达式：（任写一个即可）．（2）平移抛物线 l 1 ，使平移后的抛物线过 A ， B 两点，记为抛物线 l 2 ，如图②，求抛物线l 2 的函数表达式．（3）设抛物线l 2 的极点为C ， K 为y 轴上一点．若△△ABC ，求点 K 的坐标．S ABK S（4）请在图③上用尺规作图的方式研究抛物线 l 2 上能否存在点 P ，使 △ ABP 为等腰三角形．若存在，请判断点 P 共有几个可能的地点（保存作图印迹）；若不存在，请说明原因．yyl 2yl 1l 21AB1 AB AxCx1BxO1OO11图①图②图③解：（ 1）有多种答案，切合条件即可．比如 yx 2 1， yx 2x ， y ( x 1)22或 y x 22x 3 ， y (x2 1)2 ， y ( x 12) 2 ．yl 2（2）设抛物线 l 2 的函数表达式为 yx 2 bx c ，KQ 点 A(12)，， B(31)，在抛物线 l 2 上，GABxCOb 9 ，D F E1 b c，29 11图②2解得2抛物线 l 2 的函数表达式为 y．9 3b c 1 11.xxc222911927， C 点的坐标为9 ，7（3） yx 2 x x ．2 2 4164 16过 A ， B ，C 三点分别作 x 轴的垂线，垂足分别为 D ，E ，F ，则 AD2 ， CF7， BE 1， DE 2 ， DF5， FE3 ．1644S 梯形S 梯形15延伸 BA 交 y 轴于点 G ，设直线 AB 的函数表达式为ymx n ，Q 点 A(12)，， B(31)，在直线 AB 上，2 m， m1 ，1 55 n2直线 AB 的函数表达式为y． G 点的坐标为解得5 .x0，．1 3m n.n2222设 K 点坐标为 (0， h) ，分两种状况：若 K 点位于 G 点的上方，则KG h5．连接 AK ， BK ．2S △ ABKS △ BKG S △ AKG1 3 h 51 1 h 5h 5 ．22222Q S △ ABK15h5 15 ，解得 h55 K 点的坐标为55S △ ABC，2 16． 0，．161616若 K 点位于 G 点的下方，则KG5 h ．同理可得，h25 ．K 点的坐标为25．216 0，16（4）作图印迹如图③所示．由图③可知，点P 共有 3 个可能的地点．yl 2注：作出线段 AB 的中垂线得1 分，画出此外两段弧得1 分．ABxO图③[07 山东泰安 ]如图，在 △OAB 中， B90o ， BOA 30o ， OA 4，将 △OAB 绕点 O 按逆时针方向旋转至 △OA B ， C 点的坐标为（ 0，4）．（1）求 A 点的坐标；（2）求过 C ， A ， A 三点的抛物线 y ax2bx c 的分析式；（3）在（ 2）中的抛物线上能否存在点P ，使以 O ，A ，P 为极点的三角形是等腰直角三角形？若存在，求出全部点P 的坐标；若不存在，请说明原因解：（ 1）过点 A 作 A D 垂直于 x 轴，垂足为 D , 则四边形 OB A D 为矩形在 △ A DO 中， A DOA sinA OD 4 sin 60o 2 3yCBABOA xOD A B AB 2 点A 的坐标为 (2，2 3)（2） Q C (0，4) 在抛物线上，c 4yax 2 bx 4Q A(4，0) ， A (2，2 3) ，在抛物线 yax 2 bx 4 上16a 4b 4 0，a 1324a 2b42 解之得3b 2 3 3所求分析式为 y3 x 2 (2 3 3) x4 ．2（3）①若以点 O 为直角极点，因为 OC OA 4 ，点 C 在抛物线上，则点 C (0，4) 为知足条件的点．②若以点 A 为直角极点，则使△PAO 为等腰直角三角形的点P 的坐标应为 (4，4) 或 (4， 4) ，经计算知；此两点不在抛物线上．③若以点 P 为直角极点，则使△PAO 为等腰直角三角形的点 P 的坐标应为 (2，2) 或 (2， 2) ，经计算知；此两点也不在抛物线上．综上述在抛物线上只有一点P(0，4) 使 △OAP 为等腰直角三角形[08 广东梅州 ]如图 11 所示，在梯形 ABCD 中，已知 AB∥ CD ， AD ⊥ DB ， AD=DC=CB， AB=4．以 AB 所在直线为x轴，过 D 且垂直于AB 的直线为y 轴成立平面直角坐标系．（1）求∠ DAB 的度数及A、D 、C 三点的坐标；（2）求过 A、 D、 C 三点的抛物线的分析式及其对称轴L ．（3）若 P 是抛物线的对称轴L 上的点，那么使PDB 为等腰三角形的点P 有几个 ?（不用求点P 的坐标，只要说明原因）解：（1）DC∥ AB， AD =DC=CB，∠ CDB=∠ CBD=∠ DBA，∠ DAB =∠ CBA ，∠ DAB=2∠ DBA，∠DAB+∠ DBA =90 ，∠DAB =60，∠DBA=30 ， AB=4 ，DC =AD=2 ，Rt AOD， OA=1， OD= 3 ，.A（ - 1， 0）， D （0， 3 ），C（2， 3 ）．（ 2）依据抛物线和等腰梯形的对称性知，知足条件的抛物线必过点A（－ 1，0）， B（ 3， 0），故可设所求为y = a （ x +1）（ x -3）将点 D （ 0， 3 ）的坐标代入上式得， a =3．3所求抛物线的分析式为y =3(x1)( x3).·················7分3其对称轴L 为直线x =1．·····································8分（ 3）PDB 为等腰三角形，有以下三种状况：①因直线 L 与 DB 不平行， DB 的垂直均分线与L 仅有一个交点 P1，P1D =P1B，P1DB 为等腰三角形；······································9 分②因为以 D 为圆心，DB 为半径的圆与直线L 有两个交点 P232323、P ，DB =DP ，DB =DP ，P DB，P DB 为等腰三角形；③与②同理， L 上也有两个点 P4、 P5，使得 BD=BP4， BD=BP5．··········10 分因为以上各点互不重合，因此在直线L 上，使PDB 为等腰三角形的点P 有 5 个．[08 福建南平 ]如图，平面直角坐标系中有一矩形纸片OABC ， O 为原点，点 A ，C 分别在 x 轴， y 轴上，点 B 坐标为 (m ， 2) （此中 m0 ），在 BC 边上选用适合的点 E 和点 F ，将 △OCE 沿 OE 翻折，获得△OGE ；再将 △ ABF 沿 AF 翻折，恰巧使点 B 与点 G 重合，获得 △AGF ，且OGA 90o ．（ 1）求 m 的值；（2）求过点 O ，G ，A 的抛物线的分析式和对称轴；（ 3）在抛物线的对称轴上能否存在点 P ，使得 △OPG 是．．．等腰三角形？若不存在，请说明原因；若存在，直接答出．．．．全部知足条件的点 P 的坐标（不要求写出求解过程）．（ 1） Q B( m ， 2) ，由题意可知 AG AB2 ， OG OC2 ， OA mQ OGA 90o ，OG 2AG 2OA 22 2m 2 ．又 Q m 0 ，m 2（2）过 G 作直线 GH x 轴于 H ，则 OH 1 ， HG1，故 G (11)，．又由（ 1）知 A(2，0) ，设过 O ，G ，A 三点的抛物线分析式为yax 2 bx cQ 抛物线过原点，c 0 ．a b 1a 1又Q 抛物线过 G ， A 两点， 2b 0解得24ab所求抛物线为 yx 2 2x它的对称轴为 x1 ．（3）答：存在 ,知足条件的点 P 有 (10)，， (1， 1) ， (11，2) ， (11， 2) ．[08 湖南株洲 ]如（ 1），在平面直角坐系中，点A 的坐（ 1，- 2），点B 的坐（ 3， - 1），二次函数 yx 2 的象 l 1 .（ 1）平移抛物 l 1 ，使平移后的抛物点A ，但不点 B ，写出平移后的抛物的一个分析式（任写一个即可） .（ 2）平移抛物 l 1 ，使平移后的抛物A 、B 两点，抛物l 2 ，如（ 2），求抛物 l 2 的函数解析式及点 C 的坐 .（ 3） P y 上一点，且 S ABC S ABP ，求点 P 的坐 .（ 4）在（ 2）上用尺作的方式研究抛物l 2 上能否存在点Q ，使 QAB 等腰三角形 . 若存在，判断点 Q 共有几个可能的地点（保存作印迹）；若不存在，明原因 .yyoxoxl 1l 2（ 1）（ 2）（1） yx 2 2 x 3或 yx 24x 5等（足条件即可）⋯⋯ 1 分（2） l 2 的分析式 yx 2bx c ，立方程2 1 b c ，1 9 3bc解得： b9 , c 11， l 2 的分析式 yx 2 9 x 11 ，⋯⋯ 3 分2222点 C 的坐（ 9,7 ） ⋯⋯ 4 分4 167 ，（ 3）如答23- 1，点 A 、 B 、C 三点分作 x 的垂，垂足分 D 、E 、F ， AD2 ， CF5，FE3 . 16BE 1， DE2 ， DF4415 .得：S ABCS梯形 ABEDS梯形 BCFES梯形ACFD⋯⋯ 5 分16延 BA 交 y 于点 G ，直 AB 的分析式y1 5 ，点 G 的坐（ 0， 5），点 P 的坐2x22（ 0， h ）①当点P 位于点G 的下方，PG 5AP 、 BP，S ABP S BPG S APG5h ，h ，又22S ABC S ABP 15，得h55，点 P 的坐（0，55 ）.⋯⋯ 6 分161651625 ）.②当点 P 位于点 G 的上方，PG，同理h25，点 P 的坐（ 0，h1616 2上所述所求点P 的坐（ 0，55）或（ 0，25 ）⋯⋯ 7 分1616(4)作印迹如答 23-2 所示 .由可知，足条件的点有Q1、 Q2、Q3、 Q4，共 4 个可能的地点.⋯⋯10 分F E答 23-1答 23-211 / 12[08 浙江温州 ]如图，在 Rt △ ABC 中， A 90o ， AB 6 ， AC 8 ， D ，E 分别是边 AB ，AC 的中点，点 P 从点 D 出发沿 DE 方向运动，过点P 作 PQ BC 于 Q ，过点 Q 作 QR ∥ BA 交 AC 于R ，当点 Q 与点 C 重合时，点 P 停止运动．设 BQx ， QRy ．A（1）求点 D 到 BC 的距离 DH 的长；PR（2）求 y 对于 x 的函数关系式（不要求写出自变量的取值范围）；D E（3）能否存在点P ，使 △ PQR 为等腰三角形？若存在，BH QC恳求出全部知足要求的 x 的值；若不存在，请说明原因．解：（ 1）QARt ， AB 6 ， AC 8，BC 10 ．Q 点 D 为 AB 中点， BD 1 3 ．AB2Q DHBA 90o ， BB ． △BHD ∽△ BAC ， DH BD ， DHBDgAC3 8 12 ．ACBCBC10 5（2） Q QR ∥ AB ， QRCA 90o ．Q CC ， △ RQC ∽△ ABC ，RQ QC，y10 xABBC 610 ， A3即 y 对于 x 的函数关系式为：y6 ． DP RxE（3）存在，分三种状况：51 MBH Q2C①当 PQ PR 时，过点 P 作 PMQR 于 M ，则 QMRM ．Q 1290o ， C2 90o ，1C ．cos 1cosC8 4 ， A10 5QM 41 3 x 6 418 DPE，25，RQP5125x．5BHQC5②当 PQRQ 时，3 x 6 12 ， x 6 ． A55③当 PRQR 时，则 R 为 PQ 中垂线上的点，于是点R 为 EC 的中点，DE PR 11QR BA2 ． Q tanCBHQ CCRCE ACCR，24CA3 x 6 61518 或 6 或 15时， △ PQR 为等腰三角形． 5 ， x ．综上所述，当 x 为28 2 5 211二次函数中的存在性问题(直角三角形 )[08 辽宁十二市 ]如图 16，在平面直角坐标系中，直线y3x 3 与 x 轴交于点 A ，与 y 轴交于点C，抛物线 y ax22 3x c(a 0) 经过A，B，C三点．3（1）求过A，B，C三点抛物线的分析式并求出极点 F 的坐标；（2）在抛物线上能否存在点P ，使△ ABP 为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明原因；（3）尝试究在直线AC上能否存在一点M，使得△MBF的周长最小，若存在，求出M 点的坐标；若不存在，请说明原因．yxA O BCF图 161212 / 12。

(完整版)二次函数中的存在性问题(等腰三角形的存在性问题)

二次函数中的存在性问题(等腰三角形)[07福建龙岩]如图，抛物线254y ax ax =-+经过ABC △已知BC x ∥轴，点A 在x 轴上，点C 在y 轴上，且AC BC =．（1）求抛物线的对称轴；（2）写出A B C ，，三点的坐标并求抛物线的解析式；（3）探究：若点P 是抛物线对称轴上且在x 轴下方的动点，是否存在PAB △是等腰三角形．若存在，求出所有符合条件的点P 坐标；不存在，请说明理由．解：（1）抛物线的对称轴5522a x a -=-= （2）(30)A -， (54)B ， (04)C ，把点A 坐标代入254y ax ax =-+中，解得16a =-215466y x x ∴=-++（3）存在符合条件的点P 共有3个．以下分三类情形探索．设抛物线对称轴与x 轴交于N ，与CB 交于M ．过点B 作BQ x ⊥轴于Q ，易得4BQ =，8AQ =， 5.5AN =，2BM = ① 以AB 为腰且顶角为角A 的PAB △有1个：1P AB △．222228480AB AQ BQ ∴=+=+= 在1Rt ANP △中，1PN ==== 152P ⎛∴ ⎝⎭ ② AB 为腰且顶角为角B 的PAB △有1个：2P AB △．在2Rt BMP △中，22MP ==== 252P ⎛∴ ⎝⎭③以AB 为底，顶角为角P 的PAB △有1个，即3P AB △．画AB 的垂直平分线交抛物线对称轴于3P ，此时平分线必过等腰ABC △的顶点C ．过点3P 作3P K 垂直y 轴，垂足为K ，显然3Rt Rt PCK BAQ △∽△．312P K BQ CK AQ ∴==． 3 2.5P K = 5CK ∴= 于是1OK = 3(2.51)P ∴-，[07广西河池]如图，已知抛物线224233y x x =-++的图象与x 轴交于A ，B 两点，与y 轴交于点C ，抛物线的对称轴与x 轴交于点D ．点M 从O 点出发，以每秒1的速度向B 运动，过M 作x 轴的垂线，交抛物线于点P ，交BC 于（1）求点B 和点C 的坐标；（2）设当点M 运动了x （秒）时，四边形OBPC 的面积为S ，求S 与x 的函数关系式，并指出自变量x 的取值范围．（3）在线段BC 上是否存在点Q ，使得△DBQ 成为以BQ 等腰三角形？若存在，求出点Q 的坐标，若不存在，说明理由．（1）把x =0代入224233y x x =-++得点C 的坐标为C （0，2）把y =0代入224233y x x =-++得点B 的坐标为B （3，0）（2）连结OP ，设点P 的坐标为P （x ，y ）OBPC S 四边形=OPC S △+OPB S △ =112322x y ⨯⨯+⨯⨯= 3223x ⎛+- ⎝∵ 点M 运动到B 点上停止，∴03x ≤≤∴23324S x ⎛⎫=--+ ⎪⎝⎭（03x ≤≤）（3）存在． BC=13 ① 若BQ = DQ∵ BQ = DQ ，BD = 2 ∴ BM = 1 ∴OM = 3-1 = 2 ∴2tan 3QM OC OBC BM OB ∠=== ∴QM =23 所以Q的坐标为Q （2，23）． ② 若BQ =BD =2 ∵ △BQM ∽△BCO ，∴BQ BC =QM CO =BMBO∴=2QM∴ QM∵BQ BC =BM OB ∴ 3BM∴ BM ∴ OM = 3 ··················································· 11分所以Q 的坐标为Q （313-，13） ··················································· 12分[07年云南省]已知：如图，抛物线2y ax bx c =++经过(1,0)A 、(5,0)B 、(0,5)C 三点．（1）求抛物线的函数关系式；（2）若过点C 的直线y kx b =+与抛物线相交于点E （4，m ），请求出△CBE 的面积S 的值；（3）在抛物线上求一点0P 使得△ABP 0为等腰三角形并写出0P 点的坐标；（4）除（3）中所求的0P 点外，在抛物线上是否还存在其它的点P 使得△ABP 为等腰三角形？若存在，请求出一共有几个满足条件的点P （要求简要说明理由，但不证明）；若不存在这样的点P ，请说明理由．解：（1）∵抛物线经过点(1,0)A 、(5,0)B ∴(1)(5)y a x x =--．又∵抛物线经过点(0,5)C ∴55a =，1a =．∴抛物线的解析式为2(1)(5)65y x x x x =--=-+．（2）∵E 点在抛物线上， ∴m = 42–4×6+5 = -3．∵直线y = kx +b 过点C （0， 5）、E （4， –3）， ∴5,4 3.b k b =⎧⎨+=-⎩解得k = -2，b = 5．设直线y =-2x +5与x 轴的交点为D ，当y =0时，-2x +5=0，解得x =52．∴D 点的坐标为（52，0）． ∴S =S △BDC + S △BDE =1515(5)5+(5)32222⨯-⨯⨯-⨯=10．（3）∵抛物线的顶点0(3,4)P -既在抛物线的对称轴上又在抛物线上，∴点0(3,4)P -为所求满足条件的点．（4）除0P 点外，在抛物线上还存在其它的点P 使得△ABP 为等腰三角形．理由如下：∵220024254AP BP ==+=>，∴分别以A 、B 为圆心半径长为4画圆，分别与抛物线交于点B 、1P 、2P 、3P 、A 、4P 、5P 、6P ，除去B 、A 两个点外，其余6个点为满足条件的点．（说明：只说出P 点个数但未简要说明理由的不给分）xyC B AE–1 1 O[07山东威海]如图①，在平面直角坐标系中，点A 的坐标为(12)，，点B 的坐标为(31)，，二次函数2y x =的图象记为抛物线1l ．（1）平移抛物线1l ，使平移后的抛物线过点A ，但不过点B ，写出平移后的一个抛物线的函数表达式：（任写一个即可）．（2）平移抛物线1l ，使平移后的抛物线过A B ，两点，记为抛物线2l ，如图②，求抛物线2l 的函数表达式．（3）设抛物线2l 的顶点为C ，K 为y 轴上一点．若ABK ABC S S =△△，求点K 的坐标．（4）请在图③上用尺规作图的方式探究抛物线2l 上是否存在点P ，使ABP △为等腰三角形．若存在，请判断点P 共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由．解：（1）有多种答案，符合条件即可．例如21y x =+，2y x x =+，2(1)2y x =-+或223y x x =-+，2(1)y x =+，2(1y x =-．（2）设抛物线2l 的函数表达式为2y x bx c =++，点(12)A ，，(31)B ，在抛物线2l 上，12931b c b c ++=⎧∴⎨++=⎩，解得9211.2b c ⎧=-⎪⎪⎨⎪=⎪⎩， ∴抛物线2l 的函数表达式为291122y x x =-+．（3）229119722416y x x x ⎛⎫=-+=-+ ⎪⎝⎭，C ∴点的坐标为97416⎛⎫⎪⎝⎭，．过A B C ，，三点分别作x 轴的垂线，垂足分别为D E F ，，，则2AD =，716CF =，1BE =，2DE =，54DF =，34FE =． ABC ADEB ADFC CFEB S S S S ∴=--△梯形梯形梯形117517315(21)22122164216416⎛⎫⎛⎫=+⨯-+⨯-+⨯= ⎪ ⎪⎝⎭⎝⎭．x图①x图②x图③x延长BA 交y 轴于点G ，设直线AB 的函数表达式为y mx n =+，点(12)A ，，(31)B ，在直线AB 上，213.m n m n =+⎧∴⎨=+⎩，解得125.2m n ⎧=-⎪⎪⎨⎪=⎪⎩，∴直线AB 的函数表达式为1522y x =-+．G ∴点的坐标为502⎛⎫ ⎪⎝⎭，．设K 点坐标为(0)h ，，分两种情况：若K 点位于G 点的上方，则52KG h =-．连结AK BK ，． 151553122222ABK BKG AKG S S S h h h ⎛⎫⎛⎫=-=⨯⨯--⨯⨯-=- ⎪ ⎪⎝⎭⎝⎭△△△． 1516ABK ABC S S ==△△，515216h ∴-=，解得5516h =．K ∴点的坐标为55016⎛⎫ ⎪⎝⎭，．若K 点位于G 点的下方，则52KG h =-．同理可得，2516h =．K ∴点的坐标为25016⎛⎫⎪⎝⎭，．（4）作图痕迹如图③所示．由图③可知，点P 共有3个可能的位置．注：作出线段AB 的中垂线得1分，画出另外两段弧得1分．x[07山东泰安]如图，在OAB △中，90B ∠=，30BOA ∠=，4OA =，将OAB △绕点O 按逆时针方向旋转至OA B ''△，C 点的坐标为（0，4）．（1）求A '点的坐标；（2）求过C ，A '，A 三点的抛物线2y ax bx c =++的解析式；（3）在（2）中的抛物线上是否存在点P ，使以O A P ，，为顶点的三角形是等腰直角三角形？若存在，求出所有点P 的坐标；若不存在，请说明理由解：（1）过点A '作A D '垂直于x 轴，垂足为D ,则四边形OB A D ''为矩形在A DO '△中，A D OA ''=sin 4sin 6023A OD '∠=⨯=2OD A B AB''=== ∴点A '的坐标为(2 （2）(04)C ，在抛物线上，4c ∴= 24y ax bx∴=++(40)A ，，(2A '，在抛物线24y ax bx =++上 16440424a b a b ++=⎧⎪∴⎨++=⎪⎩，3a b ⎧=⎪⎨⎪=⎩ ∴所求解析式为23)42y x x =++．（3）①若以点O 为直角顶点，由于4OC OA ==，点C 在抛物线上，则点(04)C ，为满足条件的点． ②若以点A 为直角顶点，则使PAO △为等腰直角三角形的点P 的坐标应为(44)，或(44)-，，经计算知；此两点不在抛物线上．③若以点P 为直角顶点，则使PAO △为等腰直角三角形的点P 的坐标应为(22)，或(22)-，，经计算知；此两点也不在抛物线上．综上述在抛物线上只有一点(04)P ，使OAP △为等腰直角三角形[08广东梅州]如图11所示，在梯形ABCD 中，已知AB ∥CD ， AD ⊥DB ， AD =DC =CB ，AB =4．以AB 所在直线为x 轴，过D 且垂直于 AB 的直线为y 轴建立平面直角坐标系．（1）求∠DAB 的度数及A 、D 、C 三点的坐标；（2）求过A 、D 、C 三点的抛物线的解析式及其对称轴L ．（3）若P 是抛物线的对称轴L 上的点，那么使∆PDB 为等腰三角形的点P 有几个?（不必求点P 的坐标，只需说明理由）解：（1） DC ∥AB ，AD =DC =CB ， ∴ ∠CDB =∠CBD =∠DBA ， ∠DAB =∠CBA ， ∴∠DAB =2∠DBA ，∠DAB +∠DBA =90 ， ∴∠DAB =60 ， ∠DBA =30 ， AB =4， ∴DC =AD =2， R t ∆AOD ，OA =1，OD =3，.∴A （-1，0），D （0， 3），C （2， 3）．（2）根据抛物线和等腰梯形的对称性知，满足条件的抛物线必过点A （－1，0），B （3，0），故可设所求为 y =a （x +1）（ x -3）将点D （0，3）的坐标代入上式得， a =33-．所求抛物线的解析式为 y =).3)(1(33-+-x x ···································· 7分其对称轴L 为直线x =1． ········································································· 8分（3） ∆PDB 为等腰三角形，有以下三种情况：①因直线L 与DB 不平行，DB 的垂直平分线与L 仅有一个交点P 1，P 1D =P 1B ，∆P 1DB 为等腰三角形； ·········································································· 9分 ②因为以D 为圆心，DB 为半径的圆与直线L 有两个交点P 2、P 3，DB =DP 2，DB =DP 3， ∆P 2DB ， ∆P 3DB 为等腰三角形；③与②同理，L 上也有两个点P 4、P 5，使得 BD =BP 4，BD =BP 5． ··················· 10分由于以上各点互不重合，所以在直线L 上，使∆PDB 为等腰三角形的点P 有5个．[08福建南平]如图，平面直角坐标系中有一矩形纸片OABC ，O 为原点，点A C ，分别在x 轴，y 轴上，点B 坐标为(2)m ，（其中0m >），在BC 边上选取适当的点E 和点F ，将OCE △沿OE 翻折，得到OGE △；再将ABF △沿AF 翻折，恰好使点B 与点G 重合，得到AGF △，且90OGA ∠=．（1）求m 的值；（2）求过点O G A ，，的抛物线的解析式和对称轴；（3）在抛物线的对称轴．．．上是否存在点P ，使得OPG △是等腰三角形？若不存在，请说明理由；若存在，直接答出．．．．所有满足条件的点P 的坐标（不要求写出求解过程）．（1）(2)B m ，，由题意可知2AG AB ==2OG OC ==OA m =90OGA ∠=，222OG AG OA ∴+= 222m ∴+=．又0m >，2m ∴=（2）过G 作直线GH x ⊥轴于H ，则1OH =，1HG =，故(11)G ，．又由（1）知(20)A ，，设过O G A ，，三点的抛物线解析式为2y ax bx c =++ 抛物线过原点，0c ∴=．又抛物线过G A ，两点，1420a b a b +=⎧∴⎨+=⎩解得12a b =-⎧⎨=⎩∴所求抛物线为22y x x =-+ ∴它的对称轴为1x =．（3）答：存在,满足条件的点P 有(10)，，(11)-，，(112)，，(112)+，．[08湖南株洲]如图（1），在平面直角坐标系中，点A 的坐标为（1，-2），点B 的坐标为（3，-1），二次函数2y x =-的图象为1l .（1）平移抛物线1l ，使平移后的抛物线过点A ，但不过点B ，写出平移后的抛物线的一个解析式（任写一个即可）.（2）平移抛物线1l ，使平移后的抛物线过A 、B 两点，记抛物线为2l ，如图（2），求抛物线2l 的函数解析式及顶点C 的坐标.（3）设P 为y 轴上一点，且ABC ABP S S ∆∆=，求点P 的坐标.（4）请在图（2）上用尺规作图的方式探究抛物线2l 上是否存在点Q ，使QAB ∆为等腰三角形. 若存在，请判断点Q 共有几个可能的位置（保留作图痕迹）；若不存在，请说明理由.（1）222345y x x y x x =-+-=-+-或等（满足条件即可） ……1分（2）设2l 的解析式为2y x bx c =-++，联立方程组21193b c b c-=-++⎧⎨-=-++⎩，解得：911,22b c ==-，则2l 的解析式为291122y x x =-+-， ……3分点C 的坐标为（97,416-） ……4分（3）如答图23-1，过点A 、B 、C 三点分别作x 轴的垂线，垂足分别为D 、E 、F ，则2AD =，716CF =，1BE =，2DE =，54DF =，34FE =.得：1516ABC ABED BCFE CFD S S S S ∆=--=梯形梯形梯形A . ……5分延长BA 交y 轴于点G ，直线AB 的解析式为1522y x =-，则点G 的坐标为（0，52-），设点P 的坐y ox 图（1）yo x 图（2） l 1l 2标为（0，h ）①当点P 位于点G 的下方时，52PG h =--，连结AP 、BP ，则52ABP BPG APG S S S h ∆∆∆=-=--，又1516ABC ABP S S ∆∆==，得5516h =-，点P 的坐标为（0，5516-）. …… 6分②当点P 位于点G 的上方时，52PG h =+，同理2516h =-，点P 的坐标为（0，2516-）.综上所述所求点P 的坐标为（0，5516-）或（0，2516-） …… 7分(4) 作图痕迹如答图23-2所示.由图可知，满足条件的点有1Q 、2Q 、3Q 、4Q ，共4个可能的位置. …… 10分答图23-2EF 答图23-1[08浙江温州]如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使PQR △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=．点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△，DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=．（2）QR AB ∥，90QRC A ∴∠=∠=．C C ∠=∠，RQC ABC ∴△∽△，RQ QC AB BC ∴=，10610y x-∴=，即y 关于x 的函数关系式为：365y x =-+．（3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 10C ∴∠===，45QM QP ∴=，1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=．②当PQ RQ =时，312655x -+=，6x ∴=． ③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BA C CR CA ==， 366528x -+∴=，152x ∴=．综上所述，当x 为185或6或152时，PQR △为等腰三角形．A BCD ER P H QA BCD ER P H QM2 1 HA B CDE RPHQ二次函数中的存在性问题(直角三角形)[08辽宁十二市]如图16，在平面直角坐标系中，直线y =-x 轴交于点A ，与y 轴交于点C ，抛物线2(0)3y ax x c a =-+≠经过A B C ，，三点．（1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．x。

二次函数中的存在性问题(最新整理)

二次函数中的存在性问题1. 如图，矩形OABC在平面直角坐标系xOy中，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=4，OC=3，若抛物线的顶点在BC边上，且抛物线经过O，A两点，直线AC交抛物线于点D．（1）求抛物线的解析式；（2）求点D的坐标；（3）若点M在抛物线上，点N在x轴上，是否存在以A，D，M，N为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．4：解：（1）设抛物线顶点为E，根据题意OA=4，OC=3，得：E（2，3），设抛物线解析式为y=a（x﹣2）2+3，将A（4，0）坐标代入得：0=4a+3，即a=﹣，则抛物线解析式为y=﹣（x﹣2）2+3=﹣x2+3x；（2）设直线AC解析式为y=kx+b（k≠0），将A（4，0）与C（0，3）代入得：，解得：，故直线AC解析式为y=﹣x+3，与抛物线解析式联立得：，解得：或，则点D坐标为（1，）；（3）存在，分两种情况考虑：①当点M在x轴上方时，如答图1所示：四边形ADMN为平行四边形，DM∥AN，DM=AN，由对称性得到M（3，），即DM=2，故AN=2，∴N1（2，0），N2（6，0）；②当点M在x轴下方时，如答图2所示：过点D作DQ⊥x轴于点Q，过点M作MP⊥x轴于点P，可得△ADQ≌△NMP，∴MP=DQ=，NP=AQ=3，将y M=﹣代入抛物线解析式得：﹣=﹣x2+3x，解得：x M=2﹣或x M=2+，∴x N=x M﹣3=﹣﹣1或﹣1，∴N3（﹣﹣1，0），N4（﹣1，0）．综上所述，满足条件的点N有四个：N1（2，0），N2（6，0），N3（﹣﹣1，0），N4（﹣1，0）．2．如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C（1）求抛物线的函数解析式．（2）设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标．（3）P是抛物线上第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P，M，A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．解：（1）设抛物线的解析式为y=ax2+bx+c（a≠0），将点A（﹣2，0），B（﹣3，3），O（0，0），代入可得：，解得：．故函数解析式为：y=x2+2x．（2）当AO为平行四边形的边时，DE∥AO，DE=AO，由A（﹣2，0）知：DE=AO=2，若D在对称轴直线x=﹣1左侧，则D横坐标为﹣3，代入抛物线解析式得D1（﹣3，3），若D在对称轴直线x=﹣1右侧，则D横坐标为1，代入抛物线解析式得D2（1，3）．综上可得点D的坐标为：（﹣3，3）或（1，3）．（3）存在．如图：∵B（﹣3，3），C（﹣1，﹣1），根据勾股定理得：BO2=18，CO2=2，BC2=20，∵BO2+CO2=BC2，∴△BOC是直角三角形，假设存在点P，使以P，M，A为顶点的三角形与△BOC相似，设P（x，y），由题意知x＞0，y＞0，且y=x2+2x，①若△AMP∽△BOC，则=，即x+2=3（x2+2x），得：x1=13，x2=﹣2（舍去）．当x=13时，y=59，即P（13，59），②若△PMA∽△BOC，则=，即：x2+2x=3（x+2），得：x1=3，x2=﹣2（舍去）当x=3时，y=15，即P（3，15）．故符合条件的点P有两个，分别是P（13，59）或（3，15）．3. 如图，直线y=2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B的抛物线y=﹣x2+bx+c与直线BC交于点D（3，﹣4）．（1）求直线BD和抛物线的解析式；（2）在第一象限内的抛物线上，是否存在疑点M，作MN垂直于x轴，垂足为点N，使得以M、O、N为顶点的三角形与△BOC相似？若存在，求出点M的坐标；若不存在，请说明理由；（3）在直线BD上方的抛物线上有一动点P，过点P作PH垂直于x轴，交直线BD于点H，当四边形BOHP是平行四边形时，试求动点P的坐标．8、解答：解：（1）∵y=2x+2，∴当x=0时，y=2，∴B（0，2）．当y=0时，x=﹣1，∴A（﹣1，0）．∵抛物线y=﹣x2+bx+c过点B（0，2），D（3，﹣4），∴解得：，∴y=﹣x2+x+2；设直线BD的解析式为y=kx+b，由题意，得，解得：，∴直线BD的解析式为：y=﹣2x+2；（2）存在．如图1，设M（a，﹣a2+a+2）．∵MN垂直于x轴，∴MN=﹣a2+a+2，ON=a．∵y=﹣2x+2，∴y=0时，x=1，∴C（1，0），∴OC=1．∵B（0，2），∴OB=2．当△BOC∽△MON时，∴，∴，解得：a1=1，a2=﹣2M（1，2）或（﹣2，﹣4）；如图2，当△BOC∽△ONM时，，∴，∴a=或，∴M（，）或（，）．∵M在第一象限，（，）；∴符合条件的点M的坐标为（1，2），（3）设P（b，﹣b2+b+2），H（b，﹣2b+2）．如图3，∵四边形BOHP是平行四边形，∴BO=PH=2．∵PH=﹣b2+b+2+2b﹣2=﹣b2+3b．∴2=﹣b2+3b∴b1=1，b2=2．当b=1时，P（1，2），当b=2时，P（2，0）∴P点的坐标为（1，2）或（2，0）．4．如图，点A在x轴上，OA=4，将线段OA绕点O顺时针旋转120°至OB的位置．（1）求点B的坐标；（2）求经过点A、O、B的抛物线的解析式；（3）在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，说明理由．考点：二次函数综合题．专题：压轴题；分类讨论．分析：（1）首先根据OA的旋转条件确定B点位置，然后过B做x轴的垂线，通过构建直角三角形（2）和OB的长（即OA长）确定B点的坐标．（2）已知O、A、B三点坐标，利用待定系数法求出抛物线的解析式．（3）根据（2）的抛物线解析式，可得到抛物线的对称轴，然后先设出P点的坐标，而O、B坐标已知，可先表示出△OPB三边的边长表达式，然后分①OP=OB、②OP=BP、③OB=BP三种情况分类讨论，然后分辨是否存在符合条件的P点．解答：解：（1）如图，过B点作BC⊥x轴，垂足为C，则∠BCO=90°，∵∠AOB=120°，∴∠BOC=60°，又∵OA=OB=4，∴OC=OB=×4=2，BC=OB•sin60°=4×=2，∴点B的坐标为（﹣2，﹣2）；（2）∵抛物线过原点O和点A、B，∴可设抛物线解析式为y=ax2+bx，将A（4，0），B（﹣2．﹣2）代入，得，解得，∴此抛物线的解析式为y=﹣x2+x（3）存在，如图，抛物线的对称轴是直线x=2，直线x=2与x轴的交点为D，设点P的坐标为（2，y），①若OB=OP，则22+|y|2=42，解得y=±2，当y=2时，在Rt△POD中，∠PDO=90°，sin∠POD==，∴∠POD=60°，∴∠POB=∠POD+∠AOB=60°+120°=180°，即P、O、B三点在同一直线上，∴y=2不符合题意，舍去，∴点P的坐标为（2，﹣2）②若OB=PB，则42+|y+2|2=42，解得y=﹣2，故点P的坐标为（2，﹣2），③若OP=BP，则22+|y|2=42+|y+2|2，解得y=﹣2，故点P的坐标为（2，﹣2），综上所述，符合条件的点P只有一个，其坐标为（2，﹣2），5．如图，抛物线y=ax2+bx+c经过A（﹣3.0）、C（0，4），点B在抛物线上，CB∥x轴，且AB平分∠CAO．（1）求抛物线的解析式；（2）线段AB上有一动点P，过点P作y轴的平行线，交抛物线于点Q，求线段PQ的最大值；（3）抛物线的对称轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在，求出点M的坐标；如果不存在，说明理由．10、解答：解：（1）如图1，∵A（﹣3，0），C（0，4），∴OA=3，OC=4．∵∠AOC=90°，∴AC=5．∵BC∥AO，AB平分∠CAO，∴∠CBA=∠BAO=∠CAB．∴BC=AC．∴BC=5．∵BC∥AO，BC=5，OC=4，∴点B的坐标为（5，4）．∵A（﹣3.0）∴解得：∴抛物线的解析式为y=﹣x2+x+4．（2）如图2，设直线AB的解析式为y=mx+n，∵A（﹣3.0）、B（5，4）在直线AB上，∴解得：∴直线AB的解析式为y=x+．设点P的横坐标为t（﹣3≤t≤5），则点Q的横坐标也为t．∴y P=t+，y Q=﹣t2+t+4．∴PQ=y Q﹣y P=﹣t2+t+4﹣（t+）=﹣t2+t+4﹣t﹣=﹣t2++=﹣（t2﹣2t﹣15）=﹣[（t﹣1）2﹣16]=﹣（t﹣1）2+．∵﹣＜0，﹣3≤1≤5，∴当t=1时，PQ取到最大值，最大值为．∴线段PQ的最大值为．（3）①当∠BAM=90°时，如图3所示．抛物线的对称轴为x=﹣=﹣=．∴x H=x G=x M=．∴y G=×+=．∴GH=．∵∠GHA=∠GAM=90°，∴∠MAH=90°﹣∠GAH=∠AGM．∵∠AHG=∠MHA=90°，∠MAH=∠AGM，∴△AHG∽△MHA．∴．∴=．解得：MH=11．∴点M的坐标为（，﹣11）．②当∠ABM=90°时，如图4所示．∵∠BDG=90°，BD=5﹣=，DG=4﹣=，∴BG===．同理：AG=．∵∠AGH=∠MGB，∠AHG=∠MBG=90°，∴△AGH∽△MGB．∴=．∴=．解得：MG=．∴MH=MG+GH=+=9．∴点M的坐标为（，9）．综上所述：符合要求的点M的坐标为（，9）和（，﹣11）．6．（2009•崇左）在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，且点A（0，2），点C（﹣1，0），如图所示：抛物线y=ax2+ax﹣2经过点B．21教育网（1）求点B的坐标；（2）求抛物线的解析式；（3）在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．考点：二次函数综合题．专题：压轴题．分析：（1）根据题意，过点B作BD⊥x轴，垂足为D；根据角的互余的关系，易得B到x、y 轴的距离，即B的坐标；21（2）根据抛物线过B点的坐标，可得a的值，进而可得其解析式；（3）首先假设存在，分A、C是直角顶点两种情况讨论，根据全等三角形的性质，可得答案．解答：解：（1）过点B作BD⊥x轴，垂足为D，∵∠BCD+∠ACO=90°，∠ACO+∠CAO=90°，∴∠BCD=∠CAO，（1分）又∵∠BDC=∠COA=90°，CB=AC，∴△BCD≌△CAO，（2分）∴BD=OC=1，CD=OA=2，（3分）∴点B的坐标为（﹣3，1）；（4分）（2）抛物线y=ax2+ax﹣2经过点B（﹣3，1），则得到1=9a﹣3a﹣2，（5分）解得a=，所以抛物线的解析式为y=x2+x﹣2；（7分）（3）假设存在点P，使得△ACP仍然是以AC为直角边的等腰直角三角形：①若以点C为直角顶点；则延长BC至点P1，使得P1C=BC，得到等腰直角三角形△ACP1，（8分）过点P1作P1M⊥x轴，∵CP1=BC，∠MCP1=∠BCD，∠P1MC=∠BDC=90°，∴△MP1C≌△DBC．（10分）∴CM=CD=2，P1M=BD=1，可求得点P1（1，﹣1）；（11分）②若以点A为直角顶点；则过点A作AP2⊥CA，且使得AP2=AC，得到等腰直角三角形△ACP2，（12分）过点P2作P2N⊥y轴，同理可证△AP2N≌△CAO，（13分）∴NP2=OA=2，AN=OC=1，可求得点P2（2，1），（14分）经检验，点P1（1，﹣1）与点P2（2，1）都在抛物线y=x2+x﹣2上．（16分）练习：1. 如图，二次函数y=x 2+bx+c 的图象与x 轴交于A 、B 两点，且A 点坐标为（-3,0），经过B 点的直线交抛物线于点D （-2，-3）.（1）求抛物线的解析式和直线BD 解析式；（2）过x 轴上点E （a ，0）（E 点在B 点的右侧）作直线EF ∥BD ,交抛物线于点F ,是否存在实数a 使四边形BDFE 是平行四边形？如果存在，求出满足条件的a ；如果不存在，请说明理由.2．已知抛物线经过A （2，0）．设顶点为点P ，与x 轴的另一交点为点B ． 36232++=bx x y （1）求b 的值，求出点P 、点B 的坐标；（2）如图，在直线 y=x 上是否存在点D ，使四边形OPBD 为平行四边形？若存在，3求出点D 的坐标；若不存在，请说明理由；（3）在x 轴下方的抛物线上是否存在点M ，使△AMP ≌△AMB ？如果存在,试举例验证你的猜想；如果不存在，试说明理由．4. 如图，已知抛物线y ＝x2＋bx ＋3与x 轴交于点B （3，0），与y 轴交于点A ，P 是抛物线上的一个动点，点P 的横坐标为m （m ＞3），过点P 作y 轴的平行线PM ，交直线AB 于点M ．（1）求抛物线的解析式；（2）若以AB 为直径的⊙N 与直线PM 相切，求此时点M 的坐标；（3）在点P 的运动过程中，△APM 能否为等腰三角形？若能，求出点M 的坐标；若不能，请说明理由．3. 已知：如图一次函数y ＝x ＋1的图象与x 轴交于点A ，与y 轴交于点B ；21二次函数y ＝x 2＋bx ＋c 的图象与一次函数y ＝x ＋1的图象交于B 、C 两点，2121与x 轴交于D 、E 两点且D 点坐标为（1，0）（1）求二次函数的解析式；（2）求四边形BDEC 的面积S ；（3）在x 轴上是否存在点P ，使得△PBC 是以P 为直角顶点的直角三角形？若存在，求出所有的点P，若不存在，请说明理由．4. 如图，抛物线与x轴交于A（－1，0）、B（3，0）两点，与y轴交于点C（0，－3），设抛物线的顶点为D．（1）求该抛物线的解析式与顶点D的坐标；（2）以B、C、D为顶点的三角形是直角三角形吗？为什么？（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCD相似？若存在，请指出符合条件的点P的位置，并直接写出点P的坐标.。

(完整版)二次函数中的存在性问题(平行四边形)

二、已知三个定点，再找一个定点构成平行四边形（平面内有三个点满足）1.【08湖北十堰】已知抛物线b ax ax y ++-=22与x 轴的一个交点为A (-1,0)，与y 轴的正半轴交于点C ．⑴直接写出抛物线的对称轴，及抛物线与x 轴的另一个交点B 的坐标； ⑵当点C 在以AB 为直径的⊙P 上时，求抛物线的解析式；⑶坐标平面内是否存在点M ,使得以点M 和⑵中抛物线上的三点A 、B 、C 为顶点的四边形是平行四边形？若存在,请求出点M 的坐标；若不存在,请说明理由．解：⑴对称轴是直线：1=x ，点B 的坐标是(3,0)． ……2分说明：每写对1个给1分，“直线”两字没写不扣分．⑵如图，连接PC ，∵点A 、B 的坐标分别是A (-1,0)、B (3,0)，∴AB ＝4．∴．AB PC 242121=⨯==在Rt △POC 中，∵O P ＝PA －OA ＝2－1＝1， ∴．PO PC OC 3122222=-=-=∴b ＝．3 ………………………………3分当01=-=，y x 时，，a a 032=+--∴．a 33=………………………………4分 ∴．x x y 3332332++-= ………………5分 ⑶存在．……………………………6分理由：如图，连接AC 、BC ．设点M 的坐标为),(y x M ．①当以AC 或BC 为对角线时，点M 在x 轴上方，此时CM ∥AB ，且CM ＝AB ．由⑵知，AB ＝4，∴|x |＝4，3==OC y ．∴x ＝±4．∴点M 的坐标为)3,4()3,4(-或M ．…9分说明：少求一个点的坐标扣1分．②当以AB 为对角线时，点M 在x 轴下方．过M 作MN ⊥AB 于N ，则∠MNB ＝∠AOC ＝90°．∵四边形AMBC 是平行四边形，∴AC ＝MB ，且AC ∥MB ．∴∠CAO ＝∠MBN ．∴△AOC ≌△BNM ．∴BN ＝AO ＝1，MN ＝CO ＝3． ∵OB ＝3，∴0N ＝3－1＝2．∴点M 的坐标为(2,3)M -． ……………………………12分说明：求点M 的坐标时，用解直角三角形的方法或用先求直线解析式，然后求交点M 的坐标的方法均可，请参照给分．综上所述，坐标平面内存在点M ，使得以点A 、B 、C 、M 为顶点的四边形是平行四边形．其坐标为123(4,3),(4,3),(2,3)M M M --．说明：①综上所述不写不扣分；②如果开头“存在”二字没写，但最后解答全部正确，不扣分。

专题27 二次函数-存在性问题(全国通用)(解析版)

专题27 二次函数-存在性问题存在性问题是判断事物是否存在的问题，其知识点较广，综合性强，解题方法较灵活，对学生解决问题能力要求高，中考题中往往出现在压轴题中，其解题的一般思路是：假设存在--推理论证--得出结论---合理就存在在，反之不存在。

存在性的问题有点、线段、图形的存在等等。

解题方法多以设参数--表示点坐标--表示线段长--表示面积---建立方程等方法解决问题。

1．如图，二次函数的图象交x 轴于点()()1,0,4,0A B -，交y 轴于点()0,4,C P -是直线BC 下方抛物线上一动点．（1）求这个二次函数的表达式;（2）连接,PB PC ，是否存在点P ，使PBC ∆面积最大，若存在，求出点P 的坐标;若不存在，请说明理由．【答案】（1）234y x x =--；（2）存在点P ，使PBC ∆面积最大，点P 的坐标为()2, 6-．【分析】（1）由A 、B 、C 三点的坐标，利用待定系数法可求得抛物线解析式；（2）过P 作PE ⊥x 轴，交x 轴于点E ，交直线BC 于点F ，用P 点坐标可表示出PF 的长，则可表示出△PBC 的面积，利用二次函数的性质可求得△PBC 面积的最大值及P 点的坐标．【详解】（1）∵二次函数的图象交y 轴于点()0,4C -，∴设二次函数表达式为24y ax bx =+-，把A 、B 二点坐标代入可得4016440a b a b --=⎧⎨+-=⎩，解这个方程组，得13a b =⎧⎨=-⎩， ∴抛物线解析式为：234y x x =--；（2））∵点P 在抛物线上，∴设点P 的坐标为()2,34t t t --过P 作PE x ⊥轴于E ，交直线BC 于F设直线BC 的函数表达式y mx n =+，将B （4，0），C （0，-4）代入得404m n n +=⎧⎨=-⎩，解这个方程组，得14m n =⎧⎨=-⎩， ∴直线BC 解析式为4y x =-，∴点F 的坐标为(),4t t -，()()224344PF t t t t t ∴=----=-+， ()2114422PBC S PF OB t t ∆∴==-+⨯ ()2228t =--+，∵20a =->，∴当2t =时，PBC S ∆最大，此时223423246y t t =--=-⨯-=-，所以存在点P ，使PBC ∆面积最大，点P 的坐标为()2, 6-．【点睛】本题为二次函数的综合应用，涉及待定系数法、二次函数的性质、三角形的面积、方程思想等知识．在（1）中注意待定系数法的应用，在（2）中用P 点坐标表示出△PBC 的面积是解题的关键．2．如图,二次函数 22y ax bx =++经过点()1,0A -和点()4,0B ,与y 轴交于点C ． ()1求抛物线的解析式;()2D 为y 轴右侧抛物线上一点,是否存在点D ,使若存在2 3ABC ABD S S ∆∆=,请直接写出点D 的坐标;若不存在,请说明理由．【答案】(1) 213222y x x =-++；(2) 存在，D （1，3）或（2，3）或（5，-3）【分析】（1）利用待定系数法将点A 和点B 的坐标代入，求出a 和b 的值即可；（2）求出△ABC 的面积，根据23ABC ABD S S ∆∆=求出△ABD 的面积，得出△ABD 中AB 边上的高，从而分点D 在x 轴上方和x 轴下方分别求出点D 的坐标.【详解】解：（1）把点()1,0A -和点()4,0B 代入22y ax bx =++中,得0201642a b a b =-+⎧⎨=++⎩，解得：1232a b ⎧=-⎪⎪⎨⎪=⎪⎩， ∴抛物线的解析式为213222y x x =-++；（2）存在，()()()231,3,2,3,5,3D D D -，理由是：∵A （-1，0），B （4，0），C （0，2）， ∴()141252ABC S ∆=⨯+⨯=， ∵23ABCABD S S ∆∆=， ∴315522ABD S ∆=⨯=，在△ABD 中，∵AB=5，∴AB 边上的高，即点D 到x 轴的距离为3， ∵抛物线表达式为213222y x x =-++，若点D 的纵坐标为3，令y=3，解得x=1或2，∴点D 的坐标为（1，3）或（2，3）；若点D 的纵坐标为-3，令y=-3，解得x=5或-2（舍），∴点D 的坐标为（5，-3）.综上：存在()()()231,3,2,3,5,3D D D -，使得23ABC ABD S S ∆∆=. 【点睛】本题考查了待定系数法求二次函数的解析式，二次函数上点的坐标，解题的关键是注意分类讨论思想的运用.3．如图，在平面直角坐标系中，己知二次函数283y ax x c =++的图像与y 轴交于点B (0， 4)，与x 轴交于点A (－1，0)和点D ．(1)求二次函数的解析式；(2)求抛物线的顶点和点D 的坐标；(3)在抛物线上是否存在点P ，使得△BOP 的面积等于52？如果存在，请求出点P 的坐标？如果不存在，请说明理由．【答案】（1）248433y x x =-++；（2）D 的坐标为（3，0），顶点坐标为（1，163）；（3）满足条件的点P 有两个，坐标分别为P 1(54，214)、P 2(517,412--)．【分析】（1）利用待定系数法求出二次函数解析式即可；（2）根据二次函数的解析式得点D 的坐标，将解析式化为顶点式可得顶点的坐标；（3）设P 的坐标为P （x ，y ），到y 轴的距离为|x|，则S △BOP =12•BO •|x|，解出x=±54，进而得出P 点坐标．【详解】解：(1)把点A (－1，0)和点B (0， 4)代入二次函数283y ax x c =++中得： ()()280=1134a c c⎧-+⨯-+⎪⎨⎪=⎩ 解得：434a c ⎧=-⎪⎨⎪=⎩ 所以二次函数的解析式为：248433y x x =-++ ；（2）根据（1）得点D 的坐标为（3，0），248433y x x =-++=()()224416241333x x x --+=--+， ∴顶点坐标为（1，163）； (3)存在这样的点P ，设P 的坐标为P (x ，y )，到y 轴的距离为∣x ∣∵ S △BOP ＝12•BO •∣x ∣ ∴52＝12×4•∣x ∣ 解得：∣x ∣＝54所以x ＝±54把x ＝54代入248433y x x =-++中得： 2458543434y ⎛⎫=-⨯+⨯+ ⎪⎝⎭ 即：y ＝214，把x ＝－54代入248433y x x =-++中得： 2458543434y ⎛⎫⎛⎫=-⨯-+⨯-+ ⎪ ⎪⎝⎭⎝⎭即：y ＝－1712∴满足条件的点P 有两个，坐标分别为P 1(54，214)、P 2(517,412--)．【点睛】本题考查待定系数法求二次函数解析式、抛物线的顶点坐标以及三角形面积等知识，掌握二次函数的性质、灵活运用待定系数法是解题的关键．4．如图，已知二次函数2(1)y x a x a =-++-与x 轴交于A 、B 两点（点A 位于点B 的左侧），与y 轴交于点C ，已知BAC ∆的面积是6．（1）求a 的值；（2）在抛物线上是否存在一点P ，使ABP ABC S S ∆∆=．存在请求出P 坐标，若不存在请说明理由．【答案】（1）3a =-；（2）存在，P 点的坐标为(2,3)-或(13)-+-或(13)---．【分析】（1）根据求出A,B,C 的坐标，再由BAC ∆的面积是6得到关于a 的方程即可求解；（2）根据ABP ABC S S ∆∆=得到P 点的纵坐标为±3，分别代入解析式即可求解．【详解】（1）∵2(1)y x a x a =-++-，令0x =，则y a =-，∴(0,)C a -，令0y =，即2(1)0x a x a -++-=解得1x a =，21x =由图象知：0a <∴(,0)A a ，(1,0)B∵6ABC S ∆= ∴1(1)()62a a --= 解得：3a =-，（4a =舍去）；（2）∵3a =-，∴(0,3)C ，∵ABP ABC S S ∆∆=.∴P 点的纵坐标为±3，把3y =代入223y x x =--+得2233x x --+=，解得0x =或2x =-，把3y =-代入223y x x =--+得2233x x --+=-，解得1x =-+1x =--∴P 点的坐标为(2,3)-或(13)-+-或(13)--．【点睛】此题主要考查二次函数的图像与性质，解题的关键是熟知待定系数法的应用．5．如图所示，二次函数2y ax bx c =++的图象与x 轴交于A 、B 两点，与y 轴交于点C ，其中点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，线段OB 、OC 的长（OB OC <）是方程210160x x -+=的两个根，且A 点坐标为(60)-，．（1）求此二次函数的表达式；（2）若点E 是线段AB 上的一个动点（与点A 、B 不重合），过点E 作EF ∥AC 交BC 于点F ，连接CE . 设AE 的长为m ，△CEF 的面积为S ，求S 与m 之间的函数关系式，并写出自变量m 的取值范围；（3）在（2）的基础上试说明S 是否存在最大值，若存在，请求出S 的最大值，并求出此时点E 的坐标，判断此时△BCE 的形状；若不存在，请说明理由．【答案】（1）228833y x x =--+；（2）2142S m m =-+(0<m<8);（3）当4m =时S 有最大值8，此时点E 的坐标为(20)-，，△BCE 为等腰三角形. 【分析】（1）通过解方程x 2−10x ＋16＝0得到二次函数图象上的点B 、C 的坐标，再结合A 的坐标，利用待定系数法求出函数解析式；（2）用m 表述出AE 、BE 的长，得到△BEF ∽△BAC ，再利用相似三角形的性质得到比例式8108EF m -=，求出EF 的表达式，利用sin ∠FEG ＝sin ∠CAB ＝45得到45FG EF =，求出FG 的表达式，再根据S ＝S △BCE −S △BFE 求S 与m 之间的函数关系，m 的值不超过AB 的长．（3）将S ＝12-m 2＋4配方为S ＝12-（m −4）2＋8，求出S 的最大值，进而判断出此时△BCE 的形状．【详解】（1）方程210160x x -+=的两个根为2和8.由于OB OC <，所以2OB =，8OC =，故8c =，点B 坐标为(20)，. 因为点A 坐标为(60)-，，所以22(6)(6)802280a b a b ⎧⨯-+⨯-+=⎨⨯+⨯+=⎩．解得23a =-，83b =-. 故此二次函数的表达式为228833y x x =--+. （2）∵AB ＝8，OC ＝8，依题意，AE ＝m ，则BE ＝8−m ，∵OA ＝6，OC ＝8，∴AC ＝10．∵EF ∥AC ，∴△BEF ∽△BAC ． ∴EF BE AC AB=．即8108EF m -=． ∴EF ＝4054m -．过点F 作FG ⊥AB ，垂足为G ，则sin ∠FEG ＝sin ∠CAB ＝45． ∴45FG EF =． ∴FG ＝45•4054m -＝8−m ． ∴S ＝S △BCE −S △BFE ＝12（8−m ）×8−12（8−m ）（8−m ）＝12（8−m ）（8−8＋m ）＝12（8−m ）m ＝2142m m -+，自变量m 的取值范围是0＜m ＜8．（3）存在．理由如下：∵S ＝2142m m -+=−12（m −4）2＋8，且−12＜0， ∴当m ＝4时，S 有最大值，S 最大值＝8．∵m ＝4，∴点E 的坐标为（−2，0）．∴△BCE 为等腰三角形．【点睛】本题考查二次函数综合题，涉及函数和方程的关系、二次函数的性质、相似三角形的判定与性质、配方法求函数最大值等知识，是一道好题．6．关于x 的一元二次方程()222110k x k x --+=有两个实数根. ()1求k 的取值范围；()2是否存在实数k ，使方程的实数根互为相反数？若存在，求k ；若不存在，请说明理由.【答案】（1）14k ≤且0k ≠；（2）不存在【分析】(1)由题意，方程需满足：根的判别式大于0且二次项系数不为0，求不等式的解即可；(2)根据互为相反数的两数和等于0得方程，求解并判断即可．【详解】解：()1有题意得()22202140k k k ⎧≠⎪⎨=--≥⎪⎩，解得，14k ≤且0k ≠ ()2设方程的两根为x1,x 2,依题意， 122210k x x k -+==， ∴12k =，又∵14k ≤且0k ≠ 所以不存在【点睛】本题考查了一元二次方程根的判别式、根与系数的关系．7．如图，在平面直角坐标系xOy 中,二次函数22y x bx c =++的图象与x 轴交于A （-1,0）、B （3,0）两点, 顶点为C .(1) 求此二次函数解析式；(2) 点D 为点C 关于x 轴的对称点，过点A 作直线l ：33y x =+交BD 于点E ，过点B 作直线BK ∥AD 交直线l 于K 点.问：在四边形ABKD 的内部是否存在点P ，使得它到四边形ABKD 四边的距离都相等，若存在，请求出点P 的坐标；若不存在，请说明理由；(3) 在（2）的条件下，若M 、N 分别为直线AD 和直线l 上的两个动点，连结DN 、NM 、MK ，求DN NM MK ++和的最小值.【答案】(1)2y x =-点P 与点E 重合时，即是满足题意的点，坐标为（2(3)8【解析】试题分析：(1) ∵点A 、B 的坐标分别为（-1,0）、（3,0），∴0,230.b c b c -+=++=解得{2b c ==-∴二次函数解析式为222y x =--（2）可求点C 的坐标为（1，-∴点D 的坐标为（1，.可求直线AD的解析式为y =+由题意可求直线BK的解析式为y =-.∵直线l的解析式为y x =+∴可求出点K 的坐标为(5,易求4AB BK KD DA ====.∴四边形ABKD 是菱形.∵菱形的中心到四边的距离相等，∴点P 与点E 重合时，即是满足题意的点，坐标为（2） .(3) ∵点D 、B 关于直线AK 对称,∴DN MN +的最小值是MB .过K 作KF ⊥x 轴于F 点. 过点K 作直线AD 的对称点P ,连接KP ,交直线AD 于点Q , ∴KP ⊥AD .∵AK 是∠DAB 的角平分线,∴KF KQ PQ ===∴MB MK +的最小值是BP .即BP 的长是DN NM MK ++的最小值.∵BK ∥AD ,∴90BKP ∠=︒.在Rt △BKP 中,由勾股定理得BP =8.∴DN NM MK ++的最小值为8.考点：二次函数点评：本题难度较大，主要考查学生对二次函数性质的掌握，本题难度较高在图像分析较复杂，需要学生有扎实基础来理清思路．一般为压轴题型，基础较好的同学要多加训练，培养解题感觉．8．如图是二次函数()2y x m k =++的图象，其顶点坐标为()1,4M -．（1）直接写出m 、k 的值；（2）求二次函数的图象与x 轴的交点A ，B 的坐标；（3）在二次函数的图象上是否存在点P ，使54PAB MAB S S =△△？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）1m =-，4k =-；（2）()1,0A -，()3,0B ；（3）存在点P ，坐标为()4,5或()2,5-【分析】（1）由顶点坐标确定m 、k 的值；（2）令y=0求得图象与x 轴的交点坐标；（3）设存在这样的P 点，由于底边相同，求出△PAB 中AB 边上的高P y ，然后得出P 点纵坐标代入二次函数表达式求得P 点坐标．【详解】解：（1）由顶点坐标为M （1，-4）可知二次函数解析式为()214y x =--．∴1m =-，4k =-；（2）在()214y x =--中，令0y =得()2140x --=，解得13x =，21x =-，∴()1,0A -，()3,0B ．（3）∵PAB △与MAB △同底，且54PAB MAB S S =△△， ∴554544P M y y ==⨯=，即5P y =±．又∵点P 在()214y x =--的图象上，∴4P y ≥-，∴5P y =，∴()2145x --=，解得14x =，22x =-，∴存在点P ，坐标为()4,5或()2,5-，使54PAB MAB SS =．【点睛】本题考查了由二次函数顶点式的求法及抛物线与x 轴交点坐标的求法，以及给出面积关系求点的坐标，综合体现了数形结合的思想．9．如图，二次函数212y x bx c =++的图象交x 轴于,A D 两点，并经过B 点，已知A 点坐标是()2,0，B 点坐标是()8,6．（1）求二次函数的解析式；（2）求函数图象的顶点坐标及D 点的坐标；（3）二次函数的对称轴上是否存在一点C ，使得CBD ∆的周长最小？若C 点存在，求出C 点的坐标，若C 点不存在，请说明理由．【答案】（1）21462y x x =-+ （2）(4,−2)，(6,0)（3）存在，C(4,2)【分析】（1）只需运用待定系数法就可求出二次函数的解析式；（2）只需运用配方法就可求出抛物线的顶点坐标，只需令y=0就可求出点D 的坐标；（3）连接CA ，由于BD 是定值，使得△CBD 的周长最小，只需CD+CB 最小，根据抛物线是轴对称图形可得CA=CD ，只需CA+CB 最小，根据“两点之间，线段最短”可得：当点A 、C 、B三点共线时，CA+CB 最小，只需用待定系数法求出直线AB 的解析式，就可得到点C 的坐标．【详解】（1）把A(2，0)，B(8，6)代入212y x bx c =++，得 1402164862bx c b c ⎧⨯++=⎪⎪⎨⎪⨯++=⎪⎩ 解得46b c =-⎧⎨=⎩∴二次函数的解析式为21462y x x =-+ 故答案为：21462y x x =-+ （2）由221146(4)222y x x x =-+=--得二次函数图象的顶点坐标为(4，−2) 令y=0，得214602x x -+= 解得：x 1=2，x 2=6，∴D 点的坐标为(6，0)．故答案为：(4，−2)，(6，0)（3）二次函数的对称轴上存在一点C ，使得△CBD 的周长最小．连接CA ，如图，∵点C 在二次函数的对称轴x=4上，∴x C =4，CA=CD ，∴△CBD 的周长=CD+CB+BD=CA+CB+BD ，根据“两点之间，线段最短”，可得当点A 、C 、B 三点共线时，CA+CB 最小，此时，由于BD 是定值，因此△CBD 的周长最小．设直线AB 的解析式为y=mx+n ，把A(2，0)、B(8，6)代入y=mx+n ，得2+086m n m n =⎧⎨+=⎩解得12m n =⎧⎨=-⎩ ∴直线AB 的解析式为y=x −2当x=4时，y=4−2=2，∴当二次函数的对称轴上点C 的坐标为(4，2)时，△CBD 的周长最小．故答案为：存在，C(4，2)【点睛】本题考查了用待定系数法求二次函数的解析式，会将二次函数一般式化为顶点式，表示出顶点坐标，本题是抛物线动点问题的综合题型，在求线段和最短的时候，“两点之间，线段最短”是经常会被用到的知识点．10．如图是二次函数c bx x y ++=2的图象，其顶点坐标为M （1，－4）．（1）求出图象与x 轴的交点A ，B 的坐标；（2）在二次函数的图象上是否存在点P ，使MAB PAB S S ∆∆=45，若存在，求出P 点的坐标；若不存在，请说明理由；【答案】（1） A （-1,0） B （3,0）（2）P 1（4,5） P 2（-2,5）.【解析】试题分析：（1）将顶点M （1，-4）代入二次函数c bx x y ++=2，求出二次函数解析式，令y=0，解方程即可；（2）假设存在点P （x ，y ）满足条件，用点P 坐标分别表示出两个三角形的面积，解方程确定点P 的坐标.试题解析：：（1）因为M （1，-4）是二次函数c bx x y ++=2的顶点坐标，所以222(1)423y x bx c x x x =++=--=--，令解得 ∴A ，B 两点的坐标分别为A （-1，0），B （3，0）.（2）在二次函数的图象上存在点P ，使设P （x ，y ）则又∴即y=±5 ∵二次函数的最小值为-4∴当时，或故P 点坐标为（-2，5）或（4，5）.考点：1.二次函数的图像；2.一次函数的图像；3.二次函数的最值；4.轴对称 .11．如图，二次函数y ＝﹣14x 2+bx +c 的图象经过点A （4，0），B （﹣4，﹣4），且与y 轴交于点C ．（1）求此二次函数的解析式；（2）证明：AO 平分∠BAC ；（3）在二次函数对称轴上是否存在一点P 使得AP ＝BP ？若存在，请求出点P 的坐标；若不存在，请说明理由．【答案】（1）y ＝﹣14x 2+12x +2；（2）见解析；（3）存在．点P 的坐标为（1，﹣4）；【解析】【分析】（1）将点A （4，0）与点B （−4，-4）代入函数解析式即可；（2）求出直线AB 的解析式，求出AB 与y 轴交点D （0，−2），可得OC ＝OD ，再由AO ⊥CD ，可证AO 平分∠BAC ；（3）二次函数的对称轴为直线x ＝1，设点P 的坐标为（1，m ），AP 2＝（4−1）2＋m 2，BP 2＝（1＋4）2＋（m4）2，当AP ＝BP 时，求出m ＝−4即可；【详解】（1）∵点A （4，0）与点B （﹣4，-4）在二次函数的图象上， ∴044444b c b c =-++⎧⎨-=--+⎩，解得122b c ⎧=⎪⎨⎪=⎩，∴二次函数的解析式为y ＝211242x x -++；（2）设直线AB 的解析式为y ＝ax +n则有4040a n a n +=⎧⎨-+=⎩，解得122a b ⎧=⎪⎨⎪=-⎩，故直线AB的解析式为y＝12x﹣2，设直线AB与y轴的交点为点D，x＝0，则y＝﹣2，故点D为（0，﹣2），由（1）可知点C为（0，2），∴OC＝OD又∵AO⊥CD，∴AO平分∠BAC；（3）存在．∵y＝﹣14x2+12x+2＝﹣14（x﹣1）2+14+2，∴二次函数的对称轴为直线x＝1，设点P的坐标为（1，m），AP2＝（4﹣1）2+m2，BP2＝（1+4）2+（m4）2，当AP＝BP时，AP2＝BP2，则有9+m2＝25+m2+16+8m，解得m＝﹣4，∴点P的坐标为（1，﹣4）；【点睛】本题考查二次函数图象及性质，一次函数图象及性质；熟练掌握待定系数法求函数解析式，利用勾股定理求边长是解题的关键．12．（本题满分10分）如图是二次函数的图象，其顶点坐标为M（1，-4）．（1）求出图象与轴的交点A ，B 的坐标；（2）在二次函数的图象上是否存在点P ，使，若存在，求出P 点的坐标；若不存在，请说明理由；【答案】（1）A （－1,0） B （3,0）；（2）存在，P （－2,5）或 P （4,5）【解析】试题分析：1）由已知得，抛物线解析式令y=0，解得 ∴A （－1,0） B （3,0）（2）84421=⨯⨯=∆MAB S ∴∵AB=4 ∴令y=5，解得∴P （－2,5）或 P （4,5）考点：1．抛物线的顶点式；2．抛物线的值13．如图，二次函数212y x bx c =-++的图象经过A(2，0)，B(0，－6)两点．（1）求这个二次函数的解析式；（2）设该二次函数的对称轴与x 轴交于点C ，连接BA ，BC ，求△ABC 的面积．（3）在x 轴上是否存在一点P ，使△ABP 为等腰三角形，若存在，求出P 的坐标，若不存在，说明理由.【答案】（1）y ＝－12x 2＋4x －6；（2）S △ABC ＝6；（3）点P 坐标为（-2，0）或()2-或()2+或()80-，【解析】试题分析：（1）把A 、B 两点的坐标代入y=-12x 2+bx+c 中得到关于b 、c 的方程组，然后解方程求出b 、c 即可得到抛物线解析式；（2）先确定抛物线的对称轴方程，则可得到C 点坐标，然后根据三角形面积公式求解．（3）分类讨论，进行求解即可.试题解析：（1）∵的图象经过A （2，0）、B （0，-6）两点， ∴2206b c c -++⎧⎨-⎩＝＝，解得b=4，c=-6，∴这个二次函数的解析式为y ＝−12x 2+4x −6 （2）令-12x 2+4x-6=0 ∴x 2-8x+12=0解得：x 1=2 x 2=6∴C （4，0）∴AC=2∴S △ABC =12×2×6=6 （3）点P 坐标为（-2,0）或()(()2-80+或或， 14．如图，二次函数2y x bx c =++与x 轴交于A 、B 两点，与y 轴交于c 顶点，已知(1,0)A ，(0,3)C -.（1）求此二次函数的解析式及B 点坐标.（2）在抛物线上存在一点P 使ABP ∆的面积为10，不存在说明理由，如果存在，请求出P 的坐标.（3）根据图象直接写出33x -<<时，y 的取值范围.【答案】（1）二次函数解析式为223y x x =+-，B 点坐标为(3,0)-;（2）()4,5-，(2,5);（3）412y -<.【分析】（1）将已知的两点坐标代入抛物线中，即可求得抛物线的解析式;.（2）设()2,23P x x x +-,然后利用三角形的面积计算即可;（3）根据图象可得出y 的取值范围..【详解】解：（1）将(1,0)A ，(0,3)C -代入2y x bx c =++中，得：103b c c ++=⎧⎨=-⎩，解得23b c =⎧⎨=-⎩. 所以二次函数解析式为223y x x =+-.令0y =，即2230x x +-=，解得：11x =，23x =-.∴B 点坐标为(3,0)-.（2）设()2,23P x x x +-，∵ABP ∆的面积为10， ∴21423102x x ⨯⨯+-=，解方程2235x x +-=得14x =-，22x =，此时P 点坐标为()4,5-，(2,5).方程2235x x +-=-没有实数解.综上所述，P 点坐标为()4,5-，(2,5).（3）如图所示，当33x -<<时，当1x =-时，y 有最小值，将1x =-代入223y x x =+-中，得4y =-. 当3x =时，y 有最大值.将3x =代入223y x x =+-中，得12y =. ∴y 的取值范围是412y -<.【点睛】本题考查了二次函数解析式的确定以及图形面积的求法，不规则图形的面积通常转化为规则图形的面积的和差．15．如图，已知二次函数223y x x =+-的图象与x 轴相交于C D 、两点（点C 在点D 的左边），与y 轴交于点B ，点A 在二次函数的图像上，且AB ∥x 轴．问线段BC 上是否存在点P ，使△POC 为等腰三角形；如果存在，求出点P 的坐标；如果不存在，请说明理由．【答案】存在，点33(,)22P --或(0,3)P -或(3,22P -+-．【分析】由抛物线解析式可得出C 、B 坐标，利用待定系数法可得直线BC 的解析式为y=-x-3，分三个情况讨论：当PC PO =时，点P 在OC 的垂直平分线上，根据O 、C 坐标可得OC 中点坐标，把OC 中点的横坐标代入BC 解析式即可得P 点坐标；当PO CO =时，设P （x ，-x-3），利用两点间距离公式即可得P 点坐标；当PC CO =时，利用利用两点间距离公式即可得P 点坐标．【详解】当0y =时，2230x x +-=，解得：123,1x x =-=，∵点C 在点D 的左边，∴(3,0)C -当x=0时，y=-3，∴B （0，-3），设直线BC 的函数解析式为y kx n =+∴0330k n n=-+⎧⎨-=+⎩，解得13k n =-⎧⎨=-⎩， ∴直线BC 的解析式为y=-x-3，①当PC PO =时，点P 在OC 的垂直平分线上，∵点C （-3，0），O （0，0），∴OC 中点坐标为（32-，0），把x=32-代入y=-x-3得：y=32-3=32-， ∴点33(,)22P -- ②当PO CO =时，设P （x ，-x-3），，解得：x 1=0，x 2=-3（舍去），∴-x-3=-3，∴点(0,3)P -，③当PC CO =时，设点(,3)P x x --，3=，解得13x =-+，232x =--（不合题意，舍去）∴(3P -+∴存在，点33(,)22P --或(0,3)P -或(3,)22P -+-．【点睛】本题考查二次函数图象上的点的坐标特征、待定系数法求一次函数解析式及等腰三角形的判定，注意分类讨论思想的运用是解题关键．16．已知二次函数：2(21)2(0)y ax a x a =+++<．（1）求证：二次函数的图象与x 轴有两个交点；（2）当二次函数的图象与x 轴的两个交点的横坐标均为整数，且a 为负整数时，求a 的值及二次函数的解析式并画出二次函数的图象（不用列表，只要求用其与x 轴的两个交点A ，B （A 在B 的左侧），与y 轴的交点C 及其顶点D 这四点画出二次函数的大致图象，同时标出A ，B ，C ，D 的位置）；（3）在（2）的条件下，二次函数的图象上是否存在一点P 使75PCA ︒∠=？如果存在，求出点P 的坐标；如果不存在，请说明理由．【答案】（1）见解析；（2）1a =-，22y x x =--+，函数图象如图所示见解析；（3）存在这样的点P ，点P 的坐标为35,33⎛⎫ ⎪ ⎪⎝⎭或1)．【解析】【分析】（1）1）将解析式右边因式分解得抛物线与x 轴的交点为（−2，0）、（−1a，0），结合a ＜0即可得证；（2）根据题意求出1a =-，再求出函数与x 轴的交点，即可作图；（3）根据题意作出图像，根据题意分两种情况讨论：①当点P 在直线AC 上方时，记直线PC 与x 轴的交点为E ，根据75PCA ︒∠=求出30OEC ︒∠=，因此OC tan OEC OE ===∠E ，则可求出求得直线CE解析式为2y x =+，再联立两直线即可求出P 点坐标；②当点P 在直线AC 下方时，同理求出P 的坐标.【详解】（1）∵2(21)2(2)(1)y ax a x x ax =+++=++，且0a <，∴抛物线与x 轴的交点为(2,0)-、1,0a ⎛⎫- ⎪⎝⎭，则二次函数的图象与x 轴有两个交点；（2）∵两个交点的横坐标均为整数，且a 为负整数，∴1a =-，则抛物线与x 轴的交点A 的坐标为(2,0)-、B 的坐标为(1,0)，∴抛物线解析式为(2)(1)y x x =+-+22x x =--+21924x ⎛⎫=-++ ⎪⎝⎭，当0x =时，2y =，即(0,2)C ，函数图象如图1所示：（3）存在这样的点P ，∵2OA OC ==，∴45ACO ︒∠=，如图2，当点P 在直线AC 上方时，记直线PC 与x 轴的交点为E ，∵75PCA ︒∠=，∴120PCO ︒∠=，60OCE ︒∠=，则30OEC ︒∠=，∴OC tan OEC OE ===∠则E ，求得直线CE解析式为2y x =+，联立2232y x y x x ⎧=+⎪⎨⎪=--+⎩，解得02x y =⎧⎨=⎩或53x y ⎧=⎪⎪⎨⎪=⎪⎩，∴P ⎝⎭；如图3，当点P 在直线AC 下方时，记直线PC 与x 轴的交点为F ，∵75ACP ︒∠=，45ACO ︒∠=，∴30OCF ︒∠=，则tan 2OF OC OCF =∠==，∴F ⎫⎪⎪⎝⎭，求得直线PC解析式为2y =+，联立222y y x x ⎧=+⎪⎨=--+⎪⎩，解得：02x y =⎧⎨=⎩或11x y ⎧=⎪⎨=⎪⎩，∴1)P ，综上，点P 的坐标为⎝⎭或1)．【点睛】此题主要考查二次函数综合，解题的关键是熟知二次函数的图像与性质，一次函数的图像与性质及三角函数的应用.17．如图，二次函数2y x bx c =-++的图象经过坐标原点，与x 轴的另一个交点为A (－2，0)．（1）求二次函数的解析式（2）在抛物线上是否存在一点P ，使△AOP 的面积为3，若存在请求出点P 的坐标，若不存在，请说明理由．【答案】（1）y ＝－x 2－2x ；（2）（3，-3），（1，-3）．【分析】（1）把点（0，0）和点A （-2，0）分别代入函数关系式来求b 、c 的值；（2）设点P 的坐标为（x ，-x 2-2x ），利用三角形的面积公式得到-x 2-2x =±3．通过解方程来求x 的值，则易求点P 的坐标．【详解】解：（1）∵二次函数y =-x 2+bx +c 的图象经过坐标原点（0，0）∴c =0．又∵二次函数y =-x 2+bx +c 的图象过点A （-2，0）∴-（-2）2-2b +0=0，∴b =-2．∴所求b 、c 值分别为-2，0；（2）存在一点P ，满足S △AOP =3．设点P 的坐标为（x ，-x 2-2x ）∵S △AOP =3 ∴12×2×|-x 2-2x |=3 ∴-x 2-2x =±3．当-x 2-2x =3时，此方程无解；当-x 2-2x =-3时，解得 x 1=-3，x 2=1．∴点P 的坐标为（-3，-3）或（1，-3）．【点睛】本题考查了抛物线与x 轴的交点．解（1）题时，实际上利用待定系数法来求抛物线的解析式．18．二次函数y=ax 2+bx+c （a ≠0）的图象经过点A （3，0），B （2，﹣3），并且以x=1为对称轴．（1）求此函数的解析式；（2）作出二次函数的大致图象；（3）在对称轴x=1上是否存在一点P ，使△PAB 中PA=PB ？若存在，求出P 点的坐标；若不存在，说明理由．【答案】（1）解析式为y=x 2﹣2x ﹣3；（2）画图见解析；（3）存在，点P 的坐标为（1，﹣1）．【解析】试题分析：（1）根据对称轴的公式x =2b a -和函数的解析式，将2b a-=1和A （3，0），B （2，﹣3）代入函数解析式，组成方程组解答即可；（2）求出图象与坐标轴的交点坐标，描点即可；（3）根据两点之间距离公式解答即可．试题解析：解：（1）根据题意得：12930423b a a b c a b c ⎧-=⎪⎪++=⎨⎪++=-⎪⎩，解得：123a b c =⎧⎪=-⎨⎪=-⎩，∴解析式为y =x 2﹣2x ﹣3；（2）二次函数图象如图：（3）存在．作AB 的垂直平分线交对称轴x =1于点P ，连接PA 、PB ，则PA =PB ，设P 点坐标为（1，m ）．∵PA =PB ，∴22+m 2=（﹣3﹣m ）2+1，解得：m =﹣1，∴点P 的坐标为（1，﹣1）．点睛：（1）所用方法被称为待定系数法；（2）考查了二次函数草图的画法；（3）会用距离公式d19．如图，已知二次函数21:43L y x x =-+与x 轴交于A B 、两点（点A 在点B 的左边），与y 轴交于点C ．（1）写出A B 、两点的坐标；（2）二次函数()22:430L y kx kx k k =-+≠，顶点为P ． ①直接写出二次函数2L 与二次函数1L 有关图象的两条相同的性质；②是否存在实数k ，使ABP ∆为等边三角形？如存在，请求出k 的值；如不存在，请说明理由；③若直线8y k =与抛物线2L 交于E F 、两点，问线段EF 的长度是否发生变化？如果不会，请求出EF 的长度；如果会，请说明理由．【答案】（1）()()1,0,3,0A B ；（2）①对称轴都为直线2x =或顶点的横坐标为2；都经过()()1,0,3,0A B 两点；②存在实数k ，使ABP ∆为等边三角形，k =③线段EF 的长度不会发生变化，值为6．【分析】（1）令2430x x -+=，求出解集即可；（2）①根据二次函数2L 与1L 有关图象的两条相同的性质求解即可；②根据()22432y kx kx k k x k =-+=--，可得到结果；③根据已知条件列式2438kx kx k k -+=，求出定值即可证明．【详解】解：（1）令2430x x -+=，∴()()130x x --=，∴11x =，23x =，∵点A 在点B 的左边，∴()()1,0,3,0A B ；（2）①二次函数2L 与1L 有关图象的两条相同的性质：（I ）对称轴都为直线2x =或顶点的横坐标为2；（II ）都经过()()1,0,3,0A B 两点；②存在实数k ，使ABP ∆为等边三角形．∵()22432y kx kx k k x k =-+=--，∴顶点()2,P k -，∵()()1,0,3,0A B ，∴2AB =，要使ABP ∆为等边三角形，必满足k -=∴k =③线段EF 的长度不会发生变化．∵直线8y k =与抛物线2L 交于E F 、两点，∴2438kx kx k k -+=，∵0k ≠，∴2438x x -+=，∴11x =-，25x =，∴216EF x x =-=，∴线段EF 的长度不会发生变化．【点睛】本题主要考查了二次函数综合，结合一次函数、等边三角形的性质求解是关键．20．如图，已知二次函数y ＝x 2﹣2x +m 的图象与x 轴交于点A 、B ，与y 轴交于点C ，直线AC 交二次函数图象的对称轴于点D ，若点C 为AD 的中点．（1）求m 的值；（2）若二次函数图象上有一点Q ，使得tan ∠ABQ ＝3，求点Q 的坐标；（3）对于（2）中的Q 点，在二次函数图象上是否存在点P ，使得△QBP ∽△COA ？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）m=﹣3；（2）Q （﹣4，21）或（2，﹣3）；（3）不存在，理由见解析【分析】（1）函数的对称轴为：x=1，点C 为AD 的中点，则点A （-1，0），即可求解；（2）tan ∠ABQ=3，点B （3，0），则AQ 所在的直线为：y=±3x （x-3），即可求解；（3）分点Q （2，-3）、点Q （-4，21）两种情况，分别求解即可．【详解】（1）设对称轴交x 轴于点E ，直线AC 交抛物线对称轴于点D ，函数的对称轴为：x＝1，点C为AD的中点，则点A（﹣1，0），将点A的坐标代入抛物线表达式并解得：m＝﹣3，故抛物线的表达式为：y＝x2﹣2x﹣3…①；（2）tan∠ABQ＝3，点B（3，0），则AQ所在的直线为：y＝±3（x﹣3）…②，联立①②并解得：x＝﹣4或3（舍去）或2，故点Q（﹣4，21）或（2，﹣3）；（3）不存在，理由：△QBP∽△COA，则∠QBP＝90°①当点Q（2，﹣3）时，则BP的表达式为：y＝﹣13（x﹣3）…③，联立①③并解得：x＝3（舍去）或﹣43，故点P（﹣41339，），此时BP：PQ≠OA：AC，故点P不存在；②当点Q（﹣4，21）时，同理可得：点P（﹣21139，），此时BP：PQ≠OA：OB，故点P不存在；综上，点P不存在．【点睛】此题考查二次函数综合运用，一次函数的性质、三角形相似、中点公式的运用等，解题关键在于要注意分类求解，避免遗漏．21．如图，二次函数y ＝12x 2+bx+c 的图象交x 轴于A 、D 两点，并经过B 点，已知A 点坐标是（2，0），B 点坐标是（8，6）．（1）求二次函数的解析式；（2）求函数图象的顶点坐标及D 点的坐标；（3）二次函数的对称轴上是否存在一点C ，使得△CBD 的周长最小？若C 点存在，求出C 点的坐标；若C 点不存在，请说明理由．【答案】（1）y=12x 2﹣4x+6；（2）D 点的坐标为（6，0）；（3）存在．当点C 的坐标为（4，2）时，△CBD 的周长最小【分析】（1）只需运用待定系数法就可求出二次函数的解析式；（2）只需运用配方法就可求出抛物线的顶点坐标，只需令y=0就可求出点D 的坐标；（3）连接CA ，由于BD 是定值，使得△CBD 的周长最小，只需CD+CB 最小，根据抛物线是轴对称图形可得CA=CD ，只需CA+CB 最小，根据“两点之间，线段最短”可得：当点A 、C 、B 三点共线时，CA+CB 最小，只需用待定系数法求出直线AB 的解析式，就可得到点C 的坐标．【详解】（1）把A （2，0），B （8，6）代入212y x bx c =++，得 14202164862b c b c ⎧⨯++=⎪⎪⎨⎪⨯++=⎪⎩ 解得：46b c =-⎧⎨=⎩∴二次函数的解析式为21462y x x =+﹣；（2）由2211464222y x x x =+=﹣（﹣）﹣，得二次函数图象的顶点坐标为（4，﹣2）．令y=0，得214602x x +=﹣，解得：x 1=2，x 2=6，∴D 点的坐标为（6，0）；（3）二次函数的对称轴上存在一点C ，使得CBD 的周长最小．连接CA ，如图，∵点C 在二次函数的对称轴x=4上，∴x C =4，CA=CD ，∴CBD 的周长=CD+CB+BD=CA+CB+BD ，根据“两点之间，线段最短”，可得当点A 、C 、B 三点共线时，CA+CB 最小，此时，由于BD 是定值，因此CBD 的周长最小．设直线AB 的解析式为y=mx+n ，把A （2，0）、B （8，6）代入y=mx+n ，得208m n m n +=⎧⎨+=⎩解得：12m n =⎧⎨=-⎩ ∴直线AB 的解析式为y=x ﹣2．当x=4时，y=4﹣2=2，∴当二次函数的对称轴上点C 的坐标为（4，2）时，CBD 的周长最小．【点睛】本题考查了（1）二次函数综合题；（2）待定系数法求一次函数解析式；（3）二次函数的性质；（4）待定系数法求二次函数解析式；（5）线段的性质：（6）两点之间线段最短．22．已知：如图，二次函数y=x 2+bx+c 的图象过点A （1，0）和C （0，﹣3）（1）求这个二次函数的解析式；（2）如果这个二次函数的图象与x 轴的另一个交点为B ，求线段AB 的长．（3）在这条抛物线上是否存在一点P ，使△ABP 的面积为8？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）二次函数的解析式为223y x x =+- ；（2）=4AB ；（3）存在，点P 的坐标为1(1P -+或2(1P --或3(1,4)P --. 【分析】（1）利用待定系数法把A （1，0），C （0，-3）代入二次函数y=x 2+bx+c 中，即可算出b 、c 的值，进而得到函数解析式是y=x 2+2x-3；（2）首先求出A 、B 两点坐标，再算出AB 的长；（3）设P （m ，n ），根据△ABP 的面积为8可以计算出n 的值，然后再利用二次函数解析式计算出m 的值即可得到P 点坐标．【详解】解：（1）依题意把()0A 1，，()03C -，代入2y x bx c =++得： 103b c c ++=⎧⎨=-⎩，解得：23b c =⎧⎨=-⎩ ， ∴ 该二次函数的解析式为223y x x =+- ；（2）令0y =，则2230x x +-=，解之得：11x =，23x =- ，∴ 点B 坐标为（－3，0），。

二次函数中的存在性问题(含答案解析)(完整资料).doc

【最新整理，下载后即可编辑】2018年8月4日初中数学试卷一、综合题（共9题；共135分）1.如图所示，抛物线y=ax2+bx+c的顶点为M（﹣2，﹣4），与x轴交于A、B 两点，且A（﹣6，0），与y轴交于点C．（1）求抛物线的函数解析式；（2）求△ABC的面积；（3）能否在抛物线第三象限的图象上找到一点P，使△APC的面积最大？若能，请求出点P的坐标；若不能，请说明理由．2.（2017•乌鲁木齐）如图，抛物线y=ax2+bx+c（a≠0）与直线y=x+1相交于A （﹣1，0），B（4，m）两点，且抛物线经过点C（5，0）．（1）求抛物线的解析式；（2）点P是抛物线上的一个动点（不与点A、点B重合），过点P作直线PD⊥x轴于点D，交直线AB于点E．①当PE=2ED时，求P点坐标；②是否存在点P使△BEC为等腰三角形？若存在请直接写出点P的坐标；若不存在，请说明理由．3.（2017•赤峰）如图，二次函数y=ax2+bx+c（a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．（1）求二次函数的解析式和直线BD的解析式；（2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；（3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为2 √2？若存在求出点Q的坐标；若不存在请说明理由．4.（2017•广元）如图，已知抛物线y=ax2+bx+c过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．（1）求抛物线的解析式；（2）设点M（1，m），当MB+MD的值最小时，求m的值；（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；（4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．5.（2017•巴中）如图，已知两直线l1，l2分别经过点A（1，0），点B（﹣3，0），且两条直线相交于y轴的正半轴上的点C，当点C的坐标为（0，√3）时，恰好有l1⊥l2，经过点A，B，C的抛物线的对称轴与l1、l2、x轴分别交于点G、E、F，D为抛物线的顶点．（1）求抛物线的函数解析式；（2）试说明DG与DE的数量关系？并说明理由；（3）若直线l2绕点C旋转时，与抛物线的另一个交点为M，当△MCG为等腰三角形时，请直接写出点M的坐标．6.如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．7.如图，抛物线y=ax2+bx+c（a≠0）与x轴相交于A（﹣1，0），B（3，0），与y轴交于点C（0，3）．（1）求抛物线的解析式；（2）连接BC，点P为抛物线上第一象限内一动点，当△BCP面积最大时，求点P的坐标；（3）设点D是抛物线的对称轴上的一点，在抛物线上是否存在点Q，使以点B，C，D，Q为顶点的四边形为平行四边形？若存在，求出点Q的坐标；若不存在，说明理由．8.（2017•临沂）如图，抛物线y=ax2+bx﹣3经过点A（2，﹣3），与x轴负半轴交于点B，与y轴交于点C，且OC=3OB．（1）求抛物线的解析式；（2）点D在y轴上，且∠BDO=∠BAC，求点D的坐标；（3）点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N为顶点的四边形是平行四边形？若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．答案解析部分一、综合题1.【答案】（1）解：设此函数的解析式为y=a（x+h）2+k，∵函数图象顶点为M（﹣2，﹣4），∴y=a（x+2）2﹣4，又∵函数图象经过点A（﹣6，0），∴0=a（﹣6+2）2﹣4解得a= 14，∴此函数的解析式为y= 14（x+2）2﹣4，即y= 14x2+x﹣3；（2）解：∵点C是函数y= 14x2+x﹣3的图象与y轴的交点，∴点C的坐标是（0，﹣3），又当y=0时，有y= 14x2+x﹣3=0，解得x1=﹣6，x2=2，∴点B的坐标是（2，0），则S△ABC= 12|AB|•|OC|= 12×8×3=12；（3）解：假设存在这样的点，过点P作PE⊥x轴于点E，交AC于点F．设E（x，0），则P（x，14x2+x﹣3），设直线AC的解析式为y=kx+b，∵直线AC过点A（﹣6，0），C（0，﹣3），∴ {−6k+k=0−3=k ，解得{k=−12k=−3，∴直线AC的解析式为y=﹣12x﹣3，∴点F的坐标为F（x，﹣12x﹣3），则|PF|=﹣ 12 x ﹣3﹣（ 14x 2+x ﹣3）=﹣ 14 x 2﹣ 32x ， ∴S △APC =S △APF +S △CPF= 12 |PF|•|AE|+ 12 |PF|•|OE| =12|PF|•|OA|= 12（﹣ 14 x 2﹣ 32x ）×6=﹣ 34 x 2﹣ 92x=﹣ 34（x+3）2+274，∴当x=﹣3时，S △APC 有最大值 274 ，此时点P 的坐标是P （﹣3，﹣ 154）．【考点】二次函数的应用【解析】【分析】（1）根据顶点坐标公式即可求得a 、b 、c 的值，即可解题；（2）易求得点B 、C 的坐标，即可求得OC 的长，即可求得△ABC 的面积，即可解题；（3）作PE⊥x 轴于点E ，交AC 于点F ，可将△APC 的面积转化为△AFP 和△CFP 的面积之和，而这两个三角形有共同的底PF ，这一个底上的高的和又恰好是A 、C 两点间的距离，因此若设设E （x ，0），则可用x 来表示△APC 的面积，得到关于x 的一个二次函数，求得该二次函数最大值，即可解题．2.【答案】（1）解：∵点B （4，m ）在直线y=x+1上， ∴m=4+1=5， ∴B（4，5），把A 、B 、C 三点坐标代入抛物线解析式可得 {k −k +k =016k +4k +k =525k +5k +k =0，解得{k =−1k =4k =5， ∴抛物线解析式为y=﹣x 2+4x+5（2）解：①设P （x ，﹣x 2+4x+5），则E （x ，x+1），D （x ，0），则PE=|﹣x 2+4x+5﹣（x+1）|=|﹣x 2+3x+4|，DE=|x+1|， ∵PE=2ED，∴|﹣x 2+3x+4|=2|x+1|，当﹣x 2+3x+4=2（x+1）时，解得x=﹣1或x=2，但当x=﹣1时，P 与A 重合不合题意，舍去，∴P（2，9）；当﹣x2+3x+4=﹣2（x+1）时，解得x=﹣1或x=6，但当x=﹣1时，P与A重合不合题意，舍去，∴P（6，﹣7）；综上可知P点坐标为（2，9）或（6，﹣7）；②设P（x，﹣x2+4x+5），则E（x，x+1），且B（4，5），C（5，0），∴BE= √(k−4)2+(k+1−5)2= √2|x﹣4|，CE= √(k−5)2+(k+1)2 = √2k2−8k+26，BC= √(4−5)2+(5−0)2= √26，当△BEC为等腰三角形时，则有BE=CE、BE=BC或CE=BC三种情况，当BE=CE时，则√2|x﹣4|= √2k2−8k+26，解得x= 34，此时P点坐标为（34，11916）；当BE=BC时，则√2|x﹣4|= √26，解得x=4+ √13或x=4﹣√13，此时P 点坐标为（4+ √13，﹣4 √13﹣8）或（4﹣√13，4 √13﹣8）；当CE=BC时，则√2k2−8k+26= √26，解得x=0或x=4，当x=4时E点与B点重合，不合题意，舍去，此时P点坐标为（0，5）；综上可知存在满足条件的点P，其坐标为（34，11916）或（4+ √13，﹣4 √13﹣8）或（4﹣√13，4 √13﹣8）或（0，5）【考点】二次函数的应用，与二次函数有关的动态几何问题【解析】【分析】（1）由直线解析式可求得B点坐标，由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；（2）①可设出P点坐标，则可表示出E、D的坐标，从而可表示出PE和ED的长，由条件可知到关于P点坐标的方程，则可求得P点坐标；②由E、B、C三点坐标可表示出BE、CE和BC的长，由等腰三角形的性质可得到关于E点坐标的方程，可求得E点坐标，则可求得P点坐标．3.【答案】（1）解：∵抛物线的顶点C的坐标为（1，4），∴可设抛物线解析式为y=a（x﹣1）2+4，∵点B（3，0）在该抛物线的图象上，∴0=a（3﹣1）2+4，解得a=﹣1，∴抛物线解析式为y=﹣（x﹣1）2+4，即y=﹣x2+2x+3，∵点D在y轴上，令x=0可得y=3，∴D点坐标为（0，3），∴可设直线BD解析式为y=kx+3，把B点坐标代入可得3k+3=0，解得k=﹣1，∴直线BD解析式为y=﹣x+3（2）解：设P点横坐标为m（m＞0），则P（m，﹣m+3），M（m，﹣m2+2m+3），∴PM=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m=﹣（m﹣32）2+ 94，∴当m= 32时，PM有最大值94（3）解：如图，过Q作QG∥y轴交BD于点G，交x轴于点E，作QH⊥BD 于H，设Q（x，﹣x2+2x+3），则G（x，﹣x+3），∴QG=|﹣x2+2x+3﹣（﹣x+3）|=|﹣x2+3x|，∵△BOD是等腰直角三角形，∴∠DBO=45°，∴∠HGQ=∠BGE=45°，当△BDQ中BD边上的高为2 √2时，即QH=HG=2 √2，∴QG= √2×2 √2=4，∴|﹣x2+3x|=4，当﹣x2+3x=4时，△=9﹣16＜0，方程无实数根，当﹣x2+3x=﹣4时，解得x=﹣1或x=4，∴Q（﹣1，0）或（4，﹣5），综上可知存在满足条件的点Q ，其坐标为（﹣1，0）或（4，﹣5）【考点】二次函数的应用，与二次函数有关的动态几何问题【解析】【分析】（1）可设抛物线解析式为顶点式，由B 点坐标可求得抛物线的解析式，则可求得D 点坐标，利用待定系数法可求得直线BD 解析式；（2）设出P 点坐标，从而可表示出PM 的长度，利用二次函数的性质可求得其最大值；（3）过Q 作QG∥y 轴，交BD 于点G ，过Q 和QH⊥BD 于H ，可设出Q 点坐标，表示出QG 的长度，由条件可证得△DHG 为等腰直角三角形，则可得到关于Q 点坐标的方程，可求得Q 点坐标．4.【答案】（1）解：将A ，B ，C 点的坐标代入解析式，得 {9k −3k +k =04k −2k +k =3k =3 ，解得 {k =−1k =−2k =3，抛物线的解析式为y=﹣x 2﹣2x+3（2）解：配方，得y=﹣（x+1）2+4，顶点D 的坐标为（﹣1，4）作B 点关于直线x=1的对称点B′，如图1，则B′（4，3），由（1）得D （﹣1，4），可求出直线DB′的函数关系式为y=﹣ 15 x+ 195，当M （1，m ）在直线DN′上时，MN+MD 的值最小，则m=﹣ 15 ×1+ 195 = 185．（3）解：作PE⊥x 轴交AC 于E 点，如图2，AC的解析式为y=x+3，设P（m，﹣m2﹣2m+3），E（m，m+3），PE=﹣m2﹣2m+3﹣（m+3）=﹣m2﹣3mS△APC= 12PE•|x A|= 12（﹣m2﹣3m）×3=﹣32（m+ 32）2+ 278，当m=﹣32时，△APC的面积的最大值是278（4）解：由（1）、（2）得D（﹣1，4），N（﹣1，2）点E在直线AC上，设E（x，x+3），①当点E在线段AC上时，点F在点E上方，则F（x，﹣x2﹣2x+3），∵EF=DN∴﹣x2﹣2x+3﹣（x+3）=4﹣2=2，解得，x=﹣2或x=﹣1（舍去），则点E的坐标为：（﹣2，1）．②当点E在线段AC（或CA）延长线上时，点F在点E下方，则F（x，﹣x2﹣2x+3），∵EF=DN，∴（x+3）﹣（﹣x2﹣2x+3）=2，解得x= −3+√172或x= −3−√172，即点E的坐标为：（−3+√172，3+√172）或（−3−√172，3−√172）综上可得满足条件的点E为E（﹣2，1）或：（−3+√172，3+√172）或（−3−√172，3−√172）【考点】二次函数的性质，待定系数法求二次函数解析式，二次函数的应用，三角形的面积，轴对称-最短路线问题【解析】【分析】（1）根据待定系数法，可得答案.（2）利用轴对称求最短路径的知识，找到B点关于直线x=1的对称点B′，连接B′D，B′D与直线x=1的交点即是点M的位置，继而求出m的值.（3）根据平行于y轴的直线上两点间的距离最大的纵坐标减去较小的纵坐标，可得PE的长，根据三角形的面积，可得二次函数，根据二次函数的性质，可得答案.（4）设出点E的坐标，分情况讨论；①当点E再线段AC上时，点F在点E上方；②当点E再线段AC（或CA）延长线上时，点F在点E下方，根据平行四边形的性质，可得关于x的方程，继而求出点E的坐标.5.【答案】（1）解：设抛物线的函数解析式为y=ax2+bx+c．∵点A（1，0），点B（﹣3，0），点C（0，√3）在抛物线上，∴ {k+k+k=09k−3k+k=0k=√3，解得{k=−√33k=−2√33k=√3，∴抛物线的函数解析式为y=﹣√33x2﹣2√33x+ √3（2）解：DG=DE．理由如下：设直线l1的解析式为y=k1x+b1，将A（1，0），C（0，√3）代入，解得y=﹣√3x+ √3；设直线l2的解析式为y=k2x+b2，将B（﹣3，0），C（0，√3）代入，解得y= √33x+ √3；∵抛物线与x轴的交点为A（1，0），B（﹣3，0），∴抛物线的对称轴为直线x=﹣1，又∵点G、D、E均在对称轴上，∴G（﹣1，2 √3），D（﹣1，4√33），E（﹣1，2√33），∴DG=2 √3﹣4√33= 2√33，DE= 4√33﹣2√33= 2√33，∴DG=DE；（3）解：若直线l2绕点C旋转时，与抛物线的另一个交点为M，当△MCG为等腰三角形时，分三种情况：①以G为圆心，GC为半径画弧交抛物线于点M1、C，点M1与C关于抛物线的对称轴对称，则M1的坐标为（﹣2，√3）；②以C为圆心，GC为半径画弧交抛物线于点M2、M3，点M2与点A重合，点A、C、G在一条直线上，不能构成三角形，M3与M1重合；③作线段GC的垂直平分线，交抛物线于点M4、M5，点M4与点D重合，点D的坐标为（﹣1，4√33），M5与M1重合；综上所述，满足条件的点M只有两个，其坐标分别为（﹣2，√3），（﹣1，4√33）．【考点】待定系数法求一次函数解析式，二次函数的性质，待定系数法求二次函数解析式，二次函数的应用，与二次函数有关的动态几何问题【解析】【分析】（1）设抛物线的函数解析式为y=ax2+bx+c．分别将A（1，0），B（﹣3，0），C（0，√3）三点坐标代入得到一个三元一次方程组，解之即可得到抛物线解析式.（2）DG=DE．分别求出过A（1，0），C（0，3 ）两点的直线l1的解析式为y=﹣√3x+ √3；过B（﹣3，0），C（0，3 ）两点的直线l2的解析式为y= √33x+ √3；由二次函数的性质和已知条件求出DG和DE的长度即可.（3）若直线l2绕点C旋转时，与抛物线的另一个交点为M，当△MCG为等腰三角形时，分三种情况：①以G为圆心，GC为半径画弧交抛物线于点M1（﹣2，√3）；②以C为圆心，GC为半径画弧交抛物线于点M2、M3，；③作线段GC的垂直平分线，交抛物线于点M4、M5.6.【答案】（1）解：依题意得： {−k2k=−1k +k +k =0k =3，解之得： {k =−1k =−2k =3∴抛物线解析式为y=-x 2-2x+3∵对称轴为x=-1，且抛物线经过A （1，0）， ∴把B （-3，0）、C （0，3）分别代入直线y=mx+n ，得 {−3k +k =0k =3，解之得： {k =1k =3，∴直线y=mx+n 的解析式为y=x+3（2）解：设直线BC 与对称轴x=-1的交点为M ，则此时MA+MC 的值最小．把x=-1代入直线y=x+3得，y=2， ∴M（-1，2），即当点M 到点A 的距离与到点C 的距离之和最小时M 的坐标为（-1，2）（3）解：如图：设P （-1，t ），又∵B（-3，0），C （0，3），∴BC 2=18，PB 2=（-1+3）2+t 2=4+t 2 ， PC 2=（-1）2+（t-3）2=t 2-6t+10， ①若点B 为直角顶点，则BC 2+PB 2=PC 2 即：18+4+t 2=t 2-6t+10解之得：t=-2； ②若点C 为直角顶点，则BC 2+PC 2=PB 2即：18+t 2-6t+10=4+t 2解之得：t=4， ③若点P 为直角顶点，则PB 2+PC 2=BC 2即：4+t 2+t 2-6t+10=18解之得：t 1= 3+√172，t 2= 3−√172；综上所述P 的坐标为（-1，-2）或（-1，4）或（-1， 3+√172）或（-1，3−√172）．【考点】二次函数的应用，二次函数的实际应用-动态几何问题【解析】【分析】先把点A ，C 的坐标分别代入抛物线解析式得到a 和b ，c 的关系式，再根据抛物线的对称轴方程可得a 和b 的关系，再联立得到方程组，解方程组，求出a ，b ，c 的值即可得到抛物线解析式；把B 、C 两点的坐标代入直线y=mx+n ，解方程组求出m 和n 的值即可得到直线解析式；设直线BC 与对称轴x=-1的交点为M ，则此时MA+MC 的值最小．把x=-1代入直线y=x+3得y 的值，即可求出点M 坐标；设P （-1，t ），又因为B （-3，0），C （0，3），所以可得BC 2=18，PB 2=（-1+3）2+t 2=4+t 2 ， PC 2=（-1）2+（t-3）2=t 2-6t+10，再分三种情况分别讨论求出符合题意t 值即可求出点P 的坐标．7.【答案】（1）解：设抛物线解析式为y=a （x+1）（x ﹣3），把C （0，3）代入得a•1•（﹣3）=3，解得a=﹣1，所以抛物线解析式为y=﹣（x+1）（x ﹣3），即y=﹣x 2+2x+3 （2）解：设直线BC 的解析式为y=kx+m ，把B （3，0），C （0，3）代入得 {3k +k =0k =3 ，解得 {k =−1k =3，所以直线BC 的解析式为y=﹣x+3，作PM∥y 轴交BC 于M ，如图1，设P （x ，﹣x 2+2x+3），（0＜x ＜3），则M （x ，﹣x+3），∴PM=﹣x2+2x+3﹣（﹣x+3）=﹣x2+3x，∴S△PCB= 12•3•PM=﹣32x2+ 92=﹣32（x﹣32）2+ 278，当x= 32时，△BCP的面积最大，此时P点坐标为（32，154）（3）解：如图2，抛物线的对称轴为直线x=1，当四边形BCDQ为平行四边形，设D（1，a），则Q（4，a﹣3），把Q（4，a﹣3）代入y=﹣x2+2x+3得a﹣3=﹣16+8+3，解得a=﹣2，∴Q（4，﹣5）；当四边形BCQD为平行四边形时，设D（1，a），则Q（﹣2，3+a），把Q（﹣2，3+a）代入y=﹣x2+2x+3得3+a=﹣4﹣4+3，解得a=﹣8，∴Q（﹣2，﹣5）；当四边形BQCD为平行四边形时，设D（1，a），则Q（2，3﹣a），把Q（2，3﹣a）代入y=﹣x2+2x+3得3﹣a=﹣4+4+3，解得a=0，∴Q（2，3），综上所述，满足条件的Q点坐标为（4，﹣5）或（﹣2，﹣5）或（2，3）．【考点】二次函数的应用，与二次函数有关的动态几何问题【解析】【分析】（1）设交点式y=a（x+1）（x﹣3），然后把C点坐标代入求出a的值即可得到抛物线的解析式；（2）先利用待定系数法求出直线BC的解析式为y=﹣x+3，作PM∥y轴交BC于M，如图1，设P（x，﹣x2+2x+3），（0＜x＜3），则M（x，﹣x+3），利用三角形面积公式得到∴S△PCB= 12•3•PM=﹣32x2+ 92，然后根据二次函数的性质求解；（3）如图2，分类讨论：当四边形BCDQ为平行四边形，设D（1，a），利用点平移的坐标规律得到Q （4，a﹣3），然后把Q（4，a﹣3）代入y=﹣x2+2x+3中求出a即可得到Q点坐标；当四边形BCQD为平行四边形或四边形BQCD为平行四边形时，利用同样方法可求出对应Q点坐标．8.【答案】（1）解：由y=ax2+bx﹣3得C（0．﹣3），∴OC=3，∵OC=3OB，∴OB=1，∴B（﹣1，0），把A（2，﹣3），B（﹣1，0）代入y=ax2+bx﹣3得{4k+2k−3=−3k−k−3=0，∴ {k=1k=−2，∴抛物线的解析式为y=x2﹣2x﹣3（2）解：设连接AC，作BF⊥AC交AC的延长线于F，∵A（2，﹣3），C（0，﹣3），∴AF∥x轴，∴F（﹣1，﹣3），∴BF=3，AF=3，∴∠BAC=45°，设D（0，m），则OD=|m|，∵∠BDO=∠BAC，∴∠BDO=45°，∴OD=OB=1，∴|m|=1，∴m=±1，∴D1（0，1），D2（0，﹣1）（3）解：设M（a，a2﹣2a﹣3），N（1，n），①以AB为边，则AB∥MN，AB=MN，如图2，过M作ME⊥对称轴y于E，AF⊥x轴于F，则△ABF≌△NME，∴NE=AF=3，ME=BF=3，∴|a﹣1|=3，∴a=3或a=﹣2，∴M（4，5）或（﹣2，11）；②以AB为对角线，BN=AM，BN∥AM，如图3，则N在x轴上，M与C重合，∴M（0，﹣3），综上所述，存在以点A，B，M，N为顶点的四边形是平行四边形，M（4，5）或（﹣2，11）或（0，﹣3）．【考点】二次函数的图象，二次函数的性质，二次函数的应用【解析】【分析】（1）待定系数法即可得到结论；（2）连接AC，作BF⊥AC 交AC的延长线于F，根据已知条件得到AF∥x轴，得到F（﹣1，﹣3），设D （0，m），则OD=|m|即可得到结论；（3）设M（a，a2﹣2a﹣3），N（1，n），①以AB为边，则AB∥MN，AB=MN，如图2，过M作ME⊥对称轴y于E，AF⊥x轴于F，于是得到△ABF≌△NME，证得NE=AF=3，ME=BF=3，得到M（4，5）或（﹣2，11）；②以AB为对角线，BN=AM，BN∥AM，如图3，则N在x轴上，M与C重合，于是得到结论．。

(完整版)二次函数中的存在性问题(答案)

二次函数中的存在性问题姓名1 .已知抛物线y=-jx2等X-3与x轴交于A, B两点，与y轴交于点C.在直线CA上方的抛物线上是否存在一点D,使得4ACD 的面积最大？若存在，求出点D的坐标；若不存在，请说明理由.2.已知y=ax2+bx+c (a加)图象与直线y=kx+4相交于A (1, m) , B (4, 8)两点，与x轴交于原点及点C. (1)求直线和抛物线解析式；(2)在x轴上方的抛物线上是否存在点D,使S AOCD=2S AOAB?如果存在，求出点D坐标，如果不存在，说明理由.3 .已知直线y==x-3与x轴交于点A ,与y轴交于点C,抛物线y= --^x2+mx+n经过点A和点C.(1)求此抛物线的解析式；(2)在直线CA上方的抛物线上是否存在点D,使得4ACD的面积最大？若存在，求出点D的坐标；若不存在,4 .在平面直角坐标系xOy中，抛物线y= - x2+bx+c与x轴交于A、B两点(点A在点B的左侧)，过点A的直线y=kx+1交抛物线于点 C (2, 3).(1)求直线AC及抛物线的解析式；(2)若直线y=kx+1与抛物线的对称轴交于点E,以点E为中心将直线y=kx+1顺时针旋转90彳导到直线1,设直线1与y轴的交点为P,求△ APE的面积；(3)若G为抛物线上一点，是否存在x轴上的点F,使以B、E、F、G为顶点的四边形为平行四边形？若存在，直接写出点F的坐标；若不存在，请说明理由.5 .如图，在平面直角坐标系中，抛物线广2交x轴于A, B两点(A 在B的左侧)，交y轴于点C.(1)求直线BC的解析式；(2)求抛物线的顶点及对称轴；(3)若点Q是抛物线对称轴上的一动点，说明理由；(4)若点P是直线BC上方的一个动点, 的面积；若不存在，说明理由.线段AQ+CQ是否存在最小值？若存在,△ PBC的面积是否存在最大值？若存在,求出点Q的坐标；若不存在,求出点P的坐标及此时4PBC1 .已知抛物线y=—:\2+匪x ― 3与x轴交于A , B两点，2 .与y轴交于点C.在直线CA上方的抛物线上是否存在3 . 一点D,使得4ACD的面积最大？若存在，求出点D4 .的坐标；若不存在，请说明理由.牛目, 解：对于抛物线y= - -x2+—x - 3,4 4令y=0 ,得到--x2+i^x- 3=0, [4 4解得：x=1或x=4 ,B (1, 0), A (4, 0),令x=0,得至ij y= - 3,即 C (0, - 3), 设直线AC解析式为y=kx+b ,将A与C坐标代入得：]业上0 , 1b=-3解得：k=工，b= - 3,4・•・直线AC解析式为y=Wx-3,4设平行于直线AC,且与抛物线只有一个交点的直线方程为y/x+m,4此时直线与抛物线交于点D,使得4ACD的面积最大，与二次函数解析式联立消去y得：-总x2+"x - 3=^x+m ,4 4 4整理得：3x2- 12x+4m+12=0 ,A=144 - 12 (4m+12) =0,解得：m=0,，此时直线万程为y=^x,点D坐标为(2,―).4 42. (2008?宁波校级自主招生)已知y=ax2+bx+c (a沟)图象与直线y=kx+4相交于A (1, m), B (4, 8)两点, 与x轴交于原点及点 C.(1)求直线和抛物线解析式；(2)在x轴上方的抛物线上是否存在点D,使S AOCD=2S AOAB?如果存在，求出点D坐标，如果不存在，说明理由.解答：解：(1) 丁直线y=kx+4 过 A (1, m), B (4, 8)两点,金-Iy= - x2+6x；(2)存在.设D点纵坐标为h (h>0),由O (0, 0), A (1, 5), B (4, 8),可知S AOAB=6,把O、A、B三点坐标代入抛物线解析式，得c=0S A OCD =2S AOAB =12, —>6><h=12,解得 h=4, 2由-x 2+6x=4 ,得 x=3 父 5,•••D (3+、闻 4)或(3-V5, 4).3. (2014春？昌平区期末)已知直线 y=Cx-3与x 轴交于点A,与y 轴交于点4点A 和点C.(1)求此抛物线的解析式；(2)在直线CA 上方的抛物线上是否存在点 D,使得4ACD 的面积最大？若存在，求出点 D 的坐标；若不存在，说明理由.—3得y= - 3,则C 点坐标为(0, — 3), -3=0,解得x=4 ,则A 点坐标为(4, 0),把 A (4, 0), C (0, - 3)代入 y=--？x 2+mx+n 得4k=-7,即 y=—x+b ,4 412x+4b+12=0 ,.・・△=122-4MX (4b+12) =0,解得 b=0, 3x 2 - 12x+12=0 ,解得 x 1=x 2=2, 把 x=2 , b=0 代入 y=—x+b 得 y=—,4 2D 点坐标为(2, -1).4. (2010?孝感模拟)在平面直角坐标系 xOy 中，抛物线y= - x 2+bx+c 与x 轴交于A 、B 两点(点A 在点B 的左侧)，过点A 的直线y=kx+1交抛物线于点 C (2, 3).(1)求直线AC 及抛物线的解析式； (2)若直线y=kx+1与抛物线的对称轴交于点 E,以点E 为中心将直线y=kx+1顺时针旋转90彳导到直线1,设直线l 与y 轴的交点为P,求△ APE 的面积；解答:解得15n= - 3所以二次函数解析式为 y=- ±x 2+¥x - 3;4 4(2)存在.过D 点作直线AC 的平行线y=kx+b ,当直线y=kx+b 与抛物线只有一个公共点时，点大，此时4ACD 的面积最大， D 到AC 的距离最直线AC 的解析式为y3 「x — 3,4由直线y=—x+b 和抛物线y=-x - 3组成方程组得y=-/+b厂「¥苧一3,消去y 得至iJ 3x 2-解：(1)把x=0代入把 y=0 代入 y=-^x —3 4经过(3)若G 为抛物线上一点，是否存在 x 轴上的点F,使以B 、E 、F 、G 为顶点的四边形为平行四边形？若存在, 直接写出点F 的坐标；若不存在，请说明理由. 解答：解：(1) 丁点C (2, 3)在直线y=kx+1上,，2k+1=3 .解得k=1.直线AC 的解析式为y=x+1 . •・•点A 在x 轴上，A (T, 0).,「抛物线 y= -x 2+bx+c 过点 A 、C,I - 4f2b+c=3解得抛物线的解析式为 y= - x 2+2x+3 . (2)由 y= - x 2+2x+3= - (x-1)2+4, 可得抛物线的对称轴为 x=1, B (3, 0). • . E (1, 2).根据题意，知点 A 旋转到点B 处，直线l 过点B 、E. 设直线l 的解析式为y=mx+n . 将B 、E 的坐标代入y=mx+n 中，联立可得m= - 1, n=3. 直线l 的解析式为y= - x+3. P (0, 3).过点E 作ED^x 轴于点D.••• S APA E=S APAB - S AEAB =±AB ?PO -4AB?ED=± MX (3-2) =2.2 2 2(3)存在，点F 的坐标分别为(3-死，0), (3+,万，0), (- 1-右，0) (- 1+/6, 0).在B 的左侧)，交y 轴于点C.(1)求直线BC 的解析式； (2)求抛物线的顶点及对称轴；5. (2013秋?红安县校级月考)如图，在平面直角坐标系中，抛物线 y=+4工十2交x 轴于A , B 两点(A考点：二次函数综合题. 专题：压轴题.分析：(1)令y=0,解关于x 的一元二次方程求出点 B 的坐标，令x=0求出点C 的坐标，设直线 BC 的解析式为y=kx+b ,然后利用待定系数法求一次函数解析式解答即可；(2)把二次函数解析式整理成顶点式形式，然后写出顶点坐标与对称轴即可；(3)根据轴对称确定最短路线问题，直线 BC 与对称轴的交点即为使线段 AQ+CQ 最小的点Q,然后利用直线解析式求解即可；(4)过点P 作PD// y 轴与BC 相交于点D,根据抛物线解析式与直线BC 的解析式表示出 PD,再根据S APBC =S APCD +S APBD 列式整理，然后利用二次函数最值问题解答. 解答：解：(1)令 y=0,贝u― -^x 2+4x+2=0 ,3 3整理得，x 2 - 2x - 3=0 , 解得 x i = - 1, x 2=3,所以，点B 的坐标为(3, 0), 令 x=0 ,则 y=2,所以，点C 的坐标为(0, 2),设直线BC 的解析式为y=kx+b ,则｛:"仁。

二次函数的存在性问题(Word版解析+答案)

中考压轴题解析二次函数的存在性问题【典例分析】【考点1】二次函数与相似三角形问题【例1】已知抛物线23y ax bx =++与x 轴分别交于(3,0)A -，(1,0)B 两点，与y 轴交于点C ．（1）求抛物线的表达式及顶点D 的坐标；（2）点F 是线段AD 上一个动点． ①如图1，设AF k AD =，当k 为何值时，2CF AD =1. ②如图2，以A ，F ，O 为顶点的三角形是否与ABC ∆相似？若相似，求出点F 的坐标；若不相似，请说明理由．【变式1-1】如图，抛物线2y 2ax x c =++经过(1,0)A -，B 两点，且与y 轴交于点(0,3)C ，抛物线与直线1y x =--交于A ，E 两点．（1）求抛物线的解析式；（2）坐标轴上是否存在一点Q ，使得AQE ∆是以AE 为底边的等腰三角形？若存在，请直接写出点Q 的坐标；若不存在，说明理由．（3）P 点在x 轴上且位于点B 的左侧，若以P ，B ，C 为顶点的三角形与ABE ∆相似，求点P 的坐标．【变式1-2】如图，已知抛物线1(2)()y x x m m=-+-(m ＞0)与x 轴相交于点A ，B ，与y 轴相交于点C ，且点A 在点B 的左侧.（1）若抛物线过点（2，2），求抛物线的解析式；（2）在（1）的条件下，抛物线的对称轴上是否存在一点H ，使AH+CH 的值最小，若存在，求出点H 的坐标；若不存在，请说明理由；（3）在第四象限内，抛物线上是否存在点M ，使得以点A ，B ，M 为顶点的三角形与△ACB 相似？若存在，求出m 的值；若不存在，请说明理由.【考点2】二次函数与直角三角形问题【例2】如图，抛物线()20y ax bx c a =++≠的顶点坐标为()2,1-，图象与y 轴交于点()0,3C ，与x 轴交于A 、B 两点．()1求抛物线的解析式；()2设抛物线对称轴与直线BC 交于点D ，连接AC 、AD ，求ACD 的面积；()3点E 为直线BC 上的任意一点，过点E 作x 轴的垂线与抛物线交于点F ，问是否存在点E 使DEF 为直角三角形？若存在，求出点E 坐标，若不存在，请说明理由．【变式2-1】如图，经过x 轴上(10)(30)A B -，，，两点的抛物线2(1)4y m x m =--（0m <）交y 轴于点C ，设抛物线的顶点为D ，若以DB 为直径的⊙G 经过点C ，求解下列问题：，的坐标；（1）用含m的代数式表示出C D（2）求抛物线的解析式；△为直角三角形？如能，求出Q点的坐标，若不能，请说明理（3）能否在抛物线上找到一点Q，使BDQ由。

二次函数存在性问题(一题多问)

【原题】已知，如图1，经过点A （－3，0）的抛物线2y ax bx c =++与x 轴相交于点B （-2，-2）及原点O ．点D 是抛物线第二象限图像上的一点，AH ⊥x 轴与H 点，且tan ∠DAH =4．【问题】（1）求点D 坐标及抛物线的解析式；（2）在线段OB 下方的抛物线上有一点M ，当△MOB 的面积最大时，求点M 的坐标，并求出最大面积．A 图1xyH BDOA xyBDO（3）在（2）的条件下，抛物线上是否存在点N （不与M 重合），使得S △OBN =S △OBM ，若存在，求出N 点坐标；若不存在，请说明理由．变式练习：抛物线上是否存在点N ，使得S △OBN =14S △OBD ．（4）连接BD ，取BD 中点F ，在抛物线的对称轴上是否存在一点Q ，使得QF +QD 的值最小，求出点Q 坐标，并求出QF +QD 的最小值．变式练习：①连接BD ，取BD 中点F ，点R 、S 分别是x 轴、y 轴上的动点，当四边形DFRS 的周长最小时，求出R 、S 的坐标，并求出四边形DFRS 周长的最小值．②连接BD ，在x 轴上是否存在一点Q ，使得∣QD -QB ∣的值最大，若存在，求出点Q 坐标，并求出最大值；若不存在，请说明理由．③连接AD ，点M 、N 分别是线段OD 、AD 上的动点，连接AM ，MN ，当AM +MN 的值最小时，求出点N 的坐标．④将线段OB 向左移动m 个单位长度，得到线段O ′B ′连接O ′D 、B ′D ，是否存在这样的m ，使得O ′D +B ′D 的值最小？若存在，求出m 的值；若不存在，请说明理由．⑤已知P （0，a ）、Q （0，a +3）是y 轴上的两个动点，当四边形BDQP 的周长最小时，求a 的值．A xyBDOA xyBDO（5）在（4）的条件下，点G 是线段OD 上的动点，当△DFG 是等腰三角形时，求点G的坐标．（6）在（4）的条件下，点G 是线段OD 上的动点，把△BFG 沿着线段FG 翻折，是否存在这样的点G ,使△BFG 与△DFG 的重叠部分的面积等于△BDG 的14，若存在，求出DG 的长；若不存在，请说明理由．（7）若点K 在抛物线上，点L 在抛物线的对称轴上，且A 、O 、K 、L 为顶点的四边形是平行四边形，求点K 的坐标；A xyBDOA xyBDOA xyBDO变式练习：若点K 在抛物线上，点L 在x 轴上，且A 、B 、K 、L 为顶点的四边形是平行四边形，求点K 的坐标．（若求L 的坐标呢？）（8）若点U 是抛物线对称轴上一点，当△ADU 是Rt △时，求点U 的坐标．A xyBDOA xyBDO（9）连接BD ，点N 是直线BD 上的一点，在y 轴的正半轴，是否存在一点M ，使得∠MNO =45°，且存在唯一的N 点，若存在，求出M 点坐标；若不存在，请说明理由．变式训练：连接BD ，把△OBD 沿着OD 翻折，使得点B 落在第一象限的点B ˊ处，点P从点D 出发向点B 作匀速运动，点Q 从点B ˊ出发向点D 作匀速运动，两点同时出发，速度均为每秒一个单位长度，连接OP ，OQ ，当时间t 为多少秒时，PO 平分∠BPQ 的同时，QO 平分∠PQ B ˊ？A xyBDOA xyBDOB ˊ（10）P 是抛物线上的第一象限内的动点，过点P 作PT ⊥x 轴，垂足为T ，是否存在点P ，使得以P 、T 、A 为顶点的三角形△BOD 相似？若存在，求出点P 的坐标；若不存在，请说明理由．变式练习：P 是抛物线上的一点，过点P 作PT ⊥x 轴，垂足为T ，过点B 作BI ⊥x 轴，垂足为I ，是否存在点P ，使得以P 、T 、A 为顶点的三角形△ABI 相似？若存在，求出点P 的坐标；若不存在，请说明理由．（11）若点C 在抛物线上，且∠CDO ＝∠BDO ，试探究：在（2）的条件下，是否存在点G ，使得△GOD ∽△COB ？若存在，请求出所有满足条件的点G 坐标；若不存在，请说明理由．I A xyBDOCA xyBDO。

二次函数存在性问题(菱形、平行四边形、矩形)

今天讲解二次函数背景下的四边形存在性问题．这里的四边形存在性问题，一般是以几种特殊的四边形为主，常考察的有平行四边形、菱形、矩形、正方形．当然，三角形的存在性问题和四边形的存在性问题是一样，如等腰三角形实际上和菱形是一致的，直角三角形和矩形是一样的，等腰直角三角形和正方形是一致的．本文我们将重点讲解这类问题的求解逻辑以及注意事项，同时给大家理出一个比较通用的解题模板．1如图，抛物线y = ax 2 + bx + 3 交x 轴于点A (−1, 0) 和点B (3, 0) ，与 y 轴交于点C ，连接BC ，交对称轴于点D ．(1) 求抛物线的解析式；(2)点 P 是直线BC 上方的抛物线上点，连接PC ，PD ．求 △PCD 的面积的最大值以及此时点P 的坐标；(3)将抛物线y = ax 2 + bx + 3 向右平移 1 个单位得到新抛物线，新抛物线与原抛物线交于点E ，点F 是新抛物线的对称轴上的一点，点 G 是坐标平面内一点．当以D 、E 、F 、 G 四点为顶点的四边形是菱形时，直接写出点F 的坐标，并写出求解其中一个点F 的坐标的过程．前两小问就不详说了，直接上结论，抛物线解析式为y = −x 2 + 2x + 3 ；点 P | , | ．( 3 15 )\2 4 )第 3 小问为菱形存在性问题，以D 、E 、F 、 G 四点为顶点的四边形是菱形．四个点中， D ， E 是定点，F 是平移后新抛物线对称轴上的动点，由于点F 的横坐标是确定的，只有纵坐标在变化，我们可以称其为“G 如果只需要点F 的坐标，那么没有必要求解平移后抛物线的解析式．根据平移的性质，将原抛物线向右平移 1 个单位长度，那么原抛物线的对称轴也向右平移 1 个单位长度，因此新抛物线的对称轴为x = 2 ，几 F (2, m ) ．但由于此时E 为量抛物线的交点，因此还是要把平移后的抛物线解析式求出来，根据“左加右减”，平移后的抛物线解析式为y = − (x −1)2+ 2(x −1) + 3 = −x 2 + 4x ，联立两抛物(|y = −x 2 + 2x + 3 ( 3 15 ) 线〈|ly = −x 2 + 4x ，解得E |\2 , 4 )| ．菱形的探究相对是比较简单的，对于这类探究性问题，一般都是先从确定的信息入手．菱形是以D 、E 、F 、 G 为顶点，其中DE 为定线段，那么存在的可能有DE 是一条边，也可能是一条对对角线．前面提到，等腰三角形和菱形的分析是一致的，这里我们结合等腰三角形的存在性问题一起分析．由于 G 是“自由点”，可以随机应变，因此讨论以D 、E 、F 为顶点的三角形是等腰三角形．同样，由于定线段DE 可能是等腰三角形的一条腰，也可能是底边．当DE 为一条腰时，第一种情形是点D 为顶点，即DE = DF ，也即半动点F 到D 的距离和E 到D 的距离相等，因此点F 在以点D 为圆心， DE 为半径的圆上，作出该圆，如图 1 所示，可知此时圆与新抛物线的对称轴有两个交点F 1 ，F 2 ，结合图象可以判断，此时两个点应该都是满足的．那么再加上对应的“自由点” G ，就是以DE 为边菱形了．当DE 为一条腰时，另一种情形是点E 为顶点，即ED = EF ，也即半动点F 到E 的距离和D 到E 的距离相等，因此点F 在以点E 为圆心， ED 为半径的圆上，作出该圆，如图 2 所示，可知此时圆与新抛物线的对称轴同样有两个交点F 1 ，F 2 ，结合图象，此时的F 3 存在和DE 共线的风险，因此后续需要检验一下．根据坐标可以知道，x E =，通常像这类圆心可能为两个点中点的，一般都要留个心眼，检验一下．此时再加上对应的“自由点” G ，也是以DE 为边菱形．当DE 为底边时，则F 为顶点，即FD = FE ，即 F 到线段DE 的两端点的距离相等，可知此时F 在线段DE 的垂直平分线上，作出线段DE 的垂直平分线，如图 3 所示，可知此时有一个交点F 5 ．加上对应的“自由点” G ，此时便是以DE 为对角线的菱形．对于等腰三角形和菱形的存在性问题，如上图情形，我们称其为“两圆一线”法．由于这类题一般不需要书写完整过程，因此在解题过程中，把准备工作做好，即对应的点坐标，解析式等先求出来，动点坐标假设好，再把定线段DE ，半定线段DF 、EF 长度表示出来．根据上述分析，结合“两圆一线”分别使得三条线段两两相等建立方程，即DE = DF ，DE = EF ，DF = EF ，求解出动点坐标即可．(实际解题过程中，一般使用线段平方的形式．此外，只需关注下方解析中公式计算部分即可，文字叙述部分可忽略)此题还是比较友善的，只需求出F 坐标．如果需要求解点G 的坐标，则还要加一个步骤．这里以DEG 1F 1 为例，若要求 G 1 坐标，一般有两种比较常用的思路．一是利用菱形的对边平行且相等，即F 1G 1 可以看成是DE 平移得来的，那么点D → F 1 的平移变化也即点E → G 1 的平移变化．二是利用菱形的对角线相互平分，因此EF 1 的中点也即DG 1 的中点，利用中点坐标求解出 G 1 坐标．这两种处理在平行四边形存在性问题中也是有力手段．(|y = −x 2 + 2x + 3 ( 3 15 ) 149 ( 149 )由题， y = −x 2 + 2x + 3 向右平移 1 个单位得到新抛物线y = − (x −1)2+ 2(x −1) + 3 = −x 2 + 4x ，联立〈|ly = −x 2 + 4x ，解得 E |\2 , 4 )| ，新抛物线的对称轴为x = 2 ，设 F (2, m ) ，由于 D (1, 2) ，则DE 2 =，EF 2 = + m −2= m 2 − m +，DF 2 = 1+ (m − 2)2= m 2 − 4m + 5 ，①当DE 、DF 为一组邻边时，则 DE 2 = DF 2 ，即 = m 2 − 4m + 5 ，37 ( ) ( )②当ED 、EF 为一组邻边时，则 ED 2 = EF 2 ，即 = m 2 − m + ，16 8 16 11 ( 11)③当EF 为对角线时，则FD = FE ，即 m 2 − m + = m 2 − 4m + 5 ， 2 16解得m = ，此时 F 的坐标为|2, | ；( ) ( ) ( 149 )( 11) 当F |2, |时， y F + y D = 2y E ，x D + x F = 2x E ，即 E 为D 、F 中点，不合题意，舍去； 15 229 \ 2 )综上， F 点的坐标为||\2, 2 + 4 )|| 或||\2, 2 − 4 )|| 或(2, 2) 或|\2, 56 )| ． 56 \ 56 )解得m = 2 或m = ，此时F 的坐标为(2, 2) 或|2, | ，2 \ 2 )解得m = 2 土 4 ，此时 F 的坐标为||\2, 2 + 4 )|| 或||\2, 2 − 4 )|| ；53 15 2291 ．已知二次函数y = ax2 + bx − 2(a 丰 0)与x 轴交于A ( −, 0) ，B (4, 0) ，与 y 轴交于点C ．(1) 求抛物线的解析式；(2) 连接AC ，BC ，点 P 是直线BC 下方抛物线上一点，过 P 作PD ∥AC 交直线BC 于点D ，PE ∥x 轴交直线BC 于点， E ，求△PDE 面积的最大值及此时点， P 的坐标；(3) 在(2)的条件下，将原抛物线沿x 轴向左平移3个单位得到新抛物线，点 M 是新抛物线对称轴上一点，点 N 是平面直角坐标系内一点，当以点M 、 N 、P 、B 为顶点的四边形为菱形时，请直接写出所有符合条件的N 点的坐标；并任选其中一个N 点，写出求解过程．立〈y= − 2 x 2 + 4x − 2 ，解得D 7 , 11 ．1-1如图 1，抛物线y = ax 2 + bx + 4 交x 轴于A (−2, 0) ，B (4, 0) 两点，与y 轴交于点C ，连接 AC ， BC ．(1) 求抛物线的解析式；(2) P 是拋物线上位于直线BC 上方的一个动点，过点P 作PQ ∥y 轴交BC 于点Q ，过点P 作PE ⊥ BC 于点E ，过点 E 作EF ⊥ y 轴于点F ，求出2PQ + EF 的最大值及此时点P 的坐标；(3)如图 2，将抛物线y = ax 2 + bx + 4 沿着射线CB 的方向平移，使得新抛物线y ，过点(3,1) ，点D 为原抛物线y 与新抛物线y ，的交点，若点 G 为原抛物线的对称轴上一动点，点H 为新抛物线y ，上一动点，直接写出所有使得以 A ，D ， G ，H 为顶点的四边形为平行四边形的点H 的坐标，并把求其中一个点H 的坐标的过程写出来．抛物线解析式为y = − x 2 + x + 4 ；点 P | , | ．相当于是沿着射线BC 方向平移，故舍去，因此可得平移后抛物线的解析式为y = − x 2 + 4x − ．联2 2 ( 1 13 y = − x 2 + x +4 \2 8 )这类平行四边的探究也并不难，同样先从确定的信息入手．平行四边形是以A ，D ，G ，H 为顶点，其中AD 是定线段， G 是半动点，H 在新的抛物线上．和菱形的讨论一样，我们要考虑AD 是一条边的情形，也要考虑AD 是对角线的情形．当 AD 是一条边时，实际上此时也右两种情形，一是是平行四边形为ADHG ，也即AH ，DG 为对角线；另一种则是平行四边形为ADGH ，也即 AG ，DH 为对角线．当然，不管是那种情形，由于 AD 是一条边，根据平行四边形对边平行且相等的性质， GH 这条边可以看作是将AD 平移后得到1 (8 28 )2 \3 9 )第 3 小问中，抛物线沿着射线CB 方向平移，由于后续的点在新抛物线上，因此还是要求出平移后抛物线的解析式．这类沿着射线平移的，一般采用正交分解的形式平移，由点 C (0, 4) ，B (4, 0) 可知，沿着射线 CB 平移，即向右平移t 个单位，则向下也平移t 个单位，因此假设平移后新抛物线的解析式为y = − (x − t )2+ (x − t ) + 4 − t ，因为平移后经过点(3,1) ，代入可解得t = − 1 或t = 3 ，当 t = − 1 ， 1 13的，由于半动点 G 在原抛物线对称轴x = 1 上，那么点 G 有可能是点 A 平移后得到的，此时点H 就是点D 平移后得到的，如图 1 所示；同理，当点 G 是点D 平移后得到的，那么此时点H 就是点A 平移后得到的，如图 2 所示．设点 G (1, m )，根据平移的性质，结合点坐标的变化规律，当 A → G 时，即(−2, 0) —(1, m ) ，则有D|2 , 8 )| —H | 2 , 8 + m )| ，由于点H 在新抛物线上，且横坐标已知了，代入新抛物线即可 11 1 (13 213 13 13 (13 13 此外，除了用平移性质得到H 点的坐标外，此时 AH 是一条对角线，也利用对角线相互平分，则 A 、 H 的中点和 D 、 G 的中点是同一个，利用中点坐标则有 x A + x H = x D + x G ，故 13 13 13 (13 13 x H = x D + x G − x A = 2 ，将x = 2 代入新抛物线解析式，可求得H 点纵坐标y = − 8 ，故H | 2 , − 8 )|．当 AG 是一条对角线时，则有x A + x G = x D + x H ，故 x H = x A + x G − x D = − ，代入新抛物线解析 277 ( 9 277式，可求得此时H 的纵坐标为 − ，故H |− , − | ．8 2 8 ) 当 AD 是一条对角线时，则有x A + x D = x H + x G ，故 x H = x A + x D − x G = ，代入新抛物线解析式， 37 ( 1 37 可求得此时H 的纵坐标为 − ，故 H | , − | ．8 2 8 )同样地，在解题过程中，把准备工作做好，即对应的点坐标，解析式等先求出来，动点坐标假设好，将点坐标表示列出来(通常都是横坐标)，选定一个定点，如这里我们选定 x A ，将其与剩下三点横坐标x D 、x G 、x H 两两组合，建立中点坐标关系式，即x A + x D = x H + x G ，x A + x G = x D + x H 以及x A + x H = x D + x G ，求解出点H 横坐标，再代入解析式中求出点H 纵坐标即可．求得纵坐标 8 + m = − 2 | 2 )| + 4 2 − 2 = − 8 ，此时H | 2 , − 8 )| ． ( 7 11 (13 1113 (13 13)由题，设平移后的抛物线解析式为y = − (x − t )2+ (x − t ) + 4− t ，因为平移后经过点(3,1)，代入可解得t = − 1 (舍) 或t = 3 ，2 2联立〈y = − 2 x 2 + 4x − 2 ，解得 D 7 , 11 ， y = − x 2 + x + 4 \2 8 )则x A =−2 ，x D = ，x G = 1，设 H 点横坐标为x H ，①当AH 为一条对角线时，x A + x H = x D + x G ，则 x H = ，代入可求得此时H | , − | ； 9 ( 9 277 )1 (1 37 )综上， H 的坐标为| , − |或|− , − |或| , − | ．( 1 13 ③当AD 为一条对角线时，x A + x D = x H + x G ，则x H = ，代入可求得此时H | , − | ；(13 13) ( 9 277 ) (1 37 )2 \2 8 )\ 2 8 ) \ 2 8 ) \2 8 )②当AG 为一条对角线时，x A + x G = x D + x H ，则x H = − ，代入可求得此时H |− , − | ；2 \ 2 8 ) 2 \ 2 8 )故平移后抛物线的解析式为y = − x 2 + 4x − ，1 131．如图，在平面直角坐标系中，抛物线y= ax2 + bx+ 3(a 0) 与y轴交于点C，与x轴交于A，B两点(点A在点B的右侧)，且点A的坐标为( 3, 0) ，连接BC，过点A作AD∥BC交y轴于点D，OB= 3OA．(1) 求抛物线的解析式；(2) 如图1，点E为射线AD上一点，点P为第二象限内抛物线上一点，求四边形PBEC面积的最大值及此时点P的坐标；(3) 如图2，将原抛物线沿x轴正方向平移得到新抛物线y，y经过点C，平移后点A的对应点为点A，点N为线段AD的中点，点Q为新抛物线y的对称轴上一点，在新抛物线y上存在一点M，使以点M，Q，A，N为顶点的四边形为平行四边形，请直接写出点M的坐标，并选择一个你喜欢的点写出求解过程．2．如图，抛物线y= x2 + bx+ c与x轴相交于点A(−1, 0) 和点B，交y轴于点C，tan 三ACO= ．(1) 求抛物线的解析式；(2) 如图1 ，P点为一象限内抛物线上的一个动点，点D是BC中点，连接PD，BD，PB．求△BDP面积的最大值以及此时P点坐标；，M为新抛物线对称轴上(3) 如图2，将抛物线向左平移 1 个单位长度，得到新的抛物线y1一点，N为直线AC上一动点，在(2) 的条件下，是否存在点M，使得以点P、B、M、N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．| 4 21如图，已知抛物线y = ax 2 + bx − 4 与x 轴交于A ，B 两点，与y 轴交于点C ，且点A 的坐标为(−2, 0) ，直线BC 的解析式为y = x − 4 ．(1) 求抛物线的解析式；(2)如图 1，过点 A 作 AD ∥BC 交抛物线于点D (异于点 A )， P 是直线BC 下方抛物线上一点，过点P 作PQ ∥y 轴，交AD 于点Q ，过点 Q 作QR ⊥ BC 于点R ，连接PR ．求△PQR 面积的最大值及此时点P 的坐标；(3) 如图 2，点 C 关于x 轴的对称点为点C ，将抛物线沿射线 C A 的方向平移2个单位长度得到新的抛物线y ，新抛物线y 与原抛物线交于点M ，原抛物线的对称轴上有一动点 N ，平面直角坐标系内是否存在一点K ，使得以 D ，M ，N ，K 为顶点的四边形是矩形？若存在，请直接写出点K 的坐标；若不存在，请说明理由．抛物线解析式为y = x 2 − x − 4 ；S △PQR 的最大值为 9，点P (4, −6) ．第 3 小问中，抛物线沿着射线C A 方向平移，由于点M 为两抛物线交点，因此需求出平移后抛物线的解析式．根据A (−2, 0) ，C (0, 4) ，可知Rt △AOC 中AO : OC : AC = 1: 2 : ，因此将抛物线沿着射线C A 方向平移2个单位长度，则相当于向下平移 4 个单位长度，向左平移 2 个单位长度，因此平移后的抛物线为y = 1 (x + 2)2− 3 (x + 2) − 4 − 4 = 1 x 2 − 1 x −10 ，联立〈y = x 2 − x −10，解4 2 4 2y = x 2 − x − 4( 1得M (6, −4) ．又 BC : y = 1 x − 4 ，可知 AD : y = 1 x + 1，联立〈 y = 2 x + 1，解得D (10, 6) ．2 2 |y = 1 x 2 − 3x − 4因为以D ，M ，N ，K 为顶点的四边形是矩形，此时定线段是DM ，半动点为N ，自由点为K ．和前面讨论菱形、平行四边形时的流程基本大同小异，定线段DM 可能是矩形的边，也可能是矩形的对角线，因此要分两种情形讨论．矩形的存在性问题和直角三角形的存在性问题是一致的，如本题中，探究以D ，M ，N 为顶点的三角形是直角三角形．同样地，先以直角三角形为例，那么D ，M ，1 3 4 2在实际解题中设 K (x , y ) 即可)，利用中点关系〈 M K D N ，则〈 K，整理得N 均有可能为直角顶点．当M 为直角顶点时，过M 作DM 垂线与对称轴交点即为点N 所在位置，如图 1 所示．对于N 点坐标的求解，一方面，由于MN ⊥ DM ，则 k MN . k DM = − 1，结合点M 坐标，由此可求得直线MN 解析式，将其与对称轴方程联立即可求得点N 坐标．另一方面，可以构造如图所示的K 型相似，即构DH MH1 腰直角三角形，或者四边形中的正方形，那么可以构造此类的K 型全等求解．在此直角三角形的基础上，加上自由点K ，就变成矩形问题了．对于矩形问题，同样可以求出点N 坐标后，利用平移关系或者对角线的中点关系，求相应的点K 的坐标．当然，如果是探究矩形的存在性问题，也可以直接利用中点关系求得点K 的坐标．由点N (3, n )，设K (x K , y K ) (熟练后，(x + x = x + x (6 + x = 10 + 3 l y M + y K = y D + y N l−4 + y K = 6 + n 〈，再由对角线相等，即MK = DN ，代入即有1+ (y + 4)2= 49 + (16 − y )2，解得 y =，( 36 )同样适用．当D 为直角顶点时，三角形如图2 所示．同样，加上自由点K ，就变成矩形问题了．这里我们5 2 2 ( 44 )l y M + y N = y D + y K |y K = − \ 5 )对于直角三角形或矩形问题，如上图情形，我们可以称其为“两线一圆”．若只求点N 坐标，一般利用斜率关系，求出解析式后进一步求解．如果是矩形问题要求自由点的坐标，可以用对角线平分且相等，建立方程求解．当然，先求点N ，利用点N 作为台阶进一步求解也是没问题的，大家选用自己顺手的方法即可．造 △MN 1G ∽△DMH ，利用 = ，可求出长度，进而得到点 N 坐标．更特殊地，如果是等以垂线方式求解．由于k DM = 2 ，则 k DN = − 5 ，故此时DN : y = − 5 x + 10 ，令x = 3 ，可解得N |\3, 5 )| ，由中点可知，〈(x M + x N = x D + x K ，可解得〈(|x K = − 16 ，此时 K −1,− 6 ．l 5当N 为直角顶点时，则有NM ⊥ ND ，因此点N 在以DM 为直径的圆上．此种情形若只是求点N 坐标，策略比较多，一方面，可以利用斜率，由k ND . k NM= − 1求出点N 坐标；另一方面，可以利用线段长度求解，设DM 中点为为R ，则此时圆心为R ，因此NR = RD = DM ，由此也可求得点N 坐标，此外，还可以利用勾股定理ND 2 + NM 2 = DM 2 ．当加入自由点K ，变成矩形问题后，除了先求出点N 坐标，利用平移或中点求解点K 坐标外，也可以利用前面的对角线平分且相等来求解．故此时K |7, | ．此法借助的是矩形的对角线平分且相等的性质，该处理对于DM 是对角线的情形 \ 5 ) GM N G式和长度关系式子，即〈 M K D N 且MK 2 = DN 2 ，〈 M N D K 且MN 2 = DK 2 以及(x M + x D = x N + x K 4 2 4 2|l 4 2(x M + x K = x D + x N (6 + x = 10 + 3 (x = 7由MK 2 = DN 2 ，代入即有1+ (y + 4)2= 49 + (16 − y )2，解得 y = 36，故此时K 7,36；由MN 2 = DK 2 ，代入即有9 + (y +14)2 = 121+ (y − 6)2，解得 y = − 6 ，故此时K −1,− 6 ；(x M + x D = x N + x K (6 + 10 = 3 + x (x = 13 同样地，在解题过程中，把准备工作做好，即对应的点坐标安排到位，动点坐标假设好，选定一个定点，如这里我们选定M ，将其与剩下三点横坐标D 、 N 、K 两两组合，建立中点坐标关系 (x + x = x + x (x + x = x + xl y M + y K = y D + y N l y M + y N = y D + y K〈且MD 2 = NK 2，利用方程组求解出对应的点K 的坐标． l y M + y D = y N + y K附：坐标平面内点A (x 1 , y 1 ) ，B (x 2 , y 2 ) ，其中x 1 丰 x 2 ，则过A 、B 两点的直线的斜率k =由题，将抛物线沿着射线 C ,A 方向平移2个单位长度，即将其向下平移 4 个单位长度，向左平移 2 个单位长度，因此平移后的抛物线为y =1(x + 2)2 − 3 (x + 2) − 4 − 4 = 1 x 2 − 1 x −10 ，联立〈y = x 2− x −10，解得M (6, −4) ，y = x 2 − x − 4( 1又 BC : y = 1 x − 4 ，可知 AD : y = 1 x + 1，联立〈 y = 2 x + 1，解得D (10, 6) ，2 2 |y = 1 x 2 − 3x − 4由M (6, −4) ，D (10, 6) ，设 N (3, n ) ，K (x , y ) ，①当MK 为一条对角线时，〈，即〈，整理得〈， l y M + y K = y D + y N l −4 + y = 6 + n l n = y −105 \ 5 )②当MN 为一条对角线时，〈(x M + x N = x D + x K，即〈(6 + 3 = 10 + x，整理得〈(x = − 1l y M + y N = y D + y K l −4 + n = 6 + y l n = 10 + y5 \ 5 )③当MD 为一条对角线时，〈，即〈，整理得〈l y M + y D = y N + y K l−4 + 6 = n + y l n = 2 − y由MD 2 = NK 2 ，代入即有116 = 100 + (2 − 2y )2，解得y =− 1 或y = 3 ，故此时K (13, −1) 或(13,3) ； ( 36 ) ( 6 )综上，点K 的坐标为|7, |或|−1,− |或(13, −1) 或(13,3) ．\ 5 ) \ 5 ) y 1 − y 2． x 1 − x 21．如图1，二次函数y= ax2 + bx+ c(a丰0)与x轴交于点A(−2, 0) 、点B(点A在点B左侧)，与y轴交于点C(0,3) ，tan 三CBO= ．(1) 求二次函数解析式；(2)如图2，点P是直线BC上方抛物线上一点，PD∥y轴交BC于D，PE∥BC交x轴于点E，求PD+ BE的最大值及此时点P的坐标；(3) 在(2) 的条件下，当PD+ BE取最大值时，连接PC，将△PCD绕原点O顺时针旋转90。

中考数学二次函数存在性问题及参考答案

中考数学二次函数存在性问题及参考答案中考数学二次函数存在性问题及参考答案一、二次函数中相似三角形的存在性问题1.如图，把抛物线 $y=x^2$ 向左平移1个单位，再向下平移4个单位，得到抛物线 $y=(x-h)^2+k$。

所得抛物线与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，顶点为D。

1）写出h、k的值；2）判断△ACD的形状，并说明理由；3）在线段AC上是否存在点M，使△AOM∽△ABC？若存在，求出点M的坐标；若不存在，说明理由。

2.如图，已知抛物线经过A（$-2,0$），B（$-3,3$）及原点O，顶点为C。

1）求抛物线的解析式；2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；3）P是抛物线上的第一象限内的动点，过点P作PM⊥x 轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由。

二、二次函数中面积的存在性问题3.如图，抛物线 $y=ax^2+bx$ （$a>0$）与双曲线$y=\frac{k}{x}$ 相交于点A，B。

已知点B的坐标为（$-2,-2$），点A在第一象限内，且 $\tan\angle AOX=4$。

过点A作直线AC∥x轴，交抛物线于另一点C。

1）求双曲线和抛物线的解析式；2）计算△ABC的面积；3）在抛物线上是否存在点D，使△ABD的面积等于△ABC的面积。

若存在，请写出点D的坐标；若不存在，请说明理由。

4.如图，抛物线 $y=ax^2+c$ （$a>0$）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（$-2,0$），B（$-1,-3$）。

1）求抛物线的解析式；2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；3）在第（2）问的结论下，抛物线上的点P使$\triangle PAD=4\triangle ABM$ 成立，求点P的坐标。

(完整版)二次函数中的存在性问题(答案)

二次函数的存在性问题(面积)及答案

二次函数存在性问题

二次函数中的存在性问题(答案)(可编辑修改word版)

二次函数的存在性问题(Word版解析+答案)

二次函数中的存在性问题作业及答案

二次函数中存在性问题(等腰三角形存在性问题)

(完整版)二次函数中的存在性问题(等腰三角形的存在性问题)

二次函数中的存在性问题(最新整理)

(完整版)二次函数中的存在性问题(平行四边形)

专题27 二次函数-存在性问题(全国通用)(解析版)

二次函数中的存在性问题(含答案解析)(完整资料).doc

(完整版)二次函数中的存在性问题(答案)

二次函数的存在性问题(Word版解析+答案)

二次函数存在性问题(一题多问)

二次函数存在性问题(菱形、平行四边形、矩形)

中考数学 二次函数存在性问题 及参考答案

中考数学二次函数存在性问题及参考答案