二次函数的存在性问题
二次函数的存在性问题(面积)及答案
图12-2xCOy ABD 11二次函数的存在性问题(面积问题)1、[08云南双柏]已知：抛物线y ＝ax 2＋bx ＋c 与x 轴交于A 、B 两点，与y 轴交于点C ，其中点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，线段OB 、OC 的长（OB <OC ）是方程x 2－10x ＋16＝0的两个根，且抛物线的对称轴是直线x ＝－2． （1）求A 、B 、C 三点的坐标；（2）求此抛物线的表达式；（3）求△ABC 的面积； （4）若点E 是线段AB 上的一个动点（与点A 、点B 不重合），过点E 作EF ∥AC 交BC 于点F ，连接CE ， 设AE 的长为m ，△CEF 的面积为S ，求S 与m 之间的函数关系式，并写出自变量m 的取值范围；（5）在（4）的基础上试说明S 是否存在最大值，若存在，请求出S 的最大值，并求出此时点E 的坐标， 判断此时△BCE 的形状；若不存在，请说明理由．2、 [09湖南益阳]阅读材料：如图12-1，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a )，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算PABCAB 98SS =三角形面积的新方法：ah S ABC 21=∆，即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题：如图12-2，抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0)，交y 轴于点B .(1)求抛物线和直线AB 的解析式；(2)点P 是抛物线(在第一象限内)上的一个动点，连结PA ，PB ，当P 点运动到顶点C 时，求△CAB 的铅垂高CD 及CAB S ∆； (3)是否存在一点P ，使PABCAB98S S =若存在，求出P 点的坐标；若不存在，请说明理由.图13、[09吉林长春]如图，在直角坐标系中，矩形ABCD 的边AD 在y 轴正半轴上，点A 、C 的坐标分别 为（0，1）（2，4）．点P 从点A 出发，沿A →B →C 以每秒1个单位的速度运动，到点C 停止；点Q 在x 轴上，横坐标为点P 的横、纵坐标之和．抛物线c bx x y ++-=241经过A 、C 两点．过点P 作x 轴的垂线， 垂足为M ，交抛物线于点R ．设点P 的运动时间为t （秒），△PQR 的面积为S （平方单位）．（1）求抛物线对应的函数关系式．（2分） （2）分别求t=1和t=4时，点Q 的坐标．（3分）（3）当0＜t ≤5时，求S 与t 之间的函数关系式，并直接写出S 的最大值．（5分）4、（07云南昆明）如图，在直角坐标系中，点A 的坐标为（－2，0），连结OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB 。
二次函数存在性问题
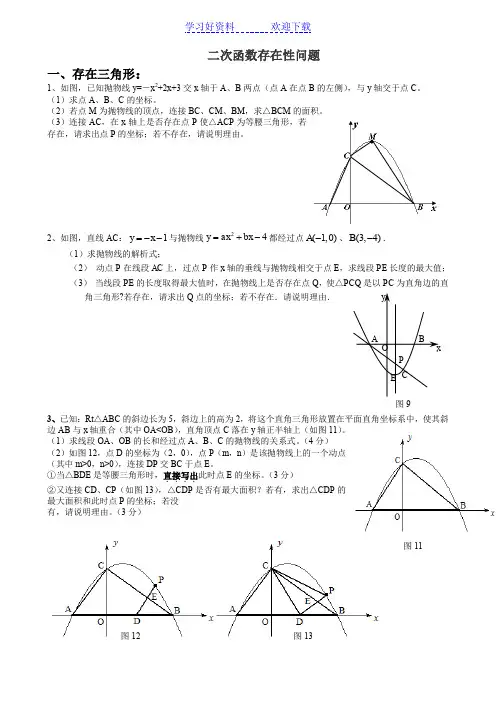
二次函数存在性问题一、存在三角形：1、如图，已知抛物线y=－x 2+2x+3交x 轴于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C 。
（1）求点A 、B 、C 的坐标。
（2）若点M 为抛物线的顶点，连接BC 、CM 、BM ，求△BCM 的面积。
（3）连接AC ，在x 轴上是否存在点P 使△ACP 为等腰三角形，若存在，请求出点P 的坐标；若不存在，请说明理由。
2、如图，直线AC ：1y x =--与抛物线24y ax bx =+-都经过点(1,0)A -、(3,4)B -．（1）求抛物线的解析式；（2） 动点P 在线段AC 上，过点P 作x 轴的垂线与抛物线相交于点E ，求线段PE 长度的最大值； （3） 当线段PE 的长度取得最大值时，在抛物线上是否存在点Q ，使△PCQ 是以PC 为直角边的直角三角形?若存在，请求出Q 点的坐标；若不存在．请说明理由．3、已知：Rt △ABC 的斜边长为5，斜边上的高为2，将这个直角三角形放置在平面直角坐标系中，使其斜边AB 与x 轴重合（其中OA<OB ），直角顶点C 落在y 轴正半轴上（如图11）。
（1）求线段OA 、OB 的长和经过点A 、B 、C 的抛物线的关系式。
（4分） （2）如图12，点D 的坐标为（2，0），点P （m ，n ）是该抛物线上的一个动点（其中m >0，n >0），连接DP 交BC 于点E 。
①当△BDE 是等腰三角形时，直接写出．．．．此时点E 的坐标。
（3分） ②又连接CD 、CP （如图13），△CDP 是否有最大面积？若有，求出△CDP 的最大面积和此时点P 的坐标；若没 有，请说明理由。
（3分）图11A B O C 图9 yx P E 图12 图13二、 存在四边形：1、如图，已知抛物线)0(2≠++=a c bx ax y 的顶点坐标为Q ()1,2-，且与y 轴交于点C ()3,0，与x 轴交于A 、B 两点（点A 在点B 的右侧），点P 是该抛物线上一动点，从点C 沿抛物线向点A 运动（点P 与A 不重合），过点P 作PD ∥y 轴，交AC 于点D ． （1）求该抛物线的函数关系式；（2）当△ADP 是直角三角形时，求点P 的坐标；（3）在问题（2）的结论下，若点E 在x 轴上，点F 在抛物线上， 问是否存在以A 、P 、E 、F 为顶点的平行四边形？若存在， 求点F 的坐标；若不存在，请说明理由．2、在平面直角坐标系中，已知抛物线经过A )0,4(-，B )4,0(-，C )0,2(三点．（1）求抛物线的解析式；（2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值． （3）若点P 是抛物线上的动点，点Q 是直线x y -=上的动点，判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标．3、如图，在平面直角坐标系中CDA Rt AOB Rt ∆≅∆,且)2,0(),0,1(B A -抛物线22-+=ax ax y 经过点C 。
二次函数存在性问题
2012年二次函数存在性问题一、二次函数中有关面积的存在性问题例1（10山东潍坊）如图所示，抛物线与x 轴交于点()()1030A B -，、，两点，与y 轴交于点()03.C -，以AB 为直径作M ⊙，过抛物线上一点P 作M ⊙的切线PD ，切点为D ，并与M ⊙的切线AE 相交于点E ，连结DM 并延长交M ⊙于点N ，连结.AN AD 、 (1）求抛物线所对应的函数关系式及抛物线的顶点坐标；(2）若四边形EAMD 的面积为求直线PD 的函数关系式；(3）抛物线上是否存在点P ，使得四边形EAMD 的面积等于DAN △的面积？若存在，求出点P 的坐标；若不存在，说明理由.答案：解：（1）因为抛物线与x 轴交于点()()1030A B -，、，两点，设抛物线的函数关系式为：()()13y a x x =+-，∵抛物线与y 轴交于点()03C -，，∴()()30103a -=+-， ∴ 1.a =所以，抛物线的函数关系式为：223y x x =--，又()214y x =--，因此，抛物线的顶点坐标为()14-，．(2）连结EM ，∵EA ED 、是M ⊙，的两条切线，∴EA ED EA AM ED MN =⊥⊥，，，∴EAM EDM △≌△又四边形EAMD的面积为∴EAM S =△∴12AM AE =· 又2AM =，∴AE =因此，点E的坐标为(11E -或(21.E --，当E 点在第二象限时，切点D 在第一象限. 在直角三角形EAM中，tan EA EMA AM ∠=== ∴60EMA ∠=°，∴60DMB ∠=° 过切点D 作DF AB ⊥，垂足为点F ，∴1MF DF ==， 因此，切点D的坐标为(2．设直线PD 的函数关系式为y kx b =+，将((12E D -、的坐标代入得2k b k b=+=-+⎪⎩解之，得33k b ⎧=-⎪⎪⎨⎪=⎪⎩所以，直线PD的函数关系式为33y x =-+当E 点在第三象限时，切点D 在第四象限.同理可求：切点D的坐标为(2，，直线PD的函数关系式为y x = 因此，直线PD 的函数关系式为33y x =-+或33y x =-(3）若四边形EAMD 的面积等于DAN △的面积 又22EAM DAN AMD EAMD S S S S ==△△△四边形， ∴AMD EAM S S =△△∴E D 、两点到x 轴的距离相等，∵PD 与M ⊙相切，∴点D 与点E 在x 轴同侧， ∴切线PD 与x 轴平行，此时切线PD 的函数关系式为2y =或 2.y =-当2y =时，由223y x x =--得，1x =当2y =-时，由223y x x =--得，1x =故满足条件的点P 的位置有4个，分别是()()()1231112P P P ++-、、、()412.P --说明：本参考答案给出了一种解题方法，其它正确方法应参考标准给出相应分数.强化训练★1、（10广东深圳）如图，抛物线y ＝ax 2＋c （a ＞0）经过梯形ABCD 的四个顶点，梯形的底AD 在x 轴上，其中A （－2,0），B （－1, －3）．(2）点M 为y 轴上任意一点，当点M 到A 、B 两点的距离之和为最小时，求此时点M 的坐标；(3）在第（2）问的结论下，抛物线上的点P 使S △P AD ＝4S △ABM 成立，求点P 的坐标．答案：（1）、因为点A 、B 均在抛物线上，故点A 、B 的坐标适合抛物线方程∴403a c a c +=⎧⎨+=-⎩ 解之得：14a c =⎧⎨=-⎩；故24y x =-为所求(2）如图2，连接BD ，交y 轴于点M ，则点M 就是所求作的点 设BD 的解析式为y kx b =+，则有203k b k b +=⎧⎨-+=-⎩，12k b =⎧⎨=-⎩，故BD 的解析式为2y x =-；令0,x =则2y =-，故(0,2)M -(3)、如图3，连接AM ，BC 交y 轴于点N ，由（2）知，易知BN=MN=1， 易求AM BM ==图2122ABM S =⨯= ；设2(,4)P x x -，依题意有：214422AD x -=⨯ ，即：2144422x ⨯-=⨯解之得：x =±0x =，故 符合条件的P 点有三个：1234),(4),(0,4)P P P --★2、．矩形OBCD 在如图所示的平面直角坐标系中，其中三个顶点分别为O (0，0)、B (0，3)、D (－2，0)，直线AB 交x 轴于点A (1，0)．(1)求直线AB 的解析式；(2)求过A 、B 、C 三点的抛物线的解析式，并写出其顶点E 的坐标；(3)过点E 作x 轴的平行线EF 交AB 于点F ．将直线AB 沿轴向右平移2个单位，与x 轴交于点G ，与EF 交于点H ．请问过A 、B 、C 三点的抛物线上是否存在点P ，使得S △P AG ＝3 4S △PEH．若存在，求点P二、二次函数中构建直角三角形与相似形的存在性问题例2 (2010甘肃）(12分) 如图，抛物线与x 轴交于A （－1，0）、B （3，0）两点，与y轴交于点C （0，－3），设抛物线的顶点为D ． （1）求该抛物线的解析式与顶点D 的坐标；（2）以B 、C 、D 为顶点的三角形是直角三角形吗？为什么？（3）探究坐标轴上是否存在点P ，使得以P 、A 、C 为顶点的三角形与△BCD 相似？若存在，请指出符合条件的点P 的位置，并直接写出点P 的坐标；若不存在，请说明理由．解：（1）设该抛物线的解析式为c bx ax y ++=2，由抛物线与y 轴交于点C （0，－3）,可知3-=c .即抛物线的解析式为32-+=bx ax y ． ………………………1分把A （－1，0）、B （3，0）代入, 得30,9330.a b a b --=⎧⎨+-=⎩解得2,1-==b a .∴ 抛物线的解析式为y = x 2－2x －3． ……………………………………………3分 ∴ 顶点D 的坐标为()4,1-. ……………………………………………………4分 说明：只要学生求对2,1-==b a ，不写“抛物线的解析式为y = x 2－2x －3”不扣分. （2）以B 、C 、D 为顶点的三角形是直角三角形. ……………………………5分理由如下：过点D 分别作x 轴、y 轴的垂线，垂足分别为E 、F.在Rt △BOC 中，OB=3，OC=3，∴ 182=BC . …………………………6分 在Rt △CDF 中，DF=1，CF=OF-OC=4-3=1，∴ 22=CD . …………………………7分 在Rt △BDE 中，DE=4，BE=OB-OE=3-1=2，∴ 202=BD . …………………………8分 ∴ 222BD CD BC =+， 故△BCD 为直角三角形. …………………………9分 （3）连接AC ，可知Rt △COA ∽ Rt △BCD ，得符合条件的点为O （0，0）． ………10分过A 作AP 1⊥AC 交y 轴正半轴于P 1，可知Rt △CAP 1 ∽ Rt △COA ∽ Rt △BCD ，求得符合条件的点为)31,0(1P ． …………………………………………11分 过C 作CP 2⊥AC 交x 轴正半轴于P 2，可知Rt △P 2CA ∽ Rt △COA ∽ Rt △BCD ， 求得符合条件的点为P 2（9，0）． …………………………………………12分 ∴符合条件的点有三个：O （0，0），)31,0(1P ，P 2（9，0）.三、二次函数中构建等腰三角形的存在性问题例3（10重庆潼南）如图, 已知抛物线c bx x y ++=221与y 轴相交于C ，与x 轴相交于A 、B ，点A 的坐标为（2，0），点C 的坐标为（0，-1）. (1）求抛物线的解析式；(2）点E 是线段AC 上一动点，过点E 作DE ⊥x 轴于点D ，连结DC ，当△DCE 的面积最大时，求点D 的坐标；(3）在直线BC 上是否存在一点P ，使△ACP 为等腰三角形，若存在，求点P 的坐标，若不存在，说明理由.答案：解：（1）∵二次函数bx x y +=221∴⎩⎨⎧-==++1022c c b解得： b =－21c =－1 ∴二次函数的解析式为21=y (2）设点D 的坐标为（m ，0∴ OD =m ∴AD =2-m 由△AD E ∽△AOC 得，AO AD =∴122DEm =- ∴DE =22m -∴△CDE 的面积=21×22m-×m=242m m +-=41)1(412+--m当m =1时，△CDE 的面积最大 ∴点D 的坐标为（1，0）(3）存在 由(1)知：二次函数的解析式为121212--=x x y 设y=0则1212102--=x x 解得：x 1=2 x 2=－1 ∴点B 的坐标为（－1，0） C （0，－1）设直线BC 的解析式为：y =kx ＋b∴ ⎩⎨⎧-==+-10b b k 解得：k =-1 b =-1∴直线BC 的解析式为: y =－x －1在Rt △AOC 中，∠AOC=900OA=2 OC=1 由勾股定理得：AC=5 ∵点B(－1,0) 点C （0，－1） ∴OB=OC ∠BCO=450①当以点C 为顶点且PC=AC=5时， 设P(k , －k －1)过点P 作PH ⊥y 轴于H题图26∴∠HCP=∠BCO=450 CH=PH=∣k ∣ 在Rt △PCH 中k 2+k 2=()25 解得k 1=210， k 2=－210 ∴P 1（210，－1210-） P 2（－210，1210-） ②以A 为顶点，即AC=AP=5设P(k , －k －1)，过点P 作PG ⊥x 轴于GAG=∣2－k ∣ GP=∣－k －1∣ 在Rt △APG 中 AG 2＋PG 2=AP 2(2－k )2+(－k －1)2=5 解得：k 1=1,k 2=0(舍)∴P 3(1, －2)③以P 为顶点，PC=AP 设P(k , －k －1) 过点P 作PQ ⊥y 轴于点Q PL ⊥x 轴于点L ，∴L(k ,0)∴△QPC 为等腰直角三角形， PQ=CQ=k 由勾股定理知CP=PA=2k∴AL=∣k -2∣, PL=｜－k －1｜在Rt △PLA 中(2k)2=(k －2)2＋(k ＋1)2 解得：k =25∴P 4(25,－27) 综上所述： 存在四个点：P 1（210，－1210-） P 2（-210，1210-） P 3(1, －2) P 4(25,－27) 三、二次函数中构建四边形的存在性问题（一）二次函数中构建梯形的存在性问题例4 (10山东临沂）如图，二次函数y = -x 2+ax +b 的图像与x 轴交于A (-21，0)、 B (2，0)两点，且与y 轴交于点C ；(1) 求该拋物线的解析式，并判断△ABC 的形状；(2) 在x 轴上方的拋物线上有一点D ，且以A 、C 、D 、B 四 点为顶点的四边形是等腰梯形，请直接写出D 点的坐标； (3) 在此拋物线上是否存在点P ，使得以A 、C 、B 、P 四点为顶点的四边形是直角梯形？若存在，求出P 点的坐标；若不存在，说明理由。
二次函数中的存在性问题
⼆次函数中的存在性问题⼆次函数中的存在性问题存在性问题是指判断满⾜某种条件的事物是否存在的问题，这类问题的知识覆盖⾯较⼴，综合性较强，题意构思⾮常精巧，解题⽅法灵活，对学⽣分析问题和解决问题的能⼒要求较⾼，是近⼏年来各地中考的“热点”。
这类题⽬解法的⼀般思路是：假设存在→推理论证→得出结论。
若能导出合理的结果，就做出“存在”的判断，导出⽭盾，就做出“不存在”的判断。
以下⼏篇内容为⼏种典型的⼆次函数中出现的存在性问题，希望⼤家在以后的学习中如果遇到此类型时能够轻松解决。
⼀、特殊三⾓形的存在性问题（⼀）⼆次函数中的等腰三⾓形存在性问题如果△ABC是等腰三⾓形，那么存在①AB＝AC，②BA＝BC，③CA＝CB三种情况．因此，解等腰三⾓形的存在性问题时，通常要进⾏分类讨论。
这类问题有⼏何法和代数法两种⽅法，我们要根据具体情况灵活选择简便的⽅法。
⼏何法⼀般分三步：分类、画图、计算．代数法⼀般也分三步：罗列三边长，分类列⽅程，解⽅程并检验．（⼆）⼆次函数中的直⾓三⾓形存在性问题如果△ABC是直⾓三⾓形，那么存在①∠A为直⾓，②∠B为直⾓，③∠C为直⾓三种情况．因此，解直⾓三⾓形的存在性问题时，通常要进⾏分类讨论。
这类问题有⼏何法和代数法两种⽅法，我们要根据具体情况灵活选择简便的⽅法。
⼏何法⼀般分三步：分类、画图、计算．代数法⼀般也分三步：罗列三边长，分类列⽅程，解⽅程并检验．（三）⼆次函数中的等腰直⾓三⾓形存在性问题在解决等腰直⾓三⾓形存在性问题时，往往要⽤到⼏何和代数相结合的⽅法，设出点的坐标后，利⽤等腰直⾓三⾓形的⼏何性质及函数关系式列⽅程求解，最常⽤到的有：①两直⾓边相等，直⾓边与斜边的⽐为1：√2；②斜边中线垂直于斜边，且等于斜边的⼀半。
③直⾓顶点处构造三垂直，得到全等三⾓形，利⽤对应边的等量关系求解。
二次函数的存在性问题(Word版解析+答案)
中考压轴题解析二次函数的存在性问题【典例分析】【考点 1】二次函数与相似三角形问题例1】已知抛物线y ax2 bx 3与 x轴分别交于A( 3,0)，B(1,0)两点，与 y轴交于点 C．2)点 F 是线段 AD 上一个动点．1AD .2ABC 相似？若相似，求出点 F 的坐标；若不相似，请说明理由．变式1-1】如图，抛物线y ax2 2x c经过A( 1,0)，B两点，且与y轴交于点C(0,3) ，抛物线与直线y x 1交于A，E 两点．(1)求抛物线的解析式；(2)坐标轴上是否存在一点Q，使得AQE是以AE为底边的等腰三角形？若存在，请直接写出点Q 的坐标；若不存在，说明理由．(3)P点在x轴上且位于点B 的左侧，若以P，B，C为顶点的三角形与ABE相似，求点P的坐AF①如图 1，设k ，当 k 为何值时，CFAD1)求抛物线的表达式及顶点 D 的坐标；标．1【变式1-2】如图，已知抛物线y m（x 2）（x m）（m > 0）与 x 轴相交于点 A，B，与 y轴相交于点 C，且点 A 在点 B 的左侧 .（ 1）若抛物线过点（ 2， 2），求抛物线的解析式；（2）在（ 1）的条件下，抛物线的对称轴上是否存在一点H ，使 AH+CH 的值最小，若存在，求出点 H 的坐标；若不存在，请说明理由；（3）在第四象限内，抛物线上是否存在点M ，使得以点 A，B，M 为顶点的三角形与△ACB 相似？若存在，求出 m 的值；若不存在，请说明理由 .考点 2】二次函数与直角三角形问题BC交于点D，连接AC 、AD ，求VACD的面积；3 点E为直线BC上的任意一点，过点E作x轴的垂线与抛物线交于点F ，问是否存在点E使VDEF 为直角三角形？若存在，求出点E 坐标，若不存在，请说明理由．例2】如图，抛物线y ax2bx c a 0的顶点坐标为2, 1 ，图象与y 轴交于点C 0,3 ，与x轴2 设抛物线对称轴与直线【变式2-1】如图，经过x 轴上A（ 1，0）， B（3，0）两点的抛物线y m（x 1）2 4m （m 0）交y 轴于点C ，设抛物线的顶点为D ，若以DB 为直径的⊙ G 经过点C ，求解下列问题：1）用含m的代数式表示出C，D 的坐标；2）求抛物线的解析式；3）能否在抛物线上找到一点Q，使△BDQ 为直角三角形？如能，求出Q点的坐标，若不能，请说明理由。
二次函数存在性问题1 教师版
x y
„ „
-3
5 -2
-2 -4
1
5 -2
2 0
„ „
(1) 求 A、B、C 三点的坐标； (2) 若点 D 的坐标为(m，0)，矩形 DEFG 的面积为 S，求 S 与 m 的函数关系，并指出 m 的取值范围； (3) 当矩形 DEFG 的面积 S 取最大值时，连接 DF 并延长至 点 M，使 FM=k·DF，若点 M 不在抛物线 P 上，求 k 的取值 范围.
二．二次函数与四边形的面积 例 1.（资阳市）25.如图 10，已知抛物线 P：y=ax2+bx+c(a≠0) 与 x 轴交于 A、B 两点(点 A 在 x 轴的正半轴上)， 与 y 轴交于点 C， 矩形 DEFG 的一条边 DE 在线段 AB 上， 顶点 F、 G 分别在线段 BC、 AC 上，抛物线 P 上部分点的横坐标对应的纵坐标如下：
2 将 C 点的横坐标 x=2 代入 y x 2x 3 得 y=-3，∴C（2，-3）∴直线 AC 的函数解析式是 y=-x-1
（2）设 P 点的横坐标为 x（-1≤x≤2）则 P、E 的坐标分别为：P（x，-x-1） ，
2 2 2 E（ ( x, x 2 x 3) ∵P 点在 E 点的上方，PE= ( x 1) ( x 2 x 3) x x 2
2 2 m2 6m 5 2 ． 当 m 6m 5 2 时， 解得 m 3 6 ． 当 m 6m 5 2 时， 解得 m 3 2 ．
2) 或 (3 6， 2) 或 (3 2， 2) 或 (3 2， 2) 时， 当点 P 运动到 (3 6， PP ∥OD ，以点 D，O，P，P 为顶点的四边形是平行四边形．
专题27 二次函数-存在性问题(全国通用)(解析版)
专题27 二次函数-存在性问题存在性问题是判断事物是否存在的问题，其知识点较广，综合性强，解题方法较灵活，对学生解决问题能力要求高，中考题中往往出现在压轴题中，其解题的一般思路是：假设存在--推理论证--得出结论---合理就存在在，反之不存在。
存在性的问题有点、线段、图形的存在等等。
解题方法多以设参数--表示点坐标--表示线段长--表示面积---建立方程等方法解决问题。
1．如图，二次函数的图象交x 轴于点()()1,0,4,0A B -，交y 轴于点()0,4,C P -是直线BC 下方抛物线上一动点．（1）求这个二次函数的表达式;（2）连接,PB PC ，是否存在点P ，使PBC ∆面积最大，若存在，求出点P 的坐标;若不存在，请说明理由．【答案】（1）234y x x =--；（2）存在点P ，使PBC ∆面积最大，点P 的坐标为()2, 6-． 【分析】（1）由A 、B 、C 三点的坐标，利用待定系数法可求得抛物线解析式；（2）过P 作PE ⊥x 轴，交x 轴于点E ，交直线BC 于点F ，用P 点坐标可表示出PF 的长，则可表示出△PBC 的面积，利用二次函数的性质可求得△PBC 面积的最大值及P 点的坐标．【详解】（1）∵二次函数的图象交y 轴于点()0,4C -，∴设二次函数表达式为24y ax bx =+-， 把A 、B 二点坐标代入可得4016440a b a b --=⎧⎨+-=⎩，解这个方程组，得13a b =⎧⎨=-⎩， ∴抛物线解析式为：234y x x =--；（2））∵点P 在抛物线上，∴设点P 的坐标为()2,34t t t --过P 作PE x ⊥轴于E ，交直线BC 于F设直线BC 的函数表达式y mx n =+，将B （4，0），C （0，-4）代入得404m n n +=⎧⎨=-⎩， 解这个方程组，得14m n =⎧⎨=-⎩， ∴直线BC 解析式为4y x =-，∴点F 的坐标为(),4t t -，()()224344PF t t t t t ∴=----=-+， ()2114422PBC S PF OB t t ∆∴==-+⨯ ()2228t =--+，∵20a =->，∴当2t =时，PBC S ∆最大，此时223423246y t t =--=-⨯-=-，所以存在点P ，使PBC ∆面积最大，点P 的坐标为()2, 6-．【点睛】本题为二次函数的综合应用，涉及待定系数法、二次函数的性质、三角形的面积、方程思想等知识．在（1）中注意待定系数法的应用，在（2）中用P 点坐标表示出△PBC 的面积是解题的关键．2．如图,二次函数 22y ax bx =++经过点()1,0A -和点()4,0B ,与y 轴交于点C ． ()1求抛物线的解析式;()2D 为y 轴右侧抛物线上一点,是否存在点D ,使若存在2 3ABC ABD S S ∆∆=,请直接写出点D 的坐标;若不存在,请说明理由．【答案】(1) 213222y x x =-++；(2) 存在，D （1，3）或（2，3）或（5，-3） 【分析】 （1）利用待定系数法将点A 和点B 的坐标代入，求出a 和b 的值即可；（2）求出△ABC 的面积，根据23ABC ABD S S ∆∆=求出△ABD 的面积，得出△ABD 中AB 边上的高，从而分点D 在x 轴上方和x 轴下方分别求出点D 的坐标.【详解】解：（1）把点()1,0A -和点()4,0B 代入22y ax bx =++中,得0201642a b a b =-+⎧⎨=++⎩，解得：1232a b ⎧=-⎪⎪⎨⎪=⎪⎩， ∴抛物线的解析式为213222y x x =-++； （2）存在，()()()231,3,2,3,5,3D D D -，理由是：∵A （-1，0），B （4，0），C （0，2）， ∴()141252ABC S ∆=⨯+⨯=， ∵23ABCABD S S ∆∆=， ∴315522ABD S ∆=⨯=， 在△ABD 中，∵AB=5，∴AB 边上的高，即点D 到x 轴的距离为3， ∵抛物线表达式为213222y x x =-++， 若点D 的纵坐标为3，令y=3，解得x=1或2，∴点D 的坐标为（1，3）或（2，3）；若点D 的纵坐标为-3，令y=-3，解得x=5或-2（舍），∴点D 的坐标为（5，-3）.综上：存在()()()231,3,2,3,5,3D D D -，使得23ABC ABD S S ∆∆=. 【点睛】本题考查了待定系数法求二次函数的解析式，二次函数上点的坐标，解题的关键是注意分类讨论思想的运用.3．如图，在平面直角坐标系中，己知二次函数283y ax x c =++的图像与y 轴交于点B (0， 4)，与x 轴交于点A (－1，0)和点D ．(1)求二次函数的解析式；(2)求抛物线的顶点和点D 的坐标；(3)在抛物线上是否存在点P ，使得△BOP 的面积等于52？如果存在，请求出点P 的坐标？如果不存在，请说明理由．【答案】（1）248433y x x =-++；（2）D 的坐标为（3，0），顶点坐标为（1，163）；（3）满足条件的点P 有两个，坐标分别为P 1(54，214)、P 2(517,412--)． 【分析】（1）利用待定系数法求出二次函数解析式即可；（2）根据二次函数的解析式得点D 的坐标，将解析式化为顶点式可得顶点的坐标；（3）设P 的坐标为P （x ，y ），到y 轴的距离为|x|，则S △BOP =12•BO •|x|，解出x=±54，进而得出P 点坐标．【详解】解：(1)把点A (－1，0)和点B (0， 4)代入二次函数283y ax x c =++中得： ()()280=1134a c c⎧-+⨯-+⎪⎨⎪=⎩ 解得：434a c ⎧=-⎪⎨⎪=⎩ 所以二次函数的解析式为：248433y x x =-++ ； （2）根据（1）得点D 的坐标为（3，0），248433y x x =-++=()()224416241333x x x --+=--+， ∴顶点坐标为（1，163）； (3)存在这样的点P ，设P 的坐标为P (x ，y )，到y 轴的距离为∣x ∣∵ S △BOP ＝12•BO •∣x ∣ ∴52＝12×4•∣x ∣ 解得：∣x ∣＝54所以x ＝±54把x ＝54代入248433y x x =-++中得： 2458543434y ⎛⎫=-⨯+⨯+ ⎪⎝⎭ 即：y ＝214， 把x ＝－54代入248433y x x =-++中得： 2458543434y ⎛⎫⎛⎫=-⨯-+⨯-+ ⎪ ⎪⎝⎭⎝⎭即：y ＝－1712∴满足条件的点P 有两个，坐标分别为P 1(54，214)、P 2(517,412--)． 【点睛】本题考查待定系数法求二次函数解析式、抛物线的顶点坐标以及三角形面积等知识，掌握二次函数的性质、灵活运用待定系数法是解题的关键．4．如图，已知二次函数2(1)y x a x a =-++-与x 轴交于A 、B 两点（点A 位于点B 的左侧），与y 轴交于点C ，已知BAC ∆的面积是6．（1）求a 的值；（2）在抛物线上是否存在一点P ，使ABP ABC S S ∆∆=．存在请求出P 坐标，若不存在请说明理由．【答案】（1）3a =-；（2）存在，P 点的坐标为(2,3)-或(13)-+-或(13)---．【分析】（1）根据求出A,B,C 的坐标，再由BAC ∆的面积是6得到关于a 的方程即可求解；（2）根据ABP ABC S S ∆∆=得到P 点的纵坐标为±3，分别代入解析式即可求解．【详解】（1）∵2(1)y x a x a =-++-，令0x =，则y a =-，∴(0,)C a -，令0y =，即2(1)0x a x a -++-=解得1x a =，21x =由图象知：0a <∴(,0)A a ，(1,0)B∵6ABC S ∆= ∴1(1)()62a a --= 解得：3a =-，（4a =舍去）；（2）∵3a =-，∴(0,3)C ，∵ABP ABC S S ∆∆=.∴P 点的纵坐标为±3，把3y =代入223y x x =--+得2233x x --+=，解得0x =或2x =-，把3y =-代入223y x x =--+得2233x x --+=-，解得1x =-+1x =--∴P 点的坐标为(2,3)-或(13)-+-或(13)--．【点睛】此题主要考查二次函数的图像与性质，解题的关键是熟知待定系数法的应用．5．如图所示，二次函数2y ax bx c =++的图象与x 轴交于A 、B 两点，与y 轴交于点C ，其中点B 在x 轴的正半轴上，点C 在y 轴的正半轴上，线段OB 、OC 的长（OB OC <）是方程210160x x -+=的两个根，且A 点坐标为(60)-，．（1）求此二次函数的表达式；（2）若点E 是线段AB 上的一个动点（与点A 、B 不重合），过点E 作EF ∥AC 交BC 于点F ，连接CE . 设AE 的长为m ，△CEF 的面积为S ，求S 与m 之间的函数关系式，并写出自变量m 的取值范围；（3）在（2）的基础上试说明S 是否存在最大值，若存在，请求出S 的最大值，并求出此时点E 的坐标，判断此时△BCE 的形状；若不存在，请说明理由．【答案】（1）228833y x x =--+；（2）2142S m m =-+(0<m<8);（3）当4m =时S 有最大值8，此时点E 的坐标为(20)-，，△BCE 为等腰三角形. 【分析】（1）通过解方程x 2−10x ＋16＝0得到二次函数图象上的点B 、C 的坐标，再结合A 的坐标，利用待定系数法求出函数解析式；（2）用m 表述出AE 、BE 的长，得到△BEF ∽△BAC ，再利用相似三角形的性质得到比例式8108EF m -=，求出EF 的表达式，利用sin ∠FEG ＝sin ∠CAB ＝45得到45FG EF =，求出FG 的表达式，再根据S ＝S △BCE −S △BFE 求S 与m 之间的函数关系，m 的值不超过AB 的长．（3）将S ＝12-m 2＋4配方为S ＝12-（m −4）2＋8，求出S 的最大值，进而判断出此时△BCE 的形状．【详解】（1）方程210160x x -+=的两个根为2和8.由于OB OC <，所以2OB =，8OC =，故8c =，点B 坐标为(20)，. 因为点A 坐标为(60)-，，所以22(6)(6)802280a b a b ⎧⨯-+⨯-+=⎨⨯+⨯+=⎩． 解得23a =-，83b =-. 故此二次函数的表达式为228833y x x =--+. （2）∵AB ＝8，OC ＝8，依题意，AE ＝m ，则BE ＝8−m ，∵OA ＝6，OC ＝8，∴AC ＝10．∵EF ∥AC ，∴△BEF ∽△BAC ． ∴EF BE AC AB=． 即8108EF m -=． ∴EF ＝4054m -． 过点F 作FG ⊥AB ，垂足为G ，则sin ∠FEG ＝sin ∠CAB ＝45． ∴45FG EF =． ∴FG ＝45•4054m -＝8−m ． ∴S ＝S △BCE −S △BFE ＝12（8−m ）×8−12（8−m ）（8−m ） ＝12（8−m ）（8−8＋m ） ＝12（8−m ）m ＝2142m m -+，自变量m 的取值范围是0＜m ＜8．（3）存在．理由如下：∵S ＝2142m m -+=−12（m −4）2＋8，且−12＜0， ∴当m ＝4时，S 有最大值，S 最大值＝8．∵m ＝4，∴点E 的坐标为（−2，0）．∴△BCE 为等腰三角形．【点睛】本题考查二次函数综合题，涉及函数和方程的关系、二次函数的性质、相似三角形的判定与性质、配方法求函数最大值等知识，是一道好题．6．关于x 的一元二次方程()222110k x k x --+=有两个实数根. ()1求k 的取值范围；()2是否存在实数k ，使方程的实数根互为相反数？若存在，求k ；若不存在，请说明理由.【答案】（1）14k ≤且0k ≠；（2）不存在 【分析】(1)由题意，方程需满足：根的判别式大于0且二次项系数不为0，求不等式的解即可；(2)根据互为相反数的两数和等于0得方程，求解并判断即可．【详解】解：()1有题意得()22202140k k k ⎧≠⎪⎨=--≥⎪⎩，解得，14k ≤且0k ≠ ()2设方程的两根为x1,x 2,依题意， 122210k x x k -+==， ∴12k =， 又∵14k ≤且0k ≠ 所以不存在【点睛】本题考查了一元二次方程根的判别式、根与系数的关系．7．如图，在平面直角坐标系xOy 中,二次函数22y x bx c =++的图象与x 轴交于A （-1,0）、B （3,0）两点, 顶点为C .(1) 求此二次函数解析式；(2) 点D 为点C 关于x 轴的对称点，过点A 作直线l ：33y x =+交BD 于点E ，过点B 作直线BK ∥AD 交直线l 于K 点.问：在四边形ABKD 的内部是否存在点P ，使得它到四边形ABKD 四边的距离都相等，若存在，请求出点P 的坐标；若不存在，请说明理由；(3) 在（2）的条件下，若M 、N 分别为直线AD 和直线l 上的两个动点，连结DN 、NM 、MK ，求DN NM MK ++和的最小值.【答案】(1)2y x =-点P 与点E 重合时，即是满足题意的点，坐标为（2(3)8【解析】试题分析：(1) ∵点A 、B 的坐标分别为（-1,0）、（3,0），∴0,230.b c b c -+=++=解得{2b c ==-∴二次函数解析式为222y x =--（2）可求点C 的坐标为（1，-∴点D 的坐标为（1，.可求直线AD的解析式为y =+由题意可求直线BK的解析式为y =-.∵直线l的解析式为y x =+∴可求出点K 的坐标为(5,易求4AB BK KD DA ====.∴四边形ABKD 是菱形.∵菱形的中心到四边的距离相等，∴点P 与点E 重合时，即是满足题意的点，坐标为（2） .(3) ∵点D 、B 关于直线AK 对称,∴DN MN +的最小值是MB .过K 作KF ⊥x 轴于F 点. 过点K 作直线AD 的对称点P ,连接KP ,交直线AD 于点Q , ∴KP ⊥AD .∵AK 是∠DAB 的角平分线,∴KF KQ PQ ===∴MB MK +的最小值是BP .即BP 的长是DN NM MK ++的最小值.∵BK ∥AD ,∴90BKP ∠=︒.在Rt △BKP 中,由勾股定理得BP =8.∴DN NM MK ++的最小值为8.考点：二次函数点评：本题难度较大，主要考查学生对二次函数性质的掌握，本题难度较高在图像分析较复杂，需要学生有扎实基础来理清思路．一般为压轴题型，基础较好的同学要多加训练，培养解题感觉．8．如图是二次函数()2y x m k =++的图象，其顶点坐标为()1,4M -． （1）直接写出m 、k 的值；（2）求二次函数的图象与x 轴的交点A ，B 的坐标；（3）在二次函数的图象上是否存在点P ，使54PAB MAB S S =△△？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）1m =-，4k =-；（2）()1,0A -，()3,0B ；（3）存在点P ，坐标为()4,5或()2,5-【分析】（1）由顶点坐标确定m 、k 的值；（2）令y=0求得图象与x 轴的交点坐标；（3）设存在这样的P 点，由于底边相同，求出△PAB 中AB 边上的高P y ，然后得出P 点纵坐标代入二次函数表达式求得P 点坐标．【详解】解：（1）由顶点坐标为M （1，-4）可知二次函数解析式为()214y x =--．∴1m =-，4k =-；（2）在()214y x =--中，令0y =得()2140x --=，解得13x =，21x =-，∴()1,0A -，()3,0B ．（3）∵PAB △与MAB △同底，且54PAB MAB S S =△△， ∴554544P M y y ==⨯=，即5P y =±． 又∵点P 在()214y x =--的图象上，∴4P y ≥-，∴5P y =，∴()2145x --=，解得14x =，22x =-，∴存在点P ，坐标为()4,5或()2,5-，使54PAB MAB SS =． 【点睛】本题考查了由二次函数顶点式的求法及抛物线与x 轴交点坐标的求法，以及给出面积关系求点的坐标，综合体现了数形结合的思想．9．如图，二次函数212y x bx c =++的图象交x 轴于,A D 两点，并经过B 点，已知A 点坐标是()2,0，B 点坐标是()8,6．（1）求二次函数的解析式；（2）求函数图象的顶点坐标及D 点的坐标；（3）二次函数的对称轴上是否存在一点C ，使得CBD ∆的周长最小？若C 点存在，求出C 点的坐标，若C 点不存在，请说明理由．【答案】（1）21462y x x =-+ （2）(4,−2)，(6,0)（3）存在，C(4,2)【分析】（1）只需运用待定系数法就可求出二次函数的解析式；（2）只需运用配方法就可求出抛物线的顶点坐标，只需令y=0就可求出点D 的坐标；（3）连接CA ，由于BD 是定值，使得△CBD 的周长最小，只需CD+CB 最小，根据抛物线是轴对称图形可得CA=CD ，只需CA+CB 最小，根据“两点之间，线段最短”可得：当点A 、C 、B三点共线时，CA+CB 最小，只需用待定系数法求出直线AB 的解析式，就可得到点C 的坐标．【详解】（1）把A(2，0)，B(8，6)代入212y x bx c =++，得 1402164862bx c b c ⎧⨯++=⎪⎪⎨⎪⨯++=⎪⎩ 解得46b c =-⎧⎨=⎩∴二次函数的解析式为21462y x x =-+ 故答案为：21462y x x =-+ （2）由221146(4)222y x x x =-+=--得二次函数图象的顶点坐标为(4，−2) 令y=0，得214602x x -+= 解得：x 1=2，x 2=6，∴D 点的坐标为(6，0)．故答案为：(4，−2)，(6，0)（3）二次函数的对称轴上存在一点C ，使得△CBD 的周长最小．连接CA ，如图，∵点C 在二次函数的对称轴x=4上，∴x C =4，CA=CD ，∴△CBD 的周长=CD+CB+BD=CA+CB+BD ，根据“两点之间，线段最短”，可得当点A 、C 、B 三点共线时，CA+CB 最小，此时，由于BD 是定值，因此△CBD 的周长最小．设直线AB 的解析式为y=mx+n ，把A(2，0)、B(8，6)代入y=mx+n ，得2+086m n m n =⎧⎨+=⎩解得12m n =⎧⎨=-⎩ ∴直线AB 的解析式为y=x −2当x=4时，y=4−2=2，∴当二次函数的对称轴上点C 的坐标为(4，2)时，△CBD 的周长最小．故答案为：存在，C(4，2)【点睛】本题考查了用待定系数法求二次函数的解析式，会将二次函数一般式化为顶点式，表示出顶点坐标，本题是抛物线动点问题的综合题型，在求线段和最短的时候，“两点之间，线段最短”是经常会被用到的知识点．10．如图是二次函数c bx x y ++=2的图象，其顶点坐标为M （1，－4）．（1）求出图象与x 轴的交点A ，B 的坐标；（2）在二次函数的图象上是否存在点P ，使MAB PAB S S ∆∆=45，若存在，求出P 点的坐标；若不存在，请说明理由；【答案】（1） A （-1,0） B （3,0） （2）P 1（4,5） P 2（-2,5）.【解析】试题分析：（1）将顶点M （1，-4）代入二次函数c bx x y ++=2，求出二次函数解析式，令y=0，解方程即可；（2）假设存在点P （x ，y ）满足条件，用点P 坐标分别表示出两个三角形的面积，解方程确定点P 的坐标.试题解析：：（1）因为M （1，-4） 是二次函数c bx x y ++=2的顶点坐标， 所以222(1)423y x bx c x x x =++=--=--，令解得 ∴A ，B 两点的坐标分别为A （-1，0），B （3，0）.（2）在二次函数的图象上存在点P ，使设P （x ，y ）则 又∴即y=±5 ∵二次函数的最小值为-4∴当时，或故P 点坐标为（-2，5）或（4，5）.考点：1.二次函数的图像；2.一次函数的图像；3.二次函数的最值；4.轴对称 .11．如图，二次函数y ＝﹣14x 2+bx +c 的图象经过点A （4，0），B （﹣4，﹣4），且与y 轴交于点C ．（1）求此二次函数的解析式；（2）证明：AO 平分∠BAC ；（3）在二次函数对称轴上是否存在一点P 使得AP ＝BP ？若存在，请求出点P 的坐标；若不存在，请说明理由．【答案】（1）y ＝﹣14x 2+12x +2；（2）见解析；（3）存在．点P 的坐标为（1，﹣4）； 【解析】【分析】 （1）将点A （4，0）与点B （−4，-4）代入函数解析式即可；（2）求出直线AB 的解析式，求出AB 与y 轴交点D （0，−2），可得OC ＝OD ，再由AO ⊥CD ，可证AO 平分∠BAC ；（3）二次函数的对称轴为直线x ＝1，设点P 的坐标为（1，m ），AP 2＝（4−1）2＋m 2，BP 2＝（1＋4）2＋（m4）2，当AP ＝BP 时，求出m ＝−4即可；【详解】（1）∵点A （4，0）与点B （﹣4，-4）在二次函数的图象上， ∴044444b c b c =-++⎧⎨-=--+⎩， 解得122b c ⎧=⎪⎨⎪=⎩，∴二次函数的解析式为y ＝211242x x -++； （2）设直线AB 的解析式为y ＝ax +n则有4040a n a n +=⎧⎨-+=⎩， 解得122a b ⎧=⎪⎨⎪=-⎩，故直线AB的解析式为y＝12x﹣2，设直线AB与y轴的交点为点D，x＝0，则y＝﹣2，故点D为（0，﹣2），由（1）可知点C为（0，2），∴OC＝OD又∵AO⊥CD，∴AO平分∠BAC；（3）存在．∵y＝﹣14x2+12x+2＝﹣14（x﹣1）2+14+2，∴二次函数的对称轴为直线x＝1，设点P的坐标为（1，m），AP2＝（4﹣1）2+m2，BP2＝（1+4）2+（m4）2，当AP＝BP时，AP2＝BP2，则有9+m2＝25+m2+16+8m，解得m＝﹣4，∴点P的坐标为（1，﹣4）；【点睛】本题考查二次函数图象及性质，一次函数图象及性质；熟练掌握待定系数法求函数解析式，利用勾股定理求边长是解题的关键．12．（本题满分10分）如图是二次函数的图象，其顶点坐标为M（1，-4）．（1）求出图象与轴的交点A ，B 的坐标；（2）在二次函数的图象上是否存在点P ，使，若存在，求出P 点的坐标；若不存在，请说明理由；【答案】（1）A （－1,0） B （3,0）；（2）存在，P （－2,5）或 P （4,5）【解析】试题分析：1）由已知得，抛物线解析式令y=0，解得 ∴A （－1,0） B （3,0）（2）84421=⨯⨯=∆MAB S ∴∵AB=4 ∴令y=5，解得∴P （－2,5）或 P （4,5）考点：1．抛物线的顶点式；2．抛物线的值13．如图，二次函数212y x bx c =-++的图象经过A(2，0)，B(0，－6)两点． （1）求这个二次函数的解析式；（2）设该二次函数的对称轴与x 轴交于点C ，连接BA ，BC ，求△ABC 的面积．（3）在x 轴上是否存在一点P ，使△ABP 为等腰三角形，若存在，求出P 的坐标，若不存在，说明理由.【答案】（1）y ＝－12x 2＋4x －6；（2）S △ABC ＝6；（3）点P 坐标为（-2，0）或()2-或()2+或()80-， 【解析】试题分析：（1）把A 、B 两点的坐标代入y=-12x 2+bx+c 中得到关于b 、c 的方程组，然后解方程求出b 、c 即可得到抛物线解析式；（2）先确定抛物线的对称轴方程，则可得到C 点坐标，然后根据三角形面积公式求解．（3）分类讨论，进行求解即可.试题解析：（1）∵的图象经过A （2，0）、B （0，-6）两点， ∴2206b c c -++⎧⎨-⎩＝＝， 解得b=4，c=-6，∴这个二次函数的解析式为y ＝−12x 2+4x −6 （2）令-12x 2+4x-6=0 ∴x 2-8x+12=0解得：x 1=2 x 2=6∴C （4，0）∴AC=2∴S △ABC =12×2×6=6 （3）点P 坐标为（-2,0）或()(()2-80+或或， 14．如图，二次函数2y x bx c =++与x 轴交于A 、B 两点，与y 轴交于c 顶点，已知(1,0)A ，(0,3)C -.（1）求此二次函数的解析式及B 点坐标.（2）在抛物线上存在一点P 使ABP ∆的面积为10，不存在说明理由，如果存在，请求出P 的坐标.（3）根据图象直接写出33x -<<时，y 的取值范围.【答案】（1）二次函数解析式为223y x x =+-，B 点坐标为(3,0)-;（2）()4,5-，(2,5);（3）412y -<.【分析】（1）将已知的两点坐标代入抛物线中，即可求得抛物线的解析式;.（2）设()2,23P x x x +-,然后利用三角形的面积计算即可;（3）根据图象可得出y 的取值范围..【详解】解：（1）将(1,0)A ，(0,3)C -代入2y x bx c =++中， 得：103b c c ++=⎧⎨=-⎩， 解得23b c =⎧⎨=-⎩. 所以二次函数解析式为223y x x =+-.令0y =，即2230x x +-=，解得：11x =，23x =-.∴B 点坐标为(3,0)-.（2）设()2,23P x x x +-，∵ABP ∆的面积为10， ∴21423102x x ⨯⨯+-=， 解方程2235x x +-=得14x =-，22x =，此时P 点坐标为()4,5-，(2,5).方程2235x x +-=-没有实数解.综上所述，P 点坐标为()4,5-，(2,5).（3）如图所示，当33x -<<时，当1x =-时，y 有最小值，将1x =-代入223y x x =+-中，得4y =-. 当3x =时，y 有最大值.将3x =代入223y x x =+-中，得12y =. ∴y 的取值范围是412y -<.【点睛】本题考查了二次函数解析式的确定以及图形面积的求法，不规则图形的面积通常转化为规则图形的面积的和差．15．如图，已知二次函数223y x x =+-的图象与x 轴相交于C D 、两点（点C 在点D 的左边），与y 轴交于点B ，点A 在二次函数的图像上，且AB ∥x 轴．问线段BC 上是否存在点P ，使△POC 为等腰三角形；如果存在，求出点P 的坐标；如果不存在，请说明理由．【答案】存在，点33(,)22P --或(0,3)P -或(3,22P -+-．【分析】由抛物线解析式可得出C 、B 坐标，利用待定系数法可得直线BC 的解析式为y=-x-3，分三个情况讨论：当PC PO =时，点P 在OC 的垂直平分线上，根据O 、C 坐标可得OC 中点坐标，把OC 中点的横坐标代入BC 解析式即可得P 点坐标；当PO CO =时，设P （x ，-x-3），利用两点间距离公式即可得P 点坐标；当PC CO =时，利用利用两点间距离公式即可得P 点坐标．【详解】当0y =时，2230x x +-=，解得：123,1x x =-=，∵点C 在点D 的左边，∴(3,0)C -当x=0时，y=-3，∴B （0，-3），设直线BC 的函数解析式为y kx n =+∴0330k n n=-+⎧⎨-=+⎩， 解得13k n =-⎧⎨=-⎩， ∴直线BC 的解析式为y=-x-3，①当PC PO =时，点P 在OC 的垂直平分线上，∵点C （-3，0），O （0，0），∴OC 中点坐标为（32-，0）， 把x=32-代入y=-x-3得：y=32-3=32-， ∴点33(,)22P -- ②当PO CO =时，设P （x ，-x-3），，解得：x 1=0，x 2=-3（舍去），∴-x-3=-3，∴点(0,3)P -，③当PC CO =时，设点(,3)P x x --，3=，解得13x =-+，232x =--（不合题意，舍去）∴(3P -+∴存在，点33(,)22P --或(0,3)P -或(3,)22P -+-． 【点睛】本题考查二次函数图象上的点的坐标特征、待定系数法求一次函数解析式及等腰三角形的判定，注意分类讨论思想的运用是解题关键．16．已知二次函数：2(21)2(0)y ax a x a =+++<．（1）求证：二次函数的图象与x 轴有两个交点；（2）当二次函数的图象与x 轴的两个交点的横坐标均为整数，且a 为负整数时，求a 的值及二次函数的解析式并画出二次函数的图象（不用列表，只要求用其与x 轴的两个交点A ，B （A 在B 的左侧），与y 轴的交点C 及其顶点D 这四点画出二次函数的大致图象，同时标出A ，B ，C ，D 的位置）；（3）在（2）的条件下，二次函数的图象上是否存在一点P 使75PCA ︒∠=？如果存在，求出点P 的坐标；如果不存在，请说明理由．【答案】（1）见解析；（2）1a =-，22y x x =--+，函数图象如图所示见解析；（3）存在这样的点P ，点P 的坐标为35,33⎛⎫ ⎪ ⎪⎝⎭或1)．【解析】【分析】（1）1）将解析式右边因式分解得抛物线与x 轴的交点为（−2，0）、（−1a，0），结合a ＜0即可得证；（2）根据题意求出1a =-，再求出函数与x 轴的交点，即可作图；（3）根据题意作出图像，根据题意分两种情况讨论：①当点P 在直线AC 上方时，记直线PC 与x 轴的交点为E ，根据75PCA ︒∠=求出30OEC ︒∠=，因此OC tan OEC OE ===∠E ，则可求出求得直线CE解析式为2y x =+，再联立两直线即可求出P 点坐标；②当点P 在直线AC 下方时， 同理求出P 的坐标.【详解】（1）∵2(21)2(2)(1)y ax a x x ax =+++=++，且0a <，∴抛物线与x 轴的交点为(2,0)-、1,0a ⎛⎫- ⎪⎝⎭， 则二次函数的图象与x 轴有两个交点；（2）∵两个交点的横坐标均为整数，且a 为负整数，∴1a =-，则抛物线与x 轴的交点A 的坐标为(2,0)-、B 的坐标为(1,0)，∴抛物线解析式为(2)(1)y x x =+-+22x x =--+21924x ⎛⎫=-++ ⎪⎝⎭， 当0x =时，2y =，即(0,2)C ，函数图象如图1所示：（3）存在这样的点P ，∵2OA OC ==，∴45ACO ︒∠=，如图2，当点P 在直线AC 上方时，记直线PC 与x 轴的交点为E ，∵75PCA ︒∠=，∴120PCO ︒∠=，60OCE ︒∠=，则30OEC ︒∠=，∴OC tan OEC OE ===∠则E ，求得直线CE解析式为2y x =+，联立2232y x y x x ⎧=+⎪⎨⎪=--+⎩， 解得02x y =⎧⎨=⎩或53x y ⎧=⎪⎪⎨⎪=⎪⎩，∴P ⎝⎭； 如图3，当点P 在直线AC 下方时，记直线PC 与x 轴的交点为F ，∵75ACP ︒∠=，45ACO ︒∠=，∴30OCF ︒∠=，则tan 2OF OC OCF =∠==，∴F ⎫⎪⎪⎝⎭，求得直线PC解析式为2y =+，联立222y y x x ⎧=+⎪⎨=--+⎪⎩， 解得：02x y =⎧⎨=⎩或11x y ⎧=⎪⎨=⎪⎩，∴1)P ，综上，点P 的坐标为⎝⎭或1)． 【点睛】此题主要考查二次函数综合，解题的关键是熟知二次函数的图像与性质，一次函数的图像与性质及三角函数的应用.17．如图，二次函数2y x bx c =-++的图象经过坐标原点，与x 轴的另一个交点为A (－2，0)．（1）求二次函数的解析式（2）在抛物线上是否存在一点P ，使△AOP 的面积为3，若存在请求出点P 的坐标，若不存在，请说明理由．【答案】（1）y ＝－x 2－2x ；（2）（3，-3），（1，-3）．【分析】（1）把点（0，0）和点A （-2，0）分别代入函数关系式来求b 、c 的值；（2）设点P 的坐标为（x ，-x 2-2x ），利用三角形的面积公式得到-x 2-2x =±3．通过解方程来求x 的值，则易求点P 的坐标．【详解】解：（1）∵二次函数y =-x 2+bx +c 的图象经过坐标原点（0，0）∴c =0．又∵二次函数y =-x 2+bx +c 的图象过点A （-2，0）∴-（-2）2-2b +0=0，∴b =-2．∴所求b 、c 值分别为-2，0；（2）存在一点P ，满足S △AOP =3．设点P 的坐标为（x ，-x 2-2x ）∵S △AOP =3 ∴12×2×|-x 2-2x |=3 ∴-x 2-2x =±3． 当-x 2-2x =3时，此方程无解；当-x 2-2x =-3时，解得 x 1=-3，x 2=1．∴点P 的坐标为（-3，-3）或（1，-3）．【点睛】本题考查了抛物线与x 轴的交点．解（1）题时，实际上利用待定系数法来求抛物线的解析式．18．二次函数y=ax 2+bx+c （a ≠0）的图象经过点A （3，0），B （2，﹣3），并且以x=1为对称轴．（1）求此函数的解析式；（2）作出二次函数的大致图象；（3）在对称轴x=1上是否存在一点P ，使△PAB 中PA=PB ？若存在，求出P 点的坐标；若不存在，说明理由．【答案】（1）解析式为y=x 2﹣2x ﹣3；（2）画图见解析；（3）存在，点P 的坐标为（1，﹣1）．【解析】试题分析：（1）根据对称轴的公式x =2b a -和函数的解析式，将2b a-=1和A （3，0），B （2，﹣3）代入函数解析式，组成方程组解答即可；（2）求出图象与坐标轴的交点坐标，描点即可；（3）根据两点之间距离公式解答即可．试题解析：解：（1）根据题意得：12930423b a a b c a b c ⎧-=⎪⎪++=⎨⎪++=-⎪⎩，解得：123a b c =⎧⎪=-⎨⎪=-⎩，∴解析式为y =x 2﹣2x ﹣3；（2）二次函数图象如图：（3）存在．作AB 的垂直平分线交对称轴x =1于点P ，连接PA 、PB ，则PA =PB ，设P 点坐标为（1，m ）．∵PA =PB ，∴22+m 2=（﹣3﹣m ）2+1，解得：m =﹣1，∴点P 的坐标为（1，﹣1）． 点睛：（1）所用方法被称为待定系数法；（2）考查了二次函数草图的画法；（3）会用距离公式d19．如图，已知二次函数21:43L y x x =-+与x 轴交于A B 、两点（点A 在点B 的左边），与y 轴交于点C ．（1）写出A B 、两点的坐标；（2）二次函数()22:430L y kx kx k k =-+≠，顶点为P ． ①直接写出二次函数2L 与二次函数1L 有关图象的两条相同的性质；②是否存在实数k ，使ABP ∆为等边三角形？如存在，请求出k 的值；如不存在，请说明理由；③若直线8y k =与抛物线2L 交于E F 、两点，问线段EF 的长度是否发生变化？如果不会，请求出EF 的长度；如果会，请说明理由．【答案】（1）()()1,0,3,0A B ；（2）①对称轴都为直线2x =或顶点的横坐标为2；都经过()()1,0,3,0A B 两点；②存在实数k ，使ABP ∆为等边三角形，k =③线段EF 的长度不会发生变化，值为6．【分析】（1）令2430x x -+=，求出解集即可；（2）①根据二次函数2L 与1L 有关图象的两条相同的性质求解即可；②根据()22432y kx kx k k x k =-+=--，可得到结果；③根据已知条件列式2438kx kx k k -+=，求出定值即可证明．【详解】解：（1）令2430x x -+=，∴()()130x x --=，∴11x =，23x =，∵点A 在点B 的左边，∴()()1,0,3,0A B ；（2）①二次函数2L 与1L 有关图象的两条相同的性质：（I ）对称轴都为直线2x =或顶点的横坐标为2；（II ）都经过()()1,0,3,0A B 两点；②存在实数k ，使ABP ∆为等边三角形．∵()22432y kx kx k k x k =-+=--，∴顶点()2,P k -，∵()()1,0,3,0A B ，∴2AB =，要使ABP ∆为等边三角形，必满足k -=∴k =③线段EF 的长度不会发生变化．∵直线8y k =与抛物线2L 交于E F 、两点，∴2438kx kx k k -+=，∵0k ≠，∴2438x x -+=，∴11x =-，25x =，∴216EF x x =-=，∴线段EF 的长度不会发生变化．【点睛】本题主要考查了二次函数综合，结合一次函数、等边三角形的性质求解是关键．20．如图，已知二次函数y ＝x 2﹣2x +m 的图象与x 轴交于点A 、B ，与y 轴交于点C ，直线AC 交二次函数图象的对称轴于点D ，若点C 为AD 的中点．（1）求m 的值；（2）若二次函数图象上有一点Q ，使得tan ∠ABQ ＝3，求点Q 的坐标；（3）对于（2）中的Q 点，在二次函数图象上是否存在点P ，使得△QBP ∽△COA ？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）m=﹣3；（2）Q （﹣4，21）或（2，﹣3）；（3）不存在，理由见解析【分析】（1）函数的对称轴为：x=1，点C 为AD 的中点，则点A （-1，0），即可求解；（2）tan ∠ABQ=3，点B （3，0），则AQ 所在的直线为：y=±3x （x-3），即可求解；（3）分点Q （2，-3）、点Q （-4，21）两种情况，分别求解即可．【详解】（1）设对称轴交x 轴于点E ，直线AC 交抛物线对称轴于点D ，函数的对称轴为：x＝1，点C为AD的中点，则点A（﹣1，0），将点A的坐标代入抛物线表达式并解得：m＝﹣3，故抛物线的表达式为：y＝x2﹣2x﹣3…①；（2）tan∠ABQ＝3，点B（3，0），则AQ所在的直线为：y＝±3（x﹣3）…②，联立①②并解得：x＝﹣4或3（舍去）或2，故点Q（﹣4，21）或（2，﹣3）；（3）不存在，理由：△QBP∽△COA，则∠QBP＝90°①当点Q（2，﹣3）时，则BP的表达式为：y＝﹣13（x﹣3）…③，联立①③并解得：x＝3（舍去）或﹣43，故点P（﹣41339，），此时BP：PQ≠OA：AC，故点P不存在；②当点Q（﹣4，21）时，同理可得：点P（﹣21139，），此时BP：PQ≠OA：OB，故点P不存在；综上，点P不存在．【点睛】此题考查二次函数综合运用，一次函数的性质、三角形相似、中点公式的运用等，解题关键在于要注意分类求解，避免遗漏．21．如图，二次函数y ＝12x 2+bx+c 的图象交x 轴于A 、D 两点，并经过B 点，已知A 点坐标是（2，0），B 点坐标是（8，6）．（1）求二次函数的解析式；（2）求函数图象的顶点坐标及D 点的坐标；（3）二次函数的对称轴上是否存在一点C ，使得△CBD 的周长最小？若C 点存在，求出C 点的坐标；若C 点不存在，请说明理由．【答案】（1）y=12x 2﹣4x+6；（2）D 点的坐标为（6，0）；（3）存在．当点C 的坐标为（4，2）时，△CBD 的周长最小【分析】（1）只需运用待定系数法就可求出二次函数的解析式；（2）只需运用配方法就可求出抛物线的顶点坐标，只需令y=0就可求出点D 的坐标；（3）连接CA ，由于BD 是定值，使得△CBD 的周长最小，只需CD+CB 最小，根据抛物线是轴对称图形可得CA=CD ，只需CA+CB 最小，根据“两点之间，线段最短”可得：当点A 、C 、B 三点共线时，CA+CB 最小，只需用待定系数法求出直线AB 的解析式，就可得到点C 的坐标．【详解】（1）把A （2，0），B （8，6）代入212y x bx c =++，得 14202164862b c b c ⎧⨯++=⎪⎪⎨⎪⨯++=⎪⎩ 解得：46b c =-⎧⎨=⎩∴二次函数的解析式为21462y x x =+﹣；（2）由2211464222y x x x =+=﹣（﹣）﹣，得二次函数图象的顶点坐标为（4，﹣2）．令y=0，得214602x x +=﹣，解得：x 1=2，x 2=6，∴D 点的坐标为（6，0）；（3）二次函数的对称轴上存在一点C ，使得CBD 的周长最小．连接CA ，如图，∵点C 在二次函数的对称轴x=4上，∴x C =4，CA=CD ，∴CBD 的周长=CD+CB+BD=CA+CB+BD ，根据“两点之间，线段最短”，可得当点A 、C 、B 三点共线时，CA+CB 最小，此时，由于BD 是定值，因此CBD 的周长最小．设直线AB 的解析式为y=mx+n ，把A （2，0）、B （8，6）代入y=mx+n ，得208m n m n +=⎧⎨+=⎩解得：12m n =⎧⎨=-⎩ ∴直线AB 的解析式为y=x ﹣2．当x=4时，y=4﹣2=2，∴当二次函数的对称轴上点C 的坐标为（4，2）时，CBD 的周长最小．【点睛】本题考查了（1）二次函数综合题；（2）待定系数法求一次函数解析式；（3）二次函数的性质；（4）待定系数法求二次函数解析式；（5）线段的性质：（6）两点之间线段最短．22．已知：如图，二次函数y=x 2+bx+c 的图象过点A （1，0）和C （0，﹣3）（1）求这个二次函数的解析式；（2）如果这个二次函数的图象与x 轴的另一个交点为B ，求线段AB 的长．（3）在这条抛物线上是否存在一点P ，使△ABP 的面积为8？若存在，求出点P 的坐标；若不存在，请说明理由．【答案】（1）二次函数的解析式为223y x x =+- ；（2）=4AB ；（3）存在，点P 的坐标为1(1P -+或2(1P --或3(1,4)P --. 【分析】（1）利用待定系数法把A （1，0），C （0，-3）代入二次函数y=x 2+bx+c 中，即可算出b 、c 的值，进而得到函数解析式是y=x 2+2x-3；（2）首先求出A 、B 两点坐标，再算出AB 的长；（3）设P （m ，n ），根据△ABP 的面积为8可以计算出n 的值，然后再利用二次函数解析式计算出m 的值即可得到P 点坐标．【详解】 解：（1）依题意把()0A 1，，()03C -，代入2y x bx c =++得： 103b c c ++=⎧⎨=-⎩，解得：23b c =⎧⎨=-⎩ ， ∴ 该二次函数的解析式为223y x x =+- ；（2）令0y =，则2230x x +-=，解之得：11x =，23x =- ，∴ 点B 坐标为（－3，0），。
二次函数解析几何--存在性问题
二次函数解析几何专题——存在性问题存在性问题是指判断满足某种条件的事物是否存在的问题，这类问题的知识覆盖面较广，综合性较强，题意构思非常精巧，解题方法灵活，对学生分析问题和解决问题的能力要求较高，是近几年来各地中考的“热点”。
这类题目解法的一般思路是：假设存在→推理论证→得出结论。
若能导出合理的结果，就做出“存在”的判断，导出矛盾，就做出不存在的判断。
由于“存在性”问题的结论有两种可能，所以具有开放的特征，在假设存在性以后进行的推理或计算，对基础知识，基本技能提出了较高要求，并具备较强的探索性，正确、完整地解答这类问题，是对我们知识、能力的一次全面的考验。
一、方法总结解存在性问题的一般步骤： （1）假设点存在；（2）将点的坐标设为参数；（3）根据已知条件建立关于参数的方程或函数。
二、常用公式（1）两点间距离公式：若A (x 1，y 1)，B (x 2，y 2)，则|AB|=221221)()(y y x x -+- （2）中点坐标公式：1212,22x x y y x y ++== （3）斜率公式：①2121y y k x x -=-；②tan k θ=（θ为直线与x 轴正方向的夹角）（4）①对于两条不重合的直线l 1、l 2，其斜率分别为k 1、k 2，则有l 1∥l 2⇔k 1＝k 2 ②如果两条直线l 1、l 2的斜率存在，设为k 1、k 2，则l 1⊥l 2⇔k 1k 2＝－1.题型一面积问题例1．如图，抛物线y＝－x2＋bx＋c与x轴交于A(1，0)，B(－3，0)两点．（1）求该抛物线的解析式；（2）在（1）中的抛物线上的第二象限内是否存在一点P，使△PBC的面积最大？，若存在，求出点P的坐标及△PBC的面积最大值；若不存在，请说明理由．变式练习：1.如图，在直角坐标系中，点A的坐标为(－2，0)，连结OA，将线段OA绕原点O顺时针旋转120°，得到线段OB．（1）求点B的坐标；（2）求经过A、O、B三点的抛物线的解析式；（3）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．2.（2009湖南益阳）如图2，抛物线顶点坐标为点C (1，4)，交x 轴于点A (3，0)，交y 轴于点B .（1）求抛物线和直线AB 的解析式； （2）求△CAB 的铅垂高CD 及S △CAB ；（3）设点P 是抛物线（在第一象限内）上的一个动点，是否存在一点P ，使S △PAB ＝89S △CAB ，若存在，求出P 点的坐标；若不存在，请说明理由.例2：如图，在坐标系xOy 中，△ABC 是等腰直角三角形，∠BAC=90°，A （1，0），B （0，2），抛物线y=21x 2+bx-2的图象过C 点． （1）求抛物线的解析式；（2）平移该抛物线的对称轴所在直线l ．当l 移动到何处时，恰好将△ABC 的面积分为相等的两部分？x CO yA B D1 1 图2变式练习：如图，抛物线y=ax 2+bx+c 关于直线x=1对称，与坐标轴交与A ，B ，C 三点，且AB=4，点D （2，23）在抛物线上，直线l 是一次函数y=kx-2（k≠0）的图象，点O 是坐标原点．（1）求抛物线的解析式；（2）若直线l 平分四边形OBDC 的面积，求k 的值；例3：将直角边长为6的等腰Rt △AOC 放在如图所示的平面直角坐标系中，点O 为坐标原点，点C 、A 分别在x 、y 轴的正半轴上，一条抛物线经过点A 、C 及点 B (–3，0)．（1）求该抛物线的解析式；（2）若点P 是线段BC 上一动点，过点P 作AB 的平行线交AC 于点E ，连接AP ，当△APE 的面积最大时，求点P 的坐标；y xCBOA变式练习：如图1，抛物线213922y x x =--与x 轴交于A 、B 两点，与y 轴交于点C ，联结BC 、AC ．（1）求AB 和OC 的长；（2）点E 从点A 出发，沿x 轴向点B 运动（点E 与点A 、B 不重合），过点E 作BC 的平行线交AC 于点D ．设AE 的长为m ，△ADE 的面积为s ，求s 关于m 的函数关系式，并写出自变量m 的取值范围；能力提升：1.（2013菏泽）如图1， △ABC 是以BC 为底边的等腰三角形，点A 、C 分别是一次函数334y x =-+的图像与y 轴、x 轴的交点，点B 在二次函数218y x bx c =++的图像上，且该二次函数图像上存在一点D 使四边形ABCD 能构成平行四边形． （1）试求b 、c 的值，并写出该二次函数的解析式；（2）动点P 从A 到D ，同时动点Q 从C 到A 都以每秒1个单位的速度运动，问：①当P 运动到何处时，由PQ ⊥AC ？②当P 运动到何处时，四边形PDCQ 的面积最小？此时四边形PDCQ 的面积是多少？2．如图，已知抛物线y=x2+bx+c的图象与x轴的一个交点为B（5，0），另一个交点为A，且与y轴交于点C（0，5）．（1）求直线BC与抛物线的解析式；（2）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值；（3）在（2）的条件下，MN取得最大值时，若点P是抛物线在x轴下方图象上任意一点，以BC为边作平行四边形CBPQ，设平行四边形CBPQ的面积为S1，△ABN的面积为S2，且S1=6S2，求点P的坐标．3.如图，二次函数的图象与x轴相交于点A（-3，0）、B（-1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y=kx-4k（k≠0）的图象过点P交x轴于点Q．（1）求该二次函数的解析式；（2）当点P的坐标为（-4，m）时，求证：∠OPC=∠AQC；（3）点M，N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．连接AN，当△AMN的面积最大时，①求t的值；②直线PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由．题型二：构造直角三角形例2．（2010四川乐山）如图所示，抛物线2y x bx c =++与x 轴交于A ，B 两点，与y 轴交于点C （0，2），连接AC ，若tan ∠OAC=2． （1）求抛物线对应的二次函数的解析式；（2）在抛物线的对称轴l 上是否存在点P ，使∠APC=90°？若存在，求出点P 的坐标；若不存在，请说明理由；变式练习： 1.函数218y x =的图象如图所示，过y 轴上一点()02M ，的直线与抛物线交于A ，B 两点，过点A ，B 分别作y 轴的垂线，垂足分别为C ，D ．（1）当点A 的横坐标为2-时，求点B 的坐标；（2）在（1）的情况下，分别过点A ，B 作AE x ⊥轴于E ，BF x ⊥轴于F ，在EF 上是否存在点P ，使APB ∠为直角．若存在，求点P 的坐标；若不存在，请说明理由；y D B MA COx3.（2010山东聊城）如图，已知抛物线y ＝ax 2+bx +c （a ≠0）的对称轴为x ＝1，且抛物线经过A （－1，0）、C （0，－3）两点，与x 轴交于另一点B ． （1）求这条抛物线所对应的函数关系式；（2）在抛物线的对称轴x ＝1上求一点M ，使点M 到点A 的距离与到点C 的距离之和最小，并求此时点M 的坐标；（3）设点P 为抛物线的对称轴x =1上的一动点，求使∠PCB ＝90º的点P 的坐标．4.（2012广州）如图1，抛物线233384y x x =--+与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ． （1）求点A 、B 的坐标；（2）设D 为已知抛物线的对称轴上的任意一点，当△ACD 的面积等于△ACB 的面积时，求点D 的坐标；（3）若直线l 过点E (4, 0)，M 为直线l 上的动点，当以A 、B 、M 为顶点所作的直角三角形有且只有．．．．三个时，求直线l 的解析式．图1E5.（2013白银）如图，在直角坐标系xOy 中，二次函数y=x 2+（2k ﹣1）x+k+1的图象与x 轴相交于O 、A 两点．（1）求这个二次函数的解析式； （2）在这条抛物线的对称轴右边的图象上有一点B ，使△AOB 的面积等于6，求点B 的坐标； （3）对于（2）中的点B ，在此抛物线上是否存在点P ，使∠POB=90°？若存在，求出点P 的坐标，并求出△POB 的面积；若不存在，请说明理由．6.（2013山西）如图1，抛物线213442y x x =--与x 轴交于A 、B 两点（点B 在点A 的右侧），与y 轴交于点C ，连结BC ，以BC 为一边，点O 为对称中心作菱形BDEC ，点P 是x 轴上的一个动点，设点P 的坐标为(m , 0)，过点P 作x 轴的垂线l 交抛物线于点Q ． （1）求点A 、B 、C 的坐标；（2）当点P 在线段OB 上运动时，直线l 分别交BD 、BC 于点M 、N ．试探究m 为何值时，四边形CQMD 是平行四边形，此时，请判断四边形CQBM 的形状，并说明理由；（3）当点P 在线段EB 上运动时，是否存在点Q ，使△BDQ 为直角三角形，若存在，请直接写出点Q 的坐标；若不存在，请说明理由．7.（2013济宁）如图，已知直线y=kx-6与抛物线y=ax2+bx+c相交于A，B两点，且点A（1，-4）为抛物线的顶点，点B在x轴上．（1）求抛物线的解析式；（2）在（1）中抛物线的第二象限图象上是否存在一点P，使△POB 与△POC全等？若存在，求出点P的坐标；若不存在，请说明理由；（3）若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标．8.（2013 绵阳）如图，二次函数y=ax2+bx+c的图象的顶点C的坐标为（0，-2），交x轴于A、B两点，其中A（-1，0），直线l：x=m（m＞1）与x轴交于D。
二次函数存在性问题(菱形、平行四边形、矩形)
今天讲解二次函数背景下的四边形存在性问题．这里的四边形存在性问题，一般是以几种特殊的四边形为主，常考察的有平行四边形、菱形、 矩形、正方形．当然，三角形的存在性问题和四边形的存在性问题是一样， 如等腰三角形实际上和 菱形是一致的， 直角三角形和矩形是一样的， 等腰直角三角形和正方形是一致的．本文我们将重点讲解这类问题的求解逻辑以及注意事项，同时给大家理出一个比较通用的解题 模板．1如图，抛物线y = ax 2 + bx + 3 交x 轴于点A (−1, 0) 和点B (3, 0) ，与 y 轴交于点C ，连接BC ， 交对称轴于点D ．(1) 求抛物线的解析式；(2)点 P 是直线BC 上方的抛物线上点，连接PC ，PD ．求 △PCD 的面积的最大值以及此时 点P 的坐标；(3)将抛物线y = ax 2 + bx + 3 向右平移 1 个单位得到新抛物线，新抛物线与原抛物线交于点E ， 点F 是新抛物线的对称轴上的一点，点 G 是坐标平面内一点．当以D 、E 、F 、 G 四点为顶点的 四边形是菱形时，直接写出点F 的坐标，并写出求解其中一个点F 的坐标的过程．前两小问就不详说了，直接上结论， 抛物线解析式为y = −x 2 + 2x + 3 ；点 P | , | ．( 3 15 )\2 4 )第 3 小问为菱形存在性问题， 以D 、E 、F 、 G 四点为顶点的四边形是菱形．四个点中， D ， E 是定点，F 是平移后新抛物线对称轴上的动点，由于点F 的横坐标是确定的，只有纵坐标在变化， 我们可以称其为“G 如果只需要点F 的坐标，那么没有必要求解平移后抛物线的解析式．根据平移的性质，将原抛物线 向右平移 1 个单位长度， 那么原抛物线的对称轴也向右平移 1 个单位长度， 因此新抛物线的对称轴 为x = 2 ，几 F (2, m ) ．但由于此时E 为量抛物线的交点，因此还是要把平移后的抛物线解析式求出 来，根据“左加右减”，平移后的抛物线解析式为y = − (x −1)2+ 2(x −1) + 3 = −x 2 + 4x ，联立两抛物(|y = −x 2 + 2x + 3 ( 3 15 ) 线〈|ly = −x 2 + 4x ，解得E |\2 , 4 )| ．菱形的探究相对是比较简单的，对于这类探究性问题，一般都是先从确定的信息入手．菱形是 以D 、E 、F 、 G 为顶点， 其中DE 为定线段，那么存在的可能有DE 是一条边，也可能是一条对 对角线．前面提到，等腰三角形和菱形的分析是一致的，这里我们结合等腰三角形的存在性问题一 起分析．由于 G 是“自由点”，可以随机应变，因此讨论以D 、E 、F 为顶点的三角形是等腰三角 形．同样， 由于定线段DE 可能是等腰三角形的一条腰，也可能是底边．当DE 为一条腰时，第一种情形是点D 为顶点，即DE = DF ，也即半动点F 到D 的距离和E 到D 的距离相等，因此点F 在以点D 为圆心， DE 为半径的圆上，作出该圆，如图 1 所示，可知此时圆与新抛物线的对称轴有两个交点F 1 ，F 2 ，结合图象可以判断，此时两个点应该都是满足的．那么 再加上对应的“自由点” G ，就是以DE 为边菱形了．当DE 为一条腰时， 另一种情形是点E 为顶点， 即ED = EF ，也即半动点F 到E 的距离和D 到E 的距离相等，因此点F 在以点E 为圆心， ED 为半径的圆上，作出该圆，如图 2 所示，可知此时 圆与新抛物线的对称轴同样有两个交点F 1 ，F 2 ，结合图象， 此时的F 3 存在和DE 共线的风险，因此后续需要检验一下．根据坐标可以知道，x E =，通常像这类圆心可能为两个点中点的，一般都要留个心眼， 检验一下．此时再加上对应的“自由点” G ，也是以DE 为边菱形．当DE 为底边时，则F 为顶点， 即FD = FE ，即 F 到线段DE 的两端点的距离相等，可知此时F 在线段DE 的垂直平分线上，作出线段DE 的垂直平分线，如图 3 所示，可知此时有一个交点F 5 ．加 上对应的“自由点” G ，此时便是以DE 为对角线的菱形．对于等腰三角形和菱形的存在性问题，如上图情形，我们称其为“两圆一线”法．由于这类题一般不需要书写完整过程，因此在解题过程中，把准备工作做好， 即对应的点坐标， 解析式等先求出来， 动点坐标假设好， 再把定线段DE ，半定线段DF 、EF 长度表示出来． 根据上 述分析，结合“两圆一线”分别使得三条线段两两相等建立方程，即DE = DF ，DE = EF ，DF = EF ， 求解出动点坐标即可．(实际解题过程中， 一般使用线段平方的形式．此外， 只需关注下方解析中公 式计算部分即可，文字叙述部分可忽略)此题还是比较友善的，只需求出F 坐标．如果需要求解点G 的坐标，则还要加一个步骤．这里 以DEG 1F 1 为例，若要求 G 1 坐标，一般有两种比较常用的思路．一是利用菱形的对边平行且相等，即F 1G 1 可以看成是DE 平移得来的， 那么点D → F 1 的平移变化也即点E → G 1 的平移变化． 二是利用菱形的对角线相互平分，因此EF 1 的中点也即DG 1 的中点，利用中点坐标求解出 G 1 坐标．这两种处理 在平行四边形存在性问题中也是有力手段．(|y = −x 2 + 2x + 3 ( 3 15 ) 149 ( 149 )由题， y = −x 2 + 2x + 3 向右平移 1 个单位得到新抛物线y = − (x −1)2+ 2(x −1) + 3 = −x 2 + 4x ，联立〈|ly = −x 2 + 4x ，解得 E |\2 , 4 )| ， 新抛物线的对称轴为x = 2 ，设 F (2, m ) ，由于 D (1, 2) ，则DE 2 =，EF 2 = + m −2= m 2 − m +，DF 2 = 1+ (m − 2)2= m 2 − 4m + 5 ，①当DE 、DF 为一组邻边时，则 DE 2 = DF 2 ，即 = m 2 − 4m + 5 ，37 ( ) ( )②当ED 、EF 为一组邻边时，则 ED 2 = EF 2 ，即 = m 2 − m + ，16 8 16 11 ( 11)③当EF 为对角线时，则FD = FE ，即 m 2 − m + = m 2 − 4m + 5 ， 2 16解得m = ，此时 F 的坐标为|2, | ；( ) ( ) ( 149 )( 11) 当F |2, |时， y F + y D = 2y E ，x D + x F = 2x E ，即 E 为D 、F 中点， 不合题意， 舍去； 15 229 \ 2 )综上， F 点的坐标为||\2, 2 + 4 )|| 或||\2, 2 − 4 )|| 或(2, 2) 或|\2, 56 )| ． 56 \ 56 )解得m = 2 或m = ，此时F 的坐标为(2, 2) 或|2, | ，2 \ 2 )解得m = 2 土 4 ，此时 F 的坐标为||\2, 2 + 4 )|| 或||\2, 2 − 4 )|| ；53 15 2291 ．已知二次函数y = ax2 + bx − 2(a 丰 0)与x 轴交于A ( −, 0) ，B (4, 0) ，与 y 轴交于点C ．(1) 求抛物线的解析式；(2) 连接AC ，BC ，点 P 是直线BC 下方抛物线上一点，过 P 作PD ∥AC 交直线BC 于点D ，PE ∥x 轴交直线BC 于点， E ，求△PDE 面积的最大值及此时点， P 的坐标；(3) 在(2)的条件下， 将原抛物线沿x 轴向左平移3个单位得到新抛物线，点 M 是新抛物线对称轴上一点， 点 N 是平面直角坐标系内一点， 当以点M 、 N 、P 、B 为顶点的四边形为菱形 时，请直接写出所有符合条件的N 点的坐标；并任选其中一个N 点，写出求解过程．立〈y= − 2 x 2 + 4x − 2 ，解得D 7 , 11 ．1-1如图 1，抛物线y = ax 2 + bx + 4 交x 轴于A (−2, 0) ，B (4, 0) 两点，与y 轴交于点C ，连接 AC ， BC ．(1) 求抛物线的解析式；(2) P 是拋物线上位于直线BC 上方的一个动点，过点P 作PQ ∥y 轴交BC 于点Q ， 过点P 作PE ⊥ BC 于点E ，过点 E 作EF ⊥ y 轴于点F ，求出2PQ + EF 的最大值及此时点P 的坐标；(3)如图 2，将抛物线y = ax 2 + bx + 4 沿着射线CB 的方向平移，使得新抛物线y ，过点(3,1) ， 点D 为原抛物线y 与新抛物线y ，的交点，若点 G 为原抛物线的对称轴上一动点，点H 为新抛物线y ， 上一动点，直接写出所有使得以 A ，D ， G ，H 为顶点的四边形为平行四边形的点H 的坐标，并 把求其中一个点H 的坐标的过程写出来．抛物线解析式为y = − x 2 + x + 4 ；点 P | , | ．相当于是沿着射线BC 方向平移，故舍去， 因此可得平移后抛物线的解析式为y = − x 2 + 4x − ．联2 2 ( 1 13 y = − x 2 + x +4 \2 8 )这类平行四边的探究也并不难， 同样先从确定的信息入手．平行四边形是以A ，D ，G ，H 为 顶点，其中AD 是定线段， G 是半动点，H 在新的抛物线上．和菱形的讨论一样，我们要考虑AD 是 一条边的情形， 也要考虑AD 是对角线的情形．当 AD 是一条边时， 实际上此时也右两种情形，一是是平行四边形为ADHG ，也即AH ，DG 为 对角线；另一种则是平行四边形为ADGH ，也即 AG ，DH 为对角线．当然，不管是那种情形，由 于 AD 是一条边，根据平行四边形对边平行且相等的性质， GH 这条边可以看作是将AD 平移后得到1 (8 28 )2 \3 9 )第 3 小问中， 抛物线沿着射线CB 方向平移， 由于后续的点在新抛物线上， 因此还是要求出平移 后抛物线的解析式．这类沿着射线平移的，一般采用正交分解的形式平移，由点 C (0, 4) ，B (4, 0) 可 知，沿着射线 CB 平移，即向右平移t 个单位，则向下也平移t 个单位，因此假设平移后新抛物线的 解析式为y = − (x − t )2+ (x − t ) + 4 − t ，因为平移后经过点(3,1) ，代入可解得t = − 1 或t = 3 ，当 t = − 1 ， 1 13的，由于半动点 G 在原抛物线对称轴x = 1 上，那么点 G 有可能是点 A 平移后得到的， 此时点H 就 是点D 平移后得到的，如图 1 所示；同理，当点 G 是点D 平移后得到的，那么此时点H 就是点A 平 移后得到的，如图 2 所示．设点 G (1, m )，根据平移的性质，结合点坐标的变化规律，当 A → G 时， 即(−2, 0) —(1, m ) ，则有D|2 , 8 )| —H | 2 , 8 + m )| ，由于点H 在新抛物线上， 且横坐标已知了，代入新抛物线即可 11 1 (13 213 13 13 (13 13 此外， 除了用平移性质得到H 点的坐标外，此时 AH 是一条对角线，也利用对角线相互平分， 则 A 、 H 的 中 点 和 D 、 G 的 中 点 是 同 一 个 ， 利 用 中 点 坐 标 则 有 x A + x H = x D + x G ，故 13 13 13 (13 13 x H = x D + x G − x A = 2 ，将x = 2 代入新抛物线解析式，可求得H 点纵坐标y = − 8 ，故H | 2 , − 8 )|．当 AG 是一条对角线时， 则有x A + x G = x D + x H ，故 x H = x A + x G − x D = − ，代入新抛物线解析 277 ( 9 277式，可求得此时H 的纵坐标为 − ，故H |− , − | ．8 2 8 ) 当 AD 是一条对角线时，则有x A + x D = x H + x G ，故 x H = x A + x D − x G = ，代入新抛物线解析式， 37 ( 1 37 可求得此时H 的纵坐标为 − ，故 H | , − | ．8 2 8 )同样地，在解题过程中， 把准备工作做好，即对应的点坐标，解析式等先求出来，动点坐标假设好， 将点坐标表示列出来(通常都是横坐标)，选定一个定点，如这里我们选定 x A ，将其与剩下 三点横坐标x D 、x G 、x H 两两组合，建立中点坐标关系式， 即x A + x D = x H + x G ，x A + x G = x D + x H 以 及x A + x H = x D + x G ，求解出点H 横坐标，再代入解析式中求出点H 纵坐标即可．求得纵坐标 8 + m = − 2 | 2 )| + 4 2 − 2 = − 8 ，此时H | 2 , − 8 )| ． ( 7 11 (13 1113 (13 13)由题， 设平移后的抛物线解析式为y = − (x − t )2+ (x − t ) + 4− t ，因为平移后经过点(3,1)，代入可解得t = − 1 (舍) 或t = 3 ，2 2联立〈y = − 2 x 2 + 4x − 2 ，解得 D 7 , 11 ， y = − x 2 + x + 4 \2 8 )则x A =−2 ，x D = ，x G = 1，设 H 点横坐标为x H ，①当AH 为一条对角线时，x A + x H = x D + x G ，则 x H = ，代入可求得此时H | , − | ； 9 ( 9 277 )1 (1 37 )综上， H 的坐标为| , − |或|− , − |或| , − | ．( 1 13 ③当AD 为一条对角线时，x A + x D = x H + x G ，则x H = ，代入可求得此时H | , − | ；(13 13) ( 9 277 ) (1 37 )2 \2 8 )\ 2 8 ) \ 2 8 ) \2 8 )②当AG 为一条对角线时，x A + x G = x D + x H ，则x H = − ，代入可求得此时H |− , − | ；2 \ 2 8 ) 2 \ 2 8 )故平移后抛物线的解析式为y = − x 2 + 4x − ，1 131．如图，在平面直角坐标系中，抛物线y= ax2 + bx+ 3(a 0) 与y轴交于点C，与x轴交于A，B两点(点A在点B的右侧)，且点A的坐标为( 3, 0) ，连接BC，过点A作AD∥BC交y轴于点D，OB= 3OA．(1) 求抛物线的解析式；(2) 如图1，点E为射线AD上一点，点P为第二象限内抛物线上一点，求四边形PBEC面积的最大值及此时点P的坐标；(3) 如图2，将原抛物线沿x轴正方向平移得到新抛物线y，y经过点C，平移后点A的对应点为点A，点N为线段AD的中点，点Q为新抛物线y的对称轴上一点，在新抛物线y上存在一点M，使以点M，Q，A，N为顶点的四边形为平行四边形，请直接写出点M的坐标，并选择一个你喜欢的点写出求解过程．2．如图，抛物线y= x2 + bx+ c与x轴相交于点A(−1, 0) 和点B，交y轴于点C，tan 三ACO= ．(1) 求抛物线的解析式；(2) 如图1 ，P点为一象限内抛物线上的一个动点，点D是BC中点，连接PD，BD，PB．求△BDP面积的最大值以及此时P点坐标；，M为新抛物线对称轴上(3) 如图2，将抛物线向左平移 1 个单位长度，得到新的抛物线y1一点，N为直线AC上一动点，在(2) 的条件下，是否存在点M，使得以点P、B、M、N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．| 4 21如图，已知抛物线y = ax 2 + bx − 4 与x 轴交于A ，B 两点， 与y 轴交于点C ，且点A 的坐标 为(−2, 0) ，直线BC 的解析式为y = x − 4 ．(1) 求抛物线的解析式；(2)如图 1，过点 A 作 AD ∥BC 交抛物线于点D (异于点 A )， P 是直线BC 下方抛物线上一 点，过点P 作PQ ∥y 轴， 交AD 于点Q ，过点 Q 作QR ⊥ BC 于点R ，连接PR ．求△PQR 面积的最 大值及此时点P 的坐标；(3) 如图 2，点 C 关于x 轴的对称点为点C ，将抛物线沿射线 C A 的方向平移2个单位长度得到新的抛物线y ，新抛物线y 与原抛物线交于点M ，原抛物线的对称轴上有一动点 N ，平面直 角坐标系内是否存在一点K ，使得以 D ，M ，N ，K 为顶点的四边形是矩形？若存在，请直接写 出点K 的坐标；若不存在， 请说明理由．抛物线解析式为y = x 2 − x − 4 ；S △PQR 的最大值为 9，点P (4, −6) ．第 3 小问中，抛物线沿着射线C A 方向平移， 由于点M 为两抛物线交点， 因此需求出平移后抛 物线的解析式．根据A (−2, 0) ，C (0, 4) ，可知Rt △AOC 中AO : OC : AC = 1: 2 : ，因此将抛物线沿着射线C A 方向平移2个单位长度，则相当于向下平移 4 个单位长度，向左平移 2 个单位长度，因此平移后的抛物线为y = 1 (x + 2)2− 3 (x + 2) − 4 − 4 = 1 x 2 − 1 x −10 ，联立〈y = x 2 − x −10，解4 2 4 2y = x 2 − x − 4( 1得M (6, −4) ．又 BC : y = 1 x − 4 ，可知 AD : y = 1 x + 1，联立〈 y = 2 x + 1，解得D (10, 6) ．2 2 |y = 1 x 2 − 3x − 4因为以D ，M ，N ，K 为顶点的四边形是矩形，此时定线段是DM ，半动点为N ，自由点为K ．和 前面讨论菱形、平行四边形时的流程基本大同小异，定线段DM 可能是矩形的边，也可能是矩形的 对角线，因此要分两种情形讨论．矩形的存在性问题和直角三角形的存在性问题是一致的，如本题 中，探究以D ，M ，N 为顶点的三角形是直角三角形． 同样地，先以直角三角形为例，那么D ，M ，1 3 4 2在实际解题中设 K (x , y ) 即可)， 利用中点关系〈 M K D N ，则〈 K，整理得N 均有可能为直角顶点．当M 为直角顶点时，过M 作DM 垂线与对称轴交点即为点N 所在位置，如图 1 所示．对于N 点 坐标的求解，一方面，由于MN ⊥ DM ，则 k MN . k DM = − 1，结合点M 坐标，由此可求得直线MN 解 析式，将其与对称轴方程联立即可求得点N 坐标．另一方面，可以构造如图所示的K 型相似，即构DH MH1 腰直角三角形， 或者四边形中的正方形， 那么可以构造此类的K 型全等求解．在此直角三角形的基础上，加上自由点K ，就变成矩形问题了．对于矩形问题，同样可以求出点N 坐标后，利用平移关系或者对角线的中点关系，求相应的点K 的坐标．当然，如果是探究矩形 的存在性问题，也可以直接利用中点关系求得点K 的坐标．由点N (3, n )，设K (x K , y K ) (熟练后，(x + x = x + x (6 + x = 10 + 3 l y M + y K = y D + y N l−4 + y K = 6 + n 〈，再由对角线相等，即MK = DN ，代入即有1+ (y + 4)2= 49 + (16 − y )2，解得 y =，( 36 )同样适用．当D 为直角顶点时，三角形如图2 所示．同样， 加上自由点K ，就变成矩形问题了． 这里我们5 2 2 ( 44 )l y M + y N = y D + y K |y K = − \ 5 )对于直角三角形或矩形问题， 如上图情形，我们可以称其为“两线一圆”．若只求点N 坐标，一 般利用斜率关系，求出解析式后进一步求解．如果是矩形问题要求自由点的坐标，可以用对角线平 分且相等， 建立方程求解．当然， 先求点N ，利用点N 作为台阶进一步求解也是没问题的， 大家选 用自己顺手的方法即可．造 △MN 1G ∽△DMH ，利用 = ，可求出长度，进而得到点 N 坐标．更特殊地，如果是等以垂线方式求解．由于k DM = 2 ，则 k DN = − 5 ，故此时DN : y = − 5 x + 10 ，令x = 3 ，可解得N |\3, 5 )| ， 由中点可知，〈(x M + x N = x D + x K ，可解得〈(|x K = − 16 ，此时 K −1,− 6 ．l 5当N 为直角顶点时，则有NM ⊥ ND ，因此点N 在以DM 为直径的圆上．此种情形若只是求点N 坐标，策略比较多， 一方面，可以利用斜率， 由k ND . k NM= − 1求出点N 坐标；另一方面，可以利用线段长度求解，设DM 中点为为R ，则此时圆心为R ，因此NR = RD = DM ，由此也可求得点N 坐 标， 此外， 还可以利用勾股定理ND 2 + NM 2 = DM 2 ．当加入自由点K ，变成矩形问题后，除了先求 出点N 坐标， 利用平移或中点求解点K 坐标外，也可以利用前面的对角线平分且相等来求解． 故此时K |7, | ．此法借助的是矩形的对角线平分且相等的性质，该处理对于DM 是对角线的情形 \ 5 ) GM N G式和长度关系式子，即〈 M K D N 且MK 2 = DN 2 ，〈 M N D K 且MN 2 = DK 2 以及(x M + x D = x N + x K 4 2 4 2|l 4 2(x M + x K = x D + x N (6 + x = 10 + 3 (x = 7由MK 2 = DN 2 ，代入即有1+ (y + 4)2= 49 + (16 − y )2，解得 y = 36，故此时K 7,36；由MN 2 = DK 2 ，代入即有9 + (y +14)2 = 121+ (y − 6)2，解得 y = − 6 ，故此时K −1,− 6 ；(x M + x D = x N + x K (6 + 10 = 3 + x (x = 13 同样地，在解题过程中， 把准备工作做好，即对应的点坐标安排到位，动点坐标假设好，选定 一个定点， 如这里我们选定M ，将其与剩下三点横坐标D 、 N 、K 两两组合， 建立中点坐标关系 (x + x = x + x (x + x = x + xl y M + y K = y D + y N l y M + y N = y D + y K〈 且MD 2 = NK 2，利用方程组求解出对应的点K 的坐标． l y M + y D = y N + y K附：坐标平面内点A (x 1 , y 1 ) ，B (x 2 , y 2 ) ，其中x 1 丰 x 2 ，则过A 、B 两点的直线的斜率k =由题， 将抛物线沿着射线 C ,A 方向平移2个单位长度， 即将其向下平移 4 个单位长度， 向左平移 2 个单位长度， 因此平移后的抛物线为y =1(x + 2)2 − 3 (x + 2) − 4 − 4 = 1 x 2 − 1 x −10 ， 联立〈y = x 2− x −10，解得M (6, −4) ，y = x 2 − x − 4( 1又 BC : y = 1 x − 4 ，可知 AD : y = 1 x + 1，联立〈 y = 2 x + 1，解得D (10, 6) ，2 2 |y = 1 x 2 − 3x − 4由M (6, −4) ，D (10, 6) ，设 N (3, n ) ，K (x , y ) ，①当MK 为一条对角线时，〈，即〈 ，整理得〈 ， l y M + y K = y D + y N l −4 + y = 6 + n l n = y −105 \ 5 )②当MN 为一条对角线时，〈(x M + x N = x D + x K，即〈(6 + 3 = 10 + x，整理得〈(x = − 1l y M + y N = y D + y K l −4 + n = 6 + y l n = 10 + y5 \ 5 )③当MD 为一条对角线时，〈 ，即〈 ，整理得〈l y M + y D = y N + y K l−4 + 6 = n + y l n = 2 − y由MD 2 = NK 2 ，代入即有116 = 100 + (2 − 2y )2，解得y =− 1 或y = 3 ，故此时K (13, −1) 或(13,3) ； ( 36 ) ( 6 )综上， 点K 的坐标为|7, |或|−1,− |或(13, −1) 或(13,3) ．\ 5 ) \ 5 ) y 1 − y 2． x 1 − x 21．如图1，二次函数y= ax2 + bx+ c(a丰0)与x轴交于点A(−2, 0) 、点B(点A在点B左侧)，与y轴交于点C(0,3) ，tan 三CBO= ．(1) 求二次函数解析式；(2)如图2，点P是直线BC上方抛物线上一点，PD∥y轴交BC于D，PE∥BC交x轴于点E，求PD+ BE的最大值及此时点P的坐标；(3) 在(2) 的条件下，当PD+ BE取最大值时，连接PC，将△PCD绕原点O顺时针旋转90。
二次函数中存在性问题
二次函数中存在性问题典例分析例1．已知，如图，已知抛物线y＝ax2+bx x轴交于A（3，0），B（-1，0）两点，与y轴交于点C，连接AC，BC，若点M是x轴上的动点（不与点B重合），MN⊥AC于点N，连接CM．（1）求抛物线的解析式；（2）当MN＝1时，求点N的坐标；（3）是否存在以点C，M，N为顶点的三角形与△ABC相似，若存在，请直接写出点M的坐标；若不存在，请说明理由．例2．如图，已知抛物线y＝ax2+bx+c的图象与x轴交于点A，B（点A在点B的右侧），且与y轴交于点C，若OA＝OC，一元二次方程ax2+bx+c＝0的两根为1和3，点P是该抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点D．（1）求该抛物线的函数关系式；（2）当△ADP是直角三角形时，求点P的坐标；（3）在题（2）的结论下，若点E在x轴上，点F在抛物线上，问是否存在以A、P、E、F 为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由．同步练习：1、如图，在平面直角坐标系中，抛物线y＝ax2-4ax＋1与x轴正半轴交于点A和点B，与y 轴交于点C，且OB＝3OC，点P是第一象限内的点，联结BC，△PBC是以BC为斜边的等腰直角三角形．（1）求这个抛物线的解析式；（2）求点P的坐标；（3）点Q在x轴上，若以Q、O、P为顶点的三角形与以C、A、B为顶点的三角形相似，求点Q的坐标．2、如图1，经过原点O的抛物线y=ax2+bx（a≠0）与x轴交于另一点A（32，0），在第一象限内与直线y=x交于点B（2，t）．（1）求这条抛物线的表达式；（2）在第四象限内的抛物线上有一点C，满足以B，O，C为顶点的三角形的面积为2，求点C的坐标；（3）如图2，若点M在这条抛物线上，且∠MBO=∠ABO，在（2）的条件下，是否存在点P，使得△POC∽△MOB？若存在，求出点P的坐标；若不存在，请说明理由．参考答案例1、答案：（1）∵抛物线ya ＝ax 2+bxx 轴交于A （3，0），B （-1，0）两点，得0930a b a b ⎧=+⎪⎨=-⎪⎩，解得：a b ⎧=⎪⎪⎨⎪=⎪⎩2y x x = （2）∵233y x x =--∴当x ＝0时，y＝，∴C （0，，∴OC∵A （3，0），∴OA ＝3，∴∠OAC ＝30°，∵MN ＝1，∠MNA ＝90°，在Rt △AMN 中，AN过点N 作NH ⊥x 轴于点H ，∴NH＝2，AH ＝32， 当点M 在点A 左侧时，N 的坐标为（32，-2）， 当点M 在点A 右侧时，N 的坐标为（，32）， 综上，点N 的坐标为（32，-32）或（，32）， （3）设M 点为（x ，0），则由（2）可得AB＝4，BC2，AC，∵BC2+AC2＝AB2，∴△ABC是直角三角形，∠BCA＝90°，又由2S△CMA＝AM×OC＝AC×MN得：MN=，∴若以点C，M，N为顶点的三角形与△ABC相似，则：①：＝，即2(3)4x-＝234x+，即6x＝6，所以x＝1，此时M为（1，0）；②：＝，即2(3)43x-＝234x+，即x2+3x＝0，解之可得：x＝0或x＝-3，∴M为（0，0）或（-3，0），综上所述，存在以点C，M，N为顶点的三角形与△ABC相似，且M的坐标为（1，0）或（0，0）或（-3，0）．分析：（1）把A、B两点坐标代入解析式求出a、b后可以得解；（2）过点N作NH⊥x轴于点H，则根据题意可以得到NH及AH的值，再分点M在点A左侧和点M在点A右侧两种情况分别写出点N坐标即可；（3）由题意可得△ABC为直角三角形，所以若以点C，M，N为顶点的三角形与△ABC相似，则MN CMCB AB=或MN CMCA AB=，由这两种情况分别求出M的坐标即可．例2、答案：（1）∵一元二次方程ax2+bx+c＝0的两根为1和3，∴OA＝OC＝3，OB＝1，∴点C（0，3），设二次函数的表达式y＝a（x-1）（x-3），∴a（0-1）（0-3）＝3，∴a＝1，∴y＝（x-1）（x-3），∴抛物线解析式为：y＝x2-4x+3；（2）分两种情况：①如图1，当点P1为直角顶点时，点P1与点B重合，则P1（1，0），②如图2，当点A为△APD2的直角顶点，∵OA＝OC，∠AOC＝90°，∴∠OAD2＝45°，当∠D2AP2＝90°时，∠OAP2＝45°，∴AO平分∠D2AP2．又∵P2D2∥y轴，∴P2D2⊥AO，∴点P2，D2关于x轴对称，设直线AC的函数关系式为y＝kx+b．由题意得：303k bb+=⎧⎨=⎩，∴13kb=-⎧⎨-⎩，∴直线AC的解析式为：y＝-x+3，∵D2在y＝-x+3上，P2在y＝x2-4x+3上，∴设D2（x，-x+3），P2（x，x2-4x+3），∴（-x+3）+（x2-4x+3）＝0，∴x2-5x+6＝0，∴x1＝2，x2＝3（舍），∴当x＝2时，y＝x2-4x+3＝22-4×2+3＝-1，∴P2的坐标为P2（2，-1），综上所得P点坐标为P1（1，0），P2（2，-1）；（3）分两种情况考虑：①以AP为边构造平行四边形，平移直线AP交x轴于点E，交抛物线于点F，∵点P 的坐标为（2，-1），∴设点F 的坐标为（x ，1），∴x 2-4x +3＝1，解得：x 1＝，x 2＝，∴点F 的坐标为（1）和（，1）；②以AP 为对角线进行构造平行四边形，∵点A ，E 的纵坐标为0，∴点F 的纵坐标为-1，此时点P ，F 重合，∴不存在这种情况，舍去．综上所述，符合条件的F 点有两个，即（，1）和（，1）．分析：（1）先求出点C 坐标，代入解析式可求解；（2）分两种情况讨论，由直角三角形的性质可求解；（3）分两种情况讨论，利用平行四边形的性质可求解．同步练习：1、解：（1）∵抛物线241y ax ax =-+∴点C 的坐标为（0,1）∵OB =3OC ∴点B 的坐标为（3,0）∴91210a a -+=∴13a =∴214133y x x =-+ （2）如图，过点P 作PM ⊥y 轴，PN ⊥x 轴，垂足分别为点M ，N ．∵∠MPC =90°-∠CPN ，∠NPB =90°-∠CPN ，∴∠MPC =∠NPB在△PCM 和△PBN 中，PMC PNB MPC NPB PC PB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△PCM ≌△PBN ，∴PM =PN ．).,(a a P 设点22PB PC = ，2222)3()1(a a a a +-=-+∴，2=a 解得，).2,2(P ∴),0,3(,2B x =该抛物线对称轴为 ).0,1(A ∴),1,0(),0,3(),0,1(),2,2(C B A P .2,22,22===∴AB AC PO,45,135 =∠=∠POB CAB 31tan ==∠∆OB OC OBC BOC Rt 中，在， ,90,45 <∠≠∠∴OCB OBC ,OA OC OAC Rt =∆中，在,45,45 <∠∴=∠∴ACB OCA左侧时：只有在点相似时，点与当O Q ABC OPQ ∆∆)0,4(,4,2222)1(-∴=∴=∴=Q OQ OQOQ OP AB AC 时，当 )0,2(,2,2222)2(-∴=∴=∴=Q OQ OQ OP OQ AB AC 时，当当点Q 在点A 右侧时，综上所述，点Q 的坐标为)0,2()0,4(--或2、解：（1）∵B （2，t ）在直线y ＝x 上，∴t ＝2，∴B （2，2），把A 、B 两点坐标代入抛物线解析式可得42293042a b a b +=⎧⎪⎨+=⎪⎩，解得23a b =⎧⎨=-⎩， ∴抛物线解析式为y ＝2x 2-3x ；（2）如图1，过C 作CD ∥y 轴，交x 轴于点E ，交OB 于点D ，过B 作BF ⊥CD 于点F ，∵点C 是抛物线上第四象限的点，∴可设C （t ，2t 2-3t ），则E （t ，0），D （t ，t ），∴OE ＝t ，BF ＝2-t ，CD ＝t -（2t 2-3t ）＝-2t 2+4t ，∴S △OBC ＝S △CDO +S △CDB ＝12CD •OE +12CD •BF ＝12（-2t 2+4t ）（t +2-t ）＝-2t 2+4t ， ∵△OBC 的面积为2，∴-2t 2+4t ＝2，解得t 1＝t 2＝1，∴C （1，-1）；（3）存在．连接AB 、OM ．设MB 交y 轴于点N ，如图2，∵B （2，2），∴∠AOB ＝∠NOB ＝45°，在△AOB 和△NOB 中=AOB NOB OB OBABO NBO ⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△AOB ≌△NOB （ASA ），∴ON ＝OA ＝32， ∴N （0，32），∴可设直线BN 解析式为y ＝kx +32， 把B 点坐标代入可得2＝2k +32，解得k ＝14，∴直线BN 的解析式为y ＝14x +32， 联立直线BN 和抛物线解析式可得2134223y x y x x ⎧=+⎪⎨⎪=-⎩，解得22x y =⎧⎨=⎩或384532x y ⎧=-⎪⎪⎨⎪=⎪⎩， ∴M （-38，4532）， ∵C （1，-1），∴∠COA ＝∠AOB ＝45°，且B （2，2），∴OB ＝OC， ∵△POC ∽△MOB ，∴OM OB OP OC=＝2，∠POC ＝∠BOM ， 当点P 在第一象限时，如图3，过M 作MG ⊥y 轴于点G ，过P 作PH ⊥x 轴于点H ，∵∠COA ＝∠BOG ＝45°，∴∠MOG ＝∠POH ，且∠PHO ＝∠MGO ，∴△MOG ∽△POH ， ∴OM MG OG OP PH OH==＝2， ∵M （-38，4532）， ∴MG ＝38，OG ＝4532， ∴PH ＝12MG ＝316，OH ＝12OG ＝4564，∴P （4564，316）． 根据对称性可知，作点P 关于直线OC 使得对称点P ′，显然△P ′OC ∽△MOB ， ∵直线OC 的解析式为y ＝-x ，∴直线PP ′的解析式为y ＝x -3364， 由3364y x y x =-⎧⎪⎨=-⎪⎩，解得3312833128y y ⎧=⎪⎪⎨⎪=⎪⎩， 设P ′（m ，n ），则有45642m +＝33128，3162n +＝-33128， 解得m ＝-316，n ＝-4564，∴P ′（-316，-4564）， 故存在满足条件的点P ，其坐标为（4564，316）或（-316，-4564）．。
中考数学 二次函数存在性问题 及参考答案
中考数学二次函数存在性问题及参考答案中考数学二次函数存在性问题及参考答案一、二次函数中相似三角形的存在性问题1.如图，把抛物线 $y=x^2$ 向左平移1个单位，再向下平移4个单位，得到抛物线 $y=(x-h)^2+k$。
所得抛物线与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，顶点为D。
1）写出h、k的值；2）判断△ACD的形状，并说明理由；3）在线段AC上是否存在点M，使△AOM∽△ABC？若存在，求出点M的坐标；若不存在，说明理由。
2.如图，已知抛物线经过A（$-2,0$），B（$-3,3$）及原点O，顶点为C。
1）求抛物线的解析式；2）若点D在抛物线上，点E在抛物线的对称轴上，且A、O、D、E为顶点的四边形是平行四边形，求点D的坐标；3）P是抛物线上的第一象限内的动点，过点P作PM⊥x 轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由。
二、二次函数中面积的存在性问题3.如图，抛物线 $y=ax^2+bx$ （$a>0$）与双曲线$y=\frac{k}{x}$ 相交于点A，B。
已知点B的坐标为（$-2,-2$），点A在第一象限内，且 $\tan\angle AOX=4$。
过点A作直线AC∥x轴，交抛物线于另一点C。
1）求双曲线和抛物线的解析式；2）计算△ABC的面积；3）在抛物线上是否存在点D，使△ABD的面积等于△ABC的面积。
若存在，请写出点D的坐标；若不存在，请说明理由。
4.如图，抛物线 $y=ax^2+c$ （$a>0$）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（$-2,0$），B（$-1,-3$）。
1）求抛物线的解析式；2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标；3）在第（2）问的结论下，抛物线上的点P使$\triangle PAD=4\triangle ABM$ 成立，求点P的坐标。
二次函数解析几何--存在性问题
二次函数解析几何专题——存在性问题存在性问题是指判断满足某种条件的事物是否存在的问题，这类问题的知识覆盖面较广，综合性较强，题意构思非常精巧，解题方法灵活，对学生分析问题和解决问题的能力要求较高，是近几年来各地中考的“热点”。
这类题目解法的一般思路是：假设存在→推理论证→得出结论。
若能导出合理的结果，就做出“存在”的判断，导出矛盾，就做出不存在的判断。
由于“存在性”问题的结论有两种可能，所以具有开放的特征，在假设存在性以后进行的推理或计算，对基础知识，基本技能提出了较高要求，并具备较强的探索性，正确、完整地解答这类问题，是对我们知识、能力的一次全面的考验。
一、方法总结解存在性问题的一般步骤：（1）假设点存在；（2）将点的坐标设为参数；（3）根据已知条件建立关于参数的方程或函数。
二、常用公式（1）两点间距离公式：若A (x 1，y 1)，B (x 2，y 2)，则|AB|=221221)()(y y x x -+-（2）中点坐标公式：1212,22x x y y x y ++==（3）斜率公式：①；②（为直线与x 轴正方向的夹角）2121y y k x x -=-tan k θ=θ（4）①对于两条不重合的直线l 1、l 2，其斜率分别为k 1、k 2，则有l 1∥l 2⇔k 1＝k 2②如果两条直线l 1、l 2的斜率存在，设为k 1、k 2，则l 1⊥l 2⇔k 1k 2＝－1.题型一 面积问题例1．如图，抛物线y ＝－x 2＋bx ＋c 与x 轴交于A (1，0)，B (－3，0)两点．（1）求该抛物线的解析式；（2）在（1）中的抛物线上的第二象限内是否存在一点P ，使△PBC 的面积最大？，若存在，求出点P 的坐标及△PBC 的面积最大值；若不存在，请说明理由．变式练习：1.如图，在直角坐标系中，点A 的坐标为(－2，0)，连结OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB ．（1）求点B 的坐标；（2）求经过A 、O 、B 三点的抛物线的解析式；（3）如果点P 是（2）中的抛物线上的动点，且在x 轴的下方，那么△PAB 是否有最大面积？若有，求出此时P 点的坐标及△PAB 的最大面积；若没有，请说明理由．O B A CyxA xy BO能力提升：1.（2013菏泽）如图1，△运动到何处时，四边形PDCQ的面积最小？此时四边形2．如图，已知抛物线y=x2+bx+c的图象与x轴的一个交点为B（5，0），另一个交点为A，且与y轴交于点C（0，5）．（1）求直线BC与抛物线的解析式；（2）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值；（3）在（2）的条件下，MN取得最大值时，若点P是抛物线在x轴下方图象上任意一点，以BC为边作平行四边形CBPQ，设平行四边形CBPQ的面积为S1，△ABN的面积为S2，且S1=6S2，求点P的坐标．3.如图，二次函数的图象与x轴相交于点A（-3，0）、B（-1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y=kx-4k（k≠0）的图象过点P交x轴于点Q．（1）求该二次函数的解析式；（2）当点P的坐标为（-4，m）时，求证：∠OPC=∠AQC；（3）点M，N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．连接AN，当△AMN的面积最大时，①求t的值；②直线PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由．yD BMA CO xE 图1的坐标，并求出△POB的面积；若不存在，请说明理由．）中抛物线的第二象限图象上是否存在一点与△POC的坐标；若不存在，请说明理由；c的图象的顶点C的坐标为（0，-2），交m（m＞1）与x轴交于D。
二次函数图象上点的存在性问题
联合函数y＝x2 可得
ቤተ መጻሕፍቲ ባይዱ
P（3，9）
M
练习：(2009—2010 昌平二模)如图，抛物线y=ax2+bx-4a经 过A(-1，0)、C(0，4)两点，与x轴交于另一点B． （1）求抛物线的解析式； （2）已知点D(m，m+1)在第一象限的抛物线上，求点D关 于直线BC对称的点的坐标； （3）在（2）的条件下，连接BD，点P为抛物线上一点， 且∠DBP=45°，求点P的坐标．
例1已知抛物线 y＝x2－2x－3 的的顶点为 D，点 P、 Q 是抛 物线上的动点，若△DPQ 是等边三角形，求△DPQ的面积。
解：根据 y＝x2－2x－3可得D（1，-4），因为△QPD是等边三
角形，所以直线DQ的斜率为 ，因为D（1，-4），
所以l DQ: y＝ x-4-
,与二次函数y＝x2－2x－3联立起来解方 程，可得xQ=1+
∵P点在抛物线上，
∴P (
)
全等、相似与角度
板块二：二次函数与多个角
技巧和方法： 在抛物线上找点，满足两角和(差)关系。
例1二次函数 y＝x2－2x－3 的图象与 x 轴交于 A、 B 两点 (点 A 在点 B 的左侧)，与 y 轴交于 C 点，在二次函数的图 象上是否存在点 P，使锐角∠PCO＞∠ACO？若存在，请你 求出 P 点的横坐标的取值范围；若不存在，请你说明理由。
例3 (2010 苏州)如图，以 A 为顶点的抛物线与 y 轴交于点 B。 已知 A、 B 两点的坐标分别为(3， 0)、 (0， 4)。 ⑶在⑵的条件下，试问：对于抛物线对称轴上的任意一点 P， PA2＋PB2＋PM2＞28 是否总成立？ 请说明理由
解：(1) （1）设y=a(x-3)2，把B（0，4）代入，得a= （2）∵m，n为正整数∴ (m-3)2 应该是9的整数，∴m是3的倍数， 又∵m>3，∴m=6，9，12...， 当m=6时，n=4，此时MA=5，MB=6， ∴四边形OAMB的四边长为3，4，5，6， 当m≥9时，MB>6，∴四边形OAMB的四边长不能是四个连续的 正整数，∴点M坐标只有一种可能（6，4）； （3）设P（3，t），MB与对称轴交点为D，
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(1)若⊙P的半径为5，则P点坐标是( ， )；A点坐标是( ， )；以P为
顶点，且经过A点的抛物线的解析式是
；
(2)在(1)的条件下，上述抛物线是否经过点C关于原点的对称点D，请说明
x （1）求证：△AOE与△BOF的面积相等； （2）记S=S△0EF－S△ECF，求当k为何值时，S有最大值，最大值为多少？ （3）请探索：是否存在这样的点F，使得将△ECF沿EF对折后，C点恰 好落在OB上？若存在，求出点F的坐标；若不存在，请说明理由．
2009年湖州市毕业生学业考试数学卷
24、已知抛物线 y x2 2x a(a 0)与轴相交于点A，顶点为M.直
线 y 1 x a 分别与x轴，y轴相交于B，C两点，并且与直线相交于点
N.
2
(1)填空：试用含a 的代数式分别表示点M与N的坐标，则M（ ，），N
（ ，）；
(2)如图，将△NAC沿y轴翻折，若点N的对应点N′恰好落在抛物线上，AN′
与x轴交于点D，连结CD，求 的值a和四边形ADCN的面积； (3)在抛物线上 y x2 2x a(a 0) 是否存在一点P，使得以P、A、C、N为
顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，试说明
理由.
y
y
C C
N
N′
N
O
B
D
x
O
B
x
A
A
M
M
二次函数与存在性 问题专题复习
夹浦中学 金晓峰
结束寄语
下课了!
•万变不离其宗. •一切皆有可能.
理由；
(3)试问：是否存在这样的直线l，当P在运动过程中，经过A、B、C三点的
抛物线的顶点都在直线l上？若存在，请求出直线l的解析式；若不存在，
请说明理由。
y
C OA
P B
(第24题图)
y 3x 5
x
2008年湖州市毕业生学业考试数学卷
24．（本小题12分）
已知：在矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴 和y轴，建立如图所示的平面直角坐标系．F是边BC上的一个动点（不与 B，C重合），过F点的反比例函数 y k (k 0)的图象与边交于点．