信道编码理论26页PPT
合集下载
信道编码中ppt课件

外语关键词
循环码:cyclic code 码多项式:code polynomial 生成多项式:generator polynomial 求模运算:modular arithmetic 系统码:systematic(regular)code 循环移位运算:cycle shift operation
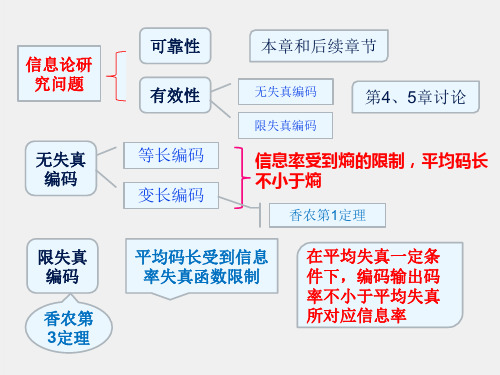
上节回顾:线性分组码
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
插件1:查表分解xn-1的方法
(1)并非所有的xn-1都具有r次的既约(不能再分解)的因式。 但只要满足n=2r-1,xn-1就具有r次的既约因式。因此 P194 页表4中只列出满足n=2m-1的xn-1的分解情况。
由对偶式 (1110011)2和187页表知m23(x)=x6+x5+x4+x+1; i=7:(111)8=(1001001)2,得知m7(x)=x6+x3+1;
对偶式还是自己。
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
本节的主要内容
❖ 码多项式 ❖ 循环移位的数学表达 ❖ 循环码的生成多项式 ❖ 循环码的编码 ❖ 循环码的译码 ❖ 编、译码的电路实现
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
循环码:cyclic code 码多项式:code polynomial 生成多项式:generator polynomial 求模运算:modular arithmetic 系统码:systematic(regular)code 循环移位运算:cycle shift operation
上节回顾:线性分组码
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
插件1:查表分解xn-1的方法
(1)并非所有的xn-1都具有r次的既约(不能再分解)的因式。 但只要满足n=2r-1,xn-1就具有r次的既约因式。因此 P194 页表4中只列出满足n=2m-1的xn-1的分解情况。
由对偶式 (1110011)2和187页表知m23(x)=x6+x5+x4+x+1; i=7:(111)8=(1001001)2,得知m7(x)=x6+x3+1;
对偶式还是自己。
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
本节的主要内容
❖ 码多项式 ❖ 循环移位的数学表达 ❖ 循环码的生成多项式 ❖ 循环码的编码 ❖ 循环码的译码 ❖ 编、译码的电路实现
烧伤病人的治疗通常是取烧伤病人的 健康皮 肤进行 自体移 植,但 对于大 面积烧 伤病人 来讲, 健康皮 肤很有 限,请 同学们 想一想 如何来 治疗该 病人
信息论与编码原理第7章信道编码的基本概念PPT课件

二进制:每个码元的信息含量为 1 比特,二进制的波特率与比特 率在数值上是相等的。
M进制:每一个码元的信息含量为 log2M。如果码元传输速率为 rs
波特,相应的比特率 rb 为:rb = rs log2M (bit/s)
05.08.2020
Department of Electronics and Information, NCUT Song Peng
▼ 在电报传送时,允许的比特差错率约为 10-4~10-5; ▼ 计算机数据传输,一般要求比特差错率小于 10-8~10-9; ▼ 遥控指令和武器系统指令中,要求误比特率更小。
05.08.2020
Department of Electronics and Information, NCUT Song Peng
第8页
7.1 信道编码在数字通信系统中的地位和作用
(2) 通信系统的主要技术指标
差错率:差错率是衡量传输质量的重要指标之一,有几种不同的定义 码元差错率:指在传输的码元总数中发生差错的码元数所占的比例 (平均值),简称误码率。 比特差错率(比特误码率):指在传输的比特总数中发生差错的比 特数所占的比例(平均值)。在二进制传输系统中,码元差错率就是 比特差错率。 码组差错率:指在传输的码组总数中发生差错的码组数所占的比例 (平均值)。 根据不同的应用场合对差错率有不同的要求。
信息论与编码原理
(第七章)
──────────────
信道编码的基本概念
05.08.2020
Department of Electronics and Information, NCUT So点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
信道编码的概念PPT课件

o 有些实际信道既有独立随机差错,也有突发性成串差错, 我们称它为混合信道。
o 从信道编码的构造方法看,信道编码的基本思路是根据一
定的规律在待发送的信息码中加入一些人为多余的码元,
以保证传输过程可靠性。信道编码的任务就是构造出以最
小多余度代价换取最大抗干扰性能的“好码”。
2021/6/4
3
信道编码通信系统的主要技术指标
根据监督元与信息元之间关系可分为:线性码 和非线性码
根据码的功能可分为:检错码和纠错码
2021/6/4
8
恒比码
非线性码
分组码
检 纠 错 码
线性码
群计数码 非循环码 循环码
奇偶校验码 汉明码 BCH码
信 道 编
卷积码
非系统卷积码
RS码
正交码
码
系统卷积码
W-A码
正
m序列
交 编
岩垂码
码
L序列
扩散码
信道编码的基本思想
2
o 信道编码的目的是为了改善数字通信系统的传输质量。由 于实际信道存在噪声和干扰,使得发送的码字与经信道传
输后所接收的码字之间存在差异,这种差异称为差错。信 道噪声、干扰越大,码字产生差错的概率也就越大。
o 在有记忆信道中,噪声、干扰的影响往往是前后相关的, 错误是成串出现的,在编码中称这类信道为突发差错信道 。实际的衰落信道、码间干扰信道均属于这类信道。
率p(R/C)。
n1
无记忆二进制信道:对任意的n都有 p(R/C) p(Ri /Ci)
则称为无记忆二进制信道。
i0
无记忆二进制对称信道/BSC/硬判决信道:无记忆二进制 信进道制的对转称移信概道率(见又下满页足)。p(0/1)=p(1/0)=pb,称为无记忆二
o 从信道编码的构造方法看,信道编码的基本思路是根据一
定的规律在待发送的信息码中加入一些人为多余的码元,
以保证传输过程可靠性。信道编码的任务就是构造出以最
小多余度代价换取最大抗干扰性能的“好码”。
2021/6/4
3
信道编码通信系统的主要技术指标
根据监督元与信息元之间关系可分为:线性码 和非线性码
根据码的功能可分为:检错码和纠错码
2021/6/4
8
恒比码
非线性码
分组码
检 纠 错 码
线性码
群计数码 非循环码 循环码
奇偶校验码 汉明码 BCH码
信 道 编
卷积码
非系统卷积码
RS码
正交码
码
系统卷积码
W-A码
正
m序列
交 编
岩垂码
码
L序列
扩散码
信道编码的基本思想
2
o 信道编码的目的是为了改善数字通信系统的传输质量。由 于实际信道存在噪声和干扰,使得发送的码字与经信道传
输后所接收的码字之间存在差异,这种差异称为差错。信 道噪声、干扰越大,码字产生差错的概率也就越大。
o 在有记忆信道中,噪声、干扰的影响往往是前后相关的, 错误是成串出现的,在编码中称这类信道为突发差错信道 。实际的衰落信道、码间干扰信道均属于这类信道。
率p(R/C)。
n1
无记忆二进制信道:对任意的n都有 p(R/C) p(Ri /Ci)
则称为无记忆二进制信道。
i0
无记忆二进制对称信道/BSC/硬判决信道:无记忆二进制 信进道制的对转称移信概道率(见又下满页足)。p(0/1)=p(1/0)=pb,称为无记忆二
信道编码定理ppt课件

p
(
y
)
2
(
1
)
2
N
[(
H
Y
)
]
|
G
(
Y
)
|
2
N
[(
H
Y
)
]
§6.3:信道编码定理的证明及其物理意义
N
• 结合AEP定理:
p(x,y) p(xn, yn)
n1
• 设随机序列对 ( X , Y ) 的
,那么对恣意小的
数δ >0,我们总能找到足够大的N使全体序列对的集合能
•
•
•
•
•
•
•
•
•
•
•
§6.2:信道编码的作用及本质
匹配信道特性: -信道编码的本质
抗白噪声:
优秀的调制、信道编码方案,
扩频方式等。
抗衰落和多径干扰:
功控抗慢衰落,
空间分集抗平滑瑞利〔空间选择〕衰落,
Rake接纳机及自顺应平衡抗频率选择性,
交错编码抗时间选择性衰落等。
抗多址干扰与远近效应:
正交码型设计,
• 资源指的提供信息传输所付出的代价
• 包括频率、时间、空间、功率等等。但不包括
实现复杂度
• 一个好的编码就是要充分利用资源,传送尽能
够多的信息
§6.2:信道编码的作用及本质
-信道编码的三种情
形
– 给定资源和可靠性要求,经过信道编码尽量提
高传输速率〔例:多电平编码〕
– 给定对信息传输的速率和可靠性要求,经过信
信道编码定理
错误概率与译码准那么、编码方法-1
(
y
)
2
(
1
)
2
N
[(
H
Y
)
]
|
G
(
Y
)
|
2
N
[(
H
Y
)
]
§6.3:信道编码定理的证明及其物理意义
N
• 结合AEP定理:
p(x,y) p(xn, yn)
n1
• 设随机序列对 ( X , Y ) 的
,那么对恣意小的
数δ >0,我们总能找到足够大的N使全体序列对的集合能
•
•
•
•
•
•
•
•
•
•
•
§6.2:信道编码的作用及本质
匹配信道特性: -信道编码的本质
抗白噪声:
优秀的调制、信道编码方案,
扩频方式等。
抗衰落和多径干扰:
功控抗慢衰落,
空间分集抗平滑瑞利〔空间选择〕衰落,
Rake接纳机及自顺应平衡抗频率选择性,
交错编码抗时间选择性衰落等。
抗多址干扰与远近效应:
正交码型设计,
• 资源指的提供信息传输所付出的代价
• 包括频率、时间、空间、功率等等。但不包括
实现复杂度
• 一个好的编码就是要充分利用资源,传送尽能
够多的信息
§6.2:信道编码的作用及本质
-信道编码的三种情
形
– 给定资源和可靠性要求,经过信道编码尽量提
高传输速率〔例:多电平编码〕
– 给定对信息传输的速率和可靠性要求,经过信
信道编码定理
错误概率与译码准那么、编码方法-1
通信原理精品第10章 信道编码幻灯片PPT

设发送端发送A和B两个消息,要表示A、B两种消息只需 要一位编码,即用“1”表示A,用“0”表示B。这种编码无冗余 度,效率最高,但同时它也无抗干扰能力。若在传输过程中发 生误码,即“1”错成“0”或“0”错成“1”,收端无法判断收到 的码元是否发生错误,因为“1”和“0”都是发送端可能发送的 码元,所以这种编码方法无纠、检错能力。
第10章 信道编码
若增加一位监督码元,增加的监督码元与信息码元相同, 即用“11”表示消息A,用“00”表示信息B。如传输过程中发 生1位错误,则“11”、“00”变成“10”或“01”。此时接收端 能发现这种错误,因为发送端不可能发送“01”或“10”。但 它不能纠错,因为“11”和“00”出现1位错误时都可变成“10” 或“01”。所以,当接收端收到“10”或“01”时,它无法确定 发送端发送的是“11”还是“00”。
第10章 信道编码
两个等长码字之间对应码元不同的数目称为这两个码字的 汉明距离,简称为码距,通常用d表示。如码字“11011”和 “00101”之间有四个对应码元不同,故码距d=4。由于两个码 字模2相加,对应码元不同的位必为1,对应码元相同的位必为 0,所以两个码字模2相加得到的新码组的重量就是这两个码字 之间的距离。如: 1101100101=11110,11110的码重为4,与上 述所得到的码距相同。
为
d0≥t+e+1
(10-2-4)
第10章 信道编码
下面举例说明给定码距时,如何根据式(10-2-2)、(10-2-3) 及(10-2-4)来确定码的纠、检错能力。仍以发送端发送A、B两 种消息为例,信源编码用“1”表示消息A,用“0”表示消息 B。信道编码器每收到一个“1”,输出一个码字“1111”; 每收到一个“0”,输出一个码字“0000”。显然,每个码字 中一个码元是信息,另三个码元是监督元,这个码共有两个码 字,这两个码字间的距离就是码的最小距离,所以这个码的最 小码距d0=4。
第10章 信道编码
若增加一位监督码元,增加的监督码元与信息码元相同, 即用“11”表示消息A,用“00”表示信息B。如传输过程中发 生1位错误,则“11”、“00”变成“10”或“01”。此时接收端 能发现这种错误,因为发送端不可能发送“01”或“10”。但 它不能纠错,因为“11”和“00”出现1位错误时都可变成“10” 或“01”。所以,当接收端收到“10”或“01”时,它无法确定 发送端发送的是“11”还是“00”。
第10章 信道编码
两个等长码字之间对应码元不同的数目称为这两个码字的 汉明距离,简称为码距,通常用d表示。如码字“11011”和 “00101”之间有四个对应码元不同,故码距d=4。由于两个码 字模2相加,对应码元不同的位必为1,对应码元相同的位必为 0,所以两个码字模2相加得到的新码组的重量就是这两个码字 之间的距离。如: 1101100101=11110,11110的码重为4,与上 述所得到的码距相同。
为
d0≥t+e+1
(10-2-4)
第10章 信道编码
下面举例说明给定码距时,如何根据式(10-2-2)、(10-2-3) 及(10-2-4)来确定码的纠、检错能力。仍以发送端发送A、B两 种消息为例,信源编码用“1”表示消息A,用“0”表示消息 B。信道编码器每收到一个“1”,输出一个码字“1111”; 每收到一个“0”,输出一个码字“0000”。显然,每个码字 中一个码元是信息,另三个码元是监督元,这个码共有两个码 字,这两个码字间的距离就是码的最小距离,所以这个码的最 小码距d0=4。
信道编码定理PPT教学课件
返回主目录
第8章
在数字通信系统中,信道的传输特性和传输过程 中噪声的存在是影响通信性能的两个主要因素。人们 总是希望在一定的传输条件下,达到最好的传输性能, 最佳接收就是在噪声干扰中如何有效地检测出信号。
所谓最佳是在某种标准下系统性能达到最佳,最 佳接收是个相对的概念,在某种准则下的最佳系统, 在另外一种准则下就不一定是最佳的。在某些特定条 件下,几种最佳准则也可能是等价的。
最小汉明距离译码
汉明距离 d(x,y), x,y中 分量不同的数目
码字先验等概 K元对称信道
p(i | i) 1 p p( j | i) p /(K 1)
最小汉明距离译码
N
ln p( y | xm ) ln p( yi | xmi ) n1 p
d ( y, xm ) ln K 1 (N d ( y, xm ))ln(1 p) N ln(1 p) d ( y, xm ) ln[(1 p)(K 1) / p]
1
j
e
jT 2
1e jt0
h(t) s(t0 t)
hs(t))
1
hs(tt))
1
0
T
Tt
2
(a)
so(t)
T 2
0
T
Tt
2
(b)
O
T
T
3T t
2
2
(c)
图8-3 信号时间波形
取t0=T,则有
H ()
1
j
e
jT 2
1e jT
h(t) s(t0 t)
(2) 匹配滤波器的输出为
s0 (t) R(t t0 ) s(x)s(x t t0 )dx
滤波器输入 滤波器输出
第8章
在数字通信系统中,信道的传输特性和传输过程 中噪声的存在是影响通信性能的两个主要因素。人们 总是希望在一定的传输条件下,达到最好的传输性能, 最佳接收就是在噪声干扰中如何有效地检测出信号。
所谓最佳是在某种标准下系统性能达到最佳,最 佳接收是个相对的概念,在某种准则下的最佳系统, 在另外一种准则下就不一定是最佳的。在某些特定条 件下,几种最佳准则也可能是等价的。
最小汉明距离译码
汉明距离 d(x,y), x,y中 分量不同的数目
码字先验等概 K元对称信道
p(i | i) 1 p p( j | i) p /(K 1)
最小汉明距离译码
N
ln p( y | xm ) ln p( yi | xmi ) n1 p
d ( y, xm ) ln K 1 (N d ( y, xm ))ln(1 p) N ln(1 p) d ( y, xm ) ln[(1 p)(K 1) / p]
1
j
e
jT 2
1e jt0
h(t) s(t0 t)
hs(t))
1
hs(tt))
1
0
T
Tt
2
(a)
so(t)
T 2
0
T
Tt
2
(b)
O
T
T
3T t
2
2
(c)
图8-3 信号时间波形
取t0=T,则有
H ()
1
j
e
jT 2
1e jT
h(t) s(t0 t)
(2) 匹配滤波器的输出为
s0 (t) R(t t0 ) s(x)s(x t t0 )dx
滤波器输入 滤波器输出
《信息论与编码》课件第6章 信道编码理论
X
信源编码
Y
差错控制 编码
Z
调制
信息错误
数据错 误一定
物理信道
条件:实
信宿
重建 符号
Xˆ
信源译码
Yˆ 差错控制 Zˆ
接收 信息
译码
接收 数据
解调
注
际信息传 输速率不 大于信道
容量,
意 1.信道一定,数据出现差错的概率一定,这是无
法改变的,与差错控制编码/译码方式无关
2.数据出现差错的概率不可改变,但是可以通过引 入差错控制编码/译码,降低信息传递中的错误
即如何选择 译码规则和 编码方法
减少信道传 输中的信息 差错
由于信道噪声或者干扰的存在, 会产生数据传输错误。
信道编码定理,也 称为香农第二定理
通信原理告诉我们,信噪声为例, 介绍虚警概率、漏报概率,以及 计算错误概率的过程和方法
原始
数
符号
信息
据
信源
(4) 纠正t个随机错误, ρ个删除,则要求码的最小距离满足 d0 ≥ ρ +2t+1
分组码的最小汉明距离满足下列关系
d0 n k 1
奇偶校验码是只有一个检验元的分组码 最小汉明距离为2,只能检测一个错误, 不能纠错。
是不等式, 不能用于计
算d0
差错 控制 译码 已知 条件
任务
6.3 译码规则
p( y)
p( y)
﹝ ❖ 考虑y的取值 两者之间比较
P(0 | y 0)
(1 pe ) p
p(1 pe ) (1 p) pe
P(1| y 0)
(1 p) pe
p(1 pe ) (1 p) pe
﹝ 两者之间比较
信源编码
Y
差错控制 编码
Z
调制
信息错误
数据错 误一定
物理信道
条件:实
信宿
重建 符号
Xˆ
信源译码
Yˆ 差错控制 Zˆ
接收 信息
译码
接收 数据
解调
注
际信息传 输速率不 大于信道
容量,
意 1.信道一定,数据出现差错的概率一定,这是无
法改变的,与差错控制编码/译码方式无关
2.数据出现差错的概率不可改变,但是可以通过引 入差错控制编码/译码,降低信息传递中的错误
即如何选择 译码规则和 编码方法
减少信道传 输中的信息 差错
由于信道噪声或者干扰的存在, 会产生数据传输错误。
信道编码定理,也 称为香农第二定理
通信原理告诉我们,信噪声为例, 介绍虚警概率、漏报概率,以及 计算错误概率的过程和方法
原始
数
符号
信息
据
信源
(4) 纠正t个随机错误, ρ个删除,则要求码的最小距离满足 d0 ≥ ρ +2t+1
分组码的最小汉明距离满足下列关系
d0 n k 1
奇偶校验码是只有一个检验元的分组码 最小汉明距离为2,只能检测一个错误, 不能纠错。
是不等式, 不能用于计
算d0
差错 控制 译码 已知 条件
任务
6.3 译码规则
p( y)
p( y)
﹝ ❖ 考虑y的取值 两者之间比较
P(0 | y 0)
(1 pe ) p
p(1 pe ) (1 p) pe
P(1| y 0)
(1 p) pe
p(1 pe ) (1 p) pe
﹝ 两者之间比较
信道编码的发展史PPT课件

第7页/共27页
信道编码的发展·卷积码
Elias在1955年提出的卷积码使得无线 通信性能有了跳跃式的发展,卷积码与 分组码的不同在于:它充分利用了各个 信息块之间的相关性。
通常卷积码记为(n,k,N)码。卷积码的 编码过程是连续进行的,依次连续将每 k个信息元输入编码器,得到n个码元, 得到的码元中的检验元不仅与本码的信 息元有关,还与以前时刻输入到编码器 的信息元(反映在编码寄存器的内容上) 有关。
紧接着,Turbo码成为通信研究的前沿,全世界各 大公司都聚焦在这个领域,包括法国电信、NTT、 DoCoMo、索尼、NEC、朗讯、三星、爱立信、诺基 亚 、 摩托罗拉和高通等等。
Turbo码成为了始于本世纪初的3G/4G移动通信技 术的核心,直到今天4.5G,我们依然在采用。
第19页/共27页
信道编码的发展·LDPC码
第14页/共27页
信道编码的发展·Turbo码
其次,与其他系统不同,Turbo码系统在发射端和接收端分别设置两个 编码器和解码器。其中一对编解码器对特定的一段比特流进行奇偶校验 码的加入和校验计算,另一对编解码器则在同一段码流经过交织扰动后 对其进行上述同样操作。
Turbo编码器结构。Turbo码编码器是由两个或多个反馈的系统卷积码编码器通过一个随机 交织器并行连接而成,编码后的校验位经过删余矩阵,从而产生不同码率的码字。
第15页/共27页
信道编码的发展·Turbo码
由于这两段码流包含同样的数据,如果没有信道噪声, 解码结果应该一致。但在噪声干扰下两组结果会产生差别。 通过上述对比特判决的可置信度信息的帮助,把这两组结 果彼此参照,可以得出第一次近似的结果。把这一结果 “反馈”到解码器前端,再进行迭代,经过几次迭代两个 解码器的结果就会互相接近(收敛)。这样就绕过了计算 复杂性问题。
信道编码的发展·卷积码
Elias在1955年提出的卷积码使得无线 通信性能有了跳跃式的发展,卷积码与 分组码的不同在于:它充分利用了各个 信息块之间的相关性。
通常卷积码记为(n,k,N)码。卷积码的 编码过程是连续进行的,依次连续将每 k个信息元输入编码器,得到n个码元, 得到的码元中的检验元不仅与本码的信 息元有关,还与以前时刻输入到编码器 的信息元(反映在编码寄存器的内容上) 有关。
紧接着,Turbo码成为通信研究的前沿,全世界各 大公司都聚焦在这个领域,包括法国电信、NTT、 DoCoMo、索尼、NEC、朗讯、三星、爱立信、诺基 亚 、 摩托罗拉和高通等等。
Turbo码成为了始于本世纪初的3G/4G移动通信技 术的核心,直到今天4.5G,我们依然在采用。
第19页/共27页
信道编码的发展·LDPC码
第14页/共27页
信道编码的发展·Turbo码
其次,与其他系统不同,Turbo码系统在发射端和接收端分别设置两个 编码器和解码器。其中一对编解码器对特定的一段比特流进行奇偶校验 码的加入和校验计算,另一对编解码器则在同一段码流经过交织扰动后 对其进行上述同样操作。
Turbo编码器结构。Turbo码编码器是由两个或多个反馈的系统卷积码编码器通过一个随机 交织器并行连接而成,编码后的校验位经过删余矩阵,从而产生不同码率的码字。
第15页/共27页
信道编码的发展·Turbo码
由于这两段码流包含同样的数据,如果没有信道噪声, 解码结果应该一致。但在噪声干扰下两组结果会产生差别。 通过上述对比特判决的可置信度信息的帮助,把这两组结 果彼此参照,可以得出第一次近似的结果。把这一结果 “反馈”到解码器前端,再进行迭代,经过几次迭代两个 解码器的结果就会互相接近(收敛)。这样就绕过了计算 复杂性问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 卷积码基础
卷积码的基本概念 卷积码的矩阵和多项式描述 初始截段码 卷积码的树图表示及其距离度量 卷积码的状态图表示
1
有记忆的编码方法
从一般的角度讲,当前的编码符号完全可以不仅受当前的信息符号控 制,而且还可受控于其它时刻的输入信息符号;
从因果的角度出发,可以只考虑受控于当前及历史上的输入符号流。 换句话说,就是编码器可以是有记忆的;
其中,gi,j表示第i个信息位对当前及后续m个子码的第j个码元的 影响。
生成多项式矩阵:
G D 11 D 1 D 2
k 0 n0 维矩阵G(D) 表示:卷积码码字中,每一段子码的n0个
码元与k0个信息位之间的关系。
卷积码的设计:
g 子生 G 成 D 编 元码电路
有限响应系统如右上图 所示:
X
Yk=iAiXk-i 由于其生成方法与线性信号 系统中的卷积相类似,因而 称为卷积码。
无限记忆系统如右下图所示: X Tk=iBiTk-i+Xk Yk=iAiTk-I
D
D
A0
A1
A2
Y
B1
B2
D
D
A0
A1
A2
Y
3
描述卷积码的参数
一般将卷积码标记为(n0, k0, m)码,其中
Step1: G ( D ) 1 D D 31 D D 2 D 3
11 11 01 11 00 00
G00 11 11 01 11 00
Step2:
c1
+
m
D
D
D
+
c2
8
Example 1
Step3:
11 11 01 11 00 00 00
Mi(1) Mi(2)
ci(1) ci(2)
(3,2,2) 卷积编码器
ci(3)
10
Example 2
Step1:
g1,1 100 g1,2 000 g1,3 101
g2,1 000 g2,2 100 g2,3 110
Step2:
100 10000 1000 0 g010 100 100000 0
Step3:
GD10
0 1
11D D2
11
Example 2
Step4:
101 000 001 000 000
011 001 000 000 000
G
101 011
000 001
001 000
000 000
101 011
p2 p1 m
图1. (3, 1, 2)卷积码编码器
4
卷积码的生成矩阵
图1的生成矩阵:
设图1编码器的初始状态为全0,若输入的信息序列M=(100…)则 输出码序列为C=(111, 010, 001, 000,…)。码序列中第m+1段以后, 后面各段取值均为0。
若M=(111…)=(100…)+(010…)+(0010…)+…,则有C=(111, 010, 001, 000,…)+ (000,111, 010, 001, 000,…)+ (000, 000, 111, 010, 001,
p0T
In0
k0
p1T 0
p0T In0k0
H
pmT 0
pmT10
p0T In0k0
pmT10
pmT10
6
Example 1
Problem formulation:
已知(2,1,3)码的子生成元为 g1,1 1101 g1,2 1111
1 求出该码的G(D)和G矩阵; 2 画出该码的编码器; 3 求出相应于信息序列M=(101)的码序列; 4 判断此码是否是系统码。
7
Example 1
000 001
001 000
12
系统卷积码
系统卷积码的生成矩阵:
g∞
Ik0 p0 0p1
0p2 0pm
Ik0 p0 0p1 0p2 0pm
G
Ik0 p0
0p1
0p2
0pm
G(D)Ik0 P(D)
13
卷积码的一致校验矩阵
000,…)+…
C=MG∞
111 010 001 000 000
G 000000
111 000
010 111
Hale Waihona Puke 001 010000 001
基本生成矩阵:
g 1 1 10 1 00 0 10 0 00 0 0
5
卷积码的生成矩阵
子生成元:
g1,1 100 g1,2 110 g1,3 101
n0:每时刻编码器输出的码元个数;其集合称为卷积码的一个码段或 子组;
k0:每时刻编码器输入的信息位个数; m:编码存贮; m+1称为编码约束度,它表示编码过程中互相约束的
子码个数; n0 (m+1)称为编码约束长度,表示编码过程中互相约束的 码元个数;
码率:R=k0/n0。
图1为一个(3, 1, 2) 卷积码编码器:
CMG10100 11 11 01 11 00 00
00 00 11 11 01 11 00
11 11 10 00 01 11 00
Step4:
非系统码。
9
Example 2
Problem formulation:
一个(3, 2, 2)系统卷积码的编码器如下图所示,请给出 该码的的子生成元、基本生成矩阵、生成矩阵多项式 和生成矩阵。
卷积码的校验矩阵:
n0k0n0矩阵
GHT 0
h 0
G D H TD 0
h1 h2
h0 h1
h0
H
h
m
h m 1
h0
0 0
hm 0
h1
14
系统卷积码的一致校验矩阵
当卷积码为系统码时,注意到 GHT 0 , 此时的校 验矩阵为:
因此输出的编码符号流也就具有了一定的相关性;
编码器的记忆可以是有限的,也可以是无限的。
对于线性系统而言,有限记忆和无限记忆就分别对应于FIR和IIR滤 波器。
当从滤波器角度看时,输入输出要用同一域中的元素。这样输入符号 流应为GF(p)上的k维矢量。输出符号流为GF(p)上的n维矢量。
2
有限响应与无限记忆
卷积码的基本概念 卷积码的矩阵和多项式描述 初始截段码 卷积码的树图表示及其距离度量 卷积码的状态图表示
1
有记忆的编码方法
从一般的角度讲,当前的编码符号完全可以不仅受当前的信息符号控 制,而且还可受控于其它时刻的输入信息符号;
从因果的角度出发,可以只考虑受控于当前及历史上的输入符号流。 换句话说,就是编码器可以是有记忆的;
其中,gi,j表示第i个信息位对当前及后续m个子码的第j个码元的 影响。
生成多项式矩阵:
G D 11 D 1 D 2
k 0 n0 维矩阵G(D) 表示:卷积码码字中,每一段子码的n0个
码元与k0个信息位之间的关系。
卷积码的设计:
g 子生 G 成 D 编 元码电路
有限响应系统如右上图 所示:
X
Yk=iAiXk-i 由于其生成方法与线性信号 系统中的卷积相类似,因而 称为卷积码。
无限记忆系统如右下图所示: X Tk=iBiTk-i+Xk Yk=iAiTk-I
D
D
A0
A1
A2
Y
B1
B2
D
D
A0
A1
A2
Y
3
描述卷积码的参数
一般将卷积码标记为(n0, k0, m)码,其中
Step1: G ( D ) 1 D D 31 D D 2 D 3
11 11 01 11 00 00
G00 11 11 01 11 00
Step2:
c1
+
m
D
D
D
+
c2
8
Example 1
Step3:
11 11 01 11 00 00 00
Mi(1) Mi(2)
ci(1) ci(2)
(3,2,2) 卷积编码器
ci(3)
10
Example 2
Step1:
g1,1 100 g1,2 000 g1,3 101
g2,1 000 g2,2 100 g2,3 110
Step2:
100 10000 1000 0 g010 100 100000 0
Step3:
GD10
0 1
11D D2
11
Example 2
Step4:
101 000 001 000 000
011 001 000 000 000
G
101 011
000 001
001 000
000 000
101 011
p2 p1 m
图1. (3, 1, 2)卷积码编码器
4
卷积码的生成矩阵
图1的生成矩阵:
设图1编码器的初始状态为全0,若输入的信息序列M=(100…)则 输出码序列为C=(111, 010, 001, 000,…)。码序列中第m+1段以后, 后面各段取值均为0。
若M=(111…)=(100…)+(010…)+(0010…)+…,则有C=(111, 010, 001, 000,…)+ (000,111, 010, 001, 000,…)+ (000, 000, 111, 010, 001,
p0T
In0
k0
p1T 0
p0T In0k0
H
pmT 0
pmT10
p0T In0k0
pmT10
pmT10
6
Example 1
Problem formulation:
已知(2,1,3)码的子生成元为 g1,1 1101 g1,2 1111
1 求出该码的G(D)和G矩阵; 2 画出该码的编码器; 3 求出相应于信息序列M=(101)的码序列; 4 判断此码是否是系统码。
7
Example 1
000 001
001 000
12
系统卷积码
系统卷积码的生成矩阵:
g∞
Ik0 p0 0p1
0p2 0pm
Ik0 p0 0p1 0p2 0pm
G
Ik0 p0
0p1
0p2
0pm
G(D)Ik0 P(D)
13
卷积码的一致校验矩阵
000,…)+…
C=MG∞
111 010 001 000 000
G 000000
111 000
010 111
Hale Waihona Puke 001 010000 001
基本生成矩阵:
g 1 1 10 1 00 0 10 0 00 0 0
5
卷积码的生成矩阵
子生成元:
g1,1 100 g1,2 110 g1,3 101
n0:每时刻编码器输出的码元个数;其集合称为卷积码的一个码段或 子组;
k0:每时刻编码器输入的信息位个数; m:编码存贮; m+1称为编码约束度,它表示编码过程中互相约束的
子码个数; n0 (m+1)称为编码约束长度,表示编码过程中互相约束的 码元个数;
码率:R=k0/n0。
图1为一个(3, 1, 2) 卷积码编码器:
CMG10100 11 11 01 11 00 00
00 00 11 11 01 11 00
11 11 10 00 01 11 00
Step4:
非系统码。
9
Example 2
Problem formulation:
一个(3, 2, 2)系统卷积码的编码器如下图所示,请给出 该码的的子生成元、基本生成矩阵、生成矩阵多项式 和生成矩阵。
卷积码的校验矩阵:
n0k0n0矩阵
GHT 0
h 0
G D H TD 0
h1 h2
h0 h1
h0
H
h
m
h m 1
h0
0 0
hm 0
h1
14
系统卷积码的一致校验矩阵
当卷积码为系统码时,注意到 GHT 0 , 此时的校 验矩阵为:
因此输出的编码符号流也就具有了一定的相关性;
编码器的记忆可以是有限的,也可以是无限的。
对于线性系统而言,有限记忆和无限记忆就分别对应于FIR和IIR滤 波器。
当从滤波器角度看时,输入输出要用同一域中的元素。这样输入符号 流应为GF(p)上的k维矢量。输出符号流为GF(p)上的n维矢量。
2
有限响应与无限记忆
