离散数学模拟试卷二
离散数学(第2学期)自测题二及参考答案

一、 单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1. 下列命题公式为重言式的是( ) A.()→∧∧P Q Q R B. ()→⌝→⌝P P QC. ()⌝→∧Q R RD. ()()()()→∧→→→P Q Q R P R2. 偏序关系一定不是..( ) A.自反的B.传递的C.反自反的D.反对称的3. 设():A x x 是实数,():B x x 是有理数,命题“有的实数是有理数”符号化为( ) A. ()()()()∃→x A x B x B. ()()()()∃∨x A x B x C. ()()()()∃∧x A x B xD. ()()()()⌝∀∧⌝x A x B x4. 设给定赋值N 如下:个体域为自然数集;特定元素0=a ;特定函数()(),,,=+=f x y x y g x y xy ;特定谓词(),F x y 为=x y 。
在赋值N 下,下列公式为真的是( )A. ()()(),,∀x F g x a xB. ()()()()()()(),,,,∀∀→x y F f x a y F f y a x C. ()()()()(),,∀∀∀x y z F f x y z D. ()()()()(),,,∀∀x y F f x y g x y5. 命题公式()P Q R ⌝∧→的成真指派是( ) A. 000,001,110 B. 001,011,101,110,111 C.全体指派D.无6. 设A B A -=,则有( ) A.⋂=∅A BB.=B AC.⊆B AD.⊆A B7. 一棵树有2个3度结点,其余结点都是叶子,则叶子数是( ) A.7B.6C.5D.48. 在整数集Z 上,下列定义的运算能构成一个群的是( ) A. {}max ,*=a b a b B. *=-a b a b C. 1*=++a b a bD. *=a b ab9. 设1R 和2R 是集合A 上的相容关系,下列关于12R R ⊕的说法正确的是( ) A.一定是相容关系B.一定不是相容关系C.可能是也可能不是相容关系D.一定是等价关系10. 设{}{}{}{}1,2,3,4,5,6,7,8A =,下列选项正确的是( ) A. 1∈AB. {}1,2,3⊆AC. {}{}4,5⊂AD. ∅∈A11. 下列的度数列,可以简单图化的是( ) A. 5,5,4,4,2,1 B. 5,4,3,2,2 C. 3,3,3,1D. 4,4,3,3,2,212. 在整数集Z 上,下列运算满足结合律的是( ) A. *=-a b a b B. 1*=+a b ab C. 2*=+a b a bD. 1*=++a b a b13. 以下必为欧拉图的是( ) A.结点度数都是偶数的连通图 B.奇数度结点最多2个的连通图 C.存在欧拉图的图D.无回路的连通图14. 下列可一笔画成的图形是( )A. B. C.D.15. 具有4个结点的非同构的无向树的数目是( ) A.2B.3C.4D.5二、 填空题(本大题共10小题,每小题2分,共20分)请在每小格的空格中填上正确答案。
离散数学考试模拟试题及详细参考答案共四套

离散模拟答案11命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c)f是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.一、简答题(共6道题,共32分)1.求命题公式(P→(Q→R))(R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)x y(x+y=4)a)y x(x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A B)-C=(A-B)(A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f gd eb ca图17.已知有限集S={a 1,a2,…,an},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N;P(N);R,R×R,{o,1}(写出即可)(6分)二、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→F)→C,B→(A∧S)B→Eb)x(P(x)→Q(x)),x(Q(x)∨R(x)),x R(x)x P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠且B≠,关系R满足:<< x1,y1>,<x2,y2>>∈R,当且仅当<x1,x2>∈R1且<y1,y2>∈R2。
离散数学期末试卷及部分答案 (2)

离散数学试题(A 卷及答案)一、证明题(10分)1)(⌝P ∧(⌝Q ∧R))∨(Q ∧R)∨(P ∧R)⇔R证明: 左端⇔(⌝P ∧⌝Q ∧R)∨((Q ∨P)∧R)⇔((⌝P ∧⌝Q)∧R))∨((Q ∨P)∧R)⇔(⌝(P ∨Q)∧R)∨((Q ∨P)∧R)⇔(⌝(P ∨Q)∨(Q ∨P))∧R ⇔(⌝(P ∨Q)∨(P ∨Q))∧R ⇔T ∧R(置换)⇔R2)∃x(A(x)→B(x))⇔ ∀xA(x)→∃xB(x)证明 :∃x(A(x)→B(x))⇔∃x(⌝A(x)∨B(x))⇔∃x ⌝A(x)∨∃xB(x)⇔⌝∀xA(x)∨∃xB(x)⇔∀xA(x)→∃xB(x) 二、求命题公式(P ∨(Q ∧R))→(P ∧Q ∧R)的主析取范式和主合取范式(10分)证明:(P ∨(Q ∧R))→(P ∧Q ∧R)⇔⌝(P ∨(Q ∧R))∨(P ∧Q ∧R))⇔(⌝P ∧(⌝Q ∨⌝R))∨(P ∧Q ∧R) ⇔(⌝P ∧⌝Q)∨(⌝P ∧⌝R))∨(P ∧Q ∧R)⇔(⌝P ∧⌝Q ∧R)∨(⌝P ∧⌝Q ∧⌝R)∨(⌝P ∧Q ∧⌝R))∨(⌝P ∧⌝Q ∧⌝R))∨(P ∧Q ∧R) ⇔m0∨m1∨m2∨m7 ⇔M3∨M4∨M5∨M6三、推理证明题(10分)1) C ∨D, (C ∨D)→ ⌝E, ⌝E →(A ∧⌝B), (A ∧⌝B)→(R ∨S)⇒R ∨S证明:(1) (C ∨D)→⌝E(2) ⌝E →(A ∧⌝B)(3) (C ∨D)→(A ∧⌝B) (4) (A ∧⌝B)→(R ∨S) (5) (C ∨D)→(R ∨S)(6) C ∨D(7) R ∨S2) ∀x(P(x)→Q(y)∧R(x)),∃xP(x)⇒Q(y)∧∃x(P(x)∧R(x))证明(1)∃xP(x) (2)P(a)(3)∀x(P(x)→Q(y)∧R(x)) (4)P(a)→Q(y)∧R(a) (5)Q(y)∧R(a) (6)Q(y) (7)R(a) (8)P(a) (9)P(a)∧R(a) (10)∃x(P(x)∧R(x)) (11)Q(y)∧∃x(P(x)∧R(x))四、设m 是一个取定的正整数,证明:在任取m +1个整数中,至少有两个整数,它们的差是m 的整数倍证明 设1a ,2a ,…,1+m a 为任取的m +1个整数,用m 去除它们所得余数只能是0,1,…,m -1,由抽屉原理可知,1a ,2a ,…,1+m a 这m +1个整数中至少存在两个数s a 和t a ,它们被m 除所得余数相同,因此s a 和t a 的差是m 的整数倍。
《离散数学》试题带答案(二)

《离散数学》试题带答案试卷九试题与答案一、 填空 30% (每空 3分)1、 选择合适的论域和谓词表达集合A=“直角坐标系中,单位元(不包括单位圆周)的点集”则A= 。
2、 集合A={Φ,{Φ}}的幂集P (A) = 。
3、 设A={1,2,3,4},A 上二元关系R={<1,2>,<2,1>,<2,3>,<3,4>}画出R的关系图。
4、 设A={<1,2>,<2 , 4 >,<3 , 3 >} , B={<1,3>,<2,4>,<4,2>},则B A ⋃= 。
B A = 。
5、 设|A|=3,则A 上有 个二元关系。
6、 A={1,2,3}上关系R= 时,R 既是对称的又是反对称的。
7、 偏序集><≤R A ,的哈斯图为,则≤R = 。
8、 设|X|=n ,|Y|=m 则(1)从X 到Y 有 个不同的函数。
(2)当n , m 满足 时,存在双射有 个不同的双射。
9、 2是有理数的真值为 。
10、Q :我将去上海,R :我有时间,公式)()(Q R R Q →∧→的自然语言为 。
11、公式)()(Q P P Q ∧⌝∧→的 主合取范式是 。
12、 若} ,, , {21m S S S S =是集合A 的一个分划,则它应满足 。
二、 选择 20% (每小题 2分)1、 设全集为I ,下列相等的集合是( )。
A 、} |{是偶数或奇数x x A =;B 、)}2( |{y x I y y x B =∧∈∃=;C 、)}12( |{+=∧∈∃=y x I y y x C ;D 、},4,4,3,3,2,2,1,1,0|{ ----=x D 。
2、 设S={N ,Q ,R},下列命题正确的是( )。
A 、S S N N ∈∈∈2 ,2则; B 、S N S Q Q N ⊂∈⊂则 ,; C 、R N R Q Q N ⊂⊂⊂则 ,; D 、S N S N ⋂⊂Φ⊂Φ⊂Φ则 ,。
离散数学形考二
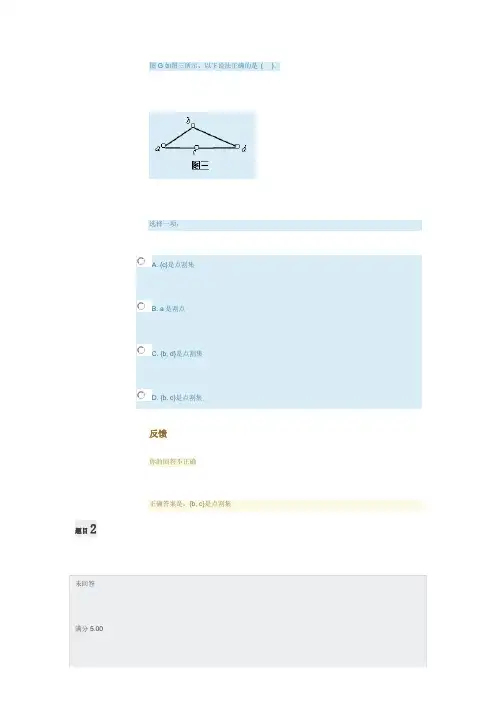
图G如图三所示,以下说法正确的是( ).选择一项:A. {c}是点割集B. a是割点C. {b, d}是点割集D. {b, c}是点割集反馈你的回答不正确正确答案是:{b, c}是点割集题目2标记题目题干如图二所示,以下说法正确的是( ).图二选择一项:A. {b, e}是点割集B. {a, e}是点割集C. {d}是点割集D. e是割点反馈你的回答不正确正确答案是:e是割点题目3未回答满分5.00标记题目题干已知无向图G的邻接矩阵为,则G有().选择一项:A. 6点,7边B. 5点,7边C. 6点,8边D. 5点,8边反馈你的回答不正确正确答案是:5点,7边题目4未回答满分5.00标记题目题干若G是一个欧拉图,则G一定是( ).选择一项:A. 汉密尔顿图B. 平面图C. 连通图D. 对偶图反馈你的回答不正确正确答案是:连通图题目5未回答满分5.00标记题目题干设无向图G的邻接矩阵为,则G的边数为( ).A. 3B. 4C. 5D. 6反馈你的回答不正确正确答案是:5题目6未回答满分5.00标记题目题干设G是有n个结点,m条边的连通图,必须删去G的( )条边,才能确定G的一棵生成树.A.B.C.D.反馈你的回答不正确正确答案是:题目7未回答满分5.00标记题目题干设无向图G的邻接矩阵为,则G的边数为( ).选择一项:A. 1B. 7C. 6D. 14反馈你的回答不正确正确答案是:7题目8题干无向简单图G是棵树,当且仅当( ).选择一项:A. G连通且边数比结点数少1B. G的边数比结点数少1C. G连通且结点数比边数少1D. G中没有回路.反馈你的回答不正确正确答案是:G连通且边数比结点数少1 题目9未回答满分5.00题干设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).图五选择一项:A. (b)是强连通的B. (a)是强连通的C. (c)是强连通的D. (d)是强连通的反馈你的回答不正确正确答案是:(a)是强连通的题目10未回答满分5.00标记题目题干无向完全图K4是().选择一项:A. 非平面图B. 树C. 欧拉图D. 汉密尔顿图反馈你的回答不正确正确答案是:汉密尔顿图标记题目信息文本判断题题目11未回答满分5.00标记题目题干设G是一个图,结点集合为V,边集合为E,则.( )选择一项:对错反馈正确的答案是“对”。
离散数学模拟试题、课后习题(附解析)超强集合

,即
r
2e 。而 ver 2 故 k
2 ver ve
k (v 2) 。 (8 分) k 2 k (v 2) ②彼得森图为 k 5, e 15, v 10 ,这样 e 不成立, k 2 2e 即得 k e
所以彼得森图非平面图。 (3 分)
二、 逻辑推演 16% 1、 证明: ①A ② A B ③ A B C D ④C D ⑤D ⑥D E ⑦D E F ⑧F ⑨A F 2、证明 ① xP( x) ② P (c ) ③ x( P ( x) Q( x)) ④ P (c ) Q ( c ) P(附加前提) US① P US③
五、计算 18%
1、设集合 A={a,b,c,d}上的关系 R={<a , b > ,< b , a > ,< b, c > , < c , d >}用矩阵运算求出 R 的传递闭包 t (R)。 (9 分)
4
离散数学模拟习题与解析 (1).doc
2、如下图所示的赋权图表示某七个城市 v1 , v 2 , , v7 及预先算出它们之间的一些直接通信线 路造价,试给出一个设计方案,使得各城市之间能够通信而且总造价最小。 (9分)
R { a, b , c, d | a, b S S , c, d S S , a d b c} 则 由
S S 上一个划分共有(
则公式 xyP( y, x) 真值为
2、 设S={a 1 ,a 2 ,…,a 8 },B i 是S的子集,则由B 31 所表达的子集是 。 3、 设 A={2 , 3 , 4 , 5 , 6} 上 的 二 元 关 系 R { x, y | x y x是质数} , 则 R=
《离散数学》模拟题
《离散数学》模拟题北航10秋学期《离散数学》模拟题⼀⼀、单项选择题(本⼤题共15⼩题,每⼩题2分,共30分)1.∑中所有有限长度的串形成的集合记为∑* ,容易证得∑*上的连接运算不满⾜交换律,但满⾜( A ) A .结合律 B .分配律 C .幂等律 D .吸收律 2.Klein 群中元素a,b,c 的阶为( B )。
A .1B .2C .3D .4 3.群G 的元素x 的所有幂的集合为G 的⼦群,称由x ⽣成的⼦群。
记为( A ). A . B .(x) C .x D .[x] 4.交换环是指乘法满⾜( A )。
A .交换律B .结合律C .分配律D .吸收律 5.⾄少有( B )元素的含单位元、⽆零因⼦环称为除环。
A .⼀ B .⼆ C .三 D .四 6.∨,∧满⾜( C )的格称为分配格A .交换律B .结合律C .分配律D .幂等律 7.若L 为有限布尔代数,则( B )正整数n ,L 与含有n 个元素的集合A 的幂集同构。
A .不存在 B .存在 C .有可能存在 8.有向图D 的顶点v 作为边的始点的次数之和称为v 的出度,记为d +(v), v 作为边的终点的次数之和称为v 的⼊度,记为d -(v),v 的度数d(v)= ( A )。
A .d +(v)+d -(v)B .d +(v)C .d -(v)D .d +(v)*d -(v) 9.若通路Г=v 0e 1v 1e 2…e 1v 1 中所有顶点互不相同(所有边⾃然互不相同)时称为( B ) A .初级回路 B .路径 C .复杂通路D .迹 10.在n 阶图中,若⼀顶点存在到⾃⾝的回路,则必存在从该顶点到⾃⾝的长度不超过( B )的回路。
A .n-1 B .n C .n+1 D .2n 11.“⼈总是要死的”谓词公式表⽰为( C )。
(论域为全总个体域)M(x):x 是⼈;Mortal(x):x 是要死的。
A .)()(x Mortal x M →; B .)()(x Mortal x M ∧C .))()((x Mortal x M x →?; D .))()((x Mortal x M x ∧?12. 公式))()((x Q x P x A →?=的解释I 为:个体域D={2},P(x):x>3, Q(x):x=4则A 的真值为( A )。
离散数学模拟试卷和答案
北京语言大学网络教育学院《离散数学》模拟试卷一注意:1.试卷保密,考生不得将试卷带出考场或撕页,否则成绩作废。
请监考老师负责监督。
2.请各位考生注意考试纪律,考试作弊全部成绩以零分计算。
3.本试卷满分100分,答题时间为90分钟。
4.本试卷分为试题卷和答题卷,所有答案必须答在答题卷上,答在试题卷上不给分。
一、【单项选择题】(本大题共15小题,每小题3分,共45分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在答题卷相应题号处。
1、在由3个元素组成的集合上,可以有()种不同的关系。
[A]3 [B]8 [C]9 [D]272、设A 1,2,3,5,8,B 1,2,5,7 ,则A B()。
[A] 3,8 [B] 3 [C]8[D] 3,83、若X是Y的子集,则一定有()。
[A]X 不属于Y [B]X ∈Y[C]X 真包含于Y [D]X∩Y=X4、下列关系中是等价关系的是()。
[A]不等关系[B] 空关系[C]全关系[D] 偏序关系5、对于一个从集合A到集合B的映射,下列表述中错误的是()。
[A]对A的每个元素都要有象[B]对A的每个元素都只有一个象[C]对B的每个元素都有原象[D]对B的元素可以有不止一个原象6、设p:小李努力学习,q: 小李取得好成绩,命题“除非小李努力学习,否则他不能取得好成绩”的符号化形式为()。
[A]p→q[B]q→p[C]┐q→┐p[D]┐p→q7、设A={a,b,c}, 则A到A的双射共有()。
[A]3 个[B]6 个[C]8个[D]9 个8、一个连通图 G 具有以下何种条件时,能一笔画出:即从某结点出发,经过图中每边仅一次回到该结点()。
[A]G 没有奇数度结点[B]G有1个奇数度结点[C]G 有2个奇数度结点[D]G 没有或有 2个奇数度结点9、设〈G,*〉是群,且|G|>1 ,则下列命题不成立的是( )。
[A]G 中有幺元 [B]G 中么元是唯一的[C]G 中任一元素有逆元 [D]G 中除了幺元外无其他幂等元10、令 p :今天下雪了, q :路滑,则命题“虽然今天下雪了,但是路不滑”可符号化 为( )[A]p [C]p →┐q ∧q [B]p [D]p ∨┐q∧┐q11、设图 G=<V,E>的结点集为 V={v1,v2,v3}, 边集为 E={<v1,v2>,<v1,v3>}.则G 的割 (点)集是()。
离散数学模拟试卷二答案
《离散数学》模拟试卷二答案一、【单项选择题】(本大题共15小题,每小题3分,共45分)二、【判断题】(本大题共8小题,每小题3分,共24分)三、【解答题】(本大题共3小题,24、25每小题10分,26小题11分,共31分)24、一次学术会议的理事会共有20个人参加,他们之间有的相互认识但有的相互不认识。
但对任意两个人,他们各自认识的人的数目之和不小于20。
问能否把这20个人排在圆桌旁,使得任意一个人认识其旁边的两个人?根据是什么?标准答案:解:可以把这20个人排在圆桌旁,使得任一人认识其旁边的两个人。
根据:构造无向简单图G=<V,E>,其中V={v1,v2,…,V20}是以20个人为顶点的集合,E中的边是若任两个人v i和v j相互认识则在v i与v j之间连一条边。
∀Vi∈V,d(v i)是与v i相互认识的人的数目,由题意知∀vi,v j∈V有d(v i)+d(v j)≥20,于是G中存在汉密尔顿回路。
设C=V i1V i2…V i20V i1是G中一条汉密尔顿回路,按这条回路的顺序按其排座位即符合要求。
复习范围或考核目标:考察无向图中的哈密尔顿图的应用,见课本211页。
25、图G=<V, E>,其中V={a, b, c, d, e, f },E={(a, b), (a, c), (a, e), (b, d), (b, e), (c, e), (d, e), (d, f), (e, f)},对应边的权值依次为5,2,1,2,6,1,9,3及8.(1)画出G的图形;(2)写出G 的邻接矩阵。
标准答案:解:(1)因为V ={a , b , c , d , e , f } E ={(a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (d , e ), (d , f ), (e , f )}, 权值依次为5,2,1,2,6,1,9,3及8 所以,G 的图形如右图所示:(2)分析:定义3.3.1 设G =<V ,E >是一个简单图,其中V ={v 1,v 2,…,v n },则n 阶方阵A (G )=(a ij )称为G 的邻接矩阵,其中⎪⎩⎪⎨⎧==.1j i v v v v a j i j i ij 不相邻或与相邻与邻接矩阵:复习范围或考核目标:考察图的矩阵表示,见课本187页。
苏XI友离散数学模拟试题2(附参考答案)
离散数学模拟试题2一、单选题(本大题共8小题,每小题2分,共16分)1.设p:天下大雨,q:我们乘公共汽车。
命题“除非天下大雨,否则我们不乘公共汽车。
”符号化为()A. p→qB. q→pC. p∧qD.⌝q →⌝ p 2.设F(x):x是兔子,G(y):y是乌龟,H(x,y):x比y跑得快。
命题“有的兔子比所有的乌龟跑得快”符号化为()A.∀x(F(x)→∃y(G(y)∧H(x,y)))B.∀x∃y((F(x)∧G(y))→H(x,y))C.∀x∃y(F(x)→(G(y)→H(x,y)))D. ∃x(F(x)∧∀y(G(y)→H(x,y))) 3.设集合A={∅,a},下面四个命题为真的是()A. a⊆AB.∅⊆AC.{∅}∈ AD.{a}∈ A 4.设集合A={a,b,c,d},A上的关系R={〈a,b〉,〈b,a〉, 〈c,d〉,〈d,c〉}∪I A,则下面命题为真的是()A. R是A上的等价关系B. R是A上的偏序关系C. R是A上的全序关系D. R是A上的全域关系5.设V=〈N,+〉,其中N为自然数集合,+为数的普通加法。
令φ:N→N,φ(x)=2x。
下面四个命题为真的是()A.是满同态B.是单自同态C.是自同构D.是V到自身的映射,但A,B,C都不是6.设Z是整数集合,∩是Z的幂集P(Z)上的交运算。
令V=〈P(Z);∩〉,则V是()A.循环群 B. 有限群 C. 无限群 D. 含幺半群7.设G是有n个顶点m条边的无向简单图,并且m=n-1,则有结论()A. G一定是树 B. G不一定是树 C.G一定不是树 D.G是森林8.完全图K4是()A. 欧拉图B.二部图C.平面图D.非平面图二、填空题(本大题共8小题,每小题3分,共24分)1.含n个命题变项的矛盾式的主析取范式为。
2.设个体域为自然数集合N,命题∀x∃y(x+y=1)的真值为。
3.设A={a,b},IA 是A上的恒等关系,则商集A/IA= 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学模拟试卷二
一、判断选择题(共20分,每小题2分)
( ) 1. 在命题逻辑中,任何命题公式的主合取范式都是存在的,并且是唯一的;( ) 2. 设A上的恒等关系I,它既是A上的等价关系也是A上的偏序关系;( ) 3. 设〈G,*〉是群,对于G中的任意元素a,b有:(a ⋅ b)-1=b-1 ⋅ a-1;( ) 4. 连通图G的任一边一定为图G的某一边割集中的一条边;
( ) 5. 图(a),(b),(c)两两同构;
(a)(b) (c)
选择题:
6设有如下命题
1)如果地上有水,则天上下雨
2)如果天上下雨,则地上有水
3)如果地上没有水,则天上不下雨
4)如果天上不下雨,则地上没有水
哪些命题等价的()
A 1)与2)等价
B 1)与3)等价
C 1)与4)等价
D 3)与4)等价
7给定A={1、2、3}上的关系R={<1, 1>, <2, 2>, <1, 3>, <3, 1>, <2, 3>}则()
A R是自反的且传递
B R不反自反且不对称
C R是反对称且不对称
D R不自反且传递
8下列叙述中错误的是()
A 空集是任何一个集合的子集
B 空集是任何一个群的子群
C 每个集合都有子集合
D 每个群都有子群
9一个简单连通无向图有n个结点,它的边数至少有()
A 一条
B n-1条
C n条
D n+1条
10一个图中,哪些分图的结点集合不是原图的结点集的划分()
A 强分图
B 单侧分图
C 弱分图
D 连通子图
三、求出下列命题公式的主析取范式。
(6分)
(P→(Q∧R))∧(⌝P→(⌝Q∧R))
四、任何人如果他喜欢步行,他就不喜欢乘汽车,对于每个人或者喜欢乘汽车或者喜欢骑自行车,有的人不爱骑自行车,因而有的人爱步行。
逻辑推证此结论的有效性。
(10分)
设M(x): x是人;Q(x);x喜欢步行
S(x); x喜欢乘汽车;R(x);x喜欢骑自行车
五、设A={a,b,c,d},其上关系R={<b,b>,<b,c>,<c,a>},S={<b,a><c,d>,<d,a>},求1)R·S
2)R的对称闭包及传递闭包(10分)
六、已知有如图的偏序关系,并求出其子集A={b,c, d, e,}的极大元、极小元、最大元、最小元、上确界、下确界。
(10分)
f g
e
d
c
b
七、设G={(a,b)︱a,b∈R,b≠0},定义运算(a,b)*(c,d)=(bc+a,bd)
求证:<G,*>是一个群。
(10分)
八、某班级有学生四十名,共有三门选修课可供选择,选修课课程名称分别为A、
B、C,其中有15名学生选A课程,有10名学生选B课程,6名学生选C课程,而且其中有5名学生三门课程都选。
问至少有多少学生三门选修课一门也没选?(10分)
九、证明下图是否为汉密尔顿图(8分)
十、设有一组数1,2,2,3,4,6,7,9,12,求相应的最优树。
并写出W(T)。
(8分)。
