计算方法-插值方法共34页
合集下载
地统计内插方法 克里金插值(Kriging)共45页
event falls within a certain range • The elevation in an area
8.1 Introduction
Some common summary statistics: –Measurements of location: mean, median –Measurements of spread: variance, standard deviation, coefficient of variation –Measurements of shape: coefficient of skewness
•What are the elevation values in an unmeasured location? •How to infer elevation values from other measurements in the same and other locations?
8.1 Introduction
8.1 Introduction
Review of Probability
•Frequency table records how often (in terms of percentage) observed values fall within certain intervals or classes.
8.2 Random Field
8.1 Introduction
Probability density function (PDF): p(u)– Discrete PDF: assigns a probability to each event • The outcome of flipping a coin • The number of road in an area Continuous PDF: determines the probability that an
8.1 Introduction
Some common summary statistics: –Measurements of location: mean, median –Measurements of spread: variance, standard deviation, coefficient of variation –Measurements of shape: coefficient of skewness
•What are the elevation values in an unmeasured location? •How to infer elevation values from other measurements in the same and other locations?
8.1 Introduction
8.1 Introduction
Review of Probability
•Frequency table records how often (in terms of percentage) observed values fall within certain intervals or classes.
8.2 Random Field
8.1 Introduction
Probability density function (PDF): p(u)– Discrete PDF: assigns a probability to each event • The outcome of flipping a coin • The number of road in an area Continuous PDF: determines the probability that an
三次埃尔米特插值
《计算方法》课程设计报告学生姓名:张学阳学号：1009300132陈洋1009300109刘睿1009300122 学院:理学院班级: 数学101题目: 分段线性及三次埃尔米特插值通用程序指导教师：宋云飞职称：讲师朱秀丽讲师尚宝欣讲师2012年12月30日目录目录 (I)一、摘要 (1)二、算法设计 (1)2.1分段线性插值 (1)2.2分段三次埃尔米特插值 (1)2.3功能框图 (1)三、例题计算 (1)四、误差及结果分析 (9)4.1例题误差分析 (1)4.2结点个数对插值结果的影响 (1)五、总结及心得体会 (12)参考文献 (13)源程序 (14)一、摘要分段线性插值与分段定义的线性插值,在相邻插值节点的区间上对应的是同一个线性函数。
由于它们的表现形式不一样从而产生为两种不同的计算方法,相应的误差表现形式也不一样.拉格朗日插值余项利用f(x)的二阶导数,要f(x)的二阶导数存在,对于二阶导数不存在的情况不能估算出它的误差,所以适用范围比较小.现在我们可以利用一阶导数就估算出误差,给计算带来许多的方便。
为了避免高次插值可能出现的大幅度波动现象，在实际应用中通常采用分段低次插值来提高近似程度，比如可用分段线性插值或分段三次埃尔米特插值来逼近已知函数，但它们的总体光滑性较差。
为了克服这一缺点，一种全局化的分段插值方法——三次样条插值成为比较理想的工具。
在代数插值过程中，人们为了获得较好的近似效果，通常情况下是增加插值节点数.由于二次插值比线性插值近似效果好，因此容易错误地认为插值多项式次数越高越好.事实上,随着插值节点的增多，插值多项式不一定收敛到被插值函数.。
通过分段低次插值或样条插值可以得到较好的近似逼近函数，分段低次插值具有公式简单、运算量小、稳定性好、收敛性有保证等优点.随着子区间长度h取得足够小，分段低次插值总能满足所要求的精度.因此分段低次插值应用十分广泛.。
分段线性插值是分段低次插值中常见的方法之一，在本文中对函数在(-5，5)上进行分段线性插值，取不同节点个数n，得到不同分段线性插值函数.并用MATLAB编写分段线性插值函数，最后比较用不同节点数所得插值函数与真实函数的误差，从而得出节点数与插值效果的关系。
一维插值
Ln ( x) an x an1 x
n
n 1
a1 x a0 (1)
a n x 0n a n1 x 0n1 a1 x 0 a 0 y 0 a n x1n a n1 x1n1 a1 x1 a 0 y1 n n a n x n a n 1 x n 1 a 1 x n a 0 y n
上一页
下一页
主 页
上一页
返 回 下一页 主 页
拉格朗日(Lagrange)多项式插值
已知三点（x0,y0), (x1,y1), (x2,y2), 求过这三点的多项式。
L2 ( x ) a 2 x 2 a1 x a 0
则
2 a 2 x 0 a1 x 0 a 0 y 0 2 a 2 x 1 a1 x 1 a 0 y1 a x 2 a x a y 1 2 0 2 2 2
称为拉格朗日插值基函数。
上一页 下一页 主 页
拉格朗日(Lagrange)多项式插值
例 将[0,/2] n等分，在g(x)=cos(x)上 取n+1个节点，作Pn(x)（取n=1,2) ,计算 Pn(/6),与 cos(/6)比较, 观察误差。 解: n=1, (x0,y0)=(0,1), (x1,y1)=(/2,0), x x0 x x1 L0 , L1 x 0 x1 x1 x 0 1 P1(x)=y0L0+y1L1=1-2x/, P1(/6)=0.6667
上一页 下一页 主 页
三次样条插值
三次样条函数 S(x), x∈[a, b] , 满足: 1) S(x) 在每一个小区间[xi-1,xi]上是 一个三次多项式函数 ； 2) 在整个区间[a,b]上，其二阶导数存在 且连续。 y
数值分析迭代加速牛顿法及弦截法
以上两式相除得
xk1 xk1
C C
xk xk
C C
2 .
据此反复递推有
xk xk
C C
x0 x0
2k
C C
.
第14页/共34页
(4.6)
记
q x0 C x0 C
整理(4.6)式，得
q2k xk C 2 C 1 q2k .
对任意初值x0>0，总有|q|<1，故由上式推知，当 k→∞时xk C ，即迭代过程恒收敛.
值x0, x1△，那么当邻域△充分小时，弦截法(5.2)将 按阶
p 1 5 1.618. 2
收敛到x*. 这里p是方程λ2-λ-1=0的正根. 定理证明可见P116.
第26页/共34页
因为(5.2)式用到前两点xk-1和xk的值，故此方法又 称为双点割线法.
如果把(5.2)式中的xk-1改为x0，即迭代公式为
比较困难，为此可以利用已求函数值 f(xk),f(xk-1),来
回避导数值 f(xk)的计算. 这类方法是建立在插值原理
基础上的，下面介绍弦截法与抛物线法.
第22页/共34页
3.5.1 弦截(割线)法
设 xk, xk-1是 f(x)=0的近似根，我们利用 f(xk), f(xk-1) 构造一次插值多项式 p1(x)，并用 p1(x)=0 的根作为方程 f(x)=0 的新的近似根 xk+1，由于
x*
x
(4.2)的计算结果.
y=f(x)
xk+2xk+1xk
第9页/共34页
牛顿迭代法的收敛性
牛顿迭代法的迭代函数为
(x) x f (x)
f ( x)
设x*是 f(x) 的一个单根，即 f(x*)=0，f(x*)≠0, 有
逐次线性插值法PPT课件
式为
I0,1,l ( x)
I0,1( x)
I0,l ( x) xl
I0,1( x) ( x x1
x1 )
计算时可由k=0到k=n-1逐次求得所需的插值多项式。计
算过程如下
x0 f (x0) I0
x பைடு நூலகம்x0
x1 f ( x1 ) I1 I0,1
x x1
x2
f (x2) I2
I I 0,2
I I 2,3
1,2,3
I 0 ,1, 2 , 3
x3 x0
x4
f (x4) I4
I I I 3,4
2,3,4
1,2,3,4
x x I0,1,2,3,4
4
0
第6页/共9页
从表上看每增加一个节点就计算一行，斜线上是 1次到4次插值多项式的值，如精度不满足要求， 再增加一个节点，前面计算完全有效，这个算法适 用于计算机上计算，且具有自动选节点并逐步比较 精度的特点，程序也比较简单。
I0,1,,k ( x)
I0,1,,k1,l ( x) I0,1,,k ( x) ( x xl xk
xk
)
(**)
上式是关于x的插值多项式，显然
I0,1,,k,l ( xi ) I0,1,,k ( xi ) f ( xi )
i=0，1，2 ,…, k-1时
第3页/共9页
而 x xk时，I0,1,,k ( xk ) I0,1,,k,l ( xk ) f ( xk )
插值结果
0.00 0.000 0
0.20 0.20134 0.23154
0.30 0.30452 0.233465 0.232118
0.50 0.52110 0.239706 0.232358
计算方法_课后习题答案
L3 x 的最高次项系数是 6，试确定 y1 。
解： l0 (x)
x x1 x0 x1
x x2 x0 x2
x x3 x0 x3
x 0.5 0 0.5
x 1 0 1
x2 02
= x3
7 2
x2
7 2
x 1
l1 ( x)
x x0 x1 x0
(2 2e1 4e0.5 )x2 (4e0.5 e1 3)x 1
2)根据Lagrange余项定理，其误差为
| R2 (x) ||
f
(3) ( 3!
)
21
(
x)
||
1 6
e
x(
x
1)(
x
0.5)
|
1 max | x(x 1)(x 0.5) |, (0,1) 6 0x1
x2 02
x4= 04
x3
7x2 14x 8 8
l1 ( x)
x x0 x1 x0
x x2 x1 x2
x x3 x1 x3
x0 1 0
x2 1 2
x4 1 4
=
x3
6x2 3
8x
l2 (x)
x x0 x2 x0
i j
而当 k 1时有
n
x jl j
j0
x
n
n
j0 i0 i j
x xi x j xi
x
j
公务员考试资料分析解题技巧
D.丁行业
当前38页，共75页，星期一。
总结
1.四舍五入(凑整)
2.除法同大同小、乘法一大一小 3.题型：计算型 、 比较型
当前39页，共75页，星期一。
速算技巧之直除法
一、比较型：
比较分数大小时，若其量级相当，首位最大(小 )数为最大（小）数。
二、计算型：
计算分数大小时，若选项首位不同，通过计算
当前19页，共75页，星期一。
【例2】表格材料1 2001至2005年国内生产总值居世界前10位国家比较(亿美元)
2001年
位次 国家和地 国内生产总 占世界的比 国家和
区
值
重(％)
地区
世界总计 315750
世界总 100
计
1
美国
100759
31.9
美国
2
日本
41624
13.2
日本
3
德国
18913
当前31页，共75页，星期一。
速算技巧之估算法
“估算法”是资料分析中的速算第一法
①：在所有计算进行之前必须考虑能否先行估算
②：很多方法都是以“估算法”作为前提
当前32页，共75页，星期一。
估算常用形式：
1.四舍五入(凑整) 2.除法同大同小；乘法一大一小；
当前33页，共75页，星期一。
估算法
【例1】706.38÷24.75=( )
饼图
标题 注释 时间 单位
关键标点、关键词、 具 段落主旨、结构 30-60秒 体
横标目、纵标目 15-30秒 数 据 横轴、纵轴、图示 10-25秒
类别名称、图示 10-20秒
当前15页，共75页，星期一。
【例1】
4 材料单价计算-插值法
主材单价插值法计算表
工程名称：珠海长隆横琴湾酒店机电安装工程—给排水施工图新增项目 合同编号：ZHCL11110353
序号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
编号：给排水施工图新增01 项目名称及规格 单位
m m m m m m 个 个 个 个 个 个 个 个 个 个 个 个 个 个 1,979.60 975.10 373.80 299.88 1,979.60 2,312.80 1,979.60 2,312.80 114.00 85.24 42.49 76.19 355.30 158.40
31.26
水补价-31 给水表 DN15 第316项 水表 DN25 第318项 水表 DN20 水换价-15 缓闭式消声止回阀 DN150 1.6Mpa 第95项 第97项 球墨铸铁缓闭式消声止回阀 DN100 PN=1.0MPa 球墨铸铁缓闭式消声止回阀 DN125 PN=1.6MPa 1.6Mpa
编号：给排水施工图新增01 项目名称及规格 单位
个 个 个 个 1.6Mpa 个 个 个 个 个 个 个 个 个 个 个 个 212.76 109.22 201.58 143.81 201.58 300.00 2,822.40 1,646.40 3,851.40 8,330.00
项目编码
单价
472.36
774.20
水补价-40 Y型过滤器 DN80 第158项 Y型过滤器 价插值法计算表
工程名称：珠海长隆横琴湾酒店机电安装工程—给排水施工图新增项目 合同编号：ZHCL11110353
序号
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
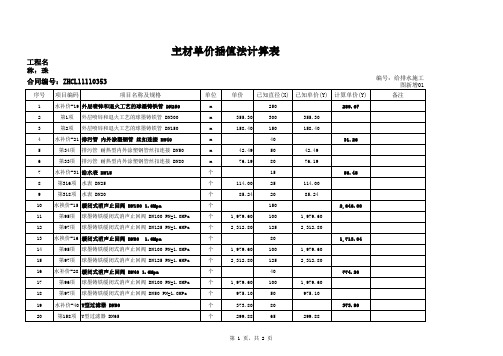
工程名称：珠海长隆横琴湾酒店机电安装工程—给排水施工图新增项目 合同编号：ZHCL11110353
序号
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
编号：给排水施工图新增01 项目名称及规格 单位
m m m m m m 个 个 个 个 个 个 个 个 个 个 个 个 个 个 1,979.60 975.10 373.80 299.88 1,979.60 2,312.80 1,979.60 2,312.80 114.00 85.24 42.49 76.19 355.30 158.40
31.26
水补价-31 给水表 DN15 第316项 水表 DN25 第318项 水表 DN20 水换价-15 缓闭式消声止回阀 DN150 1.6Mpa 第95项 第97项 球墨铸铁缓闭式消声止回阀 DN100 PN=1.0MPa 球墨铸铁缓闭式消声止回阀 DN125 PN=1.6MPa 1.6Mpa
编号：给排水施工图新增01 项目名称及规格 单位
个 个 个 个 1.6Mpa 个 个 个 个 个 个 个 个 个 个 个 个 212.76 109.22 201.58 143.81 201.58 300.00 2,822.40 1,646.40 3,851.40 8,330.00
项目编码
单价
472.36
774.20
水补价-40 Y型过滤器 DN80 第158项 Y型过滤器 价插值法计算表
工程名称：珠海长隆横琴湾酒店机电安装工程—给排水施工图新增项目 合同编号：ZHCL11110353
序号
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
g(x) f(x)
x0
x1
x2
x
x3
x4
这样的插值多项式是否存在并且唯一呢？对此，有如下结论：
定理 (唯一性) 满足 P (x i)yi,i0 ,..,n .的 n 阶插值多
项式是唯一存在的。 证明： ( p.105-106 利用Vandermonde 行列式论证)
反证：若不唯一，则除了Ln(x) 外还有另一 n 阶多项 式 Pn(x) 满足 Pn(xi) = yi 。 考察 Q n(x)P n(x)L n(x),则 Qn 的阶数 n 而 Qn 有 n + 1 个不同的根 x0 … xn
X
X0
X1
…
Xn
F(x)
F(x0)
F(x1)
…
F(xn)
这都会给研究带来困难。如何解决这类问题？当函数f(x)
比较复杂或根本无法写出解析式时，往往寻求用一个熟悉的
简单函数P(x)的去近似表示f(x),将研究f(x)的问题转化为
研究函数P(x)的问题。
插值 /* Interpolation */
当精确函数 y = f(x) 非常复杂或未知时，在一 系列节点 x0 … xn 处测得函数值 y0 = f(x0), … yn = f(xn)，由此构造一个简单易算的近似函 数 g(x) f(x)，满足条件g(xi) = f(xi) (i = 0, … n)。这里的 g(x) 称为f(x) 的插值函数。最常 用的插值函数是多…项? 式
插值方法
• 插值多项式定义 • 插值多项式的存在唯一性 • 插值余项 • 基函数构造拉氏插值多项式 • 计算机实现 • 分段线性插值 • 其它插值方法介绍
引例及问题综述
• 引例1 血药浓度问题
为试验某种新药的疗效，医生对某人用快速静脉注射方 式一次注入该药300mg后，在一定时间t(h)采取血样，
Ci
ji
( xi
1 xj)
j0
li(x)
n ji
(x xj ) (xi xj )
j0
n
Ln(x) li(x)yi i0
插值余项
p ( x ) 作为 f ( 的x ) 近似一定存在误差，用 R(x)f来(x)表p 示(x) 它的截断误差， 也称之R ( x为) 余项。下面，我们导出其具 体表达形式。
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
P1 ( x)
y0
y1 x1
y0 x0
(x
x0 )
= x x1 x0 x1
y0 +
x x0 x1 x0
1
y1 li ( x) yi i0
l0(x)
l1(x)
n1 li(x)
希望找到li(x)，i = 0, …, n 使得 li(xj)=ij ；然后令
【定理2】设 f ( n ) 在( x ) [a,b]上连续， 在f (n(a1) (,xb))内存在，节
点
ax0，x1 是L满x 足n 插b值条p ( 件x ) (2.1)的插值多项式，
则对任何 ，插值余项 x[a, b]
R (x ) f(x ) p (x )f(( n n 1 )1 ()!)(x x 0 )(x x 1 )L (x x n )
(a,b)
注： 通常不能确定 x , 而是估计 , f(n1)(x)Mn1 x(a,b)
将
Mn1 n (n1)!i0
|
xxi
|
作为误差估计上限。
当 f(x) 为任一个次数 n 的多项式时， f(n1)(x)0,
可知 Rn(x)0，即插值多项式对于次数 n 的多项式 是精确的。
Quiz: 给定 xi = i +1, i = 0, 1, 2, 3, 4, 5. 下面哪个是 l2(x)的图像？
测 得血药浓度C数据如下
试确定血药浓度C与时间t的函数关系。
引例及问题综述
引例2：标准正态分布函数
x 1
x u2
e 2 du
2
sinxx
sinxx1 x3 3!
x 充分小
引例及问题综述
在生产实际及科学研究中，经常要研究变量之间的函数 关系y=f(x)。若f(x)的表达式很复杂，或f(x)只能用一张 数据表来表示，即只知道f(x)在一系列点x0、 x1、… xn 处的函数值：
500 5
18
解： n = 1 分别利用x0, x1 以及 x1, x2 计算 x 0
x1
x2
利用
x0x /6 /4 /4 1 2 x /4 /6 /6 1 2
sin
而
501 2 内要0 端s 0 插计L.点0 1 i(通算x 51n ，1 8常的)插3 2 3 优x1 ,值R 0于所1 .7(9 效R 5 71外在1 6(果1x 8 )推的4) 较 。区这f0好(.2 2 选间0 里)(! 。0 x 择的f )( (x 7 x ) 6 s 6)2x ix ( ,s n f in ( 4 2 )) (5x 0) =s0 .i7x,6n 6x 0 4( 46 4, 3 …)
注：若不将多项式次数限制为 n ，则插值多项式不唯一。
n
例如 P(x)L n(x)p(x) (xxi)也是一个插值 i0
多项式，其中 p( x)可以是任意多项式。
拉格朗日多项式 /* Lagrange Polynomial */
求 n 次多项式 P n (x ) a 0 a 1x a n x n使得
n
Pn ( x )
li ( x )
y i
，则显然有Pn(xi)
=
yi
。
i0
每个与li节有点n 个有根关，x0而…与xi
li (x) Ci (x x0)...(x xi
f …无x关n )...(x xn
)
CiPLj no ali (ygxnroamnxgj i)eal
li (xi ) 1
y
A
y
B
y
C
1-
1-
1-
0.5-
0.5-
0.5-
01 -0.5-
2 34
✓
56 x 0 1
-0.5-
2 34
56 x 0 1
-0.5-
2 34
56 x
例：已知 si6 n1 2,si4 n1 2,si3 n2 3
分别利用 sin x 的1次、2次 Lagrange 插值计算 sin 50
并估计误差。
Pn ( xi ) yi , i 0, ... , n
条件：无重合节点，即 i j xi xj
n= 1
已称知为x拉0 氏, x基1 ;函y0数, y1/*，La求graP n1g(ex)B asa is0* /，a1x使得
P满1( 足x0 )条 件y0 l,i(Px1j)(=x1 )ij/*yK1 ronecker Delta */
x0
x1
x2
x
x3
x4
这样的插值多项式是否存在并且唯一呢？对此，有如下结论：
定理 (唯一性) 满足 P (x i)yi,i0 ,..,n .的 n 阶插值多
项式是唯一存在的。 证明： ( p.105-106 利用Vandermonde 行列式论证)
反证：若不唯一，则除了Ln(x) 外还有另一 n 阶多项 式 Pn(x) 满足 Pn(xi) = yi 。 考察 Q n(x)P n(x)L n(x),则 Qn 的阶数 n 而 Qn 有 n + 1 个不同的根 x0 … xn
X
X0
X1
…
Xn
F(x)
F(x0)
F(x1)
…
F(xn)
这都会给研究带来困难。如何解决这类问题？当函数f(x)
比较复杂或根本无法写出解析式时，往往寻求用一个熟悉的
简单函数P(x)的去近似表示f(x),将研究f(x)的问题转化为
研究函数P(x)的问题。
插值 /* Interpolation */
当精确函数 y = f(x) 非常复杂或未知时，在一 系列节点 x0 … xn 处测得函数值 y0 = f(x0), … yn = f(xn)，由此构造一个简单易算的近似函 数 g(x) f(x)，满足条件g(xi) = f(xi) (i = 0, … n)。这里的 g(x) 称为f(x) 的插值函数。最常 用的插值函数是多…项? 式
插值方法
• 插值多项式定义 • 插值多项式的存在唯一性 • 插值余项 • 基函数构造拉氏插值多项式 • 计算机实现 • 分段线性插值 • 其它插值方法介绍
引例及问题综述
• 引例1 血药浓度问题
为试验某种新药的疗效，医生对某人用快速静脉注射方 式一次注入该药300mg后，在一定时间t(h)采取血样，
Ci
ji
( xi
1 xj)
j0
li(x)
n ji
(x xj ) (xi xj )
j0
n
Ln(x) li(x)yi i0
插值余项
p ( x ) 作为 f ( 的x ) 近似一定存在误差，用 R(x)f来(x)表p 示(x) 它的截断误差， 也称之R ( x为) 余项。下面，我们导出其具 体表达形式。
可见 P1(x) 是过 ( x0 , y0 ) 和 ( x1, y1 ) 两点的直线。
P1 ( x)
y0
y1 x1
y0 x0
(x
x0 )
= x x1 x0 x1
y0 +
x x0 x1 x0
1
y1 li ( x) yi i0
l0(x)
l1(x)
n1 li(x)
希望找到li(x)，i = 0, …, n 使得 li(xj)=ij ；然后令
【定理2】设 f ( n ) 在( x ) [a,b]上连续， 在f (n(a1) (,xb))内存在，节
点
ax0，x1 是L满x 足n 插b值条p ( 件x ) (2.1)的插值多项式，
则对任何 ，插值余项 x[a, b]
R (x ) f(x ) p (x )f(( n n 1 )1 ()!)(x x 0 )(x x 1 )L (x x n )
(a,b)
注： 通常不能确定 x , 而是估计 , f(n1)(x)Mn1 x(a,b)
将
Mn1 n (n1)!i0
|
xxi
|
作为误差估计上限。
当 f(x) 为任一个次数 n 的多项式时， f(n1)(x)0,
可知 Rn(x)0，即插值多项式对于次数 n 的多项式 是精确的。
Quiz: 给定 xi = i +1, i = 0, 1, 2, 3, 4, 5. 下面哪个是 l2(x)的图像？
测 得血药浓度C数据如下
试确定血药浓度C与时间t的函数关系。
引例及问题综述
引例2：标准正态分布函数
x 1
x u2
e 2 du
2
sinxx
sinxx1 x3 3!
x 充分小
引例及问题综述
在生产实际及科学研究中，经常要研究变量之间的函数 关系y=f(x)。若f(x)的表达式很复杂，或f(x)只能用一张 数据表来表示，即只知道f(x)在一系列点x0、 x1、… xn 处的函数值：
500 5
18
解： n = 1 分别利用x0, x1 以及 x1, x2 计算 x 0
x1
x2
利用
x0x /6 /4 /4 1 2 x /4 /6 /6 1 2
sin
而
501 2 内要0 端s 0 插计L.点0 1 i(通算x 51n ，1 8常的)插3 2 3 优x1 ,值R 0于所1 .7(9 效R 5 71外在1 6(果1x 8 )推的4) 较 。区这f0好(.2 2 选间0 里)(! 。0 x 择的f )( (x 7 x ) 6 s 6)2x ix ( ,s n f in ( 4 2 )) (5x 0) =s0 .i7x,6n 6x 0 4( 46 4, 3 …)
注：若不将多项式次数限制为 n ，则插值多项式不唯一。
n
例如 P(x)L n(x)p(x) (xxi)也是一个插值 i0
多项式，其中 p( x)可以是任意多项式。
拉格朗日多项式 /* Lagrange Polynomial */
求 n 次多项式 P n (x ) a 0 a 1x a n x n使得
n
Pn ( x )
li ( x )
y i
，则显然有Pn(xi)
=
yi
。
i0
每个与li节有点n 个有根关，x0而…与xi
li (x) Ci (x x0)...(x xi
f …无x关n )...(x xn
)
CiPLj no ali (ygxnroamnxgj i)eal
li (xi ) 1
y
A
y
B
y
C
1-
1-
1-
0.5-
0.5-
0.5-
01 -0.5-
2 34
✓
56 x 0 1
-0.5-
2 34
56 x 0 1
-0.5-
2 34
56 x
例：已知 si6 n1 2,si4 n1 2,si3 n2 3
分别利用 sin x 的1次、2次 Lagrange 插值计算 sin 50
并估计误差。
Pn ( xi ) yi , i 0, ... , n
条件：无重合节点，即 i j xi xj
n= 1
已称知为x拉0 氏, x基1 ;函y0数, y1/*，La求graP n1g(ex)B asa is0* /，a1x使得
P满1( 足x0 )条 件y0 l,i(Px1j)(=x1 )ij/*yK1 ronecker Delta */