去绝对值化简(教师版)
第03讲 绝对值 有理数的大小比较(九大题型)(教师版)24-25学年六年级数学上册同步(沪教版)
第03讲绝对值有理数的大小比较(九大题型)学习目标1、了解绝对值的意义;2、会求一个数的绝对值;3、掌握绝对值的化简;4、知道对有理数大小比较的方法。
一、绝对值的意义1.定义:在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值,例如+2的绝对值等于2,记作|+2|=2;-3的绝对值等于3,记作|-3|=3.要点:(1)绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.即对于任何有理数a 都有:(2)绝对值的几何意义:一个数的绝对值就是表示这个数的点到原点的距离,离原点的距离越远,绝对值越大;离原点的距离越近,绝对值越小.(3)一个有理数是由符号和绝对值两个方面来确定的.二、绝对值性质:(1)0除外,绝对值为一正数的数有两个,它们互为相反数.(2)互为相反数的两个数(0除外)的绝对值相等.(3)绝对值具有非负性,即任何一个数的绝对值总是正数或0.三、有理数的大小比较1.数轴法:在数轴上表示出这两个有理数,左边的数总比右边的数小. 如:a 与b 在数轴上的位置如图所示,则a <b .2.法则比较法:两个数比较大小,按数的性质符号分类,情况如下:同为正号:绝对值大的数大两数同号同为负号:绝对值大的反而小两数异号正数大于负数正数与0:正数大于0-数为0负数与0:负数小于0要点:利用绝对值比较两个负数的大小的步骤:(1)分别计算两数的绝对值;(2)比较绝对值的大小:(3)判定两数的大小.拓展:3.作差法:设a 、b 为任意数,若a-b >0,则a >b ;若a-b =0,则a =b ;若a-b <0,a <b ;反之成立.4.求商法:设a 、b 为任意正数,若1a b >,则a b >;若1a b =,则a b =;若1a b <,则a b <;反之也成立.若a 、b 为任意负数,则与上述结论相反.5.倒数比较法:如果两个数都大于零,那么倒数大的反而小.【即学即练1】.123-的绝对值是 .【即学即练2】.比较大小:12- ﹣5;﹣|﹣2| ﹣(﹣2).(0)||0(0)(0)a a a a a a >ìï==íï-<î∵﹣|﹣2|=﹣2,﹣(﹣2)=2,∴﹣|﹣2|<﹣(﹣2);∵﹣23=﹣8,﹣32=﹣9,∴﹣23>﹣32.考点:实数的大小的比较【即学即练3】.用符号表述“正数的绝对值等于它本身”,正确的是( )A .(0)a a a =>B .(0)a a a =<C .()0a a a =-³D .()0a a a =-£A .3B .3-C .21x -D .12x-题型1:求一个数的绝对值【典例1】..2024-的绝对值是( )A .2024B .2024-C .12024D .12024-【答案】A【分析】本题主要考查了绝对值的意义,根据绝对值的意义解答即可.【解析】解:2024-的绝对值是2024,故选:A .【典例2】..实数3-的绝对值是 ( )A .3B .3-C .3±D .13【答案】A【分析】本题考查了实数的绝对值,掌握“一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0”是解题的关键.根据一个负数的绝对值是它的相反数即可得出答案.【解析】解:3-的绝对值是3.故选:A .题型2:绝对值与相反数【典例3】..0.2的相反数的绝对值为( )A .5-B .0.2C .5D .0.2-【典例4】..2024--的相反数是( )A .2024-B .2024C .12024-D .12024【典例5】..12024-的相反数是( )A .12024-B .12024C .2024D .-2024【答案】A【分析】本题考查了化简绝对值以及相反数的定义,根据只有符号不同的两个数互为相反数,据此即可作【典例6】..3-的绝对值的相反数是( )A .3-B .3C .13D .0【答案】A【分析】本题考查了绝对值和相反数,理解绝对值和相反数的含义是解题的关键.先求出3-的绝对值,然后根据只有符号不同的两个数互为相反数解答.【解析】3-的绝对值是3,3的相反数是3-.故选:A .【典例7】..在()4--,|1|-,|0|-,p -四个数中非负数共有( )A .1个B .2个C .3个D .4个【典例8】..绝对值是2的数是( )A .1-B .12-C .2±D .12±【答案】C【分析】本题考查绝对值的定义:绝对值是指一个数在数轴上所对应点到原点的距离叫做这个数的绝对值.理解绝对值的定义是解题的关键.【解析】根据绝对值的定义可知,2和2-的绝对值都是2.故选择:C【典例9】..如果一个数的绝对值等于23,则这个数是 .故答案为:23或23-.【典例10】..下列说法正确的是( )A .一个数的绝对值一定是正数B .一个数的相反数一定是负数C .若不相等的两个数的绝对值相等,则这两个数互为相反数D .整数的绝对值大于分数的绝对值【典例11】..绝对值不大于6的整数有 个.【答案】13【分析】本题主要考查的是有理数大小比较和绝对值,求得符合条件的数是解题的关键.依次列出绝对值不大于6的整数即可解答.【解析】解:绝对值不大于6的整数有:6±,5±,4±,3±,2±,1±,0.绝对值不大于6的整数有13个.故答案为:13.题型4:绝对值与数轴【典例12】..如图,数轴上被墨水遮盖的数的绝对值可能是( )A .72-B .52-C .72D .52【答案】C【分析】本题主要考查了有理数与数轴,求一个数的绝对值.根据数轴确定该数的绝对值在3到4之间即可判断.【解析】解:由题意得,遮住的数在4-到3-之间,∴遮住的数的绝对值在3到4之间,∴四个选项中只有C 选项符合题意,故选:C .【典例13】..如图,数轴上被遮挡住的整数的绝对值是( )A .1B .3-C .1-D .0【答案】A 【分析】本题考查数轴以及绝对值的定义,根据数轴上点的特征可知遮住的点表示的数是1-,再根据绝对值的定义求解即可.【解析】解:根据数轴上点的特征可知遮住的点表示的数是1-,1-的绝对值是1,故选A .题型5:有理数的大小比较【典例14】..比较下列各对数的大小:(1)3和7-.(2) 5.3-和( 5.4)-+.(3)45-和23-.(4)(7)--和1-.【典例15】..下列四个数中,最小的是( )A .3-B . 3.5-C .0D .|5|-【答案】B【分析】本题考查了有理数大小比较,绝对值,熟练掌握两个负数比较,绝对值小的反而大是解题的关键.根据两个负数比较,绝对值小的反而大,负数小于0,0小于正数,即可解答.【解析】解:∵|3|3-=,| 3.5| 3.5-=,∴3.53>,∴ 3.53-<-,∵|5|5-=,∴在|3, 3.5,05|---,这四个数中, 3.5305||--<-<<,∴最小的是 3.5-,故选:B .【典例16】..比 2.99-小的最大整数是 .【答案】3-【分析】此题主要考查了有理数大小比较,正确理解最大整数定义是解题关键.根据有理数大小比较即可得比 2.99-小的最大整数是3-.【解析】解:比 2.99-小的最大整数是3-.故答案为:3-.【典例17】..在有理数中,既不是正数也不是负数的数是 ;最小的非负数是 ;最大的非正数是;【答案】 0 0 0【分析】本题考查了有理数的分类,有理数包括正数,0,负数;非负数是0和正数,非正数是0和负数,根据有理数大小比较的法则即可得出正确答案.【解析】解:根据有理数包括正数,0,负数,可知既不是正数也不是负数的数是0.由于正数大于0,所以最小的非负数是0;由于负数小于0,所以最大的非正数是0.故答案为:0,0,0.【典例18】..(1)在数轴上分别表示出下列三个数:(1)--,4-,()2.5+-,(2)有理数m 、n 在数轴上的对应点如图所示:①在数轴上分别表示出数n -,m ,②把m ,n ,n -,m 这四个数从小到大用“<”号连接.较有理数的大小,掌握以上基础知识是解本题的关键.【典例19】..对于一个数,给定条件A :该数是负整数,且大于3-;条件B :该数的绝对值等于2,那么同时满足这两个条件的数是 .【答案】2-【分析】本题考查了绝对值和有理数大小比较,首先根据有理数大小比较的方法,可得大于3-的负整数有:2-、1-;然后根据绝对值即可求解;会求限定范围的负整数及一个数的绝对值是解题的关键.【解析】解:Q 大于3-的负整数有:2-、1-,绝对值等于2的数有两个:2-、2,\同时满足这两个条件的数是2-.故答案为:2-.题型6:有理数大小比较的实际应用【典例20】..2024年1月1日,我市某地4个时刻的气温(单位:C °)分别为4-,0,1,3-,其中最低的气温是.【答案】4-【分析】本题主要考查有理数的大小比较;由题意可根据有理数的大小比较进行求解.【解析】解:∵4301-<-<<,∴最低的气温是4C -°;故答案为:4-.【典例21】..检查5个足球的质量(克),把超过标准质量的克数记为正数,低于标准质量的克数记为负数,数据统计结果如下表:足球编号12345与标准质量的差(克)5+7+3-9-9+则最接近标准质量的是号足球.(只填写编号)【典例22】..在活动课上,有6名学生用橡皮泥做了6个乒乓球,直径可以有0.02毫米的误差,超过规定直径的毫米数记作正数,不足的记作负数,检查结果如下表:做乒乓球的同学李明张兵王敏余佳赵平蔡伟检测结果0.031+0.017-0.023+0.021-0.022+0.011-(1)请你指出哪些同学做的乒乓球是合乎要求的?(2)指出合乎要求的乒乓球中哪个同学做的质量最好,6名同学中,哪个同学做的质量较差?【答案】(1)张兵和蔡伟做的合乎要求(2)蔡伟做的质量最好;李明做的较差【分析】(1)绝对值大于0.02的就都是不合格的,所以张兵、蔡伟合格;(2)绝对值越小质量越好,越大质量越差,所以蔡伟最好、李明最差.【解析】(1)解:Q |0.031|0.031+=,|0.017|0.017-=,|0.023|0.023+=,|0.021|0.021-=,|0.022|0.022+=,|0.011|0.011-=,\0.0310.02>,0.0170.02<,0.0230.02>,0.0210.02>,0.0220.02>,0.0110.02<,∵直径与规定直径不超过0.02毫米的误差视为符合要求,张兵的是−0.017,蔡伟的是−0.011不超过0.02毫米的误差,∴张兵和蔡伟做的乒乓球是符合要求的;(2)解:Q |0.031||0.023||0.022||0.021||0.017||0.011|+>+>+>->->-,∴6名同学做的乒乓球质量按照最好到最差排名为:蔡伟、张兵、余佳、赵平、王芳、李明,∴蔡伟做的质量最好,李明同学做的质量最差,答:蔡伟做的质量最好;李明做的较差.【点睛】本题考查正数与负数的实际运用,涉及绝对值运算,弄清题意是解本题的关键.题型7:绝对值的非负性及应用【典例23】..若|||10|3-+-=a b ,则=a ,b = .【典例24】..若a a -=-,a 一定是( )A .正数B .非正数C .负数D .非负数【典例25】..下列说法正确的是( )A .a --一定是负数B .只有两个数相等时,它们的绝对值才相等C .若a b =,则a 与 b 一定互为相反数D .若a a =-,则a 是非正数【典例26】..若2a -与4b +互为相反数,则a b +的值为 .对值的性质是解题的关键.【典例27】..如果有理数x 、y 满足10x x y -++=,那么xy 的值是( )A .1-B .1±C .1D .2【典例28】..已知a 为有理数,则24a -+的最小值为 .【典例29】..数a ,b ,c 在数轴上对应点的位置如图所示,化简a b c -+-的结果为( )A .a b c-+-B .a b c --+C .a b c +-D.a b c-+【典例30】.当2x >时,化简2x -= .【典例31】..若有理数a b c 、、在数轴上对应的点如图,化简:a c b c a b -++--= .【典例.32】..在数轴上,a ,b ,c 对应的数如图所示,b c =.(1)确定符号:a ______0,b ______0,c _____0,b c +_____0,a c -______0;(2)化简:a c b +-;(3)化简:a a c --.c =-.【典例33】..有理数a ,b ,c 在数轴上的位置如图所示.(1)用“>”“<”或“=”填空:a b +______0,c a -______0,2b +______0.(2)化简:22a b c a b ++--+.【典例34】..如果a 表示有理数,那么a +1,|a +1|,(a +1),|a |+1中肯定为正数的有( )A .1个B .2个C .3个D .4个【答案】A【解析】根据有理数和绝对值的意义,可根据a 的值不确定,知a+1不一定是正数,(a+1)的值不确定,但是|a|≥0,可知|a+1|是正数, |a|+1一定是一个正数.故选A.【典例35】..把197201093618,,,198201193719----四个数按由大到小的顺序排列,正确的是( )A .181979362010191989372011->->->-B .189361972010199371982011->->->-C .201019793618201119893719->->->-D .201093619718201193719819->->->-【典例36】..对于任意实数x ,通常用[]x 表示不超过x 的最大整数,如[2.9]2=,下列结论正确的是( )①[]33-=- ②[]2.92-=- ③[0.9]0= ④[][]0x x +-=A .①②B .②③C .①③D .③④【答案】C【分析】根据符号[x]表示不超过x 的最大整数,依次判断可得答案.【解析】解:由题意可得,[-3]=-3,故①正确;[-2.9]=-3,故②错误;[0.9]=0,故③正确;当x 为整数时,[x]+[-x]=x+(-x )=0,当x 为小数时,如x=1.2,则[x]+[-x]=1+(-2)=-1≠0,故④错误;故选:C .【点睛】本题考查了有理数的大小比较,解答本题的关键是理解题目中的新定义.一、单选题1.32-的绝对值是( )A .23-B .32-C .23D .32A .B .C .D .A .2024-和2024-B .2024和12024C .2024-和2024D .2024-和12024A .227733æö--=--ç÷èøB .5465-<-C .()()2121--<+-D .|10|8-->【答案】B 【分析】本题考查了有理数的大小比较,掌握比较大小的方法是解题的关键.先根据绝对值和相反数的意中表示绝对值最小的数的点是()A.点A B.点B C.点C D.点D【答案】C【分析】本题考查了数轴,相反数,绝对值,有理数的大小比较的应用,解此题的关键是找出原点的位置,注意数形结合思想的运用.先根据相反数确定原点的位置,再根据点的位置确定表示绝对值最小的数的点即可.【解析】解:因为点B,D表示的有理数互为相反数,所以原点的位置在线段BD的中点处,∵离原点越近的点表示的数绝对值越小,∴表示绝对值最小的数的点是C点.故选:C.6.用数轴上的点表示下列各数,其中与原点距离最近的是()A.3-B.1C.2D.3查了四款儿童口罩,结果如下,从长度的角度看最接近标准的儿童口罩是( )A .B .C .D .A .5个B .6个C .7个D .8个( ).A .1个B .2个C .3个D .4个\011c \<-<,则()110a c a c +-=+-<;0b c +>;b a -A .1或5B .1-或5-C .1-或5D .2或4二、填空题11. 3.5-的相反数为;5-的绝对值是 ;绝对值是2的数是 .【答案】 3.5 5 2±【分析】本题主要考查了绝对值和相反数.根据相反数的定义:如果两个数只有符号不同,数字相同,那么这两个数互为相反数,0的相反数是0;绝对值的定义:正数的绝对值是它本身,负数的绝对数是它的相反数,0的绝对值是0,进行求解即可【解析】解: 3.5-的相反数为3.5;5-的绝对值是5;绝对值是2的数是2±.故答案为:3.5;5,2±.12.比较大小:(填“>”或“<”).(1)78-34-,(2)45- 34-;(3)56-- 23-.个.【答案】13【分析】本题主要考查的是有理数大小比较和绝对值,求得符合条件的数是解题的关键.依次列出绝对值不大于6的整数即可解答.【解析】解:绝对值不大于6的整数有:6±,5±,4±,3±,2±,1±,0.绝对值不大于6的整数有13个.故答案为:13.15.绝对值小于2.5的所有整数是,绝对值等于它本身的数是 .18.设表示大于的最小整数,如2.330.2012=-==、、,则下列结论:①[)2.121-=;②[)x x -的最小值是0;③[)x x -的最大值是1;④若[)0.1x x -=,则x 可以表示成0.9n +(n 为整数)的形式;⑤若整数x 满足[)2x =,则1x =±.其中正确 (填写序号).三、解答题19.写出下列各数的绝对值.(1) 1.5-;(2)83;(3)6-;(4)83 -;(5)320.已知6个有理数:52,0,4-,1(2--,32-,4-,按要求完成下列各小题.(1)互为相反数的一组数是________;(2)将上述的6个有理数表示在如图所示的数轴上,并用“<”将上面的数连接起来.∴315404222æö-<-<<--<<-ç÷èø;(2)若5a =,1=b ,且a b <,求a ,b 的值.(1)在数轴上表示a -、b -;(2)用>、=或<填空:||a ______a ,||a -______a -,||b ______b ,||b -______b-(3)试用>连接a b a b +-,,0,a b -+,【答案】(1)见解析(2)>,=,=,>(3)0a b a b a b-+>>+>-【分析】本题考查了绝对值的性质,利用数轴判断式子的正负,有理数大小比较,掌握有理数大小比较方(2)由图可知:0a b b a <-<<<-,B B 然数.(1)求A 、B 之间的距离;(2)比较点A 、B 、C 表示的数的大小;【答案】(1)2;(2)101-<<【分析】本题考查有理数的分类及数轴上两点之间的距离,(1)根据最小的正整数是1,最大的负整数是1-,最小的自然数为0代入求解即可得到答案;(2)根据正负数大小比较方法比较即可.【解析】(1)最大的负整数是1-,最小的正整数是1,最小的自然数是0,∴点A 、B 、C 是数轴上表示的数分别是1-,0,1,A \、B 之间的距离112+=;(2)由于正数大于0,负数小于0,∴101-<<;24.在活动课上,有6名学生用橡皮泥做了6个乒乓球,直径可以有0.02毫米的误差,超过规定直径的毫米数记作正数,不足的记作负数,检查结果如下表:做乒乓球的同学李明张兵王敏余佳赵平蔡伟检测结果+0.031-0.017+0.023-0.021+0.022-0.011(1)请你指出哪些同学做的乒乓球是合乎要求的?(2)指出合乎要求的乒乓球中哪个同学做的质量最好,6名同学中,哪个同学做的质量较差?(3)请你对6名同学做的乒乓球质量按照最好到最差排名;用学过的绝对值的知识说明.【答案】(1)张兵、蔡伟;(2)蔡伟;李明;(3)蔡伟、张兵、余佳、赵平、王敏、李明;说明见详解.【分析】(1)绝对值大于0.02毫米的就是不合格,所以张兵、蔡伟是合格的;(2)绝对值越小质量越好,越大质量越差,所以蔡伟做的质量最好,李明的最差;(3)按绝对值由大到小排即可.【解析】(1)Q 直径与规定直径不超过0.02毫米的误差视为合格,张兵的是0.017-,蔡伟的是0.011-,两人的都不超过0.02毫米的误差,\张兵、蔡伟做的乒乓球是合格的.(2)Q 蔡伟做的为0.011-毫米,李明做的为0.031+,\蔡伟做的质量最好,李明的最差.(3)|0.011||0.017||0.021||0.022||0.023||0.031|-<-<-<+<+<+Q ,\6名同学做的乒乓球质量按照最好到最差排名为:蔡伟、张兵、余佳、赵平、王敏、李明.【点睛】此题考查了正数与负数,以及绝对值的意义,正确理解题目的意思是解此题的关键.25.点AB 、在数轴上分别表示有理数,a b A B 、、两点之间的距离表示为AB ,在数轴上A B 、两点之间的距离AB a b =-. 已知数轴上两点A B 、对应的数分别为1-、3,点P 为数轴上一动点,其对应的数为x .(1),A B 两点之间的距离是 ;(2)设点P 在数轴上表示的数为x ,则x 与4-之间的距离表示为 ;(3)若点P 到点A 、点B 的距离相等,则点P 对应的数为 ;(4)数轴上是否存在点P ,使点P 到点A 、点B 的距离之和为8?若存在,请直接写出x 的值;若不存在,说明理由.。
绝对值(教案)
华师大版数学七年级绝对值教学设计课题绝对值单元 2.4 学科数学年级七年级学习目标1、借助数轴理解绝对值的概念,会求一个数的绝对值;2、会利用绝对值的概念进行有关绝对值的计算;3、理解绝对值的非负性质,并能应用这一性质解决问题;重点借助数轴理解绝对值的概念,会求一个数的绝对值;难点理解绝对值的非负性质,并能应用这一性质解决问题;教学过程教学环节教师活动学生活动设计意图导入新课一、复习与练习1、汽车向东行驶5千米,记作+5千米,那么汽车向西行驶5千米,记作千米;+5的相反数是;如果汽车千米耗油0.2升,那么汽车向东行驶5千米耗油升,汽车向西行驶5千米耗油升。
2、如图所示:A点表示的数是;它在原点的旁,与原点相距单位长度;B点表示的数是,它在原点的旁,与原点相距单位长度;A点和B点表示的数互为,它们与原点的距离;二、提出问题有一些量的计算中,有时并不注重其方向,如何表示这些量呢?直接回答直接回答思考复习巩固引出新课讲授新课一、绝对值的概念1、绝对值:在数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.2、举例子:(1)在数轴上表示+3的点与原点的距离是,读并理解直接回答数形结合所以+3的绝对值是,记作;(2)在数轴上表示-6的点与原点的距离是,所以-6的绝对值是,记作;(3)在数轴上表示+2.5的点与原点的距离是,所以+2.5的绝对值是,记作;(4)在数轴上表示-7.2的点与原点的距离是,所以-7.2的绝对值是,记作;(5)在数轴上表示0的点与原点的距离是,所以0的绝对值是,记作;3、绝对值符号的理解(1)|+1.8|表示的绝对值,结果是;(2)|-1.8|表示的绝对值,结果是;(3)|0|表示的绝对值,结果是;(4)|a|表示的绝对值,结果是;二、绝对值法则1、完成课本P23页的试一试。
2、绝对值法则(1)文字表述:一个正数的绝对值是它本身,零的绝对值是零,一个负数的绝对值是它的相反数。
第03讲 绝对值(教师版)

第3讲 绝对值【知识扫描】知识点一 对绝对值的几何定义的理解1. 数轴上表示数a 的点与原点的距离叫数a 的绝对值,记作|a |。
它是一个非负数,即|a |≥0。
拓展:若干个非负数之和为0,则每一个非负数都为0。
即|a |+|b |+…+=0,则有|a |=0,|b|=0,……,所以a =0,b =0,……2. 绝对值等于同一个整数的有理数有2个,它们互为相反数;反之,互为相反数的两个数绝对值相等,如|a |=5,则a =±5。
知识点二 对绝对值的代数定义的理解一个正数的绝对值是它本身;0的绝对值是0;一个负数的绝对值是它的相反数。
即:对于任何有理数a ,都有()()()⎪⎩⎪⎨⎧0000<-=>=a a a a a a知识点三 有理数的大小比较(1)两个正数比较,绝对值大的数较大; (2)正数大于0,负数小于0,正数大于负数; (3)两个负数比较,绝对值大的反而小。
【典型例题】考点一 利用绝对值的定义求解 【例1】-6的绝对值是( )A .6B .61 C .61- D .-6 【解答】A【变式】(1)在-3,-3.5,-3.75中,绝对值最小的数是________,离原点最远的是________(2)化简:|3.14-π|=____________【解答】(1)|-3|=3,|-3.5|=3.5,|-3.75|=3.75 ∵3<3.5<3.75∴绝对值最小的数是-3,离原点最远的是-3.75 (2)∵3.14-π<0∴|3.14-π|=-(3.14-π)=π-3.14考点二 已知一个数的绝对值,求这个数【例2】已知一个数的绝对值等于2018,则这个数是____________ 【解答】∵|2018|=2018,|-2018|=2018,∴绝对值等于2018的数是±2018. 故答案为:±2018.【变式】绝对值小于3的所有整数是________________ 【解答】绝对值小于3的所有整数有:-2,-1,0,1,2. 【例3】如果|a |=2,|b |=3,且a <b ,求a 、b 的值。
绝对值化简-题库教师版

⑸若x2
x 20,求x
的取值范围.
【例2】已知:⑴
a 5,b 2,且
a b:⑵
a1
2
b
20,分别求a
,b的值
【例3】已知2x
33 2x,求x的取值范围
【巩固】(4级)若a b且a b,
则下列说法正确的是(
)
A.a一定:
是正数B.a
一定是负数
C .
.b
一定是正数D
.b一定是负数
)
a
【例4】
-1 0 1
这道题目体现了一种重要的先估算+后化简+再代入求值”的思想.
(2)为研究问题首先要先将题干中条件的绝对值符号通过讨论去掉,
若a>b时,(a b)2(b
a) a b
(a
b)2
(a
b)2
0
ab,
若a b时,(a b)2(b
a) a b
(a
b)2
(b
a)2
2(a
b)2ab,
从平方的非负性我们知道
中考要求
内容
基本要求
略咼要求
较咼要求
绝对值
借助数轴理解绝对值的意义,会求实 数的绝对值
会利用绝对值的知识解决简单的化简 问题
例题精讲
绝对值的几何意义:
一个数a的绝对值就是数轴上表示数a的点与原点的距离.数a的绝对值记作a
绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
【巩固】
求出所有满足条件 非零整数m,n满足m
()
如果有理数a、b、c在数轴上的位置如图所示,求|a b b1a c1c的值.
a b 0 c 1
第2讲 绝对值的化简(教师版)

;
∴原式
.
考点 数 > 有理数 > 绝对值 > 绝对值的性质 作业4
化简:
.
答案 原式
.
解析 ①当 原式
②当 原式
③当 原式
时
; 时
; 时
;
∴原式
.
考点 数 > 有理数 > 绝对值 > 题型:零点分段法 作业5
化简:
.
答案 .
解析 ①当 原式 ②当 原式 ③当 原式 ④当 原式
时, 时, 时,
时,
.
综上所得
.
考点 数 > 有理数 > 绝对值 > 绝对值的性质
已知 、 、 为有理数,且
A.
B.
,
,则
C. 或
的值为( ). D.
答案 B
解析
,
∵
,
,
∴ , , 为三个负数,或有其中两个为正数,一个为负数,
则原式
可能出现的结果为 .
考点 数 > 有理数 > 绝对值 > 题型:|a|/a的化简
二、课后创新培养
例题1
、 、 在数轴上的位置如图所示,化简
.
答案 . 解析 略 考点 数 > 有理数 > 绝对值 > 绝对值的性质
设 , , 为非零实数,且
,
,
.化简
.
答案 解析
,
,;
,
;
,
,
所以可以得到 , , ;
考点 数 > 有理数 > 绝对值 > 绝对值的性质
模块二 绝对值的无条件化简
考点 零点分段法
知识导航
,
绝对值化简-题库教师版备课讲稿

绝对值化简- 题库教师版精品文档绝对值化简中考要求内容基本要求略高要求较高要求绝对值借助数轴理解绝对值的意义,会求实会利用绝对值的知识解决简单的化简数的绝对值问题例题精讲绝对值的几何意义:一个数 a 的绝对值就是数轴上表示数 a 的点与原点的距离.数 a 的绝对值记作 a .绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0 的绝对值是 0.注意:①取绝对值也是一种运算,运算符号是“”,求一个数的绝对值,就是根据性质去掉绝对值符号 .②绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数; 0 的绝对值是 0 .③绝对值具有非负性,取绝对值的结果总是正数或0.④任何一个有理数都是由两部分组成:符号和它的绝对值,如: 5 符号是负号,绝对值是 5 .求字母 a 的绝对值:a( a0)a(a0)a(a0)① a0( a0)②a0)③ a0)a(a0)a( a a( a利用绝对值比较两个负有理数的大小:两个负数,绝对值大的反而小 .绝对值非负性:如果若干个非负数的和为0,那么这若干个非负数都必为0.例如:若 a b c0 ,则a 0,b 0,c 0绝对值的其它重要性质:(1)任何一个数的绝对值都不小于这个数,也不小于这个数的相反数,即 a a ,且 a a ;(2)若a b ,则a b 或 a b ;(3)ab a b ;a a0) ;(bb b| a |222精品文档(5)a b a b a b ,对于 a b a b ,等号当且仅当 a 、b同号或 a 、b中至少有一个0时,等号成立;对于 a b a b ,等号当且仅当 a 、b异号或 a 、b中至少有一个0时,等号成立.板块一:绝对值代数意义及化简【例 1】(2级)⑴ 下列各组判断中,正确的是() A.若a b ,则一定有a b B.若a b ,则一定有a bC. 若a b ,则一定有 a b D .若a b ,则一定有 a22b⑵如果 a2> b 2,则()A.a b B.a>b C.a b D a<b⑶ 下列式子中正确的是( )A.a a B. a a C.a a D .a a⑷对于 m 1 ,下列结论正确的是()A.m 1≥| m |B.m 1≤| m |C.m 1≥| m | 1D.m 1≤| m | 1⑸若 x2x20 ,求 x 的取值范围.【例 2】已知:⑴ a5,b 2 ,且a2b20 ,分别求 a,b 的值b ;⑵ a 1【例 3】已知 2 x33 2 x,求 x 的取值范围【巩固】( 4 级)若a b 且a b ,则下列说法正确的是()A.a一定是正数B.a一定是负数C.b一定是正数 D .b一定是负数【例 4】求出所有满足条件 a b ab 1的非负整数对 a ,b【巩固】非零整数 m,n 满足m n50,所有这样的整数组m,n 共有如果有理数 a 、b、 c 在数轴上的位置如图所示,求a b b 1 a c1 c 的值.a b0 c 1【巩固】已知 x0z,xy0,y z x ,那么 x z y z x y【例 5】 abcde是一个五位自然数,其中 a 、b、 c 、d、 e 为阿拉伯数码,且a b c d ,则a b b c c d d e 的最大值是.【例 6】已知 y x b x20x b20,其中 0b20,b ≤ x≤ 20,那么 y 的最小值为【例 7】设 a,b,c 为整数,且 a b c a1,求 c a a b b c 的值【巩固】已知 a1,b 2,c3,且a b c,那么 a b c【例 8】(6级)(1)(第10届希望杯2试)已知x1999,则4x25x9 4 x22x23x7.(2)(第12届希望杯2试)精品文档满足 (a b) 2(b a) a b ab (ab0 )有理数a、 b ,一定不满足的关系是()A.ab0B.ab0C.a b 0D.a b 0(3)(第7届希望杯2试)已知有理数 a 、b的和a b 及差 a b在数轴上如图所示,化简2a b 2 a b 7 .a-ba+b-101这道题目体现了一种重要的“先估算+后化简+再代入求值”的思想.(2)为研究问题首先要先将题干中条件的绝对值符号通过讨论去掉,若 a ≥ b 时,( a b)2(b a) a b(a b) 2(a b)20ab ,若 a b 时,(a b) 2(b a) a b( a b)2(b a)22( a b)2ab ,从平方的非负性我们知道ab0 ,且 ab0 ,所以 ab0 ,则答案A一定不满足.(3)由图可知0 a b1, a b 1 ,两式相加可得: 2a0 , a 0 进而可判断出 b0 ,此时 2a b 0 , b 70 ,所以 2a b 2 a b7(2 a b )2(a)(b 7)7 .【巩固】( 8 级)(第9届希望杯1试)若m1998,则m211m999m222m 99920.【解析】 m211m999m(m11)999199819879990 ,m222m 999 m( m 22) 9991998 19769990 ,故(m211m999)( m222m999)20 20000 .【补充】(8 级)若x0.239,求x 1 x 3 L x 1997x x 2 L x 1996 的值.【解析】法1:∵ x0.239,则精品文档原式( x1)( x3)L( x1997)x(x2)L( x1996)x1x3x5L x1997x x 2 L x19961(32)(54)L(19971996)1 1 L 1 999法 2:由x≤a b,可得 x b x a b a ,则原式( x1x )( x3x 2 )L( x1997x1996 )11L 1 999点评:解法二的这种思维方法叫做构造法.这种方法对于显示题目中的关系,简化解题步骤有着重要作用.【例 9】(10 级)设A x b x 20x b20 ,其中0 b ≤ x ≤ 20 ,试证明 A 必有最小值【解析】因为 0 b ≤ x ≤ 20 ,所以x b ≥ 0,x20 ≤ 0,x b20 0,进而可以得到:A x 2b≥ x 2x x≥ 20 ,所以 A 的最小值为 20【例 10】(8级)若 2a45a13a 的值是一个定值,求 a 的取值范围.【解析】要想使 2a45a13a的值是一个定值,就必须使得 4 5a0,且 13a ≤ 0 ,原式 2a 45a(13a ) 3 ,即1≤ a ≤4时,原式的值永远为3. 35【巩固】(8 级)若x 1 x 2x 3 L x 2008 的值为常数,试求x 的取值范围.【解析】要使式子的值为常数,x 得相消完,当1004≤x≤1005时,满足题意.【例 11】(2级)数 a, b 在数轴上对应的点如右图所示,试化简a b b a b a aa0b 【解析】 a b b a b a aa bb a b2a b .【巩固】(2 级)实数a,b,c在数轴上的对应点如图,化简a c b a b a cb a 0c 【解析】由题意可知: a 0,c b 0,a b 0 ,a c 0 ,所以原式2c a【巩固】(2 级)若a b 且a0 ,化简 a b a b ab .b精品文档【解析】若 a b 且a0 , a0,b0 , a b0,ab0 ba b a b ab a b a b ab ab2a【例 12】(8级)(北大附中2005-2006学年度第一学期期中考试)设a,b,c为非零实数,且a a 0 , ab ab , c c 0 .化简 b a b c b a c .【解析】 a a 0 , a a ,a≤0; ab ab ,ab≥0; c c 0 , c c ,c≥0所以可以得到 a 0 , b 0 , c0 ;b a bc b a c b a b c b a c b .【例 13】(6级)如果 0m 10 并且 m ≤ x ≤ 10,化简x m x 10 x m 10 .【解析】 x m x 10x m 10 x m 10 x m 10 x20x .【巩固】( 2 级)化简:⑴ 3x ;⑵ x 1 x 23x x2 x3 x2 3≤ x1【解析】⑴原式3;⑵原式1 2x x≥ 33 x ≥12x【巩固】( 6级)若 a b ,求b a1 a b 5 的值.【解析】 b a 1 a b 5 b a 1 a b5 4 .【巩固】( 8 级)(第7届希望杯2试)若a0 , ab 0,那么 b a 1 a b 5 等于.【解析】 a 0 , ab 0 ,可得: b 0 ,所以 b a 0 , a b 0 ,b a 1 a b 5 b a 1 a b 5 4 .【巩固】(2 级)已知1≤x 5,化简 1x x 5【解析】因为 1≤ x 5 ,所以1x ≤ 0,x50 ,原式x 1 5 x 4【例 14】(8级)已知 x3,化简321x .【解析】当 x3时,3 2 1 x321x 3 3 x 3 3 xxx .【巩固】( 8 级)(第16届希望杯培训试题)已知x 1 x 1 2 ,化简 4 2 x 1 .【解析】由 x1x 1 2的几何意义,我们容易判断出1≤ x ≤1 .所以 42x 1 4 2 1 x 4 3 x 4 3 x 1 x 1 x .【例 15】(8级)若xx 2 x0 ,化简.x3 xx 2 x x 2 x3xx .【解析】x 3x x3x 3(8 级)(四中)已知a 2a4b42【巩固】 a ,b0,化简(a2b)2a2b4b32a3.【解析】∵ a a ,∴a≤0,又∵b0 ,∴ 2a4b0 ,∴ 2a4b(2 a4b)2(a2a4b2(a2b)22b) ,∴2b)2(a2b)2 a 2b(a又∵ a2b0 ,∴444 a2b(a2b ) a 2b又∵ 2a 30 ,∴222214b32a34b3(2 a3) 2 a4b2a4b a2b∴原式2413a2b a 2b a2b a2b点评:详细的过程要先判断被绝对值的式子x ,再去绝对值的符号.、【例 16】(8级)(第14届希望杯邀请赛试题)已知a,b,,c d 是有理数, a b ≤ 9,c d ≤ 16,且 a b c d25 ,求 b a d c 的值【解析】因 a b ≤ 9,c d ≤ 16 ,故 a b c d ≤ 916 25,又因为25 a b c da bd c≤ a b d c ≤ 25 ,所以 a b9,c d 16 ,故原式7板块二:关于a的探讨应用a【例 17】(6级)已知 a 是非零有理数,求aa2a3的值 .a a2a3【解析】若 a0 ,那么a a2a31113;若 a0 ,那么a a 2a31111.a a2a3a a 2a3【例 18】(10级)(2006年第二届“华罗庚杯”香港中学竞赛试题)已知 x a b c abc ,且a b c abca ,b,c 都不等于0,求 x 的所有可能值【解析】 4或0或 4【巩固】(10 级)(北京市迎春杯竞赛试题)已知a,b,c 是非零整数,且a b c0 ,求a b c abc 的值a b c abc【解析】因为 a ,b,c 是非零有理数,且a b c0 ,所以a,b,c中必有一正二负,不妨设a0,b0,c0 ,则原式a b c abca b c 11110abc【巩固】(2级)若 a0 ,则a_____ ;若a0 ,则a_____ .a a【解析】 1; 1 .重要结论一定要记得.【巩固】(6 级)当m 3 时,化简m3 m3【解析】m 3 , m 30,当 m 3 ,即 m30 时,m3m 3 ,所以m3 1 ;m3当 m 3 ,即 m30 时,m3(m 3) ,所以m3 1 . m3【例 19】(8级)(2009年全国初中数学竞赛黄冈市选拔赛试题)若0 a 1 , 2 b1,则a 1b 2a ba 1b 2a b的值是()A .0B . 1C . 3D .4【解析】 ⑴ C .特殊值法:取 a 0.5 , b1.5代入计算即可.【巩固】 (2 级)下列可能正确的是()A .C .a b 1B .ab c 2aba bca b c d D .ab c d a b c d a bc3abc d4dabcd【解析】 选 D .排除法比较好或特殊值法1 , 1, 1 , 1.【巩固】 (6 级)如果 2ab 0 ,则a1a )2等于(bbA .2B .3C .4D .5【解析】 B2002 2002 2002【例 20】 ( 8 级)如果 a b c 0,a b c 0, a b c 0,则ab c 的值等于abc( )A . 1B . 1C . 0D . 32002 20022002【解析】 易知a, b,c1 ,所以原式1,故选择 Aa 11c b【例 21】 ( 8 级)已知 abc0 ,求abac bc 的值.abacbc【解析】 ∵ abc 0 ,∴ a 、 b 、 c 三个数都不为零.若 a 、 b 、 c 三个数都是正数,则 ab 、 ac 、 bc 也都是正数,故原式值为若 a 、 b 、 c 中两正、一负,则 ab 、 ac 、 bc 中一正、两负,故原式值为若 a 、 b 、 c 中一正、两负,则 ab 、 ac 、 bc 中一正、两负,故原式值为若 a 、 b 、 c 中三负,则 ab 、 ac 、 bc 中三正,故原式值为 3.3.1.1.【巩固】 (6 级)若 a , b , c 均不为零,求a b cab.c【解析】 若 a , b , c ,全为正数,则原式3 ;若 a , b , c ,两正一负,则原式1;若 a , b , c ,一正两负,则原式 1;若 a , b , c ,全为负数,则原式3 .【例 22】(6级)(第13届希望杯 1试)如果2a b 0,求a a2 的值.1b b【解析】由 2a b 0 得 b2a ,进而有aa a1a , a a1a b2a2 a 2ab2a2a若 a0 ,则a a2111 2 3 ,1b b22若 a0 ,则a a2111 2 3 .1b b22【巩固】(6 级)若a,b,c均不为零,且a b c 0 ,求ab c.a b c【解析】根据条件可得 a ,b, c 有1个负数或2个负数,所以所求式子的值为 1 或1【例 23】(8级) a ,b, c 为非零有理数,且 a b c0 ,则a bb cc a的值等于多少?a b b c c a【解析】由 a b c 0 可知a, b ,c里存在两正一负或者一正两负;a b b c c a a b b c c aa b b c c a a b b c c a若两正一负,那么a bbcca11 1 ;b c1a b c a若一正两负,那么a bbcca11 1 .b c1a b c a综上所得a bb c c a 1 .a b b c c a【巩固】(10 级)(海口市竞赛题)三个数 a ,b, c 的积为负数,和为正数,且a b c ab ac bc xb c ab ac ,a bc求 ax3 bx2 cx 1 的值.【解析】 a ,b, c 中必为一负两正,不妨设 a 0 ,则b0,c 0 ;精品文档a b c ab ac bc xbcabac1 1 1 1 1 1 0,所以原式=1.abc【巩固】 (8 级)(第 13 届希望杯培训试题)如果 ab c0 , ab c0 , ab c0,求 ( a)2002(b) 2003 ( c)2004 的值. ab c【解析】 由 a b c 0 , a b c 0 , a b c 0 ,两两相加可得: a 0 , b 0 , c 0 ,所以原式结果为 1.若将此题变形为:非零有理数a 、b 、c ,求 b 1 等于多少?从总体出发: ( a)2008 1 ,所以原式 1 1 1 1 .a【例 24】 ( 8 级)(“祖冲之杯”初中数学邀请赛试题)设实数 a , b , c 满足 ab c 0 ,及abc0 ,若 xa bc, y a ( 1 1 ) b( 1 1 ) c( 1 1 ) ,那么代数式 x 2 y 3xy 的值| a | | b | | c | b ca c a b为.【解析】 由 ab c0 及 abc 0 ,知实数 a , b , c 中必有两个负数,一个正数,从而有 x 1 .又 y a (11 ) b( 11 ) c(11) = abc 3 ,则 x 2 y 3xy16 9 2 .b ca ca b ab c【例 25】 ( 8 级)有理数 a ,b ,c 均不为零,且 a b c0 ,设 xa b c b ca c a,则代数式b2002007的值为多少?x4x【解析】 由 ab c0 易知 a ,b ,c 中必有一正两负或两正一负,不妨设 a 0,b 0,c 0 或a0,b 0,c 0所以 xabc1 或者 xa b c1,所以 x1 ,所以原式 2004a b a c a bb c a c a b【巩固】 (8 级)有理数 a ,b ,c 均不为零,且 a b c0 ,设 xa b c,则代数式19b cac ab的值为多少?x 99x 2000【解析】 由 ab c0 易知 a ,b ,c 中必有一正两负或两正一负,不妨设 a 0,b 0,c 0 或a 0,b 0,c 0所以 xabc或者 xabc时,原式 19021 1,所以当 x 1a b a c a bb c a c a b当 x 1 时,原式 2098【巩固】 (8 级)已知 a 、 b 、 c 互不相等,求(ab)(b c) (b c)(c a) ( c a)( a b) 的值.(a b)(b c)(b c)(c a) ( c a)( a b)【解析】 由题意可得 (a b)(b c)(c a ) 0 且 ( ab) (b c) (ca)0 ,把 a b , b c , c a 当成整体分类讨论:① 两正一负,原式值为1 ;② 两负一正,原式值为 1 .【例 26】 ( 8 级)(第 18届希望杯 2试)若有理数 m 、 n 、 p 满足mn p 1 ,求2mnp的mnp3mnp值.【解析】 由mn p 1 可得:有理数 m 、 n 、 p 中两正一负,所以 mnp0 ,所以mnp1 ,m n pmnp2mnp 2 mnp 2 .3mnp3 mnp3【巩固】 (6 级)已知有理数 a ,b ,c 满足ab c 1 ,则abc()ab cabcA . 1B . 1C . 0D .不能确定【解析】 提示:其中两个字母为正数,一个为负数,即abc 0【巩固】 (8 级)有理数 a , b , c , d 满足abcd1 ,求ab c d的值.abcdabcd【解析】 由abcd1 知 abcd 0 ,所以 a , b , c , d 里含有 1 个负数或 3 个负数:abcd若含有 1 个负数,则ab c d 2 ;若含有 3 个负数,则ab c d 2 .ab c dab c d【例 27】 ( 6 级)已知 ab0 ,求ab的值ab 【解析】 ⑴ 若 a ,b 异号,则a b 0ab⑵若 a ,b 都是正数,则a b a 2b ⑶若 a ,b 都是负数,则a b a2b【巩固】 (6 级)已知 ab0,求a b的值.ab【解析】 分类讨论:当 a0 , ba b 110.当 a 0 , b 0 时,0 时,baa b ( 1)2 .a1b当 a0 , ba b 11 2.当 a 0 , b 0 时, 0 时,ba ab ( 1)0 .a1b综上所述,a b的值为2,0, 2.ab【例 28】 ( 6 级)若 a ,b ,c 均为非零的有理数,求 abc的值 a b c【解析】 ⑴ 当 a ,b ,c 都是正数时,原式a b c 3abc⑵当 a ,b ,c 都是负数时,原式 3⑶当 a ,b ,c 有两个正数一个负数时,原式 1 ⑷当 a ,b ,c 有两个负数一个正数时,原式1【巩固】( 6 级)(第 16 届希望杯培训试题)若 abc0 ,求ab c 的值.abc【解析】 由 abc 0 可得, a 、 b 、 c 中有 3个负数或 1个负数,当 a 、 b 、 c 中有 3个负数时,原式 1 1 ( 1)1 ;当 c 是负数时,原式 1 1 ( 1) 3 .板块三:零点分段讨论法(中考高端,可选讲)【例 29】(4级)(2005年云南省中考试题)阅读下列材料并解决相关问题:x x0我们知道 x0x0,现在我们可以用这一结论来化简含有绝对值的代数式,如化x x0简代数式 x1x 2 时,可令x10和 x20 ,分别求得x1,x 2 (称 1,2 分别为x 1 与 x 2 的零点值),在有理数范围内,零点值x 1和 x 2 可将全体有理数分成不重复且不易遗漏的如下3中情况:·⑴当 x1时,原式x1x2 2 x1⑵当 1≤ x 2 时,原式x 1x23⑶当 x ≥ 2 时,原式x1x22x12x 1 x1综上讨论,原式 3 1 ≤ x22 x 1 x ≥2通过阅读上面的文字,请你解决下列的问题:⑴分别求出 x2和 x 4 的零点值⑵化简代数式 x2x4【解析】⑴分别令 x20 和 x40 ,分别求得 x 2 和 x 4 ,所以x 2 和 x4的零点值分别为 x 2 和 x4⑵当 x 2 时,原式x2x4x2x 42x 2 ;当 2 ≤ x4时,原式x 2x46;当 x≥ 4 时,原式x 2x42x 22 x 2 x2所以综上讨论,原式62≤ x42x 2 x ≥4【例 30】(6级)求 m m 1m 2 的值.【解析】先找零点, m0 , m 10 , m20 ,解得 m0,1, 2.依这三个零点将数轴分为四段:m0 , 0m 1 , 1m 2 , m 2 .当 m0时,原式m m1m23m 3 ;当 0m 1 时,原式m m1m2m3;当 1m 2 时,原式m m1m2m 1 ;【例 31】 ( 4 级)化简: 2x 1 x 2 【解析】 由题意可知:零点为 x1 ,x 01时,原式2当 xx12当1≤ x 2 时,原式 3x 32当 x ≥ 2 时,原式 x 1【巩固】 ( 4 级) (2005 年淮安市中考题 )化简 x 52 x3 .【解析】 先找零点 . x5 0 , x5 ; 2 x 3 0,x3,零点可以将数轴分成三段.当 x ≥ 3, x 520 , 2x 3≥ 0 , x 5 2x 33x 2 ;2当 5 ≤ x3, x 5≥ 0, 2x3 0 , x 5 2x3 8 x ;2当 x 5 , x 5 0 , 2x 3 0 , x 5 2 x 33 x 2 .【巩固】 ( 6 级) (北京市中考模拟题 )化简: x 1 2 x 1 .【解析】 先找零点 . x1 0 , x 1. x1 0, x1.x 1 2 0 , x12 , x1 2 或 x 12 ,可得 x3 或者 x 1 ;综上所得零点有 1,-1 ,3 ,依次零点可以将数轴分成四段. ⑴ x ≥ 3 , x 1 0 , x 1 2 ≥ 0 , x 1 0 , x 1 2 x 1 2 x 2 ; ⑵ 1≤ x 3 , x 1 0 , x1 2 0 , x 1 0, x 1 2 x 1 4 ;⑶ 1≤ x 1 , x1 0 , x 12 0 , x 1≥ 0 , x 1 2 x 12 x 2 ;⑷ x 1 , x 1 0 , x 12 0 , x 1 0 , x 1 2 x 1 2x 2 .【例 32】 ( 6 级)(选讲)(北京市中考题)已知 x 2 ,求 x 3 x 2 的最大值与最小值.【解析】 法1:根据几何意义可以得到,当 x 2 时,取最大值为 5 ;当 x 2 时,取最小值为3.法 2:找到零点 3、 2 ,结合 x 2 可以分为以下两段进行分析:当 2 x 2 时, x 3 x 2 3 x x 2 1 2x ,有最值 3和 5 ;当 x2 时, x3x 2 3 x x 2 5 ;综上可得最小值为3,最大值为 5 .【巩固】 ( 8 级)(第 10届希望杯 2试)已知 0a 4 ,那么 a23 a 的最大值等于 .【解析】 (法 1):我们可以利用零点,将a 的范围分为 3 段,分类讨论(先将此分类讨论的方法,而后讲几何意义的方法,让学生体会几何方法的优越性)(2)当 2 a 3 时, a 2 3 a 1(3)当 3 a 4 时, a 23 a2a 5 ,当 a 4 时,达到最大值 3 综合可知,在 0a 4 上, a 23 a 的最大值为 5(法 2):我们可以利用零点,将a 的范围分为 3 段,利用绝对值得几何意义分类讨论,很容易发现答案:当 a 0 时达到最大值 5 .【巩固】 ( 6 级)如果 y x 1 2 x x 2 ,且 【解析】 当 1≤ x 0 时,有 yx1 2 xx 2当 0 ≤ x ≤ 2 时,有 y x 1 2 x x 2综上所述, y 的最大值为 3,最小值为1≤ x ≤ 2,求 y 的最大值和最小值2x 3 ,所以 1≤ y 3 ;3 2 x ,所以 1 ≤ y ≤ 31【巩固】 ( 6 级)( 2001 年大同市中考题)已知5 x7,求 x 取何值时 x 1x 3的最大值9与最小值.【解析】 法 1: x1 x3 表示 x 到点 1和 3 的距离差,画出数轴我们会发现当,x7时两者的距离9差最小为32,即 x 1 x 3min 32 ;当 5 x3 时,两者的距离差最大为4,即99( x 1 x3 )max4 .法 2:分类讨论:先找零点,根据范围分段,当 5 x3时, x 1 x 34;当 3 x 7 时, x1 x 32x2 ,当 x7有最小99值32;当 x3 有最大值4 .综上所得,当 5≤ x ≤ 3 时,最大值为 4;当 x7时,9 32 .9最小值为9课后练习练习 1. ( 2 级)若 abab ,则下列结论正确的是()A. a 0,b 0B. a0,b 0C. a 0,b 0D. ab【解析】 答案 BC 不完善,选择 D .练习 2. ( 2 级) (人大附期中考试 )如果有理数 a 、 b 、 c 在数轴上的位置如图所示,求a ba cb c 的值 .b-1 c 0 a 1【解析】原式(a b) (a c) (b c) 0练习 3. (6 级)已知 x0 z, xy 0, yz x ,求 xz y z x y 的值 .【解析】 由 x0 z, xy0 可得: y0 z ,又 y z x ,可得: yx z ;原式 x zyz xy 0 .练习 4. ( 8 级)(第 13届希望杯培训试题)若 x 22001,则 | x | | x1| | x 2 || x3| | x 4 | | x5|.2002【解析】 因为 x2 2001 ,所以 2 x3 ,原式 x ( x1) ( x2)( x 3) ( x 4) ( x 5) 9 .2002练习 5. ( 6 级)( 2006 年七台河市中考题)设y x b x 20x b 20 ,其中0 b 20,b x20 ,求 y 的最小值 .【解析】 y x b x 20x b 20 x b (x 20) ( x b 20) 40 x ,则 x 20时, y 有最小值为 20.练习 6.(4级)若a0 ,化简a a.【解析】 a a a a2a2a .练习 7.(6级)若a0 ,试化简2a3a.3a a2a3a2a3a5a 5 .【解析】a3a3a a4a4练习 8.(6级)若 2x 4 5x 1 3x 4 的值恒为常数,则x 应满足怎样的条件?此常数的值为多少?【解析】要使 2 x4 5 x 13x 4 的值恒为常数,那么须使45x0 , 13x 0 ,即1x4,原式 2 x 4 5x 1 3x 4 2x 45x3x 1 47 . 35练习 9.(8级)(第6届希望杯2试)a 、b、 c 的大小关系如图所示,求ab bc c a ab ac的值.a b b c c a ab aca b0 1c【解析】从图中可知 a b c 且 a 0, b0, c0 ,所以 a b0 , b c0 , c a0 , ab0 , ac0 ,所以 ab ac0 ,原式(1) (1) 1 1 2 .练习 10.(8级)若a b c0 , abc 0 ,则b cc a a b.a b c∵ a b c0 , abc0 ,∴a、 b 、c中一正二负,∴b c c a a b a b c a b c a b 1 .c练习 11.(6级)求 y x1x 5的最大值和最小值.【解析】法 1:根据几何意义可以得答案;法 2:找到零点 5 ,1,可以分为以下三段进行讨论:当 x 5 时,y x 1 x 5 1 x x 5 6 ;综上所得最小值为 6 ,最大值为 6 .练习 12.(6级)(第2届希望杯 2 试)如果 1 x 2 ,求代数式x2x1x的值.x21x x【解析】当 1 x 2 时, x0 , x 10 , x 2 0 ,原式x2x1x1111.x2x1x。
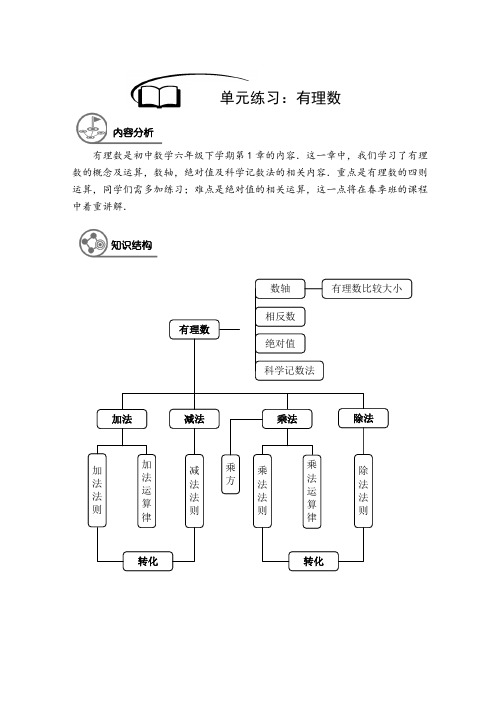
六年级寒假班第4讲:有理数章节复习-教师版
有理数是初中数学六年级下学期第1章的内容.这一章中,我们学习了有理数的概念及运算,数轴,绝对值及科学记数法的相关内容.重点是有理数的四则运算,同学们需多加练习;难点是绝对值的相关运算,这一点将在春季班的课程中着重讲解.单元练习:有理数内容分析知识结构除法有理数乘法 减法 绝对值 加法 相反数数轴 转化 转化科学记数法有理数比较大小加法法则减法法则乘法法则除法法则加法运算律乘法运算律乘方选择题【练习1】关于“零”的说法正确的是()①是整数,也是有理数;②不是正数,也不是负数;③不是整数,是有理数;④是整数,不是自然数.A.①、④B.②、③C.①、②D.①、③【难度】★【答案】C【解析】0是最小的自然数,则必为整数和有理数,但同时0非正非负,①②正确.【总结】考查数字“0”的特征,注意“0”的特殊性.【练习2】如果30%+表示增加30%,那么6%-表示()A.增加24% B.增加6% C.减少6% D.减少36%【难度】★【答案】C【解析】正负号表示相反意义的量,“+”表示增加,“-”号表示减少,故选C.【总结】考查正负号表示相反意义的量.【练习3】下列说法中,正确的是()A.存在最小的有理数B.存在最大的负有理数C.存在最小的正有理数D.存在最大的负整数【难度】★【答案】D【解析】数字的最值,只能是整数,最大的负整数是“1-”,最小的正整数是“1”,故选D.【总结】考查数的分类和数字中的一些最值问题.【练习4】数轴上表示2-的点在()A.原点的右侧B.原点的左侧C.原点D.无法确定【难度】★【答案】B【解析】数轴上表示负数都在原点的左侧,正数都在原点的右侧,故选B.【总结】考查正负数在数轴上的表示.【练习5】 一个点从数轴上的表示2-的点开始,先向右移动5个单位长度,再向左移动2个单位长度,经过两次移动后到达的终点表示( ) A .5+B .1-C .1+D .5-【难度】★【答案】C 【解析】“2-”向右移动5个单位得“3+”,“3+”向左移动2个单位得“1+”,故选C .【总结】考查数轴上点的移动.【练习6】 下列结论中,正确的是( )A .x -一定是负数B .x -一定是非正数C .x 一定是正数D .x -一定是负数【难度】★【答案】B【解析】绝对值表示距离,即为非负数,可知x -为非正数,故选B . 【总结】考查绝对值的意义,绝对值表示距离,即为非负.【练习7】 两个非零有理数的和为零,则它们的商是( )A .0B .1-C .1+D .不能确定【难度】★【答案】B【解析】两数和为零,即0a b +=,得a b =-,两有理数非零,则有()1a b b b ÷=-÷=-, 故选B .【总结】考查数轴上到原点距离相等的两个点的商.【练习8】 下列各式运算结果为正数的是( )A .425-⨯B .()4125-⨯C .()4125-⨯D .()6135-⨯【难度】★【答案】B【解析】A 选项中一个负号,积为负数;B 选项中是负数的偶数次幂,为正数;C 选项中括 号中计算差为负数,积为负数;D 选项显然为负数,故选B . 【总结】考查积的“奇负偶正”.【练习9】 若mn > 0,则关于m 、n 的说法正确的是( )A .都为正B .都为负C .同号D .异号【难度】★【答案】C 【解析】由0mn >,分类讨论可知00m n >⎧⎨>⎩或00m n <⎧⎨<⎩,即为同号,故选C .【总结】考查由两数积的正负性判断两数符号的同异.【练习10】 计算()111112234⎛⎫-++⨯- ⎪⎝⎭时,要避免通分,可运用( )A .加法交换律B .加法结合律C .乘法交换律D .乘法分配律【难度】★【答案】D【解析】2、3、4都是12的因数,可知可利用乘法分配律简便计算,故选D . 【总结】考查有理数的计算,合理利用乘法运算律.【练习11】 两数相加,其和小于每一个加数,则下列说法正确的是( )A .两个加数必有一个是0B .两个加数一正一负,且负数的绝对值较大C .两个加数都为负数D .两个加数一正一负,且正数数的绝对值较大 【难度】★★【答案】C【解析】设两数分别为a 、b ,由a b a +<且a b b +<,可知0a <且0b <,即两加数都 为负数,故选C .【总结】考查根据题目条件确定相应未知数的正负,解决问题.【练习12】 数轴上表示整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2016厘米的线段AB ,则AB 盖住的整点的个数是( ) A .2014或2015 B .2015或2016 C .2016或2017D .2017或2018【难度】★★【答案】C【解析】若线段AB 的起点在整点上,覆盖整点个数为201612017+=个;若线段AB 的起 点不在整点上,则覆盖整点个数为2016个,故选C .【总结】考查数轴上的一段距离中点的个数,注意起点位置的差别.【练习13】 如果a 、b 表示的是有理数,并且20a b +=,那么( )A .a 、b 互为相反数B .a = b = 0C .a 和b 符号相反D .a 、b 的值不存在【难度】★★【答案】B【解析】由20a b +=,0a ≥,20b ≥,可得20a b ==,则有0a b ==,故选B . 【总结】考查平方和绝对值的非负性的应用.【练习14】 如果3x =,4y =,那么x y +的结果是( )A .1B .7C .1或7D .1-或7-【难度】★★【答案】C【解析】由3x =,4y =,可得3x =±,4y =±,则1x y +=±或7±,1x y +=或7. 【总结】考查根据绝对值得到对应的未知数的取值进行解题和应用.【练习15】 下列等式,一定成立的是( )A .0a a +-=B .0a a --=C .0a a --=D .0a a --=【难度】★★【答案】C【解析】互为相反数的两数的绝对值相等,则有a a =-,故选C . 【总结】考查互为相反数的两数的关系.【练习16】 两个不为零的有理数相除,如果交换被除数与除数的位置而商不变,那么这两个数一定是( ) A .相等B .互为相反数C .互为倒数D .相等或互为相反数【难度】★★【答案】D【解析】除数与被除数交换位置商不变,说明商与商的倒数相等,即商只能为1±,由此可得 除数与被除数相等或互为相反数,故选D . 【总结】考查根据特殊条件确定相应的未知数的关系.【练习17】 某粮店出售的三种品牌的面粉袋上分别标有质量为(250.1±)千克,(250.2±)千克,(250.3±)千克的字样,从中任意拿出两袋,它们的质量最多相差( ) A .0.8千克B .0.6千克C .0.5千克D .0.4千克【难度】★★【答案】B【解析】根据面粉上的标识,可分别得到面粉产品质量范围为24.9~25.1kg ,24.8~25.2kg , 24.7~25.3kg ,质量相差最多,则应为25.324.70.6kg -=,故选B . 【总结】考查“±”符号的应用,表示一定的取值范围.【练习18】 1米长的小棒,第1次截去一半,第2次截去剩下的一半,如此下去,第7次后剩下的小棒长为( )米A .114B .164C .1128D .1256【难度】★★★【答案】C【解析】第一次截去一半,剩余长度为12m ,第二次再截去一半,则剩余长度为212m ⎛⎫⎪⎝⎭,则第7次截得剩余长度为7112128m ⎛⎫= ⎪⎝⎭,故选C .【总结】考查找规律计算的应用.【练习19】 若0a ba b+=,则下列结论中成立的是( ) A .0ab > B .0ab = C .0ab < D .0a b +<【难度】★★★【答案】C 【解析】对任一非0有理数,必有1x x=±,由0a ba b+=,可知一个为1,一个为1-,即 a 、b 两数一个为正,一个为负,得0ab <,故选C .【总结】考查根据1xx =±的应用判断未知数的正负.【练习20】 如果abcd < 0,a + b = 0,cd > 0,那么这四个数中负因数的个数至少有( )A .4个B .3个C .2个D .1个【难度】★★★【答案】D【解析】由0abcd <,可知a 、b 、c 、d 都不为0,由0a b +=,可知a 、b 必为一正一 负,由0cd >,可知c 、d 同号,则负因数应为1个或3个,即至少1个,故选D . 【总结】考查根据题目条件确定未知数的正负.【练习21】 如果1+表示比赛中赢了1局,那么2-表示___________________. 【难度】★ 【答案】输了2局.【解析】正负号表示相反意义的量,“+”表示赢,则“-”号表示输,即得“2-”表示输 了2局.【总结】考查正负号表示相反意义的量.填空题【练习22】 下列有理数中:2-, 1.0305-,47+,0,3,56-,5.21,0.016-,25.4%中,正数有_______个,负数有______个,正整数有______个,负分数有_____个. 【难度】★【答案】4,4,1,3.【解析】正数分别为47+、3、5.21、25.4%,共4个;负数分别为2-、1.0305-、56-、0.016-,共4个;正整数为3,共1个;负分数分别为 1.0305-、56-、0.016-,共3个.【总结】考查有理数的分类.【练习23】 在数轴上,距离原点3个单位长度的点表示的数为______. 【难度】★【答案】3±.【解析】根据数轴的定义,距离原点距离为3的点在原点左右两边各有一个,为3±. 【总结】考查数轴上到原点距离为定值的点,一般来说有两个,且这两个数互为相反数.【练习24】 绝对值不小于1但小于4的整数是____________________. 【难度】★【答案】1±,2±,3±.【解析】绝对值不小于1但小于4的整数,则其绝对值为1,2,3,即得相应的整数分别为1±, 2±,3±.【总结】考查数轴上的绝对值相等的点有两个,注意临界值是否能取得.【练习25】 计算:(1)22133⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭______,(2)11232⎛⎫-÷⨯= ⎪⎝⎭______,(3)321120162016⎛⎫⎛⎫-÷-= ⎪ ⎪⎝⎭⎝⎭______,(4)()4433-+-=______. 【难度】★【答案】(1)1-;(2)112-;(3)12016-;(4)0. 【解析】(1)原式221133=-=-;(2)原式()1133224=-⨯⨯=-; (3)原式12016=-; (4)原式81810=-+=. 【总结】考查有理数的计算,注意计算中一些常见易错点,运算顺序的把握等.【练习26】 2010年,我国的第6次人口普查时,全国总共约13.4亿人,写成科学记数法形式为__________人.【难度】★【答案】91.3410⨯.【解析】根据科学计数法的原则,写作()10110n a a ⨯≤<的形式,913.4 1.3410=⨯亿.【总结】考查有理数的科学计数法.【练习27】 相反数等于它本身的数是______,倒数等于它本身的数是______,平方等于它本身的数是______,立方等于它本身的数是______. 【难度】★★【答案】略【解析】0,1±,0和1,0和1±. 【总结】考查有理数中的一些满足特殊条件的数字值.【练习28】 观察下列数字的排列规律,然后填入适当的数:3,7-,11,15-,19,23-,______,______. 【难度】★★【答案】27,31-.【解析】观察数字的变化规律,发现后面一个数字的绝对值比前面一个数字的绝对值大4, 同时数字的变化满足一正一负的变化规律,可知后面两个数字分别为27和31-. 【总结】考查找规律问题,注意符号的变化.【练习29】 已知:0a b <-<,比较a 、b 、a -、b -的大小得到:______ > ______ > ______ > ______. 【难度】★★【答案】a -,b ,b -,a【解析】由0a b <-<,可知0b a <-<,即0b a <<-,由此可得a b b a ->>->. 【总结】考查根据绝对值的大小确定相应未知数以及其相反数的大小关系.【练习30】 一个有理数的倒数是327的相反数,则这个数的80%是______.【难度】★★【答案】2885-. 【解析】327的相反数的倒数即这个有理数为717-,这个数的80%即为72880%1785-⨯=-.【总结】考查根据题目条件确定相关有理数的取值解决问题.【练习31】 若3x =,则x =______;若15x-=,则x =______. 【难度】★★【答案】3±,15±.【解析】由3x =,得3x =±;由15x -=,得15x-=±,则15x =±. 【总结】考查根据数字的绝对值确定相应数字的取值.【练习32】 已知2x >,则11x x +--=______. 【难度】★★【答案】2.【解析】由2x >,则有10x +>,10x -<,则()()11112x x x x +--=++-=. 【总结】考查根据题目条件进行去绝对值的化简计算.【练习33】 如果规定运算a b a b *=--,那么()31 1.24⎛⎫*-= ⎪⎝⎭______.【难度】★★【答案】1120-.【解析】根据运算法则,可知()()33111 1.21 1.24420⎛⎫*-=---=- ⎪⎝⎭.【总结】考查新定义计算,根据新定义计算的法则用数值替换字母计算即可.【练习34】 数轴上原点右边4厘米处的点表示的有理数是32,那么数轴上原点左边10厘米处的点表示的有理数是______. 【难度】★★【答案】80-.【解析】距原点4厘米处表示的点是32,则距原点10厘米处表示的数的绝对值即为()1032480⨯÷=,点在原点左边,故为负值,即为80-. 【总结】考查数轴的单位长度处处相等.【练习35】 两滴墨水洒在一个数轴上,如图所示.试根据图中标出的数值,计算墨迹盖住的整数共有______个. 【难度】★★ 【答案】277.【解析】墨迹盖住负数部分所包含的整数从109~12--,盖住的整数个数为()()12109198---+=,墨迹盖住的正数部分包含的整数从11~189,则整数个数为 18911117-+=,即墨迹盖住的整数共98179277+=个.【总结】考查数轴上的某一段距离的整点个数,计头计尾,同时注意数轴上点的大小的变化.【练习36】 已知4x =,5y =,且x y >,则y x -=______. 【难度】★★【答案】9-或1-.【解析】由4x =,5y =,可得4x =±,5y =±,由x y >,得,5y =-,由此则 有9y x -=-或1-.【总结】考查根据题目条件确定相应未知数的值进行解题计算.109.2-11.9-10.3【练习37】 你知道20162除以3的余数是多少吗?我们通过下面的实践来解决这个问题:(1)12032=⨯+,显然12除以3的余数为2; (2)22131=⨯+,显然22除以3的余数为1; (3)32=_______,显然32除以3的余数为_______; (4)42=_______,显然42除以3的余数为_______; ……观察右侧的结果所反映的规律,我们可以猜想出20162除以3的余数是______. 【难度】★★【答案】232⨯+,2,531⨯+,1,1.【解析】由以上过程,可知2的奇数次幂除以3的余数为2,2的偶数次幂除以3的余数为1, 即猜想得到20162除以3的余数是1. 【总结】考查找规律的方法并进行猜想应用.【练习38】 a 、b 、c 三个有理数在数轴上的位置如图所示,则1c a -、1c b -、1a b-中最大的 是______. 【难度】★★★【答案】1a b-. 【解析】根据数轴上点的位置关系,可知c b a <<,则有0c a -<,0c b -<,0a b ->,由此可得10c a <-,10c b <-,10a b >-,由此可知1a b -最大. 【总结】考查根据数轴上点的位置关系确定相应字母的大小关系进行解题应用.【练习39】 ()()242340x y z ++-+-+=,则y z x x +=______. 【难度】★★★【答案】8.【解析】由()()242340x y z ++-+-+=,根据20x +≥,()230y -≥,()440z -+≥, 可得203040x y z +=⎧⎪-=⎨⎪-+=⎩,解得234x y z =-⎧⎪=⎨⎪=⎩,则有()()34228168y z x x +=-+-=-+=.【总结】考查偶次方和绝对值的非负性.【练习40】 如果51x x -++是一个常数,则这个常数的值为______. 【难度】★★★【答案】6.【解析】分类讨论得:当5x ≤时,原式()51516x x x x =--++=-+++=;当5x >时,原式()5124x x x =-++=-;综上,当5x ≤时,式子值为常数,即得常数值为6. 【总结】考查绝对值的分类去绝对值计算.【练习41】 将 2.5-,12,2,0,2--,()3--在数轴上表示出来,并用“>”把它们连接起来.【难度】★★【答案】()13202 2.52-->>>>-->-,数轴略. 【解析】22--=-,()33--=,根据数轴的特性,数轴上的数从左往右依次增大,由此 可知()13202 2.52-->>>>-->-. 【总结】考查数轴上点的表示和相应数轴上表示数的大小的变化.【练习42】 数轴上表示数a 的点到原点的距离为5,求5a -的值. 【难度】★★【答案】0或10-.【解析】表示数a 的点到原点的距离为5,可知5a =±,则有50a -=或10-. 【总结】考查数轴上到原点距离相等的点有两个,互为相反数.【练习43】 某班学生上体育课,对男生做俯卧撑测试,以规定时间内做40个为达到标准,问:(1)这10名男生成绩的达标率为多少? (2)他们共做了多少个俯卧撑?【难度】★★【答案】(1)70%;(2)408个.【解析】(1)达到40个即为达标,用正负表示0页包含在内,即达标的有7人,达标率为 710100%70÷⨯=;(2)共做俯卧撑()()()23103123231040408++-++-++-++++⨯=⎡⎤⎣⎦个. 【总结】考查相应计量标准的应用,注意计算总数量时不要忘记标准值.解答题【练习44】 已知x 、y 是有理数,且()()221210x y -++=,求x + y .【难度】★★【答案】12或32-. 【解析】由()()221210x y -++=,()210x -≥,()2210y +≥,即得10x -=,210y +=, 解得:1x =±,12y =-,由此得12x y +=或32-.【总结】考查平方的非负性,根据性质即可求得对应字母取值.【练习45】 计算:(1)()()23551110.420.2119.711.73232⎡⎤⎡⎤--+--÷-⨯+⨯⎣⎦⎢⎥⎣⎦; (2)()()()323520.3873410⎧⎫⎡⎤⎛⎫-⨯-⨯-+⨯-÷-+⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭;(3)()()2222213923133413⎡⎤-⎛⎫⎛⎫+---÷-⨯⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦; (4)22223211218538232492255⎛⎫⎛⎫⎛⎫⎛⎫⨯-÷-+⨯÷ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⨯-÷-- ⎪ ⎪⎝⎭⎝⎭.【难度】★★【答案】(1)32;(2)56-;(3)9352;(4)252-. 【解析】(1)原式()()()5553111211.719.71281323222=----⨯⨯-=--⨯⨯-=-+=⎡⎤⎣⎦; (2)原式()()()()238422856=-⨯-⨯-+=-⨯=-⎡⎤⎣⎦; (3)原式419947794779329139413133613135252⎛⎫=+-+÷⨯=+⨯=+=⎪⎝⎭; (4)原式()351498882553492436122922525⎛⎫⨯-⨯-+⨯÷+ ⎪⎝⎭===--⨯÷-. 【总结】考查有理数的四则混合运算,注意运算顺序和运算律的运用.【练习46】 有理数a 、b 、c 在数轴上的位置如图所示,若11m a b b a c c =+------,求1000m 的值.【难度】★★【答案】2000-.【解析】根据数轴上字母顺序,可知01b a c <<<<,则有0a b +<,10b -<,0a c -<, 10c ->,则有()()()()112m a b b a c c =-++-+---=-,得10002000m =-.【总结】考查去绝对值的运算,先根据绝对值中式子与0的大小关系去绝对值再代值计算.【练习47】 若201522016x =,求12345x x x x x x +-+-+-+-+-的值. 【难度】★★【答案】9.【解析】由201522016x =,可得23x <<,则0x >,10x ->,20x ->,30x -<,40x -<,50x -<,则原式()()()()()123459x x x x x x =+-+-------=.【总结】考查去绝对值的运算,先根据绝对值中式子与0的大小关系去绝对值再代值计算.【练习48】 已知三个有理数a 、b 、c 的积为负数,它们的和是正数,当a b c x abc=++时,求2018201620182017x x -+的值. 【难度】★★★【答案】2015.【解析】三个有理数积为负数,则必有三个同为负数或二正一负,又根据三数和为正数,可知必为二正一负,对任一非零数而言,必有1kk =±,本题中即可得()1111x =++-=,则20182016201820172016201820172015x x -+=-+=.【总结】考查根据条件确定数字的正负,结合1kk =±进行计算.【练习49】 化简32x x ++-. 【难度】★★★【答案】略.【解析】本题中未给出x 的具体取值范围,不能确定各绝对值中式子与0的大小关系,由此 需进行分类讨论,按照式子为0的相应x 值作为取值范围的分段: 当3x ≤-时,原式()()323221x x x x x =-+--=---+=--; 当32x -<<时,原式()()32325x x x x =+--=+-+=; 当2x ≥时,原式()()323221x x x x x =++-=++-=+. 【总结】考查绝对值的分类去绝对值计算.【练习50】 如果31x x -+-是一个常数,求x 的取值范围和这个常数的值. 【难度】★★★【答案】2,13x ≤≤.【解析】本题去绝对值需进行分类讨论,按照式子为0的相应x 值作为取值范围的分段:当1x <时,原式()()313124x x x x x =----=-+-+=-+; 当13x ≤≤时,原式()()31312x x x x =--+-=-++-=; 当3x >时,原式()()313124x x x x x =-+-=-+-=-; 综上,式子值为常数时,即为2,此时取值范围为13x ≤≤. 【总结】考查绝对值的分类去绝对值计算.。
第2讲 绝对值的化简(教师版)

,
①当 , , 都是正数时,
②当 , , 都是负数时,
③当 , , 有一个负数时,
④当 , , 有两个负数时,
考点 数 > 有理数 > 绝对值 > 绝对值的性质
例题5
若
,求
的值.
答案 -3或1
解析 当
中有三个负数或一个负数 中有三个负数时,
当 中有一个负数时,
; ;
; .
或. 考点 数 > 有理数 > 绝对值 > 绝对值的性质
例题1
、 、 在数轴上的位置如图所示,化简
.
答案 . 解析 略 考点 数 > 有理数 > 绝对值 > 绝对值的性质
设 , , 为非零实数,且
,
,
.化简
.
答案 解析
,
,;
,
;
,
,
所以可以得到 , , ;
考点 数 > 有理数 > 绝对值 > 绝对值的性质
模块二 绝对值的无条件化简
考点 零点分段法
知识导航
时,
.
答案
解析 由题:
,
,
∴ 、 、 两正一负,
∴
,
原式
.
考点 数 > 有理数 > 绝对值 > 绝对值的性质
作业8
已知 是非 有理数,求
.
答案
解析 若 是非 有理数,则 或 ; 当 时,
当 时,
∴
.
; ;
考点 数 > 有理数 > 绝对值 > 绝对值的性质
教师备选
若 、 、 为整数,且
,试计算
答案
解析 , , 均为整数,则 , 也应为整数,且
