弹塑性力学-屈服条件
弹塑性力学

ij 0 橡皮和铁盒之间无摩擦力 1 2 q, 3 q max 1 3 (1 2 ) q 1 2 2(1 )
ME6011 弹性塑性力学 21
3-3 3 3 Tresca和Mises屈服条件
研究塑性变形和作用力之间的关系及在塑性变形后 物体内部应力分布规律的学科称为塑性力学。 塑性力学问题的特点(4点) 应力与应变之间的关系(本构关系)是非线性的, 其非线性性质与具体材料有关; 应力与应变之间没有一一对应的关系,它与加载 历史有关; 在变形体中有弹性变形区 和塑性变形区,而在求 解问题时需要找出弹性区和塑性区的分界线;
xy yz
zx
xy
G
1 2 E 1 2 0 0 E
yz zxG NhomakorabeaG
1 1 1 2 [ x 0 ] x 0 [(1 ) x ] 0 E E E ex 应变偏量分量 sx 1 2G 应力偏量分量
ME6011 弹性塑性力学
9
不考虑材料强化性质
考虑材料强化性质
①理想弹塑性模型
E s ( s ) 韧性 ( s ) 材料
②线性强化弹塑性模型
( s ) E s E ( s ) ( s )
双线性强化模型
力学问题中各量间关系
ME6011 弹性塑性力学 3
• 本构关系
–反映应力应变之间的联系 映 –材料的固有特性:每一种材料,应力、应变有 着固有的关系 –广义Hook定律:线性 –增量理论:非线性,应变与应力状态和变形历 增量理论 非线性 应变与应力状态和变形历 史有关,研究应力和应变增强之间的关系
E
厚壁圆筒__弹塑性力学知识

2. 弹塑性阶段: (1) 弹性区:r r b
(1 )a 2 pe u E (b 2 a 2 ) b2 r (1 2 )r
a2 pe 1 2 2 b
ss
内半径为r ,外半径为b,在 r = r 处承受内压的厚壁筒
sq r
r rb
sq
p
r
sq r
a p
b
sq r
r b2 p a2 1 2 s s 1 l n 2 2 a b a r 2 2 2 s r a p b s 1 2 2 2 2 2 b b a r
通解:
s r C1 C2 r 2
s q C1 C2 r 2
一、弹性分析
2. 解答
通解:
s r C1 C2 r 2
s q C1 C2 r 2
er
1 1 C1 1 C 2 r 2 E 1 1 C1 1 C 2 r 2 eq E 1 1 C1r 1 C 2 r 1 u E 1 2 2 C1 2 a p b p2 1 2 b a a 2b 2 p2 p1 C2 2 2 b a
u
e
rr
u
p
rr
(1 ) r 2s s 2 2 C b ( 1 2 ) r 2 Eb 2
(1 ) r 2s s 2 2 u b ( 1 2 ) r 2 Eb 2 r
=1/2
3 r 2s s u 4 Er ul ue b2 2 a
弹性极限状态:
a p1
弹塑性力学-第五章+屈服准则v1

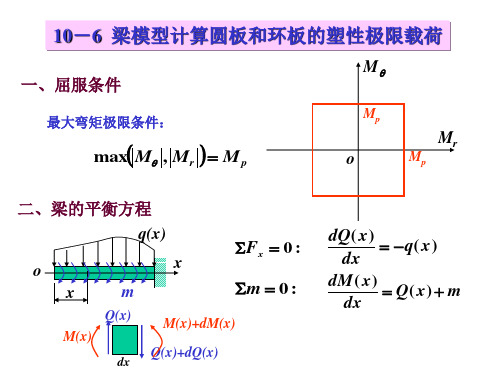
弹塑性力学10-6梁模型计算圆板和环板的塑形极限载荷(精)
r
o b
解:
o
z
r
b r a
z
a
m= 2Mp
2rM r 2 r b M p
2 r b r b 2rrq 2bq r b 2bq
b r b r 2b Mr 1 M p q r 6r
2
2
2
3
r
o
解:
o
z
r
r a
a
z
2rM r 2rM p r r 2rq 2 3
m= 2Mp
qr 2 Mr M p 6
Mr
r a
qa2 M p M p M 支圆板:
Mr
r a
0
ql 6
Mp a2
例题2:半径为 a 的简支环板,内半径为 b ,受均布载荷 q 作用,圆板单 位塑性极限弯矩为: Mp ,求塑性极限载荷。 2rq q
i 1
ai bi
( n 2) 2n 2 n
Pl M P cota i cot b i
i 1
n
正多边形(集中力作用在板中心): a i b i
( n 2) 2n 2 n
Pl M P 2 tan
i 1
n
n
Pl 2nM P tan
r
o b
解:
o
b c a
z
a
m= 2Mp
z
2 r b M p brc 2rM r 2 r b M p P r c c r a
Mr
r a
0
Pl
2 a b M p ac
弹塑性力学-15 屈服理论

●应力空间
3 P(1, 2 , 3 )
以应力分量为坐标轴—空间坐标系
主应力空间:主应力分量为坐标轴
2 1
●应力路径 一点应力状态的变化:应力点 在应力空间的运动轨迹来描述
应力空间既非几何空间又非物理空间
15.1 屈服理论分析
3. 屈服条件的一般形式
材料屈服与否取决于其所受 的应力状态和材料特性参数
S
等倾线
L P
2
一点的应力矢量 OP 1e1 2e2 3e3
15.1 屈服理论分析
2. 屈服条件的一般形式
3 QL
OP 1e1 2e2 3e3
P
n
1 3
e1
1 3
e2
1 3 e3
平面 o S
2
1
OQ OP n
1 3
(1
2
3
)
15.1 屈服理论分析
3. 屈服条件的一般形式
3. 屈服条件的一般形式
由于
f (1, 2 , 3, k) 0
I1 ii x y z 1 2 3 3 m
I2
x y
y z
z x
2 xy
2 yz
2 zx
1 2 2 3 31
I3
x
y
z
2 xy
yz
zx
x
2 yz
y
2 zx
z
2 xy
1 2 3
15.1 屈服理论分析
怎样建立屈服理论?
●根据屈服现象与机制,提出理论假设; ●基于理论假设建构屈服模型,即给出包含 屈服参数的理论公式; ●根据简单条件下的屈服试验结果,确定其 中的屈服参数; ●通过复杂应力状态下的屈服试验结果,对 理论进行检验。
塑性力学第五章(2)-简单的弹塑性问题(二)

σs
E
不变, ,保持 ε s不变,再加扭矩至 γ s =
τs
G
γ 同时拉扭进入塑性状态, 不变, (3)同时拉扭进入塑性状态,保持 ε 不变,到
ε s ,γ s
求应力分量
σ ,τ = ?
τ σ
Mises条件: 条件: 条件
σ 2 + 3τ 2 = σ s2
τ
σ
3
s
B
C A
O
σ
σ
s
γ
ε = σs
E =
应变分量(体积不可压缩): 应变分量(体积不可压缩):
σ
1 de z = d ε , de r = deθ = − d ε 2
d γ zθ = d γ
γ θr = γ rz = 0
塑性功增量: 塑性功增量:
dW d = sij deij
= s z de z + s r de r + sθ deθ + τ θz d γ θz + τ θr d γ θr + τ rz d γ rz
th
σs
σs
σ =
ch
σs
3G γ
σs
γ =
σs
3G
⇒
σ = 0 .648 σ s , τ = 0 .439 σ s
(2)先扭后拉 )
γ
σs
3G
τ
B C
σ
3
A
s
B
C A
O
σs
3G
ε
O
σ
σ
s
dγ = 0
dW d = σ d ε + τd γ = σ d ε
3Gd ε = dσ 1−
弹塑性力学——精选推荐

弹塑性⼒学应⼒应变关系应⼒应变都是物体受到外界载荷产⽣的响应。
物体由于受到外界载荷后,在物体内部各部分之间要产⽣互相之间的⼒的作⽤,由于受到⼒的作⽤就会产⽣相应的变形;或者由于变形引起相应的⼒的作⽤。
则⼀定材料的物体其产⽣的应⼒和应变也必然存在⼀定的关系。
在⼒学上由于平衡⽅程仅建⽴了⼒学参数(应⼒分量与外⼒分量)之间的关系,⽽⼏何⽅程也仅建⽴了运动学参数(位移分量与应变分量)之间的连系。
所以平衡⽅程与⼏何⽅程是两类完全相互独⽴的⽅程,它们之间还缺乏必要的联系,这种联系即应⼒和应变之间的关系。
有了可变形材料应⼒和应变之间关系和⼒学参数及运动学参数即可分析具体的⼒学问题。
由平衡⽅程和⼏何⽅程加上⼀组反映材料应⼒和应变之间关系的⽅程就可求解具体的⼒学问题。
这样的⼀组⽅程即所谓的本构⽅程。
讨论应⼒和应变之间的关系即可变为⼀定的材料建⽴合适的本构⽅程。
⼀.典型应⼒-应变关系图1-1 典型应⼒-应变曲线1)弹性阶段(OC段)该弹性阶段为初始弹性阶段OC(严格讲应该为CA’),包括:线性弹性分阶段OA段,⾮线性弹性阶段AB段和初始屈服阶段BC 段。
该阶段应⼒和应变满⾜线性关系,⽐例常数即弹性模量或杨⽒模量,记作:εσE =,即在应⼒-应变曲线的初始部分(⼩应变阶段),许多材料都服从全量型胡克定律。
2)塑性阶段(CDEF 段)CDE 段为强化阶段,在此阶段如图1中所⽰,应⼒超过屈服极限,应变超过⽐例极限后,要使应变再增加,所需的应⼒必须在超出⽐例极限后继续增加,这⼀现象称为应变硬化。
CDE 段的强化阶段在E 点达到应⼒的最⾼点,荷载达到最⼤值,相应的应⼒值称为材料的强度极限(ultimate strength ),并⽤σb 表⽰。
超过强度极限后应变变⼤应⼒却下降,直到最后试件断裂。
这⼀阶段试件截⾯积的减⼩不是在整个试件长度范围发⽣,⽽是试件的⼀个局部区域截⾯积急剧减⼩。
这⼀现象称为“颈缩”(necking )。
弹塑性力学应力应变关系

我所认识的应力和应变关系在这之前我认识了应力和应变的概念、性质以及从静力学和几何学的角度出发所得到的平衡方程和几何方程。
但是平衡方程仅反映了应力分量和外力分量的关系;几何方程仅建立了位移分量和应变分量的关系。
而谈到应力与应变的关系,对于可变形固体,在弹塑性力学中,在外力的作用下,其将发生变形。
变形分为两个阶段,弹性阶段和塑性阶段。
在弹性阶段,发生的弹性变形可以完全恢复,它是一个可逆过程。
此时,应力与应变的关系是一一对应的,是单值函数关系。
而在塑性阶段,所发生的塑性变形是不可以恢复的,是不可逆过程。
相对应的,塑性阶段的应力应变的关系是非线性关系,不存在一一对应的关系。
我所认识的应力和应变的关系就是本构关系。
本构关系也称为物理关系,它反应的是可变形材料的固有属性,实质上是一组联系力学参数和运动参数的方程式,也就是我们所说的本构方程。
在说应力与应变的关系之前,先说一下本构关系的相关影响因素,包括材料、环境、加载类型、以及加载速度。
即,),,(T t f εσ=。
另外,有各种各样的本构系,比如:弹性本构关系、塑性本构关系、粘弹性本构关系、粘塑性本构关系、各向同性本构关系、各向同性本构关系等等。
简单情况的本构关系:应力和应变的关系包括弹性和塑性的应力应变关系。
我们所说的是线性弹性体的应力应变关系,又分为简单应力状态和复杂应力状态。
在简单拉伸情况下,理想弹性材料的应力和应变的关系很简单,就是材料力学中的胡克定律: 。
而在塑性阶段,应力应变之间不再是简单的胡克定律,而是 。
另外,简单拉伸情况下的卸载定律是 。
在后继弹性阶段,也就是卸载后重新加载的材料会继续发生新的塑性变形,在此时的屈服称为后继屈服,相应的屈服点称为后继屈服点。
初始屈服和后继屈服的不同是:第一,应力的数值不一样,后继屈服的应力值更大;第二,屈服点的个数不一样。
初始屈服点只有一个,而后继屈服点会有好多个,则其对应的应力值也会有很多个。
最后,在卸载全部载荷后进行反向加载比如说把拉伸改成压缩,此时会产生Bauschinger 效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 2
cp = s
若材料强化实验曲线近似为线性,则可表示为
=s+hp 式中h是实验确定的材料常数。
混合强化
• 几何特点: 加载面大小、位置和中心都改变,它是前面两种情况的综合,
• 数学表达: f (ijij) k()= 0
与随动强化不同的是,这里k随加载的历史而变化。 • 说明:
以上关于屈服条件和加载条件的讨论都是在应力空间中进行的。 对应变软化材料来说,应变空间中讨论会更方便些。
B
*
A
s
s
C
反向屈服点
随动(运动)强化
• 几何特点(在应力空间): 形状和大小不变,中心位置,加载面作刚体移动。
• 物理意义: 材料在强化后为各向异性。
• 数学表示:
f (ijij) k = 0 ij是一个表征加载面中心移动,称为背应力(back stress)
初始屈服面
后继屈服面
Prager随动强化模型
初始屈服面
后继屈服面
O C D
B A
Mises初始屈服条件
J2
2 s
3
0
加载(后继屈服)条件
3J 2 s 0
3J 2 0
3
2
sij
sij
0
( d p )0
函数可通过单轴拉伸下实验曲线确定
单轴下的随动强化
某一个方向上的屈服极限提高,则相反方向上的屈服极限会降低。 由A点加载到B点,屈服应力由原来的s提高到*。B=*>s 再反向加载,当应力达到BC=2s时屈服, 而C<s。
• 单轴情况下
理想塑性材料的加卸载准则
加载 d
卸载?d
• 复杂应力状态下
屈服面
n
卸载?d
d 加载 ij
f(ij)<0
弹性状态
f(ij)=0, f (ij+ dij)= 0 加载
f(ij)=0, f (ij+ dij)<0
卸载
df (ij)可以表达成
df(ij) = f (ij+ dij) f (ij) =
中性变载?d
n
d 加载
卸载?d
ij
加载面
任何一种应力状态都不能位于加载面之外
• 增量前 f (ij,) = 0, • 增量后 f (ij+dij,+d) = 0
• 一致性条件:
f ij
dij
f
d
0
f (ijdij , d f (ij,
内变量的性质
• 随加载过程,内变量不断地增加 • 中性变载或者卸载时,则内变量保持不变
不会出现反向屈服。恢复掉的弹性应变是:
e
=1 E
1 s
因此,C点的应变是 C=Be=9s
(3) = 01 当= (1)s,材料产生反向屈服,当从D点到E点时,产生压缩塑
性应变是
p=
1 D h
18 s
而从C点到E点产生的弹性应变是e = (1+)s,最后的应变是
E= (1+)s18s+9s= (1+10)s
总之:内变量只会增加,不会减少。 且只有产生新的塑性变形时,它才会增加。 是塑性变形的不可逆性所决定的。
等向强化
• 几何特点(在应力空间): 加载面形状和中心位置都不变,大小变化,形状相似的扩大。
• 物理意义: 假定材料在强化后仍保持各向同性的性质。
• 数学表示: f (ij) k() = 0
f(J2,J3) k() = 0 进一步解释:等向强化可理解为材料某一方向上因加载屈服极限得到提 高,所有其它方向的屈服极限都将因此而得到同等程度的提高。
初始屈服面
后继屈服面
例1-3 简单拉伸下材料的关系曲线用线性强化模型近似表示为
E = s h p
0 s (s / E) s
其中,常数h=E/9。材料质点经历了如下单轴应力历史: = 0 10 1
其中,1= (1+)s,0<<1。试确定线性随动强化模型下的相应应变历史
解: 线性随动强化模型下,其强化条件均可表示为
• 背应力增量应平行于塑性应变增量 dij=c dipj
式中c是材料常数,由试验确定。 • 对于Mises屈服条件,该模型可写成
ij
c
p ij
3 2
sij
c
p ij
sij
c
p ij
s
单轴加载(拉伸或压缩)时
s11=
2 3
s22=s33=
1 3
1p1 p
p 22
p 33
1 2
p
强化模型式简化为:
hp=s
(1) = 0 1 当=s时,材料屈服,当s<<1即从A到B点,产生塑性变形,
B点的总应变为
(p)B
1
s h
91
E
s
9s
B=e+p
=
1 E
p
1 s
9s
110 s
得强化条件为
s=s
1
B
s
A
s
O
C
D
E
1
(2) = 10 当 = 10,材料处于卸载状态。由于<1, 在0 -1之间,
2 3
p ij
ipj
只有在塑性应变增量各分量之间的比例在整个加载过程中始终保持不 变时,两者才能相等
应力状态与屈服面的关系
当应力状态ij处在加载面上 f (ij,) = 0,
再施加增量dij,产生三种情况: (1)加载:dij指向加载面外 (2)中性变载:dij沿着加载面 (3)卸载:dij指向加载面内
f
dij
ij
f nij = ij
是屈服面外法线
加载条件还可以表示为
f(ij)=0 d•n=0 加载 f(ij)=0 d•n<0 卸载
强化材料的加卸载准则
当应力状态处在当前加载面上,再施加应力增量,产生三种情况 (1)加载:应力增量指向加载面外,推动加载面变化,
产生新的塑性变形(同时会产生弹性变形)。 (2)中性变载:应力增量沿着加载面,即与加载面相切,
累积塑性变形 塑性功
d
2 3
dipj
d
p ij
d p
பைடு நூலகம்
d ijdipj dw p
累积塑性应变与等效应变的不同
• 将整个加载过程看作是许许多多的应力增量过程d所组成。
•
将每一个应力增量过程中所产生的塑性应变增量
d
p ij
计算出 d p
然后累加起来,即计算积分 d p
• 等效塑性应变 p
p
(p)=0
C
*
B
s
A'
p
A
O
E
p
e
复杂应力状态
• 使用一组内变量(=1,2,…,n)描述塑性变形历史, • 后继屈服条件
f (ij,)=0 随塑性变形的发展,不断变化,后继屈服面或加载面也随之改变。 • 定义内变量应该根据材料内部细微结构不可逆的改变, • 通常根据宏观实验结果,引用宏观变量定义内变量
单轴拉伸下的强化
• 随加载,屈服极限会不断提高,称为强化或硬化 • 新的屈服极限:
(s)new = Max history
• 后继屈服条件(也称加载条件) =(s)new 处于屈服状态
<(s)new, 处于卸载状态 • Max history 随塑性变形历史单调增长,
Max history =(p) • 后继屈服条件即加载条件也可表示为
