信息与编码理论课后习题答案
《信息理论与编码》,答案,考试重点(1--3章)

《信息理论与编码》习题参考答案1. 信息是什么信息与消息有什么区别和联系答:信息是对事物存在和运动过程中的不确定性的描述。
信息就是各种消息符号所包含的具有特定意义的抽象内容,而消息是信息这一抽象内容通过语言、文字、图像和数据等的具体表现形式。
2. 语法信息、语义信息和语用信息的定义是什么三者的关系是什么答:语法信息是最基本最抽象的类型,它只是表现事物的现象而不考虑信息的内涵。
语义信息是对客观现象的具体描述,不对现象本身做出优劣判断。
语用信息是信息的最高层次。
它以语法、语义信息为基础,不仅要考虑状态和状态之间关系以及它们的含义,还要进一步考察这种关系及含义对于信息使用者的效用和价值。
三者之间是内涵与外延的关系。
第2章1. 一个布袋内放100个球,其中80个球是红色的,20个球是白色的,若随机摸取一个球,猜测其颜色,求平均摸取一次所能获得的自信息量答:依据题意,这一随机事件的概率空间为120.80.2X x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦其中:1x 表示摸出的球为红球事件,2x 表示摸出的球是白球事件。
a)如果摸出的是红球,则获得的信息量是()()11log log0.8I x p x =-=-(比特)b)如果摸出的是白球,则获得的信息量是()()22log log0.2I x p x =-=-(比特)c) 如果每次摸出一个球后又放回袋中,再进行下一次摸取。
则如此摸取n 次,红球出现的次数为()1np x 次,白球出现的次数为()2np x 次。
随机摸取n 次后总共所获得信息量为()()()()1122np x I x np x I x +d)则平均随机摸取一次所获得的信息量为()()()()()()()()()112211221log log 0.72 H X np x I x np x I x np x p x p x p x =+⎡⎤⎣⎦=-+⎡⎤⎣⎦=比特/次2. 居住某地区的女孩中有25%是大学生,在女大学生中有75%是身高1.6米以上的,而女孩中身高1.6米以上的占总数的一半。
信息理论与编码 答案_姚善化_清华大学出版社汇编

H X Y H X H Y X H Y 0.971 0.715 0.722
0.964 (比特/符号) (5)接收到消息 Y 后所获得的平均互信息量为:
I X ,Y H X H X Y 0.971 0.964 0.007 (比特/符号)
7. 某信源的消息符号集的概率分布和二进制代码如题表 2-5 所示。
所以
H
Y2
1 2
log
2
1 2
log
2
1
比特/符号
H Y2
X
1 4
log1
1 4
log 1
1 2
log1
0
比特/符号
I X ;Y2 H Y2 H Y2 X 1 比特/符号
因此第二个实验好些。
( 2 ) I X ;Y1Y2 H Y2Y2 H Y2Y2 X , 因 此 要 求 出 P Y1Y2 , P Y1Y2 X 和
习题 5 表
p y2 x
0 1 2
0 1 1 0
1 0 0 1
(1) 求 I X ;Y1 和 I X ;Y2 ,并判断作哪一个实验好些。
(2) 求 I X ;Y1,Y2 ,并计算作 Y1 和 Y2 两个实验比作 Y1 或 Y2 中的一个实验各可多得多少关于 X
的信息。
(3) 求 I X ;Y1 Y2 和 I X ;Y2 Y1 ,并解释它们的含义。
(3) 计算由 100 个符号构成的符号序列的熵。
答:
2
(1)信源熵为
H
X
1 4
log
4
3 4
log
4 3
0.8113
比特/符号
(2)该特定序列用 A 表示则
I
A
信息论与编码理论课后答案

信息论与编码理论课后答案【篇一:《信息论与编码》课后习题答案】式、含义和效用三个方面的因素。
2、 1948年,美国数学家香农发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
3、按照信息的性质,可以把信息分成语法信息、语义信息和语用信息。
4、按照信息的地位,可以把信息分成客观信息和主观信息。
5、人们研究信息论的目的是为了高效、可靠、安全地交换和利用各种各样的信息。
6、信息的是建立信息论的基础。
7、8、是香农信息论最基本最重要的概念。
9、事物的不确定度是用时间统计发生概率的对数来描述的。
10、单符号离散信源一般用随机变量描述,而多符号离散信源一般用随机矢量描述。
11、一个随机事件发生某一结果后所带来的信息量称为自信息量,定义为其发生概率对数的负值。
12、自信息量的单位一般有比特、奈特和哈特。
13、必然事件的自信息是。
14、不可能事件的自信息量是15、两个相互独立的随机变量的联合自信息量等于两个自信息量之和。
16、数据处理定理:当消息经过多级处理后,随着处理器数目的增多,输入消息与输出消息之间的平均互信息量趋于变小。
17、离散平稳无记忆信源x的n次扩展信源的熵等于离散信源x的熵的。
limh(xn/x1x2?xn?1)h?n???18、离散平稳有记忆信源的极限熵,。
19、对于n元m阶马尔可夫信源,其状态空间共有m个不同的状态。
20、一维连续随即变量x在[a,b] 。
1log22?ep21、平均功率为p的高斯分布的连续信源,其信源熵,hc(x)=2。
22、对于限峰值功率的n维连续信源,当概率密度均匀分布时连续信源熵具有最大值。
23、对于限平均功率的一维连续信源,当概率密度24、对于均值为0,平均功率受限的连续信源,信源的冗余度决定于平均功率的限定值p和信源的熵功率p25、若一离散无记忆信源的信源熵h(x)等于2.5,对信源进行等长的无失真二进制编码,则编码长度至少为。
2728、同时掷两个正常的骰子,各面呈现的概率都为1/6,则“3和5同时出现”这件事的自信息量是 ?mn?ki?11?mp(x)?em29、若一维随即变量x的取值区间是[0,∞],其概率密度函数为,其中:x?0,m是x的数学2期望,则x的信源熵c。
信息与编码理论课后习题答案

2.1 莫尔斯电报系统中,若采用点长为0.2s ,1划长为0.4s ,且点和划出现的概率分别为2/3和1/3,试求它的信息速率(bits/s)。
解: 平均每个符号长为:1544.0312.032=⨯+⨯秒 每个符号的熵为9183.03log 3123log 32=⨯+⨯比特/符号所以,信息速率为444.34159183.0=⨯比特/秒2.2 一个8元编码系统,其码长为3,每个码字的第一个符号都相同(用于同步),若每秒产生1000个码字,试求其信息速率(bits /s)。
解: 同步信号均相同不含信息,其余认为等概,每个码字的信息量为 3*2=6 比特;所以,信息速率为600010006=⨯比特/秒2.3 掷一对无偏的骰子,若告诉你得到的总的点数为:(a ) 7;(b ) 12。
试问各得到了多少信息量?解: (a)一对骰子总点数为7的概率是366 所以,得到的信息量为 585.2)366(log 2= 比特(b) 一对骰子总点数为12的概率是361 所以,得到的信息量为 17.5361log 2= 比特2.4经过充分洗牌后的一付扑克(含52张牌),试问:(a) 任何一种特定排列所给出的信息量是多少? (b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解: (a)任一特定排列的概率为!521, 所以,给出的信息量为 58.225!521log 2=- 比特 (b) 从中任取13张牌,所给出的点数都不相同的概率为 13131313525213!44A C ⨯=所以,得到的信息量为 21.134log 1313522=C 比特.2.5 设有一个非均匀骰子,若其任一面出现的概率与该面上的点数成正比,试求各点出现时所给出的信息量,并求掷一次平均得到的信息量。
解:易证每次出现i 点的概率为21i,所以比特比特比特比特比特比特比特398.221log 21)(807.1)6(070.2)5(392.2)4(807.2)3(392.3)2(392.4)1(6,5,4,3,2,1,21log )(2612=-==============-==∑=i i X H x I x I x I x I x I x I i ii x I i2.6 园丁植树一行,若有3棵白杨、4棵白桦和5棵梧桐。
信息论与编码习题参考答案(全)
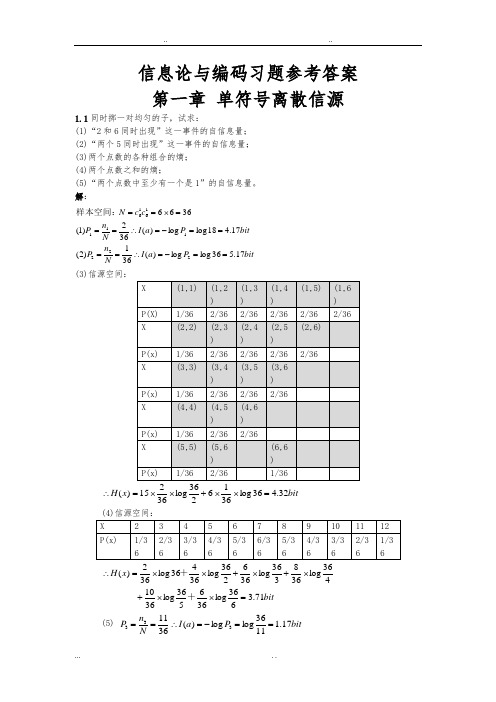
信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ (4)信源空间: bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知 bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士:“你是否是红绿色盲?”他的回答可能是:“是”,也可能“不是”。
信息理论与编码课后答案(吕锋王虹着)

第一章教材习题1.1.试述信息与知识、消息和信号之间的区别与联系,并举例说明。
1.2.详述钟义信先生的信息定义体系。
1.3.试查阅文献,说明信息具有哪些特征和性质?1.4.说明通信系统模型由哪几部分组成,并详细讨论每一部分的功能。
1.5.试述信息论的研究内容?第二章教材习题信源模型2.1试简述信源分类以及各种信源特点。
信息的描述2.2在非理想观察模型中,存在哪些不确定性,它们与信息有何关系?不确定性与信息2.3一副充分洗乱的牌(含52张),试问:(1)任一特定排列所给出的不确定性是多少?(2)随机抽取13张牌,13张牌的点数互不相同时的不确定性是多少?2.4同时扔出两个正常的骰子,也就是各面呈现的概率都是1/6,求:(1)“3和5同时出现”这事件的自信息量。
(2)“两个1同时出现”这事件的自信息量。
(3)两个点数的各种组合(无序对)的统计平均自信息量。
(4)两个点数之和(即2,3,…,12构成的子集)的熵。
(5)两个点数中至少有一个是1的自信息量。
2.5设在一只布袋中装有100只对人手的感觉完全相同的木球,每只上涂有1种颜色。
100只球的颜色有下列三种情况:(1)红色球和白色球各50只;(2)红色球99只,白色球1只;(3)红,黄,蓝,白色各25只。
求从布袋中随意取出一只球时,猜测其颜色所需要的信息量。
2.8大量统计表明,男性红绿色盲的发病率为7%,女性发病率为0.5%,如果你问一位男同志是否为红绿色盲,他回答“是”或“否”。
(1)这二个回答中各含多少信息量?(2)平均每个回答中含有多少信息量?(3)如果你问一位女同志,则答案中含有的平均信息量是多少?联合熵和条件熵2.9任意三个离散随机变量X 、Y 和Z ,求证:()()()()H XYZ H XY H XZ H X −≤−。
平均互信息及其性质2.11设随机变量12{,}{0,1}X x x ==和12{,}{0,1}Y y y ==的联合概率空间为11122122(,)(,)(,)(,)133818XY XY x y x y x y x y P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦定义一个新随机变量Z X Y =×(普通乘积)。
信息论与编码课后习题答案

1. 有一个马尔可夫信源,已知p(x 1|x 1)=2/3,p(x 2|x 1)=1/3,p(x 1|x 2)=1,p(x 2|x 2)=0,试画出该信源的香农线图,并求出信源熵。
解:该信源的香农线图为:1/3○ ○2/3 (x 1) 1 (x 2)在计算信源熵之前,先用转移概率求稳固状态下二个状态x 1和 x 2 的概率)(1x p 和)(2x p 立方程:)()()(1111x p x x p x p =+)()(221x p x x p=)()(2132x p x p +)()()(1122x p x x p x p =+)()(222x p x x p =)(0)(2131x p x p + )()(21x p x p +=1 得431)(=x p 412)(=x p马尔可夫信源熵H = ∑∑-IJi j i jix x p x xp x p )(log )()( 得 H=0.689bit/符号2.设有一个无经历信源发出符号A 和B ,已知4341)(.)(==B p A p 。
求:①计算该信源熵;②设该信源改成发出二重符号序列消息的信源,采纳费诺编码方式,求其平均信息传输速度; ③又设该信源改成发三重序列消息的信源,采纳霍夫曼编码方式,求其平均信息传输速度。
解:①∑-=Xiix p x p X H )(log )()( =0.812 bit/符号②发出二重符号序列消息的信源,发出四种消息的概率别离为1614141)(=⨯=AA p 1634341)(=⨯=AB p1634143)(=⨯=BA p 1694343)(=⨯=BB p用费诺编码方式 代码组 b i BB 0 1 BA 10 2 AB 110 3 AA 111 3无经历信源 624.1)(2)(2==X H X H bit/双符号 平均代码组长度 2B =1.687 bit/双符号BX H R )(22==0.963 bit/码元时刻③三重符号序列消息有8个,它们的概率别离为641)(=AAA p 643)(=AAB p 643)(=BAA p 643)(=ABA p 649)(=BBA p 649)(=BAB p 649)(=ABB p 6427)(=BBB p用霍夫曼编码方式 代码组 b iBBB 6427 0 0 1 BBA 649 0 )(6419 1 110 3BAB 649 1 )(6418 )(644 1 101 3ABB 649 0 0 100 3AAB 6431 )(6461 11111 5 BAA 643 0 1 11110 5ABA6431 )(6440 11101 5 AAA641 0 11100 5)(3)(3X H X H ==2.436 bit/三重符号序列 3B =2.469码元/三重符号序列3R =BX H )(3=0.987 bit/码元时刻3.已知符号集合{ 321,,x x x }为无穷离散消息集合,它们的显现概率别离为 211)(=x p ,412)(=x p 813)(=x p ···ii x p 21)(=···求: ① 用香农编码方式写出各个符号消息的码字(代码组); ② 计算码字的平均信息传输速度; ③ 计算信源编码效率。
《信息理论与编码》,答案,考试重点(1--3章)

《信息理论与编码》习题参考答案1. 信息是什么信息与消息有什么区别和联系答:信息是对事物存在和运动过程中的不确定性的描述。
信息就是各种消息符号所包含的具有特定意义的抽象内容,而消息是信息这一抽象内容通过语言、文字、图像和数据等的具体表现形式。
2. 语法信息、语义信息和语用信息的定义是什么三者的关系是什么答:语法信息是最基本最抽象的类型,它只是表现事物的现象而不考虑信息的内涵。
语义信息是对客观现象的具体描述,不对现象本身做出优劣判断。
语用信息是信息的最高层次。
它以语法、语义信息为基础,不仅要考虑状态和状态之间关系以及它们的含义,还要进一步考察这种关系及含义对于信息使用者的效用和价值。
三者之间是内涵与外延的关系。
第2章1. 一个布袋内放100个球,其中80个球是红色的,20个球是白色的,若随机摸取一个球,猜测其颜色,求平均摸取一次所能获得的自信息量答:依据题意,这一随机事件的概率空间为120.80.2X x x P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦其中:1x 表示摸出的球为红球事件,2x 表示摸出的球是白球事件。
a)如果摸出的是红球,则获得的信息量是()()11log log0.8I x p x =-=-(比特)b)如果摸出的是白球,则获得的信息量是()()22log log0.2I x p x =-=-(比特)c) 如果每次摸出一个球后又放回袋中,再进行下一次摸取。
则如此摸取n 次,红球出现的次数为()1np x 次,白球出现的次数为()2np x 次。
随机摸取n 次后总共所获得信息量为()()()()1122np x I x np x I x +d)则平均随机摸取一次所获得的信息量为()()()()()()()()()112211221log log 0.72 H X np x I x np x I x n p x p x p x p x =+⎡⎤⎣⎦=-+⎡⎤⎣⎦=比特/次2. 居住某地区的女孩中有25%是大学生,在女大学生中有75%是身高1.6米以上的,而女孩中身高1.6米以上的占总数的一半。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二章-信息量和熵习题解2.1 莫尔斯电报系统中,若采用点长为0.2s ,1划长为0.4s ,且点和划出现的概率分别为2/3和1/3,试求它的信息速率(bits/s)。
解: 平均每个符号长为:1544.0312.032=⨯+⨯秒 每个符号的熵为9183.03log 3123log 32=⨯+⨯比特/符号所以,信息速率为444.34159183.0=⨯比特/秒2.2 一个8元编码系统,其码长为3,每个码字的第一个符号都相同(用于同步),若每秒产生1000个码字,试求其信息速率(bits /s)。
解: 同步信号均相同不含信息,其余认为等概,每个码字的信息量为 3*2=6 比特;所以,信息速率为600010006=⨯比特/秒2.3 掷一对无偏的骰子,若告诉你得到的总的点数为:(a ) 7;(b ) 12。
试问各得到了多少信息量?解: (a)一对骰子总点数为7的概率是366 所以,得到的信息量为 585.2)366(log 2= 比特(b) 一对骰子总点数为12的概率是361所以,得到的信息量为 17.5361log 2= 比特2.4 经过充分洗牌后的一付扑克(含52张牌),试问:(a) 任何一种特定排列所给出的信息量是多少?(b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解: (a)任一特定排列的概率为!521, 所以,给出的信息量为 58.225!521log 2=- 比特 (b) 从中任取13张牌,所给出的点数都不相同的概率为 13131313525213!44A C ⨯=所以,得到的信息量为 21.134log 1313522=C 比特.2.5 设有一个非均匀骰子,若其任一面出现的概率与该面上的点数成正比,试求各点出现时所给出的信息量,并求掷一次平均得到的信息量。
解:易证每次出现i 点的概率为21i,所以 比特比特比特比特比特比特比特398.221log 21)(807.1)6(070.2)5(392.2)4(807.2)3(392.3)2(392.4)1(6,5,4,3,2,1,21log )(2612=-==============-==∑=i i X H x I x I x I x I x I x I i ii x I i2.6 园丁植树一行,若有3棵白杨、4棵白桦和5棵梧桐。
设这12棵树可随机地排列,且每一种排列都是等可能的。
若告诉你没有两棵梧桐树相邻时,你得到了多少关于树的排列的信息?解: 可能有的排列总数为27720!5!4!3!12=没有两棵梧桐树相邻的排列数可如下图求得,Y X Y X Y X Y X Y X Y X Y X Y图中X 表示白杨或白桦,它有⎪⎪⎭⎫ ⎝⎛37种排法,Y 表示梧桐树可以栽种的位置,它有⎪⎪⎭⎫ ⎝⎛58种排法,所以共有⎪⎪⎭⎫ ⎝⎛58*⎪⎪⎭⎫⎝⎛37=1960种排法保证没有两棵梧桐树相邻,因此若告诉你没有两棵梧桐树相邻时,得到关于树排列的信息为1960log 27720log 22-=3.822 比特2.7 某校入学考试中有1/4考生被录取,3/4考生未被录取。
被录取的考生中有50%来自本市,而落榜考生中有10%来自本市,所有本市的考生都学过英语,而外地落榜考生中以及被录取的外地考生中都有40%学过英语。
(a) 当己知考生来自本市时,给出多少关于考生是否被录取的信息?(b) 当已知考生学过英语时,给出多少有关考生是否被录取的信息?(c) 以x 表示是否落榜,y 表示是否为本市学生,z 表示是否学过英语,x 、y 和z取值为0或1。
试求H (X ),H (Y |X ),H (Z |YZ )。
解: X=0表示未录取,X=1表示录取;Y=0表示本市,Y=1表示外地;Z=0表示学过英语,Z=1表示未学过英语,由此得31(0),(1),44(0)(0)(00)(1)(01)31111,41042514(1)1,55(0)(0)(00)(1)(01)144013,55100251312(1)1,2525p x p x p y p x p y x p x p y x p y p z p y p z y p y p z y p z =========+====⨯+⨯===-======+====+⨯===-=22221313()(00)(00)(0)/(0)/104581115(10)(01)(1)/(0)/2458(00)(10)(;0)(00)log (10)log (0)(1)353588log log 3188440.4512a p x y p y x p x p y p x y p y x p x p y p x y p x y I X y p x y p x y p x p x ========⨯=========⨯=========+=====+=比特()(00)((00,0)(00)(01,0)(10))(0)/(0)19431369()/101010425104(10)((00,1)(01)(01,1)(11))(1)/(0)11211335()/225425104(;b p x z p z y x p y x p z y x p y x p x p z p x z p z y x p y x p z y x p y x p x p z I X ========+========+⨯⨯=========+========+⨯⨯=22222222(00)(10)0)(00)log (10)log (0)(1)69356935104104log log 31104104440.02698341()()log log 40.8113434()(0)(00)log (00)(0)(10)log (1p x z p x z z p x z p x z p x p x c H X H Y X p x p y x p y x p x p y x p y x ========+=====+==+=======+=====比特比特2222220)(1)(01)log (01)(1)(11)log (11)3139101111log 10log log 2log 2410410942420.6017p x p y x p y x p x p y x p y x =====+======⨯+⨯+⨯+⨯=比特2.8 在A 、B 两组人中进行民意测验,组A 中的人有50%讲真话(T ),30%讲假话(F ),20%拒绝回答(R )。
而组B 中有30%讲真话,50%讲假话和20%拒绝回答。
设选A 组进行测验的概率为p ,若以I (p )表示给定T 、F 或R 条件下得到的有关消息来自组A 或组B 的平均信息量,试求I (p )的最大值。
解:令{}{}R F T Y B A X ,,,,==,则比特得令同理03645.0)()(5.0,02.03.0)2.05.0(log 2.0)()2.05.0(log )2.05.0()2.03.0(log )2.03.0(5.0log 5.03.0log 3.0)5log )1(2.02log )1(5.0log )1(3.05log 2.0log 3.02log 5.0(2.0log 2.0)2.05.0(log )2.05.0()2.03.0(log )2.03.0()()();()(2.0)(,2.05.0)(2.03.0)1(3.05.0)()()()()(5.0max 2'2222223102231022222==∴==+-=---++-+=-+-+-+++-----++-=-===-=+=-⨯+=+==p p I p I p pp p I p p p p p p p p p p p p p p X Y H Y H Y X I p I R P p F P pp p B P B T P A P A T P T P2.9 随机掷三颗骰子,以X 表示第一颗骰子抛掷的结果,以Y 表示第一和第二颗骰子抛掷的点数之和,以Z 表示三颗骰子的点数之和。
试求H (Z |Y )、H (X |Y )、H (Z |XY ),H (XZ |Y )和H (Z |X )。
解:令X=X 1,Y=X 1+X 2,Z=X 1+X 2+X 3,H(X 1)=H(X 2)=H(X 3)=6log 2 比特 H(X)= H(X 1) =6log 2=2.585 比特 H(Y)= H(X 2+X 3)=6log 61)536log 365436log 364336log 363236log 36236log 361(2222222+++++ = 3.2744比特H(Z)= H(X 1+X 2+X 3))27216log 2162725216log 2162521216log 2162115216log 2161510216log 216106216log 21663216log 2163216log 2161(222222222++++++= = 3.5993 比特 所以H(Z/Y)= H(X 3)= 2.585 比特H(Z/X) = H(X 2+X 3)= 3.2744比特H(X/Y)=H(X)-H(Y)+H(Y/X) = 2.585-3.2744+2.585 =1.8955比特 H(Z/XY)=H(Z/Y)= 2.585比特H(XZ/Y)=H(X/Y)+H(Z/XY) =1.8955+2.585 =4.4805比特2.12 计算习题2.9中的I (Y ;Z ),I (X ;Z ),I (XY ;Z ),I (Y ;Z |X )和I (X ;Z |Y )。
解:I(Y;Z)=H(Z)-H(Z/Y) =H(Z)- H(X 3)= 3.5993-2.585 =1.0143比特 I(X;Z)=H(Z)-H(Z/X)=3.5993- 3.2744=0.3249比特 I(XY ;Z)=H(Z)-H(Z/XY) =H(Z)-H(Z/Y) =1.0143比特I(Y;Z/X)=H(Z/X)-H(Z/XY)= H(X 2+X 3)-H(X 3) =3.2744-2.585 =0.6894比特 I(X;Z/Y)=H(Z/Y)-H(Z/XY)=H(Z/Y)-H(Z/Y) =02.10 设有一个系统传送10个数字:0, 1, …, 9。
奇数在传送时以0.5的概率错成另外的奇数,而其它数字总能正确接收。
试求收到一个数字平均得到的信息量。
解:设系统输出10个数字X 等概,接收数字为Y,显然 101)(101)()()(9190===∑∑==i j p i j p i Q j w i i , H(Y)=log10 比特奇奇奇奇偶18log 81101452log 211015)(log)()()(log )()(0)(log ),()(log ),()/(22,2222=⨯⨯⨯⨯+⨯⨯⨯=--=--=∑∑∑∑∑∑∑≠====x y p x y p x p x x p x x p x p x y p y x p x y p y x p X Y H x y x i y x y x所以 I(X;Y)= 3219.2110log 2=-比特2.11 令{u l , u 2, …, u 8}为一等概消息集,各消息相应被编成下述二元码字:u l =0000,u 2=0011,u 3=0101,u 4=0110 u 5=1001,u 6=1010,u 7=1100,u 8=1111 通过转移概率为p 的BSC 传送。
