小学奥林匹克数学 容斥原理试卷(二)
容斥原理(二)含答案-
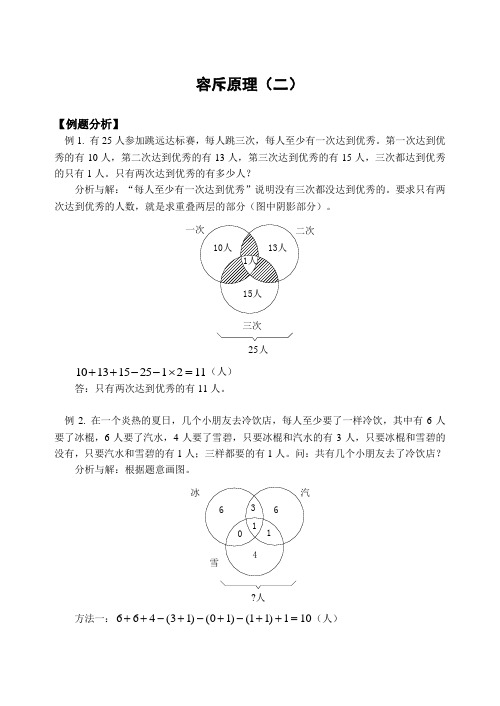
容斥原理(二)【例题分析】例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的++---⨯=(人)方法二:664311210答:共有10个小朋友去了冷饮店。
例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?30人参的有3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参7。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多多少人?最少多少人?满分的人数,即x x ≤≤78,且x ≤9,由此我们得到x ≤7。
另一方面x 最小可能是0,即没有三科都得满分的。
当x 取最大值7时,全班有()39746+=人,当x 取最小值0时,全班有()390+=39人。
答:这个班最多有46人,最少有39人。
【模拟试题】(答题时间:30分钟)1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有12的人订《数学报》,两种刊物都订的有多少人?2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两家他们住的一套房子共有多少平方米?3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
六年级奥林匹克数学十七 容斥原理(二)

A
B C
7.在一次考试中,
100分的有17人,语文得100分的有13人,两科都得100分的有7人,那么两科中至少有一科得100分的共有 人.全班45人中两科都不得100分的有 人.
8.在1,2,3,?,1000这1000个自然数中,既不是2的倍数,又不是3的倍数的数共有 个.
十七、容斥原理(二)
1.某校有500名学生报名参加学科竞赛,数学竞赛参加者共312名,作文竞赛参加者共353名,其中这两科都参加的有292名,那么这两科都没有参加的人数为 人.
2.某门诊部统计某一天挂号的病人,内科150人,外科92人,其中内、外两科都求诊的18人,这一天共来了 个病人.
3.两个正方形的纸片盖在桌面上,位置与尺寸如图所示,则它们盖住
(平方厘米).
2
4.不超过30的正整数中,是3的倍数或4的倍数的数有 个.
5.在一次运动会中,甲班参加田赛的有15人,参加径赛的有12人,参加田赛又参加径赛的有7人,没有参加比赛的有21人.那么甲班共有 人.
9.小于1000的自然数中,是完全平方.在桌面上放置着三个两两重叠的圆纸片(如图),它们的面积都是100(cm)并知A、B
222两圆重叠的面积是20(cm),A、C两圆重叠的面积为45(cm),B、C两圆重叠面积为31(cm),
2三个圆共同重叠的面积为15(cm),求盖住桌子的总面积是 平方厘米.
六年级上册奥数试题-第5讲 容斥原理 全国通用(含答案)

第5讲容斥原理知识网络我们经常会遇到这样一类问题,题目中涉及到包含与排除,也就是说有重叠部分。
解答此类问题的主要依据是容斥原理。
容斥原理一:设A、B是两类有重叠部分的量(如图1所示),若A对应的量为a,B对应的量为b,A与B重叠部分对应的量为ab,那么这两类量的总量可以用下面的公式进行计算:总量=a+b-ab容斥原理二:设A、B、C是三类有重叠部分的量(如图2所示),若A对应的量为a,B 对应的量为b,C以应的量为c,A与B重叠部分以应的量为ab,B与C重叠部分对应的量为bc,C与A重叠部分对应的量为ca,A、B、C三部分重叠部分对应的量为abc,则这三类量的总量可以用下面的公式进行计算:总量=a+b+c-ab-bc-ca+abc重点·难点容斥原理的表述虽然简单,但涉及容斥原理的题型很多,范围很广。
我们往往会遇到一些看似与容斥原理无关的问题,然而通过恰当的转化,便可利用容斥原理顺利求解。
如何分析题目,准确找到重叠部分,将问题转化成可用容斥原理解决的问题是本节的难点。
学法指导解决本节问题的最基本方法是示意图法,即通过示意图来表示题目中的数量关系,使分析、推理与计算结合起来,达到使题目的内容形象化,数量之间关系直观化的目的。
因此,这就要求我们在解题过程中,仔细分析,找出所需量并用示意图表示出来,进而通过观察示意图,确定几类量的重叠部分,然后运用容斥原理解决问题。
经典例题[例1]分母是1001的最简真分数,共有多少个?思路剖析分母是1001的真分数有共1000个,为了方便计算,增加一个分数在1001个分数中考虑问题。
由于1001=7×11×13,所心1~1001的分子里只要含有7、11、13的倍数的就一定能同分母约分,即不是最简真分数,应排除掉。
因此,首先应考虑1~1001中,有多少个7、11或13的倍数。
解答因为1001=7×11×13,所以在1~1001的自然数中,7的倍数共有(11×13)个,11的倍数共有(7×13)个,13的倍数共有(7×11)个;7、11年公倍数有13个,7、13的公倍数有11个,11、13的公倍数有7个;7、11、13的公倍数有1个(即1001)。
容斥原理(二)(含答案)-
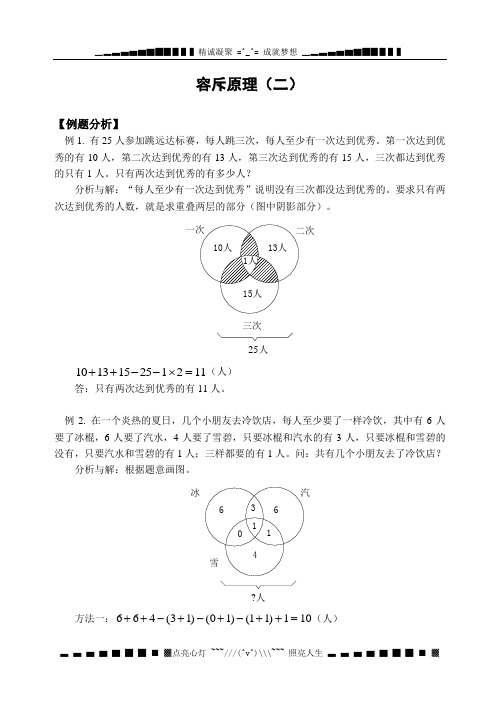
容斥原理(二)【例题分析】例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的++---⨯=(人)方法二:664311210答:共有10个小朋友去了冷饮店。
例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?30人参的有3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参7。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多多少人?最少多少人?满分的人数,即x x ≤≤78,且x ≤9,由此我们得到x ≤7。
另一方面x 最小可能是0,即没有三科都得满分的。
当x 取最大值7时,全班有()39746+=人,当x 取最小值0时,全班有()390+=39人。
答:这个班最多有46人,最少有39人。
【模拟试题】(答题时间:30分钟)1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有12的人订《数学报》,两种刊物都订的有多少人?2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两家他们住的一套房子共有多少平方米?3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
容斥原理(二)(含答案)-

容斥原理(二)【例题分析】例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的++---⨯=(人)方法二:664311210答:共有10个小朋友去了冷饮店。
例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?30人参的有3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参7。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多多少人?最少多少人?满分的人数,即x x ≤≤78,且x ≤9,由此我们得到x ≤7。
另一方面x 最小可能是0,即没有三科都得满分的。
当x 取最大值7时,全班有()39746+=人,当x 取最小值0时,全班有()390+=39人。
答:这个班最多有46人,最少有39人。
【模拟试题】(答题时间:30分钟)1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有12的人订《数学报》,两种刊物都订的有多少人?2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两家他们住的一套房子共有多少平方米?3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
小学奥数之容斥原理

五.容斥原理问题1.有100种赤贫.其中含钙的有68种,含铁的有43种,那么,同时含钙和铁的食品种类的最大值和最小值分别是( )A 43,25B 32,25 C32,15 D 43,11解:根据容斥原理最小值68+43-100=11最大值就是含铁的有43种2.在多元智能大赛的决赛中只有三道题.已知:(1)某校25名学生参加竞赛,每个学生至少解出一道题;(2)在所有没有解出第一题的学生中,解出第二题的人数是解出第三题的人数的2倍:(3)只解出第一题的学生比余下的学生中解出第一题的人数多1人;(4)只解出一道题的学生中,有一半没有解出第一题,那么只解出第二题的学生人数是( )A,5 B,6 C,7 D,8解:根据“每个人至少答出三题中的一道题”可知答题情况分为7类:只答第1题,只答第2题,只答第3题,只答第1、2题,只答第1、3题,只答2、3题,答1、2、3题。
分别设各类的人数为a1、a2、a3、a12、a13、a23、a123由(1)知:a1+a2+a3+a12+a13+a23+a123=25…①由(2)知:a2+a23=(a3+ a23)×2……②由(3)知:a12+a13+a123=a1-1……③由(4)知:a1=a2+a3……④再由②得a23=a2-a3×2……⑤再由③④得a12+a13+a123=a2+a3-1⑥然后将④⑤⑥代入①中,整理得到a2×4+a3=26由于a2、a3均表示人数,可以求出它们的整数解:当a2=6、5、4、3、2、1时,a3=2、6、10、14、18、22又根据a23=a2-a3×2……⑤可知:a2>a3因此,符合条件的只有a2=6,a3=2。
然后可以推出a1=8,a12+a13+a123=7,a23=2,总人数=8+6+2+7+2=25,检验所有条件均符。
故只解出第二题的学生人数a2=6人。
3.一次考试共有5道试题。
做对第1、2、3、、4、5题的分别占参加考试人数的95%、80%、79%、74%、85%。
四年级下奥数试题——第六讲包容与排斥(含答案)沪教版

精讲精练四年级思维数学 第六讲包容与排斥原理思维目标:根据题意,合理解决重叠部分的问题即包容与排斥原理。
数学目标:看谁算的巧思维: 两个图形分别用A 、B 表示,重叠部分用AB 表示,盖住的面积用N 表示,那么: N=A+B -AB ; AB= A+B -N ;A= N -B+AB ;B= N -A+AB 数学:先观察式子中的数字,然后进行合理巧算。
【例1】一个长为8厘米、宽为6厘米的长方形与一个边长为4厘米的正方形(如右图),放在桌子上。
它们盖住桌面的面积有多少平方厘米?金钥匙:A 面积:8×6=48(平方厘米)B 面积:4×4=16(平方厘米) AB 面积:3×3=9(平方厘米) N=A+B -AB = 48+16-9 =64-9=55(平方厘米)答:它们盖住桌面的面积有55平方厘米. 试金石:1、 四⑴班的每位学生都至少喜欢体育或文艺活动中的一种。
其中喜欢体育活动的有41人,喜欢文艺活动的有38人,两种活动都喜欢的有25人。
这个班共有学生多少人?学习目标 知识梳理AB2、某班从图书馆借来一批图书分给班上50位同学。
有30人各借到一本自然科学类书籍,有25人各借到一本文艺类书籍,既借了一本自然科学类书籍又借了一本文艺类书籍的学生有几人?【例2】某班40名学生在一次期中考试中每人至少有一门得优秀,语文得优秀的有14人,数学得优秀的有34人。
只有一门得优秀的各有多少人?金钥匙:根据题意,我们可以知道有些同学两门功课都得了优秀,在语文学科被算了一次,在数学学科也被算了一次,把两门学科得优秀的总人数去掉班级人数,多出的就是两门都得优秀的人数。
这样就能得出结果:34+14-40 数学一门:34-8=26(人)=48-40 语文一门:14-8=6(人)=8(人)答:数学一门得优秀的有26人,语文6人。
试金石:1、一次老师给全班同学做两道“动脑筋”的数学题,结果全班每人至少做对一题。
小学数学《容斥原理》练习题2
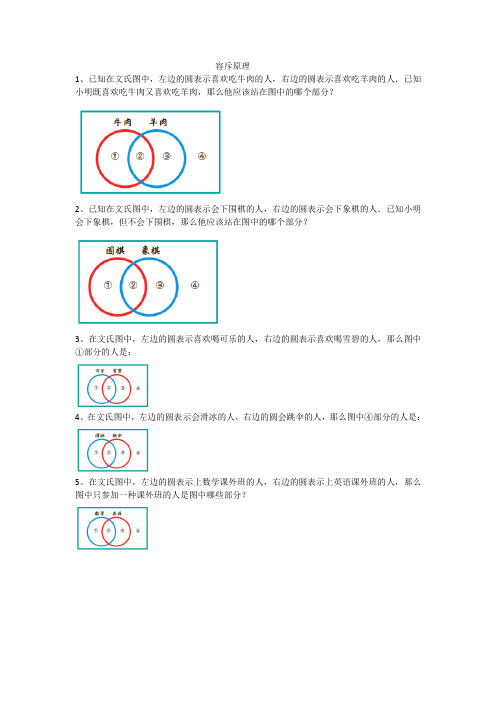
容斥原理1、已知在文氏图中,左边的圆表示喜欢吃牛肉的人,右边的圆表示喜欢吃羊肉的人.已知小明既喜欢吃牛肉又喜欢吃羊肉,那么他应该站在图中的哪个部分?2、已知在文氏图中,左边的圆表示会下围棋的人,右边的圆表示会下象棋的人.已知小明会下象棋,但不会下围棋,那么他应该站在图中的哪个部分?3、在文氏图中,左边的圆表示喜欢喝可乐的人,右边的圆表示喜欢喝雪碧的人,那么图中①部分的人是:4、在文氏图中,左边的圆表示会滑冰的人,右边的圆会跳伞的人,那么图中④部分的人是:5、在文氏图中,左边的圆表示上数学课外班的人,右边的圆表示上英语课外班的人,那么图中只参加一种课外班的人是图中哪些部分?6、在文氏图中,上面的圆表示喜欢吃西瓜的人,左下角的圆表示喜欢吃苹果的人,右下角的圆表示喜欢吃葡萄的人,那么既喜欢吃苹果又喜欢吃葡萄的是哪些部分?7、在文氏图中,上面的圆表示参加数学竞赛的人,左下角的圆表示参加英语竞赛的人,右下角的圆表示参加科技竞赛的人,那么同时参加数学竞赛和英语竞赛,但没有参加科技竞赛的人是哪些部分?8、在文氏图中,上面的圆表示有四条腿的动物,左下角的圆表示会游泳的动物,右下角的圆表示肉食动物,那么图中不吃肉的动物是哪些部分?9、在文氏图中,上面的圆表示参加数学竞赛的人,左下角的圆表示参加英语竞赛的人,右下角的圆表示参加科技竞赛的人,图中的数字表示每部分的人数,那么只参加一种竞赛的共有______人。
10、在柱助小学五年一班中,喜欢吃西瓜的有25人,喜欢吃樱桃的有20人,西瓜和樱桃都喜欢的有10人。
那么五年一班共有多少学生喜欢吃水果?11、在柱助小学五年一班中,喜欢吃西瓜的有35人,喜欢吃樱桃的有10人,西瓜和樱桃都喜欢的有5人。
那么五年一班共有多少学生喜欢吃水果?12、在柱助小学五年一班中,喜欢吃西瓜的有35人,喜欢吃樱桃的有15人,西瓜和樱桃都喜欢的有8人。
那么五年一班共有多少学生喜欢吃水果?13、华杯赛夏令营举办开营宴会,共40名学生参加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
容斥原理(二)
【例题分析】
例1. 有25人参加跳远达标赛,每人跳三次,每人至少有一次达到优秀。
第一次达到优秀的有10人,第二次达到优秀的有13人,第三次达到优秀的有15人,三次都达到优秀的只有1人。
只有两次达到优秀的有多少人?
例2. 在一个炎热的夏日,几个小朋友去冷饮店,每人至少要了一样冷饮,其中有6人要了冰棍,6人要了汽水,4人要了雪碧,只要冰棍和汽水的有3人,只要冰棍和雪碧的
++---⨯=(人)
方法二:664311210
答:共有10个小朋友去了冷饮店。
例3. 有28人参加田径运动会,每人至少参加两项比赛。
已知有8人没参加跑的项目,参加投掷项目的人数与参加跑和跳两项的人数都是17人。
问:只参加跑和投掷两项的有多少人?
30人参
的有3人,既参加数学又参加英语和既参加英语又参加语文的人数均为质数,而三种全参
7。
答:既参加英语又参加数学小组的为2人或7人。
例5. 某班同学参加升学考试,得满分的人数如下:数学20人,语文20人,英语20人,数学、英语两科满分者8人,数学、语文两科满分者7人,语文、英语两科满分者9人,三科都没得满分者3人。
问这个班最多多少人?最少多少人?
满分的人数,即x x ≤≤78,且x ≤9,由此我们得到x ≤7。
另一方面x 最小可能是0,即没有三科都得满分的。
当x 取最大值7时,全班有()39746+=人,当x 取最小值0时,全班有()390+=39人。
答:这个班最多有46人,最少有39人。
【模拟试题】(答题时间:30分钟)
1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有1
2
的人订《数学报》,两种刊物都订的有多少人?
2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两
他们住的一套房子共有多少平方米?
3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
4. 某班四年级时,五年级时和六年级时分别评出10名三好学生,又知四、五年级连续三好生4人,五、六年级连续三好生3人,四年级、六年级两年评上三好生的有5人,四、五、六三年没评过三好生的有20人,问这个班最多有多少名同学,最少有多少名同学?
【试题答案】
1. 六年级共有96人,两种刊物每人至少订其中一种,有23的人订《少年报》,有12
的人订《数学报》,两种刊物都订的有多少人?
9623961
2
961696231
2
116⨯
+⨯-=⨯+-=()()()
人或人
答:两种刊物都订的有16人。
2. 小明和小龙两家合住一套房子,门厅、厨房和厕所为公用,在登记住房面积时,两
他们住的一套房子共有多少平方米?
38441284582014128458+---=++++=()
()
平方米或平方米
答:这套房子共有58平方米。
3. 某班45名同学参加体育测试,其中百米得优者20人,跳远得优者18人,又知百米、跳远都得优者7人,跳高、百米得优者6人,跳高、跳远均得优者8人,跳高得优者22人,全班只有1名同学各项都没达优秀,求三项都是优秀的人数。
4514420182276839-=++---=()
()
人人
44395-=()人
4. 某班四年级时,五年级时和六年级时分别评出10名三好学生,又知四、五年级连续三好生4人,五、六年级连续三好生3人,四年级、六年级两年评上三好生的有5人,四、五、六三年没评过三好生的有20人,问这个班最多有多少名同学,最少有多少名同学? 设三年连续三好生人数为x 人 全班人数=⨯---++10354320x ……
全班人数=+38x
x 最大是3,最小是0
所以这个班最多有()38341+=名同学,最少有()380+=38名同学。
