六年级上册数学--圆--练习题
六年级上册数学 圆 练习题

六年级上册数学圆练习题姓名:一、填空。
1、画圆时,固定的一点叫做(),从()到()任意一点的线段叫做半径,通过()并且两端都在圆上的线段叫做()。
2、用圆规画圆时,圆规两脚之间的距离是圆的()。
3、在同一个圆内,有()条直径,有()条半径;直径的长度都是半径长度的()倍。
4、圆不论大小,它的周长总是直径的()倍多一些,这个固定的倍数叫做(),通常用字母()表示。
5、围成圆的曲线的长叫做圆的()。
6、已知圆的直径d,周长C=();已知圆的半径r,周长C=()。
7、圆是()图形,它有()条对称轴。
10、一辆汽车轮胎的外直径是1.2m,它滚动一周前进()。
11、在周长是50cm的正方形中,画一个最大的圆,这个圆的周长是(),这个圆的面积是()。
二、选择。
1、()决定圆的大小,()决定圆的位置。
A.直径B.圆心C.半径D.周长2、下面图形中()只有一条对称轴,()有无数条对称轴。
A.正方形B.等腰三角形C.圆D.长方形3、一个圆知道它的周长,要求面积,必须先要求出圆的()。
A.直径B.半径C.圆周率4、一个圆的半径扩大3倍,它的周长(),面积()。
A.扩大3倍B.扩大9倍C.缩小3倍D.缩小9倍5、一个圆的周长是6.28米,它的面积是()平方米。
A. 2B. 3.14C. 16、周长相等的长方形、正方形、平行四边形和圆,()的面积大。
A、长方形B、正方形C、圆D、平行四边形7、一个圆的周长是28.26cm,这个圆的面积是()cm2A、28.26B、50.24C、78.5D、63.685四、判断。
1、圆周率的值是3.14。
2、圆的直径是半径的2倍。
3、直径是7厘米的圆比半径是4厘米的圆大。
4、在圆内,任意一条直径都是圆的对称轴。
5、周长相等的两个圆,它们的面积也相等。
6、在同一个圆内,两条半径就是一条直径。
7、圆环是轴对称图形,它有无数条对称轴。
五、计算。
1、求下面各圆或圆环的面积。
②④六、动手操作。
1、在右边画一个周长是18.84cm2的圆,并用字母标出它圆心、半径和直径。
六年级数学上册圆练习题(打印版)

六年级数学上册圆练习题(打印版)# 六年级数学上册圆练习题## 一、选择题1. 圆的周长公式是()A. C = 2πrB. C = πdC. C = πr²D. C = 2πd2. 已知圆的半径是3厘米,圆的面积是()A. 28.26平方厘米B. 9平方厘米C. 18平方厘米D. 36平方厘米3. 圆心角是圆周角的()A. 2倍B. 4倍C. 1/2倍D. 1/4倍## 二、填空题1. 半径为4厘米的圆的周长是________厘米。
2. 一个圆的直径是14厘米,那么它的半径是________厘米。
3. 圆的面积公式是S = πr²,如果圆的半径是2厘米,那么它的面积是________平方厘米。
1. 一个圆的半径是5厘米,求它的周长和面积。
- 周长:\( C = 2πr \)- 面积:\( S = πr² \)2. 如果一个圆的周长是31.4厘米,求它的半径。
- 周长公式:\( C = 2πr \)- 解方程求半径:\( r = \frac{C}{2π} \)## 四、应用题1. 一个圆形花坛的直径是20米,如果绕花坛走一圈,需要走多少米?2. 一个圆的半径从2厘米增加到3厘米,它的面积增加了多少平方厘米?## 五、拓展题1. 一个圆的半径是4厘米,如果在这个圆内画一个最大的正方形,正方形的面积是多少?2. 一个圆的半径是3厘米,圆内接一个正六边形,求这个正六边形的边长。
答案:### 一、选择题1. A2. A3. A1. 25.122. 73. 12.56### 三、计算题1. 周长:31.4厘米,面积:78.5平方厘米2. 半径:5厘米### 四、应用题1. 62.8米2. 增加的面积:28.26平方厘米### 五、拓展题1. 32平方厘米2. 2.598厘米注意:以上题目均需学生根据圆的基本公式进行计算和解答。
希望同学们能够通过这些练习题,加深对圆的周长、面积等概念的理解和应用。
小学六年级数学上册圆的练习及答案
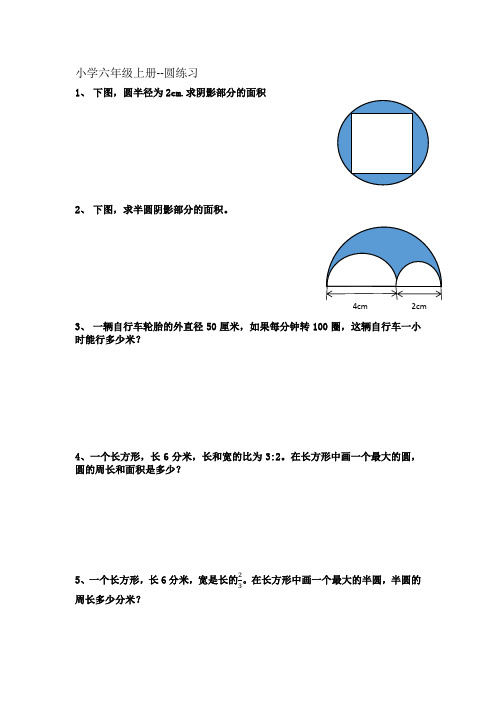
小学六年级上册--圆练习1、 下图,圆半径为2cm.求阴影部分的面积2、 下图,求半圆阴影部分的面积。
3、 一辆自行车轮胎的外直径50厘米,如果每分钟转100圈,这辆自行车一小时能行多少米?4、一个长方形,长6分米,长和宽的比为3:2。
在长方形中画一个最大的圆,圆的周长和面积是多少?5、一个长方形,长6分米,宽是长的23。
在长方形中画一个最大的半圆,半圆的周长多少分米?4cm 2cm6、挂钟分针的针尖在41小时内,正好走了25.12厘米。
它的分针长多少?7、一个环形铁片的内圆半径8厘米,外圆半径比内径多12。
求这个环形铁片的面积。
8、一种压路机的前轮直径1.5米,宽2米。
如果每分钟滚动5圈,它每分钟前进多少米?每分钟压路面多少平方米?9、一根25.12米的绳子,用它围成的正方形面积大,还是围成圆的面积大?大多少?10、如下图示,AB =4厘米,求阴影部分的面积。
参考答案:1、下图,圆半径为2cm.求阴影部分的面积解:圆的面积=3.14×22=12.56(cm 2)正方形的面积=2×2×2÷2×2=8(cm 2)12.56 - 8 = 4.56(cm 2)=4cm,高即是其半径2cm.2、下图,求半圆阴影部分的面积。
解:3.14×[(4+2)÷2]2÷2 - 3.14×(4÷ - 3.14×(2÷2)2÷2=3.14÷2×(9-4-1)2=6.28 3、一辆自行车轮胎的外直径50厘米,如果每分钟转100圈,这辆自行车一小时能行多少米?解:50×3.14×100×60=942000(cm )942000cm = 9420m4、一个长方形,长6分米,长和宽的比为3:2。
在长方形中画一个最大的圆,圆的周长和面积是多少?解:宽=6÷32=6×23 =4(分米) 周长=3.14×4=12.56(分米)面积=3.14×(4÷2)2=12.56(平方分米)5、一个长方形,长6分米,宽是长的23。
人教版六年级上册数学《圆》综合复习练习题(含答案)

人教版六年级上册数学《圆》综合复习练习题(含答案)题号一二三四五六总分得分一、填空题1.圆的与的比值是一个固定数,我们把它叫做圆周率。
2.一个圆内有条半径,用字母表示,所有的半径长度;一个圆内有条直径,用字母表示.3.一个圆形的直径是8厘米,这个圆的周长是厘米;面积是平方厘米。
4.已知扇形的圆心角为60°,弧长为6πm,则扇形的半径为,扇形面积为。
5.两个半径为2厘米的圆如右图摆放,其中四边形OABC是正方形,图中阴影部分的面积是平方厘米.6.下图阴影部分的周长是厘米.(用小数表示)(单位:厘米)7.两个圆,一个直径是6厘米,另一个直径是8厘米,这两个圆的直径之比是,周长之比是,面积之比是。
8.如图所示,小圆半径是2厘米,大圆半径是3厘米。
现在先由小圆绕大圆转一圈,再由大圆绕小圆转一圈。
那么圆心O1经过的路程圆心O2经过的路程;小圆扫过的面积大圆扫过的面积。
(填“大于”“小于”或“等于”)二、判断题9.直径是4分米的圆,它的周长与面积相等。
( )10.从正方形中剪一个周长是12.56dm的圆形,至少需要边长为4dm 的正方形纸片。
( )11.一个圆的面积是78平方厘米,剪去它的14,还剩下它的58。
( )12.圆环的面积等于外圆的面积与内圆面积的差.( )13.在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
( )三、选择题14.半径为1厘米的小圆在半径为4厘米的固定大圆外滚动一周,则小圆滚动了()周.A.3 B.4 C.5 D.615.A、B两只小蚂蚁从甲到乙分别走两条路,比较这两条路线()。
A.蚂蚁A走的长B.蚂蚁B走的长C.一样长D.无法确定16.彤彤的自行车前轮半径是0.3m,她骑车从家到大润发超市前轮转动了100圈,则从家到大润发超市的距离为()m。
A.188.4 B.94.2 C.28.26 D.113.04 17.学校要为一个面积为250m的圆形花坛安装自动旋转喷灌装置(装置安装于圆心处),以下几种射程的旋转喷灌装置,比较合适的是()。
六年级上册圆的必考练习题

六年级上册圆的必考练习题练习一:圆的基本概念1. 什么是圆?圆是平面上所有距离中心点相等的点的集合。
2. 圆的哪些要素构成了一个圆?一个圆由圆心、半径和圆周组成。
3. 如何用一个字母表示圆?我们通常用大写字母O来表示圆。
例如,O表示一个圆。
练习二:圆的性质1. 圆上的点到圆心的距离相等。
证明:设点A、B分别在圆上,O为圆心。
根据定义,OA=OB。
因此,圆上的任意两个点到圆心的距离相等。
2. 同一个圆中所有弦的长度相等。
证明:设弦AB和CD都是O的弦。
要证明AB=CD,我们可以使用数学归纳法。
首先,连接OA、OB、OC和OD。
由于OA=OB=OC=OD,我们可以得出△OAB与△OCD是等腰三角形。
根据等腰三角形的性质,我们可以得出∠AOB=∠COD,∠OAB=∠OCD。
因此,△OAB与△OCD是全等三角形。
从而,AB=CD。
3. 圆的周长是半径的2π倍。
证明:设圆的半径为r,周长为L。
我们可以将圆看作是一个分割成无数个小弧的多边形。
当我们增加小弧的数量时,这个多边形将越来越接近圆形。
当小弧的数量趋近于无穷大时,多边形的周长将趋近于圆的周长。
根据几何学的知识,我们知道一个正多边形的周长是n乘以边长。
所以,当我们将边长设为r时,正多边形的周长为nr。
当我们增加小弧的数量时,n会趋近于无穷大。
因此,L也会趋近于nr。
根据数学知识,我们可以得出nr的极限为2πr。
所以,L=2πr。
练习三:圆的计算问题1. 已知一个圆的半径为5cm,求圆的面积。
解:圆的面积可以通过公式A=πr²来计算。
将半径r代入公式中,我们得到A=π×5²=25π cm²。
2. 若一个圆的周长为30cm,求圆的直径。
解:圆的周长可以通过公式C=2πr来计算。
将周长C代入公式中,我们得到30=2πr。
解方程得到r=15/π cm。
直径d等于半径的2倍,所以d=2×15/π=30/π cm。
关于圆的数学题六年级上册

关于圆的数学题六年级上册一、填空题。
1. 圆中心的一点叫做(圆心),一般用字母(O)表示。
- 解析:这是圆的基本概念,圆心是圆的中心位置的点,是圆的重要元素,通常用字母O来表示。
2. 连接圆心和圆上任意一点的线段叫做(半径),一般用字母(r)表示。
- 解析:半径是圆的基本要素之一,它决定了圆的大小,从圆心到圆上任意一点的距离就是半径,用字母r表示。
3. 通过圆心并且两端都在圆上的线段叫做(直径),一般用字母(d)表示。
- 解析:直径也是圆的重要元素,它是圆中特殊的线段,直径的长度是半径的2倍,用字母d表示。
4. 在同一个圆里,有(无数)条半径,有(无数)条直径。
- 解析:因为圆上有无数个点,所以从圆心到圆上各点可以连接无数条线段作为半径,同理,通过圆心且两端在圆上的线段也有无数条,即直径有无数条。
5. 在同一个圆里,直径是半径的(2倍),半径是直径的((1)/(2))。
- 解析:根据直径和半径的定义,直径d = 2r,所以直径是半径的2倍,半径是直径的(1)/(2)。
6. 一个圆的半径是3厘米,直径是(6厘米)。
- 解析:因为直径d=2r,当r = 3厘米时,d = 2×3=6厘米。
7. 一个圆的直径是8分米,半径是(4分米)。
- 解析:由r=(d)/(2),当d = 8分米时,r=(8)/(2)=4分米。
8. 圆规两脚间的距离是5厘米,画出的圆的半径是(5厘米),直径是(10厘米)。
- 解析:圆规两脚间的距离就是圆的半径,所以半径是5厘米,直径d = 2r,则d=2×5 = 10厘米。
9. 圆是(轴对称)图形,它有(无数)条对称轴。
- 解析:圆沿着任意一条直径对折后,两边都能完全重合,所以圆是轴对称图形,由于圆有无数条直径,所以它有无数条对称轴。
10. 一个圆的周长总是它直径的(π)倍。
- 解析:根据圆的周长公式C=π d,C÷ d=π,π是一个常数,通常取值约为3.14。
人教版六年级数学上册第五单元《圆》测试题(含答案)

人教版六年级数学上册第五单元《圆》测试题(含答案)时间:60分钟总分:100+10分一、填一填。
(每空1分,共20分)1.画圆时,圆规两脚之间的距离为4厘米,那么这个圆的直径是( )厘米,周长是( )厘米,面积是( )平方厘米。
2.在一个长8cm、宽6cm的长方形中画出一个最大的圆,这个圆的直径是( )cm,周长是( )cm。
3.一个圆形花坛的直径是10m,这个圆形花坛的周长是( )m,面积是( )m2。
4.一个圆形喷水池的周长是25.12m,它的半径是( )m,面积是( )m2.5.圆和扇形都是轴对称图形,圆有( )条对称轴,扇形有( )条对称轴。
6.若大、小两圆的半径之比是3:2,则它们的周长之比是( ),面积之比是( )。
7.一个圆的直径扩大为原来的3倍,它的周长扩大为原来的( )倍,面积扩大为原来的( )倍。
8.若一个圆的周长是25.12分米,则与它半径相等的半圆形的周长是( )分米。
9.用一根铁丝刚好可以围成一个边长为6.28m的正方形,如果用这根铁丝围成一个圆,且铁丝无剩余,那么这个圆的面积是( )m2。
10.如图,把一个圆形纸片平均分成32份,剪拼成一个近似的长方形。
已知长方形的长是9.42m,则圆的面积是( )dm2。
11.如图,A、B两块挡板之间有一个半径为3cm的圆,圆从①号位置开始沿直线滚到②号,正好滚了5圈。
那么圆的周长是( )cm,A、B两块挡板之间的距离是( )cm。
二、判一判。
(每题1分,共7分)1.四个圆心角都是90°的扇形一定可以拼成一个圆。
()2.半径是2厘米的圆,它的周长和面积相等。
()3.任何一个圆的周长总是它直径的3.14倍。
()4.扇形面积的大小只与扇形的圆心角的大小有关。
()5.车轮的轴安装在圆心部位,是因为这点到车轮上的距离处处相等。
()6.把一个圆平均分成4个扇形,每个扇形的周长是圆周长的。
()7.左图中涂色部分与空白部分的周长相等,面积也相等。
六年级上册圆练习题及答案

六年级上册圆练习题及答案圆是我们数学学习中重要的几何概念之一,对于提升学生的几何思维和问题解决能力有重要作用。
下面是六年级上册圆练习题及答案,希望能够帮助同学们更好地掌握圆的知识。
练习题一:选择题1. 下列几何图形中符合圆的定义的是:A. 正方形B. 长方形C. 圆形D. 三角形答案:C2. 下列说法中错误的是:A. 圆的内切正方形的对角线长相等B. 圆的直径等于半径的两倍C. 圆的周长等于直径的π倍D. 圆的任意两个弦相交于圆心答案:D3. 已知一个圆的直径为20 cm,那么该圆的半径是:A. 5 cmB. 10 cmC. 20 cmD. 40 cm答案:B练习题二:计算题1. 若一个圆的半径为8 cm,求该圆的直径、周长和面积。
答案:直径:8 cm × 2 = 16 cm周长:2 × π × 8 cm ≈ 50.27 cm面积:π × 8 cm × 8 cm ≈ 201.06 cm²2. 一个圆的周长为18.84 cm,求该圆的半径和面积。
答案:周长:2 ×π × r = 18.84 cm,解得r ≈ 3 cm面积:π × 3 cm × 3 cm ≈ 28.27 cm²练习题三:应用题小明希望在水果摊上买一些苹果,他发现摊上的苹果被放在一个圆形的篮子中,篮子的直径为30 cm。
如果苹果的直径为6 cm,那么篮子最多能放多少个苹果?答案:篮子的直径为30 cm,即半径为15 cm。
苹果的直径为6 cm,即半径为3 cm。
篮子的半径除以苹果的半径得到的个数就是篮子最多能放的苹果个数。
15 cm ÷ 3 cm = 5所以篮子最多能放5个苹果。
练习题四:解答题请用直尺和铅笔画一个直径为12 cm的圆,并在图中标出圆心和半径。
答案:(请根据题目要求画图)练习题五:判断题判断下列说法是否正确,正确的在括号内打“√”,错误的在括号内打“×”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
__________________________________________________
六年级上册数学 圆 练习题
姓名: 评分: 一、填空。
(每空0.5分,共13分) 1、画圆时,固定的一点叫做( ),从( )到( )任意一点的线段叫做半径,通过( )并且两端都在圆上的线段叫做( )。
2、用圆规画圆时,圆规两脚之间的距离是圆的( )。
3、在同一个圆内,有( )条直径,有( )条半径;直径的长度都是半径长度的( )倍。
4、圆不论大小,它的周长总是直径的( )倍多一些,这个固定的倍数叫做( ),通常用字母( )表示。
5、围成圆的曲线的长叫做圆的( )。
6、已知圆的直径d ,周长C=( );已知圆的半径r ,周长C=( )。
7、圆是( )图形,它有( )条对称轴。
名称 半径(r )
直径(d ) 周长(C )
面积(
S )
自行车轮胎 5分米 钟面 2厘米 圆形花坛
62.8米
1、( )决定圆的大小,( )决定圆的位置。
A.直径 B.圆心 C.半径 D.周长
2、下面图形中( )只有一条对称轴,( )有无数条对称轴。
A.正方形 B.等腰三角形 C.圆 D.长方形
3、一个圆知道它的周长,要求面积,必须先要求出圆的( )。
A.直径 B.半径 C.圆周率
4、一个圆的半径扩大3倍,它的周长( ),面积( )。
A.扩大3倍 B.扩大9倍 C.缩小3倍 D.缩小9倍
5、一个圆的周长是6.28米,它的面积是( )平方米。
A. 2 B. 3.14 C. 1
四、判断。
(5分)
1、圆周率的值是3.14。
2、圆的直径是半径的2倍。
3、直径是7厘米的圆比半径是4厘米的圆大。
4、在圆内,任意一条直径都是圆的对称轴。
5、周长相等的两个圆,它们的面积也相等。
五、计算。
(28分) 1、求下面各圆的周长。
(12分) ①②③
2、求下面各圆或圆环的面积。
(16分) ①②
6dm
25m 8cm 2m
( ) ( )
( ) ( ) ( )
六、动手操作。
(10分)
1、
七、解决问题。
(30分)
2、一根圆形柱子的周长是6.28米,这根柱子的直径是多少米?
3、一种自行车的轮胎外直径是0.8米,每分钟转动60周,每分钟能前进多少米?
4、学校草地上有一个自动旋转洒水器,射程是20米,这个洒水器最多可以淋到多少平方米的草地?
5、右图是一个边长8dm的正方形,在正方形中作一个最大的圆,圆的周长是多少?面积是多少?
在右边画一个直径是6厘米的圆,并用字母标出
它圆心、半径和直径。
(5分)
1、一个圆形花坛,半径是10米,它的周长是多少?
__________________________________________________
6、李叔叔有471米长的铁丝,计划把它围成一个圆形牛栏,并绕牛栏3圈,这个牛栏占地多少平方米?
__________________________________________________。
