实验3 连续时间信号的卷积计算
实验3 连续时间信号的卷积计算

(1)符号法:要注意积分变量和积分限的选取
lim
0 k
f1 (k )
f2 (t
k)
如果令t=n,则
(2)数值计算法
f (n) f1(k) f2 ((n k)) k
y(t)
t
eT
u (t )
etu(t
)
t
eT
u0
ex3_1.m
y(t) [u(t) u(t 1)][u(t) u(t 1)]
– 构造 对应的时间向量k.
f (n)
y(t) [u(t) u(t 1)][u(t) u(t 1)]
ex3_3.m
实验内容:
1、绘制 f1(t) f2 (t)
采用数值与符号法
f1 (t )
f2 (t)
2、两种方式计算如下卷积
(1) f1(t) f2 (t); (2) f1(t) f3(t); (3) f1(t) f4 (t) (4) f2 (t) f3(t); (5) f2 (t) f4 (t); (6) f3(t) f4 (t)
实验目的:
1、学会运用MATLAB实现连续时间信号的卷积 2、学会运用MATLAB符号运算法求连续时间信号 的卷积 3、学会运用MATLAB数值计算方法求连续时间信 号的卷积
实验原理:
f (t) f (t) f (t) f ( ) f (t )d 1
2
1
2
f (t) f1(t) * f2 (t) f1( ) f (t )d
函数实现卷积和wconvuv?1mwnumvnm????1212ftftftfftd????????????121122112200limlimftftftfmftfmftfmftfm??????对和进行等间隔均匀抽样则当足够小的时候则1212120limmftftftfftdfmftm?????????????????????1212mmfnfmfnmfmfnm????????????????1212mftfnfmfnmftfnfn????????????用用matlab实现连续信号卷积的过程
信号卷积计算公式(一)

信号卷积计算公式(一)信号卷积1. 什么是信号卷积?信号卷积是一种在时域中计算两个信号之间的乘积并求和的方法。
它是一种重要的信号处理技术,广泛应用于图像处理、语音识别、音频处理等领域。
2. 信号卷积的计算公式信号卷积的计算公式可以表示为:∞[k]⋅ℎ[n−k]y[n]=∑xk=−∞其中,x[n]和ℎ[n]分别表示输入信号和卷积核(也称为系统的冲击响应)的值。
3. 信号卷积的示例解释离散信号的卷积信号x[n]:考虑一个离散信号x[n],其数值如下所示:n 0 1 2 3x[n] 1 2 -1 3信号ℎ[n]:接下来,我们定义另一个离散信号ℎ[n],其数值如下所示:n 0 1 2 3ℎ[n]-1 0 1 2计算卷积结果y[n]:现在,我们可以使用信号卷积的计算公式来计算卷积结果y[n],如下所示:∞[k]⋅ℎ[n−k]y[n]=∑xk=−∞当n=0时,有:y[0]=x[0]⋅ℎ[0−0]+x[1]⋅ℎ[0−1]+x[2]⋅ℎ[0−2]+x[3]⋅ℎ[0−3]=1⋅(−1)+2⋅0+(−1)⋅1+3⋅2=4依此类推,可以计算出当n=1、n=2、n=3时的y[n]。
最终,卷积结果y[n]如下所示:n 0 1 2 3y[n] 4 -1 -1 7连续信号的卷积信号x(t):如果考虑连续信号的卷积,我们可以将卷积公式稍作修改。
考虑一个连续信号x(t),其函数表达式为:x(t)=δ(t)+2δ(t−1)−δ(t−2)+3δ(t−3)其中,δ(t)表示单位冲激函数。
信号ℎ(t):接下来,我们定义另一个连续信号ℎ(t),其函数表达式为:ℎ(t)=−δ(t)+δ(t−1)+2δ(t−2)计算卷积结果y(t):现在,我们可以使用修改后的信号卷积公式来计算卷积结果y(t),如下所示:∞(τ)⋅ℎ(t−τ)dτy(t)=∫x−∞具体计算过程略。
总结信号卷积是一种重要的信号处理技术,可应用于离散信号和连续信号的处理。
通过计算输入信号与卷积核的乘积并求和,我们可以得到卷积结果。
连续时间系统卷积的计算

实验报告实验名称:连续时间系统卷积的数值计算班级:120241姓名:彭壮学号:12021327一、实验目的:1、加深对卷积概念及原理的理解;2、掌握借助计算机计算任意信号卷积的方法。
二、实验原理:卷积积分不仅可以通过直接积分或查表的方法来求解,还可以用积分的数值计算方法来求解。
在线性系统的分析过程中,有时会遇到复杂的激励信号,或者有时只是一组测试数据或曲线,冲激响应也可能出现同样的情况。
显然,此时直接计算积分或查表都有困难,而采用近似的数值计算方法可以解决这个问题,求得卷积积分。
1、卷积的定义卷积积分可以表示为2卷积计算的几何算法卷积积分的计算从几何上可以分为四个步骤:翻转→平移→相乘→叠加。
3卷积积分的应用卷积积分是信号与系统时域分析的基本手段,主要用于求系统零状态响应,它避开了经典分析方法中求解微分方程时需要求系统初始值的问题。
设一个线性零状态系统,已知系统的单位冲激响应为h(t),当系统的激励信号为e(t)时,系统的零状态响应为由于计算机技术的发展,通过编程的方法来计算卷积积分已经不再是冗繁的工作,并可以获得足够的精度。
因此,信号的时域卷积分析法在系统分析中得到了广泛的应用。
卷积积分的数值运算实际上可以用信号的分段求和来实现,即:如果我们只求当t = nΔt (n为正整数,nΔt 记为t )时r(t)的值,则由上式可以得到:当Δt 足够小时,r(t )就是e(t)和h(t)卷积积分的数值近似,由上面的公式可以得到卷积数值计算的方法如下:1 将信号取值离散化,即以 Ts 为周期,对信号取值,得到一系列宽度间隔 为 Ts 的矩形脉冲原信号的离散取值点,用所得离散取值点矩形脉冲来表示原来的连续时间信号;2 将进行卷积的两个信号序列之一反转,与另一信号相乘,并求积分,所得为 t=0 时的卷积积分的值。
以 Ts 为单位左右移动反转的信号,与另一信号相乘求积分,求的t<0和t>0时卷积积分的值;3 将所得卷积积分值与对应的t 标在图上,连成一条光滑的曲线,即为所求卷积积分的曲线。
信号与系统 连续时间信号卷积运算
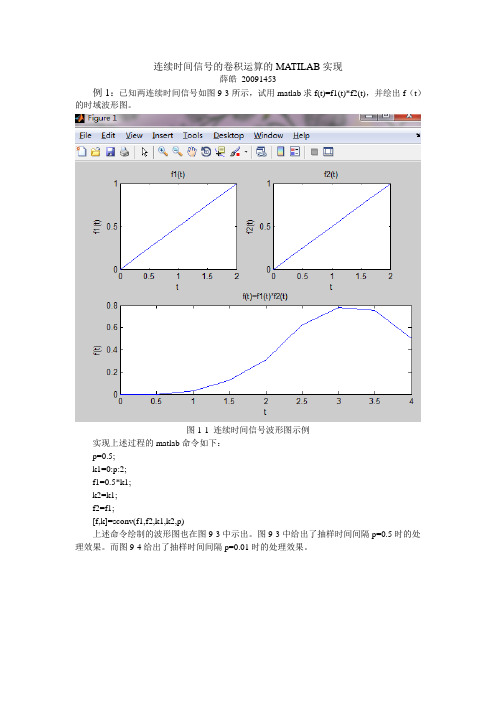
连续时间信号的卷积运算的MATILAB实现薛皓20091453例1:已知两连续时间信号如图9-3所示,试用matlab求f(t)=f1(t)*f2(t),并绘出f(t)的时域波形图。
图1-1 连续时间信号波形图示例实现上述过程的matlab命令如下:p=0.5;k1=0:p:2;f1=0.5*k1;k2=k1;f2=f1;[f,k]=sconv(f1,f2,k1,k2,p)上述命令绘制的波形图也在图9-3中示出。
图9-3中给出了抽样时间间隔p=0.5时的处理效果。
而图9-4给出了抽样时间间隔p=0.01时的处理效果。
图1-2 例1的连续时间信号波形图习题1:已知f1(t)=1(2t 1≤≤),f2(t)=1(3t 2≤≤),用matlab 实现其卷积并绘制出卷积曲线。
解:程序代码如下:>> p=0.01;k1=1:p:2;f1=ones(size(k1)).*(k1>1);k2=2:p:3;f2=ones(size(k2)).*(k2>2);f=conv(f1,f2);f=f*p;k0=k1(1)+k2(1);k3=k1(length(k1))+k2(length(k2));subplot(2,2,1)plot(k1,f1)title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(2,2,2)plot(k2,f2)title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(2,2,3)plot(k,f);h=get(gca,'position');h(3)=2.5*h(3); 0set(gca,'position',h)title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')绘制图形如图2-1所示。
连续时间信号卷积运算的MATLAB实现

连续时间信号卷积运算的MATLAB 实现一、实验目的(1)理解掌握卷积的概念及物理意义。
(2)理解单位冲激响应的概念及物理意义。
二、实验原理连续信号卷积运算定义为1212()()*()()()f t f t f t f f t d τττ∞-∞==-⎰卷积计算可以通过信号分段求和来实现,即1212120()()*()()()lim ()()k f t f t f t f f t d f k f t k τττ∞∞∆→=-∞-∞==-=∆-∆∆∑⎰ 如果只求当t n =∆(n 为整数)时()f t 的值()f n ∆,则由上式可得1212()()()()[()]k k f n f k f n k f k f n k ∞∞=-∞=-∞∆=∆∆-∆=∆∆-∆∑∑ 式中的12()[()]k f k f n k ∞=-∞∆-∆∑ 实际上就是连续信号1()f t 和2()f t 经等时间间隔∆均匀抽样的离散序列1()f k ∆和2()f k ∆的卷积和。
当∆足够小时,()f n ∆就是卷积积分的结果——连续时间信号()f t 的较好的数值近似。
三、实验程序function[f,k]=sconv(f1,f2,k1,k2,p)f=conv(f1,f2);f=f*p;k0=k1(1)+k2(1);k3=length(f1)+length(f2)-2;k=k0:p:k3*p;subplot(2,2,1)plot(k1,f1)title('f1(t)')xlabel('t')ylabel('f(1)')subplot(2,2,2)plot(k2,f2)title('t')xlabel('t')ylabel('f(2)')subplot(2,2,3)plot(k,f);h=get(gca,’position’);h(3)=2.5*h(3);set(gca,'position',h)title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')四、求解f t=cost∗sint(1)Matlab命令如下:p=0.1;k1=0:p:6;f1=sin(k1);k2=k1;f2=f1;[f,k]=sconv(f1,f2,k1,k2,p)(2)运行过程如下:图一程序截图图二运行结果五、实验小结实验结果表明,用Matlab计算出的结果与理论分析结果一致。
连续信号卷积
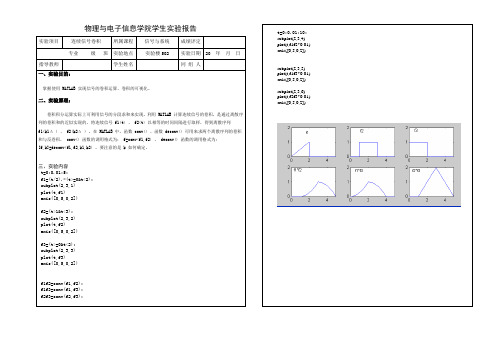
物理与电子信息学院学生实验报告t=0:0.01:10; subplot(2,3,4) plot(t,f1f2*0.01) axis([0,5,0,2])subplot(2,3,5) plot(t,f1f3*0.01) axis([0,5,0,2])subplot(2,3,6) plot(t,f2f3*0.01) axis([0,5,0,2])实验项目连续信号卷积所属课程信号与系统 成绩评定专业 级 班 实验地点 实验楼502实验日期 20 年 月 日 指导教师 学生姓名同 组 人一、实验目的:掌握使用 MATLAB 实现信号的卷积运算、卷积的可视化。
二、实验原理:卷积积分运算实际上可利用信号的分段求和来实现。
利用 MATLAB 计算连续信号的卷积,是通过离散序列的卷积和的近似实现的,将连续信号 f1(t) 、 f2(t) 以相等的时间间隔进行取样,得到离散序列 f1(k1Δ ) 、 f2(k2Δ ) 。
在 MATLAB 中,函数 conv() 、函数 deconv() 可用来求两个离散序列的卷积和与反卷积, conv() 函数的调用格式为: f=conv(f1,f2) 、 deconv() 函数的调用格式为: [f,k]=deconv(f1,f2,k1,k2) 。
要注意的是 k 如何确定。
三、实验内容 t=0:0.01:5;f1=(t/2).*(t>=0&t<2); subplot(2,3,1) plot(t,f1)axis([0,5,0,2])f2=(t>1&t<3); subplot(2,3,2) plot(t,f2)axis([0,5,0,2])f3=(t>=0&t<2); subplot(2,3,3) plot(t,f3)axis([0,5,0,2])f1f2=conv(f1,f2); f1f3=conv(f1,f3); f2f3=conv(f2,f3);四、实验总结(实验中所遇问题的原因分析及解决措施;本实验未解决的问题;对实验的改进;个人的收获等)。
运用MATLAB进行连续时间信号卷积运算

实验项目名称:运用MATLAB进行连续时间信号卷积运算(所属课程:信号与系统)院系:电子信息与电气工程专业班级:电气工程及其自动化姓名:安永军学号:201002040062实验日期:2012年4月12 号实验地点:A-07-408合作者:张德扬指导老师:李静本实验项目成绩: 教师签字: 日期:一:实验目的1,掌握连续时间信号的基本运算的实现方法。
2,熟悉连续LTI 系统在典型激励信号下的响应及其特征。
3、掌握连续LTI 系统单位冲激响应的求解方法。
4、重点掌握用卷积法计算连续时间系统的零状态响应。
5、熟悉MATLAB 相关函数的调用格式及作用。
6、会用MATLAB 对系统进行时域分析。
二、实验原理1、信号的运算包括:信号的基本运算,包括加、减、乘、除等;信号的时域变换,包括信号的平移、翻转、尺度变换等;两个信号的卷积运算等。
2、连续时间线性时不变系统(LTI )可以用如下的线性常系数差分方程来描述:()(1)()(1)110110()()()()()()()()n n m m n m n n r t r t r t r t e t e t e t e t a a a a b b b b ----++++=++++''其中,n m ≥,系统的初始条件为(0)r -,(0)r -',(0)r -'', (1)(0)n r--。
系统的响应一般包括两个部分,即由当前输入所产生的响应(零状态响应)和由历史输入(初始状态)所产生的响应(零输入响应)。
对于低阶系统,一般可以通过解析的方法得到响应。
但对于高阶系统,手工计算就比较困难,这时MATLAB 强大的计算功能就能比较容易地确定系统的各种响应,如冲激响应、阶跃响应、零输入响应、零状态响应、全响应等。
1)直接求解法在MATLAB 中,要求以系数相量的形式输入系统的微分方程。
因此,在使用前必须对系统的微分方程进行变换,得到其传递函数。
连续时间信号的卷积运算

实验二连续时间信号的卷积运算与LTI系统的时域分析实验人:Mr.yan1 实验目的(1)熟悉卷积的定义和表示;(2)掌握利用计算机进行卷积运算的原理和方法;(3)熟悉连续信号卷积运算函数conv的应用。
(4)熟悉连续LTI系统在典型激励信号下的响应及其特征;(5)掌握连续LTI系统单位冲激响应的求解方法;(6)掌握用卷积法计算连续时间系统的零状态响应;(7)能够应用Matlab对系统进行时域分析。
2 实验原理(1)卷积的定义、卷积的几何解法、卷积积分的应用(求系统的零状态响应)(2)对于一般的n阶LTI连续系统,如果n的数值比较小时,可以通过解析的方法得到响应。
但是,对于高阶系统,手工运算比较困难,要利用一些计算工具软件。
3 涉及的Matlab函数(1)conv函数:实现信号的卷积运算。
调用格式:w=conv(u,v)计算两个有限长度序列的卷积。
说明:该函数假定两个序列都从零开始。
(2)lsim函数:计算并画出系统在任意输入下的零状态响应。
调用格式:lsim(b,a,x,t)其中:a和b是由描述系统的微分方程系数决定的表示该系统的两个行向量;x和t是表示输入信号的行向量。
该调用格式将会绘出由向量a和b所定义的连续系统在输入为向量x 和t所定义的信号时,系统的零状态响应的时域仿真波形,且时间范围与输入信号相同。
(3)impulse函数:计算并画出系统的冲激响应。
调用格式:impulse(b,a)该调用格式以默认方式绘出向量a和b定义的连续系统的冲激响应的时域波形。
impulse(b,a,t)该调用格式将绘出向量a和b定义的连续系统在0-t时间范围内的冲激响应波形。
impulse(b,a,t1:p:t2)该调用格式将绘出向量a和b定义的连续系统在t1-t2时间范围内,且以时间间隔p均匀取样的冲激响应波形。
(4)step函数:计算并画出系统阶跃响应曲线调用格式:该函数与函数impulse()一样,也有相似的调用格式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、学会运用MATLAB实现连续时间信号的卷积 2、学会运用MATLAB符号运算法求连续时间信号 的卷积 3、学会运用MATLAB数值计算方法求连续时间信 号的卷积
实验原理:
f (t) f (t) f (t) f ( ) f (t )d 1
2
1
2
f (t) f1(t) * f2 (t) f1( ) f (t )d
f1(m ) f2[(n m) ]
m
f (t) [ f1(n) f2 (n)]
• 用MATLAB实现连续信号卷积的过程:
– 将连续信号 f1(t与) f以2 (时t) 间间隔 抽样, 得
到
f1(k), f2(k)
– 构造与 f1(k), f相2(k对)应的时间变量k1和k2.
– 调用conv()函数计算卷积积分f(t)的近似向量
f1 (t )
lim 0
f1 (m
),
f2 (t)
lim 0
f2 (m
)
f (t) f1(t) f2 (t) f1( ) f2 (t )d
lim 0 m
f1 (m
) f2 (t m
)
f (n ) f1(m ) f2 (n m ) m
f1(m ) f2[(n m) ]
m
f (t) f (n )
(1)符号法:要注意积分变量和积分限的选取
lim
0 k
f1 (k )
f2 (t
k)
如果Байду номын сангаасt=n,则
(2)数值计算法
f (n) f1(k) f2 ((n k)) k
y(t)
t
eT
u (t )
etu(t
)
t
eT
u(
)
e (t
)u(t
)
0
ex3_1.m
y(t) [u(t) u(t 1)][u(t) u(t 1)]
– 构造 对应的时间向量k.
f (n)
y(t) [u(t) u(t 1)][u(t) u(t 1)]
ex3_3.m
实验内容:
1、绘制 f1(t) f2 (t)
采用数值与符号法
f1 (t )
f2 (t)
2、两种方式计算如下卷积
(1) f1(t) f2 (t); (2) f1(t) f3(t); (3) f1(t) f4 (t) (4) f2 (t) f3(t); (5) f2 (t) f4 (t); (6) f3(t) f4 (t)
ex3_2.m
MATLAB中:w conv(u,v) 函数实现卷积和
w(n) u(m)v(n 1 m)
m
f (t) f1(t) f2 (t) f1( ) f2 (t )d
对f1(t)和f2 (t)进行等间隔 均匀抽样, 则f1(t) f1(m ),f2 (t) f2 (m ), 当 足够小的时候,则
