高等流体力学各章习题汇总
高等流体力学各章习题汇总

式中是 u 速度, dS 是流动方向的微元弧长. 7. 试证明对于滞止焓 h0 有以下方程成立
t ( h0 ) x j ( u j h0 ) p t x j ( ij u i k T x j ) fiu i
滞止焓
h0 h
1 u u 2
8.一个物质体系V 分为V1和V2 两部分, Σ 是V1和V2的分界面, S 是V的 边界曲面, 设交界面Σ以速度 u 运动,在 Σ 两侧物理量 F 有一个跃变. 试导出推广的雷诺输运公式
Dt
V
D
FdV
V
F t
dV
S
F V nd S
第五章 教科书 5.5, 5.6, 5.7 4. 证明在球坐标系下 (
A r
2
co s B r ) sin
2 2
可表示不可压缩流体
某轴对称无旋流动中的流函数,并求其速度势.
5. 已知流体绕流圆球的势函数
的力.
( r , ) U ( r
a
3 2
) co s
2r
, 式中 a 是
2
2
(1)沿下边给出的封闭曲线积分求速度环量,
0 x 10, y 0; 0 y 5, x 10; 0 x 10, y 5; 0 y 5, x 0.
(2)求涡量 ,然后求
n dA
A
式中A是 (1) 中给出的矩形面积, 是此面积的外单位法线矢量。
u i t u
j
t
u j
x
ij j
x k
《流体力学》所有做过的习题答案
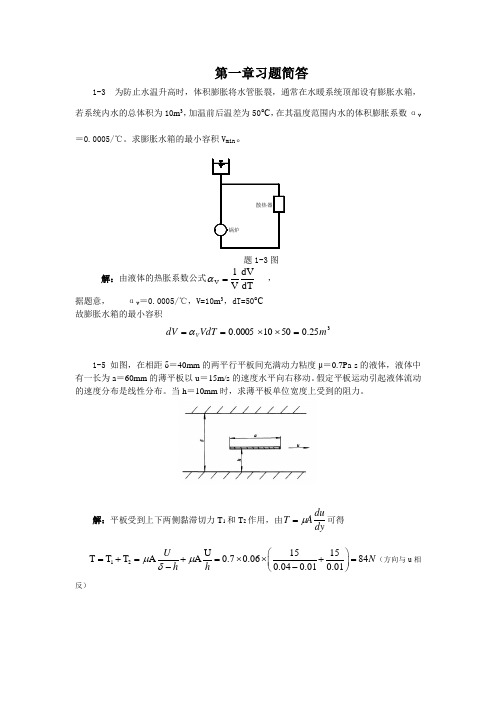
第一章习题简答1-3 为防止水温升高时,体积膨胀将水管胀裂,通常在水暖系统顶部设有膨胀水箱,若系统内水的总体积为10m 3,加温前后温差为50°С,在其温度范围内水的体积膨胀系数αv=0.0005/℃。
求膨胀水箱的最小容积V min 。
题1-3图解:由液体的热胀系数公式dTdVV 1V =α , 据题意, αv =0.0005/℃,V=10m 3,dT=50°С 故膨胀水箱的最小容积325.050100005.0m VdT dV V =⨯⨯==α1-5 如图,在相距δ=40mm 的两平行平板间充满动力粘度μ=0.7Pa·s 的液体,液体中有一长为a =60mm 的薄平板以u =15m/s 的速度水平向右移动。
假定平板运动引起液体流动的速度分布是线性分布。
当h =10mm 时,求薄平板单位宽度上受到的阻力。
解:平板受到上下两侧黏滞切力T 1和T 2作用,由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭(方向与u 相反)1-7 温度为20°С的空气,在直径为2.5cm 的管中流动,距管壁上1mm 处的空气速度为3cm/s 。
求作用于单位长度管壁上的黏滞切力为多少?解:温度为20°С的空气的黏度为18.3×10-6 Pa·s 如图建立坐标系,且设u=ay 2+c 由题意可得方程组⎪⎩⎪⎨⎧+-=+=ca ca 22)001.00125.0(03.00125.00 解得a = -1250,c =0.195 则 u=-1250y 2+0.195则y dy y d dy du 2500)195.01250(2-=+-= Pa dyduAT 561048.4)0125.02500(1025.0103.18--⨯-=⨯-⨯⨯⨯⨯⨯==∴πμ (与课本后的答案不一样。
大学科目《流体力学》习题及答案

一、选择题1.按连续介质的概念,流体质点是指A .流体的分子; B. 流体内的固体颗粒; C . 无大小的几何点; D. 几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
2.作用在流体的质量力包括A. 压力;B. 摩擦力;C. 重力;D. 惯性力。
3.单位质量力的国际单位是:A . N ; B. m/s ; C. N/kg ; D. m/s 2。
4.与牛顿内摩擦定律直接有关系的因素是A. 切应力和压强; B. 切应力和剪切变形速率; C. 切应力和剪切变形。
5.水的粘性随温度升高而A . 增大; B. 减小; C. 不变。
6.气体的粘性随温度的升高而 A. 增大;B. 减小;C. 不变。
7.流体的运动粘度υ的国际单位是A. m 2/s ;B. N/m 2 ; C. kg/m ;D. N ·s/m2 8.理想流体的特征是A. 粘度是常数;B. 不可压缩;C. 无粘性; D. 符合pV=RT 。
9.当水的压强增加1个大气压时,水的密度增大约为A. 200001; B. 100001;C. 40001 。
10.水力学中,单位质量力是指作用在A. 单位面积液体上的质量力;B. 单位体积液体上的质量力; C. 单位质量液体上的质量力;D. 单位重量液体上的质量力 11.以下关于流体粘性的说法中不正确的是A. 粘性是流体的固有属性;B. 粘性是在运动状态下流体具有抵抗剪切变形速率能力的量度C. 流体的粘性具有传递运动和阻滞运动的双重作用;D. 流体的粘性随温度的升高而增大。
12.已知液体中的流速分布µ-y 如图所示,其切应力分布为 A.τ=0;B.τ=常数; C. τ=ky (k 为常数)。
13.以下关于液体质点和液体微团的正确论述是A. 液体微团比液体质点大;B. 液体微团包括有很多液体的质点; C. 液体质点没有大小,没有质量;D. 液体质点又称液体微团。
14.液体的汽化压强随温度升高而 A. 增大;B. 减小;C. 不变;15.一封闭容器盛以水,当其从空中自由下落时(不计空气阻力),其单位质量力为 A. 0 ; B. -g ; C. mg ;D. –mg 。
高等流体力学课后习题

⎧ y = c′x 2 ⎨ 3 ⎩ z = c′′x
1.5 已知流体质点的空间位置表示如下,
x = x0 , y = y0 + x0 ( e −2 t − 1), z = z0 + x0 ( e −3t − 1) ,
求 (1) 速度的欧拉表示; (2) 加速度的欧拉和拉格朗日表示; (3) 过点 (1,1,1) 的流线及 t = 0 时在 ( x0 , y0 , z0 ) = (1,1,1) 处的流体质点的迹线; (4)散度、旋度及涡线; (5)应变率张量和 旋转张量。 解: (1)速度欧拉表示
x = c1t , y = c2 et , z = c3
由 t = τ 时 ( x, y , z ) = ( x∗ , y∗ , z∗ )得
c1 = x∗τ −1 , c2 = y∗e −τ , c3 = z∗
将以上常数代入迹线方程,
高 等 流 体 力 学 习 题
第一章 课后练习题解
1.2 一速度场用 u =
x 2y 3z 描述, (1)求加速度的欧拉描述; (2)先求 , v= , w= 1+ t 1+ t 1+ t
矢径表示式 r = r ( x0 , y0 , z0 , t ) ,再求此加速度的拉格朗日描述; (3)求流线。
涡线方程,
x = c1 dy dz = −3 t −2e −2 t 3e ⇒ z=− 2 t ye + c2 3
(5)应变率张量和旋转张量
⎛ ⎜ 0 ⎜ S = ⎜ e −2 t ⎜ 3 −3t ⎜− e ⎝ 2
1.8
e −2 t 0 0
3 ⎞ ⎛ − e −3t ⎟ ⎜ 0 2 ⎟ ⎜ 0 ⎟ , A = ⎜ − e −2 t ⎟ ⎜ 3 −3 t 0 ⎟ ⎜− e ⎠ ⎝ 2
高等流体力学第一章配套例题

r ez r ez
θ
P
σ Rω
a
σ Rθ
r r r pn = σ RR eR + σ Rθ eθ r 3µU r = − p0 eR + ez 2a
x
ω
y
z
σ RR
P
r 2π π r 2 3µU r r F = ∫ ∫ pn a sin θ dθ dω = 4π a 2 ez = 6πµUaez 2a 0 0
u = ay , v = w = 0 试求:
r
sij
aij s ijδ x j 和旋转速度 a ij δ x j
r r r i j k r r 1) ∇ × u = ∂ / ∂x ∂ / ∂y ∂ / ∂z = −ak ay 0 0
2)
0 a / 2 0 sij = a / 2 0 0 0 0 0
r + dr ,θ +
dθ dz ,z+ 2 2
dθ dz r ,θ + , z + 2 2
}dθ dz
dr
dθ
r+
dr dz ,θ + dθ , z + 2 2 dr ,θ , z + 2 2 r+ dz ]dzdr
r
θ
x
r+
r r r +{[(σ zr er + σ zθ eθ + σ zz ez )r ] r r r −[(σ zr er + σ zθ eθ + σ zz ez )r ]
θ
σ Rω
a
σ Rθ
ω
又解 :
y
x
r r F = ez ∫ (σ RR cosθ − σ Rθ sin θ ) 2π a sin θ a dθ
(完整word版)流体力学总题库内部吐血整理

2h
(3)
即
h 2H h1
(4)
等角速度旋转容器中液体相对平衡时等压面的方程为
2r2 gz C
2
(5)
r d z h 对于自由液面,C=0。圆筒以转速 n1 旋转时,自由液面上,边缘处,
,
,则
2
2
d 2
2
gh
0
(6)
2
得
2 2gh
d
(7)
由于
2 n1
60
(8)
n1
30
30
d δ
n L
2.在温度不变的条件下,体积为 由流体压缩系数计算公式可知:
的水,压强从
增到
,体积减少了
,试求水的压缩率。
3.某种油的运动黏度是 4.28x10∧-7 ㎡/s,密度是 ρ=678kg/m³,试求其动力黏度。
解:油的运动黏度 v=4.28x10∧-7 ㎡/s。ρ=678kg/m³
v=u/p 得 u=pv=4.28x10*-7x678=2.9x10∧-4Pa.s 4.(习题 1-8)
h= 因此,可以计算 h 得到:
pA -pB Hg g
(2.7+2.9) 104 = 13.55103 9.8
=0.422m
6、如图所示,一直立的煤气管,为求管中煤气的密度,在高度差 H=20m 的两个断面上安装 U 形管测压计,其内工
m h h 的密度 =1.28kg/ 3 ,测压计读数 1 =100mm, 2 =115mm。若忽略 U 形管测压计中空气密度的影响,试求煤气管中煤气的密度。解:
,间隙
,间隙内润滑油的动力黏度
,消耗的功率
解 油层与轴承接触面上的速度为零,与轴接触面上的速度等于轴面上的线速度
(完整word版)《高等流体力学》习题集

《高等流体力学》复习题一、 基本概念1. 什么是理想流体?正压流体,不可压缩流体? [答]:教材P57当流体物质的粘度较小,同时其内部运动的相对速度也不大,所产生的粘性应力比起其它类型的力来说可以忽略不计时,可把流体近似地看为是无粘性的,这样无粘性的流体称为理想流体。
内部任一点的压力只是密度的函数的流体,称为正压流体。
流体的体积或密度的相对变化量很小时,一般可以看成是不可压缩的,这种流体就被称为不可压缩流体。
2. 什么是定常场;均匀场;并用数学形式表达。
[答]:如果一个场不随时间的变化而变化,则这个场就被称为定常场。
其数学表达式为:)(ϕϕ=如果一个场不随空间的变化而变化,即场中不显含空间坐标变量r ,则这个场就被称为均匀场。
其数学表达式为:)(t ϕϕ=3. 理想流体运动时有无切应力?粘性流体静止时有无切应力?静止时无切应力是否无粘性?为什么? [答]:理想流体运动时无切应力。
粘性流体静止时无切应力。
但是,静止时无切应力,而有粘性。
因为,粘性是流体的固有特性。
4. 流体有势运动指的是什么?什么是速度势函数?无旋运动与有势运动有何关系? [答]:教材P119-123如果流体运动是无旋的,则称此流体运动为有势运动。
对于无旋流动来说,其速度场V 总可以由某个速度标量函数(场)),(t r φ的速度梯度来表示,即φ∇=,则这个标量函数(场)),(t φ称为速度场V 的速度势函数。
无旋运动与有势运动的关系:势流运动与无旋运动是等价的,即有势运动是无旋的,无旋运动的速度场等同于某个势函数的梯度场。
5. 什么是流函数?存在流函数的流体具有什么特性?(什么样的流体具有流函数?) [答]:6. 平面流动中用复变位势描述的流体具有哪些条件(性质)? [答]:教材P126-127理想不可压缩流体的平面无旋运动,可用复变位势描述。
7. 什么是第一粘性系数和第二粘性系数?在什么条件下可以不考虑第二粘性系数?Stokes 假设的基本事实依据是什么? [答]:教材P89第一粘性系数μ:反映了剪切变形对应力张量的贡献,因此称为剪切变形粘性系数; 第二粘性系数μ’:反映了体变形对应力张量的贡献,因而称为体变形粘性系数。
高等流体力学复习总结

m y 2 x 2 y 2
四、倒数函数-偶极子
m 1 m x yi w( z ) i 2 2 2 x yi 2 x y
m 1 w( z ) 2 z
m是实数
dw m 1 iQ dw dz dz 0 2 c c dz c 2 z
正压流体
流体在流动过程中,若流体的密度仅
是压力的函数,则该流动是正压的。或
者,若等密度面与等压面重合,则流动 正压。
d ( )v ( v) dt
1 1 F p v ( v) 3
直角坐标系中的形式
u 2 u v w p xx p 2 x y z x 3 v 2 u v w p yy p 2 x y z y 3 w 2 u v w p zz p 2 x y z z 3
w( z ) a ln z
a是实数
i
w( z ) i a ln(re ) a ln r i
Q a 2 Q w( z ) ln z 2
点源 若点源不在坐标原点而在z0点,则复位势为: 点汇
Q w( z ) ln( z z0 ) 2
w( z) ib ln z b是实数 z re i w( z ) i bi ln(re ) bi(ln r i ) b bi ln r
第二章 流体力学的基本概念
一 流体的定义和特征
二、流体连续介质假设
三 描述流体运动的两种方 法
四 迹线与流线 P104 例题 P140习题 五 速度分解定理 变形速度二阶张量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1). 证明圆周 x 2
y a
2
2
上的任意一点的速度都与 y 轴平行,且此
速度大小与 y 成反比. (2). 求 y 轴上的速度最大点;
(3). 证明 y 轴是一条流线.
7. 已知速度势φ, 求相应流函数ψ. (1). (2).
xy
x x y
2 2
b
b
U p
8. 求图示不脱体绕流平板上下表面压强, 压强系数和速度分布.
2
2
(1)沿下边给出的封闭曲线积分求速度环量,
0 x 10, y 0; 0 y 5, x 10; 0 x 10, y 5; 0 y 5, x 0.
(2)求涡量 ,然后求
n dA
A
式中A是 (1) 中给出的矩形面积, 是此面积的外单位法线矢量。
u i t u
j
t
u j
x
ij j
x k
u j u k
ij
xi
f
j
可简化为
u i x
j
fi
6. 流体在弯曲的变截面细管中流动,设 A 为细管的横断面积, 在 A 断面上的流动物理量是均匀的,试证明连续方程具有下述形式,
L1
C
L2
第四章 教科书 4.1, 4.4, 4.7, 4.12 5. 设复位势为
F ( z ) m ln ( z 1 z )
(1). 问流动是由哪些基本流动组成; (2). 求流线方程;
(3). 求通过 z i 和 z
1 2
两点连线的流体体积流量.
6. 在点 (a, 0), ( -a, 0) 上放置等强度的点源,
第三章 教科书3.2, 3.3
3. 证明理想气体,质量力有势时有
D ( Dt
)(
1 )u 3 p
是涡量.
4.设等截面直角形管道,铅直段长为L1,
水平段长为 L2, 管中盛满了理想不可 压缩均质的水(如图示). C 处有一阀门, 当阀门打开后,管中的流动在各截面上 是均匀分布的. 求当铅直段中液面高为 h 时,管中的压强分布.
(2) 垂直于该平面的应力矢量分量; (3)
n 与 p n 之间的夹角。
1.4 设流动速度分布为 求各切应力。
u yzt , v zxt , w 0 .
粘度系数为
0 .0 1 N s/m ,
1.5 (教科书 2.3 )已知流场
u 1 6 x y , v 1 0, w yz
第五章 教科书 5.5, 5.6, 5.7 4. 证明在球坐标系下 (
A r
2
co s B r ) sin
2 2
可表示不可压缩流体
某轴对称无旋流动中的流函数,并求其速度势.
5. 已知流体绕流圆球的势函数
的力.
( r , ) U ( r
a
3 2
) co s
2r
, 式中 a 是
练习题
第一章 1.1 设速度场
u x 1 t ,
v 2y 1 t ,
w 3z 1 t ,
(1) 求其加速度的欧拉描述; (2) 先求矢径表示式 r r ( x 0 , y 0 , z 0 , t ) ,再由此求加速度的拉 格朗日描述; (3) 求流线及迹线。 1.2 设
n
1.6 (教科书 2.6) 计算下列二维流场在任意点
(R, )
的涡量,
(1).
(2)
u R 0, u R
u R 0, u 2 R
上式中 R 和 是柱坐标变量, 1.7 (教科书1.8)
, 为常数。
第二章 教科书: 1.4, 1.7, 1.9 (增加 Φ 证明大于零), 1.10 5. 证明方程
( F1 F 2 ) u d S
V1
Σ Leabharlann n 和 分别是 S 和 Σ 的法向单位矢 式中
S
n
量,其指向如图所示, F1 - F2 为 Σ 两侧 F 函数的跳跃.
V2
9. 设物体表面是不可穿透的,且表面形状在初始时刻可用 F(x,y,z)=0 来表示,如果此物体从初始时刻开始做下列不同运动: (1). 以速度 U 做等速运动, 速度沿 X 轴的负方向; (2). 以速度V= f (t) 做变速直线运 动,速度沿 X 轴的正方向.试写出在静止坐标系中粘性流体在物面上 的速度,物面在运动过程中的表达式,并计算速度在物面法线上的分量.
滞止焓
h0 h
1 u u 2
8.一个物质体系V 分为V1和V2 两部分, Σ 是V1和V2的分界面, S 是V的 边界曲面, 设交界面Σ以速度 u 运动,在 Σ 两侧物理量 F 有一个跃变. 试导出推广的雷诺输运公式
Dt
V
D
FdV
V
F t
dV
S
F V nd S
w b ( a x y ),
2 2 2
u v 0,
求应变率张量及旋转张量。
1.3 在P点的应力张量如下
7 0 2 0 5 0 2 0 4
求 (1) P点与单位法向矢量
pn ; 垂直的平面上的应力矢量
2 1 2 n , , 3 3 3
A t S ( Au ) 0
式中是 u 速度, dS 是流动方向的微元弧长. 7. 试证明对于滞止焓 h0 有以下方程成立
t ( h0 ) x j ( u j h0 ) p t x j ( ij u i k T x j ) fiu i
圆球半径. 试求圆球表面的压强分布,并计算流体作用在圆球上
6. 求半径为 a 的圆球在无限流场中由于重力而下沉的运动规律。 设 圆球运动阻力
D 1 2 C D V A
2
,C 是阻力系数, A
D
a
2
,称为
迎风面积。
