重叠子阵平面相控阵ADBF的方向图控制
平面相控阵天线方向图测量中的栅瓣问题仿真与分析研究

李 玮,刘 震,田书林,黄建国
(成都电子科技大学 自动化工程学院 四川成都 611731)
【摘要】在相控阵雷达天线实际测量与设计仿真过程中,经常会遇到栅瓣问题。栅瓣的出现会产生测角多 值性,致使雷达接收机锁定栅瓣而导致误跟踪。传统的文章侧重分析线性相控阵天线的栅瓣问题,而很少 关注平面相控阵天线的栅瓣问题。文章首先从理论上分析了平面相控阵天线栅瓣出现的原因、位置以及如 何抑制栅瓣出现的措施,并通过仿真实验验证了结论的正确性。本文的工作将对工程实践中遇到的栅瓣问 题起到一定的指导作用。 【关键词】相控阵;天线测量;方向图仿真;栅瓣
0 -2
-5 -5 -10 -15 -20 -25 -20 0 0
-4
( dB)
-8 -10 -12 -14 -20 -10 0 10 20
( dB)
-15 -20 -25 -20
( dB)
-6
-10
-10
0
10
20
-10
0
10
20
(
)
(
)
(
)
(a) d x = d y = 0.5λ
(b) d x = d y = 1.5λ
F (θ , ϕ ) = Fax (θ , ϕ ) • Fay (θ , ϕ )
M −1
(2)
其 中
Fax (θ , ϕ ) = ∑ I m e jm ( kd x sin θ cos ϕ +α x ) 为 沿 x 方 向 间 距 为 d x , 步 进 相 位 为
m =0 N −1 jn ( kd y sin θ sin ϕ +α y )
(1)
其中 f (θ , ϕ ) 称为单元天线的方向函数,即元因子,虽然天线阵中各个阵元之间存在互耦, 每个天线元的电流分布必然受到其他天线元的影响, 靠近边缘的阵元所受的影响与阵中心所 受的影响必然不同,不过,这些影响都比较小,通常认为阵中所有天线元具有相同的方向函 数,即 f (θ , ϕ ) = 1 。 F (θ , ϕ ) 称为阵因子,它与阵中各天线元的位置、激励电流幅度和相位 有关。因此,在阵列天线中,方向性主要由阵因子来决定。在平面相控阵天线中,有:
利用耦合实现相控阵平顶单元方向图的方法

Fi 1 S o e e ’ a al l p a e wa e ui e a r y mo e g. k b l v S p r le l t v g d r a d l
等 。但 馈 电网络 的设计 一般 过于 复杂而 加介 质棒 的 方法会增 加相控 阵 的质 量 , 此并 不 能 很 好 地满 足 因 星载相控 阵的应用 要求 。
( 国 空 间技 术 研 究 院 总 体 部 ,北 京 109 ) 中 00 4
摘 要 :提 出 了一 种 用 于 低 轨 卫 星 有 限 扫 描 相 控 阵 的 新 型 波 导 辐 射 单 元 。该 辐 射 单 元 利 用 缝 隙耦 合 实 现 平 顶 的单 元 方 向 图 以解 决 有 限 扫 描 相 控 阵 由于 采 用 大 间 距 设 计 时 引 起 的扫 描 边 缘 增 益 跌 落 和 栅 瓣 的 问 题 。分 析 采 用 多 模 散 射 矩 阵 的 方法 , 算 速 度 快 、 度 高 。 数 值 计 算 和 测 试 结 果 表 明 这 种 辐 射 单 元 可 以 用 于 扫 描 角 度 宽 达 计 精 ±2。 5的有 限 扫 描 相 控 阵 的 设 计 。计 算 结 果 同 时 表 明 该 辐 射 单 元 至 少 可 以 满 足 1 %的 频 带 宽 度 。 0 关 键 词 :有 限 扫 描 相 控 阵 ;栅 瓣 ;平 顶 单 元 方 向 图 ;多 模 散 射 矩 阵
耦合 量就 可 以综合 出平 顶 的单 元 方 向图 。根据 Fo l— qe( ut弗洛 奎) 定理 , 2的无 限平面波 导相控 阵等效 图 为 图 3所示 的单元胞 室 (n e ) u icl 。 t 1
二维面阵子阵划分及PADBF算法研究

()=[ t , () t ()…, r
爪 f ( ) = s 0 o ̄ M , i cs n
t ( , = s Oi ̄ v 0 ) i s n n
() 1
则 有
() £
S()x t 仃 ktep 一
(
)+
f) 2
S ={ , ) t , )=△) ( l ( Y I( Y 。 f=12 …L 6 ,, )()
维面阵 , 出了等功 率噪声 法与 遗传算 法 ( A) 结合 的子 提 G 相
阵划分方法 , 该方法可使 同一子 阵单元 紧密相邻 同时避免栅 瓣 出现 , 能够 降低 子阵划分工程实现 的复杂度 。 在部分 自适应数字波束形成算法方 面, 国内外对 子阵级 部分 自适应数字波束形成技术进行 了大量研 究 , 基本是针 但
式 ( )中 , , 6 ( Y )表示 阵元 的位置 , ( , t Y)是 g q 量化 后
的幅 度 权 函 数 , △, ( , 12, )表 示 量 化 区 间 , 量 化 l= , … L是 的 阶数 。
Yv0, )/ m ( ] A}+n () t 式 ( )中 , ()为第一个阵元接收到 的第 k个干扰源的 2 st 复包 络 , t 为第 m 个 阵元 中与 干扰不相关 的高斯加性 白 n() 噪声 , 设各阵元 的噪声功率均 为 o 。 r
Re e r h o u r a vso nd PADBF g rt m s a c n S ba r y Di ii n a Al o ih
f r Two-d m e i n Pl n r Ar a o i nso a a r y
DONG Ye, IRu , IXio L i L a —mi g n
相控阵天线单元在阵中方向图研究
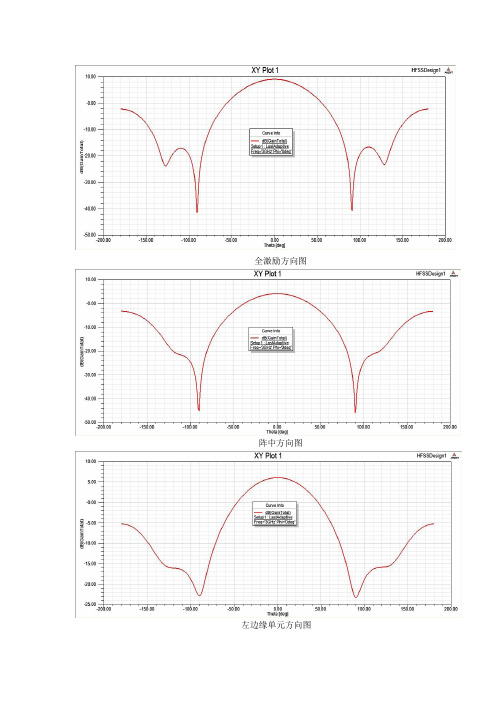
全激励方向图阵中方向图左边缘单元方向图左临边单元方向图右临边单元方向图右边缘单元方向图阵中(5号单元)方向图边缘单元(1号单元)方向图边缘单元(2号单元)方向图边缘单元(3号单元)方向图边缘单元(4号单元)方向图边缘单元(6号单元)方向图边缘单元(7号单元)方向图边缘单元(8号单元)方向图边缘单元(9号单元)方向图全激励方向图阵中方向图Unit 1(1) a flash in the pan昙花一现的人物,一时的成功★The low inflation rate will be no flash in the pan.(2) a matter of 关于...的问题;大约★To be promoted or to fall behind is not a matter of salary but even more a matter of self-respect. ★John cost a matter of 500 yuan for the coat.(3) a number of 一系列,一连串;大部分★When American’s National Research Council sent two engineers to supervise a series of industrial experiments at a large telephone-parts factory called the Hawthorne Plant near Chicago in 1924, it hoped they would learn how shop-floor lighting affected workers’ productivity.★A majority of immigrants spoke English well or very well after ten years of residence.(4)a majority of 种种,各种★A variety of small clubs can provide multiple opportunities for leadership, as well as for practice in successful group dynamics.(5) abide by 恪守,遵守,服从★Californians and New Englanders speak the same language and abide by the same federal laws.(6)above all 首要,尤其★Among the many shaping factors, I would single out the country’s excellent elementary schools; and above all the American genius。
相控阵形式

相控阵形式相控阵(Phased Array)是一种利用多个天线元件组成的阵列天线,通过控制每个天线元件的相位来实现波束的方向图变化。
相控阵技术在雷达、通信、无线电等领域具有广泛的应用前景。
本文将对相控阵的基本概念、原理、分类以及应用领域进行详细介绍。
一、相控阵的基本概念相控阵是一种由多个天线元件组成的阵列天线,通过对每个天线元件的相位进行独立控制,实现对波束方向图的动态调整。
相控阵的核心思想是将传统的机械扫描方式改为电子扫描方式,从而提高天线的性能和灵活性。
二、相控阵的原理相控阵的工作原理是通过改变阵列中每个天线元件的相位,使得阵列波束在一个平面内实现动态扫描。
当所有天线元件的相位相同时,阵列波束最大;当相邻天线元件的相位差为180度时,阵列波束为零;当相邻天线元件的相位差为任意值时,阵列波束将沿着相位差的方向逐渐减小。
通过改变每个天线元件的相位,可以实现对波束方向图的动态调整。
三、相控阵的分类根据阵列中天线元件的数量和排列方式,相控阵可以分为以下几类:1. 线阵:线阵是由一系列沿直线排列的天线元件组成,适用于需要大范围扫描的场景。
线阵可以分为一维线阵和二维线阵。
一维线阵只有一个维度上的天线元件,适用于单向扫描;二维线阵有两个维度上的天线元件,适用于双向扫描。
2. 面阵:面阵是由一系列分布在一个平面内的天线元件组成,适用于需要高分辨率的场景。
面阵可以分为矩形面阵和圆形面阵。
矩形面阵中的天线元件呈矩形排列,适用于需要高增益的场景;圆形面阵中的天线元件呈圆形排列,适用于需要低副瓣的场景。
3. 子阵列:子阵列是由一组相互独立的子阵列组成,每个子阵列可以独立控制其相位。
子阵列可以提高系统的可靠性和灵活性,适用于需要快速响应的场景。
四、相控阵的应用相控阵技术在雷达、通信、无线电等领域具有广泛的应用前景。
以下是一些典型的应用场景:1. 雷达系统:相控阵雷达通过控制阵列中每个天线元件的相位,实现对波束方向图的动态调整,从而实现对目标的快速跟踪和高分辨率成像。
理解相控阵天线的方向图

理解相控阵天线的方向图考虑一维阵列天线,由一排间隔很近的发射单元组成,每个阵元在所有方向上发射一个振幅、相位和频率相同的波。
为了测量这些波在不同方位角下的总强度,我们把一个场强探测器放在足够远的地方,使得从探测器到所有发射单元的视线几乎平行。
从阵列垂直平分线上的一个点开始,我们将场强探测器沿固定半径的弧线从阵列中心移动。
在任何一点上,场强取决于接收波的相对相位,而相对相位又取决于发射单元之间的距离差。
如果我们从阵列的一端画一条垂直于视线到探测器的直线(AB),那么这些差异就能很好地显示出来。
这条线与阵列的夹角等于探测器的方位角θ。
现在,如果θ为零,并且探测器远离阵列,则探测器到所有发射器的距离基本上是相同的。
这些波是同相位的,它们的场强叠加成一个很大的值。
但是,如果θ大于零,那么探测器到发射单元的距离就会逐渐增大。
因此,接收波的相位都略有不同,场强之和没有θ为零时那么大。
随着方位角的增大,距离差增大。
最终达到了一个点,如探测器至第一发射器(第1号)的距离与至中心发射器(第7号)距离之差为半波长。
那么,1号接收波与7号接收波相互抵消。
从2号和8号收到的波也是如此。
以此类推,从所有发射器接收到的波强度之和为零。
探测器已经到达了天线辐射强度总和为零的方位角。
如果θ进一步增加,阵列末端发射器的波将不再完全抵消,并且之和会增加。
当探测器到阵列首末两端的距离之差为1.5个波长时,会达到另一个峰值。
3到10发射单元发出的波依然对消,但两头发射器发出的波,1和2以及11和12,相加能够产生一个可观的结果。
探测器的位置位于阵列第一旁瓣的中心。
如果θ进一步增加,发生对消的部分就会增加,并且重复上述过程。
场强与方位角的关系如图所示,可由下列方程表示。
其中E是场强,x与θ成正比。
这被称为sinx/x或sinc函数。
实际上,x=π(L/λ)sinθ。
其中是波长。
所以只有当θ值比较小时,x与θ成正比。
随着θ的增加,逐渐小于θ,导致高阶旁瓣的幅度逐渐减小。
远距离支援干扰下DBF雷达作用距离分析

(o r ) ( , ) 0 , 。 “ 。 p
用权 矢 量 w 对 子 阵 输 出进 行 加 权 ,F )一 ( , W“ ( , 表 示子 阵级 阵 因子 的方 向图 ,F 妒 a O ) ( , )
表示 子 阵 的 方 向 图 ,平 面 相 控 阵 的 方 向 图 为
G ( ) 这时平 面 阵输 出 的信 号 功 率 、 , 。 干扰 功 率
P 一 G ( o ) 。 0,
P 一 G ( k ) 。 O,
P 一 ・L ・L
和噪 声功 率分别 为
( 1) 1
( 2) 1 ( 3) 1
空 间相位差 , 为 Krn ce 积 , “ 和 a ( ) o o ekr a ( ) 分
2 信 号 模 型
设矩 形平 面相 控 阵位于 w y平面 上 , o 由全 向阵 元 组成 。 第 一个 阵元位 于坐 标原 点上 , 向和 Y 设 方
身 , 正结合 实 际战情 , 真 对平 面 相 控 阵 雷达 应 用 子 阵级 DB 技 术 的 研 究 较 少 。 本 文 研 究 子 阵 级 F
s a d o fi t r e e e n D BF a ard t c i a ge i n l z d Si u a i e ulsde onsr t h tDBF t t n — f n e f r nc s o r d e e ton r n s a a y e . m l ton r s t m taeta a s ba r y l v lc n l r l nc e s a a t c in a e,whih i l ult n l z h nt—nt re e c e — u r a e e a a gey i r a e r d rde e to r ng c shepf o a a y e t e a i i e f r n e p r f m a eofDBF a r or nc r da .
一种天线阵方向图综合法

一种天线阵方向图综合法
单秋山;邓维波;赵淑青
【期刊名称】《电子学报》
【年(卷),期】1994(000)009
【摘要】首先把待求阵因子分解为若干组子阵因子的叠加,每个子阵对应一组相位线性递变,幅度按一定规律加权的空间电流谐波,子阵阵因子的空间指向对应一定的空间抽样点。
各空间谐波之和即为阵元和总数励,它对应等求的阵因子,调整空间谐波的个数,相对幅度及空间抽样点位置,即可综合出理想的方向图,综出一个设计实例以说明这种综合方法。
【总页数】1页(P93)
【作者】单秋山;邓维波;赵淑青
【作者单位】不详;不详
【正文语种】中文
【中图分类】TN820.15
【相关文献】
1.一种应用于天线阵方向图综合的改进遗传算法 [J], 杨莘元;杨林
2.一种基于双正交模的新型天线阵方向图综合方法 [J], 张云峰;曹伟
3.一种超宽带相控阵天线阵方向图栅瓣抑制方法 [J], 姜建华;胡梦中
4.一种脉冲天线阵列方向图的快速计算方法 [J], 冯菊;廖成
5.一种新的天线阵方向图综合演化算法 [J], 薄亚明
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第29卷 第12期系统工程与电子技术Vol.29 No.122007年12月Systems Engineering and Electronics Dec.2007文章编号:1001 506X(2007)12 2001 05收稿日期:2007-01-23;修回日期:2007-07-09。
基金项目:航天支撑项目基金资助课题(2003-HG18)作者简介:胡航(1968-),男,博士,硕士生导师,主要研究方向为阵列信号处理技术在相控阵雷达、电子侦察及电子反对抗中的应用。
E mail:h uhang@重叠子阵平面相控阵ADBF 的方向图控制胡 航,李绍滨,邓新红(哈尔滨工业大学电子与信息技术研究院,黑龙江哈尔滨150001)摘 要:提出了二维子阵级ADBF 的信号模型,适用于任意的平面相控阵。
研究了基于失配最优检测器的二维子阵级ADBF,它是对常规二维子阵级ADBF 的一种修正,通过引入一个失配的导向向量,可对方向图进行有效的控制。
该方法在无干扰时可得到所希望的静态方向图,因而解决了ADBF 在自适应与非自适应工作模式之间的转换问题;而在存在干扰的情况下,与常规方法相比,明显改善了旁瓣电平。
基于失配最优检测器的方法对重叠子阵和非重叠子阵均适用,克服了基于归一化的方法只适用于非重叠子阵的局限性。
仿真结果证明了所提出方法的有效性。
关键词:子阵级相控阵;自适应数字波束形成;失配最优检测器;方向图控制;旁瓣抑制中图分类号:T N 957.51;T N 911.7 文献标志码:APattern control for planar phased array ADBF with overlapped subarraysH U H ang ,LI Shao bin,DENG Xin hong(School of E lectronics and I nf ormation T echnology ,H arbin Inst.of Technology,H arbin 150001,China) Abstract:The signal model of 2 D ADBF at subarray level suitable f or any planar phased array is present ed.2 D A DBF at subarray level based on mismat ched opt im um det ector is studied w hich is a modification for conventional 2 D ADBF at subarray level.By introducing a mismat ched st eering vector,this m ethod achieves t he desired qu iescent patt ern in the absence of jamm er,thereby the conversion problem bet w een adaptive and non adaptive w ork modes of A DBF is resolved.On the ot her hand,it im proves th e sidelobe level markedly com pared w ith the conventional m ethod in the presence of jamm er.T he m ethod based on m ism atched opt im um de t ector is su itable for both non overlapped and overlapped subarrays and overcom es t he limitation that t he m ethod based on norm alizat ion processing only su its non overlapped subarrays.Sim ulation results indicate t he validity of t he int roduced m ethod.Keywords:phased array at subarray level;adaptive digit al beamform ing;m ismatched optimum detect or;pattern control;sidelobe suppression0 引 言对自适应数字波束形成(adapt ive digital beamforming,ADBF)的研究进行了30余年,提出了很多有效的方法,但这些方法多是阵元级方法。
ADBF 技术在相控阵雷达中具有重要应用,此时阵列常常包含成百上千个阵元,通常采用子阵结构,为此必须采用子阵级ADBF [1]。
在子阵级AD BF 中,通常阵元级的锥削加权用于抑制和方向图的旁瓣,而子阵级加权用于进行自适应[2]。
国外对子阵级ADBF 进行了一些研究,但大多集中在单一的DBF 技术上,如自适应干扰抑制[3]。
然而在雷达系统中ADBF 不应被看作是一个孤立的部分,当利用其进行干扰抑制时,还应支持其它一些功能。
例如对子阵输出进行最优自适应滤波将破坏所期望的由锥削加权得到的和方向图,并导致旁瓣电平显著增加;在没有干扰(仅存在热噪声)的情况下这种影响尤为严重。
我们希望在不存在干扰时,自适应方向图能够与静态方向图一致,这样可使系统不必在自适应和非自适应工作模式之间进行转换,这就是静态方向图控制问题。
国内外对子阵级ADBF 的静态方向图控制问题研究得很少。
其中文献[2]提出了一种通过对子阵输出进行归一2002系统工程与电子技术第29卷化,以使各子阵噪声功率相同从而进行方向图控制的方案,但只适用于非重叠子阵而不适用于重叠子阵。
文献[4]提出了一种基于失配最优检测器(mismatched opt imum de t ect or,M OD)的自适应方法,适用于重叠子阵;但该文献主要讨论的是方向图控制而不是子阵级ADBF 的问题,并只研究了线阵的情况。
1 信号模型设由M 个全向阵元组成的平面阵位于xoy 平面上,如图1所示。
其中第1个阵元位于坐标原点为参考阵元,第m(m =1, ,M)个阵元的坐标为(x m ,y m )。
在阵元级上通过移相器实现波束指向。
第m 个阵元的幅度加权为g m 。
用( , )表示仰角和方位角,且设波束指向为( 0, 0)。
有K 个远场窄带干扰入射,其中第k(k =1, ,K )个干扰的方向为(k , k )。
阵列共被划分为L 个子阵,子阵间可以是重叠或非重叠的。
图1 平面阵示意图设阵元输出的干扰加噪声为x (t)=[x 1(t), ,x m (t), ,x M (t)]T令( , )=sin cos !( , )=sin sin则有x m (t)=!Kk =1s k(t)exp {-j2∀[x m ( k , k )+y m !( k , k )]/#}+n m (t)(1)式中,s k (t)为第一个阵元接收到的第k 个干扰源的复包络,n m (t)为第m 个阵元中与干扰不相关的高斯加性白噪声,设各阵元的噪声功率均为∃2n 。
子阵转换矩阵可表示为[5-6]T =P 0T 0(2)式中,T 0为M ∀L 的子阵形成矩阵,在其第l(1#l #L )列的所有元素中,只有与第l 个子阵的阵元序号相对应的元素值为1,其余均为0(在非重叠子阵的情况下,T 0的列向量相互正交),而P 0=diag (g m e-j2∀[x m ( 0, 0)+y m !( 0, 0)]/#)m =1, ,M(3)子阵输出的干扰加噪声可表示为x sub (t)=T Hx (t)(4)其协方差矩阵为R sub =T H RT(5)式中R =E [x (t)x (t)H ]2 二维重叠子阵ADBF 的方向图控制方法二维子阵级A DBF 可由一维阵元级LCM V 波束形成方法[7]直接推广到子阵级平面相控阵得到,本文将这种方法称为常规的二维子阵级ADBF,简称为常规方法,它是一种最优波束形成器。
常规方法的自适应权向量为w 2D_CM =%(R sub )-1a sub ( 0, 0)(6)式中,%为一非零常数,而a sub ( 0, 0)=T Ha ( 0, 0)(7)式中a ( 0, 0)=[ 1( 0, 0), , m ( 0, 0), , M ( 0, 0)]T且m ( 0, 0)=exp {-j2∀[x m ( 0, 0)+y m !( 0, 0)]/#} 但是常规方法存在局限性,即与静态方向图相比,其自适应方向图的旁瓣电平大大增加。
因而研究二维子阵级ADBF 的方向图控制方法是十分必要的。
2.1 基于归一化的二维子阵级ADB F 及其局限性基于归一化的二维子阵级ADBF 的原理是,在自适应前对每个子阵进行归一化,以得到相同的噪声功率;而在进行自适应后首先对子阵输出重新进行调整,再与一个静态控制向量相结合以得到无干扰情况下的静态方向图。
下面给出其具体实现过程。
考虑无干扰的情况。
为方便起见设∃2n =1。
此时R(0)=I M ∀M (8)上标(0)表示无干扰的情况。
设阵列由非重叠子阵构成。
定义c l =!m ∃U l(gm)21/2(9)式中,U l 为第l 个子阵所包含的所有阵元的序号的集合。
此时R (0)sub =diag {(c l )2}l=0, ,L-1(10)为对子阵输出进行归一化[4],引入一个归一化矩阵G ,即G =diag (1/c l )l=0, ,L-1(11)利用G 进行归一化处理后,干扰加噪声的协方差矩阵为R sub_Norm =G HR sub G(12)令q 表示各元素均为1的L 维列向量,称其为静态方向控制向量。
基于归一化处理的方法的自适应权向量为w 2D_No rm =G (R sub_Norm )-1G -1q (13)式中,G -1的作用是使天线主瓣方向的增益保持不变。
第12期胡航等:重叠子阵平面相控阵ADBF 的方向图控制2003由于R(0)sub_Norm=I L ∀L (14)因而w (0)2D_Norm =q (15)显然此时各加权系数均为1,因而得到的自适应方向图与静态方向图相同。
但是,上述结论是在非重叠子阵的前提下得到的。
对于重叠子阵,T 0的各个列向量不正交,根据式(2)和(3),T的各个列向量也不正交。
而由式(8)和(5)可得R (0)sub =T H T ,因而R (0)sub 不是对角阵,根据式(12)可知R (0)sub_No rm不是对角阵,因而式(14)不成立,即w (0)2D_Norm %q ,故无法实现方向图控制。
