振动力学期末考试试题和答案

《振动力学》习题集(含答案)

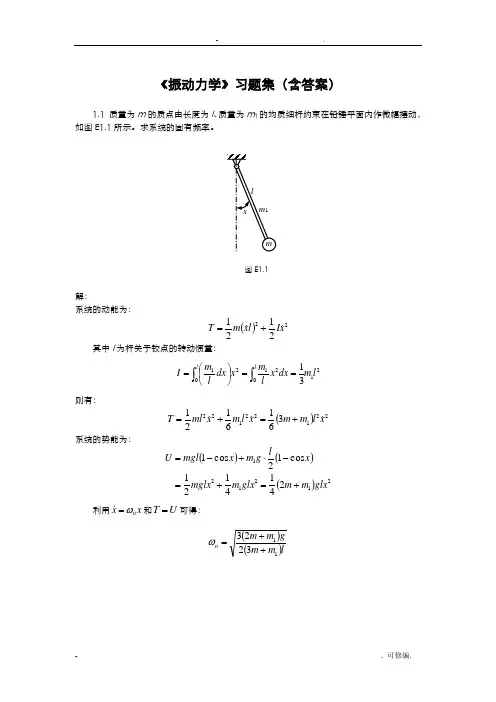
《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集(含答案)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》作业资料(含答案解析)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得：()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得：()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集(含答案)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

振动力学考题集[1]

1、四个振动系统中，自由度为无限大的是（）。

A. 单摆；B. 质量-弹簧；C. 匀质弹性杆；D. 无质量弹性梁；2、两个分别为c1、c2的阻尼原件,并连后其等效阻尼是（）。

A. c1+c2；B. c1c2/(c1+c2)；C. c1-c2；D. c2-c1；3、（）的振动系统存在为0的固有频率。

A. 有未约束自由度；B. 自由度大于0；C. 自由度大于1；D. 自由度无限多；4、多自由度振动系统中，质量矩阵元素的量纲应该是（）。

A. 相同的，且都是质量；B. 相同的，且都是转动惯量；C. 相同的，且都是密度；D. 可以是不同的；5、等幅简谐激励的单自由度弹簧-小阻尼-质量振动系统，激励频率（）固有频率时，稳态位移响应幅值最大。

A. 等于；B. 稍大于；C. 稍小于；D. 为0；6、自由度为n的振动系统，且没有重合的固有频率，其固有频率的数目（A ）。

A. 为n；B. 为1；C. 大于n；D. 小于n；7、无阻尼振动系统两个不同的振型u(r)和u(s)，u(r)T Mu(s)的值一定（）。

A. 大于0；B. 等于0；C. 小于0；D. 不能确定；8、无阻尼振动系统的某振型u(r)，u(r)T Ku(r)的值一定（）。

A. 大于0；B. 等于0；C. 小于0；D. 不能确定；9、如果简谐激励力作用在无约束振动系统的某集中质量上，当激励频率为无限大时，该集中质量的稳态位移响应一定（）。

A. 大于0；B. 等于0；C. 为无穷大；D. 为一常数值；10、相邻固有频率之间的间隔呈近似无限等差数列的振动系统是（）。

A. 杆的纵向振动；B. 弦的横向振动；C. 一般无限多自由度系统；D. 梁的横向振动；11、两个刚度分别为k1、k2串连的弹簧,其等效刚度是（）。

A. k1+k2；B. k1k2/(k1+k2)；C. k 1-k 2；D. k 2-k 1；12、无阻尼振动系统两个不同的振型u (r )和u (s )，u (r )T Ku (s )的值一定（）。

振动力学习题集含答案

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+= 系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集[含答案]

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得：()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得：()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222121212121θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集(附答案解析)

，
代入各单元状态变量的第一元素，即：
得到模态：
，
5.10在图E5.10所示系统中，已知GIpi(i= 1 , 2)，li(i= 1 , 2)和Ji(i= 1 , 2)。用传递矩阵法计算系统的固有频率和模态。
图E5.10
解：
两自由端的边界条件为：，。
其中：，。
由自由端边界条件得频率方程：
，
代入各单元状态变量的第一元素，即：
图 T 2-26答案图 T 2-25
解：
受力如答案图T 2-26。对O点取力矩平衡，有：
4.7 两质量均为m的质点系于具有力F的弦上，如图E4.7所示。忽略振动过程中弦力的变化写出柔度矩阵，建立频率方程。求系统的固有频率和模态，并计算主质量、主刚度、简正模态，确定主坐标和简正坐标。
图E4.7答案图E4.7(1)
（3）
故：
由（3）得：
2.5在图E2.3所示系统中，已知m，c，k，和，且t=0时，，，求系统响应。验证系统响应为对初值的响应和零初值下对激励力响应的叠加。
图E2.3
解：
，
求出C，D后，代入上面第一个方程即可得。
2.7 由一对带偏心质量的等速反向旋转齿轮构成的振动机械安装在弹簧和阻尼器构成的支承上，如图E2.7所示。当齿轮转动角速度为时，偏心质量惯性力在垂直方向大小为。已知偏心重W= 125.5N，偏心距e=15.0cm，支承弹簧总刚度系数k= 967.7N/cm，测得垂直方向共振振幅，远离共振时垂直振幅趋近常值。求支承阻尼器的阻尼比及在运行时机器的垂直振幅。
故频率方程为：
5.1质量m、长l、抗弯刚度EI的均匀悬臂梁基频为3.515(EI/ml3)1/2，在梁自由端放置集中质量m1。用邓克利法计算横向振动的基频。

《振动力学》习题集(含答案)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

振动力学_上海交通大学中国大学mooc课后章节答案期末考试题库2023年

振动力学_上海交通大学中国大学mooc课后章节答案期末考试题库2023年1.对于任意初始激励，二自由度系统的响应都是两个主振型的叠加。

答案:正确2.如图所示的系统中，四个物体的质量均为m，由三根刚度系数均为k的弹簧连接，系统的刚度矩阵为：【图片】答案:3.如图所示两自由度系统，系统的固有频率分别为【图片】和【图片】。

系统的模态矩阵为：【图片】答案:4.如图所示两自由度系统，系统的固有频率分别为【图片】和【图片】，系统的模态矩阵为【图片】，系统存在初始条件【图片】和【图片】。

系统的响应分别为：【图片】答案:5.如图所示柔性悬臂梁，梁两端的物理边界条件为：【图片】答案:左端挠度为零、截面转角为零，右端弯矩为零、剪力为零6.一个无阻尼单自由度弹簧质量系统，在【图片】时间间隔内受到如图所示的突加的矩形脉冲力作用【图片】，已知系统的固有频率为【图片】。

采用杜哈梅积分所求得的系统响应为：【图片】答案:7.如图所示等截面梁，长度为l，弹性模量为E，横截面对中性轴的惯性矩为I，梁材料密度为【图片】。

集中质量为m，卷簧刚度为【图片】，直线弹簧刚度为【图片】。

【图片】为梁x位置的截面在t时刻的振动位移。

写出系统的动能和势能表达式：动能为（），势能为（）。

【图片】答案:_8.只有一个机械系统的全部元件即弹簧、质量块和阻尼都是非线性的，这个系统的振动才是非线性振动答案:错误9.单自由度线性振动系统有可能会有两个及以上的固有频率。

答案:错误10.粘性阻尼系统的运动微分方程是非线性的。

答案:错误11.无阻尼单自由度系统的振幅随时间变化答案:错误12.对于一个单自由度振动系统，假定系统受到简谐外部激励的作用，如下说法正确的是答案:系统的稳态响应是以外部激励的频率为振动频率进行振动的13.叠加原理适用于线性振动系统分析，也适用于非线性振动系统分析。

答案:错误14.如下说法是否正确：柔性悬臂梁的固有频率和模态函数可以通过梁的动力学方程求得。

(完整版)大学物理振动习题含答案

一、选择题：1．3001：把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度θ ，然后由静止放手任其振动，从放手时开始计时。

若用余弦函数表示其运动方程，则该单摆振动的初相为(A) π (B) π/2 (C) 0 (D) θ ［］2．3002：两个质点各自作简谐振动，它们的振幅相同、周期相同。

第一个质点的振动方程为x 1 = A cos(ωt + α)。

当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处。

则第二个质点的振动方程为：(A))π21cos(2++=αωt A x (B) )π21cos(2-+=αωt A x (C))π23cos(2-+=αωt A x (D) )cos(2π++=αωt A x ［］3．3007：一质量为m 的物体挂在劲度系数为k 的轻弹簧下面，振动角频率为ω。

若把此弹簧分割成二等份，将物体m 挂在分割后的一根弹簧上，则振动角频率是(A) 2 ω (B) ω2 (C) 2/ω (D) ω /2 ［］4．3396：一质点作简谐振动。

其运动速度与时间的曲线如图所示。

若质点的振动规律用余弦函数描述，则其初相应为 (A) π/6 (B) 5π/6 (C) -5π/6 (D) -π/6 (E) -2π/3 ［］5．3552：一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2。

将它们拿到月球上去，相应的周期分别为1T '和2T '。

则有(A) 11T T >'且22T T >' (B) 11T T <'且22T T <'(C) 11T T ='且22T T =' (D) 11T T ='且22T T >' ［］ 6．5178：一质点沿x 轴作简谐振动，振动方程为)312cos(1042π+π⨯=-t x (SI)。

2008年振动力学期末考试试题第三题

第三题（20分）
在图示振动系统中，已知：物体的质量m1、m2及弹簧的
刚度系数为k1、k2、k3、k4。

（1）采用影响系数方法建立系统的振动微分方程；（2）若k1= k3=k4= k0，又k2=2 k0，求系统固有频率；（3）取k0 =1，m1=8/9，m2 =1，系统初始位移条件为x1(0)=9和x2(0)=0，初始速度都为零，采用模态叠加法求系统响应。

解：
（1）系统可以简化为二自由度振动系统。

当x1＝1，x2＝0时，有：
k11＝k1+k2+k4，k21＝－k2
当x2＝1，x2＝1时，有：k22＝k2+k3，k12＝－k2。

因此，系统刚度矩阵为：
系统质量矩阵为：
系统动力学方程为：
（2）当，时，运动微分方程用矩阵表示为：
频率方程为：
求得：
（3）当k0=1，m1=8/9，m2 =1时，系统质量阵：
系统刚度阵：
固有频率为：
，
主模态矩阵为：
主质量阵：
主刚度阵：
模态空间初始条件：
，
模态响应：
，
即：
因此有：。

《振动力学》习题集(含答案)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集(含答案解析)

《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T +=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T +=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得： ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得： ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得： ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。

《振动力学》习题集(含标准答案)

《振动力学》习题集(含答案)————————————————————————————————作者：————————————————————————————————日期：《振动力学》习题集（含答案）1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动，如图E1.1所示。

求系统的固有频率。

图E1.1解：系统的动能为：()222121x I l x m T &&+=其中I 为杆关于铰点的转动惯量：2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有：()221221223616121x l m m x l m x ml T &&&+=+=系统的势能为：()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω=&和U T =可得： ()()lm m gm m n 113223++=ωml m 1 x1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动，在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧，如图E1.2所示。

求系统的固有频率。

图E1.2解：如图，令θ为柱体的转角，则系统的动能和势能分别为：22222243212121θθθ&&&mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn =&和U T =可得： ()mkR a R mR a R k n 343422+=+=ωkk A Ca R θ1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ，2k 和3k 的轴约束，如图E1.3所示。

求系统的固有频率。

图E1.3解：系统的动能为：221θ&J T =2k 和3k 相当于串联，则有：332232 , θθθθθk k =+=以上两式联立可得：θθθθ32233232 , k k k k k k +=+=系统的势能为：()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn =&和U T =可得： ()()3232132k k J k k k k k n +++=ωkk 2 kJ1.4 在图E1.4所示的系统中，已知()b a m i k i , ,3,2,1 和=，横杆质量不计。