2017 模拟试题(九)及答案
2017九语一模试卷及答案

2017年中考精英班中考押题卷(A卷)参考答案及评分标准语文题号分值参考答案及评分标准一、(24分)110分本题共5小题,每句错、漏、多一字都扣0.5分。
(1)1分不义而富且贵(2)1分芳草萋萋鹦鹉洲(3)2分青树翠蔓,蒙络摇缀(4)2分年少万兜鍪,坐断东南战未休(5)4分黄梅时节家家雨,青草池塘处处蛙。
有约不来过夜半,闲敲棋子落灯花。
24分(1)攫取(2)谰语(3)转弯抹角(4)顶礼膜拜33分D(妙笔生花,比喻杰出的写作才能,含褒义)43分C(句式杂糅,去掉“来围观”或把“挤满了”改为“有”)54分示例:如果忘记是秋季里残败的荷花,那么铭记就是灿烂的金菊。
如果忘记是冬季里凋零的瘦菊,那么铭记就是傲雪的红梅!二(46分)(一)(10分)63分(1)得到(1分)(2)提出(1分)(3)通“肢”,四肢(1分)(不写通假或者不解释意思均不给分)74分(1)有时遭到他的训斥,表情(脸色)更为恭敬,礼貌更为周到,不敢答复一句话或:有时;叱咄:训斥;色:表情,脸色;至:周到。
其中一个没翻译出来扣0.5分,句子不通顺扣1分)(2)同学舍的求学者都穿着锦绣衣服,戴着有红色帽带、饰有珍宝的帽子,腰间挂着白玉环。
(被:穿着;腰,动词。
其中一个没有翻译出来扣0.5分,句子不通顺扣1分)83分B(嗜学为主观条件,家贫为客观条件,两个对应关系不对)(二)(9分)93分D(A.准备/助词,不译;B.好处/增加;C.信用/通“伸”,伸张;D.军队)103分明恕而行/要之以礼/虽无有质/谁能间之113分①两国信用不是发自内心(1分)②依靠互换人质来获取信任,但没有按照礼义去履行盟约(1分)(只答到交换人质不给分。
)③郑国派军队收割了周地的麦子、稻谷(1分)(三)(10分)123分C(没有对比论证)133分B(强调学习的重要性)144分答案示例:本文认为要想取得某方面的成功,不能只依靠天资优越,而应该勤奋刻苦,肯下笨功夫。
我坚持每天练字摘抄,形成了良好的书写习惯和写作能力,成绩有了很大提升。
2017年高考模拟试卷(9)参考答案

2017年高考模拟试卷(9)参考答案南通市数学学科基地命题一、填空题1. {}2,5.2. 15. 3.-4. 4. 0.5. 5. 26y x =-. 6. 60.7. 30. 线性规划或待定系数法,设甲、乙混货物分别为x ,y 克,由题意3x+4y 1005x+2y 120≥⎧⎨≥⎩,设x+y=34)(52)x y x y λμ+++(,解得,31==λμ,,即可. 8.. 9.. 设CA=x,则PQ=2CPcos<CAP=([3,))x ∈+∞,PQ ≤<. 10. 1e. 易知函数()f x 在(],0-∞上有一个零点,所以由题意得方程ln 0ax x -=在()0+∞,上恰有一解,即ln x a x =在()0+∞,上恰有一解. 令ln ()x g x x =,21ln ()0x g x x -'==,得e x =,当()0,e x ∈时,()g x 单调递增,当()e ,+x ∈∞时,()g x 单调递减,所以()1e e a g ==.11.9.223331212922k x x x x x=+=++≥=,也可以求导. 12. 116-.设弦AB 中点为M ,则()OP BP OM MP BP MP BP ⋅=+⋅=⋅ , 若MP BP ,同向,则0OP BP ⋅> ;若MP BP ,反向,则0OP BP ⋅< , 故OP BP ⋅的最小值在MP BP ,反向时取得,此时1||||2MP BP += ,2||||1||||()216MP BP OP BP MP BP +⋅=-⋅-=- ≥, 当且仅当1||||4MP BP == 时取等号,即OP BP ⋅ 的最小值是116-.13.(方法一)由题意,得sin sin ααββ⎧=⎪⎨=⎪⎩所以αβ,是方程sin x x即方程()πsin 3x -5ππ()26k k αβ+=+∈Z,所以tan()αβ+=(方法二)同上,αβ,sin 0x x -的两根.设()sin f x x x -()cos f x x x '=-.令()0f x '=,得0tan x =,所以02x αβ+=,所以(方法三)直线210x y +-=交单位圆于A B ,两点, 过O 作OH AB ⊥,垂足为H ,易知OH =因为OC 60COH ∠=︒,即1502αβ+=︒,所以tan()tan300αβ+=︒=14.9⎧-⎨⎩⎭.32()322x x a x f x x a x a x ⎧--⎪=⎨⎪--+-<⎩,≥,,,当x a ≥时,320x x --=,得11x =-,23x =,结合图形知,① 当1a <-时,313x -,,成等差数列,则35x =-,代入3220x a --+-=得,9a =-; ② 当13a -≤≤时,方程3220x a x--+-=,即22(1)30x a x +-+=的根为34x x ,, 则343x x =,且3432x x +=,解得4x ,又342(1)x x a +=-,所以a .③ 当3a >时,显然不符合. 所以a 的取值集合95⎧-⎨⎩⎭. 二、解答题:本大题共6小题,共90分.15. (1)因为tan α=2,所以sin αcos α=2,即sin α=2cos α.又sin 2α+cos 2α=1,所以5cos 2α=1,即cos 2α=15. 所以 cos2α=2cos 2α-1=-35.(2)由α∈(0,π),且tan α=2>1,得α∈(π4,π2),所以2α∈(π2,π). 由题知cos2α=-35,所以sin2α=45.又因为β∈(0,π),cos β=-7210∈(-1,0),所以β∈(π2,π), 所以sin β=210,且2α-β∈(-π2,π2).因为sin(2α-β)=sin2αcos β-cos2αsin β=45×(-7210)-(-35)×210=-22, 所以2α-β=-π4.16.(1)因为BD 垂直平分AC ,所以BA BC =,在△ABC 中,因为120ABC ∠=︒, 所以30BAC ∠=︒.因为△ACD 是正三角形,所以60DAC ∠=︒, 所以90BAD ∠=︒,即AD AB ⊥.因为=1AB ,120ABC ∠=︒,所以AD AC == 又因为1PA =,2PD =,由222PA AD PD +=, 知90PAD ∠=︒,即AD AP ⊥.因为AB AP ⊂,平面PAB ,AB AP A = , 所以AD ⊥平面PAB .(2)(方法一)取AD 的中点H ,连结CH ,NH . 因为N 为PD 的中点,所以HN ∥PA , 因为PA ⊂平面PAB ,HN ⊄平面PAB , 所以HN ∥平面PAB .由△ACD 是正三角形,H 为AD 的中点,所以CH AD ⊥.由(1)知,BA AD ⊥,所以CH ∥BA , 因为BA ⊂平面PAB ,CH ⊄平面PAB ,HPA BCDMN所以CH ∥平面PAB .因为CH HN ⊂,平面CNH ,CH HN H = , 所以平面CNH ∥平面PAB . 因为CN ⊂平面CNH , 所以CN ∥平面PAB .(方法二)取PA 的中点S ,过C 作CT ∥AD 交AB 的延长线于T ,连结ST ,SN .因为N 为PD 的中点,所以SN ∥AD ,且12SN AD =,因为CT ∥AD ,所以CT ∥SN . 由(1)知,AB AD ⊥,所以CT AT ⊥, 在直角△ CBT 中,1BC =,60CBT ∠=︒,得CT =由(1)知,AD =12CT AD =,所以CT SN =.所以四边形SNCT 是平行四边形, 所以CN ∥TS .因为TS ⊂平面PAB ,CN ⊄平面PAB , 所以CN ∥平面PAB .17.(1)由题意知,124()2b b =-=,解得a =1b =,所以椭圆的方程为2212x y +=. (2)① 由(2)N t ,,(01)A ,,(01)B -,,则 直线NA 的方程为11y x t =+,直线NB 的方程为31y x t=-.P A BCDMNTS由221122y x t x y ⎧=+⎪⎨⎪+=⎩,得,222422.2t x t t y t ⎧=-⎪+⎨-⎪=+⎩,,故()2224222t t t t P --++,. 由223122y x t x y ⎧=-⎪⎨⎪+=⎩,得,222121818.18t x t t y t ⎧=⎪+⎨-⎪=+⎩,,故()22212181818t t t t Q -++,. 所以直线PM 的斜率222221262482PMt t t k t t t ---+==-+, 直线QM 的斜率22218161812818QMt t t k t t t ---+==+, 所以PM QM k k =,故P M Q ,,三点共线.② 由①知,11k t =,213k t =,2368t k t-=. 所以21323122463182t k k k k k k t t t-+-=⨯-=-, 所以132312k k k k k k +-为定值1-.18.(1)设OP =r ,则l =r ·2θ,即r =l2θ,所以S 1=12lr =l 24θ,θ∈(0,π2).(2)设OC =a ,OD =b .由余弦定理,得l 2=a 2+b 2-2ab cos2θ,所以 l 2≥2ab -2ab cos2θ.所以 ab ≤l 22(1-cos2θ),当且仅当a =b 时“=”成立.所以S △OCD =12ab sin2θ≤l 2sin2θ4(1-cos2θ)=l 24tan θ,即S 2=l 24tan θ.(3)1S 2-1S 1=4l 2(tan θ-θ),θ∈(0,π2),. 令f (θ)=tan θ-θ,则f '(θ)=(sin θcos θ)'-1=sin 2θcos 2θ.当θ∈[0,π2)时,f '(θ)>0,所以f (θ)在区间[0,π2)上单调增.所以,当θ∈(0,π2)时,总有f (θ)>f (0)=0,即1S 2-1S 1>0,即S 1>S 2.答:为使养殖区面积最大,应选择方案一. 19. (1)易得2143a =.(2)由111241n n n a a S +-=-,得11241n nn n n a a a a S ++-=-,所以11241n n n n na a S a a ++-=-①.所以12121241n n n n n a a S a a +++++-=-②,由②-①,得12112112n n n n n n n n na a a aa a a a a +++++++=---.因为10n a +≠,所以22112n nn n n na a ++++=-. 所以121112n n n n n n a a a a a a +++++-=--,即12111n nn n n na a a a a a ++++-=--,即11n n b b +-=,所以数列{}n b 是公差为1的等差数列. 因为112134a b a a ==-,所以数列{}n b 的通项公式为14n b n =-.(3)由(2)知,114n n n a n a a +=--,所以11431141n n an a n n ++=+=--,所以14(1)141n n a a n n +=+--,所以数列41n a n ⎧⎫⎨⎬-⎩⎭是常数列.由124113a =⨯-,所以2(41)3n a n =-.(方法一)由m p r a a a ,,(m p r <<)成等比数列,则41m -,41p -,41r -成等比数列,所以2(41)(41)(41)p m r -=--, 所以2168164()0p p mr m r --++=,即2424()0p p mr m r --++=(*). (途径一)(*)式即为2424()4p p mr m r mr -=-+<-,所以2211(2))22p -<,即11222p -<,所以p <2p mr <.(途径二)(*)式即为24241p p rm r -+=-.由222222(42)(42)(41)()0414141p p r p p r r r p p r mr p r p r r r -+-+----=⋅-==>---,所以2p mr <.(方法二)由m p r a a a ,,(m p r <<)成等比数列, 则41m -,41p -,41r -成等比数列, 记4m α=,4p β=,4r γ=(1αβγ<<<), 则有1α-,1β-,1γ-成等比数列,所以2(1)(1)(1)βαγ-=--,即22()ββαγαγ-=-+.若2βαγ=,即2p mr =时,则2αγβ+=,所以αβγ==,矛盾; 若2βαγ>,则22()0βαγβαγ-+=->,所以1()12βαγ>+>,所以[][]2221(2)()()()()()0αγββαγαγαγαγαγαγ+---+>-+--+=->, 矛盾.所以2βαγ<,即2p mr <.20. (1) 由题意知曲线()y f x =过点(1,0),且'(1)e f =;又因为222'()ln e x a f x a x b x x+=-++⎛⎫ ⎪⎝⎭,则有(1)e(2)0,'(1)e()e,f b f a b =+==+=⎧⎨⎩解得3,2a b ==-.(2) ①当2a =-时,函数()y f x =的导函数22'()e 2ln 0x f x x b x=--+=⎛⎫ ⎪⎝⎭,若'()0f x =时,得222ln b x x =+, 设22()2ln g x x x =+(0)x > .由2332424'()x g x x x x-=-=0=,得x =1ln 2g =+.当0x <<'()0g x <,函数()y g x =在区间上为减函数,()(1ln 2,)g x ∈++∞;仅当1ln 2b >+时,()b g x =有两个不同的解,设为1x ,2x 12()x x <.此时,函数()y f x =既有极大值,又有极小值.②由题意2e ln x a x b xkx ++⎛⎫≥ ⎪⎝⎭对一切正实数x 恒成立,取1x =得(2)e k b ≤+.下证2e ln e (2)x a x b xb x ++⎛⎫≥+ ⎪⎝⎭对一切正实数x 恒成立.首先,证明e e xx ≥. 设函数()e e xu x x =-,则'()e e xu x =-,当1x >时,'()0u x >; 当1x <时,'()0u x <;得e e (1)0xx u -=≥,即e e xx ≥,当且仅当都在1x =处取到等号.再证1ln 1x x+≥. 设1()ln 1v x x x=+-,则21'()x v x x -=,当1x >时,'()0v x >;当1x <时,'()0v x <;得()(1)0v x v =≥,即1ln 1x x+≥,当且仅当都在1x =处取到等号. 由上可得2e ln (2)e x a x b xb x ++⎛⎫≥+ ⎪⎝⎭,所以min()(2)e f x b x ⎛⎫=+⎪⎝⎭, 即实数k 的最大值为(2)e b +.数学Ⅱ(附加题)21. A. 连结PQ ,因为四边形ACQP 是1O 的内接四边形, 所以A PQD ∠=∠, 又在2O 中,PBD PQD ∠=∠,所以A PBD ∠=∠, 所以AC ∥BD .B .(1) 设1234A ⎛⎫= ⎪⎝⎭,则12234A ==-, 1213122A --⎛⎫ ⎪∴= ⎪-⎝⎭, 21582131461122M -⎛⎫⎛⎫⎛⎫ ⎪∴== ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭. (2)11112x x x x x M M y y y y y -'''-⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=∴== ⎪ ⎪ ⎪ ⎪ ⎪⎪'''-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ ,即,2,x x y y x y ''=-⎧⎨''=-+⎩ 代入22221x xy y ++=可得 ()()()()2222221x y x y x y x y ''''''''-+--++-+=,即22451x x y y ''''-+=,故曲线C '的方程为22451x xy y -+=.C. (1)曲线1C :22(1)2x y ++=,极坐标方程为22cos 10ρθ+-= 曲线2C 的直角坐标方程为1y x =-; (2) 曲线1C 与曲线2C 的公共点的坐标为(0,1)-,极坐标为3(1,)2π. D. 因为0x >,0y >,0z >,所以1233x y z++,2463y x z++, 所以1239()()2462yx z x y z ++++≥.当且仅当::1:2:3x y z =时,等号成立.22.(1)从7个顶点中随机选取3个点构成三角形,共有37=35C种取法.其中X ABF ,这类三角形共有6个.因此(376635P X C ===. (2)由题意,X2,其中X ABF ,这类三角形共有6个;其中2X =的三角形有两类,如△PAD (3个),△PAB (6个),共有9个;其中X PBD ,这类三角形共有6个;其中X =CDF ,这类三角形共有12个;其中X =BDF ,这类三角形共有2个.因此(635P X =,()9235P X ==,(635P X =,(1235P X ==,(235P X ==. 所以随机变量X 的概率分布列为:所求数学期望()E X 69612223535353535+⨯++. 23. (1)①当n =2时,a 2=2,不等式成立.②假设当n =k (k ≥2)时不等式成立,即a k ≥2,则当n =k +1时,a k +1=(1+1k (k +1))a k +12k >2.所以,当n =k +1时,不等式也成立. 根据①,②可知,对所有n ≥2,a n ≥2成立.(2)当n ≥2时,由递推公式及(1)的结论有a n +1=(1+1n 2+n )a n +12n ≤(1+1n 2+n +12n +1)a n (n ≥2).两边取对数,并利用已知不等式ln(1+x )<x ,得 ln a n +1≤ln(1+1n 2+n +12n +1)+ln a n <ln a n +1n 2+n +12n +1,第 11页,共 11页 故 ln a n +1-ln a n <1n 2+n +12n +1(n ≥2), 求和可得ln a n -ln a 2<12⨯3+1 3⨯4+…+1 (n -1)n+123+124+…+12n =(12-13)+(13-14)+…+(1n -1-1n )+123·1-12n -21-12=12-1n +122-12n <34. 由(1)知,a 2=2,故有ln a n 2<34,即a n <2e 34(n ≥2),而a 1=1<2e 34,所以对任意正整数n ,有a n <2e 34.。
江西省2017年普通高等学校招生全国统一考试仿真卷理科综合能力测试(九)化学试题含解析

2017年普通高等学校招生全国统一考试仿真卷理科综合能力测试(九)化学试题第Ⅰ卷一、选择题:本大题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
7。
化学源于生活,又高于生活.下列说法正确的是( )A.石油裂化、石油分馏、石油裂解、石油的催化重整都是化学变化B.分子式为C3H4Cl2的有机物中,与乙烯含有相同官能团的共有5种C.高纯度的晶体硅可以制备晶体管等半导体、电脑芯片和光导纤维D.酒精、NaCl溶液、CuSO4溶液、浓HNO3都可使蛋白质发生变性【解析】石油分馏是物理变化,A项错误;该有机物含有碳碳双键,可能的同分异构体为:,B项正确;制备光导纤维的不是晶体硅,而是SiO2,C项错误;NaCl属于无机轻金属盐,不会导致蛋白质变性,而是盐析,D项错误。
【答案】B8。
用N A表示阿伏加德罗常数的值,下列叙述正确的是( )A。
标准状况下,22。
4L SO3含有N A个分子B。
6。
4g氧气和3.2g臭氧(O3)混合气体所含有的氧原子数为0。
6N AC.过氧化钠与CO2反应时,0.1mol过氧化钠转移的电子数为0。
2N AD.标准状况下,2。
24L Cl2与过量的稀FeCl2溶液反应,转移电子总数为0。
1N A【解析】标准状况下,SO3是固体,所以标准状况下,22.4L SO3含有的分子数大于N A个,故A错。
氧气和臭氧都是由氧原子构成的,因此在该题中的氧原子的物质的量为氧气和臭氧的总质量除以氧原子的摩尔质量,为0.6mol,故B正确.过氧化钠与CO2反应时,1mol过氧化钠反应转移1mol电子,所以0.1mol过氧化钠转移的电子数为0。
1N A,故C错.标准状况下,2。
24L Cl2为0.1mol,氯气与足量的氯化亚铁反应时,氯气全部反应,氯气中氯元素的化合价从0价降为—1价,所以标准状况下,2。
24 L Cl2与过量的稀FeCl2溶液反应,转移电子总数为0.2N A,故D错.【答案】B9.有机物A的分子式为CmHn02,其中氧的质量分数约为18。
2017年高考模拟试卷(9)参考答案

2017年高考模拟试卷(9)参考答案南通市数学学科基地命题一、填空题1. {}2,5.2. 15. 3.-4. 4. 0.5. 5. 26y x =-. 6. 60.7. 30. 线性规划或待定系数法,设甲、乙混货物分别为x ,y 克,由题意3x+4y 1005x+2y 120≥⎧⎨≥⎩,设x+y=34)(52)x y x y λμ+++(,解得,31==1414λμ,,即可. 8.. 9.. 设CA=x,则PQ=2CPcos<CAP=([3,))x ∈+∞,PQ ≤<. 10. 1e. 易知函数()f x 在(],0-∞上有一个零点,所以由题意得方程ln 0ax x -=在()0+∞,上恰有一解,即ln x a x =在()0+∞,上恰有一解. 令ln ()x g x x =,21ln ()0x g x x -'==,得e x =,当()0,e x ∈时,()g x 单调递增,当()e ,+x ∈∞时,()g x 单调递减,所以()1e e a g ==.11.9.223331212922k x x x x x=+=++≥=,也可以求导. 12. 1-.设弦AB 中点为M ,则()OP BP OM MP BP MP BP ⋅=+⋅=⋅,若MP BP ,同向,则0OP BP ⋅>;若MP BP ,反向,则0OP BP ⋅<, 故OP BP ⋅的最小值在MP BP ,反向时取得, 此时1||||2MP BP +=,2||||1||||()216MP BP OP BP MP BP +⋅=-⋅-=-≥, 当且仅当1||||4MP BP ==时取等号,即OP BP ⋅的最小值是116-.13.(方法一)由题意,得sin sin ααββ⎧=⎪⎨=⎪⎩所以αβ,是方程sin x x即方程()πsin 3x -5ππ()26k k αβ+=+∈Z,所以tan()αβ+=(方法二)同上,αβ,sin 0x x -的两根.设()sin f x x x -()cos f x x x '=-.令()0f x '=,得0tan x =,所以02x αβ+=,所以(方法三)直线210x y +-=交单位圆于A B ,两点, 过O 作OH AB ⊥,垂足为H ,易知OH =因为OC 60COH ∠=︒,即1502αβ+=︒,所以tan()tan300αβ+=︒=14.9⎧-⎨⎩⎭.32()322x x a x f x x a x a x ⎧--⎪=⎨⎪--+-<⎩,≥,,,当x a ≥时,320x x --=,得11x =-,23x =,结合图形知,① 当1a <-时,313x -,,成等差数列,则35x =-,代入3220x a --+-=得,9a =-; ② 当13a -≤≤时,方程3220x a x--+-=,即22(1)30x a x +-+=的根为34x x ,, 则343x x =,且3432x x +=,解得4x ,又342(1)x x a +=-,所以a .③ 当3a >时,显然不符合. 所以a 的取值集合95⎧-⎨⎩⎭. 二、解答题:本大题共6小题,共90分.15. (1)因为tan α=2,所以sin αcos α=2,即sin α=2cos α.又sin 2α+cos 2α=1,所以5cos 2α=1,即cos 2α=15. 所以 cos2α=2cos 2α-1=-35.(2)由α∈(0,π),且tan α=2>1,得α∈(π4,π2),所以2α∈(π2,π). 由题知cos2α=-35,所以sin2α=45.又因为β∈(0,π),cos β=-7210∈(-1,0),所以β∈(π2,π), 所以sin β=210,且2α-β∈(-π2,π2).因为sin(2α-β)=sin2αcos β-cos2αsin β=45×(-7210)-(-35)×210=-22, 所以2α-β=-π4.16.(1)因为BD 垂直平分AC ,所以BA BC =,在△ABC 中,因为120ABC ∠=︒, 所以30BAC ∠=︒.因为△ACD 是正三角形,所以60DAC ∠=︒, 所以90BAD ∠=︒,即AD AB ⊥.因为=1AB ,120ABC ∠=︒,所以AD AC == 又因为1PA =,2PD =,由222PA AD PD +=, 知90PAD ∠=︒,即AD AP ⊥. 因为AB AP ⊂,平面PAB ,AB AP A =,所以AD ⊥平面PAB .(2)(方法一)取AD 的中点H ,连结CH ,NH . 因为N 为PD 的中点,所以HN ∥PA , 因为PA ⊂平面PAB ,HN ⊄平面PAB , 所以HN ∥平面PAB .由△ACD 是正三角形,H 为AD 的中点,所以CH AD ⊥.由(1)知,BA AD ⊥,所以CH ∥BA , 因为BA ⊂平面PAB ,CH ⊄平面PAB ,HPA BCDMN所以CH ∥平面PAB . 因为CH HN ⊂,平面CNH ,CH HN H =,所以平面CNH ∥平面PAB . 因为CN ⊂平面CNH , 所以CN ∥平面PAB .(方法二)取PA 的中点S ,过C 作CT ∥AD 交AB 的延长线于T ,连结ST ,SN .因为N 为PD 的中点,所以SN ∥AD ,且12SN AD =,因为CT ∥AD ,所以CT ∥SN . 由(1)知,AB AD ⊥,所以CT AT ⊥, 在直角△ CBT 中,1BC =,60CBT ∠=︒,得CT =由(1)知,AD =12CT AD =,所以CT SN =.所以四边形SNCT 是平行四边形, 所以CN ∥TS .因为TS ⊂平面PAB ,CN ⊄平面PAB , 所以CN ∥平面PAB .17.(1)由题意知,124()2b b =-=,解得a =1b =,所以椭圆的方程为2212x y +=. (2)① 由(2)N t ,,(01)A ,,(01)B -,,则 直线NA 的方程为11y x t =+,直线NB 的方程为31y x t=-.P A BCDMNTS由221122y x t x y ⎧=+⎪⎨⎪+=⎩,得,222422.2t x t t y t ⎧=-⎪+⎨-⎪=+⎩,,故()2224222t t t t P --++,. 由223122y x t x y ⎧=-⎪⎨⎪+=⎩,得,222121818.18t x t t y t ⎧=⎪+⎨-⎪=+⎩,,故()22212181818t t t t Q -++,. 所以直线PM 的斜率2222162482PMt t t k t t t ---+==-+, 直线QM 的斜率222181261812818QMt t t k t t t ---+==+, 所以PM QM k k =,故P M Q ,,三点共线.② 由①知,11k t =,213k t =,2368t k t-=.所以21323122463182t k k k k k k t t t-+-=⨯-=-, 所以132312k k k k k k +-为定值12-.18.(1)设OP =r ,则l =r ·2θ,即r =l2θ,所以S 1=12lr =l 24θ,θ∈(0,π2).(2)设OC =a ,OD =b .由余弦定理,得l 2=a 2+b 2-2ab cos2θ,所以 l 2≥2ab -2ab cos2θ.所以 ab ≤l 22(1-cos2θ),当且仅当a =b 时“=”成立.所以S △OCD =12ab sin2θ≤l 2sin2θ4(1-cos2θ)=l 24tan θ,即S 2=l 24tan θ.(3)1S 2-1S 1=4l 2(tan θ-θ),θ∈(0,π2),. 令f (θ)=tan θ-θ,则f '(θ)=(sin θcos θ)'-1=sin 2θcos 2θ.当θ∈[0,π2)时,f '(θ)>0,所以f (θ)在区间[0,π2)上单调增.所以,当θ∈(0,π2)时,总有f (θ)>f (0)=0,即1S 2-1S 1>0,即S 1>S 2.答:为使养殖区面积最大,应选择方案一.19. (1)易得2143a =.(2)由111241n n n a a S +-=-,得11241n nn n n a a a a S ++-=-,所以11241n n n n na a S a a ++-=-①.所以12121241n n n n n a a S +++++-=②,由②-①,得12112112n n n n n n n n na a a aa a a a a +++++++=---.因为10n a +≠,所以22112n nn n n na a a a a a ++++=---. 所以121112n n n n n n a a a a a a +++++-=--,即12111n nn n n na a a a a a ++++-=--,即11n n b b +-=,所以数列{}n b 是公差为1的等差数列. 因为11213a b ==,所以数列{}n b 的通项公式为14n b n =-.(3)由(2)知,114n n n a n a a +=--,所以114311414n n an a n n ++=+=--,所以1n n a a +=,所以数列41n a n ⎧⎫⎨⎬-⎩⎭是常数列.由12a =,所以2(41)3n a n =-.(方法一)由m p r a a a ,,(m p r <<)成等比数列,则41m -,41p -,41r -成等比数列,所以2(41)(41)(41)p m r -=--, 所以2168164()0p p mr m r --++=,即2424()0p p mr m r --++=(*). (途径一)(*)式即为2424()4p p mr m r mr -=-+<-,所以2211(2))22p -<,即11222p -<,所以p <2p mr <.(途径二)(*)式即为24241p p rm r -+=-.由222222(42)(42)(41)()0414141p p r p p r r r p p r mr p r p r r r -+-+----=⋅-==>---,所以2p mr <.(方法二)由m p r a a a ,,(m p r <<)成等比数列, 则41m -,41p -,41r -成等比数列, 记4m α=,4p β=,4r γ=(1αβγ<<<), 则有1α-,1β-,1γ-成等比数列,所以2(1)(1)(1)βαγ-=--,即22()ββαγαγ-=-+.若2βαγ=,即2p mr =时,则2αγβ+=,所以αβγ==,矛盾; 若2βαγ>,则22()0βαγβαγ-+=->,所以1()12βαγ>+>,所以[][]2221(2)()()()()()024αγββαγαγαγαγαγαγ+---+>-+--+=->, 矛盾.所以2βαγ<,即2p mr <.20. (1) 由题意知曲线()y f x =过点(1,0),且'(1)e f =;又因为222'()ln e x a f x a x b xx+=-++⎛⎫ ⎪⎝⎭,则有(1)e(2)0,'(1)e()e,f b f a b =+==+=⎧⎨⎩解得3,2a b ==-.(2) ①当2a =-时,函数()y f x =的导函数22'()e 2ln 0x f x x b x =--+=⎛⎫ ⎪⎝⎭,若'()0f x =时,得222ln b x x =+, 设22()2ln g x x x =+(0)x > .由2332424'()x g x x x x-=-=0=,得x =1ln 2g =+.当0x <<'()0g x <,函数()y g x =在区间上为减函数,()(1ln 2,)g x ∈++∞;仅当1ln 2b >+时,()b g x =有两个不同的解,设为1x ,2x 12()x x <.此时,函数()y f x =既有极大值,又有极小值.②由题意2e ln x a x b xkx ++⎛⎫≥ ⎪⎝⎭对一切正实数x 恒成立,取1x =得(2)e k b ≤+.下证2e ln e (2)x a x b xb x ++⎛⎫≥+ ⎪⎝⎭对一切正实数x 恒成立.首先,证明e e xx ≥. 设函数()e e xu x x =-,则'()e e xu x =-,当1x >时,'()0u x >; 当1x <时,'()0u x <;得e e (1)0xx u -=≥,即e e xx ≥,当且仅当都在1x =处取到等号.再证1ln 1x x+≥. 设1()ln 1v x x x=+-,则21'()x v x x -=,当1x >时,'()0v x >;当1x <时,'()0v x <;得()(1)0v x v =≥,即1ln 1x x+≥,当且仅当都在1x =处取到等号. 由上可得2e ln (2)e x a x b xb x ++⎛⎫≥+ ⎪⎝⎭,所以min()(2)e f x b x ⎛⎫=+⎪⎝⎭, 即实数k 的最大值为(2)e b +.数学Ⅱ(附加题)21. A. 连结PQ ,因为四边形ACQP 是1O 的内接四边形, 所以A PQD ∠=∠, 又在2O 中,PBD PQD ∠=∠,所以A PBD ∠=∠, 所以AC ∥BD .B .(1) 设1234A ⎛⎫= ⎪⎝⎭,则12234A ==-, 1213122A --⎛⎫⎪∴= ⎪-⎝⎭, 21582131461122M -⎛⎫⎛⎫⎛⎫ ⎪∴== ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭. (2)11112x x x x x M M y y y y y -'''-⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=∴== ⎪ ⎪ ⎪ ⎪ ⎪⎪'''-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,即,2,x x y y x y ''=-⎧⎨''=-+⎩ 代入22221x xy y ++=可得()()()()2222221x y x y x y x y ''''''''-+--++-+=,即22451x x y y ''''-+=,故曲线C '的方程为22451x xy y -+=.C. (1)曲线1C :22(1)2x y ++=,极坐标方程为22cos 10ρθ+-= 曲线2C 的直角坐标方程为1y x =-; (2) 曲线1C 与曲线2C 的公共点的坐标为(0,1)-,极坐标为3(1,)2π. D. 因为0x >,0y >,0z >,所以1233++,246y x z++, 所以1239()()2462yx z x y z ++++≥.当且仅当::1:2:3x y z =时,等号成立.22.(1)从7个顶点中随机选取3个点构成三角形,共有37=35C种取法.其中X ABF ,这类三角形共有6个.因此(376635P X C ===. (2)由题意,X2,其中X ABF ,这类三角形共有6个;其中2X =的三角形有两类,如△PAD (3个),△PAB (6个),共有9个;其中X PBD ,这类三角形共有6个;其中X =CDF ,这类三角形共有12个;其中X =BDF ,这类三角形共有2个.因此(635P X =,()9235P X ==,(635P X =,(1235P X ==,(235P X ==. 所以随机变量X 的概率分布列为:所求数学期望()E X 69612223535353535+⨯++. 23. (1)①当n =2时,a 2=2,不等式成立.②假设当n =k (k ≥2)时不等式成立,即a k ≥2,则当n =k +1时,a k +1=(1+1k (k +1))a k +12k >2.所以,当n =k +1时,不等式也成立. 根据①,②可知,对所有n ≥2,a n ≥2成立.(2)当n ≥2时,由递推公式及(1)的结论有a n +1=(1+1n 2+n )a n +12n ≤(1+1n 2+n +12n +1)a n (n ≥2).两边取对数,并利用已知不等式ln(1+x )<x ,得 ln a n +1≤ln(1+1n 2+n +12n +1)+ln a n <ln a n +1n 2+n +12n +1,故 ln a n +1-ln a n <1n 2+n +12n +1(n ≥2), 求和可得ln a n -ln a 2<12⨯3+1 3⨯4+…+1 (n -1)n+123+124+…+12n =(12-13)+(13-14)+…+(1n -1-1n )+123·1-12n -21-12=12-1n +122-12n <34. 由(1)知,a 2=2,故有ln a n 2<34,即a n <2e 34(n ≥2),而a 1=1<2e 34,所以对任意正整数n ,有a n <2e 34.。
2017年高考模拟试卷(9)
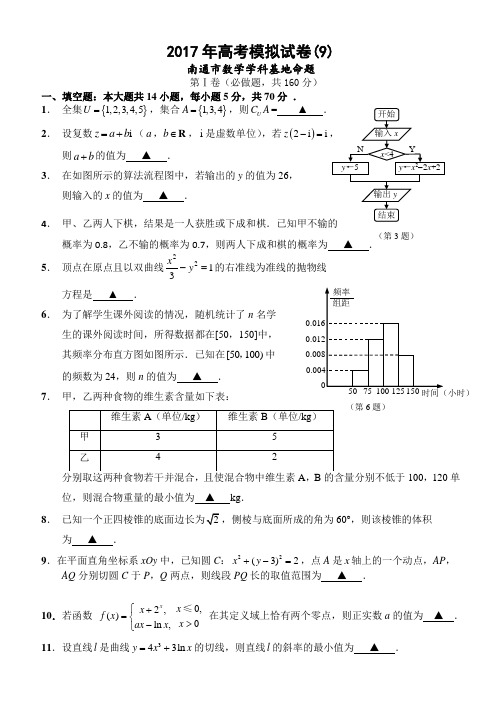
(第3题)(第6题)2017年高考模拟试卷(9)南通市数学学科基地命题第Ⅰ卷(必做题,共160分)一、填空题:本大题共14小题,每小题5分,共70分 .1. 全集{}1,2,3,4,5U =,集合{}1,3,4A =,则U C A = ▲ .2. 设复数i z a b =+(a b ∈,R ,i 是虚数单位),若()2i i z -=则a b +的值为 ▲ .3. 在如图所示的算法流程图中,若输出的y 的值为26,则输入的x 的值为 ▲ .4. 概率为0.8,乙不输的概率为0.7,则两人下成和棋的概率为 ▲ .5. 顶点在原点且以双曲线1322=-y x 的右准线为准线的抛物线 方程是 ▲ .6. 为了解学生课外阅读的情况,随机统计了n 名学生的课外阅读时间,所得数据都在[50,150]中, 其频率分布直方图如图所示.已知在[50 100),中 的频数为24,则n 的值为 ▲. 7. 甲,乙两种食物的维生素含量如下表:100,120单位,则混合物重量的最小值为 ▲ kg .8. 60°,则该棱锥的体积为 ▲ .9.在平面直角坐标系xOy 中,已知圆C :22(3)2x y +-=,点A 是x 轴上的一个动点,AP ,AQ 分别切圆C 于P ,Q 两点,则线段PQ 长的取值范围为 ▲ . 10.若函数 0,2,()0ln ,≤x x x f x x ax x ⎧+=⎨>-⎩在其定义域上恰有两个零点,则正实数a 的值为 ▲ .12.扇形AOB 中,弦1AB =,C 为劣弧AB 上的动点,AB 与OC 交于点P ,则OP BP ⋅的最小值是 ▲ .13.在平面直角坐标系xOy 中,已知(cos sin )A αα,,(cos sin )B ββ,是直线y =上的两点,则tan()αβ+的值为 ▲ .14.已知函数3()2f x x a a =--+-有且仅有三个零点,且它们成等差数列,则实数a 的取值集合为 ▲ .二、解答题:本大题共6小题,共90分. 15.(本小题满分14分)已知tan α=2,cos β=- 7210,且α,β∈(0,π), (1)求cos2α的值; (2)求2α-β的值. 16.(本小题满分14分)如图,在四棱锥P ABCD -中,△ACD 是正三角形,BD 垂直平分AC ,垂足为M ,ABC ∠=120° ,=1PA AB =,2PD =,N 为PD 的中点.(1)求证:AD ⊥平面PAB ; (2)求证:CN ∥平面PAB .17. (本小题满分14分)在平面直角坐标系xOy 中,已知A B ,分别是椭圆22221(0)yx a b a b+=>>的上、下顶点,点()102M ,为线段AO的中点,AB =.(1)求椭圆的方程;(2)设(2)N t ,(0t ≠),直线NA ,NB 分别交椭圆于点P Q ,,直线NA ,NB ,PQ 的斜率分别为1k ,2k ,3k . ① 求证:P M Q ,,三点共线; D(第16题)PAPBPCM N18.(本小题满分16分)如图,一个角形海湾AOB ,∠AOB =2θ(常数θ为锐角).拟用长度为l (l 为常数)的围网围成一个养殖区,有以下两种方案可供选择: 方案一:如图1,围成扇形养殖区OPQ ,其中⌒PQ =l ; 方案二:如图2,围成三角形养殖区OCD ,其中CD =l ;(1)求方案一中养殖区的面积S 1 ;(2)求证:方案二中养殖区的最大面积S 2=l 24tan θ;(3)为使养殖区的面积最大,应选择何种方案?并说明理由.19.(本小题满分16分)已知数列{}n a 的首项为2,前n 项的和为n S ,且111241n n n a a S +-=-(*n ∈N ).(1)求2a 的值; (2)设1nn n na b a a +=-,求数列{}n b 的通项公式;(3)若m p r a a a ,,(*m p r ∈,,N ,m p r <<,)成等比数列,试比较2p 与mr 的大小,并证明.20.(本小题满分16分)已知函数2()ln )xf x e a x b x=++(,其中,a b R ∈. 2.71828e =是自然对数的底数. (1)若曲线()y f x =在1x =处的切线方程为(1)y e x =-.求实数,a b 的值;(2)① 若2a =-时,函数()y f x =既有极大值,又有极小值,求实数b 的取值范围; ② 若2a =,2b ≥-.若()f x kx ≥对一切正实数x 恒成立,求实数k 的最大值llAOBAOB图1Q PAOBC D 图2(第18题)2θ2θ2θ1O2O ABPQDC第II 卷(附加题,共40分)21.【选做题】本题包括A, B,C,D 四小题,每小题10分,请选定其中两小题,并在相应的答题.......区域内作答...... A ,(选修4-1;几何证明选讲)如图,1O ,2O 交于两点P Q ,,直线AB 过点P ,与1O ,2O 分别交于点A B ,,直线CD 过点Q ,与1O ,2O 分别交于点C D ,. 求证:AC ∥BD . B .(选修4-2:矩阵与变换)若二阶矩阵M 满足:12583446M ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭. (1)求二阶矩阵M ;(2)若曲线22:221C x xy y ++=在矩阵M 所对应的变换作用下得到曲线C ',求曲线C '的方程.C .(选修4-4:坐标系与参数方程)已知点(1)P αα-(其中[)0,2)απ∈,点P 的轨迹记为曲线1C ,以坐标原点 为极点,x 轴的正半轴为极轴建立极坐标系,点Q 在曲线21:)4C ρπθ=+上. (1)求曲线1C 的极坐标方程和曲线2C 的直角坐标方程;(2)当0,02ρθπ≥≤<时,求曲线1C 与曲线2C 的公共点的极坐标. D .(选修4-5:不等式选讲)已知实数0x >,0y >,0z >,证明:1239()()2462yx z x y z ++++≥.【选做题】第22题、23题,每题10分,共计20分.22.已知正六棱锥S ABCDEF -的底面边长为2,高为1.现从该棱锥的7个顶点中随机选取3个点构成三角形,设随机变量X 表示所得三角形的面积.(1)求概率(P X 的值;(2)求X 的分布列,并求其数学期望()E X .23.已知数列{a n }满足:a 1=1,对任意的n ∈N *,都有a n +1=(1+1n 2+n)a n +12n .(1)求证:当n ≥2时,a n ≥2;(2)利用“∀x >0,ln(1+x )<x ”,证明:a n <2e 34(其中e 是自然对数的底数).2017年高考模拟试卷(9)参考答案南通市数学学科基地命题一、填空题1. {}2,5.2. 15.3.-4. 4. 0.5. 5. 26y x =-.6. 60.7. 30. 线性规划或待定系数法,设甲、乙混货物分别为x ,y 克,由题意3x+4y 1005x+2y 120≥⎧⎨≥⎩,设x+y=34)(52)x y x y λμ+++(,解得,31==1414λμ,,即可. 8.. 9.[3. 设CA=x,则PQ=2CPcos<CAP=([3,))x ∈+∞,PQ ≤<. 10. 1e. 易知函数()f x 在(],0-∞上有一个零点,所以由题意得方程ln 0ax x -=在()0+∞,上恰有一解,即ln x a =在()0+∞,上恰有一解. 令ln ()x g x x =,21ln ()0x g x x -'==,得e x =,当()0,e x ∈时,()g x 单调递增,当()e ,+x ∈∞时,()g x 单调递减,所以()1e e a g ==.11.9.223331212922k x x x x x=+=++≥,也可以求导. 12. 116-.设弦AB 中点为M ,则()OP BP OM MP BP MP BP ⋅=+⋅=⋅ , 若MP BP ,同向,则0OP BP ⋅> ;若MP BP ,反向,则0OP BP ⋅< , 故OP BP ⋅的最小值在MP BP ,反向时取得,此时1||||2MP BP += ,2||||1||||()216MP BP OP BP MP BP +⋅=-⋅-=- ≥, 当且仅当1||||4MP BP == 时取等号,即OP BP ⋅ 的最小值是116-. 13.(方法一)由题意,得sin sin ααββ⎧=+⎪⎨=+⎪⎩所以αβ,是方程sin x x即方程()πsin 3x -5ππ()26k k αβ+=+∈Z,所以tan()αβ+=(方法二)同上,αβ,sin 0x x -的两根.设()sin f x x x -()cos f x x x '=-.令()0f x '=,得0tan x =,所以02x αβ+=,所以(方法三)直线210x y +-=交单位圆于A B ,两点, 过O 作OH AB ⊥,垂足为H ,易知OH =因为OC 60COH ∠=︒,即1502αβ+=︒,所以tan()tan300αβ+=︒=14.9⎧-⎨⎩⎭.32()322x x a x f x x a x a x ⎧--⎪=⎨⎪--+-<⎩,≥,,,当x a ≥时,320x x --=,得11x =-,23x =,结合图形知,① 当1a <-时,313x -,,成等差数列,则35x =-,代入3220x a --+-=得,9a =-; ② 当13a -≤≤时,方程3220x a x--+-=,即22(1)30x a x +-+=的根为34x x ,, 则343x x =,且3432x x +=,解得4x ,又342(1)x x a +=-,所以a .③ 当3a >时,显然不符合. 所以a 的取值集合95⎧-⎨⎩⎭. 二、解答题:本大题共6小题,共90分. 15. (1)因为tan α=2,所以sin αcos α=2,即sin α=2cos α. 又sin 2α+cos 2α=1,所以5cos 2α=1,即cos 2α=15.所以 cos2α=2cos 2α-1=-35.(2)由α∈(0,π),且tan α=2>1,得α∈(π4,π2),所以2α∈(π2,π).由题知cos2α=-35,所以sin2α=45.又因为β∈(0,π),cos β=-7210∈(-1,0),所以β∈(π2,π), 所以sin β=210,且2α-β∈(-π2,π2). 因为sin(2α-β)=sin2αcos β-cos2αsin β=45×(-7210)-(-35)×210=-22,所以2α-β=-π4.16.(1)因为BD 垂直平分AC ,所以BA BC =,在△ABC 中,因为120ABC ∠=︒, 所以30BAC ∠=︒.因为△ACD 是正三角形,所以60DAC ∠=︒, 所以90BAD ∠=︒,即AD AB ⊥.因为=1AB ,120ABC ∠=︒,所以AD AC == 又因为1PA =,2PD =,由222PA AD PD +=, 知90PAD ∠=︒,即AD AP ⊥.因为AB AP ⊂,平面PAB ,AB AP A = , 所以AD ⊥平面PAB .(2)(方法一)取AD 的中点H ,连结CH ,NH . 因为N 为PD 的中点,所以HN ∥PA , 因为PA ⊂平面PAB ,HN ⊄平面PAB , 所以HN ∥平面PAB .由△ACD 是正三角形,H 为AD 的中点,所以CH AD ⊥.由(1)知,BA AD ⊥,所以CH ∥BA , 因为BA ⊂平面PAB ,CH ⊄平面PAB , HPABCDMN因为CH HN ⊂,平面CNH ,CH HN H = , 所以平面CNH ∥平面PAB . 因为CN ⊂平面CNH , 所以CN ∥平面PAB .(方法二)取PA 的中点S ,过C 作CT ∥AD 交AB 的延长线于T ,连结ST ,SN .因为N 为PD 的中点,所以SN ∥AD ,且12SN AD =,因为CT ∥AD ,所以CT ∥SN . 由(1)知,AB AD ⊥,所以CT AT ⊥, 在直角△ CBT 中,1BC =,60CBT ∠=︒, 得CT =由(1)知,AD 12CT AD =,所以CT SN =.所以四边形SNCT 是平行四边形, 所以CN ∥TS .因为TS ⊂平面PAB ,CN ⊄平面PAB , 所以CN ∥平面PAB .17.(1)由题意知,124()2b b =-=,解得a =1b =,所以椭圆的方程为2212x y +=.(2)① 由(2)N t ,,(01)A ,,(01)B -,,则 直线NA 的方程为11y x t =+,直线NB 的方程为31y x t=-.P ABCDMNTS由221122y x t x y ⎧=+⎪⎨⎪+=⎩,得,222422.2t x t t y t ⎧=-⎪+⎨-⎪=+⎩,,故()2224222t t t t P --++,. 由223122y x t x y ⎧=-⎪⎨⎪+=⎩,得,222121818.18t x t t y t ⎧=⎪+⎨-⎪=+⎩,,故()22212181818t t t t Q -++,. 所以直线PM 的斜率2222162482PMt t t k t t t ---+==-+, 直线QM 的斜率222181261812818QMt t t k t t t ---+==+, 所以PM QM k k =,故P M Q ,,三点共线.② 由①知,11k t =,213k t =,2368t k t-=.所以21323122463182t k k k k k k t t t-+-=⨯-=-, 所以132312k k k k k k +-为定值12-.18.(1)设OP =r ,则l =r ·2θ,即r =l2θ,所以S 1=12lr =l 24θ,θ∈(0,π2).(2)设OC =a ,OD =b .由余弦定理,得l 2=a 2+b 2-2ab cos2θ,所以 l 2≥2ab -2ab cos2θ.所以 ab ≤l 22(1-cos2θ),当且仅当a =b 时“=”成立.所以S △OCD =12ab sin2θ≤l 2sin2θ4(1-cos2θ)=l 24tan θ,即S 2=l 24tan θ.(3)1S 2-1S 1=4l 2(tan θ-θ),θ∈(0,π2),. 令f (θ)=tan θ-θ,则f '(θ)=(sin θcos θ)'-1=sin 2θcos 2θ.当θ∈[0,π2)时,f '(θ)>0,所以f (θ)在区间[0,π2)上单调增.所以,当θ∈(0,π2)时,总有f (θ)>f (0)=0,即1S 2-1S 1>0,即S 1>S 2.19. (1)易得2143a =.(2)由111241n n n a a S +-=-,得11241n nn n n a a a a S ++-=-,所以11241n n n n na a S a a ++-=-①.所以12121241n n n n n a a S +++++-=②,由②-①,得12112112n n n n n n n n na a a aa a a a a +++++++=---.因为10n a +≠,所以22112n nn n n na a a a a a ++++=---. 所以121112n n n n n n a a a a a a +++++-=--,即12111n nn n n na a a a a a ++++-=--,即11n n b b +-=,所以数列{}n b 是公差为1的等差数列. 因为11213a b ==,所以数列{}n b 的通项公式为14n b n =-.(3)由(2)知,114n n n a n a a +=--,所以114311414n n an a n n ++=+=--,所以1n n a a +=,所以数列41n a n ⎧⎫⎨⎬-⎩⎭是常数列.由12a =,所以2(41)3n a n =-.(方法一)由m p r a a a ,,(m p r <<)成等比数列,则41m -,41p -,41r -成等比数列,所以2(41)(41)(41)p m r -=--, 所以2168164()0p p mr m r --++=,即2424()0p p mr m r --++=(*). (途径一)(*)式即为2424()4p p mr m r mr -=-+<-,所以2211(2))22p -<,即11222p -<,所以p <2p mr <.(途径二)(*)式即为24241p p rm r -+=-.由222222(42)(42)(41)()0p p r p p r r r p p r mr p r p -+-+----=⋅-==>,所以2p mr <.(方法二)由m p r a a a ,,(m p r <<)成等比数列, 则41m -,41p -,41r -成等比数列, 记4m α=,4p β=,4r γ=(1αβγ<<<), 则有1α-,1β-,1γ-成等比数列,所以2(1)(1)(1)βαγ-=--,即22()ββαγαγ-=-+.若2βαγ=,即2p mr =时,则2αγβ+=,所以αβγ==,矛盾; 若2βαγ>,则22()0βαγβαγ-+=->,所以1()12βαγ>+>,所以[][]2221(2)()()()()()024αγββαγαγαγαγαγαγ+---+>-+--+=->, 矛盾.所以2βαγ<,即2p mr <.20. (1) 由题意知曲线()y f x =过点(1,0),且'(1)e f =;又因为222'()ln e x a f x a x b x x+=-++⎛⎫ ⎪⎝⎭,则有(1)e(2)0,'(1)e()e,f b f a b =+==+=⎧⎨⎩解得3,2a b ==-.(2) ①当2a =-时,函数()y f x =的导函数22'()e 2ln 0x f x x b x=--+=⎛⎫ ⎪⎝⎭,若'()0f x =时,得222ln b x x =+, 设22()2ln g x x x =+(0)x > .由2332424'()x g x x x x-=-=0=,得x =1ln 2g =+.当0x <<时,'()0g x <,函数()y g x =在区间()上为减函数,()(1ln 2,)g x ∈++∞;仅当1ln 2b >+时,()b g x =有两个不同的解,设为1x ,2x 12()x x <.此时,函数()y f x =既有极大值,又有极小值.②由题意2e ln x a x b xkx ++⎛⎫≥ ⎪⎝⎭对一切正实数x 恒成立,取1x =得(2)e k b ≤+.下证2e ln e (2)x a x b xb x ++⎛⎫≥+ ⎪⎝⎭对一切正实数x 恒成立.首先,证明e e xx ≥. 设函数()e e xu x x =-,则'()e e xu x =-,当1x >时,'()0u x >; 当1x <时,'()0u x <;得e e (1)0xx u -=≥,即e e xx ≥,当且仅当都在1x =处取到等号.再证1ln 1x x+≥. 设1()ln 1v x x x=+-,则21'()x v x x -=,当1x >时,'()0v x >;当1x <时,'()0v x <;得()(1)0v x v =≥,即1ln 1x x+≥,当且仅当都在1x =处取到等号. 由上可得2e ln (2)e x a x b xb x ++⎛⎫≥+ ⎪⎝⎭,所以min()(2)e f x b x ⎛⎫=+⎪⎝⎭,即实数k 的最大值为(2)e b +.数学Ⅱ(附加题)21. A. 连结PQ ,因为四边形ACQP 是1O 的内接四边形, 所以A PQD ∠=∠, 又在2O 中,PBD PQD ∠=∠,所以A PBD ∠=∠, 所以AC ∥BD .B .(1) 设1234A ⎛⎫= ⎪⎝⎭,则12234A ==-,1213122A --⎛⎫⎪∴= ⎪-⎝⎭, 21582131461122M -⎛⎫⎛⎫⎛⎫ ⎪∴== ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭. (2)11112x x x x x M M y y y y y -'''-⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=∴== ⎪⎪ ⎪ ⎪ ⎪⎪'''-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭, 即,2,x x y y x y ''=-⎧⎨''=-+⎩ 代入22221x xy y ++=可得 ()()()()2222221x y x y x y x y ''''''''-+--++-+=,即22451x x y y ''''-+=,故曲线C '的方程为22451x xy y -+=.C. (1)曲线1C :22(1)2x y ++=,极坐标方程为22cos 10ρθ+-= 曲线2C 的直角坐标方程为1y x =-; (2) 曲线1C 与曲线2C 的公共点的坐标为(0,1)-,极坐标为3(1,)2π. D. 因为0x >,0y >,0z >,所以123x y z++,2463y x z++, 所以1239()()yx z ++++≥.当且仅当::1:2:3x y z =时,等号成立.22.(1)从7个顶点中随机选取3个点构成三角形,共有37=35C种取法.其中X ABF ,这类三角形共有6个.因此(376635P X C ===. (2)由题意,X2,其中X ABF ,这类三角形共有6个;其中2X =的三角形有两类,如△P AD (3个),△P AB (6个),共有9个;其中X PBD ,这类三角形共有6个;其中X =CDF ,这类三角形共有12个;其中X =BDF ,这类三角形共有2个.因此(635P X =,()9235P X ==, (635P X =,(1235P X ==,(235P X ==. 所以随机变量X 的概率分布列为:所求数学期望()E X 69612223535353535+⨯+++. 23. (1)①当n =2时,a 2=2,不等式成立.②假设当n =k (k ≥2)时不等式成立,即a k ≥2,则当n =k +1时,a k +1=(1+1k (k +1))a k +12k >2.所以,当n =k +1时,不等式也成立. 根据①,②可知,对所有n ≥2,a n ≥2成立.(2)当n ≥2时,由递推公式及(1)的结论有a n +1=(1+1n 2+n )a n +12n ≤(1+1n 2+n +12n +1)a n (n ≥2).两边取对数,并利用已知不等式ln(1+x )<x ,得 ln a n +1≤ln(1+1n 2+n +12n +1)+ln a n <ln a n +1n 2+n +12n +1,故 ln a n +1-ln a n <1n 2+n +12n +1(n ≥2),求和可得ln a n -ln a 2<12⨯3+1 3⨯4+…+1 (n -1)n +123+124+…+12n=(12-13)+(13-14)+…+(1n -1-1n )+123·1-12n -21-12=12-1n +122-12n <34. 由(1)知,a 2=2,故有ln a n 2<34,即a n <2e 34(n ≥2),而a 1=1<2e 34,所以对任意正整数n ,有a n <2e 34.。
2017年浙江省普通高校招生选考科目考试模拟卷9

2017年浙江省普通高校招生选考科目考试模拟卷(九)(时间:45分钟满分:50分)一、选择题(本大题共12小题,每小题2分,共24分。
每小题列出的四个备选项中只有一个符合题目要求,不选、多选、错选均不得分)1.某用户在根据导航软件设置好的导航路径行驶,途中高德地图提示前方有拥堵现象,建议改道,并实时提供新的导航路径,该实例最能体现信息的() A.载体依附性B.时效性C.共享性D.真伪性B[本题主要考查信息及其特征。
导航系统提供最新的实时路况信息,最能体现信息特征的“时效性”,因此选择B。
]2.某网页文件如图所示,对该网页文件的分析如下:①该网页标题为:中国国家图书馆·中国国家数字图书馆②该网站的URL为http:///③HTTP是超文本标记语言④可将网页中的图片、文字、超链接等添加到收藏夹中⑤可使用“FrontPage”软件编辑其中正确的是()A.①②③④⑤B.③④⑤C.②③④D.①②⑤D[本题考查的主要是网站、网页的基本知识。
URL:统一资源地址,又称网址;HTTP是超文本传输协议;收藏夹的功能是收藏网址;FrontPage、DreamWeaver、记事本都可以编辑网页;网页的标题可以从浏览器标题栏中看出。
所以本题正确的有①②⑤。
]3.下列应用中,没有使用智能处理技术的是( ) A .利用指纹快速解锁手机 B .用Siri 语音功能启动QQ 软件 C .使用在线翻译实现中英文转换 D .将书籍扫描成图像保存到计算机中D [本题主要考查了智能处理的知识。
选项D “将书籍扫描成图像保存到计算机中”没有使用智能处理,只是使用了扫描而没有使用智能识别功能。
本题其他几个选项都使用了智能处理技术。
因此答案是D 。
]4.使用Access 软件创建数据表,存储如下表所示的图书信息:C [ 本题考查Access 数据库知识。
“编号”字段包含“SN -”,属于文本类型,“自动编号”属于数字类型,因此B 、D 都不符合要求;“书价”字段有货币符号,可能是货币类型或是文本类型,“出版时间”可能为日期/时间型或文本型。
江西省2017年普通高等学校招生全国统一考试仿真卷理科综合能力测试(九)物理试题含解析

2017年普通高等学校招生全国统一考试仿真卷理科综合能力测试(九)物理试题第Ⅰ卷二、选择题:本题共8小题,每题6分,在每小题给出的四个选项中,第14~18题只有一个选项符合题目要求。
第19~21题有多选项题目要求。
全部答对的得6分,选对但不全的得3分,有选错的的0分。
14.关于光电效应,下列说法正确的是()A.极限频率越大的金属材料逸出功越大B.只要光照射的时间足够长,任何金属都能产生光电效应C.从金属表面出来的光电子的最大初动能越大,这种金属的逸出功越小D.入射光的光强一定时,频率越高,单位时间内逸出的光电子数就越多【解析】根据W=hγc知,极限频率越大的金属材料逸出功越大.故选项A正确;发生光电效应的条件是入射光的频率大于极限频率,与入射光照射的时间无关.故选项B错误;根据光电效应方程E k=hγ-W知,光电子的最大初动能与入射光的频率和逸出功两个因素有关,光电子的最大初动能越大,这种金属的逸出逸出功不一定越小,也可能是因为入射光的频率高的缘故.故选项C错误;光的强度影响的是单位时间发出光电子数目,与入射光的强度无关.故D错误。
【答案】A15. 如图所示,在x轴相距为L的两点固定两个等量异种点电荷+Q、-Q,虚线是以+Q所在点为圆心、L/2为半径的圆,a、b、c、d是圆上的四个点,其中a、c两点在x轴上,b、d两点关于x轴对称。
下列判断不正确的是()A.b、d两点处的电势相同B.四点中c点处的电势最低C.b、d两点处的电场强度相同D.将一试探电荷+q沿圆周由a点移至c点,+q的电势能减小【解析】由图知,b、d两点到两电荷的距离一样远,所以电势相等,A正确;四个点到正电荷的距离一样远,故正电荷在四点的电势相等,根据沿电场线的方向电势降低,负电荷点c 点的电势最低,且为负值,叠加后,c 点电势最低,所以B 正确;b 、d 两点处的电场强度的方向不同,所以C 错误; a 的电势高于c 点的电势,正电荷由高电势移动到低电势,电场力做正功,电势能减小,D 正确。
2017年普通高等学校招生全国统一考试高考模拟信息卷(九)理综生物试卷

2017年普通高等学校招生全国统一考试高考模拟信息卷(九)理综生物试卷1.糖类、蛋白质、脂质是生物体的三大能源物质,下列有关叙述正确的是A.细胞通过氧化分解各种单糖来生成ATPB.细胞内丧失活性的蛋白质会被分解,生成的氨基酸主要用于新蛋白质的合成C.脂防除储存能量外,还是构成动物细胞生物膜系统的重要组成成分D.机体可以通过将蛋白质(氨基酸)、脂质等非糖物质转化为糖原来升高血糖2.下图是影响几种小分子物质进出细胞的因素与运输速率的相关曲线。
下列相关叙述正确的是A.图中①、②所表示的物质运输方式均不需要消耗能量B.性激素和K+进入细胞,前者可以用曲线①和③来描述,后者可用②和④来描述C.图②中最终限制运输速率不再增加的原因是载体数量有限D.如果将图④的横轴换成氧气浓度,则④中的曲线一定不变3.下图的核基因模型为控制某种酶的基因内部和周围的DNA片段情况。
距离以千碱基对(kb)表示,但未按比例画出,基因长共8kb,人为划分出a-g这7个区间,转录直接生成的mRNA 中d区间所对应的区域会被加工切除,成为成熟的mRNA。
下列相关分析正确的是A.该酶是由299个氨基酸组成的B.起始密码子对应的位点是RNA聚合酶结合的位点C.一次细胞有丝分裂过程中核基因只进行一次转录过程D.mRNA上某一特定位点对应的氨基酸可以由几种特定的tRNA将它转运到核糖体上4.下图虚线框表示人体的体液组成及相互关系。
下列相关叙述正确的是A.图中的②、③、⑤可分别表示淋巴、组织液、血液B.图中②和③的组成成分更接近,⑤的蛋白质含量最高C.图中⑤的渗透压的维持只与Na+和Cl-有关,⑥的渗透压的维持与K+密切相关D.图中的①、④、⑥内部都能进行ATP的合成以及水解5.下列关于科学研究和实验方法的叙述,不正确的是A.摩尔根等人通过假说——演绎法,证明了基因在染色体上B.“建立血糖的调节模型”采用的研究方法是模型方法,模拟活动本身就是在构建动态的物理模型,之后再根据活动中的体会构建概念模型C.在低温诱导植物细胞染色体数目变异实验中,卡诺氏液处理根尖后,需要蒸馏水冲洗2次D.在土壤中小动物类群丰富度的研究中,不适于用样方法或标志重捕法进行调查6.下列有关种群和群落的叙述,正确的是A.种群密度越大种群个体数越多B.种群数量的“S”型曲线在K/2之前等同于“J”型曲线C.群落的丰富度越大,生态系统的营养结构相对越复杂D.随着演替的进行,群落的物种组成、生物量都将增大29.(10分)下图1是番茄光合作用过程图解,图2是在密闭、透明的玻璃小室中培养番茄幼苗的实验装置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年苏州市初三英语模拟试题(九)一、单项填空( )1. Life is like ocean: Only strong-willed can reach the other shore(海岸).A. an; theB. the; aC. the; /D. /; a( )2. If you don't know the to the science museum, here is a map of the city.A. dateB. wayC. priceD. time( )3. Pay no attention to those who laugh at you. What most is how you see yourself.A. mattersB. mindsC. caresD. values( )4. There is only one more day to go your favourite music group play live.A. sinceB. whileC. whenD. before( )5.—Are you going to Tom's party this weekend?—not. I may have to work.A. ProbablyB. CertainlyC. EspeciallyD. Properly( )6. Many Internet users, especially women, showed pictures of with an A4-sized piece of paper.A. herselfB. themselvesC. himselfD. itself( )7.一Have you watched the boat races this Dragon Boat Festival?一Yes. wonderful races!A. What anB. What aC. WhatD. How( )8. The fridge doesn't work. Why not consider a new one?A. buyB. boughtC. to buyD. buying( )9.一Tom said he planned to sell his shop and go to a medical school. It be true, right?—Well,you're probably wrong. He always wants to learn medicine, you know.A. shouldn'tB. can'tC. needn'tD. mustn't( )10. "I want to go to Mars, because it's a place that no one to before, "said Carson.A. has goneB. has beenC. wasD. went( )11.The population of China is than that of Australia.A. far moreB. far lessC. much smallerD. much larger( )12. It that the method didn't work well. He had to try another one.A. ran outB. found outC. turned outD. worked out( )13.一it is from our own planet Earth to Mars!一Yes. It takes months to travel to Mars by spacecraft.A. How soonB. How farC. How longD. How often( )14.一Excuse me, could you tell me ?一There's a bank on the second floor. You can make it there.A. if there's a bank near hereB. how I can get to the bankC. where 1 can change moneyD. where the bank is( )15.一Hi, Jack. We will go on an outing this weekend. Would you like to join us?一. That's the last thing in the world I would ever want to do.A. It dependsB. With pleasureC. It's up to youD. No, thanks二、完形填空The first note I ever wrote to my mother said "Hi,Mom! Have a nice day! Love,Marie! " I was twelve when I wrote it, and I folded(折叠)the note into her change purse.My mother worked as a cleaner in a clothing factory. I knew that when she 16 meals in the dining hall,she would have to look for change in her purse. I didn't know that she would 17 that note, and always carry it with her.From the day that I 18 folded the small piece of paper into my mother's change purse, she and I left each other 19 notes. They would be put in the fridge, under a lamp, or beside the TV set. I 20 found one hidden in my shoe. From the outside, our notes may have been general 21 of our days, ideas and wishes. But to my mother and me, they were a lifeline- the communication between each other that no one else 22 .On October 20,2009,my mother died after a long illness. I stood near her bed,holding her hand. I didn't cry the day my mother died, 23 I didn't cry a week later when I went to collect her things. I was so thankful that she no longer had aches and pains.Recently, I found a note that my mom had left me. It had been hidden in the 24 of my favourite childhood book for years. It read "Dear Marie. I love you always. Miss you a lot. Don't forget me. Be 25 ! Love, Mom." That day, I cried.( )16. A. prepared B. sold C. bought D. cooked( )17. A. forget B. keep C. lose D. pick( )18. A. carefully B. wisely C. quickly D. carelessly( )19. A. big B. funny C. secret D. beautiful( )20. A. hardly B. never C. even D. seldom( )21. A. programs B. courses C. excuses D. records( )22. A. shared B. believed C. promised D. remembered( )23. A. and B. but C. or D. because( )24. A. lines B. poems C. pages D. pictures( )25. A. serious B. happy C. patient D. strict三、阅读理解AWith an announcement made on 1 April, 2017, Xiongan has become a well-known name in China overnight. Xiongan New Area, about 100 kilometers south-west of Beijing, covers three counties: Xiongxian, Rongcheng and Anxin.26. Xiongan New Area is ______.A. in TianjinB. in BeijingC. in Hebei ProvinceD. in Baoding27. Which of the following is TRUE?A. Xiongan New Area covers four counties.B. Xiongan New Area will become larger and larger.C. Xiongan New Area is 100 kilometres north-west of Beijing.D. Xiongan New Area will cover about 200 square km in the long term.BWhile many young people were enjoying the summer vacation, Zach Bonner was working his hardest. Zach started walking from Valrico, Florida, his hometown, on Christmas, 2009. He reached Los Angeles nine months later in September, 2010. He covered a total of 2,478 miles and raised $120,000 for kids in need. Along the way, Zach attended school online. His mother, brother and sister took turns to walk or drive together with him.Although he is very young, Zach has a long history of helping others. When a terrible storm hit town in 2004, Zach, when six, pulled a wagon(小推车)through his community and collected food for people in need.He has raised $400,000 for his Little Red Wagon Foundation since then. It gives money to projects which help homeless children. In 2007, Zach began walking to support a children's charity in Tampa, Florida. He finished his journey 23 days later, 280 miles away in Tallahassee. Then in the summer of 2009, he trekked(跋涉) about 670 miles from Atlanta to Washington, D.C., in just two months."As long as there are homeless kids, I will never stop walking for them. " Zach says.( )28. We can learn from Paragraph 2 that Zach .A. began to help people at a very early ageB. made money to pay for his educationC. enjoyed playing around in his communityD. worked very hard for his family( )29. At what age did Zach start walking to support a Tampa children's charity?A. At six.B. At nine.C. At eleven.D. At twelve.( )30. Which of the following best describes Zach?A. Friendly and shy.B. Silly but lovely.C. Kind and helpful.D. Clever but lazy.CIt is most difficult for parents to decide whether to have a second child or not.It is often heard that a single child is like to be a lonely child. There are no other children inthe family for the child to talk or play with. An only child is not able to get along well with children of his age. Some parents regretted making the decisions to have only one child.But the number of parents choosing to have only one child is increasing in many parts of the world. In the US, for example, more than14 % of women between 18 and 34 plan to have just one child. The same can be seen in the UK. In Japan, the average(平均) number of children born per family had gone down to 1.42 by 1996.For some single-child parents, especially who are busy working every day, time and energy seem to beoverwhelming. They don't have enough time and energy to share with more children. For other people, money is their first consideration. Many couples in Japan choose not to have large families as the cost of supporting a child up to the age of 18 reaches around US$160,000.( )31.What do people not think about when they choose to have a second child ?A. timeB. energyC. moneyD. food( )32.What does the underlined word "overwhelming" mean in the last paragraphA. 压倒一切的B. 宽松的C. 流行的D. 充足的( )33. Parents choose not to have a second child because .A. The cost of supporting a child is so high.B. Parents are too busy working every day to share their time and energy with more children.C. Some parents regretted making the decisions to have only one child.D. Both A and B.DPhysical activity has many advantages. It makes bones and muscles(肌肉)stronger. improves mental health and mood,lowers blood pressure, and reduces the risk of cardiovascular(心血管的)disease, and all kinds of cancers. Exercise is also good for your brain. It may not be a cure-all for obesity(肥胖),however.Though better nutrition(营养)together with exercise has long been the good treatment for losing weight and avoiding obesity, a new study suggests diet,in fact,plays the key role.Researchers compare African-American women in Chicago with women in the countries of Nigeria. On average(平均),the Chicago women weighed 184 pounds and the Nigerian women weighed 127 pounds. Researchers had expected to find that the slimmer Nigerian women would be more physically active. To their surprise, they found no important difference between the two groups in the amount of calories burned during physical activity."Less physical activity may not be the main drive of obesity. " said Richard Cooper, a member of the study team. "People burn more calories when they exercise. The thing is, they make up by eating more. We would love to say that physical activity has a positive effect on weight control, but that does not appear to be the case. "Diet is a more likely explanation than physical activity expenditure(消耗)for why Chicago women weigh more than Nigerian women, Cooper said. She noted the Nigerian diet is low in fat and animal protein(动物蛋白).Lout the Chicago diet is 40 percent to 45 percent in fat.More research seems to be needed,however, as the new finding is different from other studies. A study found that Old Order Amish people who had a gene(基因)related to obesity stayed thin because they exercised a lot.( )34. By saying the underlined words in Paragraph 4,Cooper meant that .A. exercise may not do good to your brainB. less exercise may not lead to obesity at allC. exercise doesn't play a key role in losing weightD. people need to eat more to do enough physical activity( )35. At the mention of Old Order Amish people,the writer wants to prove that .A. obesity is a serious medical problemB. the result of the new study is reasonableC. obesity is mainly related to one's genesD. the result of the new study needs to be tested further ( )36. What can we know about Chicago women and Nigerian women from the passage?A. They don't like doing physical activities.B. They burn almost the same amount of calories during physical activity.C. Chicago women are slimmer than Nigerian women.D. Nigerian women like to do more exercise than Chicago women.( )37. The writer's purpose of writing the passage is to expect us to_.A. control our diet to stay thinB. take more exercise to lose weightC. do more physical activity to avoid diseasesD. find a way that can treat obesity completely四、词汇检测38. Try to calm down and not to get (急躁的)while facing much stress.39. Everyone hopes to live (和平地)with their family in the world.40. The coal and oil we are burning is of poor quality and don't meet the (标准)for environmental protection.41. The point we must insist on (保持不变)to be discussed.42. (以,凭借)his efforts he succeeded in making so many useful inventions.43. Thank you for giving me some useful (建议). It's of great value to me.44. Shirley was standing at the door .Her long hair (垂下)down to the chest.45.一Yesterday, my father bought me a new mobile phone as a present,but I don't know how to use it.一Why not read the first before using it?46.一Who is the most modest boy in your class?一Daniel. He often wins some prizes but never off in public.2017年苏州市初三英语模拟试题(九)参考答案一、1一5 ABADA 6-10 BCDBB 11一15 DCBCD二、16一20 CBACC 2.1一25 DAACB三、26一30 CBABC 31一35 DADCD 36一37 BA四、38. impatient 39. peacefully 40. standard 41. remains42. Through 43. advice 44. hung 45. instructions46. shows 47. lasted五、48. More and more parents begin to pay attention to children's safety.49. The robot seems to be out of control.50. These silk scarves are made by hand.51. Could you tell why you didn't try out for the school team then?52. The 70-year-old man was considered to be/as the best dancer at last night's competition.六、53. Upton Sinclair.54. They tell people important information about food and help people to make good choices.55. Yes. Because food safety is closely related to our daily life./No. As the saying goes, we must eat a peck of dirtbefore we die, so we don't need to pay too much attention to food safety.七、I like films best, especially English films. Why?Firstly, I can learn many English words and practice listening and speaking by watching English films. secondly, most of the English films are educational. Some of them can make you more confident. Thirdly, I can know some famous actors and actresses, such as Audrey Hepburn. She was considered a superstar, not only for her acting in the films but for her efforts in charity. Finally, I can also learn about the culture of England and America.However, there is a problem. I have no time to watch films because of too much homework. I hope to balance the relationship between study and hobbies.。
