第九节 多面体与球[详版课资]
合集下载
高三数学多面体与球(新编201912)
2.性质 (1)球心和截面圆心的连线垂直于截面；
(2)球心到截面的距离d与球的半径R及截面半径r 有如下关系：
3.球面距离 径.)
为A、B对球心的张角，R为球半
4.表面积与体积
返回
课前热身
1.一个四面体的所有棱长都为2，四个顶点在同一球面 上，则此球的表面积为( A )
(A)
(B)
(C)
(D)Leabharlann 2.已知一个简单多面体的各个顶点处都有三条棱，则顶 点数V与面数F满足的关系式是( A )
(A)2F+V=4
(B)2F-V=4
(C)2F+V=2
(D)2F-V=2
3.一个凸多面体的顶点数为20，棱数为30.则它的各面 多边形的内角总和为( A )
(A)2160° (B)5400° (C)6480° (D)7200°
4.将棱长为3的正四面体的各棱长三等分，经过靠近顶 点的各分点，将原正四面体各顶点均截去一个棱长为1 的小正四面体，剩下的多面体的棱数为( A )
(A)16
(B)17
(C)18
(D)19
5.地球表面上从A地(北纬45°，东经120°)到B地(北纬 45°，东经30°)的最短距离为(地球半径为R)( A )
(3)每个面都是有相同边数的正多边形，且以每 个顶点为其一端都有相同数目的棱的凸多面 体，叫正多面体.
；我爱查吧 https:/// 我爱查吧
；
文字有三句话，各有一处语病，请选择两句加以修改。(4分) ①在甲型H1N1流感防控工作的关键时刻，在我省一套信息化应急指挥系统正式启动。②通过这套指挥系统，使省疾病预防控制中心工作人员可随时向省领导汇报全省甲型HlNl流感的防控情况，省领导也可以通过该系统对防控工作发出 指令。③采取信息化应急指
高三数学多面体与球
πR 的弧长等于 (R为地球半径)，求甲、乙两地间的距离. 2
【解题回顾】求球面上两点的距离，就是求过这两点 的大圆的劣弧长，而不是纬线上的劣弧长，求解的关 键在于求两点的球心角的大小，利用弧长公式来求 出：L=θ•R即为所求球面距离.
3. 设一个凸多面体有 V个顶点，求证它的各面多边形 的内角总和为(V-2)•360°.
2010届高考数学复习 强化双基系列课件
56《立体几何 －多面体与球》
多面体与球
• 要点·疑点·考点 •课 前 热 身 • 能力·思维·方法 • 延伸·拓展 •误 解 分 析
要点·疑点·考点
一、多面体 1. 概念 (1)若干个平面多边形围成的几何体，叫多面体. (2)把多面体的任何一面伸展为平面，如果所有 其他各面都在这个平面的同侧，这样的多面体 叫凸多面体. (3)每个面都是有相同边数的正多边形，且以每 个顶点为其一端都有相同数目的棱的凸多面 体，叫正多面体.
(A)R (C) πR
(B) πR (D) πR
3
2
返回
能力·思维·方法
1. 已知凸多面体每个面都是五边形，每个顶点都有三 条棱，试求该多面体的面数、顶点数和棱数.
【解题回顾】用欧拉公式 V+F-E=2 解题时，要善于发
nF 现棱数E与面数F、顶点数V的关系，一般有E 2 mV 和E 2
2. 在北纬 60°圈上，有甲常转化为小圆半径，大圆 半径及球心到截面距离来解决. 返回
误解分析
1.在涉及球内接正方体或长方体的题目中，作出的截 面一般过多面体的对角线，且对角线长为球的直径 若过对棱中点作横截面，将会出错.
2. 球面上两点间距离不是直线距离，也不是纬度圈上 的劣弧长，而是指过这两点的球大圆上 的劣弧长，不 能错啊!
高考数学总复习 9.11简单多面体和球精品课件 文 新人教B版
6.两点的球面距离：球面上两点之间的最短距离，
就是经过两点的大圆在这两点间的一段劣弧的长度， 我们把这个弧长叫做两点的球面距离，l＝Rφ(φ为球心 角的弧度数). 7.球的表面积和体积公式：S＝4πR2，V＝ πR3.
1.球面距离是弧长，而非两点间的直线距离；求A、
B两点的球面距离的步骤是：⑴求弦长|AB| ，⑵求球心
6．(2004年北京，理11)某地球仪上北纬30°纬线 的长度为12π cm，该地球仪的半径是________cm，表 面积是________cm2.
例1
已知球的两个平行截面的面积分别为49π、
400π，且两个截面之间的距离为9，求球的表面积． [分析] 先画出过球心且垂直于已知截面的球的大 圆截面，再根据球的性质和已知条件列方程求出球的
3.球的概念：与定点距离等于或小于定长的点的
集合，叫做球体，简称球，定点叫球心，定长叫球的 半径，与定点距离等于定长的点的集合叫做球面．一 个球或球面用它的球心的字母表示，例如球O. 4.球的截面：
(1)球的截面是一个圆；
(2)球心和截面圆心的连线垂直于截面； (3)球心到截面的距离d与球的半径R及截面圆的半 径r满足r＝ . 球面被经过球心的平面截得的圆叫做大圆，被不
一、选择题 1．下列四个命题中错误的个数是 ( )
①经过球面上任意两点，可以作且只可以作一
个球的大圆；②球的表面积是它大圆面积的四倍； ③球面上两点的球面距离，是这两点所在截面圆上 以这两点为端点的劣弧的长． A．0 C．2 [解析] ①③错误． [答案] C B．1 D．3
2．一平面截一球得到直径为6 cm的圆面，球心到
经过球心的平面截得的圆叫做小圆．
5.经度、纬度： 经线：球面上从北极到南极的半个大圆． 纬线：与赤道平面平行的平面截球面所得的小 圆． 经度：某地的经度就是经过这点的经线与地轴确 定的半平面与0°经线及轴确定的半平面所成的二面角 的度数． 纬度：某地的纬度就是指过这点的球半径与赤道 平面所成角的度数．
2010高考数学一轮复习 第九讲 多面体与球课件 新人教版
答案：D
第十五页，编辑于星期五：五点 二十四分。
2．长方体的一个顶点上的三条棱长分别是3、4、5，
且它的8个顶点都在同一球面上，则这个球的表面积是
()
A．25π B．50π C．125π D．都不对
解析：设长方体的体对角线长为l，外接球半径为R，
则l2＝32＋42＋52＝50，又R＝，
∴S球表＝4πR2＝4π× 答案：B
答案：B
第九页，编辑于星期五：五点 二十四分。
3．如图，已知直平行六面体ABCD－A1B1C1D1的各条 棱长均为3，∠BAD＝60°，长为2的线段MN的一个端点M
在DD1上运动，另一端点N在底面ABCD上运动，则MN的 中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体
的体积为
()
第十页，编辑于星期五：五点 二十四分。
面截球所得的圆面面积为π，则球的体积为
()
第七页，编辑于星期五：五点 二十四分。
解题思路：设球半径为R，截面圆半径为r，根据πr2＝ π⇒r＝1.
又∵OQ1＝1，∴R＝ 从而得球的体积
第八页，编辑于星期五：五点 二十四分。
失分警示：对球的性质掌握不好，OO1⊥截面圆O1及 Rt△OO1A中勾股定理的运用，还有球的表面积公式的应用 不够灵活，导致该题失分．
【例2】 设地球的半径为R，在北纬45°圈上有两个 点A、B，A在西经40°，B在东经50°，求A、B两点间纬线 圈的弧长及A、B两点间的球面距离．
[解析] 如图，设45°纬线圈中心为O1，地球中心为 O，则∠AO1B＝40°＋50°＝90°.
又∵OO1⊥圆O1所在平面， ∴OO1⊥O1A，OO1⊥O1B. 又∵A、B在北纬45°圈上， ∴∠OBO1＝∠OAO1＝45°.
第十五页，编辑于星期五：五点 二十四分。
2．长方体的一个顶点上的三条棱长分别是3、4、5，
且它的8个顶点都在同一球面上，则这个球的表面积是
()
A．25π B．50π C．125π D．都不对
解析：设长方体的体对角线长为l，外接球半径为R，
则l2＝32＋42＋52＝50，又R＝，
∴S球表＝4πR2＝4π× 答案：B
答案：B
第九页，编辑于星期五：五点 二十四分。
3．如图，已知直平行六面体ABCD－A1B1C1D1的各条 棱长均为3，∠BAD＝60°，长为2的线段MN的一个端点M
在DD1上运动，另一端点N在底面ABCD上运动，则MN的 中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体
的体积为
()
第十页，编辑于星期五：五点 二十四分。
面截球所得的圆面面积为π，则球的体积为
()
第七页，编辑于星期五：五点 二十四分。
解题思路：设球半径为R，截面圆半径为r，根据πr2＝ π⇒r＝1.
又∵OQ1＝1，∴R＝ 从而得球的体积
第八页，编辑于星期五：五点 二十四分。
失分警示：对球的性质掌握不好，OO1⊥截面圆O1及 Rt△OO1A中勾股定理的运用，还有球的表面积公式的应用 不够灵活，导致该题失分．
【例2】 设地球的半径为R，在北纬45°圈上有两个 点A、B，A在西经40°，B在东经50°，求A、B两点间纬线 圈的弧长及A、B两点间的球面距离．
[解析] 如图，设45°纬线圈中心为O1，地球中心为 O，则∠AO1B＝40°＋50°＝90°.
又∵OO1⊥圆O1所在平面， ∴OO1⊥O1A，OO1⊥O1B. 又∵A、B在北纬45°圈上， ∴∠OBO1＝∠OAO1＝45°.
多面体与球
多面体与球1.三棱锥顶点在底面上的射影为三角形的外心⇔三侧棱相等或三侧棱与底面所成的角相等；内心⇔三侧面与底面所成的二面角相等；垂心⇔相对的棱垂直。
正三棱锥中相对的棱垂直；三棱锥三侧棱（侧面）两两垂直⇒顶点在底面上的射影为三角形的垂心；三棱锥一个顶点在对面上的射影为三角形的垂心⇒三棱锥其余顶点在对面上的射影也为三角形的垂心。
[举例1] 已知三棱锥S －ABC 的底面是正三角形，点A 在侧面SBC 上的射影H 是△SBC 的垂心，SA=a ，则此三棱锥体积最大值是 解析：∵点A 在侧面SBC 上的射影H 是△SBC 的垂心，∴点S 在底面ABC 上的射影O 为△ABC 的垂心；又△ABC 为正三角形，∴O 为△ABC 的中心，即三棱锥S －ABC 为正三棱锥。
记SO=h （h< a ），则AO=22h a -，于是有：AB=)(322h a -,记三棱锥S －ABC 体积为f(h)，则f(h)=h h a )(4322-， f /(h)=)3(4322h a -，∴f max (h)=)33(a f =63a .[举例2] 下面是关于三棱锥的四个命题：①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥.②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥. ③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥.④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱；其中，真命题的编号是 （写出所有真命题的编号）.解析：①侧面与底面所成的二面角都相等，则顶点在底面上的射影O 是底面的内心，又底面是等边三角形，故O 是底面三角形的中心，所以三棱锥是正三棱锥；②在三棱锥S －ABC 中，令AB=BC=CA=SA=SB=2，SC=3，该三棱锥不是正三棱锥；③底面是等边三角形且侧面的面积都相等，则顶点到底面三边的距离相等，即顶点在底面上的射影O 到底面三边的距离相等，但这不意味着O 是底面三角形的内心，还有可能是旁心（一个内角的平分线与另一个角的外角平分线的交点），故三棱锥未必是正三棱锥；④侧棱与底面所成的角都相等，则顶点在底面上的射影O 是底面的外心，侧面与底面所成的二面角都相等，则O 是底面的内心，底面三角形的内、外心重合，则必为正三角形且O 为其中心，故该三棱锥是正三棱锥。
球体构成多面体立体构成课堂课资
对球体的变化
上课复习
面的处理 切孔、切折、附加、凹入 凸出等处理 （效果：坚实或轻巧）
边的处理 进行变化
角的处理
反折、剪边、平折等手段 剪角或内折等方法
9
1、面的处理
面的处理是在多面体的面上进行开窗、 附加、凹入凸出等变化 O 开窗——在面的某一部位按照设计的需要切
口形成窗口状 O 附加——在面上家如别的形态，使原有的面
O 凸边——将边向外突出，求得形态的变化
上课复习
12
①本体变化
①本体变化 就是在多面体的造型上直接进行加工，不除
量，也不增形。
A 棱边处理 单线变复线，将多面体棱边处理为双线，这
样棱边形成了一个狭窄棱面，棱角由尖锐变成了平钝。
上课复习
13
折痕线变形 将多面体原来笔直的棱边折痕线变成曲线的处 理，幅度不宜过大，可使原来严肃的形体变得优美起来。
31
上课复习
32
上课复习
33
上课复习
34
上课复习
35
上课复习
36
上课复习
37
上课复习
38
上课复习
39
上课复习
40
O 阿基米德多面体一共有13个，包括十四面 体、十六面体、二十六面体等。
上课复习
6
截半立方体
上课截复半习十二面体
7
多面体变异 无论是柏拉图多面体，还是阿
基米德多面体，由于表面具有平面几何形的数理性， 若以此作为基本结构，对其表面、棱边、棱角进行 处理，多面体将呈现出更加多样的异形变化，营造 出更加全新的视觉听觉心理感受。
上课复习
1
柏 拉 图 多 面 体
上课复习
2
多面体与球.doc
a过球面上两点可确定一个球的大圆b过球面上三点可确定一个球的大圆c过球面上两点只有一个球的小圆d过球面上两点只有一个半径最小的球小圆2过球的一条半径的中点作垂直于这条半径的球截面则此截面面积是球大圆面积的b13c34d143设地球的半径为r求北纬600的纬线长在球面上aob小于求ab两点间的球面距离4三个球的半径之比是1
4、三个球的半径之比是1：2：3，则最大球的体积等于其他两个球体积和的倍。
５、设地球的半径为R，在北纬450圈上有A、B两地，它们的纬度圈上的弧长等于 R，求A、B两地间的球面距离。
６、已知球的半径为25，有两个截面的面积为49 、400 ，求平行截面间的距离。
７已知各棱长都相等的三棱锥内接在一个体积为36 的球内，求这个棱锥的高？
８、若球的半径为R，求其内接正四面体的体积？
９分与面数．
１０球面上三点A、B、C组成这个球的一个截面的内接三角形，AB=18,BC=24,AC=30,且球心到截面的距离为球半径的一半，（１）求球的体积，（２）求AC两点的球面距离．
１１、有一轴截面为正三角形的圆锥形容器，内部盛水的高度为Ｈ，放入一个球后，水面恰好与球相切，求球的半径？
C、过球面上两点只有一个球的小圆D、过球面上两点只有一个半径最小的球小圆
２、过球的一条半径的中点作垂直于这条半径的球截面，则此截面面积是球大圆面积的（）
A、/2 B、1/3 C、3/4 D、1/4
３、设地球的半径为R，求北纬600的纬线长
球O的半径R，点A、B在球面上，∠AOB= （小于 ），求A、B两点间的球面距离
姓名
班级
学号
时间
课题
多面体与球
设计
一、方法点拨：（1）了解多面体、正多面体的概念，理解欧拉公式，并利用欧拉公式解决有关
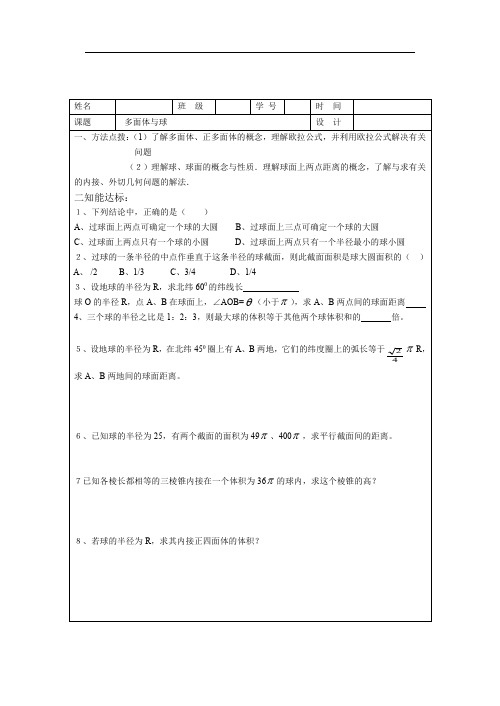
4、三个球的半径之比是1：2：3，则最大球的体积等于其他两个球体积和的倍。
５、设地球的半径为R，在北纬450圈上有A、B两地，它们的纬度圈上的弧长等于 R，求A、B两地间的球面距离。
６、已知球的半径为25，有两个截面的面积为49 、400 ，求平行截面间的距离。
７已知各棱长都相等的三棱锥内接在一个体积为36 的球内，求这个棱锥的高？
８、若球的半径为R，求其内接正四面体的体积？
９分与面数．
１０球面上三点A、B、C组成这个球的一个截面的内接三角形，AB=18,BC=24,AC=30,且球心到截面的距离为球半径的一半，（１）求球的体积，（２）求AC两点的球面距离．
１１、有一轴截面为正三角形的圆锥形容器，内部盛水的高度为Ｈ，放入一个球后，水面恰好与球相切，求球的半径？
C、过球面上两点只有一个球的小圆D、过球面上两点只有一个半径最小的球小圆
２、过球的一条半径的中点作垂直于这条半径的球截面，则此截面面积是球大圆面积的（）
A、/2 B、1/3 C、3/4 D、1/4
３、设地球的半径为R，求北纬600的纬线长
球O的半径R，点A、B在球面上，∠AOB= （小于 ），求A、B两点间的球面距离
姓名
班级
学号
时间
课题
多面体与球
设计
一、方法点拨：（1）了解多面体、正多面体的概念，理解欧拉公式，并利用欧拉公式解决有关
大纲版数学理科高考总复习9-7多面体与球
• 题型二 球面距离 • 典例2 设地球的半径为R，在北纬 45°圈上有两个点A、B，A在西经40°， B在东经50°，求A、B两点间纬线圈的 弧长及A、B两点间的球面距离．
• 【解】 如图所示，设 45°纬度圈的 中心为O1，地球中心为O， • 则∠AO1B＝40°＋50°＝90°. • 又∵OO1⊥圆O1所在平面， • ∴OO1⊥O1A，OO1⊥O1B. • 又∵A、B在北纬45°圈上， • ∴∠OBO1＝∠OAO1＝45°.
•大圆 ②球面被经过球心的平面所截得的圆 叫做 ，被不经过球心的平面 小圆 所截得的圆叫做 ； 截面 • ③球心和截面圆心的连线垂直 ； • ④球心到截面的距离 2.与球的半径 R 及 d2＝R2－rd 截面的半径r，有下面的关系：
• (3)球面距离 大圆在这两点间的一段劣弧 • 经过球面上两点的 的 长度，叫做两点的球面距离．
• 变式1 给出下列命题，其中正确的有 ( ) • ①底面是正多边形，而侧棱长与底面 边长相等的棱锥是正多面体； • ②正多面体的面不是三角形就是正方 形；
• ③长方体的各个面是正方形时，它就 是正多面体； • ④正三棱锥是正四面体． • A．①② B．③ • C．②③ D．③④
• 解析： 对于①，正多面体各面必须是 全等多边形，如果是一个正四棱锥， 且侧棱长与底面边长相等，符合条件， 但它不是正多面体；对于②，正多面 体的面在正四面体、正八面体、正二 十面体中是正三角形，在正方体中是 正方形，而在正十二面体中则是正五 边形；对于③长方体的各个面是正方 形时，它是正方体，因而是正多面体； 对于④，正三棱锥中，若侧棱长与底 面边长不相等，则它不是正多面体． • 答案：B
• 变式 3 球 O 的球面上有三点 A ， B ， C ， BC＝5 cm，∠BAC＝30°，过A，B，C 三点作球O的截面，球心到截面的距离 为12 cm. • (1)求截面的面积； • (2)求球的表面积； • (3)求球的体积．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
课堂优质
30
课堂优质
31
• 2．(2009年江西卷)体积为8的一个正方体， 其全面积与球O的表面积相等，则球O的 体积等于________．
• 【解析】 设正方体棱长为a，球半径为r.
• ∵a3＝8，∴a＝2.∵4πr2＝6a2，
课堂优质
32
课堂优质
33
课堂优质
3
• 2．球
• (1)球面和球的概念
• 半圆以它的直径 为旋转轴，旋转所成的曲
面叫做球面，球面所球围体成的几何体叫做 ，
简称球．
等于
• 球也可以看作是与定点(球心)的距离
定长(半径)的所有点的集合(轨迹)．
• (2)球的截面的性质
• ①用一个平面去截一个球，截面是大一圆 个圆 面；
小圆
• ②球面被经过球心课的堂优质平面所截得的圆叫做 4
课堂优质
25
• 【解析】 (1)证明：连结BD，因为AD⊥ 底面BCDE，AC⊥BC，AE⊥BE，所以 △ABC、△ABE、△ABD均是以AB为斜边的 直角三角形，从而点A、B、C、D、E都 在以AB为直径的同一球面上．
• (2)取AB的中点O，则O为球心，因为 ∠CBE＝90°，DE为AE在面BCDE上的射影， AE⊥BE，所以DE⊥BE，
• 【解析】 如图所示，
• ∵2πr＝12π，∴r＝6(cm)．
• 设地球仪半径为R，
课堂优质
11
课堂优质
12
• 在北纬45°圈上有A、B两点，沿该纬 线圈上A、B两点的劣弧长为 πR(R为地 球半径)，求：A、B两点的球面距离．
• 【思路点拨】 先据已知条件找出北纬 45°圈的小圆半径与地球半径的关系，再 求出AB的长，进而求距离．
间的球面距离)．
课堂优质
6
• 1．下列结论正确的是
()
• A．过球面上两点，可确定球的一个大圆
• B．过球直径的三等分点的平面不可能平 分球
• C．过球面上三点，可确定一个大圆
• D．若A、B、C是球面上三点，则过三点
的球的截面圆周是△ABC的外接圆
• 【答案】 D
课堂优质
7
• 2．(2008年湖北卷)用与球心距离为1的平
• ∴截面的面积为πr2＝25π(cm2)． • (2)∵球心到截面距离为12 cm， • ∴R2－r2＝122，R2＝122＋52＝132， • ∴R＝13. • ∴S球＝4πR2＝676π(cm2)．
课堂优质
16
•
解球的截面问题，关键是利用球
的截面圆半径、球心到截面的距离、球半
径三者之间的关系建立等式．球的表面积
课堂优质
5
•
(1)要分清球和球面的区别．球面
是曲面，是球的表面，是空间中与定点的
距离等于定长的点的集合，球是球体的简
称，是几何体，是空间中与定点的距离等
于或小于定长的点的集合．
• (2)球面距离(如A、B两点距离)的计算方法： • ①计算线段AB的长； • ②计算∠AOB； • ③求过A、B的大圆的劣弧长(即A、B两点
• (1)求证：平面ABD⊥平面ADC；
• (2)如果BD∶DC＝ ∶2，求二面角B－AC －D的大小．
课堂优质
20
• 【解析】 (1)证明：如图，设截面圆BCD 的圆心为O1，则OO1⊥面BCD.连结BD.
• 在△ABC中，O，O1分别为AC，BC的中点， ∴OO1綊
• AB，
• ∴AB⊥平面BCD，
DF⊥AC， • ∴∠DFE是二面角B－AC－D的平面角． • 设球的半径为2，则OO1＝1，AB＝2，
课堂优质
22
• ∴二面角B－AC－D的大小为60°.
课堂优质
23
•
解决有关的外接球问题时，一般
作一个适当的截面，将问题转化为平面问
题解决，这个截面通常指圆锥的轴截面，
球的大圆，多面体的对角面等，在这个截
• 第九节 多面体与球
课堂优质
1
课堂优质
2
• 1．多面体与正多面体
• (1)多面体：若干平个面多边形 体叫做多面体．
围成的几何
• (2)凸多面体：把多面体的任何一个面伸展
为平面，如果所有其他各同一面侧都在这个平面
的
，这样的多面体叫做凸多面体．
• (3)正多面，体且：以每每个个面顶都点是为有其相一同端正边都多数边有的形相 同数目的棱的凸多面体，叫做正多面体．
课堂优质
26
课堂优质
27
课堂优质
28
• 在高考中，主要考查球的性质、球面上两 点间距离、球的表面积、体积的计算以及
球的内接多面体和外切多面体等问题，多 以选择题和填空题的形式进行考查．
课堂优质
29
• 1．(2009年陕西卷)如图，球O的半径为2， 圆O1是一小圆，OO1＝ ，A、B是圆O1 上两点，若A、B两点间的球面距离为 ， 则∠AO1B＝________.
面中应包括每个几何体的主要元素，且这
个截面必须能反映出几何的主要位置关系
和数量关系．
课堂优质
24
•
2．四棱锥A—BCDE中，AD⊥底
面BCDE，AC⊥BC，AE⊥BE.
• (1)求证：A、B、C、D、E都在以AB为直 径的同一球面上；
• (2)若∠CBE＝90°，CE＝ ，AD＝1，求 B、D两点的球面距离．
和体积都是关于球半径的函数，因此要注
意运用函数与方程的思想方法去处理．
课堂优质
17
•
1．在球心的同侧有相距9 cm的
两个平行截面，它们的面积分别为49π
cm2和400π cm2，求球的表面积和体积．
课堂优质
18
课堂优质
19
• 球O的截面BCD到球心的距离等于球 的半径的一半，BC是截面圆的直径，D是 截面圆圆周上一点，CA是球O的直径．
• ∴AB⊥CD.又BC是⊙O1的直径， • ∴CD⊥BD，∴CD⊥平面ABD，
• CD⊂面ACD
• ∴平面ABD⊥平面ADC.，AB⊥平面BCD， • ∴平面BCD⊥平面ABC. • 作DE⊥BC于E，则DE⊥平面ABC， • 作EF⊥AC于F，连结DF.由三垂线定理知
课堂优质
13
课堂优质
14
•
球O的球面上有三点A，B，C，BC＝
5 cm，∠BAC＝30°，
• 过A，B，C三点作球O的截面，球心到截 面的距离为12 cm.
• (1)求截面的面积；
• (2)求球的表面积；
• (3)求球的体积．
• 【思路点拨】 画示意图，求出小圆半径 及球的半径．
课堂优质
15
• 【解析】 (1)设过A，B，C三点的外接圆 的半径为r，球的半径为R，
面去截球，所得的截面面积为π，则球的
体积为
()
【答案】 B
课堂优质
8
• 3．已知正方体的外接球的体积是 π， 则这个正方体的棱长是
()
【答案】 D
课堂优质
9
【答案】 2
课堂优质
10
• 5．某地球仪上北纬30°纬线的长度为12π cm，该地球仪的半径是________cm，表 面积是________cm2.
• ③球心和截面圆心的连垂直线截面
；
• ④球心到截面的距离d与球的半径R及截面 的半径r，有R2＝下d2面＋r的2. 关系：
• (3)球面距离
• 经过球面上两点的大圆在这两点间的劣弧的长度， 叫做两点的球面距离．
• (4)球的表面积与体积
• 半径是R的球的表面积S球4面πR＝2
V球π＝R3
.
；体积