控制工程基础第2章答案资料
控制工程基础第二章参考答案

第二章 参考答案2-1 (1) 不是 (2) 是 (3) 不是 (4) 不是 2-2 (a))()()(3)(2222t u t u dtt du RC dt t u d C R i o o o =++ (b) )()()()()()()()(2211222121222111222121t u dtt du C R C R dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (c ) )()()()()()(33221312221t u R dtt du C R R t u R R dt t du C R R R R R i i o o +=++++(d))()()()()()()()(1211222121211211222121t u dtt du C R C R dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (e))()()()()()()()(221222121211222222121t u dtt du R C C dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (f) )()()()()()()(22121221t u R dtt du L t u R R dt t du L C R R dt t u d CL R i i oo o +=++++ 2-3 (a) )]()([)()()(23213121t u R dtt du C R R t u R dt t du C R R R R i i o o +=++-(b) )()()()(4141232022213210t u R R t u R R dt t du C R R R dt t u d C C R R R R i o o o -=++ (c))]()()([)(32321t u R R dtt du C R R t u R i i o ++=-(d) )()()()()(221122212121t u dt t du C R C R dt t u d C C R R dt t du C R i i i o +++=- (e) )()()()(2412222142t u dtt du C R C R dt t u d C C R R o o o +++ )}()(])([)({21213224223221432132t u dtt du R R C C R R C R dt t u d R R C C R R R R R R i i i +++++++=- 2-4 (a) dt t dx f dt t dx f f dt t x d m i o o )()()()(12122=++ (b) dt t dx f k t x k k dt t dx f k k i o o )()()()(12121=++ (c) )()()()()(121t x k dt t dx f t x k k dt t dx f i i o o +=++ (d) )()()()()()(112121t x k dtt dx f t x k k dt t dx f f i i o o +=+++2-5 (a))(1)()()()(1)()()(2112212221211*********t u C C dt t du C R C R dt t u d R R t u C C dt t du C R C R C R dt t u d R R i i i o o o +++=++++ (b))()()()()()()()(2112212221211211212221t x k k dtt dx k f k f dt t x d f f t x k k dt t dx k f k f k f dt t x d f f i i i o o o +++=++++ 由(a)(b)两式可以看出两系统具有相同形式的微分方程,所以(a)和(b)是相似系统。
控制工程基础第二章参考答案

第二章 参考答案2-1 (1) 不是 (2) 是 (3) 不是 (4) 不是 2-2 (a))()()(3)(2222t u t u dtt du RC dt t u d C R i o o o =++ (b) )()()()()()()()(2211222121222111222121t u dtt du C R C R dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (c ) )()()()()()(33221312221t u R dtt du C R R t u R R dt t du C R R R R R i i o o +=++++(d))()()()()()()()(1211222121211211222121t u dtt du C R C R dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (e))()()()()()()()(221222121211222222121t u dtt du R C C dt t u d C C R R t u dt t du C R C R C R dt t u d C C R R i i i o o o +++=++++ (f) )()()()()()()(22121221t u R dtt du L t u R R dt t du L C R R dt t u d CL R i i oo o +=++++ 2-3 (a) )]()([)()()(23213121t u R dtt du C R R t u R dt t du C R R R R i i o o +=++-(b) )()()()(4141232022213210t u R R t u R R dt t du C R R R dt t u d C C R R R R i o o o -=++ (c))]()()([)(32321t u R R dtt du C R R t u R i i o ++=-(d) )()()()()(221122212121t u dt t du C R C R dt t u d C C R R dt t du C R i i i o +++=- (e) )()()()(2412222142t u dtt du C R C R dt t u d C C R R o o o +++ )}()(])([)({21213224223221432132t u dtt du R R C C R R C R dt t u d R R C C R R R R R R i i i +++++++=- 2-4 (a) dt t dx f dt t dx f f dt t x d m i o o )()()()(12122=++ (b) dt t dx f k t x k k dt t dx f k k i o o )()()()(12121=++ (c) )()()()()(121t x k dt t dx f t x k k dt t dx f i i o o +=++ (d) )()()()()()(112121t x k dtt dx f t x k k dt t dx f f i i o o +=+++2-5 (a))(1)()()()(1)()()(2112212221211*********t u C C dt t du C R C R dt t u d R R t u C C dt t du C R C R C R dt t u d R R i i i o o o +++=++++ (b))()()()()()()()(2112212221211211212221t x k k dtt dx k f k f dt t x d f f t x k k dt t dx k f k f k f dt t x d f f i i i o o o +++=++++ 由(a)(b)两式可以看出两系统具有相同形式的微分方程,所以(a)和(b)是相似系统。
控制工程基础第2章答案
第2章系统的数学模型(习题答案)2.1什么是系统的数学模型?常用的数学模型有哪些?解:数学模型就是根据系统运动过程的物理、化学等规律,所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。
常用的数学模型有微分方程、传递函数、状态空间模型等。
2.2 什么是线性系统?其最重要的特性是什么?解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要的特性就是它满足叠加原理。
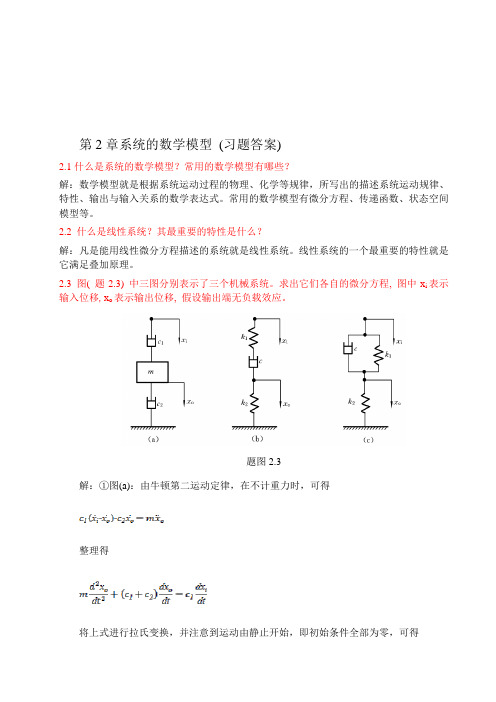
2.3 图( 题2.3) 中三图分别表示了三个机械系统。
求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。
题图2.3解:①图(a):由牛顿第二运动定律,在不计重力时,可得整理得将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[]于是传递函数为②图(b):其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并记其初始条件为零,得系统传递函数为③图(c):以的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2.4试建立下图(题图2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电压)(t u r 和位移)(t x r 为输入量;电压)(t u c 和位移)(t x c 为输出量;1,k k 和2k 为弹簧弹性系数;f 为阻尼系数。
+-+-u )tfC)+-+-f)(a )(b )(c )(d R题图2.4【解】:)(a方法一:设回路电流为i ,根据克希霍夫定律,可写出下列方程组:⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量,整理得:dtdu RC u dt du RCrc c =+方法二:dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量,各受力点任何时刻均满足∑=0F ,则有:cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ,根据牛顿运动定律,可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论:)(a 、)(b 互为相似系统,)(c 、)(d 互为相似系统。
控制工程基础第2章答案资料

函数。 (2) 以 N(s)为输入,当 R(s) = 0 时,分别以 C(s),Y(s) ,B(s),E(s) 为输出的闭环传递函
解:凡是能用线性微分方程描述的系统就是线性系统。线性系统的一个最重要的特性就是 它满足叠加原理。
2.3 图 ( 题 2.3) 中三图分别表示了三个机械系统。求出它们各自的微分方程 输入位移 , xo 表示输出位移 , 假设输出端无负载效应。
, 图中 xi 表示
题图 2.3 解:①图 (a):由牛顿第二运动定律,在不计重力时,可得 整理得
对上式进行拉氏变换,并注意到运动由静止开始,即 则系统传递函数为
2.4 试建立下图(题图 2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点, 其中电压 ur (t ) 和位移 xr (t ) 为输入量;电压 uc (t ) 和位移 xc (t ) 为输出量; k , k1 和 k2 为弹簧弹 性系数; f 为阻尼系数。
RC duc dt
uc
RCdu r dt
方法二:
Uc( s ) Ur( s )
R R1
Cs
RCs RCs 1
RC duc dt
uc
RC dur dt
由于无质量,各受力点任何时刻均满足
F 0 ,则有:
f ( dx r dt
dxc ) dt
kx c
f dxc k dt
xc
f dx r k dt
U c (s) U r (s)
( 题 图 2.15) 所示 。已知 电位器最大 工作 角 度
控制工程基础第2章答案

第2章系统的数学模型(习题答案)2.1什么是系统的数学模型?常用的数学模型有哪些?解:数学模型就是根据系统运动过程的物理、化学等规律,所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。
常用的数学模型有微分方程、传递函数、状态空间模型等。
2.2 什么是线性系统?其最重要的特性是什么?解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要的特性就是它满足叠加原理。
2.3 图( 题2.3) 中三图分别表示了三个机械系统。
求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。
题图2.3解:①图(a):由牛顿第二运动定律,在不计重力时,可得整理得将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[]于是传递函数为②图(b):其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并记其初始条件为零,得系统传递函数为③图(c):以的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2.4试建立下图(题图2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电压)(t u r 和位移)(t x r 为输入量;电压)(t u c 和位移)(t x c 为输出量;1,k k 和2k 为弹簧弹性系数;f 为阻尼系数。
+-+-u )tfC)+-+-f)(a )(b )(c )(d R题图2.4【解】:)(a方法一:设回路电流为i ,根据克希霍夫定律,可写出下列方程组:⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量,整理得:dtdu RC u dt du RCrc c =+方法二:dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量,各受力点任何时刻均满足∑=0F ,则有:cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ,根据牛顿运动定律,可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论:)(a 、)(b 互为相似系统,)(c 、)(d 互为相似系统。
《控制工程基础》第二版 (董景新 著)课后习题答案 清华出版社

Xi
G1 G2
1+G1 H1+ G2 H2 +G1G2 H3 +G1G2H1H2 )
X0
G (s) =
G 1G 2 1 + G 1 H 1 + G 2 H 2 + G 1G 2 H 3 + G 1G 2 H 1 H 2
第二章习题解
2-7: 求X0(s) 和Xi2(s) (s)之间的闭环传递函数; 求X0(s) 和Xi1(s (s)之间的闭环传递函数;
G (s) =
G1G 2G 3G 4G 5 H 1 1 + G 4 + G1G 2 + G1G 2G 4 − G1G 4G 5 H 1H 2
第二章习题解
4):求出
X 02 ( s ) X i1 ( s )
-
解:第一步,方框图整理
-
G2 G1
Xi1 +
+
+
①
H2 H1
+
② G4 ③
X02 G5 G6
( g )解:设中间变量 : xa (t ) Q k ′ = (Ds + k1 )
x 0(t) k1 k2 m x a(t) (t)
(t) fi(t)
k ′x0 (t ) = k 2 [xa (t ) − x0 (t )] k ′ + k2 D x0 (t ) ∴ xa (t ) = k2 x 又:f i (t ) = m&&a (t ) + k 2 [xa (t ) − x0 (t )] k2 ∴ G (s ) = mDs 3 + m(k1 + k 2 )s 2 + k 2 Ds + k1k 2
机械控制工程基础习题答案

第二章习题答案2-1试求下列函数的拉氏变换,假设0<t 时,0)(=t f(1))3cos 1(5)(t t f -= 答案:⎪⎭⎫⎝⎛+-=22315)(s s s s F (2)t et f t10cos )(5.0-= 答案:2210)5.0(5.0)(+++=s s s F (3))35sin()(π+=t t f 答案:22225235521)(+⋅++⋅=s s s s F (4)atn e t t f =)( 答案:1)(!)(+-=n a s n s F 2-2求下列函数的拉氏变换(1)te t t tf 33232)(-++= 答案:32182)(42+++=s ss s F (2))0(4sin 2cos )(333≥++=---t te t e e t tf t t t答案:222244)3(42)1(1)3(6)(++++++++=s s s s s F(3)te t t tf 22)1()2(15)(-+-⋅= 答案:)2(32)2(25)(----+=s s e s e s s F (4)⎩⎨⎧><≤≤=ππt t t tt f ,000sin )(答案:提示)sin(sin )(π-+=t t t f ,se s s s F π-+++=1111)(22 2-3已知)1(10)(+=s s s F(1)利用终值定理,求∞→t 时)(t f 值 答案:10)1(10lim )(lim )(lim 0=+==→→∞→s s ss sF t f s s t(2)通过取)(s F 的拉氏反变换,求∞→t 时)(t f 值答案:[]()101)(10lim 11110lim )(lim )(lim 11=-⋅=⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+-==-∞→-∞→-∞→∞→tt t t t e t s s L s F L t f 2-4已知2)2(1)(+=s s F (1)利用初值定理,求)0(f 和)0(f '的值。
机械控制工程基础第二章的答案及解析
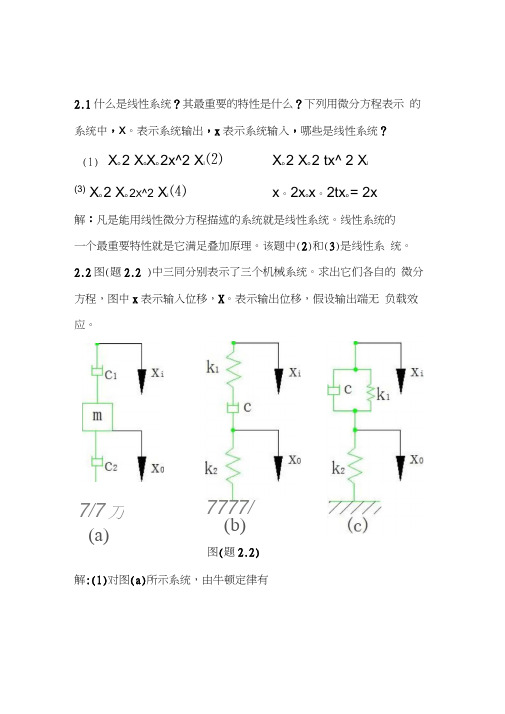
2.1什么是线性系统?其最重要的特性是什么?下列用微分方程表示 的系统中,x 。
表示系统输出,x 表示系统输入,哪些是线性系统? (1)X o2 X oX o2x^2 X i⑵X o2 X o 2 tx^ 2 Xi(3)X o2 X o2X ^2 X i⑷x 。
2x ox 。
2tx o= 2x解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的 一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系 统。
2.2图(题2.2 )中三同分别表示了三个机械系统。
求出它们各自的 微分方程,图中x 表示输入位移,X 。
表示输出位移,假设输出端无 负载效应。
图(题2.2)解:(1)对图(a)所示系统,由牛顿定律有7/7刀 (a)7777/ (b)c i( x —x 。
) —C 2X 。
二 mx 。
mx 。
( c iC 2)x 。
二 c iXi(X j-x)k i= c(x-x 。
)c(xx °) = k 2x 。
(1) (2)消除中间变量有c (总- k 2)x 。
- k ik zx 。
二 ckix(3) 对图(c)所示系统,由牛顿定律有c ( X - x 。
) k i( X - x 。
)= k zx 。
1c x°+ ( ki+ k 2)x °=cx+ kix2.3 求出图(题2.3)所示电系统的微分方程。
(a)图(题2.3)解:(1)对图⑻ 所示系统,设j 1为流过R 的电流,j 为总电流,则有1 u 厂 R ?iidtC2□ 一 u 。
二 R i j i对图(b)所示系统,引入一中间变量 x,并由牛顿定律有RiCiUiUnR解:设系统输入为M (即),输出二(即),分别对圆盘和质块进行动 力学分析,列写动力学方程如下:1U i-U 。
(i-i i)dtC1消除中间变量,并化简有C 1R 2U(1RC ) U 。
-= 0^+(肯+ C2)⑵ 对图(b )所示系统,设i 为电流,则有1CR 2U 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章系统的数学模型(习题答案)2.1什么是系统的数学模型?常用的数学模型有哪些?解:数学模型就是根据系统运动过程的物理、化学等规律,所写出的描述系统运动规律、特性、输出与输入关系的数学表达式。
常用的数学模型有微分方程、传递函数、状态空间模型等。
2.2 什么是线性系统?其最重要的特性是什么?解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的一个最重要的特性就是它满足叠加原理。
2.3 图( 题2.3) 中三图分别表示了三个机械系统。
求出它们各自的微分方程, 图中x i表示输入位移, x o表示输出位移, 假设输出端无负载效应。
题图2.3解:①图(a):由牛顿第二运动定律,在不计重力时,可得整理得将上式进行拉氏变换,并注意到运动由静止开始,即初始条件全部为零,可得[]于是传递函数为②图(b):其上半部弹簧与阻尼器之间,取辅助点A,并设A点位移为x,方向朝下;而在其下半部工。
引出点处取为辅助点B。
则由弹簧力与阻尼力平衡的原则,从A和B两点可以分别列出如下原始方程:消去中间变量x,可得系统微分方程对上式取拉氏变换,并记其初始条件为零,得系统传递函数为③图(c):以的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:移项整理得系统微分方程对上式进行拉氏变换,并注意到运动由静止开始,即则系统传递函数为2.4试建立下图(题图2.4)所示各系统的微分方程并说明这些微分方程之间有什么特点,其中电压)(t u r 和位移)(t x r 为输入量;电压)(t u c 和位移)(t x c 为输出量;1,k k 和2k 为弹簧弹性系数;f 为阻尼系数。
+-+-C)(t u r )(t u c )(t r )(t x c f1k 2k CR)(t u r )(u c +-+-f)(t r )(t x c )(a )(b )(c )(d R 2R题图2.4【解】:)(a方法一:设回路电流为i ,根据克希霍夫定律,可写出下列方程组:⎪⎩⎪⎨⎧=+=⎰i R u u dt i C u cc r 1消去中间变量,整理得:dtdu RC u dt du RCrc c =+方法二:dtdu RC u dt du RCRCs RCs CsR R s U s U rc c r c =+⇒+=+=11)()( 由于无质量,各受力点任何时刻均满足∑=0F ,则有:cc r kx dt dxdt dx f =-)(dtdx k f x dt dx k f rc c =+⇒()r r c c r c u dtduC R u dt du C R R Cs R R Cs R Cs R R CsR s U s U +=++⇒+++=+++=221212212)(1111)()( 设阻尼器输入位移为a x ,根据牛顿运动定律,可写出该系统运动方程r rc c aa c a r c r x dtdx k f x dt dx f k k k k dt dx f x x k x x k x x k +=++⇒⎪⎩⎪⎨⎧=--=-22121221)()()( 结论:)(a 、)(b 互为相似系统,)(c 、)(d 互为相似系统。
四个系统均为一阶系统。
2.5试求下图(题图2.5)所示各电路的传递函数。
)(t +_1R ++__u )1R ++u )__)(a ++__C u ))(b )(c )(d题图2.5【解】:可利用复阻抗的概念及其分压定理直接求传递函数。
(a)1212212222212)()(1//)1(//)1()()(R s L C R R LCs R R s LCR R CsR Ls R Cs R LsR Cs s U s U r c ++++=+⨯+++= (b)1)(1)(1)1//(1//1)()(21221122121221122121221111+++++++=++-=s C R C R C R s C C R R s C R C R s C C R R sC R s C R sC R s U s U r c (c) 2121212212)()//(1)//(1)()(R R s L C R R LCs R Ls R Ls R CsR Ls R Cs s U s U r c +++++=+++= (d)sC R Rs C R s C R R sC R s C R s C R sC s U s U r c 121121211//)1(//)1(1//)1(1)()(+⨯++++++=1)2(1221221212212+++++=s RC RC s C C R s RC s C C R2.6求图( 题图2.6) 所示两系统的微分方程。
题图2.6解(1)对图(a )所示系统,由牛顿定律有即(2)对图(b )所示系统,由牛顿定律有其中2.7 求图( 题图2.7) 所示机械系统的微分方程。
图中M为输入转矩,C m为圆周阻尼,J 为转动惯量。
圆周半径为R,设系统输入为M(即M(t)),输出为(即),题图2.7解:分别对圆盘和质块进行动力学分析,列写动力学方程如下:消除中间变量x,即可得到系统动力学方程+k(c)2.8 求图( 题图2.8) 所示系统的传递函数(f(t)为输入,y2(t)为输出)。
解分别对,进行受力分析,列写其动力学方程有对上两式分别进行拉氏变换有消除得2.9 若系统传递函数方框图如图(题图2.9) 所示, 求:(1) 以R(s)为输入,当N(s) = 0 时,分别以C(s),Y(s),B(s),E(s) 为输出的闭环传递函数。
(2) 以N(s)为输入,当R(s) = 0 时,分别以C(s),Y(s),B(s),E(s) 为输出的闭环传递函数。
(3) 比较以上各传递函数的分母,从中可以得出什么结论。
题图2.8 题图2.9解(1)以为输入,当N()=0时:若以C()为输出,有若以Y ()为输出,有若以B ()为输出,有若以E ()为输出,有(2)以为输入,当R()=0时:若以C ()为输出,有若以Y ()为输出,有若以B ()为输出,有若以E ()为输出,有(3)从上可知:对于同一个闭环系统,当输入的取法不同时,前向通道的传递函数不同,反馈回路的传递函数不同,系统的传递函数也不同,但系统的传递函数分母保持不变,这是因为这一分母反映了系统的固有特性,而与外界无关。
2.10 求出图( 题图2 .10) 所示系统的传递函数)(/)(S X S X i o 。
题图2.10G 1G 2G 3G 4H 1H 3G 4H 3H 4G 4-+--X 0(s)-G 1G 2G 4H 1H 3 -H 3G 4---Xi(s)X 0(s)G 31+G 3G 4H 4-G 4H 3 -H 3G 4-Xi(s)X 0(s)G 1G 2G 31+G 3G 4H 4-G 2G 3H 3-解方法一:利用公式(2.3.1),可得方法二:利用方框图简化规则,有图(题2.16.b )2.11 求出图( 题图2 .11) 所示系统的传递函数)(/)(S X S X i o 。
解根据方框图简化的规则,有图(题2.17.b )题图2.11H 3+Xi(s)X 0(s)G 4+G 4+-G 4G 1G 3G 5H 3-Xi(s)X 0(s)G 4+G 1G 2G 3G 1G 2G 3G 1G 2G 31+G 1G 2G 3H 3H 42.12 图(题图2 .12) 所示为一个单轮汽车支撑系统的简化模型。
1m 代表汽车质量,B 代表振动阻尼器,1K 为弹簧,2m 为轮子的质量,2K 为轮胎的弹性,试建立系统的数学模型。
题图2.12问题2 质点振动系统。
这是一个单轮汽车支撑系统的简化模型。
代表汽车质量,B 代表振动阻尼器,为弹簧,为轮子的质量,为轮胎的弹性,建立质点平移系统数学模型。
解答:拉氏变换:2.13 液压阻尼器原理如图(题图2.13)所示。
其中,弹簧与活塞刚性联接,忽略运动件的惯性力,且设i x 为输入位移,o x 为输出位移,k 弹簧刚度,c 为粘性阻尼系数,求输出与输入之间的传递函数。
X 0X tk题图2.13解:1)求系统的传递函数 活塞的力平衡方程式为)]()([)(t x t x dtdct kx o i o -= 经拉氏变换后有)]()([)(s X s X cs s kX o i o -=解得传递函数为1)()()(+==Ts Tss X s X s G i o 式中,RC T =为时间常数。
2.14 由运算放大器组成的控制系统模拟电路图如图(题图2.14)所示,试求闭环传递函数)(/)(s U s U r cR 0R 1— K — K — KC 1C 2R 0R 0R 0R 2uU题图2.14解:式(1)(2)(3)左右两边分别相乘得即所以:2.15 某位置随动系统原理方块图如图(题图 2.15)所示。
已知电位器最大工作角度0max 330=θ,功率放大级放大系数为3K ,要求:(1) 分别求出电位器传递系数0K 、第一级和第二级放大器的比例系数1K 和2K ; (2) 画出系统结构图;(3) 简化结构图,求系统传递函数)(/)(s s i o θθ;10k+SMTG30k20k10k— K 1— K 2+15V-15V+15V -15VK 0θ10k10k功放K 3K 0θ+题图2.15 位置随动系统原理图解: (1)=3=2(2)系统结构图如下:(3)系统传递函数2.16 设直流电动机双闭环调速系统的原理图如图(题图2.16)所示,要求: (1)分别求速度调节器和电流调节器的传递函数;(2)画出系统结构图(设可控电路传递函数为)1/(32+s K τ;电流互感器和测速发电机的传递函数分别为4K 和5K );(3)简化系统结构图,求系统传递函数)(/)(s U s i Ω。
RC 1+—负载SMTGU iRR 1R 2RRC 2— K— KU a速度调节器电流调节器电流互感器晶闸管电路扼流圈ωU f题图2.16 直流电动机调速系统原理图解:(1)速调流调(2)系统结构图如下(3)简化结构图,求系统传递函数因为求系统传递函数,所以令,系统结构图如下:所以:。
