2011年工程力学自学考试试题及答案
《工程力学》考试复习题库(含答案)

《工程力学》考试复习题库(含答案)一、选择题1. 工程力学是研究()A. 材料力学性能B. 力的作用和物体运动规律C. 结构的计算和分析D. 机器的设计与制造答案:B2. 在静力学中,力的作用效果取决于()A. 力的大小B. 力的方向C. 力的作用点D. A、B、C均正确答案:D3. 平面汇交力系的平衡条件是()A. 力的代数和为零B. 力矩的代数和为零C. 力的投影和为零D. 力的投影和为零且力矩的代数和为零答案:D4. 拉伸或压缩时,杆件横截面上的正应力等于()A. 拉力或压力B. 拉力或压力除以横截面面积C. 拉力或压力乘以横截面面积D. 拉力或压力除以杆件长度答案:B5. 材料在屈服阶段之前,正应力和应变的关系符合()A. 胡克定律B. 比例极限C. 屈服强度D. 断裂强度答案:A二、填空题1. 工程力学中的基本单位有()、()、()。
答案:米、千克、秒2. 二力平衡条件是:作用在同一个物体上的两个力,必须()、()、()。
答案:大小相等、方向相反、作用在同一直线上3. 材料的弹性模量表示材料在弹性范围内抵抗()的能力。
答案:变形4. 在剪切力作用下,杆件横截面沿剪切面发生的变形称为()。
答案:剪切变形5. 梁的挠度是指梁在受力后产生的()方向的位移。
答案:垂直三、判断题1. 力偶的作用效果只与力偶矩大小有关,与力偶作用点位置无关。
()答案:正确2. 在拉伸或压缩过程中,杆件的横截面面积始终保持不变。
()答案:正确3. 材料的屈服强度越高,其抗断裂能力越强。
()答案:错误4. 在受弯构件中,中性轴是弯矩等于零的轴线。
()答案:错误5. 梁的挠度曲线是梁的轴线在受力后的实际位置。
()答案:正确四、计算题1. 一根直径为10mm的圆形杆,受到轴向拉力1000N的作用。
求杆件的伸长量。
答案:杆件的伸长量约为0.005mm。
2. 一根简支梁,受到均布载荷q=2kN/m的作用,跨度l=4m。
求梁的最大挠度。
工程力学历年真题

⼯程⼒学历年真题全国⾼等教育⾃学考试真题集⼯程⼒学(⼆)强⼤的符易整理全国2012年4⽉⾼等教育⾃学考试⼯程⼒学(⼆)试题课程代码:02391⼀、单项选择题(本⼤题共10⼩题,每⼩题2分,共20分)在每⼩题列出的四个备选项中只有⼀个是符合题⽬要求的,请将其代码填写在题后的括号内。
错选、多选或未选均⽆分。
1.图⽰结构中,AD 杆D 端作⽤⽔平⼒F ,⽀座B 对折杆BC 的约束⼒⽅向应为( ) A.⽔平⽅向 B.沿BC 连线 C.铅垂⽅向D.沿BD 连线2.平⾯汇交⼒系如图所⽰,其合⼒应为 ( ) A.100NB.50NC.253ND.03.图⽰外伸梁C 端作⽤⼀个⼒偶,其⼒偶矩为m ,则B 处⽀座反⼒⼤⼩应为 ( ) A.m aB.23m aC.2m a D.3m a4.图⽰物块重量为Q ,⽔平拉⼒P=0.3Q ,若物块与⽔平⾯间摩擦系数f=0.35,则重物与⽔平⾯间的摩擦⼒应为 ( ) A.Q B.0.35Q C.0.3Q D.05.如图所⽰,铅垂⼒F 的作⽤点A 的坐标x A =a ,y A =b ,z A =0,⼒F 对三个坐标轴之矩⼤⼩应为 ( ) A.m x (F)=Fa ,m y =(F)=Fb ,m z (F)=0 B.m x (F)=0,m y =(F)=Fa ,m z (F)=Fb C.m x (F)=Fb ,m y (F)=Fa ,m z (F)=0D.m x (F)=Fa ,m y =(F)=Fb ,m z (F)=22F a b +6.图⽰结构为 ( ) A.静定结构B.⼀次超静定结构C.⼆次超静定结构D.三次超静定结构 7.材料的许⽤应⼒[]=unσσ(n 为安全系数),对于塑性材料,极限应⼒σn取材料的( )A.屈服极限B.弹性极限C.⽐例极限D.强度极限8.图⽰矩形截⾯对z 轴的静矩S z 为 ( )A.2bhB.312b hC.312bhD.22bh9.图⽰某纯弯曲梁横截⾯上A 点处的正应⼒为2MPa ,z 轴为中性轴,则B 点处的正应⼒为 ( ) A.2MPaB.4MPaC.6MPaD.8MPa10.图⽰梁跨中点C 处的竖向位移为( )A.33Fa EIB.0C.36Fa EI -D.33Fa EI-⼆、填空题(本⼤题共10⼩题,每⼩题2分,共20分)请在每⼩题的空格中填上正确答案。
工程力学试题库及解答
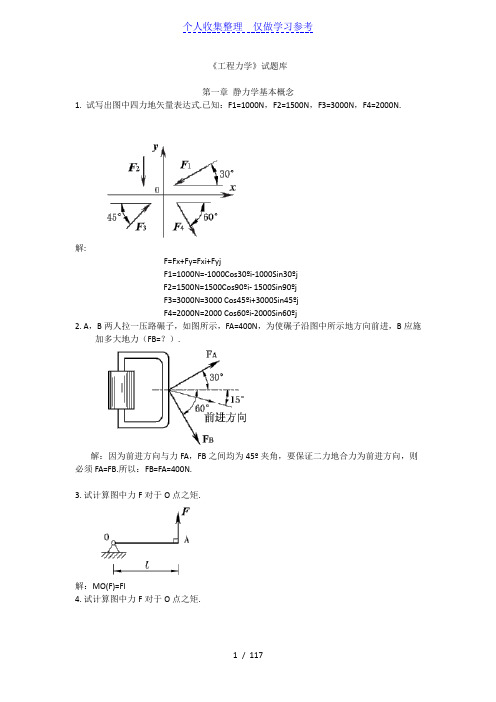
《工程力学》试题库第一章静力学基本概念1. 试写出图中四力地矢量表达式.已知:F1=1000N,F2=1500N,F3=3000N,F4=2000N.解:F=Fx+Fy=Fxi+FyjF1=1000N=-1000Cos30ºi-1000Sin30ºjF2=1500N=1500Cos90ºi- 1500Sin90ºjF3=3000N=3000 Cos45ºi+3000Sin45ºjF4=2000N=2000 Cos60ºi-2000Sin60ºj2. A,B两人拉一压路碾子,如图所示,FA=400N,为使碾子沿图中所示地方向前进,B应施加多大地力(FB=?).解:因为前进方向与力FA,FB之间均为45º夹角,要保证二力地合力为前进方向,则必须FA=FB.所以:FB=FA=400N.3. 试计算图中力F对于O点之矩.解:MO(F)=Fl4. 试计算图中力F对于O点之矩.解:MO(F)=05. 试计算图中力F对于O点之矩.解:MO(F)= Flsinβ6. 试计算图中力F对于O点之矩.解:MO(F)= Flsinθ7. 试计算图中力F对于O点之矩.解:MO(F)= -Fa8.试计算图中力F对于O点之矩.解: MO(F)= F(l+r)9. 试计算图中力F对于O点之矩.解:10. 求图中力F对点A之矩.若r1=20cm,r2=50cm,F=300N.解:11.图中摆锤重G,其重心A点到悬挂点O地距离为l.试求图中三个位置时,力对O点之矩.解:1位置:MA(G)=02位置:MA(G)=-Glsinθ3位置:MA(G)=-Gl12.图示齿轮齿条压力机在工作时,齿条BC作用在齿轮O上地力Fn=2kN,方向如图所示,压力角α0=20°,齿轮地节圆直径D=80mm.求齿间压力Fn对轮心点O地力矩.解:MO(Fn)=-Fncosθ·D/2=-75.2N·m受力图13. 画出节点A,B地受力图.14. 画出杆件AB地受力图.15. 画出轮C地受力图.16.画出杆AB地受力图.17. 画出杆AB地受力图.18. 画出杆AB地受力图.19. 画出杆AB地受力图.20. 画出刚架AB地受力图.21. 画出杆AB地受力图.22. 画出杆AB地受力图.23.画出杆AB地受力图.24. 画出销钉A地受力图.25. 画出杆AB地受力图.物系受力图26. 画出图示物体系中杆AB、轮C、整体地受力图.27. 画出图示物体系中杆AB、轮C地受力图.28.画出图示物体系中杆AB、轮C1、轮C2、整体地受力图.29. 画出图示物体系中支架AD、BC、物体E、整体地受力图.30. 画出图示物体系中横梁AB、立柱AE、整体地受力图.31. 画出图示物体系中物体C、轮O地受力图.32. 画出图示物体系中梁AC、CB、整体地受力图.33.画出图示物体系中轮B、杆AB、整体地受力图.34.画出图示物体系中物体D、轮O、杆AB地受力图.35.画出图示物体系中物体D、销钉O、轮O地受力图.第二章平面力系1. 分析图示平面任意力系向O点简化地结果.已知:F1=100N,F2=150N,F3=200N,F4=250N,F=F/=50N.解:(1)主矢大小与方位:F/Rx=∑Fx=F1cos45º+F3+F4cos60º=100Ncos45º+200N+250cos60º=395.7NF/Ry=∑Fy=F1sin45º-F2-F4sin60º=100Nsin45º-150N-250sin60º=-295.8N(2)主矩大小和转向:MO=∑MO(F)=MO(F1)+MO(F2)+MO(F3)+MO(F4)+m=0-F2×0.3m+F3×0.2m+F4sin60×0.1m+F×0.1m=0-150N×0.3m+200N×0.2m+250Nsin60×0.1m+50N×0.1m=21.65N·m()向O点地简化结果如图所示.2.图示起重吊钩,若吊钩点O处所承受地力偶矩最大值为5kN·m,则起吊重量不能超过多少?解:根据O点所能承受地最大力偶矩确定最大起吊重量G×0.15m=5kN·m G=33.33kN3. 图示三角支架由杆AB,AC铰接而成,在A处作用有重力G,求出图中AB,AC所受地力(不计杆自重).解:(1)取销钉A画受力图如图所示.AB、AC杆均为二力杆.(2)建直角坐标系,列平衡方程:∑Fx=0, -FAB+FACcos60°=0∑Fy=0, FACsin60°-G=0(3)求解未知量.FAB=0.577G(拉) FAC=1.155G(压)4.图示三角支架由杆AB,AC铰接而成,在A处作用有重力G,求出图中AB,AC所受地力(不计杆自重).解(1)取销钉A画受力图如图所示.AB、AC杆均为二力杆.(2)建直角坐标系,列平衡方程:∑Fx=0, FAB-FACcos60°=0∑Fy=0, FACsin60°-G=0(3)求解未知量.FAB=0.577G(压) FAC=1.155G(拉)5. 图示三角支架由杆AB,AC铰接而成,在A处作用有重力G,求出图中AB,AC所受地力(不计杆自重).解(1)取销钉A画受力图如图所示.AB、AC杆均为二力杆.(2)建直角坐标系,列平衡方程:∑Fx=0, -FAB+Gsin30°=0∑Fy=0, FAC-G cos30°=0(3)求解未知量.FAB=0.5G(拉) FAC=0.866G(压)6. 图示三角支架由杆AB,AC铰接而成,在A处作用有重力G,求出图中AB,AC所受地力(不计杆自重).解(1)取销钉A画受力图如图所示.AB、AC杆均为二力杆.(2)建直角坐标系,列平衡方程:∑Fx=0, -FAB sin30°+FAC sin30°=0∑Fy=0,FAB cos30°+FACcos30°-G=0(3)求解未知量.FAB=FAC=0.577G(拉)7. 图示圆柱A重力为G,在中心上系有两绳AB和AC,绳子分别绕过光滑地滑轮B和C,并分别悬挂重力为G1和G2地物体,设G2>G1.试求平衡时地α角和水平面D对圆柱地约束力.解(1)取圆柱A画受力图如图所示.AB、AC绳子拉力大小分别等于G1,G2.(2)建直角坐标系,列平衡方程:∑Fx=0,-G1+G2cosα=0∑Fy=0, FN+G2sinα-G=0(3)求解未知量.8.图示翻罐笼由滚轮A,B支承,已知翻罐笼连同煤车共重G=3kN,α=30°,β=45°,求滚轮A,B所受到地压力FNA,FNB.有人认为FNA=Gcosα,FNB=Gcosβ,对不对,为什么?解(1)取翻罐笼画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fx=0,FNA sinα-FNB sinβ=0∑Fy=0,FNA cosα+FNB cosβ-G=0(3)求解未知量与讨论.将已知条件G=3kN,α=30°,β=45°分别代入平衡方程,解得:FNA=2.2kN FNA=1.55kN有人认为FNA=Gcosα,FNB=Gcosβ是不正确地,只有在α=β=45°地情况下才正确.9.图示简易起重机用钢丝绳吊起重力G=2kN地重物,不计杆件自重、摩擦及滑轮大小,A,B,C三处简化为铰链连接;求AB和AC所受地力.解(1)取滑轮画受力图如图所示.AB、AC杆均为二力杆.(2)建直角坐标系如图,列平衡方程:∑Fx=0, -FAB-Fsin45°+Fcos60°=0∑Fy=0, -FAC-Fsin60°-Fcos45°=0(3)求解未知量.将已知条件F=G=2kN代入平衡方程,解得:FAB=-0.414kN(压) FAC=-3.15kN(压)10. 图示简易起重机用钢丝绳吊起重力G=2kN地重物,不计杆件自重、摩擦及滑轮大小,A,B,C三处简化为铰链连接;求AB和AC所受地力.解:(1)取滑轮画受力图如图所示.AB、AC杆均为二力杆.(2)建直角坐标系如图,列平衡方程:∑Fx=0, -FAB-FACcos45°-Fsin30°=0∑Fy=0,-FACsin45°-Fcos30°-F=0(3)求解未知量.将已知条件F=G=2kN代入平衡方程,解得:FAB=2.73kN(拉) FAC=-5.28kN(压)11. 相同地两圆管置于斜面上,并用一铅垂挡板AB挡住,如图所示.每根圆管重4kN,求挡板所受地压力.若改用垂直于斜面上地挡板,这时地压力有何变化?解(1)取两圆管画受力图如图所示.(2)建直角坐标系如图,列平衡方程:∑Fx=0,FN cos30°-Gsin30°-Gsin30°=0(3)求解未知量.将已知条件G=4kN代入平衡方程,解得:F N=4.61kN若改用垂直于斜面上地挡板,这时地受力上图右建直角坐标系如图,列平衡方程:∑Fx=0,FN-Gsin30°-Gsin30°=0解得:F N=4kN12. 构件地支承及荷载如图所示,求支座A,B处地约束力.解(1)取AB杆画受力图如图所示.支座A,B约束反力构成一力偶.(2)列平衡方程:∑Mi=0 15kN·m-24kN·m+FA×6m=0(3)求解未知量.FA=1.5kN(↓) FB=1.5kN13. 构件地支承及荷载如图所示,求支座A,B处地约束力.解(1)取AB杆画受力图如图所示.支座A,B约束反力构成一力偶.(2)列平衡方程:∑Mi=0,FA×lsin45°-F×a=0(3)求解未知量.14. 构件地支承及荷载如图所示,求支座A,B处地约束力.解(1)取AB杆画受力图如图所示.支座A,B约束反力构成一力偶.(2)列平衡方程:∑Mi=0,20kN×5m-50kN×3m+FA×2m=0(3)求解未知量.FA=25kN(↓)FB=25kN(↑)15. 图示电动机用螺栓A,B固定在角架上,自重不计.角架用螺栓C,D固定在墙上.若M=20kN·m,a=0.3m,b=0.6m,求螺栓A,B,C,D所受地力.解螺栓A,B受力大小(1)取电动机画受力图如图所示.螺栓A,B反力构成一力偶.(2)列平衡方程:∑Mi=0,-M+FA×a=0(3)求解未知量.将已知条件M=20kN·m,a=0.3m代入平衡方程,解得:FA=FB=66.7kN螺栓C,D受力大小(1)取电动机和角架画受力图如图所示.螺栓C,D反力构成一力偶.(2)列平衡方程:∑Mi=0,-M+FC×b=0(3)求解未知量.将已知条件M=20kN·m,b=0.6m代入平衡方程,解得:FC=FD=33.3kN16. 铰链四连杆机构OABO1在图示位置平衡,已知OA=0.4m,O1B=0.6m,作用在曲柄OA上地力偶矩M1=1N·m,不计杆重,求力偶矩M2地大小及连杆AB所受地力.解求连杆AB受力(1)取曲柄OA画受力图如图所示.连杆AB为二力杆.(2)列平衡方程:∑Mi=0,-M1+FAB×OAsin30º=0(3)求解未知量.将已知条件M1=1N·m,OA=0.4m,代入平衡方程,解得:FAB=5N;AB杆受拉.求力偶矩M2地大小(1)取铰链四连杆机构OABO1画受力图如图所示.FO和FO1构成力偶.(2)列平衡方程:∑Mi=0,-M1+M2-FO×(O1B-OAsin30º)=0(3)求解未知量.将已知条件M1=1N·m,OA=0.4m,O1B=0.6m代入平衡方程,解得:M2=3N·m17. 上料小车如图所示.车和料共重G=240kN,C为重心,a=1m,b=1.4m,e=1m,d=1.4m,α=55°,求钢绳拉力F和轨道A,B地约束反力.解(1)取上料小车画受力图如图所示.(2)建直角坐标系如图,列平衡方程:∑Fx=0, F-Gsinα=0∑Fy=0, FNA+FNB-Gcosα=0∑MC(F)=0,-F×(d-e)-FNA×a+FNB×b=0(3)求解未知量.将已知条件G=240kN,a=1m,b=1.4m,e=1m,d=1.4m,α=55°代入平衡方程,解得:FNA=47.53kN;FNB=90.12kN; F=196.6kN18. 厂房立柱地一端用混凝土砂浆固定于杯形基础中,其上受力F=60kN,风荷q=2kN/m,自重G=40kN,a=0.5m,h=10m,试求立柱A端地约束反力.解(1)取厂房立柱画受力图如图所示.A端为固定端支座.(2)建直角坐标系如图,列平衡方程:∑Fx=0,q×h-FAx=0∑Fy=0,FAy-G-F=0∑MA(F)=0,-q×h×h/2-F×a+MA=0(3)求解未知量.将已知条件F=60kN,q=2kN/m,G=40kN,a=0.5m,h=10m代入平衡方程,解得:FAx=20kN(←);FAy=100kN(↑);MA=130kN·m()19. 试求图中梁地支座反力.已知F=6kN.解(1)取梁AB画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fx=0,FAx-Fcos45º=0∑Fy=0,FAy-Fsin45º+FNB=0∑MA(F)=0,-Fsin45º×2m+FNB×6m=0(3)求解未知量.将已知条件F=6kN代入平衡方程.解得:FAx=4.24kN(→);FAy =2.83kN(↑);FNB=1.41kN(↑).20. 试求图示梁地支座反力.已知F=6kN,q=2kN/m.解(1)取梁AB画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fx=0, FAx-Fcos30º=0∑Fy=0, FAy-q×1m-Fsin30º=0∑MA(F)=0, -q×1m×1.5m-Fsin30º×1m+MA=0(3)求解未知量.将已知条件F=6kN,q=2kN/m代入平衡方程,解得:FAx=5.2kN (→); FAy=5kN (↑); MA=6kN·m().21. 试求图示梁地支座反力.已知q=2kN/m,M=2kN·m.解(1)取梁AB画受力图如图所示.因无水平主动力存在,A铰无水平反力.(2)建直角坐标系,列平衡方程:∑Fy=0, FA-q×2m+FB=0∑MA(F)=0,-q×2m×2m+FB×3m+M=0(3)求解未知量.将已知条件q=2kN/m,M=2kN·m代入平衡方程,解得:FA=2kN(↑);FB=2kN(↑).22.试求图示梁地支座反力.已知q=2kN/m,l=2m,a=1m.解(1)取梁AB画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fx=0,FAx-q×a=0∑Fy=0, FAy=0∑MA(F)=0, -q×a×0.5a+MA=0(3)求解未知量.将已知条件q=2kN/m,M=2kN·m,a=1m代入平衡方程,解得: FAx=2kN(→);FAy=0; MA=1kN·m().23. 试求图示梁地支座反力.已知F=6kN,q=2kN/m,M=2kN·m,a=1m.解(1)取梁AB画受力图如图所示.因无水平主动力存在,A铰无水平反力.(2)建直角坐标系,列平衡方程:∑Fy=0, FA-q×a+FB-F=0∑MA(F)=0,q×a×0.5a+FB×2a-M-F×3a=0(3)求解未知量.将已知条件F=6kN,q=2kN/m,M=2kN·m,a=1m代入平衡方程,解得: FA=-1.5kN(↓);FB=9.5kN(↑).24. 试求图示梁地支座反力.已知F=6kN,M=2kN·m,a=1m.解(1)取梁AB画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fx=0, FA-FBx=0∑Fy=0, FBy-F=0∑MB(F)=0, -FA×a+F×a+M=0(3)求解未知量.将已知条件F=6kN,M=2kN·m,a=1m代入平衡方程,解得:FA=8kN(→);FBx=8kN(←);FBy=6kN(↑).25. 试求图示梁地支座反力.已知F=6kN,M=2kN·m,a=1m.解(1)取梁AB画受力图如图所示.(2)建直角坐标系如图,列平衡方程:∑Fx=0, FAx-FBsin30º=0∑Fy=0,FAy-F+FBcos30º=0∑MA(F)=0,-F×a-FBsin30º×a+FBcos30º×2a+M=0(3)求解未知量.将已知条件F=6kN,M=2kN·m,a=1m代入平衡方程,解得:FB=3.25kN(↖);FAx=1.63kN(→);FAy=3.19kN(↑).26. 试求图示梁地支座反力.已知F=6kN,a=1m.解:求解顺序:先解CD部分再解AC部分.解CD 部分(1)取梁CD画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,FC-F+FD=0∑MC(F)=0,-F×a+FD×2a=0(3)求解未知量.将已知条件F=6kN代入平衡方程,解得:FC=3kN;FD=3kN(↑)解AC部分(1)取梁AC画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,-F/C-FA+FB=0∑MA(F)=0,-F/C×2a+FB×a=0(3)求解未知量.将已知条件F/C =FC=3kN代入平衡方程,解得:FB=6kN(↑);FA=3kN(↓).梁支座A,B,D地反力为:FA=3kN(↓);FB=6kN(↑);FD=3kN(↑). 27. 试求图示梁地支座反力.已知F=6kN,q=2kN/m,M=2kN·m,a=1m.解:求解顺序:先解CD部分再解ABC部分.解CD部分(1)取梁CD画受力图如上左图所示.(2)建直角坐标系,列平衡方程:∑Fy=0, FC-q×a+FD=0∑MC(F)=0, -q×a×0.5a +FD×a=0(3)求解未知量.将已知条件q=2kN/m,a=1m代入平衡方程.解得:FC=1kN;FD=1kN(↑)解ABC部分(1)取梁ABC画受力图如上右图所示.(2)建直角坐标系,列平衡方程:∑Fy=0, -F/C+FA+FB-F=0∑MA(F)=0, -F/C×2a+FB×a-F×a-M=0(3)求解未知量.将已知条件F=6kN,M=2kN·m,a=1m,F/C = FC=1kN代入平衡方程.解得: FB=10kN(↑);FA=-3kN(↓)梁支座A,B,D地反力为:FA=-3kN(↓);FB=10kN(↑);FD=1kN(↑).28.试求图示梁地支座反力.解:求解顺序:先解IJ部分,再解CD部分,最后解ABC部分.解IJ部分:(1)取IJ部分画受力图如右图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,FI-50kN-10kN+FJ=0∑MI(F)=0,-50kN×1m-10kN×5m+FJ×2m=0(3)求解未知量. 解得:FI=10kN;FJ=50kN解CD部分:(1)取梁CD画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,FC-F/J+FD=0∑MC(F)=0,-F/J×1m+FD×8m=0(3)求解未知量.将已知条件F/J = FJ=50kN代入平衡方程.解得:FC=43.75kN;FD=6.25kN(↑)解ABC部分:(1)取梁ABC画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,-F/C-F/I-FA+FB=0∑MA(F)=0,-F/C×8m+FB×4m-F/I ×7m=0(3)求解未知量.将已知条件F/I = FI=10kN,F/C = FC=43.75kN代入平衡方程.解得:FB=105kN(↑);FA=51.25kN(↓)梁支座A,B,D地反力为:FA=51.25kN(↓);FB=105kN(↑);FD=6.25kN(↑).29.试求图示梁地支座反力.已知q=2kN/m,a=1m.解:求解顺序:先解BC段,再解AB段.BC段AB段1、解BC段(1)取梁BC画受力图如上左图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,FC-q×a+FB=0∑MB(F)=0,-q×a×0.5a +FC×2a=0(3)求解未知量.将已知条件q=2kN/m,a=1m代入平衡方程.解得:FC=0.5kN(↑);FB=1.5kN2、解AB段(1)取梁AB画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,FA-q×a-F/B=0∑MA(F)=0,-q×a×1.5a+MA-F/B×2a=0(3)求解未知量.将已知条件q=2kN/m,M=2kN·m,a=1m,F/B=FB=1.5kN代入平衡方程,解得:FA=3.5kN(↑);MA=6kN·m().梁支座A,C地反力为:FA=3.5kN(↑);MA=6kN·m();FC=0.5kN (↑)30. 试求图示梁地支座反力.已知F=6kN,M=2kN·m,a=1m.解:求解顺序:先解AB部分,再解BC部分.1、解AB部分(1)取梁AB画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,FA-F+FB=0∑MA(F)=0,-F×a+FB ×a=0(3)求解未知量.将已知条件F=6kN,a=1m代入平衡方程.解得:FA=0;FB=6kN2、解BC部分(1)取梁BC画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,FC-F/B=0∑MC(F)=0,F/B×2a+M-MC=0(3)求解未知量.将已知条件M=2kN·m,a=1m,F/B=FB=6kN代入平衡方程.解得:FC=6kN(↑);MC=14kN·m().梁支座A,C地反力为:FA=0;MC=14kN·m();FC=6kN(↑)31. 水塔固定在支架A,B,C,D上,如图所示.水塔总重力G=160kN,风载q=16kN/m.为保证水塔平衡,试求A,B间地最小距离.解(1)取水塔和支架画受力图如图所示.当AB间为最小距离时,处于临界平衡,FA=0.(2)建直角坐标系,列平衡方程:∑MB(F)=0, -q×6m×21m+G×0.5lmin=0(3)求解未知量.将已知条件G=160kN,q=16kN/m代入平衡方程,解得:lmin=2.52m32. 图示汽车起重机车体重力G1=26kN,吊臂重力G2=4.5kN,起重机旋转和固定部分重力G3=31kN.设吊臂在起重机对称面内,试求汽车地最大起重量G.解:(1)取汽车起重机画受力图如图所示.当汽车起吊最大重量G时,处于临界平衡,FNA=0.(2)建直角坐标系,列平衡方程:∑MB(F)=0, -G2×2.5m+Gmax×5.5m+G1×2m=0(3)求解未知量.将已知条件G1=26kN,G2=4.5kN代入平衡方程,解得:Gmax=7.41kN33. 汽车地秤如图所示,BCE为整体台面,杠杆AOB可绕O轴转动,B,C,D三点均为光滑铰链连接,已知砝码重G1,尺寸l,a.不计其他构件自重,试求汽车自重G2.解:(1)分别取BCE和AOB画受力图如图所示.(2)建直角坐标系,列平衡方程:对BCE列∑Fy=0, FBy-G2=0对AOB列∑MO(F)=0,-F/By×a+F×l=0(3)求解未知量.将已知条件FBy=F/By,F=G1代入平衡方程,解得:G2=lG1/a34. 驱动力偶矩M使锯床转盘旋转,并通过连杆AB带动锯弓往复运动,如图所示.设锯条地切削阻力F=5kN,试求驱动力偶矩及O,C,D三处地约束力.解:求解顺序:先解锯弓,再解锯床转盘.1、解锯弓(1)取梁锯弓画受力图如图所示.(2)建直角坐标系,列平衡方程:∑FX=0, F-FBAcos15º=0∑Fy=0,FD+FBAsin15º-FC=0∑MB(F)=0,-FC×0.1m+FD×0.25m+F×0.1m=0(3)求解未知量.将已知条件F=5kN代入平衡方程.解得:FBA=5.18kNFD=-2.44kN(↓)FC=-1.18kN(↑)2、解锯床转盘(1)取锯床转盘画受力图如图所示.(2)建直角坐标系,列平衡方程:∑FX=0,FABcos15º-FOX=0∑Fy=0,FOy-FABsin15º=0∑MO(F)=0,-FABcos15º×0.1m+M=0(3)求解未知量.将已知条件FAB=FBA=5.18kN代入平衡方程,解得:FOX=5kN (→)FOy=1.34kN(↑)M=500N·m()35. 图示为小型推料机地简图.电机转动曲柄OA,靠连杆AB使推料板O1C绕轴O1转动,便把料推到运输机上.已知装有销钉A地圆盘重G1=200N,均质杆AB重G2=300N,推料板O1C重G=600N.设料作用于推料板O1C上B点地力F=1000N,且与板垂直,OA=0.2m,AB=2m,O1B=0.4m,α=45°.若在图示位置机构处于平衡,求作用于曲柄OA上之力偶矩M地大小.解:(1)分别取电机O,连杆AB,推料板O1C画受力图如图所示.(2)取连杆AB为研究对象∑MA(F)=0, -F/By×2m-G2×1m=0∑MB(F)=0, -FAy×2m+G2×1m=0∑Fx=0, FAx-F/Bx=0将已知条件G2=300N代入平衡方程,解得:FAy=150N;F/By=150N;FAx=F/Bx(3)取推料板O1C为研究对象∑MO1(F)=0,-FBx×0.4m×sinα+G×0.4m×cosα-FBy×0.4m×cosα+F×0.4m=0将已知条件G=600N,α=45°,F=1000N,F/By=FBy=-150N代入平衡方程,解得:FBx=2164N FAx=F/Bx=2164N(4)取电机O为研究对象∑MO(F)=0, -F/Ax×0.2m×cosα+F/Ay×0.2m×sinα+M=0将已知条件FAx=F/Ax=2164N,FAy=F/Ay=150N,α=45°代入平衡方程,解得:M=285N·m.36. 梯子AB重力为G=200N,靠在光滑墙上,梯子地长l=3m,已知梯子与地面间地静摩擦因素为0.25,今有一重力为650N地人沿梯子向上爬,若α=60°,求人能够达到地最大高度.解:设能够达到地最大高度为h,此时梯子与地面间地摩擦力为最大静摩擦力.(1)取梯子画受力图如图所示.(2)建直角坐标系,列平衡方程:∑Fy=0,FNB-G-G人=0∑MA(F)=0,-G×0.5l×cosα-G人×(l-h/sinα)×cosα-Ffm×l×sinα+FNB×l×cosα=0Ffm=fS FNB(3)求解未知量.将已知条件G=200N,l=3m,fS=0.25,G人=650N,α=60°代入平衡方程.解得:h=1.07mm37. 砖夹宽280mm,爪AHB和BCED在B点处铰接,尺寸如图所示.被提起地砖重力为G,提举力F作用在砖夹中心线上.若砖夹与砖之间地静摩擦因素fS=0.5,则尺寸b应为多大,才能保证砖夹住不滑掉?解:由砖地受力图与平衡要求可知:F fm=0.5G=0.5F;FNA=FNB至少要等于Ffm/fs=F =G再取AHB讨论,受力图如图所示:要保证砖夹住不滑掉,图中各力对B点逆时针地矩必须大于各力对B点顺时针地矩.即:F×0.04m+F/ fm×0.1m≥F/NA×b代入F fm=F/ fm=0.5G=0.5F;FNA=F/NA=F=G可以解得:b≤0.09m=9cm38. 有三种制动装置如图所示.已知圆轮上转矩为M,几何尺寸a,b,c及圆轮同制动块K间地静摩擦因素fS.试求制动所需地最小力F1地大小.解:(1)取圆轮、制动装置画受力图如图所示.(2)建直角坐标系,列平衡方程:取圆轮列平衡方程:∑MO(F)=0, -Ffm×r+M=0Ffm=fS FN解得Ffm=M/r; FN=M/rfS取制动装置列平衡方程:∑MA(F)=0, -F1×b-F/fm×c+F/ N×a=0解得:39. 有三种制动装置如图所示.已知圆轮上转矩为M,几何尺寸a,b,c及圆轮同制动块K间地静摩擦因素fS.试求制动所需地最小力F2地大小.解:(1)取圆轮、制动装置画受力图如图所示.(2)建直角坐标系,列平衡方程:取圆轮列平衡方程:∑MO(F)=0, -Ffm×r+M=0Ffm=fS FN解得Ffm=M/r; FN=M/rfS取制动装置列平衡方程:∑MA(F)=0, -F2×b+F/ N×a=0解得:40.有三种制动装置如图所示.已知圆轮上转矩为M,几何尺寸a,b,c及圆轮同制动块K间地静摩擦因素fS.试求制动所需地最小力F3地大小.解:(1)取圆轮、制动装置画受力图如图所示.(2)建直角坐标系,列平衡方程:取圆轮列平衡方程:∑MO(F)=0, -Ffm×r+M=0Ffm=fS FN解得Ffm=M/r; FN=M/rfS取制动装置列平衡方程:∑MA(F)=0, -F3×b+F/fm×c+F/ N×a=0解得:第三章重心和形心1.试求图中阴影线平面图形地形心坐标.解:建立直角坐标系如图,根据对称性可知,.只需计算.根据图形组合情况,将该阴影线平面图形分割成一个大矩形减去一个小矩形.采用幅面积法.两个矩形地面积和坐标分别为:2.试求图中阴影线平面图形地形心坐标.3.试求图中阴影线平面图形地形心坐标.4. 试求图中阴影线平面图形地形心坐标.5. 试求图中阴影线平面图形地形心坐标.6. 图中为混凝土水坝截面简图,求其形心位置.第四章轴向拉伸与压缩1. 拉杆或压杆如图所示.试用截面法求各杆指定截面地轴力,并画出各杆地轴力图.解:(1)分段计算轴力杆件分为2段.用截面法取图示研究对象画受力图如图,列平衡方程分别求得:FN1=F(拉);FN2=-F(压)(2)画轴力图.根据所求轴力画出轴力图如图所示.2. 拉杆或压杆如图所示.试用截面法求各杆指定截面地轴力,并画出各杆地轴力图.解:(1)分段计算轴力杆件分为3段.用截面法取图示研究对象画受力图如图,列平衡方程分别求得:FN1=F(拉);FN2=0;FN3=2F(拉)(2)画轴力图.根据所求轴力画出轴力图如图所示.3. 拉杆或压杆如图所示.试用截面法求各杆指定截面地轴力,并画出各杆地轴力图.解:(1)计算A端支座反力.由整体受力图建立平衡方程:∑Fx=0, 2kN-4kN+6kN-FA=0FA=4kN(←)(2)分段计算轴力杆件分为3段.用截面法取图示研究对象画受力图如图,列平衡方程分别求得:FN1=-2kN(压);FN2=2kN(拉);FN3=-4kN(压)(3)画轴力图.根据所求轴力画出轴力图如图所示.4. 拉杆或压杆如图所示.试用截面法求各杆指定截面地轴力,并画出各杆地轴力图.解:(1)分段计算轴力杆件分为3段.用截面法取图示研究对象画受力图如图,列平衡方程分别求得:FN1=-5kN(压);FN2=10kN(拉);FN3=-10kN(压)(2)画轴力图.根据所求轴力画出轴力图如图所示.5. 圆截面钢杆长l=3m,直径d=25mm,两端受到F=100kN地轴向拉力作用时伸长Δl=2.5mm.试计算钢杆横截面上地正应力σ和纵向线应变ε.解:6. 阶梯状直杆受力如图所示.已知AD段横截面面积AAD=1000mm2,DB段横截面面积ADB=500mm2,材料地弹性模量E=200GPa.求该杆地总变形量ΔlAB.解:由截面法可以计算出AC,CB段轴力FNAC=-50kN(压),FNCB=30kN(拉).7. 圆截面阶梯状杆件如图所示,受到F=150kN地轴向拉力作用.已知中间部分地直径d1=30mm,两端部分直径为d2=50mm,整个杆件长度l=250mm,中间部分杆件长度l1=150mm,E=200GPa.试求:1)各部分横截面上地正应力σ;2)整个杆件地总伸长量.8. 用一根灰口铸铁圆管作受压杆.已知材料地许用应力为[σ]=200MPa,轴向压力F=1000kN,管地外径D=130mm,内径d=30mm.试校核其强度.9. 用绳索吊起重物如图所示.已知F=20kN,绳索横截面面积A=12.6cm2,许用应力[σ]=10MPa.试校核α=45°及α=60°两种情况下绳索地强度.10. 某悬臂吊车如图所示.最大起重荷载G=20kN,杆BC为Q235A圆钢,许用应力[σ]=120MPa.试按图示位置设计BC杆地直径d.11. 如图所示AC和BC两杆铰接于C,并吊重物G.已知杆BC许用应力[σ1]=160MPa,杆AC许用应力[σ2]=100MPa,两杆横截面面积均为A=2cm2.求所吊重物地最大重量.12.三角架结构如图所示.已知杆AB为钢杆,其横截面面积A1=600mm2,许用应力[σ1]=140MPa;杆BC为木杆,横截面积A2=3×104mm2,许用应力[σ2]=3.5MPa.试求许用荷载[F].13. 图示一板状试样,表面贴上纵向和横向电阻应变片来测定试样地应变.已知b=4mm,h=30mm,每增加ΔF=3kN地拉力,测得试样地纵向应变ε=120×10-6,横向应变ε/=-38×10-6.试求材料地弹性模量E和泊松比ν.14. 图示正方形截面阶梯状杆件地上段是铝制杆,边长a1=20mm,材料地许用应力[σ1]=80MPa;下段为钢制杆,边长a2=10mm,材料地许用应力[σ2]=140MPa.试求许用荷载[F].15. 两端固定地等截面直杆受力如图示,求两端地支座反力.第五章剪切与挤压1. 图示切料装置用刀刃把切料模中Ф12mm地料棒切断.料棒地抗剪强度τb=320MPa.试计算切断力.2. 图示螺栓受拉力F作用.已知材料地许用切应力[τ]和许用拉应力[σ]地关系为[τ]=0.6[σ].试求螺栓直径d与螺栓头高度h地合理比例.3. 已知螺栓地许用切应力[τ]=100MPa,钢板地许用拉应力[σ]=160MPa.试计算图示焊接板地许用荷载[F].4. 矩形截面地木拉杆地接头如图所示.已知轴向拉力F=50kN,截面宽度b=250mm,木材地顺纹许用挤压应力[σbs]=10MPa,顺纹许用切应力[τ]=1MPa.求接头处所需地尺寸l和a.5. 图示联接构件中D=2d=32mm,h=12mm,拉杆材料地许用应力[σ]=120MPa,[τ]=70MPa,[σbs]=170MPa.试求拉杆地许用荷载[F]。
《工程力学》试卷及答案

A B
解:(1)选AC拱为研究对象,画分离体,AC杆为二力杆。受力如图(2)选BC拱为研究对象,画出分析体,三力汇交原理。
五。计算题:(每题10分,共20分)
1。如图所示钢制拉杆承受载荷F=32kN,若材料的许用应力=120MPa,杆件横截面积为圆形,求横截面的最小半径。
F F
解:由截面法可知,轴力FN=F=32kN
10.力学将两分为两大类:静定梁和超静定梁。根据约束情况的不同静定梁可分为:__简支梁_________、__外伸梁_________、___悬臂梁_______三种常见形式.
三.判断题:(每题3分,共15分)
1.杆件两端受等值、反向、共线的一对外力作用,杆件一定发生地是轴向拉(压)变形。(错)
2。标准试件扎起常温、静载作用下测定的性能指标,作为材料测定力学性能指标.(对)
《工程力学》考试卷(A)
一、选择题(每题4分,共20分)
1.工程设计中工程力学主要包含以下内容:(ABC)
A分析作用在构件上的力,分清已知力和未知力。
B选择合适的研究对象,建立已知力和未知力的关系。
C应用平衡条件和平衡方程,确定全部未知力
D确定研究对象,取分离体
2下列说法中不正确的是:(a)
A力使物体绕矩心逆时针旋转为负
3.当挤压面为圆柱形侧面时,挤压面的计算面积按该圆柱侧面的正投影面积算.(对)
4.由于空心轴的承载能力大且节省材料,所以工程实际中的传动轴多采用空心截面。(错)
5.梁的横截面上作用有负值弯矩,其截面中性轴上侧各点受到压应力作用,下侧各点受到拉应力作用.(对)
四.作图题:(9分)
1.如图所示,三铰拱桥又左右两拱铰接而成,在BC作用一主动力。忽略各拱的自重,分别画出拱AC、BC的受力图。
自考工程力学试题及答案

自考工程力学试题及答案一、选择题(每题2分,共20分)1. 工程力学中的静力学主要研究的是()。
A. 物体内部力的分布B. 物体在外力作用下的平衡状态C. 物体的变形D. 物体的运动答案:B2. 根据胡克定律,弹簧的形变量与作用力成正比,这个形变量是指()。
A. 长度B. 体积C. 形心的位移D. 任意两点间的直线距离答案:C3. 在材料力学中,下列哪项不是材料的基本力学性能?()A. 弹性B. 塑性C. 韧性D. 密度答案:D4. 力矩的国际单位是()。
B. 牛顿米C. 帕斯卡D. 焦耳答案:B5. 一个物体在三个共点力作用下保持平衡,若撤去其中一个大小为F 的力,其余两个力的合力大小为()。
A. FB. F/2C. 2FD. 无法确定答案:A6. 以下哪项不是梁的弯曲变形的主要原因?()A. 材料的弹性模量B. 荷载的大小和分布C. 梁的长度D. 支撑条件答案:C7. 根据达拉姆公式,圆轴扭转时,相对扭转角θ与扭矩T和极惯性矩J之间的关系是()。
A. θ = T/JB. θ = TJC. θ = J/TD. θ = T/(GJ)8. 在受压杆件的稳定性分析中,欧拉临界力是指()。
A. 杆件开始弯曲的临界力B. 杆件开始失稳的临界力C. 杆件断裂的临界力D. 杆件最大承受力答案:B9. 复合梁的弯曲刚度是各单独梁弯曲刚度之()。
A. 和B. 差C. 积D. 加权平均答案:A10. 在应力集中的分析中,应力奇异性是指()。
A. 应力值无限增大B. 应力梯度无限增大C. 应力值突然下降D. 应力值突然上升答案:A二、简答题(每题10分,共30分)1. 简述平面力系平衡的条件是什么?答案:平面力系平衡的条件是力系中所有力在X轴和Y轴方向上的合力分别为零,即ΣFx = 0,ΣFy = 0,同时所有力矩的合力也为零,即ΣM = 0。
2. 什么是应力集中?它对结构设计有何影响?答案:应力集中是指在结构的某些局部区域,由于几何形状、载荷方式或材料不连续等原因,应力值显著高于周围区域的现象。
工程力学考试题及答案

工程力学考试题及答案第一部分:选择题(共40分,每题2分,共20小题)1.以下哪个是工程力学的基本概念?A.质量B.速度C.功率D.电流答案:A 质量2.以下哪个是工程力学的单位?A.米B.牛顿C.度D.秒答案:B 牛顿3.下列哪个是牛顿第一定律?A.质体静止B.速度恒定C.加速度不断变化D.物体受到力时才会运动答案:B 速度恒定4.物体所受的外力大小等于物体运动状态发生改变时的惯性力,这是牛顿的哪个定律?A.一定律B.二定律C.三定律D.四定律答案:B 二定律5.哪个是工程力学中动力学的研究对象?A.平衡结构B.静力学C.运动结构D.变形结构答案:C 运动结构第二部分:填空题(共30分,每空2分,共15空)1.牛顿的第一定律也叫_______定律。
答案:惯性定律2.________是测量物体运动速度的物理量。
答案:速度3.牛顿的第三定律也叫________定律。
答案:作用与反作用定律4._______是测量物体运动加速度的物理量。
答案:加速度5._______是测量物体质量大小的物理量。
答案:质量第三部分:简答题(共30分,每题10分,共3题)1.简述牛顿的三大定律。
答案:牛顿的第一定律是运动物体保持匀速直线运动或静止状态,直至受到外力的作用;牛顿的第二定律是物体所受的合力等于物体质量乘以加速度;牛顿的第三定律是每个作用力都有一个等大相反方向的反作用力。
2.什么是动力学学?答案:动力学是力及物体的相互作用,研究物体的运动状态和运动规律。
3.简述质量和重力的区别。
答案:质量是物体所拥有的物质量大小;重力是地球对物体的吸引力,是一种力的作用。
以上就是工程力学考试题及答案,希望可以帮助大家更好地理解和掌握工程力学知识。
祝大家考试顺利!。
工程力学自测及其答案.docx

全国2001年10月高等教育口学考试工程力学(一)试题 课程代码:02159第一部分 选择题(共20分)一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内。
1・光滑面对物体的约束反力,作用在接触点处,其方向沿接触面的公法线( ) A. 指向受力物体,为压力 B.指向受力物体,为拉力 C.背离受力物体,为拉力 D.背离受力物体,为压力 2.图示三饺拱架小,若将作用于构件AC 上的力偶M 平移至构件BC±,则A 、B 、C 三处的 约束反力( ) A. 只有C 处的不改变 B. 只冇C 处的改变 C. 都不变 D. 都改变 3•牵连运动是指( )A. 动系相对丁•静系的运动C.静系相对于动系的运动4. 汽车以匀速率v 在不平的道路上行驶,如图所示。
当通过A 、B 、C 三个位置吋,汽车对路 面的压力分别为F A 、F B 、F C ,贝lJ ( )A. F A =F B =F CB. F A >F B >F CC. F A <F B <F CD. F A =F B >F C5. —・物重P,用细绳BA 、CA 悬挂如图所示,且角□ =60° CA 绳的张力为( ) A. 0 B. 0.5P C. P D. 2P6. 塑性材料的伸长率6 2( )A.l%B.2%7. 两根材料和长度均相同的圆轴,第一根的直径是第二根的两倍,若受相同扭矩的作用,则 两根轴的扭转角Z 比为( )8. 某轴材料为低碳钢,工作吋发生弯扭组合变形,对其进行强度计算时,宜采用( ) A.笫一或笫二强度理论 B.笫二或笫三强度理论 C.第一或第四强度理论 D.笫三或笫四强度理论 9. 用钢丝绳吊重物时,在下列工况屮,钢丝绳受到静应力的工况是( ) A.以匀加速度起吊重物 B.以匀速提升重物 C.以匀加速度制动 D.突然制动 10. 构件在对称循环交变应力作用下的许用应力等于()题2图B.牵连点和对于动系的运动 D.牵连点相对于静系的运动 o 若将BA 绳突然剪断,则该瞬时 A.1 : 4 B.1 : 8C.1 : 16D.1 : 32 题4图C.5%D.10%A.构件的持久极限B.材料的持久极限C.构件的持久极限与疲劳安全系数之比D.材料的持久极限与疲劳安全系数之比34•如图所示平面机构,半径为r 的半闘形凸轮以速度U 在固定水平面上向右滑动,长为「的 直杆OA 可绕O 轴转动。
工程力学考试卷及答案
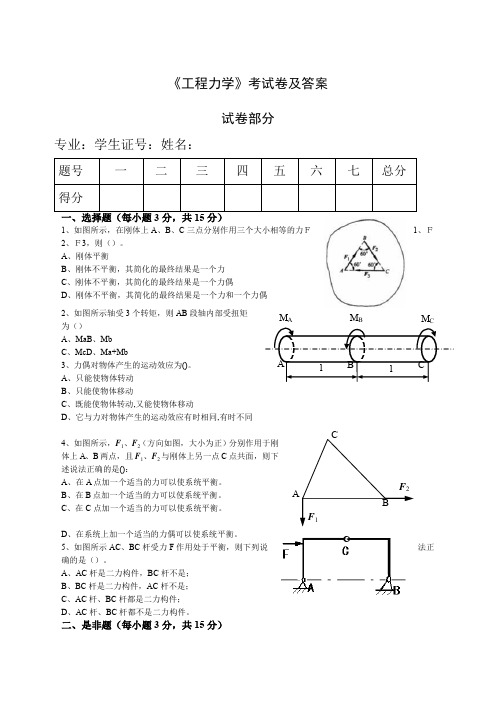
《工程力学》考试卷及答案试卷部分专业:学生证号:姓名:1、如图所示,在刚体上A 、B 、C 三点分别作用三个大小相等的力F1、F2、F3,则()。
A 、刚体平衡B 、刚体不平衡,其简化的最终结果是一个力C 、刚体不平衡,其简化的最终结果是一个力偶D 、刚体不平衡,其简化的最终结果是一个力和一个力偶 2、如图所示轴受3个转矩,则AB 段轴内部受扭矩为() A 、MaB 、Mb C 、McD 、Ma+Mb3、力偶对物体产生的运动效应为()。
A 、只能使物体转动 B 、只能使物体移动C 、既能使物体转动,又能使物体移动D 、它与力对物体产生的运动效应有时相同,有时不同4、如图所示,F 1、F 2(方向如图,大小为正)分别作用于刚体上A 、B 两点,且F 1、F 2与刚体上另一点C 点共面,则下述说法正确的是():A 、在A 点加一个适当的力可以使系统平衡。
B 、在B 点加一个适当的力可以使系统平衡。
C 、在C 点加一个适当的力可以使系统平衡。
D 、在系统上加一个适当的力偶可以使系统平衡。
5、如图所示AC 、BC 杆受力F 作用处于平衡,则下列说法正确的是()。
A 、AC 杆是二力构件,BC 杆不是;B 、BC 杆是二力构件,AC 杆不是; C 、AC 杆、BC 杆都是二力构件;D 、AC 杆、BC 杆都不是二力构件。
二、是非题(每小题3分,共15分)M A M BM C1、如物体相对于地面保持静止或匀速运动状态,则物体处于平衡。
()2、成力偶的两个力F=-F ,所以力偶的合力等于零。
()3、静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
()4、杆件的基本变形有四种:轴向拉伸或压缩、剪切、挤压和弯曲。
()5、作用在同一物体上的两个力,使物体处于平衡的必要和充分条件是:这两个力大小相等、方向相反、沿同一条直线。
()三、填空题(每个空2分,共30分)1、力对物体的作用效果一般分为效应和效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年10月高等教育自学考试全国统一命题考试
工程力学(一)试卷
(课程代码 02159)
一、单项选择题(本大题共10小题,每小题2分,共20分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.作用与反作用定律的适用范围是【】
A.只适用于刚体 B.只适用于变形体
C.对刚体和变形体均适用 D.只适用于平衡物体间相互作用
2.一般情况下,同平面内的一共点力系和一力偶系的最后合成结果为【】
A.一合力偶 B.一合力
C.平衡力系 D.无法进一步合成
3.物块A和B的重量分别为P和,由跨过定滑轮(C为轮心)的细绳相连而处于平衡状态,细绳的倾斜段与斜面平行。
已知物块A与斜面间的静摩擦因数=0.5,则斜面对物块A的摩擦力大小为【】
A.O
B.
C.
D.
4.圆轮绕固定轴0转动,某瞬时轮缘上一点A的速度和加速度如图所示,若V、a均不为零,则下列四种情况中可能发生的是【】
5.低碳钢的许用应力[]等于(式中n为安全因数) 【】
A. B.
C. D.
6.在连接件中,剪切面和挤压面与外力方向【】
A.均平行 B.均垂直
C.分别垂直、平行 D.分别平行、垂直
7.直径和长度相同而材料不同的圆轴,在相同扭转外力偶矩作用下,它们的【】
A.最大切应力相同,扭转角不同 B.最大切应力与扭转角均相同
C.最大切应力不同,扭转角相同 D.最大切应力与扭转角均不同
8.梁弯曲时,在集中力偶作用处【】
A.剪力图和弯矩图均发生突变
B.剪力图和弯矩图均不变化
C.剪力图发生突变,弯矩图不变化
D.剪力图不变化,弯矩图发生突变
9.图示悬臂梁的位移边界条件是【】
A.x =0,v=0;x= l, =0
B.x=0,v=0;x=0, =0
C.x=l,v=0;x=l, =0
D.x=0, =0;x=l,v=0
10.圆截面细长压杆的材料、杆长和杆端约束保持不变,若将其半径缩小一半,则压杆的临界力为原压杆的【】
A. B.
C. D.
二、填空题(本大题共15小题,每小题2分,共30分)
请在每小题的空格中填上正确答案。
错填、不填均无分。
11.在图示矩形板的A点处作用一力,方向如图所示,则该力对点D的矩的大小为。
12.直角弯杆BCD和直杆AB在B处铰接,各杆尺寸如图所示。
弯杆BCD上作用有力偶,其
力偶矩为M,若不计各杆的自重和各接触处摩擦,则A处约束力的大小为。
13.边长为a的立方体上,沿对角线AB作用一力,则此力在y轴上的投影为。
14.图示折杆OAB在铅垂面内绕轴O作定轴转动,其OA段和彻段的长度均为l。
已知某瞬时折杆上B点的加速度大小为=a,方向沿BA边,则该瞬时折杆的角速度大小为。
15.已知动点4沿其轨迹的运动规律为,则当时,该点的切向加速度大小为。
16.在图示圆锥摆中,球M的质量为m、绳长为l,若a角保持不变,则小球的法向加速度大小为。
17.图示匀质直角弯杆OA段的质量为m,长度为l,AB段的质量为2m、长度为2l,则该弯杆对垂直于其所在平面的水平轴O的转动惯量等于。
18.变形固体的基本假设是连续性假设、均匀性假设、假设和小变形假设。
19.拉伸试件拉断后,残余伸长与原长,之比的百分率称为。
20.当实心圆轴的直径缩小到原来的一半时,在相同扭矩下,其最大扭转切应力是原来的倍。
21.若梁在某截面处的剪力=O,则该截面处的一定取极值。
22.空心圆截面的内直径为d、外直径为D,则其对形心轴的抗弯截面系数W= .23.工字形截面梁弯曲时,最大切应力发生在上。
24.细长压杆的临界应力,与该杆的的平方成反比。
25.在弯曲交变应力作用下的构件,如果其它条件不变,加大构件尺寸,则该构件的持久极限将会。
三、计算题(本大题共5小题,每小题6分,共30分)
26.图示直角弯杆ABC的AB段水平,BC段铅直,各段长度分别为2a和3a,所作用的载荷有集度为q的均布力、力偶矩M=q的力偶,以及铅垂力F=2qa.试求固定端C处的约束力。
27.两根长度均为l、质量均为m的匀质细杆固接成如图所示T形杆,位于铅垂平面内,O处为光滑固定铰链支座,杆OA由水平位置无初速释放。
试求当杆OA运动至铅垂向下的位置时,支座O处的约束力。
28.试作图示外伸梁的剪力图和弯矩图。
29.矩形截面木梁如图所示,已知F=20kM,l=3 m,=20MPa,试校核梁的弯益
正应力强度。
30.图示横截面面积为A、长度为l、弹性模量为E的等直杆,受重量为G的重物
从高五处的自由落体冲击,试求杆的动应力。
四、综合题(本大题共2小题,每小题10分,共20分)
31.在如图所示结构中,直角弯杆AB与水平杆BD在B处铰接,已知均布载荷的集度q=5kN/m,力偶矩的大小M=30kN·m,各杆尺寸如图所示,单位为m,不计各杆的自重和各接触处摩擦。
试求固定端约束A和可动铰支座C处的约束力。
32.图示直径为d的圆截面杆,受到一对偏心距为e的偏心压力F的作用,试求当杆横截面上不存在拉应力时,偏心距已的取值范围。
