迭代法求平方根
开平方根的算法

开平方根的算法是一种常用的数学运算方法,可以用于求一个数的平方根。
常见的开平方根算法有以下几种:
1. 迭代法:迭代法是一种基于逐步逼近的方法,即通过对取平方根的数进行逐步逼近,直至误差足够小。
迭代公式为:X(n+1) = (X(n) + S/X(n)) / 2,其中X(n)为第n次逼近的平方根,S为待开平方根的数。
通过多次迭代计算,逼近的结果即为待开平方根的平方根。
2. 牛顿迭代法:牛顿迭代法也是一种逐步逼近的方法,但由于使用了函数的导数,因此迭代速度更快。
迭代公式为:X(n+1) = (X(n) + S/X(n)) / 2,其中X(n)为第n次逼近的平方根,S为待开平方根的数。
通过多次迭代计算,逼近的结果即为待开平方根的平方根。
3. 二分法:二分法是将待开平方根的值按照大小平分为两部分,然后判断目标数属于哪部分,再将该部分继续平分,直至误差足够小。
二分公式为:X(n+1) = (a + b)/2,其中a为待开平方根数的下限,b为待开平方根数的上限,X(n)为第n次逼近的平方根。
通过多次二分计算,逼近的结果即为待开平方根的平方根。
这些算法均可用于开平方根运算,具体使用哪种算法,需要根据具体情况而定。
迭代法求平方根C语言实验报告

实验五: 迭代法求平方根
物理学416班赵增月F12 2011412194 日期: 2013年10月31日
一·实验目的
1.熟练掌握程序编写步骤;
2.学习使用循环结构。
二·实验器材
1.电子计算机;
2.VC6.0
三·实验内容与流程
1.流程图
2.输入以下程序#include<stdio.h>
#include<math.h>
void main()
{
float x2,x1,a;
printf("请输入实数a=");
scanf("%f",&a);
x2=a*0.5;
do
{ x1=x2;
x2=0.5*(x1+a/x1);
}while(fabs(x2-x1)>1e-5);
printf("a 的平方根是: %f\n",x2);
}
四·实验结果
运行显示如下:
请输入实数a=4
a 的平方根是: 2.000000
Press any key to continue
五·实验总结与反思
1.注意循环的初始值的设定, 要保证循环可以进行;
2.循环必须有结束的条件, do while结构中, 不满足循环条件跳出循环。
3.。
平方根的计算方法

平方根的计算方法导言:平方根(square root)是数学中常见的运算,用于求一个数的平方根。
计算平方根可以帮助我们解决很多实际问题,例如在几何学、物理学和工程学中的应用。
本文将介绍几种计算平方根的方法,并探讨它们的优缺点。
一、牛顿法(Newton's Method)牛顿法是一种迭代法,通过不断逼近平方根的值来得到更加精确的结果。
该方法基于牛顿-拉夫逊法则,其迭代公式如下:x_(x+1) = x_x - (x_x^2 - x)/(2x_x)其中,x为需要求平方根的数,x为迭代次数,x_x为迭代过程中的近似值。
通过迭代计算,x_x将逐渐逼近平方根。
牛顿法的优点是收敛速度快、迭代次数较少,适用于求解大部分整数和实数的平方根。
但是,牛顿法需要选择一个合适的初始值,否则可能导致结果偏离真实值。
二、二分法(Bisection Method)二分法是一种基于区间划分的方法,通过不断将区间缩小,逐渐逼近平方根的值。
该方法的思路是,如果一个数的平方大于待求平方根的数,那么这个数的平方根必然在该数左侧;反之,如果一个数的平方小于待求平方根的数,那么这个数的平方根必然在该数右侧。
通过不断将区间一分为二,可以逐步缩小范围。
二分法的优点是简单易实现,并且收敛性较好。
然而,与牛顿法相比,二分法的收敛速度较慢,需要更多的迭代次数。
三、连分数(Continued Fraction)法连分数法是一种将平方根表示为连分数的方法,通过截断连分数的展开式,可以近似计算平方根的值。
以求解正整数的平方根为例,设平方根为一个无限连分数:√x = x_0 + 1/(x_1 + 1/(x_2 + 1/(x_3 + 1/(x_4 + ...))))其中,x_x为连分数的系数。
通过不断截断、逼近连分数的展开,可以得到近似的平方根。
连分数法的优点是可以提供较为准确的结果,并且在计算机实现时能够保持高精度。
然而,连分数法的计算步骤繁琐,对于非整数的平方根计算较为复杂。
用迭代法求a的平方根的原理

用迭代法求a的平方根的原理
迭代法是一种通过反复逐步逼近的方法,用于求解一个方程的近似解。
对于求平方根的问题,迭代法的原理可以描述如下:
1. 假设我们要求一个数a 的平方根,我们可以猜测一个初始的近似解x0。
2. 我们利用这个近似解x0 来更新我们的猜测,并得到一个更好的近似解x1。
这个更新的过程可以使用如下的迭代公式来进行:
x_{k+1} = (x_k + a / x_k) / 2
其中,x_{k+1} 表示新的近似解,x_k 表示上一次的近似解。
3. 我们不断地重复上述的更新过程,直到我们得到一个满足我们要求的精度或近似解为止。
可以通过设定一个迭代次数或者定义一个收敛准则来判断何时停止迭代。
4. 当满足停止条件后,我们得到的近似解x_k 可以作为a 的平方根的近似值。
迭代法的原理在不断逼近的过程中,通过近似解的不断更新,逐渐靠近真实解。
这样的方法常用于求解无法直接求解的方程或函数,包括求解平方根、方程根、最优解等,并且具有广泛的应用。
平方根和立方根的计算

平方根和立方根的计算计算平方根和立方根是数学中常见的运算,它们在各个领域都有重要的应用。
本文将介绍如何计算平方根和立方根,并提供一些实际问题中的应用示例。
一、平方根的计算平方根是指一个数的二次方等于该数的非负实数解。
计算平方根有多种方法,下面将介绍两种常用的方法:试位法和牛顿迭代法。
1. 试位法试位法是通过不断逼近目标值来计算平方根的方法。
以计算一个数a的平方根为例,首先选择一个初始的近似值x0,然后通过迭代的方式逐步逼近真实的平方根。
假设x0是a的一个近似平方根,将x0代入方程x^2 = a,得到x1 = (x0 + a / x0) / 2。
再将x1代入方程,得到x2,以此类推,直到得到满足精度要求的近似平方根。
2. 牛顿迭代法牛顿迭代法也是一种常用的计算平方根的方法。
该方法通过不断求导和迭代来逼近平方根的值。
以计算一个数a的平方根为例,假设初始近似值x0,通过迭代的方式更新近似值,即x1 = (x0 + a / x0) / 2,再将x1代入得到x2,以此类推,直到满足精度要求的近似平方根。
二、立方根的计算立方根是指一个数的三次方等于该数的实数解。
计算立方根也有多种方法,下面介绍两种常用的方法:试位法和二分法。
1. 试位法试位法计算立方根的步骤与计算平方根类似。
假设x0是一个近似值,将x0代入方程x^3 = a,得到x1 = (2 * x0 + a / (x0^2)) / 3。
再将x1代入得到x2,以此类推,直到满足精度要求的近似立方根。
2. 二分法二分法是一种通过不断二分区间来逼近立方根的方法。
假设a是待求的数,选择一个区间[x, y],使得x^3 <= a <= y^3。
然后计算区间的中点m = (x + y) / 2,如果m^3与a的差值足够小,则可以认为m就是近似的立方根。
否则,根据与a的大小关系调整区间,并重复以上步骤,直到满足精度要求的近似立方根。
三、应用示例平方根和立方根的计算在实际问题中有广泛的应用,下面列举一些例子:1. 几何学中的应用:计算物体的体积、表面积等需要用到平方根和立方根的问题。
牛顿迭代法求平方根
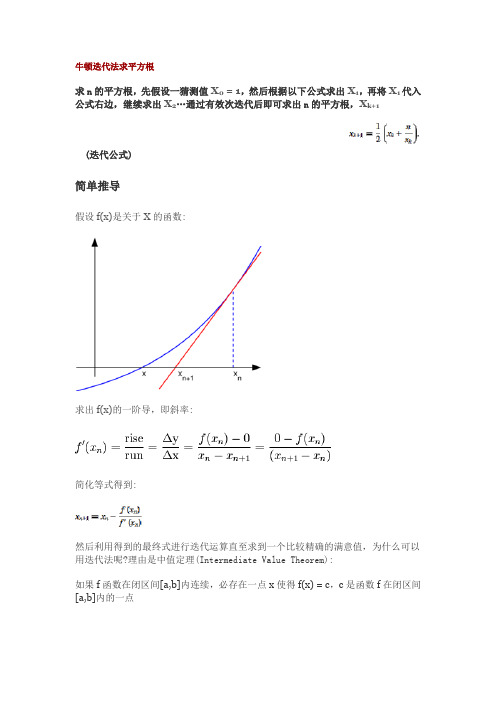
牛顿迭代法求平方根求n的平方根,先假设一猜测值X0 = 1,然后根据以下公式求出X1,再将X1代入公式右边,继续求出X2…通过有效次迭代后即可求出n的平方根,X k+1(迭代公式)简单推导假设f(x)是关于X的函数:求出f(x)的一阶导,即斜率:简化等式得到:然后利用得到的最终式进行迭代运算直至求到一个比较精确的满意值,为什么可以用迭代法呢?理由是中值定理(Intermediate Value Theorem):如果f函数在闭区间[a,b]内连续,必存在一点x使得f(x) = c,c是函数f在闭区间[a,b]内的一点我们先猜测一X初始值,例如1,当然地球人都知道除了1本身之外任何数的平方根都不会是1。
然后代入初始值,通过迭代运算不断推进,逐步靠近精确值,直到得到我们主观认为比较满意的值为止。
例如要求768的平方根,因为252 = 625,而302 = 900,我们可先代入一猜测值26,然后迭代运算,得到较精确值:27.7128。
回到我们最开始的那个”莫名其妙”的公式,我们要求的是N的平方根,令x2 = n,假设一关于X的函数f(x)为:f(X) = X2 - n求f(X)的一阶导为:f'(X) = 2X代入前面求到的最终式中:X k+1 = X k - (X k2 - n)/2X k化简即得到我们最初提到的那个求平方根的神奇公式了:用泰勒公式推导我之前介绍过在The Art and Science of C一书中有用到泰勒公式求平方根的算法,其实牛顿迭代法也可以看作是泰勒公式(Taylor Series)的简化,先回顾下泰勒公式:仅保留等式右边前两项:令f(X0+ε) = 0,得到:再令X1 = X0+ ε0,得到ε1…依此类推可知:转化为:引申从推导来看,其实牛顿迭代法不仅可以用来求平方根,还可以求立方根,甚至更复杂的运算。
同样,我们还可以利用pascal语言来实现下那个最简单的求平方根的公式(尽管我们可以直接用sqrt()完成)program asd (input,output);vara,x,n,i:real;beginwriteln('Please input a!');read(a);x:=1;n:=1000;i:=1;while i<=n dobeginx:=(x+(a/x))/2;i:=i+1;end;writeln(x:10:3);readln;end.2007年赣州市信息学奥赛高中组上机测试题第2题:编程求平方根(15分)任给常数b,编程求b的算术平方根,要求准确到小数点后3位,注意不能调用高级语言系统的开平方根函数。
C语言复习---迭代法,牛顿迭代法,二分法求根

C语⾔复习---迭代法,⽜顿迭代法,⼆分法求根⼀:⽤迭代法求 x=√a。
求平⽅根的迭代公式为:X(n+1)= (Xn+a/Xn) /2。
#define _CRT_SECURE_NO_WARNINGS#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1, x2;float a;scanf("%f", &a);x2 = 1.0;do{x1 = x2;x2 = (x1 + a / x1) / 2;} while (fabs(x1-x2)>pow(10,-5));printf("value:%lf", x2);system("pause");return0;}⼆:⽤求⽅程在1.5附近的根(2x3-4x2+3x-6=0)例:⽅程求根⽜顿迭代法求⽅程 f(x)=x3+x2-3x-3=0在1.5附近的根f(x)=x^3+x^2-3x-3f'(x)=3x^2+2x-3x(n+1)=xn-f(xn)/f'(xn)令x1=1.5x2=1.777778x3=1.733361x4=1.732052x5=1.732051x6=1.732051如果精确到0.000001,则x=1.732051准确值=根号3重要公式#include <stdio.h>#include <stdlib.h>#include <math.h>int main(){double x1=0, x2;double fx1, fx2;x2 = 1.5;while (fabs(x1 - x2)>=1e-6){x1 = x2;fx1 = 2 * x1*x1*x1 - 4 * x1*x1 + 3 * x1 - 6; //f(xn)fx2 = 6 * x1*x1 - 8 * x1 + 3; //f(xn)'x2 = x1 - fx1 / fx2;}printf("value:%lf", x2);system("pause");return0;}三:⼆分法求⽅程的根给定精确度ξ,⽤⼆分法求函数f(x)零点近似值的步骤如下:1确定区间[a,b],验证f(a)·f(b)<0(这是前提,选取的区间必须满⾜这个条件),给定精确度ξ. 2求区间(a,b)的中点c.3计算f(c).(1) 若f(c)=0,则c就是函数的零点;(2) 若f(a)·f(c)<0,则令b=c;(3) 若f(c)·f(b)<0,则令a=c.(4) 判断是否达到精确度ξ:即若|a-b|<ξ,则得到零点近似值a(或b),否则重复2-4.#include <stdio.h>#include <stdlib.h>#include <math.h>double fx(double x){return2 * x*x*x - 4 * x*x + 3 * x - 6;}int main(){double x1 , x2;double fx1, fx2;double e = 1e-6;do{printf("enter (x1,x2):\n");scanf("%lf", &x1);scanf("%lf", &x2);if (x1>x2){double temp = x1;x1 = x2;x2 = temp;}fx1 = fx(x1);fx2 = fx(x2);} while (fx1*fx2>0);if (fabs(fx1) < e)printf("solution1:%lf\n", x1);else if (fabs(fx2) < e)printf("solution2:%lf\n", x2);else{while (fabs(x1 - x2) >= e){double mid = (x1 + x2) / 2;if (fx(mid)*fx2 < 0)x1 = mid;elsex2 = mid;}printf("solution3:%lf", x2);}system("pause");return0;}。
平方根和立方根的计算方法

平方根和立方根的计算方法在数学中,平方根和立方根是基本的运算之一。
计算平方根和立方根的方法有多种,下面将介绍几种常见的计算方法。
一、平方根的计算方法:1. 牛顿迭代法牛顿迭代法是一种常用的求解方程近似解的方法,也可以用来计算平方根。
设要计算的数为x,初始估计值为a,根据迭代公式:a = (a + x / a) / 2反复迭代,直到a的平方与x的差小于预设的误差范围,即可得到x的平方根。
2. 二分法二分法是一种逐步逼近的方法。
设要计算的数为x,初始估计值为a,设区间左端点为low,右端点为high,mid为区间中点,计算mid 的平方与x的差,若差小于预设的误差范围,则mid即为所求的平方根;若差大于0,则将区间缩小至low和mid之间,否则将区间缩小至mid和high之间。
反复迭代,直到满足条件的mid被找到。
二、立方根的计算方法:1. 二分法与计算平方根的二分法类似,设要计算的数为x,初始估计值为a,设区间左端点为low,右端点为high,mid为区间中点,计算mid的立方与x的差,若差小于预设的误差范围,则mid即为所求的立方根;若差大于0,则将区间缩小至low和mid之间,否则将区间缩小至mid和high之间。
反复迭代,直到满足条件的mid被找到。
2. 牛顿迭代法与计算平方根的牛顿迭代法类似,设要计算的数为x,初始估计值为a,根据迭代公式:a = (2 * a + x / (a * a)) / 3反复迭代,直到a的立方与x的差小于预设的误差范围,即可得到x的立方根。
三、总结:平方根和立方根的计算方法可以通过牛顿迭代法和二分法来实现。
牛顿迭代法通过逐步逼近求解方程的近似解,而二分法则通过逐步缩小区间来逼近方程的解。
选择适当的方法,根据需要的精度和效率来计算平方根和立方根,可以得到准确的结果。
以上就是关于平方根和立方根的计算方法的介绍。
通过牛顿迭代法和二分法,我们可以方便地计算平方根和立方根,为数学和科学研究提供了便利。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
迭代法求平方根是一种有效的计算方法,它可以用来快速求出一个数的平方根。
这种方法基于牛顿迭代法,它使用一个初始值作为起始点,然后不断地重复应用牛顿迭代公式来收敛到正确的解。
具体而言,要使用迭代法求平方根,首先要选取一个初始值x0作为起始点。
然后不断地重复应用牛顿迭代公式xn+1=1/2(xn+a/xn)来得到新的值xn+1,直到误差小于所定义的误差界限ε时即可得出正确的解。
例如:要求9的平方根时,我们可以将x0设为3.5(因为3.5^2=12.25>9),然后不断地重复应用上式即可得出正确的解3。
总之,迭代法是一种有效、快速、易于理解和实施的求平方根方法。
在大部分情况中都能够得出正确而有效地优化效果。
