(完整版)空间几何体练习题含答案
(完整版)空间几何体练习题含答案
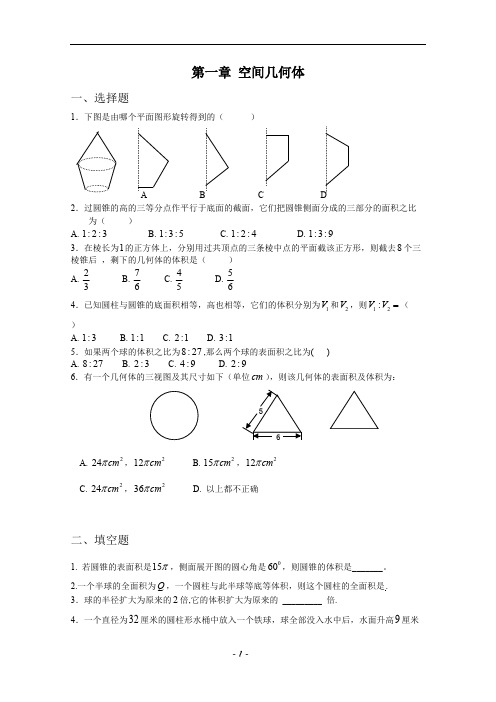
第一章空间几何体一、选择题1.下图是由哪个平面图形旋转得到的()A B C D2.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()A. B. C. D.1:2:31:3:51:2:41:3:93.在棱长为的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去个三18棱锥后,剩下的几何体的体积是()A. B. C. D.237645564.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为和,则(1V2V12:V V=)A. B. C. D.1:31:12:13:15.如果两个球的体积之比为,那么两个球的表面积之比为( )8:27A. B. C. D.8:272:34:92:96.有一个几何体的三视图及其尺寸如下(单位),则该几何体的表面积及体积为:cmA. ,B. ,224cmπ212cmπ215cmπ212cmπC. ,D. 以上都不正确224cmπ236cmπ二、填空题1. 若圆锥的表面积是,侧面展开图的圆心角是,则圆锥的体积是_______。
15π0602.一个半球的全面积为,一个圆柱与此半球等底等体积,则这个圆柱的全面积是.Q3.球的半径扩大为原来的倍,它的体积扩大为原来的_________ 倍.24.一个直径为厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高厘米329则此球的半径为_________厘米.5.已知棱台的上下底面面积分别为,高为,则该棱台的体积为___________。
4,163三、解答题1. (如图)在底半径为,母线长为的圆柱,求圆柱的表面积242.如图,在四边形中,,,,,ABCD 090DAB ∠=0135ADC ∠=5AB =CD =,求四边形绕旋转一周所成几何体的表面积及体积.2AD =ABCD AD参考答案一、选择题1.A 几何体是圆台上加了个圆锥,分别由直角梯形和直角三角形旋转而得2.B 从此圆锥可以看出三个圆锥,123123::1:2:3,::1:2:3,r r r l l l == 12312132::1:4:9,:():()1:3:5S S S S S S S S =--=3.D 111115818322226V V -=-⨯⨯⨯⨯⨯=正方体三棱锥4.D 121:():()3:13V V Sh Sh ==5.C 121212:8:27,:2:3,:4:9V V r r S S ===6.A 此几何体是个圆锥,23,5,4,33524r l h S πππ====⨯+⨯⨯=表面 2134123V ππ=⨯⨯=二、填空题1. 设圆锥的底面半径为,母线为,则,得,r l 123r l ππ=6l r =,得,圆锥的高226715S r r r r ππππ=+⋅==r =h =21115337V r h ππ==⨯=2. 109Q 22223,S R R R Q R πππ=+===全 32222221010,,2233339V R R h h R S R R R R Q πππππ==⋅==+⋅==3. 821212,8r r V V ==4. 12234,123V Sh r h R R ππ=====5. 28'11()(416)32833V S S h =++=⨯+⨯= 三、解答题1.解:圆锥的高,h ==1r =22(2S SS πππ=+=+=侧面表面底面 2.解:S S S S=++表面圆台底面圆台侧面圆锥侧面25(25)2πππ=⨯+⨯+⨯⨯⨯1)π=+ V V V=-圆台圆锥222112211()331483r r r r h r h πππ=++-=。
高一数学空间几何体试题答案及解析

高一数学空间几何体试题答案及解析1.如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF平面EFDC.(Ⅰ)当,是否在折叠后的AD上存在一点,且,使得CP∥平面ABEF?若存在,求出的值;若不存在,说明理由;(Ⅱ)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.【答案】(1)存在点,;(2)当时,三棱锥的最大值.【解析】(1)与立体几何有关的探索问题:第一步:假设符合条件的结论存在;第二步:从假设出发,利用空间中点、线、面的位置关系求解;第三步,确定符合要求的结论存在或不存在;第四步:给出明确结果;第五步:反思回顾,查看关键点;(2)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;四是利用线面平行的定义,一般用反证法;(3)在求所列函数的最值时,若用基本不等式时,等号取不到时,可利用函数的单调性求解;(4)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,常常用于比较数的大小或证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好利用基本不等式的切入点.试题解析:解:(Ⅰ)假设存在使得满足条件CP∥平面ABEF在平面内过点作交于,在平面内作直线交于点,连结 3分∵∴ 4分∵5分又∴平面∥平面 6分又∵∴,故点就是所求的点 7分又∵∴ 8分(Ⅱ)因为平面ABEF平面EFDC,平面ABEF平面EFDC=EF,又AF EF,所以AF⊥平面EFDC 10分由已知BE=x,所以AF=x(),则FD=8x.∴ 12分故当且仅当,即=4时,等号成立所以,当=4时,有最大值,最大值为 14分解法二:故所以,当=4时,有最大值,最大值为 14分【考点】(1)探究性问题;(2)求体积的最大值.2.下图中的几何体是由哪个平面图形旋转得到的()【答案】A【解析】几何体的上半部分是一个圆锥,下半部分是一个圆台,故选A【考点】简单旋转体的概念3.一个正方体的顶点都在球面上,它的棱长为,则球的表面积是()A.B.C.D.【答案】B【解析】因为一个正方体的棱长为为2,则该正方体的对角线长为.又因为该正方体的顶点都在球面上,所以球的直径就是正方体的对角线,即球的半径.又因为球的表面积.故选B.【考点】1.球的内接正方体.2.球的表面积公式.3.长方体的对称性.4.若圆锥的表面积,侧面展开图的圆心角为,则该圆锥的体积为______.【答案】【解析】设该圆锥的底面圆的半径为,母线长为,因为侧面展开图的圆心角为,所以,因为圆锥的表面积,所以,所以该圆锥的体积为【考点】本小题主要考查圆锥的侧面积和表面积的关系以及圆锥的体积计算.点评:解决本题的关键是正确运用圆锥中相应的计算公式、圆锥的侧面展开图的关系等求出,进而求出圆锥的高,然后利用圆锥的体积公式计算体积.5.某高速公路收费站入口处的安全标识墩如图1所示。
必修二_1.3_空间几何体的表面积和体积同步练习和详细答案

1.3空间几何体的表面积和体积【知识总结】1. 多面体的面积和体积公式名称 侧面积(S 侧) 全面积(S 全)体积(V )棱 棱柱 直截面周长x IS 侧+2S 底S底• h=S 直截面• h柱直棱柱 chS 底• h「棱锥棱锥 各侧面积之和1S 底• h3 正棱锥 1『 —ch 2S 侧+S 底棱台各侧面面积之和1—h(S 上底+S 下底+3棱 台正棱台1一 (c+c ' )h '2S 侧+S 上底+S 下底S 下底’S 下底)表中表示面积,'、分别表示上、下底面周长,表斜咼,'表示斜咼,表示侧棱长。
2 .旋转体的面积和体积公式名称圆柱圆锥圆台球S 侧 2 n rl n rl n (r 1+「2)lS 全 2 n r(l+r) n r(l+r) 2 2n (r 1+r 2)l+ n (r 1+r24 n RVn r 2h(即 n r 2l)1r 2h —n r h312 2—n h(r 1+r 1「2+r 2)3 43—n R3 表中I 、h 分别表示母线、咼,r 表示圆柱、圆锥与球冠的底半径,r i 、「2分别表示圆台上、下底面半径,R 表示半径。
【知能训练】A:多面体的表面积和体积 一•选择题1.如图,在直三棱柱 ABC-ABC i 中,AA=AB=2 BC=1, / ABC=90,若规 定主(正)视方向垂直平面 ACCA ,则此三棱柱的左视图的面积为 ( )A.—— B . 2 - C . 4 D . 22•某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底 边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、 高为4的等腰三角形,则该几何体的表面积为()3.—个棱锥被平行于底面的平面所截,如果截面面积与底面面积之比为1: 2,则截面把棱锥的一条侧棱分成的两段之比是()A . 1 : 4B . 1 : 2C . 1 : ( "- 1 )D . 1: ( 一+1 ) 4.正六棱台的两底边长分别为1cm, 2cm,高是1cm,它的侧面积为()A . 80B . 24 一+88C. 24 一+40 D . 118A .9 ~ 2cm2B . 9 cmC. - cm 22D. 3 cm5. 要制作一个容积为 4卅,高为1m 的无盖长方体容器,已知该容器的底面造价是每平方米 20元,侧面造价是每平方米 10元,则该容器的最低总造价是( )A . 80 元B . 120 元C . 160 元D. 240 元6. (文) 四棱锥S-ABCD 的底面是矩形,锥顶点在底面的射影是矩形对角线的交点,四棱 锥及其三视图如图(AB 平行于主视图投影平面)则四棱锥 A . 24 B . 18 C . - - D . 87. 某空间组合体的三视图如图所示,则该组合体的体积为( A . 48B . 56C . 64D. 72&各棱长均为a 的三棱锥的表面积为( )A. 4 _a 2B . 3 "a 2C .2 _a 2D9.已知一个四棱锥的高为 3,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为()10. 如图,在三棱柱 ABC-ABC 中,D, E , F 分别是AB, AC, AA 的中点,设三棱锥 F-ADE的体积为V 1,三棱柱 ABG-ABC 的体积为V 2,则V 1: V ___________________________________ .11. _______ 将边长为2的正方形沿对角线 AC 折起,以A, B, C, D 为顶点的三棱锥的体积最大值等 于 ____ .12.如图,一个三棱柱形容器中盛有水,且侧棱AA=8.若AAB 1B 水平放置时,液面恰好过AC BC, AC , BC 的中点,则当底面 ABC 水平放置时,液面的高为 _________________ . 13. 四棱锥P-ABCD 的底面ABCE 为正方形,且PD 垂直于底面 ABCD N 为PB 中点,则三棱锥 P-ANC 与四棱锥P-ABCD 的体积比为 ________________ .14.已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示.若该四棱锥的侧视图为S-ABCD 的体积=( )A .B . 6C. -D . 2直角三角形,则它的体积为_________________15.如图所示,在三棱柱ABC-ABQ 中,AB=AC=AA=2, BC=2 ;且/ AAB=/ A i AC=60,则该三棱柱的体积是_________________________ .B:旋转体的表面积和体积1•如果圆锥的底面半径为,高为2,那么它的侧面积是()A. 4 n B . 2 n C . 2 n D . 4 n2.一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是()A. 5 nB. 4 nC. 3 nD. 2 n3•如果圆锥的轴截面是正三角形(此圆锥也称等边圆锥),则此圆锥的侧面积与全面积的比是()A. 1 : 2 B. 2: 3 C. 1 : 一 D. 2: _4•圆锥侧面积为全面积的,则圆锥的侧面展开图圆心角等于()A. - nB. nC. 2 nD.以上都不对5.圆台的上、下底面半径和高的比为 1 : 4: 4,母线长为10,则圆台的侧面积为()A. 81 nB. 100 nC. 14 nD. 169 n6.已知球的直径SC=8 A, B是该球球面上的两点,AB=2 ,/ SCAN SCB=60,则三棱锥S-ABC 的体积为()A. 2 ~B. 4 ~C. 6 ~D. 8 ~7.若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为S、S,则S:Sa=()A. 1 : 1B. 2: 1C. 3: 2D. 4: 1&若两个球的表面积之比为1: 4,则这两个球的体积之比为()A. 1 : 2B. 1 : 4C. 1 : 8D. 1 : 169.体积相等的正方体、球、等边圆柱(即底面直径与母线相等的圆柱)的全面积分别为S , S, S3,那么它们的大小关系为()A. S1 v S2 v S3B. S1 v S3V S2C. S2V S3 v S1D. S2 v S1 v S3二.填空题(共5小题)10.圆锥和圆柱的底面半径和高都是R,则圆锥的全面积与圆柱的全面积之比为________________n和n的矩形, 11 .已知一个圆柱的侧面展开图是一个长和宽分别为则该圆柱的体积是____________________12.在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,则斜截圆柱的侧面面积S= cm 2.13.球的体积与其表面积的数值相等,则球的半径等于14•已知一圆柱内接于球O,且圆柱的底面直径与母线长均为2,则球为O的表面积为15.已知A, B, C是球面上三点,且AB=AC=4cm/ BAC=90,若球心O到平面ABC的距离为2 ,则该球的表面积为cm3.11.正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为1,此时四面体ABCD7卜接球表面积为三.解答题(共3小题)16•如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成•已知球的直径是6cm,圆柱筒长2cm.(1)这种“浮球”的体积是多少cm (结果精确到0.1 ) ?(2 )要在这样2500个“浮球”表面涂一层胶质,如果每平方米需要涂胶100克,共需胶多少?17.(文)如图,球O的半径长为10(1)求球O的表面积;(2)求球O的体积;(3)若球O的小圆直径AB=3Q求A、B两点的球面距离.18.设底面直径和高都是4厘米的圆柱的内切球为O.(1)求球O的体积和表面积;(2)与底面距离为1的平面和球的截面圆为M AB是圆M内的一条弦,其长为2 ,求AB 两点间的球面距离.参考答案: A:I、A 2、B 3、C 4、A 5、C 6、D 7、C 8、D 9、D10、解:因芮D,E,分S]是Ab肌的中自所以血虫DE;S AA BC=1:仆又F是宜納的中点,所以A T aS面的范离H为F到虧面距离h的2倍• 即三複栓盘卩1门-2匚的壽是三棱穩F-ME高的7倍-斷以如;畑空兰空=4T=1:西.故答案为1; 24.II、铅:妇也肪示,评正方也就口叭対術钱M * 3DSt + iO>甲n折更启的位豈为F・连揺即‘ *苛一TAZJLBC,AC l-BD* - BaflD- QrO--ACX 耶®IT g匡b> =楼帕的作祗対V D -kBC"v^EOC' -^Vc-BCC~ ;BCD' k AO*j52kBOD' x J S^ISOD_卞航:王方世的迪丢为2・可J?■■- BOD ft AH - To LABC谜劉昴尢值■*:S/\ 二 0D* =? x j^x忑小血乂目□力'二w in上aoii *’,丄i ?rv「.q-TTY-M' l「=丄工」•王5V.怡巧「此t」导.乂RJ农虻-土故告案为;半12、解:不妨令此三棱柱为直三棱柱,如图当侧面AA1B1B水平放置时,水的形状为四棱柱形,底面是梯形.设△ ABC的面积为S,贝U S梯形ABFE= S,V水=S? AA1=6S .当底面ABC水平放置时,水的形状为三棱柱形,设水面高为h,则有V水=Sh,••• 6S=Sh,.•• h=6 .故当底面ABC水平放置时,液面高为6 .故答案为:613、1:4 14、15、2解:團柱的側面展开囹星长利员务别为和TT的矩用,当毋线为戈氏时,區1桂的庙面半襌是扌此时囿桂体粮是(l)1 2Ttx3it=^;当母线为H时,圆柱酌展面半轻是学此时圆柱的体釈是(芥II"二竺匕£-t 4综上所求圈柱的体稅杲:—16、解:(1 )T该“浮球”的圆柱筒直径d=6cm ,•••半球的直径也是6cm,可得半径R=3cm,•两个半球的体积之和为V球=-冗R = - n ? 27 = 6 n cm3 * S 6…(2分)斗412、解:将相同的两个几何体,对接为圆柱,则圆柱的侧面展开,侧面展开图的面积 S=[ ( 50+80) X 20 n x 2]/2=2600 n cm2. 故答案为:2600 n13、 3 14、8 n 15、64 n学习参考而V 圆柱=n R ? h= n X 9X = n cm3…(2 分)•该“浮球”的体积是:V=V球+V圆柱=36 n +18 n =54 n" 169.6cm 3…(4分)(2)根据题意,上下两个半球的表面积是S 球表= n R = Xn X 9= 6 n cm?…(6 分)而“浮球”的圆柱筒侧面积为:S圆柱侧=2 n Rh=2 Xn X 3 X 2=12 n cm2…(8分)6 n n n• 1个“浮球”的表面积为S = —0一= —m因此,2500个“浮球”的表面积的和为2500 S = 00 X —= n m2…(10分)•/每平方米需要涂胶100克,•总共需要胶的质量为:100 X 12 n =1200 n (克)…(12分)答:这种浮球的体积约为169.6cm 3;供需胶1200 n克.…(13分)17、解:(1)球的表面积为4 n r 2=1200 n ; …(4分)(2)球的体积V=-n r3= 4000 _n ; …(8 分)(3)设球心为O,在△ AOB中,球O的小圆直径AB=30,球O的半径长为10解得Z AOB=",所以A、B两点的球面距离为0 n n . …(15分)18、解:(1)•••底面直径和高都是4厘米的圆柱的内切球为O,•球O的半径为2cm,.•.球O的体积为-n ? 2=,表面积4 n ? 22=16 n ;(2)•/ AB是圆M内的一条弦,其长为2 ,• Z AOB= n , • AB两点间的球面距离为".。
空间几何体的表面积与体积习题附答案

空间几何体的表面积与体积习题附答案1.圆柱的侧面积可以通过展开图计算,展开图是一个正方形,边长为2πr,所以侧面积为4πr^2,即4πS,因此选项为A。
2.根据三视图可以看出该几何体由两个同底的半圆锥组成,底面半径为1,高为3,因此体积为2×(1/3)πr^2h=π,因此选项为D。
3.根据三视图可以看出该几何体是一个组合体,由一个底面为等腰直角三角形的直三棱柱和一个底面为等腰直角三角形的三棱锥组成。
直三棱柱的高为2,三棱锥的高为2,因此梯形的高为2,底边为2和4,面积为(2+4)×2/2=6,共有2个梯形,因此梯形的面积之和为12,因此选项为B。
4.根据三视图可以看出该几何体为一个圆柱挖去一个同底的圆锥,圆锥的高为圆柱高的一半,因此圆锥的高为2,圆柱的底面积为π,侧面积为4π,圆锥的侧面积为2π×5/2=5π,因此表面积为π+4π+5π=9π+5π,因此选项为A。
5.根据三视图可以看出该几何体为一个直三棱柱削去一个同底的三棱锥,三棱柱的高为5,三棱锥的高为3,三棱锥与三棱柱的底面均为两直角边分别为3和4的直角三角形,因此三棱柱的体积为底面积×高=3×4×5=60,三棱锥的体积为1/3×底面积×高=1/3×3×4×3=4,因此该几何体的体积为60-4=56,因此选项为C。
C1F=4,连接EF,交AD于点G,求三角形AEF和四边形ABCG的面积和长方体ABCD-A1B1C1D1的体积.解:首先可以求出AE=BF=6,EF=8,再根据三角形相似可以求出AG=12,GD=4,因此AD=16,AGD为等腰直角三角形,所以GD=DG=4,因此CG=10,BG=AB-AG =4,所以ABCG为梯形,其面积为(AB+CG)×4=56.三角形AEF的面积为1/2×AE×EF=24.长方体ABCD-A1B1C1D1的体积为16×10×8=1280.题目1:一长方体被平面α分成两个高为10的直棱柱,求平面α把该长方体分成的两部分体积的比值。
高中空间立体几何经典例题精选全文完整版

可编辑修改精选全文完整版立体几何一、选择题1.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是 ( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D2 2.(20XX 年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C 【答案】A3 3.(20XX 年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A4 4.(20XX 年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1B .2C .2-12D .2+12【答案】C5.(20XX 年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,底面是边长为3.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为( )A.512πB .3πC.4πD.6π【答案】B6.(20XX年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为()A.5603B.5803C.200D.240【答案】C7.(20XX年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为,m n,那么m n+=()A.8 B.9 C.10 D.11【答案】A二、填空题8.(20XX年高考北京卷(理))如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为__________.1D1BPD1CCEBA1A【答案】2559.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2410.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-11.(20XX 年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于球构成一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π12.(20XX 年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A B C D -中,异面直线1A B 与1B C 所成角的大小为_______AB C1A D EF1B 1C【答案】3π三、解答题13.(20XX 年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB是圆的直径,PA 垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值D 1 C 1 B 1A 1D C AB14.(20XX 年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,113tan 6233BC CC BC C =⋅∠==从而2333ABC S BC ∆==因此该三棱柱的体积为1336183ABC V S AA ∆=⋅==15.(20XX 年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))B 1 A 1C 1ACB如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点.求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点 ∵E.F 分别是SA.SB 的中点 ∴EF ∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF ∥平面ABC 同理:FG ∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC ∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBC 平面SAB 平面SBC =BC AF ⊆平面SAB AF ⊥SB∴AF ⊥平面SBC 又∵BC ⊆平面SBC ∴AF ⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC ⊥平面SAB 又∵SA ⊆平面SAB ∴BC ⊥SA16.(20XX 年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11A【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C; 直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯=而1AD C ∆中,11AC DC AD ==故132AD C S ∆= AB CSGFE所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.17.(20XX 年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE =O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CD B '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===连结,OD OE,在OCD ∆中,由余弦定理可得OD=由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥,理可证A O OE '⊥, 又OD OE O =,所以A O '⊥平面BCDE . (Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故2OH =,从而2A H '== 所以cos OH A HO A H '∠=='所以二面角ACD B '--向量法:以O 点为原点,建立空间直角坐标系O -.CO BDEA CDOBE'A图1图2C DO BE'AH则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,1,n =- 由(Ⅰ)知,(OA '=为平面CDB 的一个法向量,所以3cos ,3n OA n OA n OA'⋅'===',即二面角A CD B '--的平面角的余弦值为5.18.(20XX年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD-A1B1C1D1中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点.(Ⅰ) 证明B1C1⊥CE;(Ⅱ) 求二面角B1-CE-C1的正弦值.(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1所成角的正弦值为2, 求线段AM的长.6【答案】19.(20XX年高考陕西卷(理))如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD,12AB AA==(Ⅰ) 证明: A1C⊥平面BB1D1D;(Ⅱ) 求平面OCB1与平面BB1D1D的夹角θ的大小.1A【答案】解:(Ⅰ) BDOAABCDBDABCDOA⊥∴⊂⊥11,,面且面;又因为,在正方形AB CD 中,BDCAACACAACABDAACOABDAC⊥⊂⊥=⋂⊥11111,,故面且面所以;且.在正方形AB CD中,AO = 1 . .111=∆OAOAART中,在OECAOCEAEDB1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又OOBDDDBBODDBBBD=⋂⊂⊂111111E.E,DDBBCA111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O为原点,以OC为X轴正方向,以OB为Y轴正方向.则)1,0,1()1,1,1(),10(),1(,0,1,0111-=⇒CABACB,,,,)(.由(Ⅰ)知, 平面BB1D1D的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OCOBCAn设平面OCB1的法向量为,则0,0,2122=⋅=⋅OCnOBnn).1-,1,0(法向量2=n为解得其中一个21221||||||,cos|cos212111=⋅=⋅=><=nnnnnnθ.所以,平面OCB1与平面BB1D1D的夹角θ为3π1A。
(完整版)空间几何体的表面积与体积练习题.及答案

For personal use only in study and research; not forcommercial use空间几何体的表面积与体积专题一、选择题1.棱长为2的正四面体的表面积是( C ).A. 3 B .4 C .4 3 D .16解析 每个面的面积为:12×2×2×32= 3.∴正四面体的表面积为:4 3.2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的 ( B ). A .2倍 B .22倍 C.2倍 D.32倍解析 由题意知球的半径扩大到原来的2倍,则体积V =43πR 3,知体积扩大到原来的22倍.3.如图是一个长方体截去一个角后所得多面体的三视图,则该多面体的体积为( B ). A.1423 B.2843 C.2803D.1403解析 根据三视图的知识及特点,可画出多面体 的形状,如图所示.这个多面体是由长方体截去 一个正三棱锥而得到的,所以所求多面体的体积 V =V 长方体-V 正三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843. 4.某几何体的三视图如下,则它的体积是( A) A .8-2π3 B .8-π3C .8-2π D.2π3解析 由三视图可知该几何体是一个边长为2的正方体内部挖去一个底面半径为1,高为2的圆锥,所以V =23-13×π×2=8-2π3.5.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为( A)A .24-32π B .24-π3 C .24-π D .24-π2据三视图可得几何体为一长方体内挖去一个半圆柱,其中长方体的棱长分别为:2,3,4,半圆柱的底面半径为1,母线长为3,故其体积V =2×3×4-12×π×12×3=24-3π2.6.某品牌香水瓶的三视图如图 (单位:cm),则该几何体的表面积为( C )A.⎝ ⎛⎭⎪⎫95-π2 cm 2B.⎝ ⎛⎭⎪⎫94-π2 cm 2C.⎝ ⎛⎭⎪⎫94+π2 cm 2D.⎝⎛⎭⎪⎫95+π2 cm 2解析 这个空间几何体上面是一个四棱柱、中间部分是一个圆柱、下面是一个四棱柱.上面四棱柱的表面积为2×3×3+12×1-π4=30-π4;中间部分的表面积为2π×12×1=π,下面部分的表面积为2×4×4+16×2-π4=64-π4.故其表面积是94+π2.7.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S-ABC 的体积为( C).A .3 3B .2 3 C. 3 D .1解析 由题可知AB 一定在与直径SC 垂直的小圆面上,作过AB 的小圆交直径SC 于D ,设SD =x ,则DC =4-x ,此时所求棱锥即分割成两个棱锥S-ABD 和C-ABD ,在△SAD 和△SBD 中,由已知条件可得AD =BD =33x ,又因为SC 为直径,所以∠SBC =∠SAC =90°,所以∠DCB =∠DCA =60°,在△BDC 中 ,BD =3(4-x ),所以33x =3(4-x ),所以x =3,AD =BD =3,所以三角形ABD 为正三角形,所以V =13S △ABD ×4= 3.二、填空题8.三棱锥PABC 中,PA ⊥底面ABC ,PA =3,底面ABC 是边长为2的正三角形,则三棱锥PABC 的体积等于__3______.解析 依题意有,三棱锥PABC 的体积V =13S △ABC ·|PA |=13×34×22×3= 3.9.一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为_ 3∶2_______.解析 设圆柱的底面半径是r ,则该圆柱的母线长是2r ,圆柱的侧面积是2πr ·2r =4πr 2,设球的半径是R ,则球的表面积是4πR 2,根据已知4πR 2=4πr 2,所以R =r .所以圆柱的体积是πr 2·2r=2πr 3,球的体积是43πr 3,所以圆柱的体积和球的体积的比是2πr 343πr 3=3∶2.10.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是___26_____. 解析 由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V =13×1×1×22=26. 11.如图,半径为R 的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是____2πR 2____.解析 由球的半径为R ,可知球的表面积为4πR 2.设内接圆柱底面半径为r ,高为2h ,则h 2+r 2=R 2.而圆柱的侧面积为2πr ·2h =4πrh ≤4πr 2+h 22=2πR 2(当且仅当r =h 时等号成立),即内接圆柱的侧面积最大值为2πR 2,此时球的表面积与内接圆柱的侧面积之差为2πR 2.12.如图,已知正三棱柱ABCA 1B 1C 1的底面边长为2 cm ,高为5 cm ,则一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点A 1的最短路线的长为___13_____cm. 解析 根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 (cm). 三、解答题13.某高速公路收费站入口处的安全标识墩如图1所示,墩的上半部分是正四棱锥PEFGH ,下半部分是长方体ABCDEFGH .图2、图3分别是该标识墩的正视图和俯视图. (1)请画出该安全标识墩的侧视图; (2)求该安全标识墩的体积.解析 (1)侧视图同正视图,如图所示:(2)该安全标识墩的体积为V =V PEFGH +V ABCDEFGH =13×402×60+402×20=64 000(cm 3).14 .一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为3,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.(1)求该几何体的体积V ;(2)求该几何体的表面积S.解析 (1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为3,所以V =1×1×3= 3.(2)由三视图可知,该平行六面体中,A1D ⊥平面ABCD ,CD ⊥平面BCC1B1, 所以AA1=2,侧面ABB1A1,CDD1C1均为矩形, S =2×(1×1+1×3+1×2)=6+2 3.15.已知某几何体的俯视图是如右图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ;(2)求该几何体的侧面积S .解析 由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h 1的等腰三角形,左、 右侧面均为底边长为6,高为h 2的等腰三角形,如右图所示. (1)几何体的体积为:V =13·S 矩形·h =13×6×8×4=64.(2)正侧面及相对侧面底边上的高为:h 1=42+32=5.左、右侧面的底边上的高为:h 2=42+42=4 2.故几何体的侧面面积为:S =2×⎝ ⎛⎭⎪⎫12×8×5+12×6×42=40+24 2. 1.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( ). .解:设展开图的正方形边长为a ,圆柱的底面半径为r ,则2πr =a ,2ar π=,底面圆的面积是24a π,于是全面积与侧面积的比是2221222a a a πππ++=, 2.在棱长为 1 的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去与8个顶点相关的8个三棱锥后 ,剩下的几何体的体积是( ).2.解:正方体的体积为1,过共顶点的三条棱中点的平面截该正方体截得的三棱锥的体积是111111()3222248⨯⨯⨯⨯=,于是8个三棱锥的体积是61,剩余部分的体积是65, 3.一个直棱柱(侧棱垂直于底面的棱柱)的底面是菱形,对角线长分别是6cm 和8cm ,高是5cm ,则这个直棱柱的全面积是 。
新人教版空间几何体测试题及答案
第一章《空间几何体》单元测试题(时间:60分钟,满分:100分)班别 座号 姓名 成绩 一、选择题(本大题共10小题, 每小题5分,共50分) 1、 图(1)是由哪个平面图形旋转得到的( )A B C D2、过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分 的面积之比为( )A.1:2:3B.1:3:5C.1:2:4 D1:3:9 3、棱长都是1的三棱锥的表面积为( )A. 3B. 23C. 33D. 434、已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V 1和V 2,则V 1:V 2=A. 1:3B. 1:1C. 2:1D. 3:15、如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:96、有一个几何体的三视图及其尺寸,则该几何体的表面积及体积为:A.24πcm 2,12πcm 3B.15πcm 2,12πcm3C.24πcm 2,36πcm 3D.以上都不正确7、一个球的外切正方体的全面积等于6 cm 2,则此球的体积为 ( ) A.334cm π B.386cm π C. 361cm π D. 366cm π 8、一个体积为38cm 的正方体的顶点都在球面上,则球的表面积是A .28cm πB .212cm πC .216cm πD .220cm π 9、一个正方体的顶点都在球面上,此球与正方体的表面积之比是( )A. 3πB. 4πC. 2πD. π10、如右图为一个几何体的 三视图,其中府视图为 正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为(A)6+3 (B)24+3 (C)24+23 (D)32A B 1 C 正视图侧视图府视图题号 1 2 3 4 5 6 7 8 9 10 _______________.答案二、填空题(本大题共4小题,每小题5分,共20分)11. 长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为12.一个半球的全面积为Q,一个圆柱与此半球等底等体积,则这个圆柱的全面积是______.13、球的半径扩大为原来的2倍,它的体积扩大为原来的 _________ 倍.14、一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是_________.三、解答题(本大题共3小题,每小题10分,共30分)15.将圆心角为1200,面积为3 的扇形, 16. (如图)在底半径为2母线长为4的作为圆锥的侧面,求圆锥的表面积和体积. 圆锥中内接一个高为3的圆柱,求圆柱的表面积*16、如图,在四边形ABCD中,,,,,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.参考答案:1.A ;2.B ;3.A ;4.D ;5.C ;6.A ;7.C ;8.B ;9.C ;10.C.11.15;12.910Q;13.8;14.2:1 15.解:l=3,R=1;S=4π;V=322π.16.R=1,h=3,S=2π+2π3.17.S=60π+4π2;V=52π-38π=3148π.。
空间几何体练习试题和答案解析
(数学 2 必修)第一章空间几何体[ 基础训练A组]一、选择题1.有一个几何体的三视图如下图所示,这个几何体应是一个( )A. 棱台B. 棱锥C. 棱柱D. 都不对主视图左视图俯视图2.棱长都是1的三棱锥的表面积为()A. 3B. 2 3C. 3 3D. 4 33.长方体的一个顶点上三条棱长分别是3, 4,5 ,且它的8 个顶点都在同一球面上,则这个球的表面积是()A.25 B.50 C.125 D.都不对4.正方体的内切球和外接球的半径之比为()A. 3 :1 B.3: 2 C.2: 3 D.3:35.在△ABC中,AB BC ABC ,若使绕直线BC 旋转一周,2, 1.5, 120则所形成的几何体的体积是()A. 92B.72C.52D.326.底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为 5 ,它的对角线的长分别是9和15 ,则这个棱柱的侧面积是()A.130 B.140 C.150 D.160二、填空题1.一个棱柱至少有_____个面,面数最少的一个棱锥有________个顶点,. .专业知识分享. .顶点最少的一个棱台有________条侧棱。
2.若三个球的表面积之比是1: 2 :3,则它们的体积之比是_____________。
3.正方体ABCD A1B1C1D1 中,O是上底面ABCD 中心,若正方体的棱长为a,则三棱锥O AB D 的体积为_____________。
1 14.如图,E,F 分别为正方体的面ADD1 A1 、面BCC1B1 的中心,则四边形B F D1E 在该正方体的面上的射影可能是____________ 。
5.已知一个长方体共一顶点的三个面的面积分别是 2 、 3 、 6 ,这个长方体的对角线长是___________;若长方体的共顶点的三个侧面面积分别为3,5,15 ,则它的体积为___________.三、解答题1.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M ,高4M ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4M (高不变);二是高度增加4M (底面直径不变)。
8.1空间几何体;8.2斜二测画法练习题(含答案)
(D)4 个
()
4. 对于棱柱下列说法正确的是 (A)只有两个面互相平行 (C)所有的面都是平行四边形
() (B)所有的棱都互相平行 (D)两底面互相平行,且各侧棱也互相平行
5. 关于空间几何体的结构特征,下列说法不正确的是
(A)棱锥的侧棱长都相等
(B)棱柱的侧棱长都相等
(C)三棱台的上、下底面是相似三角形
第八章 立体几何初步
§8.1 空间几何体——多面体
班
姓名
2020 年 3 月 11 日
一、 选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 下列各组几何体中,都是多面体的一组是 (A)三棱柱,四棱台,球,圆锥 (C)三棱柱,四棱台,正方体,六棱锥
() (B)三棱柱,四棱台,正方体,圆台 (D)圆锥,圆台,球,半球
{ 棱台的侧棱所在直线均相交于同一点.
其中,真命题的个数为
(A)1 个
(B)2 个
(C)3 个
(D)4 个
()
答案: D
4. 对于棱柱下列说法正确的是 (A)只有两个面互相平行 (C)所有的面都是平行四边形
() (B)所有的棱都互相平行 (D)两底面互相平行,且各侧棱也互相平行
答案: D
5. 关于空间几何体的结构特征,下列说法不正确的是
(A)棱锥的侧棱长都相等
(B)棱柱的侧棱长都相等
(C)三棱台的上、下底面是相似三角形
(D)有的棱台的侧棱长都相等
()
第八章 立体几何初步
2020 年 3 月 11 日
答案: A
6. 下列说法中正确的是 (A)正方体和长方体都是特殊的直四棱柱 (C)棱锥的侧面都是等腰三角形
(B)棱柱的侧面可以是三角形 (D)棱柱的各条棱都相等
2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练【含答案】
2025年高考数学一轮复习-空间几何体的结构、表面积和体积-专项训练一、基本技能练1.下列说法中,正确的是()A.棱柱的侧面可以是三角形B.若棱柱有两个侧面是矩形,则该棱柱的其他侧面也是矩形C.正方体的所有棱长都相等D.棱柱的所有棱长都相等2.如图所示的等腰梯形是一个几何图形的斜二测直观图,其底角为45°,上底和腰均为1,下底为2+1,则此直观图对应的平面图形的面积为()A.1+2B.2+2C.2+22D.4+223.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为()A.4B.43D.3C.234.已知在梯形ABCD中,∠ABC=π2,AD∥BC,BC=2AD=2AB=2,则将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的表面积为() A.(5+2)π B.(4+2)πC.(5+22)πD.(3+2)π5.如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷、佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为45°,则该正四棱锥的一个侧面与底面的面积之比为()A.3∶2B.2∶2C.3∶3D.3∶46.过圆锥的轴作截面,如果截面为正三角形,则称该圆锥为等边圆锥.已知在一等边圆锥中,过顶点P 的截面与底面交于CD ,若∠COD =90°(O 为底面圆心),且S △PCD =72,则这个等边圆锥的表面积为()A.2π+2πB.3πC.2π+3πD.π+3π7.如图,四边形ABCD 是边长为2的正方形,ED ⊥平面ABCD ,FC ⊥平面ABCD ,ED =2FC =2,则四面体ABEF 的体积为()A.13B.23C.1D.438.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为5-12,约为0.618.这个比例被公认为是最能引起美感的比例,因此被称为黄金比.在几何世界中有很多黄金图形,在三角形中,如果相邻两边之比等于黄金比,且它们夹角的余弦值为黄金比值,那么这个三角形一定是直角三角形,且这个三角形称为黄金分割直角三角形.在正四棱锥中,以黄金分割直角三角形的长直角边作为正四棱锥的高,黄金分割直角三角形的短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离),斜边作为正四棱锥的斜高,这样得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中,以该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为()A.5-12B.5+12C.1D.149.如图,在棱长为2的正方体ABCD-A′B′C′D′中,点E,F,G分别是棱A′B′,B′C′,CD的中点,则由点E,F,G确定的平面截正方体所得的截面多边形的面积等于________.10.已知圆锥的顶点为S,底面圆周上的两点A,B满足△SAB为等边三角形,且面积为43,又知圆锥轴截面的面积为8,则圆锥的侧面积为________.11.如图,已知正三棱柱ABC-A1B1C1的各棱长均为2,点D在棱AA1上,则三棱锥D-BB1C1的体积为________.12.已知三棱锥S-ABC中,∠SAB=∠ABC=π2,SB=4,SC=213,AB=2,BC =6,则三棱锥S-ABC的体积为________.二、创新拓展练13.(多选)攒尖是我国古代建筑中屋顶的一种结构形式,宋代称为撮尖,清代称攒尖,通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖,也有单檐和重檐之分,多见于亭阁式建筑、园林建筑.下面以四角攒尖为例,如图,它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为θ,这个角接近30°.若取θ=30°,侧棱长为21米,则()A.正四棱锥的底面边长为6米B.正四棱锥的底面边长为3米C.正四棱锥的侧面积为243平方米D.正四棱锥的侧面积为123平方米14.(多选)如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=12,则下列结论中错误的是()A.AC⊥AFB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.△AEF的面积与△BEF的面积相等15.(多选)《九章算术》是《算经十书》中最重要的一部,其中将有三条棱互相平行且有一个面为梯形的五面体称为“羡除”,则()A.“羡除”有且仅有两个面为三角形B.“羡除”一定不是台体C.不存在有两个面为平行四边形的“羡除”D.“羡除”至多有两个面为梯形16.(多选)如图,四边形ABCD为正方形,ED⊥平面ABCD,FB∥ED,AB=ED=2FB.记三棱锥E-ACD,F-ABC,F-ACE的体积分别为V1,V2,V3,则()A.V3=2V2B.V3=V1C.V3=V1+V2D.2V3=3V1参考答案与解析一、基本技能练1.答案C解析棱柱的侧面都是平行四边形,选项A错误;其他侧面可能是平行四边形,选项B错误;棱柱的侧棱与底面边长并不一定相等,选项D错误;易知选项C正确.2.答案B解析∵平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,∴平面图形为直角梯形,且直角腰长为2,上底边长为1,下底边长为2+1,∴平面图形的面积S=1+1+22×2=2+ 2.故选B.3.答案B解析易知该几何体是由上、下两个全等的正四棱锥组成的,其中正四棱锥底面边长为2,棱锥的高为1,所以该多面体的体积V =2×13×(2)2×1=43.4.答案A解析因为在梯形ABCD 中,∠ABC =π2,AD ∥BC ,BC =2AD =2AB =2,所以将梯形ABCD 绕AD 所在的直线旋转一周得到的几何体是一个底面半径为1,高为2的圆柱挖去一个底面半径为1,高为1的圆锥后剩余的部分,如图所示.所以该几何体的表面积S =π×12+2π×1×2+π×1×12+12=(5+2)π.5.答案D解析设塔顶是正四棱锥P -ABCD (如图),PO 是正四棱锥的高.设正四棱锥底面边长为a ,则底面面积S 1=a 2,因为AO =22a ,∠PAO =45°,所以PA =2×22a =a ,所以△PAB 是正三角形,其面积为S 2=34a 2,所以S 2∶S 1=34a 2∶a 2=3∶4.6.答案B解析如图,连接PO ,设圆锥的母线长为2a ,则圆锥的底面圆的半径为a ,高为PO =3a .由已知得CD =2a ,PC =PD =2a ,则S △PCD =12×2a ×(3a )2+22a 2=72,从而可得a =1,圆锥的表面积为πa ×2a +πa 2=3πa 2=3π.7.答案B解析∵ED ⊥平面ABCD 且AD ⊂平面ABCD ,∴ED ⊥AD .∵在正方形ABCD 中,AD ⊥DC ,又DC ∩ED =D ,DC ,ED ⊂平面CDEF ,∴AD ⊥平面CDEF .易知FC =ED2=1,V A -BEF =V ABCDEF -V F -ABCD -V A -DEF .∵V E -ABCD =13·ED ·S 正方形ABCD =13×2×2×2=83,V B -EFC =13·BC ·S △EFC =13×2×2×1×12=23,∴V ABCDEF =V E -ABCD +V B -EFC =83+23=103.又V F -ABCD =13·FC ·S 正方形ABCD =13×1×2×2=43,V A -DEF =13·AD ·S △DEF =13×2×2×2×12=43,∴V A -BEF =V ABCDEF -V F -ABCD -V A -DEF =103-43-43=23.故选B.8.答案D解析如图,在黄金分割正四棱锥P -ABCD 中,O 是正方形ABCD 的中心,PE 是正四棱锥的斜高,设OE =a ,则CD =2a ,∴Rt△POE为黄金分割直角三角形,则OEPE=5-12,∴PE=5+12,则PO=PE2-OE2=1+52a,∴以该正四棱锥的高为边长的正方形的面积S=PO2=1+52a2,又正四棱锥的四个侧面是全等的,∴S侧=4S△PCD=4×12×CD×PE=2(1+5)a2,∴该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为1 4 .9.答案332解析分别取AD,CC′和AA′的中点为P,M,N,可得出过E,F,G三点的平面截正方体所得截面为正六边形EFMGPN,则正六边形的边长MG=CG2+CM2=222+2221,故截面多边形的面积S=6×34×12=332.10.答案82π解析设圆锥的母线长为l,由△SAB为等边三角形,且面积为43,所以12l 2sin π3=43,解得l =4;又设圆锥底面半径为r ,高为h ,则由轴截面的面积为8,得rh =8;又r 2+h 2=l 2=16,解得r =h =22,所以圆锥的侧面积S =πrl =π·22·4=82π.11.答案233解析如图,取BC 的中点O ,连接AO .∵正三棱柱ABC -A 1B 1C 1的各棱长均为2,∴AC =2,OC =1,则AO = 3.∵AA 1∥平面BCC 1B 1,∴点D 到平面BCC 1B 1的距离为3.又S △BB 1C 1=12×2×2=2,∴V D -BB 1C 1=13×2×3=233.12.答案43解析∵∠ABC =π2,AB =2,BC =6,∴AC =AB 2+BC 2=22+62=210.∵∠SAB =π2,AB =2,SB =4,∴AS =SB 2-AB 2=42-22=2 3.由SC =213,得AC 2+AS 2=SC 2,∴AC ⊥AS .又∵SA ⊥AB ,AC ∩AB =A ,AC ,AB ⊂平面ABC ,∴AS ⊥平面ABC .∴AS 为三棱锥S -ABC 的高,∴V 三棱锥S -ABC =13×12×2×6×23=4 3.二、创新拓展练13.答案AC解析如图,在正四棱锥S -ABCD 中,O 为正方形ABCD 的中心,H 为AB 的中点,则∠SHO 为侧面SAB 与底面ABCD 所成的锐二面角,且SH ⊥AB ,∠SHO =30°,设底面边长为2a ,所以OH =AH =a ,OS =33a ,SH =233.在Rt △SAH 中,a 2=21,解得a =3,所以正四棱锥的底面边长为6米,侧面积为S =12×6×23×4=243(平方米).14.答案AD解析由题意及图形知,当点F 与点B 1重合时,∠CAF =60°,故A 错误;由正方体ABCD -A 1B 1C 1D 1的两个底面平行,EF ⊂平面A 1B 1C 1D 1,知EF ∥平面ABCD ,故B 正确;由几何体的性质及图形知,三角形BEF 的面积是定值,点A 到平面DD 1B 1B 的距离是定值,故可得三棱锥A -BEF 的体积为定值,故C 正确;由图形可以看出,B 到直线EF 的距离与A 到直线EF 的距离不相等,故△AEF 的面积与△BEF 的面积不相等,故D 错误.故选AD.15.答案ABC解析由题意知AE ∥BF ∥CD ,四边形ACDE 为梯形,如图所示.选项A ,由题意知“羡除”有且仅有两个面为三角形,故A 正确;选项B ,因为AE ∥BF ∥CD ,所以“羡除”一定不是台体,故B 正确;选项C ,假设四边形ABFE 和四边形BCDF 为平行四边形,则AE ∥BF ∥CD ,且AE =BF =CD ,即四边形ACDE 为平行四边形,与已知四边形ACDE 为梯形矛盾,故不存在,故C 正确;选项D ,若AE ≠BF ≠CD ,则“羡除”有三个面为梯形,故D 错误.故选ABC.16.答案CD 解析如图,连接BD 交AC 于O ,连接OE ,OF .设AB =ED =2FB =2,则AB =BC =CD =AD =2,FB =1.因为ED ⊥平面ABCD ,FB ∥ED ,所以FB ⊥平面ABCD ,所以V 1=V E -ACD =13S △ACD ·ED =13×12AD ·CD ·ED =13×12×2×2×2=43,V 2=V F -ABC =13S △ABC ·FB =13×12AB ·BC ·FB =13×12×2×2×1=23.因为ED ⊥平面ABCD ,AC ⊂平面ABCD ,所以ED ⊥AC ,又AC ⊥BD ,且ED ∩BD =D ,ED ,BD ⊂平面BDEF ,所以AC ⊥平面BDEF .因为OE ,OF ⊂平面BDEF ,所以AC ⊥OE ,AC ⊥OF .易知AC=BD=2AB=22,OB=OD=12BD=2,OF=OB2+FB2=3,OE=OD2+ED2=6,EF=BD2+(ED-FB)2=(22)2+(2-1)2=3,所以EF2=OE2+OF2,所以OF⊥OE.又OE∩AC=O,OE,AC⊂平面ACE,所以OF⊥平面ACE,所以V3=V F-ACE=13S△ACE·OF=13×12AC·OE·OF=13×12×22×6×3=2,所以V3≠2V2,V1≠V3,V3=V1+V2,2V3=3V1,所以选项A,B不正确,选项C,D正确.故选CD.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章空间几何体一、选择题
1.下图是由哪个平面图形旋转得到的()
A C D
2.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为()
A. 1:2:3
B. 1:3:5
C. 1:2:4
D. 1:3:9
3.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,则截去8个三棱锥后,剩下的几何体的体积是()
A.
2
3
B.
7
6
C.
4
5
D.
5
6
4.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为
1
V和
2
V,则
12
:
V V=()A. 1:3 B. 1:1 C. 2:1 D. 3:1
5.如果两个球的体积之比为8:27,那么两个球的表面积之比为( )
A. 8:27
B. 2:3
C. 4:9
D. 2:9
6.有一个几何体的三视图及其尺寸如下(单位cm),则该几何体的表面积及体积为:A. 2
24cm
π,2
12cm
π B. 2
15cm
π,2
12cm
π
C. 2
24cm
π,2
36cm
π D. 以上都不正确
二、填空题
1. 若圆锥的表面积是15π,侧面展开图的圆心角是0
60,则圆锥的体积是_______。
2.一个半球的全面积为Q,一个圆柱与此半球等底等体积,则这个圆柱的全面积是.
3.球的半径扩大为原来的2倍,它的体积扩大为原来的_________ 倍.
4.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.
5.已知棱台的上下底面面积分别为4,16,高为3,则该棱台的体积为___________。
三、解答题
1. (如图)在底半径为2,母线长为4的圆锥中内接一个高为3的圆柱,求圆柱的表面积
2.如图,在四边形ABCD 中,
090DAB ∠=,0135ADC ∠=,5AB =,22CD =,2AD =,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.
参考答案
一、选择题
1.A 几何体是圆台上加了个圆锥,分别由直角梯形和直角三角形旋转而得
2.B 从此圆锥可以看出三个圆锥,123123::1:2:3,::1:2:3,r r r l l l ==
12312132::1:4:9,:():()1:3:5S S S S S S S S =--=
3.D 111115818322226V V -=-⨯⨯⨯⨯⨯
=正方体三棱锥 4.D 121:():()3:13
V V Sh Sh ==
5.C 121212:8:27,:2:3,:4:9V V r r S S ===
6.A 此几何体是个圆锥,23,5,4,33524r l h S πππ====⨯+⨯⨯=表面 2134123
V ππ=⨯⨯=
二、填空题
1.
设圆锥的底面半径为r ,母线为l ,则123
r l ππ=,得6l r =,226715S r r r r ππππ=+⋅==
,得r =
h =
211153377
V r h ππ==⨯= 2.109
Q
22223,S R R R Q R πππ=+===全 32222221010,,2233339
V R R h h R S R R R R Q πππππ==⋅==+⋅== 3.8 21212,8r r V V ==
4.12
2
34,123
V Sh r h R R ππ===== 5.28
'11()(416)32833V S S h =+=⨯+⨯= 三、解答题
1.
解:圆锥的高h ==,圆柱的底面半径1r =,
22(2S S S πππ
=+=+=+侧面表面底面
2.解:S S S S =++表面圆台底面圆台侧面圆锥侧面
25(25)2πππ=⨯+⨯+⨯⨯⨯
1)π=
V V V =-圆台圆锥
222112211()331483
r r r r h r h πππ=++-=。
