《新编基础物理学答案》_第9章
新编基础物理学上册1-2单元课后答案

新编物理基础学(上、下册)课后习题详细答案王少杰,顾牡主编第一章1-1.质点运动学方程为:cos()sin(),r a t i a t j btk ωω=++r r r r其中a ,b ,ω均为正常数,求质点速度和加速度与时间的关系式。
分析:由速度、加速度的定义,将运动方程()r t r对时间t 求一阶导数和二阶导数,可得到速度和加速度的表达式。
解:/sin()cos()==-++r r r r rv dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦r r r r1-2. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2/d d v v K t -=, 式中K 为常量.试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kx v v e -= 。
其中0v 是发动机关闭时的速度。
分析:要求()v v x =可通过积分变量替换dxdvvdt dv a ==,积分即可求得。
证:2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v0Kx v v e -=1-3.一质点在xOy 平面内运动,运动函数为22,48x t y t ==-。
(1)求质点的轨道方程并画出轨道曲线;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
分析:将运动方程x 和y 的两个分量式消去参数t ,便可得到质点的轨道方程。
写出质点的运动学方程)(t r ρ表达式。
对运动学方程求一阶导、二阶导得()v t r 和()a t r ,把时间代入可得某时刻质点的位置、速度、加速度。
解:(1)由2,x t =得:,2x t =代入248y t =-可得:28y x =-,即轨道曲线。
《新编基础物理学》_第10章

第10章 导体和电介质中的静电场10-1 如题图10-1所示,三块平行的金属板A ,B 和C ,面积均为2cm 200, A 与B 相距mm 4,A 与C 相距mm 2,B 和C 两板均接地,若A 板所带电量C 100.37-⨯=Q ,忽略边缘效应,求:(1)B 和C 上的感应电荷;(2)A 板的电势(设地面电势为零)。
分析:当导体处于静电平衡时,根据静电平衡条件和电荷守恒定律,可以求得导体的电荷分布,又因为B 、C 两板都接地,所以有AC AB U U =.解:(1)设B 、C 板上的电荷分别为B q 、C q 。
因3块导体板靠的较近,可将6个导体面视为6个无限大带电平面。
导体表面电荷分布均匀,且其间的场强方向垂直于导体表面。
作解图10-1中虚线所示的圆柱形高斯面。
因导体达到静电平衡后,内部场强为零,故由高斯定理得:1A C q q =-2A B q q =-即()A B C q q q =-+ ①又因为AC AB U U =即2AC AB dE E d ⋅=⋅所以2A C A B E E =可得002C B q qS Sεε =⋅ 即 2C B q q = ② 联立①②求得题图10-1解图10-1d7210C C q -=-⨯7110C B q -=-⨯(2) A 板的电势00222C C A AC AC q d d d U U E S σεε ==⋅=⋅=⋅ 733412210210 2.2610(V)200108.8510----⨯=⨯⨯=⨯⨯⨯⨯ 10-2 如题图10-2所示,平行板电容器充电后,A 和B 极板上的面电荷密度分别为σ+和σ-,设P 为两极板间任意一点,略去边缘效应,求:(1)A ,B 板上的电荷分别在P 点产生的场强A E ,B E;(2)A ,B 板上的电荷在P 点产生的合场强E;(3) 拿走B 板后P 点处的场强E '。
分析:运用无限大均匀带电平板在空间产生的场强表达式及场强叠加原理求解。
《新编基础物理学答案》_第11章

第11章 恒定电流与真空中的恒定磁场11-1 电源中的非静电力与静电力有什么不同?答:在电路中,电源中非静电力的作用是,迫使正电荷经过电源内部由低电位的电源负极移动到高电位的电源正极,使两极间维持一定的电位差。
而静电场的作用是在外电路中把正电荷由高电位的地方移动到低电位的地方,起到推动电流的作用;在电源内部正好相反,静电场起的是抵制电流的作用。
电源中存在的电场有两种:1、非静电起源的场;2、稳恒场。
把这两种电场与静电场比较,静电场由静止电荷所激发,它不随时间的变化而变化。
非静电场不由静止电荷产生,它的大小决定于单位正电荷所受的非静电力,kF E q=。
当然电源种类不同,k F 的起因也不同。
11-2静电场与恒定电场有什么相同处和不同处?为什么恒定电场中仍可应用电势概念? 答:稳恒电场与静电场有相同之处,即是它们都不随时间的变化而变化,基本规律相同,并且都是位场。
但稳恒电场由分布不随时间变化的电荷产生,电荷本身却在移动。
正因为建立稳恒电场的电荷分布不随时间变化,因此静电场的两条基本定理,即高斯定理和环路定理仍然适用,所以仍可引入电势的概念。
11-3一根铜导线表面涂以银层,当两端加上电压后,在铜线和银层中,电场强度是否相同?电流密度是否相同?电流强度是否相同?为什么? 答:此题涉及知识点:电流强度d sI =⋅⎰j s ,电流密度概念,电场强度概念,欧姆定律的微分形式j E σ=。
设铜线材料横截面均匀,银层的材料和厚度也均匀。
由于加在两者上的电压相同,两者的长度又相等,故铜线和银层的场强E 相同。
由于铜线和银层的电导率σ不同,根据j E σ=知,它们中的电流密度j 不相同。
电流强度d sI =⋅⎰j s ,铜线和银层的j 不同但相差不太大,而它们的横截面积一般相差较大,所以通过两者的电流强度,一般说来是不相同的。
11-4一束质子发生侧向偏转,造成这个偏转的原因可否是: (1)电场? (2)磁场?(3)若是电场或者是磁场在起作用,如何判断是哪一种场?答:造成这个偏转的原因可以是电场或磁场。
新编物理学基础课后习题答案
i AB CD
0 I vl 1 1 ( ) 2 a vt a b vt
I
aA b D l
方向为顺时针方向。 (2) 选面积元dS = ldr a b 0 I 0 l I a b Φ a l dr ln 2 r 2 a
r v
B
C
dr
I aA b D l B C
v
解:(1) 任意时刻 t,AB、CD边到导线的距离分别 为 a +v t 和 a +b + v t 0 I 0 I BAB BCD 2 (a vt ) 2 (a b vt )
AB l vBAB (A B)
CD l vBCD (D C)
0 0 0
3-7 如图所示,长直导线AB中的电流 I沿导线向上, 并以 dI/dt=2A/s的变化率均匀增长。导线附近放一个 与之共面的直角三角形线框,其一边与导线平行,位 置及线框尺寸如图(设a =10cm, b=20cm, c = 5.0cm) 所示。求此线框中产生的感应电动势的大小和方向。 A Y 0 I 解: dx 处 的B 2 x I 0.15 0 I Φ s B dS 0.05 y dx b 2 x y 0.15 x y y 2(0.15 x ) O x dx X 0.1 0.2 a B c
k
R rk 2eR (2k 1) 2 rk2 1 12 1 k 50.5 50 (条) 4 R 2 0.5 10 400 2
2
4-15 波长范围在450~650nm之间的复色平行光垂直 照射在每厘米有5000条刻线的光栅上,屏幕放在透镜 的焦平面处,屏上第二级光谱各色光在屏上所占范围 的宽度为35.1cm,求透镜的焦距f 。 1 cm 解: a b (a b)sin k 2 5000 21 2 450 0 sin 1 0.45 26.74 1 a b 2 103
大学物理第九章振动学基础习题答案

第九章 振动学习题9-1 一小球与轻弹簧组成的振动系统,按(m) 3ππ8cos 05.0⎪⎭⎫ ⎝⎛+=t x ,的规律做自由振动,试求(1)振动的角频率、周期、振幅、初相、速度最大值和加速度最大值;(2)t=1s ,2s ,10s 等时刻的相位;(3)分别画出位移、速度和加速度随时间变化的关系曲线。
解:(1)ω=8πs -1,T=2π/ω=0.25s ,A=0.05m ,ϕ0=π/3,m A ω=v ,2m a A ω=(2)π=8π3t φ+ (3)略9-2 一远洋货轮质量为m ,浮在水面时其水平截面积为S 。
设在水面附近货轮的水平截面积近似相等,水的密度为ρ,且不计水的粘滞阻力。
(1)证明货轮在水中做振幅较小的竖直自由运动是谐振动;(2)求振动周期。
解:(1)船处于静止状态时gSh mg ρ=,船振动的一瞬间()F gS h y mg ρ=-++ 得F gSy ρ=-,令k gS ρ=,即F ky =-,货轮竖直自由运动是谐振动。
(2)ω==,2π2T ω==9-3 设地球是一个密度为ρ的均匀球体。
现假定沿直径凿通一条隧道,一质点在隧道内做无摩擦运动。
(1)证明此质点的运动是谐振动;(2)计算其振动周期。
解:以球心为原点建立坐标轴Ox 。
质点距球心x 时所受力为324433x mF G G mx x πρπρ=-=-令43k G m πρ=,则有F kx =-,即质点做谐振动。
(2)ω==2πT ω== 9-4 一放置在水平桌面上的弹簧振子,振幅A =2.0 ×10-2 m ,周期T s 。
当t =0时,(1)物体在正方向端点;(2)物体在平衡位置,向负方向运动;(3)物体在x ×10-2m 处,向负方向运动;(4)物体在x =-×10-2 m 处,向正方向运动。
求以上各种情况的振动方程。
解:ω=2π/T=4πs -1(1)ϕ0=0,0.02cos4(m)x t π=(2)ϕ0=π/2,0.02cos 4(m)2x t ππ⎛⎫=+ ⎪⎝⎭(3)ϕ0=π/3,0.02cos 4(m)3x t ππ⎛⎫=+ ⎪⎝⎭(4)ϕ0=4π/3,40.02cos 4(m)3x t ππ⎛⎫=+ ⎪⎝⎭9-5 有一弹簧,当其下端挂一质量为m 的物体时,伸长量为9.8 ×10-2 m 。
新编基础物理学上册答案

新编基础物理学上册答案【篇一:新编基础物理学上册1-2单元课后答案】class=txt>王少杰,顾牡主编第一章????1-1.质点运动学方程为:r?acos(?t)i?asin(?t)j?btk,其中a,b,?均为正常数,求质点速度和加速度与时间的关系式。
?分析:由速度、加速度的定义,将运动方程r(t)对时间t求一阶导数和二阶导数,可得到速度和加速度的表达式。
?????解:v?dr/dt??a?sin(?t)i?a?cos(?t)j?bk????2a?dv/dt??a???cos(?t)i?sin(?t)j??1-2. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即dv/dt??kv2,式中k为常量.试证明电艇在关闭发动机后又行驶x距离时的速度为v?v0e?kx 。
其中v0是发动机关闭时的速度。
dvdv分析:要求v?v(x)可通过积分变量替换a?,积分即可求得。
?vdtdxdvdvdxdv???v??kv2dtdxdtdxdv??kdxvv1xvv???v0v?0kdx ,lnv0??kx证:v?v0e?kx1-3.一质点在xoy平面内运动,运动函数为x?2t,y?4t2?8。
(1)求质点的轨道方程并画出轨道曲线;(2)求t=1 s和t=2 s 时质点的位置、速度和加速度。
分析:将运动方程x和y的两个分量式消去参数t,便可得到质点的轨道方程。
写出质点的???运动学方程r(t)表达式。
对运动学方程求一阶导、二阶导得v(t)和a(t),把时间代入可得某时刻质点的位置、速度、加速度。
解:(1)由x?2t,得:t?,代入y?4t2?8可得:y?x2?8,即轨道曲线。
画图略???(2)质点的位置可表示为:r?2ti?(4t2?8)j?????由v?dr/dt则速度:v?2i?8tj????由a则加速度:a?8j ?dv/dt????????则:当t=1s时,有r?2i?4j,v?2i?8j,a?8j????????当t=2s时,有r?4i?8j,v?2i?16j,a?8j1-4.一质点的运动学方程为x?t2,y?(t?1)2,x和y均以m为单位,t以s为单位。
新物理高考第九章参考答案共28页

第九章 参考答案第一节 第一节 磁场及其描述考点知识梳理(一)4.特殊物质6.N 极受力;N 极;磁铁的磁场和电流的磁场一样,都是由电荷的运动产生的。
(二)磁场力;不受;吸引;排斥;磁场;磁场力;磁场(三)有方向的曲线;强弱;切线方向;磁感应强度;N ;S ;S ;N ;磁场的方向;不一定;电流方向;平行且距离相等(四)对放入其中的电流或磁极有力的作用;最大;磁场力为零;磁感应强度;矢量;B=F IL ;垂直;切线;N 极;N 极;牛/安米;特斯拉;T ;处处相等;矢量和;矢量运算法则(五)乘积;韦伯;Wb ;磁通量表示穿过某一面积的磁感线条数多少;穿过单位面积的磁通量;标量考能训练答案:1.解析:因在地球的内部地磁场从地球北极指向地球的南极,根据右手螺旋定则可判断出地球表现环形电流的方向应从东到西,而地球是从西向东自转,所以只有地球表面带负电荷才能形成上述电流。
答案:A2.解析:由安培定则判断,凡是垂直纸面向外的磁感线都集中在是线圈内,因磁感线是闭合曲线,则必有相应条数的磁感线垂直纸面向里,这些磁总线分布在线圈是外,所以B 、C 两圆面都有垂直纸面向里和向外的磁感线穿过,垂直纸面向外磁感线条数相同,垂直纸面向里的磁感线条数不同,B 圆面较少,c 圆面较多,但都比垂直向外的少,所以 B 、C 磁通方向应垂直纸面向外,φB >φC ,所以A 、C 正确.分析磁通时要注意磁感线是闭合曲线的特点和正反两方向磁总线条数的多少,不能认为面积大的磁通就大.答案:AC3. 解析:由IL F B =可知1特安·米牛1=。
由==特可知1SB φ2米韦。
由1安秒库1=及 安·米牛特11=,可知1特秒库·米牛/1=。
由1焦=1牛·米=1库·伏,可知 1牛=1库·伏/米,又知1特=秒库·米牛/1,从而可知1特秒米米伏//1=。
答案:A 、B 、C 、D 。
新编基础物理学上册1-2单元课后答案

新编物理基础学(上、下册)课后习题详细答案王少杰,顾牡主编第一章1-1。
质点运动学方程为:cos()sin(),r a t i a t j btk ωω=++其中a ,b ,ω均为正常数,求质点速度和加速度与时间的关系式。
分析:由速度、加速度的定义,将运动方程()r t 对时间t 求一阶导数和二阶导数,可得到速度和加速度的表达式。
解:/sin()cos()==-++v dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦1-2. 一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度方向与速度方向相反,大小与速度平方成正比,即2/d d v v K t -=, 式中K 为常量.试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kx v v e -= 。
其中0v 是发动机关闭时的速度。
分析:要求()v v x =可通过积分变量替换dxdvvdt dv a ==,积分即可求得。
证:2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v 0Kx v v e -=1-3.一质点在xOy 平面内运动,运动函数为22,48x t y t ==-。
(1)求质点的轨道方程并画出轨道曲线;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
分析:将运动方程x 和y 的两个分量式消去参数t ,便可得到质点的轨道方程。
写出质点的运动学方程)(t r 表达式。
对运动学方程求一阶导、二阶导得()v t 和()a t ,把时间代入可得某时刻质点的位置、速度、加速度。
解:(1)由2,x t =得:,2x t =代入248y t =-可得:28y x =-,即轨道曲线。
画图略(2)质点的位置可表示为:22(48)r ti t j =+- 由/v dr dt =则速度:28v i tj =+由/a dv dt =则加速度:8a j =则:当t=1s 时,有24,28,8r i j v i j a j =-=+=当t=2s 时,有48,216,8ri j v i j a j =+=+=1-4.一质点的运动学方程为22(1)x t y t ==-,,x 和y 均以m 为单位,t 以s 为单位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电荷与真空中的静电场9-1两个小球都带正电,总共带有电荷5.0 105C,如果当两小球相距2.0m时, 任一球受另一球的斥力为1.0N.试求:总电荷在两球上是如何分配的。
分析:运用库仑定律求解。
解:如解图9-1所示,设两小球分别带电q1,q2则有q1+q25. C 1 10 5①解图9-1由库仑定律得F qq?厂29 109盹1②4 n °r4由①②联立解得9-2两根6.0 10 2m长的丝线由一点挂下,每根丝线的下端都系着一个质量为0.5 10 3kg的小球.当这两个小球都带有等量的正电荷时,每根丝线都平衡在与沿垂线成60°角的位置上。
求每一个小球的电量。
分析:对小球进行受力分析,运用库仑定律及小球平衡时所受力的相互关系求解。
解:设两小球带电q,小球受力如解图9-2所示2F T cos30 ①4n 0R 解图9-2mg T sin30 ②联立①②得叫E tan30。
③q其中代入③式,得r9-3在电场中某一点的场强定义为E —,q。
若该点没有试验电荷,那么该点是否存在电场?为什么?答:若该点没有试验电荷,该点的场强不变.因为场强是描述电场性质的物理量,仅与场源电荷的分布及空间位置有关,与试验电荷无关,从库仑定律知道,试验rr —电荷q°所受力F与q0成正比,故E 一是与q°无关的。
q。
9-4直角三角形ABC 如题图9-4所示,AB 为斜边,A 点上 J有一点荷q i 1.8 10 9C ,B 点上有一点电荷q 2 4.8 10 9C ,已知BC 0.04m , AC 0.03m ,求C 点电场强度E 的大小和;超方向(cos37 0.8,sin370.6).分析:运用点电荷场强公式及场强叠加原理求解。
解:如解图9-4所示C 点的电场强度为E E r1 E 2C 点电场强度E 的大小方向为C即方向与BC 边成33.7 °9-5两个点电荷q 1 4 10 6C, q 2 8 10 6C 的间距为0.1m ,求距离它们都是0.1m 处的电场强度E 。
分析:运用点电荷场强公式及场强叠加原理求解。
解:如解图9-5所示E 1,E 2沿x 、y 轴分解 电场强度为9-6有一边长为a 的如题图9-6所示的正六角形,四个顶点 都放有电荷q ,两个顶点放有电荷一q 。
试计算图中在六角 形中心O 点处的场强。
分析:运用点电荷场强公式及场强叠加原理求解。
解:如解图 9-6 所示.设 q 1 q 2 q 3 q 6=q , q 4 q 5 =分析:将带电直线无限分割,取一段电荷元,运用点电荷场强公式表示电荷元的 场强,再积分求解。
注意:先将电荷元产生的场强按坐标轴分解然后积分,并利 用场强对称性。
解:如解图9-7建立坐标,带电直线上任一电荷元在 P 点产生的场强大小为题图9-4解图9-4解图9-5点电荷在o 点产生的电场强度大小均为E E 1E 2 E 3 L E 6q 24 n Q 3各电场强度方向如解图9-6所示, E 3与E 6抵消.根据矢量合成,按余弦定理有 解得 方向垂直向下.9-7电荷以线密度 均匀地分布在长为I 的直线上, 电直线的中垂线上与带电直线相距为 R 的点的场强。
求带——Hy v\ A题图9-6解图9-6根据对称性分析,合场强 首的方向沿y 轴的方向9-8两个点电荷q i 和q 2相距为I ,若(1)两电荷同号;(2) 两电荷异号,求电荷连线上电场强度为零的点的位置 •分析:运用点电荷场强公式及场强叠加原理求解。
解:如解图9-8所示建立坐标系,取q i 为坐标原点,指向 q 2的方向为x 轴正方向.(1)两电荷同号.场强为零的点只可能在q i 、q 2之间,设距q i 为x 的A 点.据题意有E i E 2即解图9-8解得⑵ 两电荷异号•场强为零的点在q i q 2连线的 延长线或反向延长线上,即E i =E 2解之得:xdEdx4 o (R 2 x 2)解图9-79-9无限长均匀带电直线,电荷线密度为 入被折成互成直角的 两部分•试求如题图9-9所示的P 点和P'点的电场强度. 分析:运用均匀带电细棒附近的场强公式及场强叠加原理求解。
解:以P 点为坐标原点,建立如解图9-10 (a)所示坐标系 均匀带电细棒产生的场强公式 E(cos 1 cos 2)i (sin 2 sin Jj4 n o a在P 点n1, 2n4所以竖直棒在P 点的场强为1 水平棒在P 点的场强为 所以在P 点的合场强 即P 点的合场强的大小为 方向与x 轴正方向成45° 同理以P 点为坐标原点,建立如图题 9-10解图⑵坐标在P 点 3 1 冗,2 n4 所以竖直棒在P 点的场强为 水平棒在P 点的场强为 i\ + \ +\ + \ + 4 \r+ |7 +a +A—所以在P 点的合场强为即P 点的合场强的大小为 方向与x 轴成-135 ° 9-10无限长均匀带电棒h 上的线电荷密度为1,12上的线 电荷密度为 2 , h 与〔2平行,在与h , J 垂直的平面上有一 点P,它们之间的距离如题图9-10所示,求P 点的电场强度。
分析:运用无限长均匀带电细棒的场强公式及场强叠加原 理求解。
解:h 在P 点产生的场强为 12在P 点产生的场强大小为 方向如解图9-11所示。
把E 2写成分量形式,有题图9-10在P 点产生的合场强为r r rE E 1 E 210.8 n 0解图9-109-11 一细棒被弯成半径为R 的半圆形,其上部均匀分布有电荷Q ,下部均匀分布电荷 Q ,如题图9-11所示,求圆心0 点处的电场强度。
分析:在半圆环说上取电荷元,运用点电荷场强公式及场强 叠加原理积分求解。
将带电半圆环分割成无数个电荷元, 运 用点电荷场强公式表示电荷元场强。
将电荷元电场进行矢量题图9-11分解,再进行对称性分析,然后积分求解。
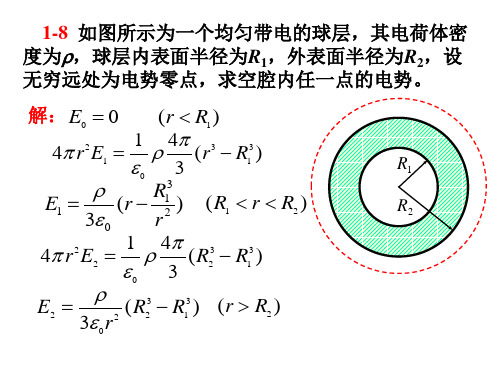
2Q r解:把圆环分成无限多线元dl ,dl 所带电量为dq 2Qdl ,产生的场强为dE n R则dE 的大小为解图9-11把dE 分解成dE x 和dE y ,则由于Q 、 Q 带电量的对称性,x 轴上的分量相互抵 消,则所以圆环在0点产生的场强为9-12.一均匀带电球壳内半径 R 1 6cm ,外半径 R> 10cm ,电荷体密度为2 10 5C m3 4,求:到球心距离r 分别为5cm 、8cm 、12cm 处场点的场强.分析 此题属于球对称性电场,三个场点分别位于球层内半径以内、内外半径之 间、外半径以外三个区域,由高斯定理做高斯面求解。
解:根据高斯定理E dSr 12cm 时,4 n 3 3—(R ; R 13)3沿半径向外.9-13两平行无限大均匀带电平面上的面电荷密度分别为 + 6和-2®如题图9-13所示,(1) 求图中三个区域的场强E 1,E 2,E 3的表达式;33rR 142—3.48 10 N C 4 n o r当r 5 cm 时,q 0,得r 8 cm 时, q/ 33(rR;)方向沿半径向外.题图9-13(2)若 4.43 10 6C m 2,那么,E i , E ? , E 3各多大?分析:首先确定场强正方向,然后利用无限大均匀带电平板场强及场强叠加原理 求解。
解:(1)无限大均匀带电平板周围一点的场强大小为在I 区域U 区域川区域 (2)若 4.43 10 6C m 2 则9-14点电荷q 位于一边长为a 的立方体中心,试求(1) 在该点电荷电场中穿过立方体的任一个面的电通量;(2) 若将该场源点电荷移动到该立方体的一个顶点上,这时穿过立方体各面的 电通量是多少? 分析此题需结合高斯定理以及对称性关系来求解。
解:(1) 由高斯定理可知,通过立方体的总的电通量■ E dS 2s 0立方体有六个面,当q 在立方体中心时,每个面上电通量相等,所以 通过每个面的电通量为(2)电荷在顶点时,将立方体延伸为边长2a 的立方体,使q 处于边长2a 的立方体中心,则通过边长2a 的正方形上电通量边长2a 的正方形共有四个边长a 的正方形,由于对称性,则通过边长 为a 的正方形的电通量为q 24 09-15 一均匀带电半圆环,半径为分析:将带电半圆环分割成无数个电荷元, 根据点电荷电势公式表示电荷元的电 势,再利用电势叠加原理求解。
解:把半圆环无穷分割,如解图 9-15取线元dl ,其带电量为dq —d|,则其n R在圆心0的电势为:. dq Qdl解图9-15duR ,电量为+Q ,求环心处的电势。
4 n 0R 4 n 0 R n R所以整个半圆环在环心 0点处的电势为9-16 一面电荷密度为 的无限大均匀带电平面,若以该平面处为电势零点,求带电平面周围的电势分布。
分析:利用无限大均匀带电平面的场强公式及电势与电场 强度的积分关系求解。
解图9-16解:如解图9-16所示建立坐标系,所以无限大平面周围 的场强分布为取该平面电势为零,则周围任一点 P 的电势为9-17 如题图 9-17所示,已知 a 8 102m ,b 6 10 2m ,8 8q 1 3 10 Cq 3 10 C ,D 为qg 连线中点,求: (1) D 点和B 点的电势;(2) A 点和C 点的电势;(3) 将电量为2 10 9C 的点电荷q o 由A 点移到C 点, 电场力所做的功;(4将q 0由B 点移到D 点,电场力所做的功。
分析:由点电荷的电势的公式及叠加原理求电势。
静电力 是保守力,保守力做功等于从初位置到末位置势能增量的 负值。
解:(1)建立如解图9-17所示坐标系,由点电荷产生的 电势的叠加得 同理,可得(2) U A 」 ------------- _:4n 0b 4 n 0Jb 2 a 2(3) 将点电荷q 0由A 点移到C 点,电场力所做的功 (4) 将q 0由B 点移到D 点,电场力所做的功9-18如题图9-18所示,在A ,B 两点处放有电量分别为 q , q 的点电荷,AB 间距离为2R ,现将另一正试验点电荷q 。
从O 点经过半圆弧移到C 点,求移动过程中电 场力做的功. 分析同上题。
解:O 点的电势为C 点的电势为所以9-19两点电荷q 1=1.5 X 0-8C ,q ? =3.0 X 0-8C ,相距*=42cm ,要把它们之间的距.4*C* 1£-------- (7 --------题图9-17解图9-17离变为r2 =25cm,电场力做功为多少此题用电场力做功定义式积分求解,需注意电场力做功的正负值半径为R i 和R 2(R 2 > R i )的两无限长同轴圆柱面,单位长度上分别带有电量和,试求:(1) 空间场强分布; (2) 两圆柱面之间的电势差。
