电子在电磁场中的运动规律-实验报告
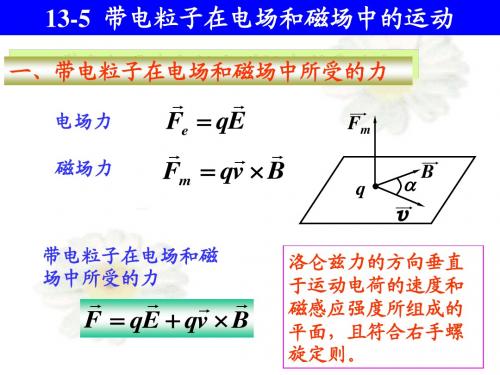
带电粒子在电场或磁场中的运动

通过特定设计的磁场结构,可以将带电粒子约束在某一特定区域内,实现带电粒子的稳定运动。
04
带电粒子在复合场中的运动
电场与磁场的相互作用
电场与磁场相互垂直
当电场与磁场相互垂直时,带电粒子在复合场中的运动轨迹为圆 周或螺旋线。
电场与磁场同向平行
当电场与磁场同向平行时,带电粒子在复合场中的运动轨迹为直线 或抛物线。
拓展应用领域
目前带电粒子在电场或磁场中的运动主要应用于 科研和工业生产,未来可以拓展其在环保、医疗 等领域的应用。
THANKS感谢观看将带电粒子注入固体材料 中,改变材料的性质,用 于半导体制造、表面改性 等领域。
未来研究方向与挑战
1 2 3
探索更高能量粒子的运动规律
随着科技的发展,需要研究更高能量粒子的运动 规律,以推动相关领域的研究进展。
实现更精确的粒子控制
目前粒子控制技术还存在一定的局限性,未来需 要探索更精确的粒子控制方法,提高相关设备的 性能。
粒子运动的能量守恒
带电粒子在电场或磁场中的运动过程中,其动能和势能之 间相互转化,总能量保持守恒。
在科技领域的应用前景
粒子加速器
利用电场加速带电粒子, 提高粒子的能量,用于核 物理、高能物理等领域的 研究。
电子显微镜
利用磁场约束和引导电子, 提高成像的分辨率,广泛 应用于生物学、医学等领 域。
离子注入技术
复合场中的粒子加速器
直线加速器
通过逐步增加电场强度,使带电粒子在 电场中不断加速,最终获得高能量。
VS
回旋加速器
利用磁场和电场的共同作用,使带电粒子 在环形轨道中不断加速,最终获得高能量 。
05
带电粒子运动的实验观察与验证
电磁场与电磁波实验报告

电磁场与电磁波实验报告电磁场与电磁波实验报告引言:电磁场和电磁波是物理学中非常重要的概念。
电磁场是由电荷产生的一种物理场,它的存在和变化会影响周围空间中的其他电荷。
而电磁波则是电磁场的一种传播形式,它以电磁场的振荡和传播为基础,具有波动性质。
本次实验旨在通过实际操作和测量,深入了解电磁场和电磁波的特性。
实验一:测量电磁场强度在实验一中,我们使用了一个电磁场强度计来测量不同位置的电磁场强度。
首先,我们将电磁场强度计放置在一个固定的位置,记录下此时的电磁场强度。
然后,我们将电磁场强度计移动到其他位置,重复测量过程。
通过这些数据,我们可以得出不同位置的电磁场强度的分布情况。
实验结果显示,电磁场强度随着距离的增加而逐渐减弱。
这符合电磁场的特性,即电荷产生的电磁场在空间中以一定的规律传播,而传播的强度会随着距离的增加而减弱。
这一实验结果验证了电磁场的存在和变化对周围环境的影响。
实验二:测量电磁波频率和波长在实验二中,我们使用了一个频率计和一个波长计来测量电磁波的频率和波长。
首先,我们将频率计和波长计设置好,并将它们与电磁波源连接。
然后,我们观察频率计和波长计的测量结果,并记录下来。
通过这些数据,我们可以得出电磁波的频率和波长的数值。
实验结果显示,不同频率的电磁波具有不同的波长。
频率越高的电磁波,波长越短;频率越低的电磁波,波长越长。
这符合电磁波的特性,即电磁波的振荡频率和波长之间存在一定的关系。
这一实验结果验证了电磁波的波动性质,以及频率和波长之间的关系。
实验三:观察电磁波的干涉和衍射现象在实验三中,我们使用了一块光栅和一个狭缝装置来观察电磁波的干涉和衍射现象。
首先,我们将光栅放置在光源前方,并调整光源的位置和光栅的角度。
然后,我们观察到在光栅后方的屏幕上出现了一系列明暗相间的条纹。
这些条纹是由电磁波的干涉和衍射效应引起的。
实验结果显示,当电磁波通过光栅时,会发生干涉和衍射现象。
干涉现象表现为明暗相间的条纹,而衍射现象表现为条纹的扩散和交替。
电子自旋共振实验报告

微波电子自旋共振【摘要】本文通过电子自旋共振实验,解释恒定磁场中的电子自旋磁矩在射频电磁场的作用下会发生磁能级间的共振跃迁现象。
一、引言电子自旋的概念首先由Pauli 于1924年提出。
而电子自旋共振实验则是从1945年开始才发展起来的一项新技术。
电子自旋共振研究的对象是具有未偶电子的物质,如具有奇数个电子的原子、分子、内电子壳层未被充满的离子、受辐射作用产生的自由基及半导体、金属等。
通过共振谱线的研究,可以获得有关分子、原子及离子中未偶电子的状态及其周围环境方面的信息,从而得到有关物质结构和化学键的信息,故电子自旋共振是一种重要的近代物理实验技术,在物理、化学、生物、医学等领域有广泛用途。
“自旋”概念的明确提出:1925年,两位年轻的荷兰学生乌伦贝克和哥德斯密特,“为了解释反常塞曼效应”,受泡利不相容原理的启发,明确提出了电子具有自旋的概念,并证明了“自旋”就是泡利提出的“新自由度”。
1926年,海森伯和约旦引进自旋S ,用量子力学理论对反常塞曼效应作出了正确的计算。
1927年,泡利引入了泡利矩阵作为自旋操作符号的基础,引发了保罗-狄拉克发现描述相对论电子的狄拉克方程式。
电子自旋共振(ESR ,Electron Spin Resonance)是一种奇妙的实验现象,也被称为电子顺磁共振(EPR ,Electron Paramagnetic Resonance)。
它利用具有未偶电子的物质在外加恒定磁场作用下对电磁波的共振吸收特性,来探测物质中的未偶电子,研究其与周围环境的相互作用,从而获得有关物质微观结构的信息。
电子自旋共振现象直到1944年才由苏联喀山大学的扎沃伊斯基.Зabouchu ǔ)在实验中观察到。
二、实验原理1、量子力学解释电子具有自旋,其自旋角动量Pe 和自旋磁矩e μ的关系为:图1 自旋能级在磁场中的取向e B e P h g ρρμμ-=g 为朗德因子,B μ为玻耳磁子,其值为×1O-11MevT-1。
北理电磁实验报告(3篇)

第1篇一、实验目的1. 理解电磁场的基本概念和性质。
2. 掌握电磁场的基本测量方法。
3. 分析电磁场在不同介质中的传播特性。
4. 熟悉电磁场实验设备的操作。
二、实验原理电磁场是电场和磁场的总称,它们在空间中以波的形式传播。
本实验通过搭建电磁场实验平台,观察和分析电磁场在不同介质中的传播特性,以及电磁场与电荷、电流的相互作用。
三、实验器材1. 电磁场实验平台2. 电磁场发生器3. 电磁场传感器4. 信号发生器5. 示波器6. 测量仪器(如:电流表、电压表、频率计等)7. 实验用线、连接器等四、实验内容1. 电磁场基本性质观察(1)搭建电磁场实验平台,观察电磁场在不同介质中的传播特性。
(2)通过电磁场发生器产生电磁波,观察电磁波在空气、水、金属等介质中的传播情况。
2. 电磁场测量(1)利用电磁场传感器测量电磁场强度。
(2)通过信号发生器产生已知频率和强度的电磁波,与传感器测量结果进行对比。
3. 电磁场与电荷、电流的相互作用(1)观察电磁场对电荷的作用,如电场力、洛伦兹力等。
(2)观察电磁场对电流的作用,如安培力、法拉第电磁感应等。
4. 电磁场实验设备操作(1)学习电磁场实验平台各部分的功能和操作方法。
(2)掌握电磁场传感器、信号发生器、示波器等仪器的使用方法。
五、实验步骤1. 搭建电磁场实验平台,连接好各部分仪器。
2. 观察电磁场在不同介质中的传播特性,记录实验数据。
3. 利用电磁场传感器测量电磁场强度,与信号发生器产生的电磁波强度进行对比。
4. 观察电磁场对电荷和电流的作用,记录实验数据。
5. 学习电磁场实验设备操作,熟悉各仪器使用方法。
六、实验结果与分析1. 电磁场在不同介质中的传播特性:电磁波在空气中传播速度最快,在水、金属等介质中传播速度较慢。
2. 电磁场强度测量:通过传感器测量得到的电磁场强度与信号发生器产生的电磁波强度基本一致。
3. 电磁场与电荷、电流的相互作用:电磁场对电荷的作用表现为电场力,对电流的作用表现为安培力。
带电粒子在电场磁场中的运动
磁流体发电
气体在3000K高温下将 + 高温 等离 子气
+ + +
v v
I
发生电离,成为正、负离子,
将高温等离子气体以 1000m/s的速度进入均匀磁
fm
+ -
–
B
场B中,
根据洛仑兹力公式
f qv B
– – –
fm
正电荷聚集在上板,负电荷聚集在下板,因而可向外供电。
B
•电子偶:理论和实验都表明,正电子总是伴随着 电子一起出现的,犹如成对成双的配偶,故称之为 电子——正电子偶,简称电子偶或电子对。
3、磁聚焦
速度与磁场有一个夹角θ, 把速度分解成平行于磁场 的分量与垂直于磁场的分 量 v // v cos v v sin 在平行于磁场的方向: F//=0 ,作匀速直线运动; 在垂直于磁场的方向: F⊥=qvBsinθ,匀速圆周运动 故带电粒子同时参与两个运动,结果粒子作螺旋线向前运动, 轨迹是螺旋线。 mv mv 螺距——粒子回转一周 sin 回旋半径 R qB qB 所前进的距离
0
q B R0 2m
2
2
2
2
从原理上说,要增大粒子的能量,可以从增大电磁铁的截面 (即增大半圆盒的面积)着手,但实际上这里很困难的。
我国最大的三个加速器
北京正负电子对撞机
合肥同步辐射加速器
兰州重离子加速器
4、霍耳效应
•现象 1879年霍耳发现把一载流导体 d 放在磁场中,如果磁场方向与 电流方向垂直,则在与磁场和 电流二者垂直的方向上出现横 uH b 向电势差,这一现象称之为霍 耳效应。相应的电势差称为霍 耳电压。
电磁场与电磁波实验报告

实验一 静电场仿真1.实验目的建立静电场中电场及电位空间分布的直观概念;2.实验仪器计算机一台3.基本原理当电荷的电荷量及其位置均不随时间变化时,电场也就不随时间变化,这种电场称为静电场;点电荷q 在无限大真空中产生的电场强度E 的数学表达式为204qE r r πε= r 是单位向量 1-1真空中点电荷产生的电位为04qr ϕπε= 1-2其中,电场强度是矢量,电位是标量,所以,无数点电荷产生的电场强度和电位是不一样的,电场强度为1221014ni n i i i q E E E E r r πε==+++=∑ i r 是单位向量1-3 电位为121014ni n i i q r ϕϕϕϕπε==+++=∑ 1-4 本章模拟的就是基本的电位图形;4.实验内容及步骤1 点电荷静电场仿真题目:真空中有一个点电荷-q,求其电场分布图;程序1:负点电荷电场示意图clearx,y=meshgrid-10:1.2:10;E0=8.85e-12;q=1.610^-19;r=;r=sqrtx.^2+y.^2+1.010^-10m=4piE0r;m1=4piE0r.^2;E=-q./m1.r;surfcx,y,E;负点电荷电势示意图clearx,y=meshgrid-10:1.2:10; E0=8.85e-12;q=1.610^-19;r=;r=sqrtx.^2+y.^2+1.010^-10m=4piE0r;m1=4piE0r.^2;z=-q./m1surfcx,y,z;xlabel'x','fontsize',16ylabel'y','fontsize',16title'负点电荷电势示意图','fontsize',10程序2clearq=2e-6;k=9e9;a=1.0;b=0;x=-4:0.16:4;y=x; X,Y=meshgridx,y;R1=sqrtX+1.^2+Y.^2+1.010^-10;R2=sqrtX-1.^2+Y.^2+1.010^-10;Z=qk1./R2-1./R1;ex,ey=gradient-Z;ae=sqrtex.^2+ey.^2;ex=ex./ae;ey=ey./ae; cv=linspaceminminZ,maxmaxZ,40; contourX,Y,Z,cv,'k-';hold onquiverX,Y,ex,ey,0.7;clearq=2e-6;k=9e9;a=1.0;b=0;x=-4:0.15:4;y=x; X,Y=meshgridx,y;R1=sqrtX+1.^2+Y.^2+1.010^-10;R2=sqrtX-1.^2+Y.^2+1.010^-10;U=qk1./R2-1./R1;ex,ey=gradient-U;ae=sqrtex.^2+ey.^2;ex=ex./ae;ey=ey./ae; cv=linspaceminminU,maxmaxU,40; surfcx,y,U;实验二恒定电场的仿真1.实验目的建立恒定电场中电场及电位空间分布的直观概念;2.实验仪器计算机一台3.基本原理电场的大小和方向均不随时间变化的场称为恒定电场,如直流导线,虽说电荷在导线内运动,但电场不随时间变化而变化,所以,直流导线形成的电场是恒定电场;对于恒定电场,我们可以假设其为静电场,假设有静止不动的分布在空间中的电量q产生了这一电场;通过一些边界条件等确定自己所需要的变量,然后用静电场的方法来求解问题;4.实验内容及步骤1高压直流电线表面的电场分布仿真题目:假设两条高压导线分别是正负电流,线间距2m,线直径0.04m,电流300A,两条线电压正负110kV,求表面电场分布;程序clearx,y=meshgrid -2:0.1:2; r1=sqrtx+1.^2+y.^2+0.14; r2=sqrtx -1.^2+y.^2+0.14; k=100/log1/0.02; E=k1./r1-1./r2; surfcx,y,E;xlabel'x','fontsize',16 ylabel'y','fontsize',16 title'E','fontsize',10 RR D=2m X Y P 图2-1高压直流电线示意图 R2 R1clearx,y=meshgrid-2:0.1:2;r1=sqrtx+1.^2+y.^2+0.14; r2=sqrtx-1.^2+y.^2+0.14; k=100/log1/0.02;m=log10r2./r1;U=km;surfcx,y,U;xlabel'x','fontsize',16 ylabel'y','fontsize',16title'U','fontsize',10实验三 恒定磁场的仿真1.实验目的建立恒定磁场中磁场空间分布的直观概念;2.实验仪器计算机一台3.基本原理磁场的大小和方向均不随时间变化的场,称为恒定磁场; 线电流i 产生的磁场为:024IdldB r μπ=说明了电流和磁场之间的关系,运动的电荷能够产生磁场;4.实验内容及步骤圆环电流周围引起的磁场分布仿真题目:一个半径为0.35的电流大小为1A 的圆环,求它的磁场分布;分析:求载流圆环周围的磁场分布,可以用毕奥—萨伐尔定律给出的数值积分公式进行计算:图3-1载流圆环示意图程序 clear x=-10:0.5:10; u0=4pi10^-7; R=0.35;I=1;B=u0IR.^2./2./R.^2+x.^2.^3/2; plotx,B;RrpxdB实验四电磁波的反射与折射1.实验目的1熟悉相关实验仪器的特性和使用方法2掌握电磁波在良好导体表面的反射规律2.实验仪器DH1211型3厘米信号源1台、可变衰减器、频率调节器、电流指示器、喇叭天线、金属导体板1块、支座一台;3.基本原理电磁波在传播过程中如遇到障碍物,必定要发生反射;当电磁波入射到良好导体近似认为理想导体平板上时将发生全反射;电磁波入射到良好导体近似认为理想导体平板时,分为垂直入射和以一定角度入射称为斜入射;如图4-1所示;入射线与分界面法线的夹角为入射角,反射线与分界面法线的夹角为反射角;垂直入射斜入射入射角0°、反射角0°入射角45°、反射角45°图4-1用一块金属板作为障碍物,测量当电波以某一入射角投射到此金属板上的反射角,验证电磁波的反射规律:1电磁波入射到良好导体近似认为理想导体平板上时将发生全反射; 2入射角等于反射角;4.实验内容及步骤1熟悉仪器的特性和使用方法 2连接仪器,调整系统3测量入射角和反射角反射全属板放到支座上时,应使金属板平面与支座下面的小圆盘上的某一对刻线一致;而把带支座的金属反射板放到小平台上时,应使圆盘上的这对与金属板平面一致的刻线与小平台上相应900刻度的一对刻线一致;这时小平台上的00刻度就与金属板的法线方向一致;转动小平台,使固定臂指针指在某一角度处,这一角度的读数就是入射角,然后转动活动臂在表头上找到一个最大指示,此时活动臂上的指针所指的刻度就是反射角;支座 喇叭天线金属导体铝板频率调节器DH1121B 3厘米信号源可变衰减器电流指示器检波器活动臂。
第二章电磁场中电子的运动

电子光学第二章(Kang) P.17
牛顿运动方程
直角坐标系、圆柱坐标系以及一般正交坐标系运 动方程
将x和y的微分形式用r和 ψ 的微分形式代入,上述方程可以得到圆柱 坐标方程下的牛顿方程:
2) Fr m0 ( r r
r ) F m0 (2r m0 d 2 ) (r r dt
sin cos r sin cos r 2 cos2 ) Fr m0 ( r cos2 2r cos sin r cos sin r 2 sin 2 ) m0 ( rsin 2 2r 2 (sin 2 cos2 )] m0 [ r(sin 2 cos2 ) r 2) m0 ( r r
拉格朗日方程
直角坐标系下推演拉格朗日方程
拉格朗日函数
静电场是位场,因此将位能和动能函数带入到拉格朗日函数后,得到静电 场中的拉各朗日函数 2 0
m L eU 2
电子自旋实验报告

【摘要】电子自旋的概念首先由Pauli于1924年提出,1925年S.A.Goudsmit与G.Uhlenbeek利用这个概念解释某些光谱的精细结构。
近代观测核自旋共振技术,随后用它去观察电子自旋。
本实验目的是观察电子自选共振现象,测量DPPH中电子的g因数。
【原理】(一)电子的轨道磁矩与自旋磁矩由原子物理可知,对于原子中电子的轨道运动,与它相应的轨道磁矩μl为μl = —ep l/2m e式中p l为电子轨道运动的角动量,e为电子电荷,m e为电子质量,其轨道磁矩方向与轨道角动量的方向相反,数值大小分别为p l = (l(l+1))^0.5*h μl = (l(l+1))^0.5*eh/2m e原子中电子除轨道运动外还存在自旋运动。
根据狄拉克提出的电子的相对论性波动方程,电子自旋运动的量子数为S = 1/2,自选运动角动量p s与自旋磁矩μsμs = —ep s/m e其数值大小分别为p s = (s(s+1))^0.5*h μs = (s(s+1))^0.5*eh/m e比较上式可知,自旋运动电子磁矩与角动量之间的比值是轨道运动磁矩与角动量之间比值的二倍。
原子中电子的轨道磁矩与自旋磁矩合成原子的总磁矩。
对于单电子原子总磁矩μj与角动量p j之间有μj = -gep j/2m e g = 1 + (j(j+1)-l(l+1)+s(s+1))/2j(j+1)g称为朗德g因数。
对于单纯轨道运动g = 1,对于单纯自旋运动g = 2。
引入回磁比γ,μj = -γp jγ = -ge/2m e在外磁场中,μj和p j的空间去向是量子化的。
p j在外磁场方向上的投影为p z = mh m = j,j-1,……,-j相应的磁矩μj在外磁场方向上的投影为μz = γmh = mgμBμB称为波尔磁子,电子的磁矩通常都用玻尔磁子μB作单位来量度。
μB = 9.274009*10^-24 J/T h = 6.626068*10^-34 J·S(二)电子顺磁共振既然总磁矩uj的空间取向是量子化的,磁矩与外磁场B的相互作用也是不连续的,其能量为E=-u j*B=mgu B B不同量子数m所对应的状态上的电子具有不同的能量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子在电磁场中的运动特性研究 一、实验目的 1、 测试电偏转 2、 测试磁偏转 3、 测试电聚焦 4、 测试磁聚焦 二、实验原理 (一)电偏转
电子从阴极发射出来后,受阳极作用而加速。
如果电子逸出阴极时的初始动
能可以忽略不计,那么它从2A 射出时的动能就由下式确定:22
2
1eV mv z
v =
√
2ee 2
e
过阳极A2的电子以v 的速度进入两个分别平行的平行板电容器间。
若在某个平行板间加上电压U ,板间距离为d ,则板间电场(近似视为匀强电场)E =e
e。
设电子速度方向为z ,电场方向为Y 轴,平行板正中央为x 轴。
初,v z =v ;v y =0;电子通过板所需时间为t=e e
; 电子在平行板间加速度为a e =
−ee
e
,则射出平行板时y 方向上位移y 1=12
e e e 2
=⋯=
ee 2
4e 2e
速度e e =e e e ,V e =e ,tan e =
ee ee
=
ee
2e 2e
又由图知,D=y 1+Ltan θ所以
D =
12ee e 2e (e
2
+e )
(二)电聚焦
聚焦阳极和第二阳极是由同轴的金属圆筒组成。
由于各电极上电位不同,在他们之间形成了弯曲的等位面,电力线。
这样就使电子束的路径发生弯曲,这样的组合称为电子透镜。
改变等位面的弯曲程度,可以改变聚焦的位置。
(三)磁偏转
同(一),电子飞出加速电场后,在匀强磁场中受洛伦兹力F=evB,速度大小不变,方
向变化。
电子做匀速圆周运动evB=ee 2
e ,R=ee
ee。
电子离开磁场后直射荧光屏。
(四)磁聚焦和电子荷质比
同(一),若平行板间没有电压,可在荧光屏上得到一小亮点。
若给其中一对偏转板加上交变电压,电子将获得垂直于轴向的分速度Vy。
若加上一平行于轴向的磁场B,平行轴向分速度Vx不产生洛伦兹力,所以F洛=eVyB,这个力使电子在前进的过程中在垂直于轴向的
平面做圆周运动,周期T=2ee
e e =2ee
ee。
最终轨迹为一螺线,螺距h=VxT=2e
e √2ee2
e。
由上两式可发现,T、h均与Vy无关。
从同一点出发的电子会在一个周期后距出发点一个螺距的地方相遇。
由上式得,荷质比
e e =
8ee2
e2e2
此实验所用长直螺线管的磁感应强度B可由下式计算:
B=
eee
所以,e e
⁄=8e2e2(e2+e2)/(eeee)
μ=4π*10-7亨/米
N=526±2
L=0.234m
D=0.09m
螺距h=0.145m
三、实验仪器
DH4521电子束测试仪
四、实验步骤
1、开启电源,适当调节辉度、聚焦,使屏上光点聚成一细点。
2、光点调零。
在“X(或Y)调节”处调节,先使电压表示数为零,然后调节调零旋钮,使
光点位于中心点。
3、电偏转:测量偏转量D随偏转电压U的变化。
给定阳极电压U2,改变偏转电压,测量一
组数据,再改变U2,测量另一组数据。
先测Y轴,再测X轴上的,并求电偏转灵敏度D/U d。
4、电聚焦:固定阳极电压U2,调节对应聚焦旋钮,使光点达到最佳聚焦效果,读出聚焦电
压U1,再改变阳极电压重新测量。
计算U2/U1。
5、磁偏转:给定U2,测量偏转量D与偏转电流I的变化。
将磁偏转电流输出与输入相连。
调节电流改变D。
再改变U2,再测数据。
求灵敏度D/I,并解释为什么U2不同,灵敏度不同?
6、磁聚焦:将“电子束-荷质比”打至荷质比,U2调至700V。
将励磁电流调节旋钮逆时针
调节到头,并将励磁电流输入与输出相连。
电流换向开关打向正向,调节输出调节旋钮,加大电流,直至荧光屏上直线一边旋转一边缩短至一个小光点,读取电流值I正。
再将开关打至反向,同理得I反。
再改变U2重复上述步骤。
测出荷质比e/m。
五、数据记录与处理
(一)电偏转
灵敏度600V时为1.25mm/V,700V时为1.08mm/V。
灵敏度600V时为0.722mm/V,700V时为0.639mm/V。
(二)电聚焦
(三)磁偏转
灵敏度600V时为0.1005m/A,700V时为0.0925m/A。
(四)磁聚焦
平均值:1.59754E+11(C/kg)
标准值:e/m=1.76E+11(C/kg)
百分差E=10%
六、实验结论与误差分析
1、理论上,阳极电压越大,粒子进入偏转板速度越大,在y方向上加速时间越短,所以偏
转量越小。
因而电偏转中,电压越低,偏转灵敏度越高。
图像比较符合理论,误差为偶然误差,读数偏差。
2、电聚焦中,比例约为4.4。
图像比较不符合理论,截距太大,可能原因:1、低电压时读数不准、偏大;2、仪器故障。
3、磁偏转中,阳极电压不同,粒子初速不同,磁场中偏转半径不同,因而灵敏度不同。
图像比较符合理论,误差为偶然误差,读数偏差。
4、磁聚焦结果与实际值接近,但偏小10%。
可发现数据中I反明显大于I正,可能是读数
时I反读大了;同时也有π计算时取小了的原因(影响不大)。
