保险精算(三).ppt
合集下载
保险精算课程三(寿险精算)
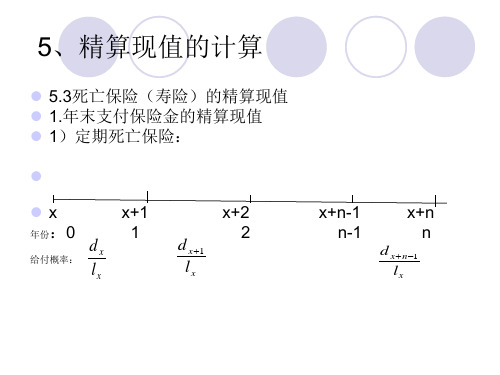
N N Dx
x
xn
x
xh
2.终身寿险的年缴纯保费
h Px
Ax ax:h|
Mx Nx Nxh
3.两全保险的年缴纯保费
P h x：n|
Ax:n| ax:h |
Mx
M xn Dxn Nx Nxh
课堂练习:
1.某人30岁投保20年期，延期10年，5年限期缴费的定期 人寿险,保险金额为100000元，求年缴纯保险费?
N x N x1 Dx
S x N x N x1
(Ia) x
Sx Dx
( Ia) x
S x 1 Dx
( Ia) x:n |
S x 1
S x n1 Dx
nN x n1
作业：
1.某人30岁(女)时投保寿险,约定45岁前死亡给付保险金 150000元,40岁至60岁之间死亡给付保险金为100000 元,60岁以后给付保险金50000元,求趸缴纯保险费?
(In| A)x (IA)1x:n| n|Ax
Rx Rxn nM xn N M xn
Dx
Dx
标准递减也可以看作：
A1 x:n |
A1 x:n 1|
A1 x:n 2|
A1 x:1|
nM x [Rx1 Rxn1 ] Dx
课堂练习
（x）=30，定期寿险保单。第一年死亡给付1000元， 第二年死亡给付1200元，第三年1400元，这样依次按 200元比例递增，n=20，求保险金的精算现值：
x:n |
Dx
Ax:n|
Mx
M xn Dx
Dxn
Ax
Mx Dx
m| Ax
M xm Dx
A1 x :n|
Mx
M Dx
x
xn
x
xh
2.终身寿险的年缴纯保费
h Px
Ax ax:h|
Mx Nx Nxh
3.两全保险的年缴纯保费
P h x：n|
Ax:n| ax:h |
Mx
M xn Dxn Nx Nxh
课堂练习:
1.某人30岁投保20年期，延期10年，5年限期缴费的定期 人寿险,保险金额为100000元，求年缴纯保险费?
N x N x1 Dx
S x N x N x1
(Ia) x
Sx Dx
( Ia) x
S x 1 Dx
( Ia) x:n |
S x 1
S x n1 Dx
nN x n1
作业：
1.某人30岁(女)时投保寿险,约定45岁前死亡给付保险金 150000元,40岁至60岁之间死亡给付保险金为100000 元,60岁以后给付保险金50000元,求趸缴纯保险费?
(In| A)x (IA)1x:n| n|Ax
Rx Rxn nM xn N M xn
Dx
Dx
标准递减也可以看作：
A1 x:n |
A1 x:n 1|
A1 x:n 2|
A1 x:1|
nM x [Rx1 Rxn1 ] Dx
课堂练习
（x）=30，定期寿险保单。第一年死亡给付1000元， 第二年死亡给付1200元，第三年1400元，这样依次按 200元比例递增，n=20，求保险金的精算现值：
x:n |
Dx
Ax:n|
Mx
M xn Dx
Dxn
Ax
Mx Dx
m| Ax
M xm Dx
A1 x :n|
Mx
M Dx
保险精算第三讲
1 死亡即刻赔付
1.1 n年期定期寿险 1.2 终身寿险 1.3 延期m年 终身寿险
1.4 n年期生存保险
1.5 n年期两全保险
1.6 延期m年的 n年期两全保险
1.7 递增寿险 1.8 递减寿险
1 , t m bt 0 , t m
v , t m zt bt vt 0 , t m
e2 t fT (t )dt E ( zt )2
m
1.4 n年期生存保险
1.5 n年期两全保险
记
2 m
Ax e2 t fT (t )dt
m
1.6 延期m年的 n年期两全保险
1.7 递增寿险 1.8 递减寿险
所以方差等价于
Var ( zt ) A ( m Ax )
,x 0
1.6 延期m年的 n年期两全保险
1.7 递增寿险 1.8 递减寿险
求： (1)
10
Ax
(2)Var(zt )
2 计算基数
例3.3答案
S ( x t ) (1) fT (t ) 0.04e0.04t S ( x) A e m x
10 0.06 t
1 死亡即刻赔付
1.1 n年期定期寿险 1.2 终身寿险 1.3 延期m年 终身寿险
10
0.04e
0.04 t
dt 0.04 e0.1t dt 0.147 0.04e0.16t
10
1.4 n年期生存保险
1.5 n年期两全保险
(2) Ax e
2 m 10
0.12 t
0.16 Var ( zt ) m2 Ax ( m Ax )2 0.0288
保险精算第3章(3)
s(x t)
t px
1 ty px t px
1
pxt y pxt
1
p
y x
y p xt pxy
26
例：在常数死力下求： q5 75.25
l75 56799 l76 54239 l80 43180 l81 40208
p 5 75.25 p 0.75 75.25 4 p76 0.25 p80
5 p20 0.2 p25 (10.8 p25.2 2 p26 0.6 p28 )
l25 l20
(1
0.2q25 )[1
(1
0.8q25 1 0.2q25
)
l28 l26
(1
0.6q28 )
0.00248
24
二、年龄内常数死力假设(几何插值法)
还可以怎么写？
• 令： s(x t) s(x)1t s(x 1)t 0 t 1
p0.75 75
l80 l76
p 0.25 80
0.75545
q5 75.25 0.24455
27
三、调和插值法（Balducci假设）
• 令： 1 1 t t
s(x t) s(x) s(x 1)
0t 1
• 生存函数：
t
px
s(x t) s(x)
1 1t t s(x) s(x 1)
0 t 1
1.t qx
lx
lxt lx
td x lx
tqx
2.t px
lxt lx
lx tdx lx
1 tqx
3. y qxt
lxt
lxt y lxt
yd x lx tdx
yqx 1 tqx
21
第六章：财产保险精算介绍PPT
（二）财产保险费率厘定的原则
1．法律原则 2．业务原则 3．促进防灾防损的原则
下一张
法律原则
（1）费率适当，保证保障的原则——费率的厘定必须 足以赔付所有正常的损失和支付所有的费用。
（2）公平合理的原则——这是指实现费率计算上的公 平，对类似的风险单位应收取相同的费率，对不同的 危险单位应收取不同的费率。
1．保额损失率。 2．稳定系数 3．附加均方差。
1．保额损失率。
（1）保额损失率 （2）保额损失率的保险含义 （3）平均保额损失率的计算
（1）保额损失率
就是保险赔偿金额（赔款）与承保责任 金额（保险金额）之比。
如：的保额损失率为：保额损失率=60万元 /3亿元=2‰ 也就是说，发生的保险事故中每1000元 保险财产要损失2元。
（二）未到期责任准备金
1．未到期责任准备金的概念 2．未到期责任准备金的计算方法
1、未到期责任准备金的概念
（1）未到期责任 ：由于财产保险业务大都是定期的，而保险的 会计核算则是以年度来办理决算，即从每年的1月份起到12月31日 止。在这种情况下，只有当年1月1日出单的业务，才会在12月31 日到期，其全部有效期都在同一个会计年度内，而其他日期出单 的业务，或多或少有一部分有效期是在会计核算的第二年度之内， 这种超过会计年度的保单有效期的业务就叫“未到期责任”。 （2）未到期责任准备金（unearned Liability Reserves）：又 称保费准备金、未满期责任准备金、未了责任准备金、未满期保 费准备金。是保险人在会计年度决算时将保险责任期尚未届满， 应属于下一年度的部分保费提存出来形成的准备金。
2．产生未决赔款的原因
（1）未决赔款：被保险人提出索赔，但保险 人对事故的认定，赔偿金额的大小难以确定时 需提存； （2）已决未付额：保险人对索赔案件已调查 结束，应赔金额亦已确定，但由于结算原因， 支付过程尚未完成； （3）已发未报案件：在年内发生，但由于被 保险人尚未索赔，需要在次年赔付的保险责任 案件。
保险精算精选PPT演示文稿
偿付能力测试等重要工作。
•1
❖ 由于精算师是一项非常专门的职业，一般需要经过资格考试来认定从业资格。国际 上著名的精算学会有：北美精算学会、英国精算学会、日本精算学会和澳大利亚精 算学会，不同的精算师学会具有不同的资格认证和考试课程和制度。其中在国际上 最具代表性和权威性，规模最大、拥有最多会员精算师的组织是美国的北美精算师 协会（Society of Actuaries，简称SOA），享有极高的声誉。目前拥有正式会员 和准会员约16，500名。作为一个国际性的精算教育和研究机构，SOA的主要任务 是提供人寿保险、健康保险、员工福利和养老金领域的精算教育计划，以后续教育 的方式提高精算师的咨询和解决涉及不确定事件的金融、保险、财务及社会问题的 能力。
•4
我国的精算师考试
❖ 准精算师考试基础课程
课程编号 课程名称
学分
001
数学基础Ⅰ
30
002
数学基础Ⅱ
30
003
复利数学
20
004
寿险精算数学
50
005
风险理论
20
006
生命表基础
30
007
寿险精算实务
30
008
非寿险精算数学与实务 30
009
综合经济基础
30
❖ 每门报名200元
考试时间 3 3 2 4 2 3 3 3 3
备注 必考 必考 必考 必考 必考 必考 必考 必考 必考
•5
❖ 精算师考试高级课程
课程编号 课程名称
学分
011
财务
30
012
保险法规
30
013
资产/负债管理
30
014
社会保险
寿险精算学课件-(3)精选全文
费用分类
成分
投资费用
（1）投资分析成本（2）购买、销售及服务成本
1、新契约费 （1）销售费用，包括代理人佣金及宣传广告费（2）风
保
险分类，包括体检费用（3）准备新保单及记录
险 2、维持费 （1）保费收取及会计
费
（2）给付变更及理陪选择权准备
用
（3）与保单持有人进行联络
3、营业费用 （1）研究、开发新险种费用（2）精算及一般法律服务 （3）普通会计（4）税金、许可证等费用
0
Ax
P( Ax )ax
0
P( Ax )
Ax ax
方差确定
Var(L)
Var[vt
P(
Ax
)
1
v d
k
1
]
Var[v(k 1)(s1)
P
(
Ax
)
1
v d
k
1
]
Var[(vs1 P( Ax ) )vk1] d
记Z s
vs1
P( Ax d
)
，Z
k
vk 1
由于分数剩余寿命和整值剩余寿命相互独立，
(
Z
k
)
方差的确定
终身寿险场合有
E
(Z
2 k
)
2 Ax，Var(Zk
)
2 Ax
-
Ax
2
在分数期死亡服从均匀分布的假定下，有
E(Zs )
E
v
s-1
P( Ax )
d
i
P( Ax ) d
Var(Zs
)
Var
v
s-1
P( Ax d
)
Var (v s -1 )
寿险精算学(第3版)课件：期缴保费
• 以例5.8进行讲解，每年的净保费等于133.07元，每年的 毛保费等于178.47元，也就是说每年缴纳的毛保费里面有 45.4元是覆盖费用的费用保费。但实际上第一年的真实费 用等于：
40.5+205+78%178.47=279.71
• 第一年收取的费用45.4元是完全不够支付第一年的真实费 用的。费用不够的部分是由保险公司现行垫付。这就产生 了寿险产品的新业务压力（new business strain）。也就 是说寿险公司只要新卖出一份保险产品，第一年就要承担 初年费用不够的资金压力。
毛保费的构成图示
经营费用
• 所谓经营费用是指保险公司支出的除了风险赔付之外, 其他维持 保险公司正常运作的所有费用支出的统称。
• 经营费用包括管理费用和佣金两大部分, 其中, 管理费用通常由 投资费用和保险费用两部分构成。
– 投资费用包括与投资相关的分析、 购买、 销售及服务成本。 由 于这些费用直接与投资收入的产生有关, 所以投资费用通常从总投 资收入中扣除, 在传统寿险产品保费计算时通常不单独考虑。
缴费频率与赔付频率不一致时， 期缴净保费的厘定
• 实务中, 有时保费的缴纳频率会和赔付的给付频率不一致
– 比如有可能保费每年期初缴纳, 但死亡即刻给付; – 再比如保费每年缴纳m 次, 而死亡年末赔付或死亡即刻赔付。
• 这时，期缴净保费的厘定, 通常需要借助不同频率之间精 算函数的变换来实现。
例5.6
未来损失变量
• 未来损失变量（Future Loss），t时刻的未来损失变量记作Lt
Lt =未来支出贴现到t 时刻的现值 - 未来收入贴现到t 时刻的现值
– 如果Lt >0, 意味着对保险人而言未来收不抵支, 将会产生亏损 (loss) – 如果Lt <0, 意味着对保险人而言未来收入会大于支出, 将会产生利润
40.5+205+78%178.47=279.71
• 第一年收取的费用45.4元是完全不够支付第一年的真实费 用的。费用不够的部分是由保险公司现行垫付。这就产生 了寿险产品的新业务压力（new business strain）。也就 是说寿险公司只要新卖出一份保险产品，第一年就要承担 初年费用不够的资金压力。
毛保费的构成图示
经营费用
• 所谓经营费用是指保险公司支出的除了风险赔付之外, 其他维持 保险公司正常运作的所有费用支出的统称。
• 经营费用包括管理费用和佣金两大部分, 其中, 管理费用通常由 投资费用和保险费用两部分构成。
– 投资费用包括与投资相关的分析、 购买、 销售及服务成本。 由 于这些费用直接与投资收入的产生有关, 所以投资费用通常从总投 资收入中扣除, 在传统寿险产品保费计算时通常不单独考虑。
缴费频率与赔付频率不一致时， 期缴净保费的厘定
• 实务中, 有时保费的缴纳频率会和赔付的给付频率不一致
– 比如有可能保费每年期初缴纳, 但死亡即刻给付; – 再比如保费每年缴纳m 次, 而死亡年末赔付或死亡即刻赔付。
• 这时，期缴净保费的厘定, 通常需要借助不同频率之间精 算函数的变换来实现。
例5.6
未来损失变量
• 未来损失变量（Future Loss），t时刻的未来损失变量记作Lt
Lt =未来支出贴现到t 时刻的现值 - 未来收入贴现到t 时刻的现值
– 如果Lt >0, 意味着对保险人而言未来收不抵支, 将会产生亏损 (loss) – 如果Lt <0, 意味着对保险人而言未来收入会大于支出, 将会产生利润
保险精算学3-生命表
Pr(K (x) k) Pr(k T (x) k 1) k px qxk
设S(x)为x岁人在其死亡年度中所活过的不足一年的 部分。 S(x)是（0，1）上的连续分布，有：
T (x) K(x) S(x)
K(x)的期望值是简约平均余命：
ex E(K (x)) k k px qxk k ( k px k1 px ) p k1 x
3050253031303030053030050530300530303070700514069700505139525505002555505552550025525505255001094501090250105454401090105042245025010901050847440253030530305303030530300569569ln05695生命表可以依据实际同时出生的一批人资料编制不过编制这种生命表需要纵向追踪一批人从生到死的全部过程而且在实际中很难取得完整的原始资料同时该表也只是历史的追述不能说明现在某个时期的死亡水平因此一般不采用实际同批人方法编制生通常采用假设同批人方法编制即把某一时期各个年龄的死亡水平当做同时出生的一批人在一生中经历的各个年龄时的死亡水平看待从而描述某一时期处于不同年龄人群的死亡水平
1、tLx：x岁的人在x~x+t岁间的生存人年数。
人年数（复合单位）：人群存活时间的复合单位。1 个人存活1年是1人年，2个人每人存活半年也是1人 年。
在死亡均匀分布的假设下，x~x+t岁间死亡的人数
tdx平均存活t/2年，活到lx+t的人则存活t年，故有：
t Lx
t lxt
t 2
t dx
t 2
二、x岁余命的生命函数
T(x)：x岁的人未来能生存的时间。其分布函数为：
设S(x)为x岁人在其死亡年度中所活过的不足一年的 部分。 S(x)是（0，1）上的连续分布，有：
T (x) K(x) S(x)
K(x)的期望值是简约平均余命：
ex E(K (x)) k k px qxk k ( k px k1 px ) p k1 x
3050253031303030053030050530300530303070700514069700505139525505002555505552550025525505255001094501090250105454401090105042245025010901050847440253030530305303030530300569569ln05695生命表可以依据实际同时出生的一批人资料编制不过编制这种生命表需要纵向追踪一批人从生到死的全部过程而且在实际中很难取得完整的原始资料同时该表也只是历史的追述不能说明现在某个时期的死亡水平因此一般不采用实际同批人方法编制生通常采用假设同批人方法编制即把某一时期各个年龄的死亡水平当做同时出生的一批人在一生中经历的各个年龄时的死亡水平看待从而描述某一时期处于不同年龄人群的死亡水平
1、tLx：x岁的人在x~x+t岁间的生存人年数。
人年数（复合单位）：人群存活时间的复合单位。1 个人存活1年是1人年，2个人每人存活半年也是1人 年。
在死亡均匀分布的假设下，x~x+t岁间死亡的人数
tdx平均存活t/2年，活到lx+t的人则存活t年，故有：
t Lx
t lxt
t 2
t dx
t 2
二、x岁余命的生命函数
T(x)：x岁的人未来能生存的时间。其分布函数为：
中国海洋大学寿险精算讲义[3]
![中国海洋大学寿险精算讲义[3]](https://img.taocdn.com/s3/m/1c71e7e0172ded630b1cb6c7.png)
第一节
生存年金简介 introduction of life annuities
1、生存年金的定义
生存年金的定义： 以被保险人存活为条件，间隔相等的时期（年、半年、季、 月）支付一次保险金的保险类型 (life annuity is a series of payments made continuously or at equal intervals(year, semi-year,quarter,month )while a given life survives) 分类 初付年金/延付年金(annuities-due /annuities-immediate) 连续年金/离散年金(annuities-continuous /annuities-discrete) 定期年金/终身年金(term annuities/whole life annuities) 非延期年金/延期年金(non-deferred annuities/deferred annuities)
第三章中英文单词对照
生存年金 初付年金 延付年金 确定性年金 当期支付技巧 综合支付技巧
Life annuity Annuities-due Annuities-immediate Annuities-certain Current payment technique Aggregate payment technique
2、终身连续生存年金精算现值的估计一 ——综合支付技巧
步骤一：计算到死亡发生时间T为止的所有已支 付的年金的现值之和（record the interest only present value of all paymnet to be made by the auunity if death occurs at time t) 1 vT Y aT
《保险精算》之三--生命表
∫
x+n
x
µ y dy = − ∫
x+n
x
s'( y) d y = − lns(y) | x + n = − [ln s ( x + n ) − ln s ( x )] x s( y)
= − ln 故有
n
s( x + n) = − ln n p x s( x)
−
x+n
p x = e ∫xµBiblioteka y dy∞ 0ex
正是T(x)随机变量的期望值
p xµ
∞ 0 t
e
x
= E [T ( x )] =
∫
t
t
x + t
dt =
∫
p xdt
23
死亡力
生命表x岁死亡人数dx正是生存人数函数lx+t与死亡力之积在 0~1上的积分
d x = ∫ lx + t µ x + t dt
0
1
生命表x岁生存人年数Lx正是生存人数函数lx+t在0~1上的积分
26
例3.6：已知F0 (t ) = 1 − e
− λt
, λ > 0, 计算µ x 。
解：由已知条件知，f 0 (t ) = λ e − λt , 有 f 0 ( x) λ e−λ x = −λ x = λ; µx = 1 − F0 (t ) e
27
整值平均余寿与中值余寿
x岁的整值平均余寿是指x岁未来平均存活的整数年数， 不包括不满1年的零数余寿，它是整值余寿随机变量K(x) 的期望值，以ex表示，
d x + n lx + n − lx + n + m = = n px − n + m px = n px ⋅m qx + n n｜m q x＝ lx lx
保险精算人寿保险趸缴纯保费-PPT精品文档
常见概念中英文单词对照(2)
定期人寿保险 终身人寿保险 两全保险 生存保险 延期保险 变额受益保险
Term life insurance Whole life insurance Endowment insurance Pure endowment insurance Deferred insurance Varying benefit insurance
人寿保险的分类
受益金额是否恒定
定额受益保险 变额受益保险
保障标的的不同
保单签约日和保障期 期始日是否同时进行
人寿保险（狭义） 生存保险 两全保险 定期寿险 终身寿险
保障期是否有限
即期保险 延期保险
人寿保险的特点
保障的长期性
这使得从投保到赔付期间的投资收益（利息）成为 不容忽视的因素。 人寿保险的赔付金额和赔付时间依赖于被保险人的 生命状况。被保险人的死亡时间是一个随机变量。 这就意味着保险公司的赔付额也是一个随机变量， 它依赖于被保险人剩余寿命分布。 这意味着，保险公司可以依靠概率统计的原理计算 出平均赔付并可预测将来的风险。
主要险种的趸缴纯保费的厘定
终身寿险 n年期定期寿险 n年期生存保险 n年期两全保险 延期m年的终身寿险 延期m年的n年期的两全保险 递增终身寿险 递减n年定期寿险
1、终身寿险
定义 保险人对被保险人在投保后任何时刻发生的保险责任 范围内的死亡均给付保险金的险种。 假定： ( x ) 岁的人，投保保额bt=1元终身寿险 基本函数关系
力 和 fT(x)( t) 、 fX( t) 的关系是怎样的 x
保险精算-第3章2-生命表
3.2.2 生命表的内容
基数: 在生命表中,首先选择初始年龄且假定在 该年龄生存的一个合适的人数. 一般0为初始年龄,基数用 l 0 表示 需要规定极限年龄,用 表示
常用符号
x ：年龄
lx
：生存数，指从初始年龄至满 x 岁尚生存的人。 （1）l x 表示自出生至满 x 岁尚存活人数的期望值。
年龄 x 30 31 32 33 34 35 36 37 38 39 未来一年内死亡概率 q x 0.00133 算出各种 0.00134 0.00137 有用的概率 ： 0.00142 p 34 , q 34 , 2 p 34 , 2 q 34 0.00150 q 34 0.00159 2| 0.00170 0.00183 0.00197 0.00213
q x m p x m 1 p x m p x n q x m
例3.1
已知
l x 10000 (1 x 100 )
计算下面各值：
（1）d ,
30 20
p 30 ,
30
q 30 ,
10
q 30
（2）20岁的人在50~55岁死亡的概率。 （3）该人群平均寿命。
例3.1答案
• 国民生命表是以全体国民或特定地区的人口生 存状况统计资料编制成的 • 经验表是人寿保险公司依据过去其承保的被保 险人实际的生存状况统计资料编制的。
在同一时期内， 国民生命的死亡率一般要高于经验表的死亡率。
国民生命表
1.完全生命表（complete life table） 2.简易生命表（abridged life table） • 完全生命表是根据准确的人口普查资料，依 年龄分别计算死亡率、生存率、平均余命等 生命函数而编制的。 • 简易生命表则采取每年的人口生存状况动态 统计资料和人口抽样调查的资料，按年龄段 （如5岁或10岁为一段）计算的死亡率、生 存率、平均余命等生命函数。
保险精算 第3章1 生命函数.
例：Pr(X 50) 1 F(50)
表示新生儿50岁仍然生存的概率 或50岁以后死亡的概率。
3.1.2 生存函数
生存函数 S(x) Pr(X x) x 0
意义：新生儿能活过 x 岁的概率。
与分布函数的关系：S(x) 1 F(x) 与密度函数的关系：f (x) S(x) 例
Pr(X 50) S(50)
S(0) 1
前面我们讲分布函数和生存函数都是从年龄 x 0 开
始考虑的，但实际购买保险的被保险人往往已经活到
某个年龄x 岁的人，这时我们关心的是x 岁的人剩
余寿命X x 的分布。 (x) 表示一个 x 岁的人或已经活到 x 岁的人.
T (x) X x 表示 (x) 未来寿命的随机变量,即剩余
寿命,简称余命.
关于T的分布,就是 X x 时,X 的条件分布.
（X :出生婴儿的未来寿命.）
练习：设 x
F (x) 80
(0 x 80)
1 (x 80)
求：
1） s(x)
2）新生儿在30岁前死亡的概率； 3）新生儿活过50岁的概率； 4）新生儿在30岁和50岁之间死亡的概率。
Fx t F 1 Fx
x
S(x)
S(x S(x)
t)
剩余寿命 T 的生存函数,记作 t px ：
t px Pr(T (x) t) Pr( X x t X t) s(x t) s(x)
t px 表示 x 岁的人在 x t 岁时仍活着的概率.
生存状况
从数学的角度，生存状况是一个简单的过程。 这个过程有如下的特征： 1.存在两种状态：生存和死亡。 2.生命个体可从“生存”状态到“死亡”状态，但不能
表示新生儿50岁仍然生存的概率 或50岁以后死亡的概率。
3.1.2 生存函数
生存函数 S(x) Pr(X x) x 0
意义：新生儿能活过 x 岁的概率。
与分布函数的关系：S(x) 1 F(x) 与密度函数的关系：f (x) S(x) 例
Pr(X 50) S(50)
S(0) 1
前面我们讲分布函数和生存函数都是从年龄 x 0 开
始考虑的，但实际购买保险的被保险人往往已经活到
某个年龄x 岁的人，这时我们关心的是x 岁的人剩
余寿命X x 的分布。 (x) 表示一个 x 岁的人或已经活到 x 岁的人.
T (x) X x 表示 (x) 未来寿命的随机变量,即剩余
寿命,简称余命.
关于T的分布,就是 X x 时,X 的条件分布.
（X :出生婴儿的未来寿命.）
练习：设 x
F (x) 80
(0 x 80)
1 (x 80)
求：
1） s(x)
2）新生儿在30岁前死亡的概率； 3）新生儿活过50岁的概率； 4）新生儿在30岁和50岁之间死亡的概率。
Fx t F 1 Fx
x
S(x)
S(x S(x)
t)
剩余寿命 T 的生存函数,记作 t px ：
t px Pr(T (x) t) Pr( X x t X t) s(x t) s(x)
t px 表示 x 岁的人在 x t 岁时仍活着的概率.
生存状况
从数学的角度，生存状况是一个简单的过程。 这个过程有如下的特征： 1.存在两种状态：生存和死亡。 2.生命个体可从“生存”状态到“死亡”状态，但不能
保险精算第6章(3)
A25：40 0.114592 ，A25：140 0.0811675 ，i 61) a
25:40 15.6422
25:40
d
A
100000P 25:40
100000
25:40
a
732.85
25:40
(2)Ga 100000A 100A1 (75 0.15G) (25 0.1G)a
1）死亡事件发生时产生的费用精算现值。
(20000 18 0.1 20)Ax
2）各年与每份保单相关的费用的精算现值。
34.5 6ax
15
3）各年与每千元保额相关的费用的精算现值。
(4.5 0.5ax ) 20
4）各年与保费相关的费用的精算现值。
(6%ax 2.5%ax：15 +1%ax：9 68.5%)G
12
未来保险费用的分配
分类
1、新契约费 （1）销售费用
佣金 销售事务 其它 （2）分类 （3）发行与记录 2、维持费 3、营业费用 （1）（2）（3） （4）税金 小计 4、给付费用
每份
12.5 18 4 2
4 40.5
第一年
每千 保费百分 元 比（%）
每份
每千元
续年 保费百分比（%）
2-9年 10-15年 16年以上
25:40
25:40
25:40
25:40
100000A 100A1 75 25a
G
25:40
25:40
25:40
0.9a 0.15
25:40
A1 25:40
A 25:40
A1 25:40
0.033425
G 856.45
18
例6.8
25:40 15.6422
25:40
d
A
100000P 25:40
100000
25:40
a
732.85
25:40
(2)Ga 100000A 100A1 (75 0.15G) (25 0.1G)a
1）死亡事件发生时产生的费用精算现值。
(20000 18 0.1 20)Ax
2）各年与每份保单相关的费用的精算现值。
34.5 6ax
15
3）各年与每千元保额相关的费用的精算现值。
(4.5 0.5ax ) 20
4）各年与保费相关的费用的精算现值。
(6%ax 2.5%ax：15 +1%ax：9 68.5%)G
12
未来保险费用的分配
分类
1、新契约费 （1）销售费用
佣金 销售事务 其它 （2）分类 （3）发行与记录 2、维持费 3、营业费用 （1）（2）（3） （4）税金 小计 4、给付费用
每份
12.5 18 4 2
4 40.5
第一年
每千 保费百分 元 比（%）
每份
每千元
续年 保费百分比（%）
2-9年 10-15年 16年以上
25:40
25:40
25:40
25:40
100000A 100A1 75 25a
G
25:40
25:40
25:40
0.9a 0.15
25:40
A1 25:40
A 25:40
A1 25:40
0.033425
G 856.45
18
例6.8
《寿险精算学(第3版)》 PPT-ch3
函数为
0 , 0 t n Zt vn ,t n
• 定期生存险趸缴净保费
A 1 x:n
E(Zt )
n
vn
fx
(t)dt
vn
n
px
• 现时值方差
Var(Zt )
A 2 1 x：n
A1 x:n
2
其中：2
A1 x:n
=
v2n
n
px
例3.4
• （30）购买10年定期生存险，10年末生存给付1。假设复 利计息，年实质利率为5%，寿命服从（0,100）的de Moivre分布。请计算：
140 ln1.05
（3）对于定期寿险而言，赔付现时值是一个分段函数，因 为 v10=1.0510 0.6139 A310:10，也就是说只要是在10年内发生理赔的 被保险人他们所缴纳的趸缴净保费都小于赔付现时值，他们 保费不足的部分是由那些活过10年，没有发生任何赔付的被 保险人补齐的，即
Pr(Zt
(
x)
1
x 100
例3.2解
,0 x 100 ，所以
f30
(t)
1 70
, 0 t 70
且已知复利计息，年实质利率为5%，则 δ = ln(1+ i) = ln1.05
所以趸缴净保费为
A30 E(Zt )
e 70 t
1
e t dt =
0 70 70
0
1
1 1.0570 =
0.2832
• 赔付现值变量是未来寿命的单调减函数。未来寿命短的被保险 人, 由于贴现时期短,赔付现值会大于平均赔付成本。 反之, 未 来寿命长的被保险人, 由于贴现时期长, 赔付现值会小于平均赔 付成本。 本例中, 收支平衡的时间点出现在未来寿命为25.8577 年的时刻点上。未来寿命长于25.8577 年的被保险人（63%） 会补贴哪些未来寿命短于25.8577年的被保险人（37%）。
保险精算课件第3章寿险精算现值
4.2 死亡即付的人寿保险
死亡即付就是指如果被保险人在保障 期内发生保险责任范围内的死亡 ，保险公 司将在死亡事件发生之后，立刻给予保险 赔付。
死亡即刻赔付时刻是一个连续型随机 变量，它距保单生效日的时期长度就等于 被保险人签约时的剩余寿命。
1.终身寿险 对(x) 的1单位元终身寿险，死亡即付现值 随机变量为
死亡时存活的整数年数，这时的变额寿险称为 标准递增的变额寿险。
标准递增的终身寿险
Z (K 1)vK 1, K 0,1, 2,
1
…
11
…
x x+1 x+2
…
1…
1
1…
…
1
1…
1
1…
x+n-1 x+n
其精算现值以 (IA)x 表示，有
(IA)x E(Z ) (k 1)vk1k qx k 0
k 0
qx
1 lx
x 1
d xk v k 1
k 0
●赔付现值随机变量的方差：
Var(Z ) E(Z 2 ) [E(Z )]2
E(Z 2)
v2(k1) k qx
e q 2 (k 1) kx
k 0
k 0
E(Z 2) 相当于以计算趸缴净保费利息力
Ax E(Z )
0
vt
t
px
x t dt
v k 1 t
k
t
px
x t dt
k 0
v1 sk
0
sk
px
xsk ds
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
选择-终极生命表
选择-终极生命表构造的原因
需要构造选择生命表的原因：刚刚接受体检 的新成员的健康状况会优于很早以前接受体 检的老成员。
需要构造终极生命表的原因：选择效力会随 时间而逐渐消失
选择-终极生命表的使用
选择-终极表实例
[x]
选择表
终极表
q[ x] q[ x1] q q [ x2] [ x3] q[ x4] qx5 x 5
意义：新生儿能活到 x 岁的概率。
与分布函数的关系：S(x) 1 F(x)
与密度函数的关系：f (x) S(x) 新生儿将在x岁至z岁之间死亡的概率：
Pr(x X z) s(x) s(z)
剩余寿命
定义：已经活到x岁的人（简记(x)），还 能继续存活的时间，称为剩余寿命，记 作T(x)。
用X 表示出生婴儿未来寿命的随机变量，则X的分
布函数F x Pr X x x 0
即0岁的人在x岁之前死亡的概率。x 0
X的概率密度函数记为f x,则f x F x，x 0
那么Pr X 50表示什么？
表示x岁的人在50岁以后死亡的概率，即在50岁仍然 生存的概率。
Pr X 50 1 Pr X 50 1 F 50
T分布函数记为 FT t
FT t Pr(T (X ) t) Pr(x X x t X x) ＝F x t F x 1 F x
s(x) s(x t) s(x)
T的概率密度函数记为fT
t
,
fT
t
FT
t
sx t sx
在精算学中，用国际通用的符号来表示有关T x
的各种概率。
生命表的定义
根据已往一定时期内各种年龄的死亡统生命表的发展历史
1662年,Jone Graunt,根据伦敦瘟疫时期的洗礼和死亡名单,写 过《生命表的自然和政治观察》。这是生命表的最早起源。
1693年，Edmund Halley,《根据Breslau城出生与下葬统计表 对人类死亡程度的估计》，在文中第一次使用了生命表的形 式给出了人类死亡年龄的分布。人们因而把Halley称为生命表 的创始人。
0 t px dt
剩余寿命的期望与方差
剩余寿命的方差
o2
Var(T (x)) E(T (x)2 ) E2T (x) 2 t t pxdt ex
0
整值剩余寿命的期望与方差
期望整值剩余寿命：(x) 整值剩余寿命的期望值
(均值),简记 ex
ex E(K (x))
k ( k px k1 px ) k 0 1 px 2 px 2 2 px 3 px 3 3 px 4 px
Tx x lydy
o
ex
Tx lx
生命表中列有的lx和dx的值会给计算各种概率带来方便。
k
px
lxk lx
,
k qx
1
k
px
lx
lxk lx
k m qx k px km px
lxk lxkm
lx
lx
lxk lxkm lx
生命表实例（美国全体人口生命表）
年龄区 死亡比
间
例
x~ xt t qx
70 .0175 .0249 .0313 .0388 .0474 .0545 75
71 .0191 .0272 .0342 .0424 .0518 .0596 76
72 .0209 .0297 .0374 .0463 .0566 .0652 77
73 .0228 .0324 .0409 .0507 .0620 .0714 78
1/ 70
2、30 5q20
l50 l55 l20
1/16
e 0
3、
T0
100
(1
x )dx 50
0 l0
0
100
生命表的类型
国民生命表 经验生命表
国民生命表：是根据全国范围内的人口 统计资料构造出来的，反映的是一个特 定时期内全国人口的寿命分布情况。
经验生命表：是人寿保险公司经营寿险 业务死亡率的经验结果，它是以人寿保 险公司的被保险人群体为对象。它分为 终极表、选择表和综合表。
ln[s(x)]
死亡效力与生存函数的关系
死亡效力与生存函数的关系
两边积分，
x
0 ydy
x 0
ln
s
y
dy
ln s y
x 0
x 0
y
dy,
ln
s
x
x
0 ydy
x
s x e0 ydy
xt
从而，t px
s
xt sx
0
y dy
e e x
xt
x
y dy
e 0 ydy
q k1 x k qx k px p k1 x
剩余寿命的期望与方差
期望剩余寿命：(x) 剩余寿命的期望值(均值),简
记
o
ex o
ex
E(T (x))
tfT
0
t dt
t(
0
sx t s x )dt
0
t(
t
px
)dt
t
t
px
0
0
t
px dt
t t px
0
0 t px dt
2-3
.00065 98648 64
98617
剩余寿命 总数
Tx
期初存活者平 均剩余寿命
ex
7387758 7387485 7385850
73.88 74.22 74.38
7387758 7288785 7190091
73.88 73.82 72.89
例3.1：
已知
lx
10000(1 x ) 100
78 .0357 .0508 .0641 .0796 .0973 .1121 83
1.给出生存函数s x ex2 2500 ,求：（1）人在50岁至
60岁之间死亡的概率；（2）50岁的人在60岁以前死 亡的概率；（3）人能活到70岁的概率；（4）50岁 的人能活到70岁的概率。
1 Pr(50 X 60)
生命表的特点
构造原理简单、数据准确（大样本场合）、不依赖总体分布 假定（非参数方法）
生命表的构造
原理
在大数定理的基础上，用观察数据计算各年龄人 群的生存概率。（用频数估计频率）
常用符号 新生生命组个体数：l0
年龄：x 极限年龄：
生命表的构造
l0个新生生命能生存到年龄X的期望个数：lx
计算下面各值： （1）d30,20 p30,30 q30,10 q30
（2）20岁的人在50~55岁死亡的概率。
（3）该人群平均寿命。
例3.1答案
1、d30 l30 l31 100
p 20 30
l50 l30
5/7
q 30 30
l30 l60 l30
3/ 7
q 10 30
l40 l41 l30
第三章
生命表函数与生命表构造
本章重点
生命表函数
生存函数 剩余寿命 死亡效力
生命表的构造
有关寿命分布的参数模型 生命表的起源 生命表的构造 选择与终极生命表
有关分数年龄的三种假定
第一节 生命表函数
分布函数
一个人的寿命从出生到死亡的时间长度， 是无法事先确定的，在概率上称之为随 机变量，记为X。是连续型随机变量。
表示x岁的人在x t岁仍活着的概率。
特别：
x p0 s(x)
剩余寿命
px ：x岁的人至少能活到x+1岁的概率
px 1 px
qx ：x岁的人将在1年内去世的概率
qx 1qx
t u qx：X岁的人活过t年后在往后u年内去
世的概率即在x＋t岁到x＋t＋u岁之间死 亡的概率。
t u qx Pr t T x t u Pr[T x t u] Pr T x t
天
期初生 存数
lx
期间死亡 数
t dx
在年龄区间 共存活年数
t Lx
0-1
.00463 100000 463
273
1-7
.00246 99537 245
1635
7-28 .00139 99292 138
5708
年
0-1
.01260 10000 1260
98973
1-2
.00093 98740 92
98694
1 px 2 px 3 px
p k1 x k 0
整值剩余寿命的期望与方差
整值剩余寿命的方差
Var(K (x)) E(K 2 ) E2 (K ) (2k 1) k1 px ex2 k 0
死亡效力
定义：(x) 的瞬时死亡率，简记 x
x
s(x) s(x)
f (x) s(x)
＝s 50 s 60
e 1
36
e 25
0.3679 0.2369 0.1310
2
q 10 50
s 50
s 50 s 50
10
e 1
36
e 25
e 1
0.37 0.24 0.37
0.35
3 Pr X
70
s 70
49
e 25
0.14086
4
20
p50
s 50 20 s 50
有关寿命分布的参数模型
Makeham模型(1860)
x A Bcx
s(x) exp{Ax B(cx 1) / ln c} , B 0,A -B,c 1,x 0 Weibull模型(1939)
x kxn
s(x) exp{kxn1 /(n 1)} , k 0, n 0, x 0