工程力学课后习题答案(20210219023826)
大学《工程力学》课后习题解答-精品
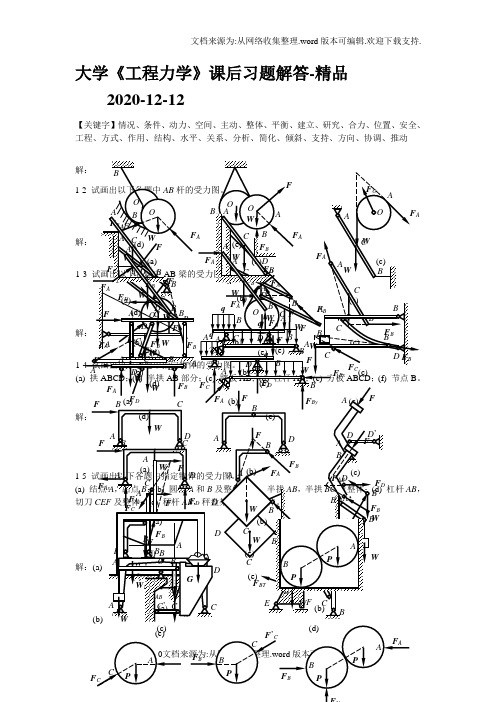
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
工程力学课后习题答案(静力学和材料力学)
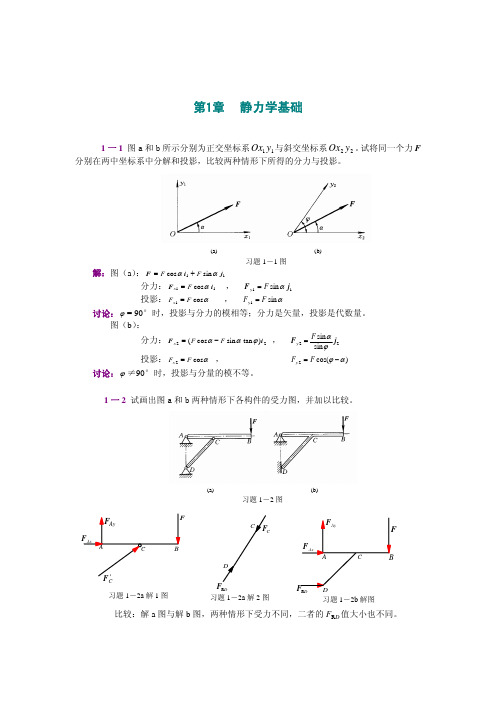
解:图(a):θ = arcsin 4 ,
5
∑ Fx = 0 ,
F sin(60° − θ ) − W sinθ = 0 , F = 1672 N
图(b):θ = 53.13° ,
∑ Fx = 0 , F cos(θ − 30°) − W sinθ = 0 , F = 217N
Fy
x
30D B
Wθ
y
可推出图(b)中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1-12 解 1 图
F AB 习题 1-12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点,滚子搁置在倾斜的光滑刚性平面上,如
图所示。对于给定的θ 角,试求平衡时的 β 角。
=
25 kN 6
即
FR
= ( 5 , 10 )kN 23
作用线方程: y = 4 x + 4 3
讨论:本题由于已知数值的特殊性,实际 G 点与 E 点重合。
2-3三个小拖船拖着一条大船,如图所示。每根拖缆的拉力为5kN。试求:(1)作用于大 船上的合力的大小和方向。(2)当A船与大船轴线x的夹角θ为何值时,合力沿大船轴线方向。
投影: Fx1 = F cosα , Fy1 = F sinα
讨论: ϕ = 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
图(b):
分力: Fx2 = (F cosα − F sin α tan ϕ )i2 ,
Fy2
=
F sinα sinϕ
j2
投影: Fx2 = F cosα ,
Fy2 = F cos(ϕ − α )
(完整版)工程力学课后详细答案
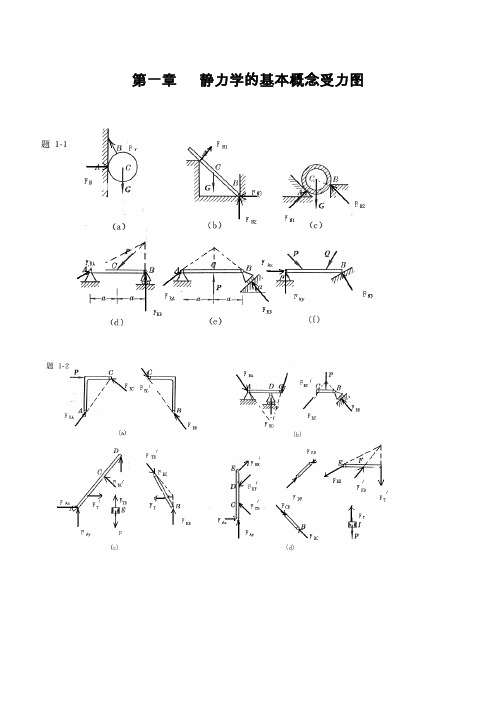
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
工程力学课后习题答案

2-7 已知梁AB上作用一力偶,力偶矩为M,梁长为l,梁重不计。求在图a,b,两三种情况下,支座A和B的约束反力。
(a) (b)
题2-7图
(a) (注意,这里,A与B处约束力为负,表示实际方向与假定方向相反,结果应与你的受力图一致,不同的受力图其结果的表现形式也不同)
(b)
2-8 在题图所示结构中二曲杆自重不计,曲杆AB上作用有主动力偶,其力偶矩为M,试求A和C点处的约束反力。
题3-1图
3-2 图示力系中,F1=100N,F2=300N,F3=200N,各力作用线的位置如图所示。将力向原点O简化
题3-2图
3-3 边长为a的等边三角形板,用六根杆支持在水平面位置如图所示。若在板面内作用一力偶,其矩为M,不计板重,试求各杆的内力。
题3-3图
3-4 如图所示的空间构架由三根杆件组成,在D端用球铰链连接,A、B和C端也用球铰链固定在水平地板上。今在D端挂一重物P=10kN,若各杆自重不计,求各杆的内力。
题6-2图
6-3题6-2图所示圆截面杆,已知载荷 , , 段的直径 ,如欲使 与 段横截面上的正应力相同,试求 段的直径。
6-4设图示结构的1和2两部分皆为刚体,刚拉杆 的横截面直径为 ,试求拉杆内的应力。
题6-4图
1做受力图
2列平衡方程求解
解得F=6kN, FN=3kN, AB杆的应力为:
6-5某受扭圆管,外径 ,内径 ,横截面上的扭矩 ,试计算距轴心21mm处圆管横截面与纵截面上的扭转切应力。
题2-4图
作BD两节点的受力图
联合解得:
2-5在四连杆机构ABCD的铰链B和C上分别作用有力F1和F2,,机构在图示位置平衡。求平衡时力F1和F2的大小间的关系。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交2-4 图示为一拔桩装置。
在木桩的点A 上系一绳,将绳的另一端固定在点C ,在绳的点B 系另一绳BE ,将它的另一端固定在点E 。
然后在绳的点D 用力向下拉,并使绳BD 段水平,AB 段铅直;DE 段与水平线、CB 段与铅直线成等角α=(弧度)(当α很小时,tan α≈α)。
如向下的拉力F=800N ,求绳AB 作用于桩上的拉力。
题2-4图 作BD 两节点的受力图 联合解得:kN F F F A 80100tan 2=≈=α2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2,,机构在图示位置平衡。
(完整版)工程力学课后习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)2 第一章静力学基础(d)(e)(f)(g)第一章静力学基础 3 1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)4 第一章静力学基础1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)第一章静力学基础 5 (b)(c)(d)6 第一章静力学基础(e)第一章静力学基础7 (f)(g)8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如第二章 平面力系 9图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
《工程力学》详细版习题参考答案

∑ Fx
=FAx
+
FBx
+
FCx
=− 1 2
F
+
F
−
1 2
F
=0
∑ Fy
= FAy
+
FBy
+
FCy
= − 3 2
F
+
3 F = 0 2
∑ M B= FBy ⋅ l=
3 Fl 2
因此,该力系的简化结果为一个力偶矩 M = 3Fl / 2 ,逆时针方向。
题 2-2 如图 2-19(a)所示,在钢架的 B 点作用有水平力 F,钢架重力忽 略不计。试求支座 A,D 的约束反力。
(a)
(b)
图 2-18
解:(1)如图 2-18(b)所示,建立直角坐标系 xBy。 (2)分别求出 A,B,C 各点处受力在 x,y 轴上的分力
思考题与练习题答案
FAx
= − 12 F ,FAy
= − 3 F 2
= FBx F= ,FBy 0
FCx
= − 12 F ,FCy
= 3 F 2
(3)求出各分力在 B 点处的合力和合力偶
(3)根据力偶系平衡条件列出方程,并求解未知量
∑ M =0 − aF + 2aFD =0
《工程力学》
可解得 F=Ay F=D F /2 。求得结果为正,说明 FAy 和 FD 的方向与假设方向相同。 题 2-3 如 图 2-20 ( a ) 所 示 , 水 平 梁 上 作 用 有 两 个 力 偶 , 分 别 为
3-4 什么是超静定问题?如何判断问题是静定还是超静定?请说明图 3-12 中哪些是静定问题,哪些是超静定问题?
(a)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB, BC或ABC 的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
b)c)e)g)第二章平面力系2-1 电动机重P=5000N,放在水平梁AC 的中央,如图所示。
梁的 A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为 30 0。
如忽略撑杆与梁的重量,求绞支座 A、 B 处的约束反力。
题2-1 图F x 0,F B cos30 F A cos30 0PF y 0,FA sin30 FB sin30解得: A F B P 5000N2-2 物体重 P=20kN ,用绳子挂在支架的滑轮 B 上,绳子的另一端接在绞车 D 上,如 图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,ABF y 0, F BC sin30 P cos30 P 02-3 如图所示,输电线 ACB 架在两电线杆之间,形成一下垂线,下垂距离 CD = f =1 m , 两电线杆间距离 AB =40m 。
电线 ACB 段重P=400N ,可近视认为沿 AB 直线均匀分布,求电 线的中点和两端的拉力。
A 、F x 0, F AB F BC cos30 P sin 30 0 3.732P2.732P B 、C题 2-2图 题 2-3F x 0,F A cos F C ,F y 0,F A sin F Gtan 1/10 解得:F A 201N F C 2000N2-4 图示为一拔桩装置。
在木桩的点A 上系一绳,将绳的另一端固定在点C,在绳的点B 系另一绳BE,将它的另一端固定在点E 。
然后在绳的点D 用力向下拉,并使绳BD 段水平,AB段铅直;DE段与水平线、CB段与铅直线成等角=0.1rad(弧度)(当很小时,tan )。
如向下的拉力F=800N ,求绳AB 作用于桩上的拉力。
D节点:F x 0,F E cos FBD , Fy0,FEsin以 AC 段电线为研究对象,三力汇交题2-4图作 BD 两节点的受B节点:F x 0,F C sin F BD, F y 0,F C cos F A以 B 、 C 节点为研究对象,作受力图B 节点: F x2 0,F 2 cos30 F BC 0F 16 解得:F 242-6 匀质杆重 W=100N ,两端分别放在与水平面成 300和 600 倾角的光滑斜面上,求平 衡时这两斜面对杆的约束反力以及杆与水平面间的夹角。
联合解得: F Atan2100F 80kN2-5 在四连杆机构 ABCD 的铰链 B 和 C 上分别作用有力 F 1 和 F 2,,机构在图示位置平F x1 0,F BC cos45 F 1 0 C 节点:2-7 已知梁AB 上作用一力偶,力偶矩为况下,支座A 和B 的约束反力。
M,梁长为l,梁重不计。
求在图 a,b,两三种情M.(注.意.,.这.里.,.A.与.B.处.约.束.力.为.负.,.表.示.实.际.方.向.与.假.定.方.向.相.反.,.结.果.应.与.你.的.受.力.图.一.致.,.不.同.的.受.力.图.其.结.果.的.表.现.形.式.也.不.同..)题2-6图b)题2-7图a) F A F B2-8 在题图所示结构中二曲杆自重不计,曲杆 AB 上作用有主动力偶,其力偶矩为 M , 试求 A 和 C 点处的约束反力。
BC 是二力杆, AB 只受力偶作用,因此 A 、B 构成一对力偶。
即 F AF BM A 0, 2F B ' a 2F B ' 3a M22 各尺寸如图。
求支座 A 的约束反力。
(b) FA FBM l cos 作两曲杆的受力图, F B '2M 4aF A F B2M4a2-9 在图示结构中, 各构件的自重略去不计, 在构件 BC 上作用一力偶矩为 M 的力偶,1 作受力图2、BC 只受力偶作用,力偶只能与力偶平衡3、构件 ADC 三力汇交20, 22 F A 2Ml2-10 四连杆机构 ABCD 中的 AB =0.1m , CD =0.22m ,杆AB 及CD 上各作用一力偶。
在图 示位置平衡。
已知 m 1=0.4kN.m, 杆重不计,求 A 、D 两绞处的约束反力及力F C ' 0题 2-9 图FB偶矩m2。
题 2-10 图AB 杆: M 0,F B l AB sin30 M1 CD 杆 M 0,F B l CDsin75 M2解得: M 21.7kNm2-11 滑道摇杆机构受两力偶作用, 在图示位置平衡。
已知 OO 1=OA=0.4m ,m 1=0.4kN.m, 求另一力偶矩 m 2。
及 O 、O 1 处的约束反力。
曲柄上应加多大的力偶矩 M 方能使机构在图示位置平衡?OB 杆和滑块: M 0,F A ' 0.4 sin60 CD 杆 M 0,F A 3 0.4 M 2 解得: F A 1.15kN , M 2 0.8kNm F O F O1 F A 1.15kNM12-12 图示为曲柄连杆机构。
主动力 F 400N 作用在活塞上。
不计构件自重,试问在2-13图示平面任意力系中 F1 40 2N,F2 80N,F3 40N,F4 110N ,M 2000N mm 。
各力作用位置如图所示,图中尺寸的单位为m m 。
求:( 1)力系向O点简化的结果;(2)力系的合力并在图中标出作用位置。
题2-13 图F3 193kN ,桥墩重量P 5280kN ,风力的合力F示。
求力系向基底截面中心O 的简化结果;如能简化为一合力,求合力作用线位置并在图中标出。
2-15 试求图示各梁支座的约束反力。
设力的单位为k N ,力偶矩的单位为kN.m,长度2-14 某桥墩顶部受到两边桥梁传来的铅直力F1 1940kN ,F2 800kN ,水平力140kN 。
各力作用线位置如图所题2-14图a)b)8 1.6 20 2.4 FY 20 0.8 20223 F Y 2 2 2 1 20,F Ay0.80.4 FB0,3 2 2 0,F A FB MAFx 33 重。
求固定端 A 处的约束力。
精选文档题 2-12 图受力分析如图:解得: F A 15kN,F B 21kN受力分析如图:的单位为 m ,分布载荷集度为kN/m 。
M A 0,20 2-16 在图示刚架中,已知 q3kN/m , F 6 2 kN , M 10kN m ,不计刚架自解得: 0,F AxF Ax 2.12kN , F Ay0.33kN, F B 4.23kN2-17 在图示 a ,b 两连续梁中, 已知 q ,M ,a ,及 ,不计梁的自重。
求各连续梁在 A , B ,C 三处的约束反力。
2-13 在图示 a ,b 两连续梁中, 已知 q ,M ,a ,及 ,不计梁的自重。
求各连续梁在 A , B ,C 三处的约束反力。
acos2.对 AB 杆列平衡方程a)b)题 2-13 图1 作受力图, BC 杆受力偶作用F X 0,F AxMFB'sin tanF Y 0,F AyMF B'cosMA(F) 0,MAFB'cos a MF X 0,F Bx F C sinF Y 0,F By qa F C cos 012MB(F) 0,FCcos a qa2B C2qa1.以 AB 为研究对象,列平衡方程所以:F AxF AyM tanaMA1.以 BC 为研究对象,列平衡方程F Bx q2a tanqa2cosF ByF X 0,F Ax F BxqatanF Y 0,F Ay F By qa 2B(F) 0,M A F By 12 2qa2F Ax F Bx F Ay F By qatan2 qa 2M A112qaqa2cosA,B,C 构成,已知每个半拱重P=300kN ,2-18 如图所示,三绞拱由两半拱和三个铰链以整体为研究对象,由对称性知:F Ax F BxF Ay F By P 300kN 以 BC 半拱为研究对象3l lM C 0,P F Bx h F By82F Bx F Ax 120kN2-19 图示构架中,物体重 1200N,由细绳跨过滑轮E 而水平系于墙上,尺寸如图所示,不计杆和滑轮的重量。
求支承A 和B 处的约束反力以及杆BC的内力F BC。
题2-19 图以整体为研究对象F X 0,F AxF Y 0,F Ay F BM A(F) 0,F B (2 r)P (1.5 r) 0F Ax解得:F AyF B 1200N 150N 1050N以 CDE 杆和滑轮为研究对象M D (F) 0,F B21.52 221.51.5 0解得:F B 1500N2-20 在图示构架中,各杆单位长度的重量为300N/m ,载荷P=10kN ,A处为固定端,B,C,D 处为绞链。
求固定端A 处及B,C 为绞链处的约束反力。
F X 0,F Ax 0F Y 0,F Ay P P1 P2 P3 15.1kN 以 ABC 杆为研究对象题2-20 图显然:P1 1800N P2以整体为研究对象1800N P3 1500N M A(F) 0,M A P 6 P2 3 P3 2 68.4kNF X 0,F Ax F Bx F Cx 0(式1)F Y 0,F Ay F By F Cy P(1 式2)M A(F) 0,M A F Bx 3 F Ax (6 式3)以 CD 杆为研究对象M D (F) 0,F Cy 4 P2 1由 1、2、3、4 式得:F Bx 22.8kN , F By 17.85NP 2 (式 4)F Cx 22.8kN , F Cy 4.55kN2-21 试用节点法求图示桁架中各杆的内力。
F 为已知,除杆 2 和杆 8 外,其余各杆长度均相等。
2-22 平面桁架结构如图所示。
节点D 上作用一载荷F,试求各杆内力。
题2-22图F1 10kN, F2 F3 20kN 。
试求桁架 4,5,7,102-24 平面桁架的支座和载荷如图所示,求杆2 杆,用截面法分析;再取 C 节点)1,2和 3 的内力。
(提示:先截断AD、3、各杆的内力。
题2-23图2-23桁架受力如图所示,已知题2-24 图2-25 两根相同的均质杆AB 和BC,在端点B 用光滑铰链连接,A,C 端放在不光滑的水平面上,如图所示。
当ABC 成等边三角形时,系统在铅直面内处于平衡状态。
求杆端与水平面间的摩擦因数。
以整体为研究对象M A(F) 0,N C PM C (F) 0,N A P 以 AB杆为研究对象1M B(F) 0,N A 12l 得:F A2P3f N A题2-25 图2-26 图示两无重杆在 B 处用套筒式无重滑块连接,在 AD 杆上作用一力偶,其力偶矩 M A =40N.m ,滑块和 AD 间的摩擦因数 f s =0.3。
