向量的极化恒等式与等和线的应用学生版

合集下载

向量复习专题二极化恒等式

向量复习专题二极化恒等式一、极化恒等式：222214
a b AD BC AM BM ⎡⎤⋅=-=-⎣⎦
二、极化恒等式的应用
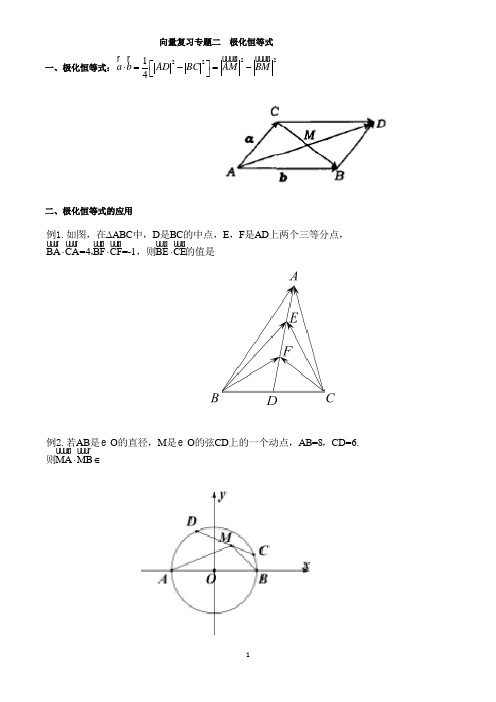
ABC D BC E F AD BA CA=4BF CF=-1BE CE ∆⋅⋅⋅ 例1.如图，在中，是的中点，，是上两个三等分点，，，则的值是
AB O M O CD AB=8CD=6.MA MB ⋅∈
例2.若是的直径，是的弦上的一个动点，，则
例 4.在中,,,已知点是内一点,则的最
小值是_______.
()
ABCD OB OC ⋅ 例5.如图放置的边长为1的正方形顶点分别在x 轴，y 轴正半轴含原点滑动，则的最大值为
.3,2,()P ABO OA OB P AB OP OA OB ∆==⋅- 例3为所在平面内一点，线段在线段的垂直平分线上，则
的值为
例6.（2013浙江理7）在ABC ∆中，0P 是边AB 上一定点，满足AB B P 410=，且对于边AB 上任一点P ，恒有C P B P PC PB 00∙≥∙，则
A. 2π=
∠ABC B. 2π=∠BAC C. AC AB = D. BC AC =
例7.已知圆的半径为，是圆上的两点，且，是圆的任意一条直径，
若点满足，则的最小值为
O 1,A B 3AOB π
∠=MN O C 1(1)()2
OC OA OB R λλλ=+-∈ CM CN ⋅。

向量的极化恒等式与等和线的应用-学生版

向量的极化恒等式与等和线的应用-学生版向量的极化恒等式与等和线的应用-学生版结论：平行四边形对角线的平方和等于两条邻边平方和的两倍?思考1:如果将上面(1) (2)两式相减，能得到什么结论呢？对于上述恒等式，用向量运算显然容易证明。

那么基于上面的引例，你觉得极化恒等式的几何意义是什么？几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的丄.4即：；b = 4〔AC 2-DB 2】(平行四边形模式)极化恒等式引例：平行四边形是表示向量加法和减法的几何模型。

你能用向量方法证明：平行四边形的对角线的平方和等于两条邻边平方和的两倍? 证明：不妨设AB = a, AD = b,贝V AC 二 a b,DB =a —b, ___ , 2 AC 二 AC 二 a b (1).2 DB r 2 a ___ 2 ? ■ 2 =DB 二 a — b ? r r 2 -2a b + b(1) (2)两式相加得:ab =;_a b极化恒等式思考：在图1的三角形ABD中（M为BD的中点），此恒等式如何表示呢？因为AC=2AM，所以ai=|AMp-1|DB|2（三角形模式）例1. （2012年浙江文15）在ABC中川是BC的中点AM =3,BC =10，则AB TAC =BMC目标检测（2012北京文 13改编）已知正方形 ABCD 的边长为 1, 点E 是AB 边上的动点，贝V DE DA 的值为_______________________________________ .例2.（自编）已知正三角形 ABC 内接于半径为2的圆O ,点P 是圆O 上的一个动点, 则PA PB 的取值范围是 _________________ .目标检测2 2（2010福建文11）若点O 和点F 分别为椭圆中上 =1的中心和左焦点，点P 为椭圆上的任意一点，则OP FP 的最大值为（）A2 B.3 C.6 D.8例3. （2013浙江理7）在ABC 中,P o是边AB 上一定点，满足P°B*AB ，且对于边AB 上任一点4 7PB 卩C HRB PC 。

极化恒等式学生版

极化恒等式(学生版) 极化恒等式是线性代数中的一个重要恒等式，它反映了矩阵和向量之间的内在关系。

这个恒等式可以表示为：A⋅(β+γ)=Aβ+Aγ，其中A是一个矩阵，β和γ是向量，A⋅表示矩阵A和向量的乘积。

在证明极化恒等式之前，我们需要先了解一下矩阵和向量的乘法。

矩阵和向量的乘法是通过将矩阵的每一行与向量相乘，然后将这些乘积相加得到的。

例如，如果A是一个3×2的矩阵，β是一个2×1的向量，那么A⋅β可以通过以下步骤计算：1.将第一行a11a12与向量β相乘得到第一个乘积a11β1+a12β2，将第二行a21a22与向量β相乘得到第二个乘积a21β1+a22β2，将第三行a31a32与向量β相乘得到第三个乘积a31β1+a32β2。

2.将上述三个乘积相加得到A⋅β=(a11β1+a12β2)+(a21β1+a22β2)+(a31β1+a32β2)=a11β1+a12β2 +a21β1+a22β2+a31β1+a32β2=∑i=13∑j=12Aijβj。

现在我们可以证明极化恒等式。

首先，我们需要将矩阵A拆分成两个部分，即A=A−+A+，其中A−=(A−1)ij=−∑k=1nAkij(i=1,m;j=1,n)是一个(m×n)矩阵，A+=εijk(i=1,m;j=1,n;k=−m−(+j)=i)也是一个(m×n)矩阵。

其中εijk是一个排列符号，当i、j、k三个指标循环排列时，其值为1或−1。

根据矩阵拆分的定义，我们可以将极化恒等式表示为：(A−+A+)⋅(β+γ)=A−⋅β+A−⋅γ+A+⋅β+A+⋅γ对于右侧第一项A−⋅β，根据矩阵和向量的乘法计算规则可得：A−⋅β=(−∑k=1nAkij)⋅β=(−Akij)⋅βk=(−∑k=1n(Aiuj)⋅Bvkaj)⋅ɛvka)=(−∑k= 1n(Aui)⋅Bk)(ɛik⋅ɛivk)=(−∑k=1n(Aui⋅Bk))⋅ɛik=(−Aui⋅B)⋅eivi=(−Aui⋅B)⋅βi= tika⋅Mk耿 ltiZMn耿 wnow瓣towZMn耿 +yla"owe看来及。

最全归纳平面向量中的范围与最值问题 (十大题型)(学生版)

最全归纳平面向量中的范围与最值问题目录题型一：三角不等式题型二：定义法题型三：基底法题型四：几何意义法题型五：坐标法题型六：极化恒等式题型七：矩形大法题型八：等和线题型九：平行四边形大法题型十：向量对角线定理方法技巧总结技巧一．平面向量范围与最值问题常用方法：(1)定义法第一步：利用向量的概念及其基本运算将所求问题转化为相应的等式关系第二步：运用基木不等式求其最值问题第三步：得出结论(2)坐标法第一步：根据题意建立适当的直角坐标系并写出相应点的坐标第二步：将平面向量的运算坐标化第三步：运用适当的数学方法如二次函数的思想、基本不等式的思想、三角函数思想等求解(3)基底法第一步：利用其底转化向量第二步：根据向量运算律化简目标第三步：运用适当的数学方法如二次函数的思想、基本不等式的思想、三角函数思想等得出结论(4)几何意义法第一步：先确定向量所表达的点的轨迹第二步：根据直线与曲线位置关系列式第三步：解得结果技巧二．极化恒等式(1)平行四边形平行四边形对角线的平方和等于四边的平方和：|a +b |2+|a -b |2=2(|a|2+|b |2)证明：不妨设AB =a ,AD =b ，则AC =a +b ，DB =a -bAC 2=AC 2=a +b 2=a 2+2a ⋅b +b 2①DB 2=DB 2=a -b 2=a 2-2a ⋅b +b 2②①②两式相加得：AC 2+DB 2=2a 2+b 2=2AB 2+AD 2 (2)极化恒等式：上面两式相减，得：14a +b 2-a -b 2----极化恒等式①平行四边形模式：a ⋅b =14AC 2-DB 2几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14．②三角形模式：a ⋅b =AM 2-14DB 2(M 为BD 的中点)技巧三．矩形大法矩形所在平面内任一点到其对角线端点距离的平方和相等已知点O 是矩形ABCD 与所在平面内任一点，证明：OA 2+OC 2=OB 2+OD 2．【证明】(坐标法)设AB =a ,AD =b ，以AB 所在直线为轴建立平面直角坐标系xoy ，则B (a ,0),D (0,b ),C (a ,b )，设O (x ,y )，则OA 2+OC 2=(x 2+y 2)+[(x -a )2+(y -b )2]OB 2+OD 2=[(x -a )2+y 2]+[x 2+(y -b )2]∴OA 2+OC 2=OB 2+OD 2技巧四．等和线(1)平面向量共线定理已知OA =λOB +μOC ，若λ+μ=1，则A ,B ,C 三点共线；反之亦然．(2)等和线平面内一组基底OA ,OB 及任一向量OP ，OP =λOA +μOB(λ,μ∈R )，若点P 在直线AB 上或者在平行于AB 的直线上，则λ+μ=k (定值)，反之也成立，我们把直线AB 以及与直线AB 平行的直线称为等和线．①当等和线恰为直线AB 时，k =1；②当等和线在O 点和直线AB 之间时，k ∈(0,1)；③当直线AB 在点O 和等和线之间时，k ∈(1,+∞)；④当等和线过O 点时，k =0；⑤若两等和线关于O 点对称，则定值k 互为相反数；技巧五．平行四边形大法1.中线长定理2AO 2=AB 2+AD 2-12DB 22.P 为空间中任意一点，由中线长定理得：2PO 2=PA 2+PC 2-12AC 22PO 2=PD 2+PB 2-12DB 2两式相减：PA 2+PC 2-PD 2+PB 2=AC2-BD 22=2AB ⋅AD技巧六．向量对角线定理AC ⋅BD =(AD 2+BC 2)-(AB 2+CD2)2必考题型归纳题型一:三角不等式1(2023·全国·高三专题练习)已知向量a ,b ,c 满足|a |=2,|b |=1,|c -a -b |=1，若对任意c ，(c -a )2+(c-b )2≤11恒成立，则a ⋅b 的取值范围是.2(2023·全国·高三专题练习)已知平面向量a ,b ,c 满足：|a|=1,b ⋅a =-1，若对满足条件的任意向量b ，|c -b |≥|c -a |恒成立，则cos c +a ,a 的最小值是．3已知向量a ,b ,c 满足a =b =c =2，a ⋅b =0，若关于t 的方程ta +b2-c=12有解，记向量a ,c 的夹角为θ，则sin θ的取值范围是.1.已知e 1 ,e 2 ,e 3 是平面向量，且e 1 ,e 2 是互相垂直的单位向量，若对任意λ∈R 均有e 3 +λe 1的最小值为e 3 -e 2 ，则e 1 +3e 2 -e 3 +e 3-e 2 的最小值为．2.已知平面向量e 1 ,e 2 满足2e 2 -e 1 =2，设a =e 1 +4e 2 ,b =e 1 +e 2 ，若1≤a ⋅b ≤2，则|a|的取值范围为．3.(2023·浙江金华·统考一模)已知平面向量a ，b ，c 满足a ⋅b =74，|a -b|=3，(a -c )(b -c )=-2，则c的取值范围是．1已知向量a ，b 的夹角为π3，且a ⋅b =3，向量c 满足c =λa +1-λ b 0<λ<1 ，且a ⋅c =b ⋅c ，记x =c ⋅aa ，y =c ⋅b b，则x 2+y 2-xy 的最大值为.2(2023·四川成都·高二校联考期中)已知向量a ，b ，c 满足a =1，b=2，a ⋅b=-1，向量c -a 与向量c -b 的夹角为π4，则c 的最大值为．3(2023·浙江绍兴·高二校考学业考试)已知向量a ，b 满足a =1，b=3，且a ⊥b ，若向量c 满足c -a -b =2a -b ，则c的最大值是．1.已知向量a ，b 满足a =1，b =3，且a ⋅b =-32，若向量a -c 与b -c 的夹角为30°，则|c |的最大值是. 2.已知向量a ，b ，满足a =2b =3c =6，若以向量a ，b 为基底，将向量c 表示成c =λa+μb (λ，μ为实数)，都有λ+μ ≤1，则a ⋅b的最小值为 3.已知向量a 、b 满足：a -b=4，a =2b .设a -b 与a +b 的夹角为θ，则sin θ的最大值为.1.已知菱形ABCD 的边长为2，∠BAD =120°，点E ，F 分在边BC ，CD 上，BE =λBC ，DF=μDC ．若λ+μ=23，则AE ⋅AF 的最小值为．2.(2023·天津·高三校联考阶段练习)已知菱形ABCD 的边长为2，∠BAD =120°，点E 、F 分别在边BC ，CD 上，BE =λBC ，DF =μDC ，若2λ+μ=52，则AE ⋅AF 的最小值．3.如图，菱形ABCD 的边长为4，∠BAD =30°，M 为DC 的中点，若N 为菱形内任意一点(含边界)，则AM ⋅AN的最大值为．4.菱形ABCD 的边长为4，∠BAD =30°，若N 为菱形内任意一点(含边界)，则AB ⋅AN的最大值为．5.如图，菱形ABCD 的边长为4,∠BAD =60°,M 为DC 的中点，若N 为菱形内任意一点(含边界)，则AM ⋅AN的最大值为.6.平面四边形ABCD 是边长为2的菱形，且∠A =120°，点N 是DC 边上的点，且DN =3NC，点M 是四边形ABCD 内或边界上的一个动点，则AM ⋅AN的最大值为.7.(2023·全国·高三专题练习)已知向量a ，b 满足a +b =3，a ⋅b =0．若c =λa+1-λ b ，且c ⋅a =c ⋅b，则c 的最大值为．8.已知平面向量a ，b ，c 满足a =2，b =1，a ⋅b =-1，且a -c 与b -c 的夹角为π4，则c 的最大值为．9.已知平面向量a 、b 、c 满足a=4，b =3，c =2，b ⋅c =3，则a -b 2a -c 2-a -b⋅a -c 2最大值为.10.在△ABC 中，M 为边BC 上任意一点，N 为AM 的中点，且满足AN =λAB +μAC，则λ2+μ2的最小值为.题型四:几何意义法1(2023·全国·模拟预测)已知a ，b ，c 是平面向量，满足a -b =a +b ，a =2b =2，c +a -b=5，则向量c 在向量a上的投影的数量的最小值是.2(2023·上海浦东新·上海市建平中学校考三模)已知非零平面向量a ，b ，c 满足：a ，b 的夹角为π4，c -a与c -b 的夹角为3π4，a -b=2，c -b =1，则b ⋅c 的取值范围是.3(2023·全国·高三专题练习)已知平面向量a ,b 夹角为π3，且平面向量c 满足c -a =c -b =1,c -a ⋅c -b =-12,记m 为f t =ta +1-t b (t ∈R )的最小值，则m 的最大值是． 1.(2023·全国·高三专题练习)已知平面向量a ，b ，c 满足a ⋅b =-3，a -b=4，c -a 与c -b 的夹角为π3，则c -a -b 的最大值为． 2.(2023·四川内江·高二四川省内江市第六中学校考开学考试)已知非零平面向量a ，b ，c 满足：a ，b 的夹角为π3，c -a 与c -b的夹角为2π3，a -b =23，c -b =2，则b ⋅c 的取值范围是．3.已知非零平面向量a ，b ，c 满足a -b =2，且(c -a )⋅(c -b )=0，若a 与b 的夹角为θ，且θ∈π6,π3，则|c |的最大值是.4.(2023·全国·高三专题练习)平面向量a ,b ,c 满足：a ,b 的夹角为π3，|a -b|=|b -c |=|a -c |=23，则b ⋅c的最大值为. 5.(2023·广东阳江·高二统考期中)已知非零平面向量a ，b ，c 满足a -b =4，且a -c⋅b -c =-1，若a 与b 的夹角为θ，且θ∈π3,π2，则c 的模取值范围是. 6.(2023·浙江·高三专题练习)已知平面向量a ，b ，c ，若a =b =a -b =1，且2a -c+2b +c =23，则a -c的取值范围是.7.(2023·安徽阜阳·高三安徽省临泉第一中学校考期末)已知向量a ，b 满足a =b =1，且a ⋅b=0，若向量c 满足c +a +b=1，则c 的最大值为.8.(2023·浙江·模拟预测)已知向量a ，b ，c 满足a -b +c=2b =2，b -a 与a 的夹角为3π4，则c 的最大值为．9.(2023·全国·高三专题练习)已知平面向量a ,b ,c 满足：a -b =5，向量a与向量b 的夹角为π3，a -c=23，向量a -c 与向量b -c 的夹角为2π3，则a 2+c 2的最大值为.题型五:坐标法1(2023·全国·高三专题练习)已知向量a ，b 满足2a +b=3，b =1，则a +2a +b 的最大值为.2(2023·江苏常州·高三统考期中)已知平面向量a ,b ,c 满足|a |=2，|b |=4，a ，b 的夹角为π3，且(a -c )⋅(b -c )=2，则|c |的最大值是.3设平面向量a ，b ，c 满足a =b =2，a 与b 的夹角为2π3，a -c ⋅b -c =0则c 的最大值为．1.(2023·安徽滁州·校考三模)已知平面向量a ，b ，c 满足|a|=1，|b |=3，a ⋅b =0，c -a 与c -b 的夹角是π6，则c ⋅b -a 的最大值为.2.(2023·河北·统考模拟预测)如图，在边长为2的正方形ABCD 中．以C 为圆心，1为半径的圆分别交CD ，BC 于点E ，F ．当点P 在劣弧EF 上运动时，BP ⋅DP的最小值为．3.(2023·山东·山东省实验中学校考一模)若平面向量a ，b ，c 满足a =1，b ⋅c =0，a ⋅b =1，a⋅c=-1，则b +c 的最小值为．4.(2023·四川眉山·仁寿一中校考一模)如图，在平面四边形ABCD 中，∠CDA =∠CBA =90°，∠BAD =120°，AB =AD =1，若点E 为CD 边上的动点，则AE ⋅BE的最小值为．5.(2023·安徽滁州·校考模拟预测)已知a=1，b +a +b -a =4，则b -14a 的最小值是.6.(2023·浙江·模拟预测)已知向量a ，b 满足a=3，且b -λa 的最小值为1(λ为实数)，记a,b =α，a ,a -b=β，则b ⋅b -a cos α+β最大值为.7.在矩形ABCD 中，AB =4，AD =3，M ，N 分别是AB ，AD 上的动点，且满足2AM +AN =1，设AC =xAM +yAN ，则2x +3y 的最小值为()A.48B.49C.50D.51题型六:极化恒等式1(2023·山东师范大学附中模拟预测)边长为1的正方形内有一内切圆，MN 是内切圆的一条弦，点P 为正方形四条边上的动点，当弦MN 的长度最大时，PM ⋅PN的取值范围是．2(2023·湖北省仙桃中学模拟预测)如图直角梯形ABCD 中，EF 是CD 边上长为6的可移动的线段，AD =4，AB =83，BC =12，则BE ⋅BF的取值范围为． 3(2023·陕西榆林·三模)四边形ABCD 为菱形，∠BAC =30°，AB =6，P 是菱形ABCD 所在平面的任意一点，则PA ⋅PC的最小值为． 1.(2023·福建莆田·模拟预测)已知P 是边长为4的正三角形ABC 所在平面内一点，且AP=λAB +(2-2λ)AC (λ∈R )，则PA ⋅PC 的最小值为()A.16B.12C.5D.42.(2023·重庆八中模拟预测)△ABC 中，AB =3，BC =4，AC =5，PQ 为△ABC 内切圆的一条直径，M 为△ABC 边上的动点，则MP ⋅MQ的取值范围为()A.0,4B.1,4C.0,9D.1,9题型七:矩形大法1已知圆C 1:x 2+y 2=9与C 2:x 2+y 2=36，定点P (2,0)，A 、B 分别在圆C 1和圆C 2上，满足PA ⊥PB ，则线段AB 的取值范围是．2在平面内，已知AB 1 ⊥AB 2 ，OB 1 =OB 2 =1，AP =AB 1 +AB 2 ，若|OP |<12，则|OA |的取值范围是()A.0,52B.52,72C.52,2D.72,23(2023·全国·高三专题练习)已知圆Q :x 2+y 2=16，点P 1,2 ，M 、N 为圆O 上两个不同的点，且PM⋅PN =0若PQ =PM +PN ，则PQ的最小值为．1.设向量a ，b ，c满足|a |=|b |=1，a ⋅b =12，(a -c )⋅(b -c )=0，则|c |的最小值是()A.3+12B.3-12C.3D.1题型八:等和线1如图，边长为2的等边三角形的外接圆为圆O ，P 为圆O 上任一点，若AP =xAB +yAC，则2x +2y 的最大值为()A.83B.2C.43D.12在△ABC 中，M 为BC 边上任意一点，N 为线段AM 上任意一点，若AN =λAB +μAC(λ，μ∈R )，则λ+μ的取值范围是()A.0,13B.13,12C.[0,1]D.[1,2]3(2023·全国·高三专题练习)如图,OM ∥AB ，点P 在由射线OM 、线段OB 及AB 的延长线围成的区域内(不含边界)运动,且OP =xOA +yOB .当x =-12时，y 的取值范围是()A.0，+∞ B.12，32C.12，+∞ D.-12，321.(2023·全国·高三专题练习)在扇形OAB 中，∠AOB =60°，C 为弧AB 上的一动点，若OC=xOA +yOB，则3x +y 的取值范围是．2.(2023·江西上饶·统考三模)在扇形OAB 中，∠AOB =60°，C 为弧AB 上的一个动点.若OC=xOA +yOB ，则2x +y 的取值范围是.3.(2023·全国·高三专题练习)在扇形OAB 中，OA =1，∠AOB =π3，C 为弧AB 上的一个动点，若OC =xOA +yOB ，则x +3y 的取值范围是.4.(2023·福建三明·高二三明一中校考开学考试)如图，在扇形OAB 中，∠AOB =π3，C 为弧AB 上的一个动点，若OC =xOA +yOB，则x +4y 的取值范围是.5.(2023·全国·高三专题练习)如图，OM ⎳AB ，点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内(不含边界).且OP =xOA +yOB，则实数对x ,y 可以是()A.-14,34B.-15,75C.14,-12D.-23,236.如图，B 是AC 的中点，BE =2OB ，P 是平行四边形BCDE 内(含边界)的一点，且OP=xOA +yOBx ,y ∈R ，则下列结论正确的个数为()①当x =0时，y ∈2,3②当P 是线段CE 的中点时，x =-12，y =52③若x +y 为定值1，则在平面直角坐标系中，点P 的轨迹是一条线段④x -y 的最大值为-1A.1B.2C.3D.47.(2023·全国·高三专题练习)在△ABC 中，AB =AC=AB ⋅AC=2，点Q 在线段BC (含端点)上运动，点P 是以Q 为圆心，1为半径的圆及内部一动点，若AP =λAB +μAC，则λ+μ的最大值为()A.1B.33C.3+33D.328.在△ABC 中，AD 为BC 上的中线，G 为AD 的中点，M ，N 分别为线段AB ，AC 上的动点(不包括端点A ，B ，C )，且M ，N ，G 三点共线，若AM =λAB ，AN =μAC，则λ+4μ的最小值为()A.32 B.52C.2D.949.(2023·全国·高三专题练习)在ΔABC 中，AC =2,AB =2,∠BAC =120°,AE =λAB ,AF=μAC ，M 为线段EF 的中点，若AM=1，则λ+μ的最大值为()A.73B.273C.2D.21310.在扇形OAB 中，∠AOB =60o ，OA =1，C 为弧AB 上的一个动点，且OC =xOA +yOB．则x +4y 的取值范围为()A.[1,4)B.[1,4]C.[2,3)D.[2,3]11.(2023·全国·高三专题练习)如图，在扇形OAB 中，∠AOB =600，C 为弧AB 上且与A ,B 不重合的一个动点，且OC =xOA +yOB，若u =x +λy (λ>0)存在最大值，则λ的取值范围为()A.(1,3)B.13,3C.12,1D.12,2题型九:平行四边形大法1如图，圆O 是半径为1的圆，OA =12，设B ，C 为圆上的任意2个点，则AC ⋅BC 的取值范围是.2如图，C ，D 在半径为1的⊙O 上，线段AB 是⊙O 的直径，则AC ⋅BD的取值范围是.3(2023·浙江·模拟预测)已知e 为单位向量，平面向量a ，b 满足|a +e |=|b -e |=1，a ⋅b的取值范围是.1.(2023·江西宜春·校联考模拟预测)半径为1的两圆M 和圆O 外切于点P ，点C 是圆M 上一点，点B 是圆O 上一点，则PC ⋅PB的取值范围为.2.(2023·福建·高三福建师大附中校考阶段练习)设圆M ，圆N 的半径分别为1，2，且两圆外切于点P ，点A ，B 分别是圆M ，圆N 上的两动点，则PA ⋅PB的取值范围是()A.-8,12B.-16,34C.-8,1D.-16,1题型十:向量对角线定理1已知平行四边形ABCD ，AB ⊥BC ，AB =BC =AD =2，CD =3，AC 与BD 交于点O ，若记a =OA⋅OB ，b =OB ⋅OC ，c =OC ⋅OD ，则()A.a <b <cB ．a <c <bC ．c <a <bD ．b <a <c2如图，在圆O 中，若弦AB =3，弦AC =5，则AO ⋅BC的值是()A.-8B ．-1C ．1D ．83如图，在四边形ABCD 中，AB ⊥BC ，AD ⊥BC 若，AB =a ，AD =b ，则AC ⋅BD 等于()A.b 2-a 2B.a 2-b 2C.a 2+b 2D.a 2⋅b 2。

平面向量的极化恒等式及其应用

平面向量的极化恒等式及其应用2AB22AC2BC2则动点P的轨迹一定通过ABC的------A.外心B.内心C.重心D.垂心平面向量的极化恒等式及其应用一、极化恒等式的由来定理：平行四边形的对角线的平方和等于相邻两边平方和的两倍。

证法1（向量法）：设 $AB=a,AD=b$，则$AC=a+b,DB=a-b$，$AC+DB=2(a+b)=2(AB+AD)$。

证法2（解析法）：证法3（余弦定理）：推论1：由 $AC+DB=2(AB+AD)$ 知，$2AO+2OB=2(AB+AD)$，即 $AB+AD=2(AO+OB)$。

推论2：$a\cdot b=\dfrac{1}{4}(a+b)^2-\dfrac{1}{4}(a-b)^2$，即 $AB\cdot AD=AO-OB$。

推论3：在 $\triangle ABC$ 中，$O$ 是边 $BC$ 的中点，则 $AB\cdot AC=AO-OB$，即极化恒等式的几何意义。

二、平行四边形的一个重要结论平行四边形的对角线的平方和等于相邻两边平方和的两倍。

AC+DB=2(AB+AD)$。

三、三角形中线的一个性质AB+AC=2(AO+OB)$。

推论1：$AO=\dfrac{1}{2}(AB+AC)-OB$。

推论2：$AO=\dfrac{1}{2}(AB+AC)-BC$。

应用】已知点 $P$ 是直角三角形 $ABC$ 斜边 $AB$ 上中线 $CD$ 的中点，则 $\dfrac{PA+PB}{PC^2}=-\dfrac{1}{2}$。

四、三角形“四心”的向量形态1.$O$ 是平面上一定点，$A,B,C$ 是平面上不同的三点，动点 $P$ 满足 $\dfrac{AP}{AB}+\dfrac{AP}{AC}=\infty$，则动点 $P$ 的轨迹一定通过 $\triangle ABC$ 的外心 $O$，即$OP=OA+\lambda\cdot\overrightarrow{AB}+\mu\cdot\overrighta rrow{AC}$，$\lambda,\mu\in\mathbb{R}$。

极化恒等式与等和(高)线定理【四大题型】(学生版)

极化恒等式与等和(高)线定理【四大题型】【题型1利用极化恒等式求值】【题型2利用极化恒等式求最值(范围)】【题型3利用等和线求基底系数和的值】【题型4利用等和线求基底系数和的最值(范围)】1.极化恒等式与等和(高)线定理极化恒等式是平面向量中的重要等式，是解决平面向量的数量积问题的重要工具，有平行四边形模型和三角形模型两大重要模型，可以建立起向量与几何长度之间的等量关系；等和(高)线定理是平面向量中的重要定理，由三点共线结论推导得出，在求基底系数和的值、最值(范围)中有着重要作用.【知识点1极化恒等式】1.极化恒等式的证明过程与几何意义(1)平行四边形对角线的平方和等于四边的平方和：|a +b |2+|a -b |2=2(|a |2+|b |2).证明：不妨设AB =a ,AD =b ，则AC =a +b ，DB =a -b，AC 2=AC 2=a +b 2=a 2+2a ⋅b +b 2①，DB 2=DB 2=a -b 2=a 2-2a ⋅b +b 2②，①②两式相加得：AC 2+DB 2=2a 2+b 2=2AB 2+AD 2.(2)极化恒等式：上面两式相减，得：14a +b2-a -b 2 ----极化恒等式平行四边形模式：a ⋅b =14AC 2-DB 2 .2.几何解释：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14．(1)平行四边形模型：向量的数量积等于以这组向量为邻边的平行四边形的“和对角线长”与“差对角线长”平方差的14，即14a +b2-a -b 2 (如图).(2)三角形模型：向量的数量积等于第三边的中线长与第三边长的一半的平方差，即(M 为BC 的中点)(如图).极化恒等式表明，向量的数量积可以由向量的模来表示，可以建立起向量与几何长度之间的等量关系.【知识点2等和(高)线定理】1.等和(高)线定理(1)由三点共线结论推导等和(高)线定理：如图，由三点共线结论可知，若(λ,μ∈R )，则λ+μ=1，由△OAB 与△OA 'B '相似，必存在一个常数k ,k ∈R ，使得，则，又(x ,y ∈R )，∴x +y =kλ+kμ=k ；反之也成立.(2)平面内一个基底及任一向量，(λ,μ∈R )，若点P '在直线AB 上或在平行于AB 的直线上，则λ+μ=k (定值)；反之也成立，我们把直线AB 以及与直线AB 平行的直线称为等和(高)线.①当等和线恰为直线AB 时，k =1；②当等和线在O 点和直线AB 之间时，k ∈(0,1)；③当直线AB 在O 点和等和线之间时，k ∈(1,+∞)；④当等和线过O 点时，k =0；⑤若两等和线关于O 点对称，则定值k 1，k 2互为相反数；⑥定值k 的变化与等和线到O 点的距离成正比.【题型1利用极化恒等式求值】1.(2024·贵州毕节·三模)如图，在△ABC 中，D 是BC 边的中点，E ，F 是线段AD 的两个三等分点，若BA⋅CA =7，BE ⋅CE =2，则BF ⋅CF =()A.-2B.-1C.1D.22.(23-24高三上·福建厦门·期末)如图，BC 、DE 是半径为1的圆O 的两条直径，BF =2FO ，则FD ⋅FE =()A.-34B.-89C.-14D.-493.(2024高三·江苏·专题练习)如图，在平面四边形ABCD 中，O 为BD 的中点，且OA =3，OC =5.若AB⋅AD =-7，则BC ⋅DC 的值是．4.(23-24高二下·湖南长沙·开学考试)如图，在平行四边形ABCD 中，AB =1，AD =2，点E ，F ，G ，H 分别是AB ，BC ，CD ，AD 边上的中点，则EF ⋅FG +GH ⋅HE等于．【题型2利用极化恒等式求最值(范围)】5.(2024高三·全国·专题练习)半径为2的圆O 上有三点A 、B 、C 满足OA +AB +AC =0，点P 是圆内一点，则P A ⋅PO +PB ⋅PC 的取值范围为()A.[-4，14)B.[0，4)C.[4，14]D.[4，16]6.(23-24高一下·江苏南通·期中)正三角形ABC 的边长为3，点D 在边AB 上，且BD =2DA ，三角形ABC 的外接圆的一条弦MN 过点D ，点P 为边BC 上的动点，当弦MN 的长度最短时，PM ⋅PN的取值范围是()A.[-1,5]B.[-1,7]C.[0,2]D.[1,5]7.(2024·重庆·模拟预测)已知△OAB 的面积为1,AB =2，动点P ,Q 在线段AB 上滑动，且PQ =1，则OP⋅OQ的最小值为.8.(23-24高三上·上海浦东新·阶段练习)在面积为2的平行四边形中ABCD 中，∠DAB =π6，点P 是AD 所在直线上的一个动点，则PB 2+PC 2-PB ⋅PC 的最小值为．【题型3利用等和线求基底系数和的值】9.(2024·四川成都·模拟预测)如图，在平行四边形ABCD 中，BE =23BC ，DF =34DE ，若AF =λAB +μAD，则λ+μ=()A.32B.-112C.112D.010.(2023·河北沧州·模拟预测)在△ABC 中，BE =12EC ,BF =12BA +BC，点P 为AE 与BF 的交点，AP =λAB +μAC ，则λ+μ=()A.0B.14C.12D.3411.(23-24高一上·江苏常州·期末)在平行四边形ABCD 中，E 为BC 的中点，F 在线段DC 上，且CF =2DF ．若AC =λAE +μAF，λ,μ均为实数，则λ+μ的值为．12.(23-24高一上·江苏苏州·期末)如图，在矩形ABCD 中，M ，N 分别为线段BC ，CD 的中点，若MN =λ1AM +λ2BN ，λ1,λ2∈R ，则λ1+λ2的值为.【题型4利用等和线求基底系数和的最值(范围)】13.(2024·山东烟台·三模)如图，边长为2的等边三角形的外接圆为圆O ，P 为圆O 上任一点，若AP =xAB+yAC ，则2x +2y 的最大值为()A.83B.2C.43D.114.(23-24高三上·河北沧州·期中)如图，△BCD 与△ABC 的面积之比为2，点P 是区域ABCD 内任意一点(含边界)，且AP =λAB +μACλ,μ∈R ，则λ+μ的取值范围是()A.0,1B.0,2C.0,3D.0,415.(23-24高一下·福建泉州·阶段练习)在△ABC 中，M 为BC 边上任意一点，N 为线段AM 上任意一点，若AN =λAB +μAC (λ，μ∈R )，则λ+μ的取值范围是.16.(23-24高一下·广西桂林·期末)已知O 为△ABC 内一点，且4OA +8OB +5OC =0 ，点M 在△OBC 内(不含边界)，若AM =λAB +μAC，则λ+μ的取值范围是．一、单选题1.(2024·四川绵阳·三模)如图，在△ABC 中，AF =BF =6,EF =5，则EA ⋅EB =()A.-11B.-13C.-15D.152.(2024·陕西西安·一模)在△ABC 中，点D 是线段AC 上一点，点P 是线段BD 上一点，且CD =DA ，AP=23AB+λAC ，则λ=()A.16B.13C.23D.563.(2024高三·全国·专题练习)在△ABC 中，D 是BC 边上的中点，且AE =13AD ，AF =2AE ，AB ⋅AC=6，FB ⋅FC =-2，则EB ⋅EC =()A.-1B.2C.-12D.14.(2024·陕西榆林·三模)在△ABC 中，E 在边BC 上，且EC =3BE ,D 是边AB 上任意一点，AE 与CD 交于点P ，若CP =xCA +yCB，则3x +4y =()A.34B.-34C.3D.-35.(23-24高三下·湖南长沙·阶段练习)向量的数量积可以表示为：以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的四分之一，即如图所示，a ⋅b =14AD 2-BC 2，我们称为极化恒等式.已知在△ABC 中，M 是BC 中点，AM =3，BC =10，则AB ⋅AC=()A.-16B.16C.-8D.86.(2024·全国·模拟预测)如图，在△ABC 中，AN =tNC (t >0)，BP =λPN (λ>0)，若AP =34AC -14BC ，则λ+t 的值为()A.7B.6C.5D.47.(23-24高三上·山东潍坊·期末)已知正方形ABCD 的边长为2，MN 是它的内切圆的一条弦，点P 为正方形四条边上的动点，当弦MN 的长度最大时，PM ⋅PN的取值范围是()A.[0，1]B.0,2C.[1，2]D.-1,18.(2024·河北沧州·三模)对称美是数学美的重要组成部分，他普遍存在于初等数学和高等数学的各个分支中，在数学史上，数学美是数学发展的动力.如图，在等边△ABC 中，AB =2，以三条边为直径向外作三个半圆，M 是三个半圆弧上的一动点，若BM =λAB +μAC，则λ+μ的最大值为()A.12B.33C.1D.32二、多选题9.(23-24高一下·江苏南京·期中)在△ABC 中，点D 是线段BC 上任意一点，点M 是线段AD 的中点，若存在λ,μ∈R 使BM =λAB +μAC，则λ,μ的取值可能是()A.λ=-35,μ=110B.λ=1,μ=-32C.λ=-910,μ=25D.λ=-710,μ=3510.(23-24高一下·四川成都·阶段练习)如图，正方形ABCD 中，E 为AB 中点，M 为线段AD 上的动点，若BM =λBE +μBD ，则λ+μ的值可以是()A.32B.12C.1D.211.(23-24高一下·陕西西安·阶段练习)(多选)如图，在四边形ABCD 中，∠B =60°，AB =3，BC =6，且AD =λBC λ∈R ，AD ⋅AB =-32，则()A.AB ·BC =9B.实数λ的值为16C.四边形ABCD 是梯形D.若M ，N 是线段BC 上的动点，且MN =1，则DM ⋅DN 的最小值为132三、填空题12.(2024·新疆·二模)在等腰梯形ABCD 中，AB =2DC ，点E 是线段BC 的中点，若AE =λAB +μAD ，则λ+μ=.13.(23-24高一下·黑龙江大庆·期末)如图，在△ABC 中，D 是BC 的中点，E ，F 是AD 上的两个三等分点BA ⋅CA =5，BF ⋅CF =-2，则BE ⋅CE 的值是.14.(23-24高三·广东阳江·阶段练习)在面积为2的平行四边形ABCD 中，点P 为直线AD 上的动点，则PB ⋅PC +BC 2的最小值是．四、解答题15.(23-24高一下·甘肃白银·阶段练习)如图，在平行四边形ABCD 中，AC 与BD 相交于点O ．E 是线段OD 的中点，AE 的延长线与CD 交于点F ．(1)用AB ，AD 方表示AE ；(2)若AF =λAB +μAD ，求λ+μ的值．16.(23-24高一下·江苏苏州·期中)阅读一下一段文字：a +b 2=a 2+2a ⋅b +b 2，a -b 2=a 2-2a ⋅b +b 2，两式相减得(a +b )2-(a -b )2=4a ·b ⇒a ·b =14[(a +b )2-(a -b)2]我们把这个等式称作“极化恒等式”，它实现了在没有夹角的参与下将两个向量的数量积运算化为“模”的运算．试根据上面的内容解决以下问题：如图，在△ABC 中，D 是BC 的中点，E ，F 是AD 上的两个三等分点．(1)若AD =6，BC =4，求AB ⋅AC 的值；(2)若AB ⋅AC =4，FB ⋅FC =-1，求EB ⋅EC 的值．17.(23-24高一上·辽宁大连·期末)在三角形ABC 中，AB =a ，AC =b ，BE =2EC，D 为线段AC 上任意一点，BD 交AE 于O .(1)若CD =2DA .①用a ，b表示AE ；②若AO =λAE ，求λ的值；(2)若BO =xBA +yBC ，求12x +13y +1的最小值.18.(23-24高一下·湖南邵阳·期末)如图，已知四边形ABDE 为平行四边形，点C 在AB 延长线上，点M 在线段AD 上，且AB =12BC ,AM =13AD ，设AB =a ,AE =b .(1)用向量a ，b表示CD ；(2)若线段CM 上存在一动点P ，且AP =ma +nb m ,n ∈R ，求n 2+mn 的最大值.1119.(23-24高一下·广东潮州·阶段练习)阅读以下材料，解决本题：我们知道①(a +b )2=a 2+2a ⋅b +b 2；②(a -b)2=a 2-2a ⋅b +b 2.由①-②得(a +b )2-(a -b )2=4a ⋅b ⇔a ⋅b =(a +b )2-(a -b )24，我们把最后推出的式子称为“极化恒等式”，它实现了没有夹角参与的情况下将两个向量的数量积化为“模”的运算.如图所示的四边形ABCD 中，BD =8,AB ⋅AD =48，E 为BD 中点.(1)若cos ∠BAD =1213，求△ABD 的面积；(2)若2AE =EC ，求CB ⋅CD 的值；(3)若P 为平面ABCD 内一点，求P A ⋅PB +PD 的最小值.。

平面向量系数和(等和线、等值线)问题(高阶拓展、竞赛适用)(学生版) 2025年高考数学一轮复习学案

第04讲平面向量系数和（等和线、等值线）问题（高阶拓展、竞赛适用）（5类核心考点精讲精练）平面向量与代数、几何融合考查的题目综合性强，难度大，考试要求高。

平面向量是有效连接代数和几何的桥梁，已成为高考数学的一个命题热点。

近年，高考、模考中有关“系数和（等和线）定理”背景的试题层出不穷，学生在解决此类问题时，往往要通过建系或利用角度与数量积处理，结果因思路不清、解题繁琐，导致得分率不高，而向量三点共线定理与等和线巧妙地将代数问题转化为图形关系问题，将系数和的代数运算转化为距离的比例运算，数形结合思想得到了有效体现，同时也为相关问题的解决提供了新的思路，大家可以学以致用如图，P 为AOB ∆所在平面上一点，过O 作直线//l AB ，由平面向量基本定理知：存在,x y R ∈，使得OP xOA yOB=+下面根据点P 的位置分几种情况来考虑系数和x y +的值①若P l ∈时，则射线OP 与l 无交点，由//l AB 知，存在实数λ，使得OP AB λ=而AB OB OA =- ，所以OP OB OA λλ=-，于是=-=0x y λλ+②若P l ∉时，（i ）如图1，当P 在l 右侧时，过P 作//CD AB ，交射线OA OB ，于,C D 两点，则OCD OAB ∆~∆，不妨设OCD ∆与OAB ∆的相似比为k由,P C D ，三点共线可知：存在R λ∈使得：(1)(1)OP OC OD k OA k OBλλλλ=+-=+- 所以(1-)x y k k kλλ+=+=（ii ）当P 在l 左侧时，射线OP 的反向延长线与AB 有交点，如图1作P 关于O 的对称点P '，由（i ）的分析知：存在存在R λ∈使得：(1)(1)OP OC OD k OA OB λλλλ'=+-=+- 所以--(1)OP k OA OBλλ'=+- 于是--(1-)-x y k k kλλ+=+=综合上面的讨论可知：图中OP 用,OA OB线性表示时，其系数和x y +只与两三角形的相似比有关。

平面向量中极化恒等式、等和(高)线定理及最值(范围)问题--备战2022年高考数学一轮复习配套试题

平面向量中极化恒等式、等和(高)线定理及最值(范围)问题)知识梳理1．极化恒等式：a ·b ＝14[(a ＋b )2－(a －b )2]．(1)几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14.(2)平行四边形PMQN ，O 是对角线交点．则： ①PM →·PN→＝14[|PQ |2－|NM |2](平行四边形模式)； ②PM →·PN→＝|PO |2－14|NM |2(三角形模式)． 2．等和(高)线定理(1)由三点共线结论推导等和(高)线定理：如图，由三点共线结论可知，若OP →＝λOA→＋μOB →(λ，μ∈R )，则λ＋μ＝1，由△OAB 与△OA ′B ′相似，必存在一个常数k ，k ∈R ，使得OP ′→＝kOP →，则OP ′→＝kOP →＝kλOA →＋kμOB →，又OP ′→＝xOA →＋yOB →(x ，y ∈R )，∴x ＋y ＝kλ＋kμ＝k ；反之也成立．(2)平面内一组基底OA→，OB →及任一向量OP ′→，OP ′→＝λOA →＋μOB →(λ，μ∈R )，若点P ′在直线AB 上或在平行于AB 的直线上，则λ＋μ＝k (定值)；反之也成立，我们把直线AB 以及与直线AB 平行的直线成为等和(高)线．①当等和线恰为直线AB 时，k ＝1；②当等和线在O 点和直线AB 之间时，k ∈(0，1)； ③当直线AB 在O 点和等和线之间时，k ∈(1，＋∞)； ④当等和线过O 点时，k ＝0；⑤若两等和线关于O 点对称，则定值k 互为相反数；⑥定值k 的变化与等和线到O 点的距离成正比． 3．平面向量中的最值(范围)问题(1)向量投影、数量积、向量的模、夹角的最值(或范围)． (2)向量表达式中字母参数的最值(或范围)．题型一极化恒等式的应用【例1】 (1)已知AB 是圆O 的直径，AB 长为2，C 是圆O 上异于A ，B 的一点，P 是圆O 所在平面上任意一点，则(P A →＋PB →)·PC →的最小值为( )A ．－14B ．－13C ．－12 D ．－1(2)(2020·天津卷)如图，在四边形ABCD 中，∠B ＝60°，AB ＝3，BC ＝6，且AD →＝λBC →，AD →·AB→＝－32，则实数λ的值为__________；若M ，N 是线段BC 上的动点，且|MN →|＝1，则DM →·DN→的最小值为__________．答案 (1)C (2)16 132解析 (1)P A →＋PB →＝2PO →，∴(P A →＋PB →)·PC →＝2PO →·PC →，取OC 中点D ，由极化恒等式得，PO →·PC →＝|PD |2－14|OC |2＝|PD |2－14，又|PD |2min＝0，∴(P A →＋PB →)·PC →的最小值为－12.(2)法一依题意得AD ∥BC ，∠BAD ＝120°，由AD →·AB →＝|AD →|·|AB →|·cos ∠BAD ＝－32|AD →|＝－32，得|AD →|＝1，因此λ＝|AD →||BC→|＝16.取MN 的中点E ，连接DE ，则DM →＋DN →＝2DE →，DM →·DN →＝14[(DM →＋DN →)2－(DM →－DN →)2]＝DE →2－14NM →2＝DE →2－14.注意到线段MN 在线段BC 上运动时，DE 的最小值等于点D 到直线BC 的距离，即AB ·sin B ＝332，因此DE →2－14的最小值为⎝ ⎛⎭⎪⎫3322－14＝132，即DM →·DN →的最小值为132.法二因为AD →＝λBC →，所以AD ∥BC ，则∠BAD ＝120°，所以AD →·AB →＝|AD →|·|AB →|·cos 120°＝－32，解得|AD→|＝1.因为AD→，BC →同向，且BC ＝6，所以AD→＝16BC →，即λ＝16. 在四边形ABCD 中，作AO ⊥BC 于点O ，则BO ＝AB ·cos 60°＝32，AO ＝AB ·sin 60°＝332.以O 为坐标原点，以BC 和AO 所在直线分别为x ，y 轴建立平面直角坐标系．如图，设M (a ，0)，不妨设点N 在点M 右侧，则N (a ＋1，0)，且－32≤a ≤72.又D ⎝ ⎛⎭⎪⎫1，332，所以DM →＝⎝ ⎛⎭⎪⎫a －1，－332， DN→＝⎝ ⎛⎭⎪⎫a ，－332，所以DM →·DN →＝a 2－a ＋274＝⎝ ⎛⎭⎪⎫a －122＋132.所以当a ＝12时，DM →·DN→取得最小值132.感悟升华 (1)极化恒等式多用于向量的数量积； (2)注意在三角形、平行四边形中的应用．【训练1】 (1)(2021·杭州二中模拟)在△ABC 中，M 是BC 的中点，AM ＝3 ，BC ＝10，则AB →·AC→＝________．(2)已知正三角形ABC 内接于半径为2的圆O ，点P 是圆O 上的一个动点，则P A →·PB→的取值范围是________．答案 (1)－16 (2)[－2，6]解析 (1)因为M 是BC 的中点，由极化恒等式得AB →·AC→＝|AM |2－14|BC |2＝9－14×100＝－16.(2)取AB 的中点D ，连接CD ，因为三角形ABC 为正三角形，所以O 为三角形ABC 的重心，O 在CD 上，且OC ＝2OD ＝2，所以CD ＝3，AB ＝2 3. 又由极化恒等式得P A →·PB→＝PD 2－14AB 2＝PD 2－3，因为P 在圆O 上，所以当P 在点C 处时，PD max ＝3，当P 在CO 的延长线与圆O 的交点处时，PD min ＝1，所以P A →·PB →∈[－2，6]．题型二等和线定理的应用【例2】 (1)如图，平面内有三个向量OA →，OB →，OC →，其中〈OA →，OB →〉＝120°，〈OA →，OC →〉＝30°，且|OA →|＝|OB →|＝1，|OC →|＝23，若OC →＝mOA →＋nOB →，则m ＋n ＝________．(2)在扇形OAB 中，∠AOB ＝60°，C 为AB ︵上的一个动点，若OC →＝xOA →＋yOB →，则3x ＋y 的取值范围是________．答案 (1)6 (2)[1，3]解析 (1)法一连接AB ，交OC 于点D ，则 ∠DOA ＝∠OAD ＝30°，∠BOD ＝90°， |OD →|＝|OB →|tan 30°＝33，|OD →|＝|DA →|＝33，|DB →|＝233，由平面向量基本定理得OD→＝23OA →＋13OB →，|OC →|＝23＝6|OD →|，∴OC →＝6⎝ ⎛⎭⎪⎫23OA →＋13OB →＝4OA→＋2OB →，m ＋n ＝6.法二根据等高线定理可得|OC ||OD |＝k ＝m ＋n ，k ＝|OC→||OD →|＝2333＝6，∴m ＋n ＝6.(2)取D 使得OD →＝13OA →，OC →＝xOA →＋yOB →＝3xOD →＋yOB →，作一系列与BD 平行的直线与圆弧相交，当点C 与点B 重合时，3x ＋y 取得最小值1，当点C 与点A 重合时，3x ＋y 取得最大值3，故3x ＋y 的取值范围是[1，3]．感悟升华 (1)“等和线”的解题步骤 ①确定值为1的等和线；②过动点作该线平行线，结合动点的可行域，分析在何点处取得最值； ③利用长度比或该点的位置，求得最值或范围．(2)“等和线”多用于向量线性表示式中有关系数的最值、范围问题． (3)此类问题也可建系，用坐标法解决．【训练2】如图，四边形OABC 是边长为1的正方形，点D 在OA 的延长线上，且AD ＝1，点P 是△BCD (含边界)的动点，设OP →＝λOC →＋μOD →，则λ＋μ的最大值为________．答案 32解析当点P 位于B 点时，过点B 作GH ∥DC ，交OC ，OD 的延长线于G ，H ，则OP →＝xOG →＋yOH →，且x ＋y ＝1， ∵△GCB ∽△COD ，∴GC CO ＝CB OD ＝12，∴OP →＝OB →＝xOG →＋yOH →＝32xOC →＋32yOD →＝λOC →＋μOD →，所以λ＝32x ，μ＝32y ⇒λ＋μ＝32x ＋32y ＝32.故答案为32. 题型三平面向量中的最值(范围)问题角度1 函数型【例3－1】 (1)(一题多解)(2020·浙江卷)已知平面单位向量e 1，e 2满足|2e 1－e 2|≤ 2.设a ＝e 1＋e 2，b ＝3e 1＋e 2，向量a ，b 的夹角为θ，则cos 2θ的最小值是__________． (2)(2021·宁波十校联考)设向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，记a *b ＝x 1x 2－y 1y 2，若圆C ：x 2＋y 2－2x ＋4y ＝0上的任意三个点A 1，A 2，A 3，且A 1A 2⊥A 2A 3，则|OA 1→*OA 2→＋OA 2→*OA 3→|(O 为坐标原点)的最大值是________．答案 (1)2829 (2)16解析 (1)法一设e 1＝(1，0)，e 2＝(x ，y )，则a ＝(x ＋1，y )，b ＝(x ＋3，y )．由2e 1－e 2＝(2－x ，－y )，故|2e 1－e 2|＝（2－x ）2＋y 2≤2，得(x －2)2＋y 2≤2. 又有x 2＋y 2＝1，得(x －2)2＋1－x 2≤2，化简，得4x ≥3，即x ≥34，因此34≤x ≤1. cos 2θ＝⎝ ⎛⎭⎪⎫a ·b |a |·|b |2 ＝⎝ ⎛⎭⎪⎫（x ＋1）（x ＋3）＋y 2（x ＋1）2＋y 2（x ＋3）2＋y 22＝⎝ ⎛⎭⎪⎫4x ＋42x ＋26x ＋102＝4（x ＋1）2（x ＋1）（3x ＋5）＝4（x ＋1）3x ＋5＝43（3x ＋5）－833x ＋5＝43－833x ＋5，当x ＝34时，cos 2θ有最小值，为4⎝ ⎛⎭⎪⎫34＋13×34＋5＝2829.法二单位向量e 1，e 2满足|2e 1－e 2|≤2，所以|2e 1－e 2|2＝5－4e 1·e 2≤2，即e 1·e 2≥34. 因为a ＝e 1＋e 2，b ＝3e 1＋e 2，a ，b 的夹角为θ，所以cos 2θ＝（a ·b ）2|a |2|b |2＝[（e 1＋e 2）·（3e 1＋e 2）]2|e 1＋e 2|2·|3e 1＋e 2|2＝（4＋4e 1·e 2）2（2＋2e ·e 2）（10＋6e 1·e 2）＝4＋4e 1·e 25＋3e 1·e 2.不妨设t ＝e 1·e 2，则t ≥34，cos 2θ＝4＋4t 5＋3t ，又y ＝4＋4t 5＋3t 在⎣⎢⎡⎭⎪⎫34，＋∞上单调递增．所以cos 2θ≥4＋35＋94＝2829. 所以cos 2θ的最小值为2829. 法三由题意，不妨设e 1＝(1，0)，e 2＝(cos x ，sin x )．因为|2e 1－e 2|≤2，所以（2－cos x ）2＋sin 2x ≤2，得5－4cos x ≤2，即cos x ≥34. 易知a ＝(1＋cos x ，sin x )，b ＝(3＋cos x ，sin x )，所以a ·b ＝(1＋cos x )(3＋cos x )＋sin 2x ＝4＋4cos x ，|a |2＝(1＋cos x )2＋sin 2x ＝2＋2cos x ，|b |2＝(3＋cos x )2＋sin 2x ＝10＋6cos x ，所以cos 2θ＝（a ·b ）2|a |2|b |2＝（4＋4cos x ）2（2＋2cos x ）（10＋6cos x ）＝4＋4cos x5＋3cos x.不妨设m ＝cos x ，则m ≥34，cos 2θ＝4＋4m 5＋3m ，又y ＝4＋4m 5＋3m 在⎣⎢⎡⎭⎪⎫34，＋∞上单调递增，所以cos 2θ≥4＋35＋94＝2829，所以cos 2θ的最小值为2829. (2)由O ，A 1，A 2，A 3四点共圆，且A 1A 2⊥A 2A 3，可知A 1A 3为圆C 的直径，故OA 1→＋OA 3→＝2OC →.由圆C 的标准方程设OA 2→＝(1＋5cos θ，－2＋5sin θ)，又点C (1，－2)，则|OA 1→*OA 2→＋OA 2→*OA 3→|＝|(OA 1→＋OA 3→)*OA 2→|＝2|OC →*OA 2→|＝2|(1＋5cos θ)＋2(－2＋5sin θ)|＝2|5sin(θ＋φ)－3|≤16，其中tan φ＝12，当且仅当θ＝2k π－π2－φ，k ∈Z 时等号成立，所以所求最大值为16.感悟升华此类问题可归结为函数、三角函数求最值、值域问题．【训练3－1】 (1)如图，在扇形OAB 中，OA ＝2，∠AOB ＝90°，M 是OA 的中点，点P 在AB ︵上，则PM →·PB →的最小值为________．(2)(2017·浙江卷)已知向量a ，b 满足|a |＝1，|b |＝2，则|a ＋b |＋|a －b |的最小值是________，最大值是________．答案 (1)4－25 (2)4 2 5 解析(1)如图，以O 为坐标原点，OA→为x 轴的正半轴，OB →为y 轴的正半轴建立平面直角坐标系，则M (1，0)，B (0，2)，设P (2cos θ，2sin θ)，θ∈⎣⎢⎡⎦⎥⎤0，π2，所以PM →·PB→＝(1－2cos θ，－2sin θ)·(－2cos θ，2－2sin θ)＝4－2cos θ－4sin θ＝4－2(cos θ＋2sin θ)＝4－25sin(θ＋φ)⎝ ⎛⎭⎪⎫其中sin φ＝55，cos φ＝255，所以PM →·PB→的最小值为4－2 5.(2)由题意，不妨设b ＝(2，0)，a ＝(cos θ，sin θ)(θ∈[0，2π))，则a ＋b ＝(2＋cos θ，sin θ)，a －b ＝(cos θ－2，sin θ)．令y ＝|a ＋b |＋|a －b |＝（2＋cos θ）2＋sin 2θ＋（cos θ－2）2＋sin 2θ＝5＋4cos θ＋5－4cos θ，则y 2＝10＋225－16cos 2θ∈[16，20]．由此可得(|a ＋b |＋|a －b |)max ＝20＝25， (|a ＋b |＋|a －b |)min ＝16＝4，即|a ＋b |＋|a －b |的最小值是4，最大值是2 5. 角度2 解不等式型【例3－2】 (1)(2021·金丽衢十二校二联)设t ∈R ，已知平面向量a ，b 满足|a |＝2|b |＝2，且a ·b ＝1，向量c ＝x a ＋(t －x )b ，若存在两个不同的实数x ∈[0，t ]，使得c 2－2a ·c ＋3＝0，则实数t ( ) A ．有最大值为2，最小值为32 B ．无最大值，最小值为32 C ．有最大值为2，无最小值 D ．无最大值，最小值为0(2)已知不共线向量OA →，OB →夹角为α，|OA →|＝1，|OB →|＝2，OP →＝(1－t )OA →，OQ →＝tOB →(0≤t ≤1)，|PQ →|在t ＝t 0处取最小值，当0<t 0<15时，则α的取值范围为( ) A.⎝ ⎛⎭⎪⎫0，π3 B.⎝ ⎛⎭⎪⎫π3，π2 C.⎝ ⎛⎭⎪⎫π2，2π3 D.⎝ ⎛⎭⎪⎫2π3，π 答案 (1)B (2)C解析 (1)设向量a ，b 的夹角为θ，∵a ·b ＝|a ||b |cos θ＝2cos θ＝1，∴cos θ＝12.∵θ∈[0，π]，∴θ＝π3.由题意得c ·a ＝[x a ＋(t －x )b ]·a ＝x a 2＋(t －x )b ·a ＝4x ＋t －x ＝3x ＋t ，c 2＝[x a ＋(t －x )b ]2＝x 2a 2＋2x (t －x )a ·b ＋(t －x )2·b 2＝4x 2＋2xt －2x 2＋t 2－2xt ＋x 2＝3x 2＋t 2.存在两个不同的实数x ∈[0，t ]，使得c 2－2a ·c ＋3＝0，即存在两个不同的实数x ∈[0，t ]，使得3x 2－6x ＋t 2－2t ＋3＝0，即f (x )＝3x 2－6x ＋t 2－2t＋3在[0，t ]内有两个不同的零点，则⎩⎪⎨⎪⎧f （0）≥0，f （t ）≥0，Δ>0，0<－－66<t ，即⎩⎨⎧t 2－2t ＋3≥0，4t 2－8t ＋3≥0，0<t <2，t >1，解得t ∈⎣⎢⎡⎭⎪⎫32，2，则实数t 的最小值为32，无最大值，故选B. (2)由题意，不共线向量OA→，OB →夹角为α，|OA →|＝1，|OB →|＝2，OP →＝(1－t )OA →，OQ →＝tOB →(0≤t ≤1)，得PQ →＝OQ →－OP →＝tOB →－(1－t )OA →，所以|PQ →|2＝[tOB →－(1－t )OA →]2＝(5＋4cos α)t 2－2(1＋2cos α)t ＋1，由二次函数的图象和性质知，当t ＝t 0＝1＋2cos α5＋4cos α时，|PQ→|取最小值，即0<1＋2cos α5＋4cos α<15，解得－12<cos α<0，因为α∈[0，π]，所以α∈⎝ ⎛⎭⎪⎫π2，2π3，故选C.感悟升华此类问题最后化为解不等式(组)问题解决．【训练3－2】 (1)(2021·丽水测试)已知|c |＝2，向量b 满足2|b －c |＝b ·c .当b ，c 的夹角最大时，|b |＝________．(2)(2021·金华十校调研)已知平面向量a ，b ，c 满足|a |≤1，|b |≤1，|2c －(a ＋b )|≤|a －b |，则|c |的最大值为________．答案 (1)22 (2) 2解析 (1)设〈b ，c 〉＝θ，则由2|b －c |＝b ·c 得4(b －c )2＝(b ·c )2，即4|b |2sin 2θ－16|b |cos θ＋16＝0，则4cos θ＝|b |sin 2θ＋4|b |≥2|b |sin 2θ·4|b |＝4sin θ，当且仅当|b |sin 2θ＝4|b |，即|b |＝2sin θ时，等号成立，∵4cos θ≥4sin θ，则tan θ＝sin θcos θ≤1，所以θ≤π4，当θ＝π4时，|b |＝2 2.(2)因为|2c －(a ＋b )|≤|a －b |，所以|2c |－|a ＋b |≤|a －b |，即|2c |≤|a ＋b |＋|a －b |，将a ，b 的起点移到同一点，以a ，b 为邻边构造平行四边形，则a ＋b ，a －b 为平行四边形的两条对角线．在平行四边形ABCD 中，|AC |2＝|AB |2＋|AD |2＋2|AB |·|AD |cos ∠BAD ，|BD |2＝|AB |2＋|AD |2－2|AB |·|AD |cos ∠BAD ，则|AC |2＋|BD |2＝2|AB |2＋2|AD |2，易得当|AB |，|AD |最大且|AC |＝|BD |时，|AC |＋|BD |取得最大值，所以当|a |＝1，|b |＝1且|a ＋b |＝|a －b |时，|a ＋b |＋|a －b |取得最大值22，则|2c |≤|a ＋b |＋|a －b |≤22，即|c |≤2，所以|c |的最大值为 2.角度3 重要不等式型【例3－3】 (1)(一题多解)(2021·义乌市联考)已知平面向量a ，b ，c 满足a ＋b ＋c ＝0，a ，b 的夹角为α，|a |＝1，|b |＋|c |＝2，则cos α的取值范围是________． (2)(2016·浙江卷)已知向量a ，b ，|a |＝1，|b |＝2.若对任意单位向量e ，均有|a ·e |＋|b ·e |≤6，则a ·b 的最大值是________．答案 (1)[－1，1] (2)12解析 (1)法一由题意可知－c ＝a ＋b ，则|b |－|a |≤|c |≤|b |＋|a |，所以|b |－1≤2－|b |≤|b |＋1，则12≤|b |≤32.不妨设|b |＝t ，t ∈⎣⎢⎡⎦⎥⎤12，32，则|c |＝2－t .又由－c ＝a ＋b 两边平方得1＋t 2＋2t cos α＝(2－t )2＝4－4t ＋t 2，则cos α＝3－4t 2t ∈[－1，1]．法二如图所示，椭圆方程为x 2＋4y 23＝1.当向量a ，b ，c 共线时，α取最大值或最小值，即cos α＝1或－1，所以cos α∈[－1，1]． (2)由已知可得6≥|a ·e |＋|b ·e |≥|a ·e ＋b ·e |＝|(a ＋b )·e |，由于上式对任意单位向量e 都成立． ∴6≥|a ＋b |成立．∴6≥(a ＋b )2＝a 2＋b 2＋2a ·b ＝12＋22＋2a ·b . 即6≥5＋2a ·b ，∴a ·b ≤12. 感悟升华常用不等式(1)基本不等式：a ＋b ≥2ab (a >0，b >0)； (2)三角不等式：||a |－|b ||≤|a ±b |≤|a |＋|b |； (3)数量积不等式：|a ·b |≤|a ||b |.【训练3－3】 (1)(2021·浙江新高考仿真三)设平面向量a ，b 满足1≤|a |≤2，2≤|b |≤3，则|a ＋b |＋|a －b |的取值范围是________．(2)(一题多解)(2021·浙江五校联考)已知a |＝3，|b |＝|c |＝4，若c ⊥a ，则|a －b －c |的最大值为________．答案 (1)[6，213] (2)9解析 (1)|a ＋b |2＋|a －b |2＝2(|a |2＋|b |2)①，由基本不等式，得|a ＋b |2＋|a －b |2≥（|a ＋b |＋|a －b |）22②.又|a |∈[1，2]，|b |∈[2，3]，由①②得(|a ＋b |＋|a －b |)2≤4(|a |2＋|b |2)≤52，即|a ＋b |＋|a －b |≤213.又由三角不等式有|a ＋b |＋|a －b |≥|(a ＋b )±(a －b )|，即|a ＋b |＋|a －b |≥2|a |，|a ＋b |＋|a －b |≥2|b |，故|a ＋b |＋|a －b |≥6，综上，有6≤|a ＋b |＋|a －b |≤213.(2)法一 |a －b －c |＝a 2＋b 2＋c 2－2a ·b ＋2b ·c ＝41＋2b ·（c －a ）.∵c ⊥a ，∴|c －a |＝5，则b ·(c －a )≤|b ||c －a |＝20，所以|a －b －c |≤41＋40＝9.法二由|a |＝3，|b |＝|c |＝4知，a 在以O 为圆心，3为半径的圆上运动，b ，c 均在以O 为圆心，4为半径的圆上运动，如图，又a ⊥c ，则|a －b －c |＝|(a －c )－b |＝|CA→－OB →|≤|CA →|＋|OB →|＝5＋4＝9. 角度4 轨迹型【例3－4】 (2021·名校仿真训练四)直线ax ＋by ＋c ＝0与圆O ：x 2＋y 2＝4相交于两点M ，N .若c 2＝a 2＋b 2，P 为圆O 上任意一点，则PM →·PN →的取值范围是________．答案 [－2，6] 解析如图，取MN 的中点A ，连接OA ，则OA ⊥MN ，∵c 2＝a 2＋b 2，∴O 点到直线MN 的距离OA ＝|c |a 2＋b2＝1，圆O 的半径r ＝2，∴Rt △AON 中，设∠AON ＝θ，得cos θ＝OA ON ＝12，得θ＝π3，cos ∠MON ＝cos 2θ＝cos 2π3＝－12，由此可得OM →·ON →＝|OM →|·|ON →|cos ∠MON ＝2×2×⎝ ⎛⎭⎪⎫－12＝－2，则PM →·PN →＝(OM →－OP →)·(ON→－OP →)＝OM →·ON →＋OP →2－OP →·(OM →＋ON →)＝－2＋4－2OP →·OA →＝2－2|OP →|·|OA →|·cos ∠AOP ＝2－4cos ∠AOP ，当OP→，OA →同向时，取得最小值2－4＝－2，当OP →，OA →反向时，取得最大值2＋4＝6，则PM →·PN→的取值范围是[－2，6]．感悟升华利用向量及其运算的几何意义，结合轨迹图形求解，并注意分析临界状态．【训练3－4】 (2021·湖州期末质检)正方形ABCD 的边长为2，E ，M 分别为BC ，AB 的中点，点P 是以C 为圆心，CE 为半径的圆上的动点，点N 在正方形ABCD 的边上运动，则PM →·PN →的最小值是________．答案 1－ 5 解析由题意得PM →·PN →＝(PC →＋CM →)·(PC →＋CN →)＝1＋PC →·CM →＋(PC →＋CM →)·CN →＝1＋PC →·CM →＋PM →·CN →.由图易得向量PM →，CN →的夹角恒为锐角，则PM →·CN →≥0，则当点N 与点C 重合，点P 为CM 与圆C 的交点时，PC →·CM →取得最小值－5，PM →·CN →取得最小值0，此时PM →·PN →取得最小值1－ 5. 角度5 投影与函数分析型【例3－5】 (1)如图是蜂巢结构图的一部分，正六边形的边长均为1，正六边形的顶点称为“晶格点”．若A ，B ，C ，D 四点均位于图中的“晶格点”处，且A ，B 的位置如图所示，则AB →·CD→的最大值为________．(2)(2019·浙江卷)已知正方形ABCD 的边长为1，当每个λi (i ＝1，2，3，4，5，6)取遍±1时，|λ1AB →＋λ2BC →＋λ3CD →＋λ4DA →＋λ5AC →＋λ6BD →|的最小值是________，最大值是________．答案 (1)24 (2)0 2 5解析 (1)先建立平面直角坐标系如图，因为正六边形的边长均为1，所以B (0，0)，A ⎝ ⎛⎭⎪⎫32，92，当CD→在AB →方向上的投影最大时，AB →·CD →最大，此时取C (0，5)，D (－3，0)，即(AB →·CD →)max ＝⎝ ⎛⎭⎪⎫－32，－92·(－3，－5)＝32＋452＝24. (2)如图，以A 为原点，AB 所在直线为x 轴，AD 所在直线为y 轴建立平面直角坐标系，则AB→＝(1，0)，AD →＝(0，1)．设a ＝λ1AB →＋λ2BC →＋λ3CD →＋λ4DA →＋λ5AC →＋λ6BD →＝λ1AB →＋λ2AD →－λ3AB →－λ4AD →＋λ5(AB →＋AD →)＋λ6(AD →－AB →) ＝(λ1－λ3＋λ5－λ6)AB →＋(λ2－λ4＋λ5＋λ6)AD → ＝(λ1－λ3＋λ5－λ6，λ2－λ4＋λ5＋λ6)．故|a|＝（λ1－λ3＋λ5－λ6）2＋（λ2－λ4＋λ5＋λ6）2. ∵λi (i ＝1，2，3，4，5，6)取遍±1，∴当λ1－λ3＋λ5－λ6＝0，λ2－λ4＋λ5＋λ6＝0(λ1＝λ3＝λ4＝λ5＝λ6＝1，λ2＝－1)时，|λ1AB →＋λ2BC →＋λ3CD →＋λ4DA →＋λ5AC →＋λ6BD →|取得最小值0.考虑到λ5－λ6，λ5＋λ6有相关性，要确保所求模最大，只需使|λ1－λ3＋λ5－λ6|，|λ2－λ4＋λ5＋λ6|尽可能取到最大值，即当λ1－λ3＋λ5－λ6＝2，λ2－λ4＋λ5＋λ6＝4(λ1＝λ2＝λ5＝λ6＝1，λ3＝λ4＝－1)时可取到最大值，∴|λ1AB →＋λ2BC →＋λ3CD →＋λ4DA →＋λ5AC →＋λ6BD →|的最大值为4＋16＝2 5. 感悟升华 (1)关于数量积问题常用投影分析法；(2)当向量线性表达式系数较多且给出其取值范围时，常用系数分析法．【训练3－5】 (1)已知正三角形ABC 的边长为4，O 是平面ABC 内的动点，且∠AOB ＝π3，则OC →·AB →的最大值为________． (2)(2021·浙江名师预测一)已知等边△ABC 的边长为1，当每个λi (i ＝1，2，3)在{－1，0，1}中取值时，则|λ1AB →－λ2BC →＋λ3CA →|的最小值是________，最大值是________．答案 (1)1633 (2)0 2解析 (1)如图，圆E 2为△ABC 的外接圆，圆E 1与圆E 2关于直线AB 对称，由题意知O 在圆E 1，E 2的优弧AB ︵上(圆E 1，E 2半径相等)，设AB 的中点为D ，OC →·AB →＝(DC →－DO →)·AB→＝BA →·DO →＝|BA →|·|DO →|·cos ∠ADO ，易知DO →在BA →方向上的射影最大时，OC →·AB →取得最大值，易知DO →在BA →方向上射影的最大值为△ABO 外接圆的半径，故所求最大值为4×42sin π3＝1633. (2)当λi (i ＝1，2，3)中三个均为0时，|λ1AB →－λ2BC →＋λ3CA →|＝0；当λi (i ＝1，2，3)中恰有2个为0时，|λ1AB →－λ2BC →＋λ3CA →|≤1；当λi (i ＝1，2，3)中恰有1个为0时，1≤|λ1AB →－λ2BC →＋λ3CA →|≤3；当λi (i ＝1，2，3)中均不为0时，0≤|λ1AB →－λ2BC →＋λ3CA →|≤2，综上所述，|λ1AB →－λ2BC →＋λ3CA →|的最小值是0，最大值是2.一、选择题1．若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则OP →·FP →的最大值为( ) A ．2 B ．3 C ．6 D ．8 答案 C解析如图，由已知|OF |＝1，取FO 中点E ，连接PE ，由极化恒等式得OP →·FP→＝|PE |2－14|OF |2＝|PE |2－14， ∵|PE |2max ＝254，∴OP →·FP→的最大值为6. 2.如图，菱形ABCD 的边长为2，∠BAD ＝60°，M 为DC 的中点，若N 为菱形内任意一点(含边界)，则AM →·AN→的最大值为( )A ．3B ．2 3C ．6D ．9 答案 D解析由平面向量数量积的几何意义知，AM →·AN →等于|AM →|与AN →在AM →方向上的投影之积，所以(AM →·AN →)max ＝AM →·AC →＝⎝ ⎛⎭⎪⎫12AB →＋AD →·(AB →＋AD →)＝12AB →2＋AD →2＋32AB →·AD→＝9.3．(一题多解)(2020·新高考山东卷)已知P 是边长为2的正六边形ABCDEF 内的一点，则AP →·AB→的取值范围是( )A ．(－2，6)B ．(－6，2)C ．(－2，4)D ．(－4，6) 答案 A解析法一如图，取A 为坐标原点，AB 所在直线为x 轴建立平面直角坐标系，则A (0，0)，B (2，0)，C (3，3)，F (－1，3)．设P (x ，y )，则AP →＝(x ，y )， AB→＝(2，0)，且－1＜x ＜3. 所以AP →·AB →＝(x ，y )·(2，0)＝2x ∈(－2，6)．故选A.法二 AP →·AB →＝|AP →|·|AB →|·cos ∠P AB ＝2|AP →|cos ∠P AB ，又|AP →|cos ∠P AB 表示AP →在AB→方向上的投影，所以结合图形可知，当P 与C 重合时投影最大．当P 与F 重合时投影最小．又AC →·AB →＝23×2×cos 30°＝6，AF →·AB →＝2×2×cos 120°＝－2，故当点P 在正六边形ABCDEF 内部运动时，AP →·AB →∈(－2，6)．故选A. 4．(2021·镇海中学检测)已知向量m ，n 满足(m ＋n )·(m －2n )＝0，(m －n )·(m ＋2n )＋1＝0，则|n |的最小值为( ) A.14 B.12 C.22 D ．1 答案 C解析因为(m ＋n )·(m －2n )＝0，所以m 2－m ·n －2n 2＝0.因为(m －n )·(m ＋2n )＋1＝0，所以m 2＋m ·n －2n 2＋1＝0，所以m ·n ＝－12，且m 2＝2n 2－12>0.因为(m ·n )2＝14≤|m |2·|n |2＝⎝ ⎛⎭⎪⎫2|n |2－12·|n |2，解得|n |2≥12，所以|n |≥22，即|n |的最小值为22，故选C.5.如图，△BCD 与△ABC 的面积之比为2，点P 是区域ABDC 内的任一点(含边界)．且AP →＝λAB →＋μAC →，则λ＋μ的取值范围是( )A ．[0，1]B ．[0，2]C ．[0，3]D ．[0，4] 答案 C解析过点P 作GH ∥BC ，交AC 、AB 的延长线于G ，H ，则AP→＝xAG →＋yAH →，且x ＋y ＝1，当点P 位于D 点时，G ，H 分别位于C ′，B ′，∵△BCD 与△ABC 的面积之比为2，∴AC ′＝3AC ，AB ′＝3AB ，∴OP →＝xAG →＋yAH →＝xAC ′→＋yAB ′→＝x ·3·AC →＋y ·3·AB →＝λAB →＋μAC →，所以λ＝3y ，μ＝3x ⇒λ＋μ＝3x ＋3y ＝3.当点P 位于A 点时，显然有λ＋μ＝0，选C.6．(一题多解)已知点C 为扇形AOB 的弧AB 上任意一点，且∠AOB ＝120°，若OC →＝λOA→＋μOB →(λ，μ∈R )，则λ＋μ的取值范围是( ) A ．[－2，2] B ．(1，2] C ．[1，2] D ．[1，2] 答案 D解析法一 (常规方法)设半径为1，由已知可设OB 为x 轴的正半轴，O 为坐标原点，建立直角坐标系，其中A ⎝ ⎛⎭⎪⎫－12，32；B (1，0)；C (cos θ，sin θ)(其中∠BOC ＝θ⎝ ⎛⎭⎪⎫0≤θ≤2π3，有OC→＝λOA →＋μOB →(λ，μ∈R )，即(cos θ，sin θ)＝λ⎝ ⎛⎭⎪⎫－12，32＋μ(1，0)，整理得－12λ＋μ＝cos θ；32λ＝sin θ，解得λ＝2sin θ3，μ＝cos θ＋sin θ3，则λ＋μ＝2sin θ3＋cos θ＋sin θ3＝3sin θ＋cos θ＝2sin ⎝ ⎛⎭⎪⎫θ＋π6，θ∈⎣⎢⎡⎦⎥⎤0，2π3，易得λ＋μ∈[1，2]．法二 (等和线定理) 设λ＋μ＝k ，当C 位于A 或B 时，A 、B 、C 三点共线，所以k ＝λ＋μ＝1，当点运动到AB ︵的中点C 时，k ＝λ＋μ＝2，∴λ＋μ∈[1，2]．7．设θ为两个非零向量a ，b 的夹角，已知对任意实数t ，|b ＋t a |的最小值为1，则( )A ．若θ确定，则|a |唯一确定B ．若θ确定，则|b |唯一确定C ．若|a |确定，则θ唯一确定D ．若|b |确定，则θ唯一确定答案 B解析 |b ＋t a |2＝b 2＋2a ·b ·t ＋t 2a 2 ＝|a |2t 2＋2|a |·|b |cos θ·t ＋|b |2. 因为|b ＋t a |min ＝1，所以4|a |2·|b |2－4|a |2·|b |2cos 2θ4|a |2＝|b |2(1－cos 2θ)＝1.所以|b |2sin 2θ＝1，所以|b |sin θ＝1，即|b |＝1sin θ. 即θ确定，|b |唯一确定．8．(2021·龙湾中学检测)已知平面向量a ，b ，c 满足|a |＝|b |＝a ·b ＝2，(a －c )·(b －2c )＝1，则|b －c |的最小值为( ) A.7－52 B.7－32 C.5－32 D.3－12答案 A解析由|a |＝|b |＝a ·b ＝2得〈a ，b 〉＝π3，则不妨设a ＝OA →＝(1，3)，b ＝OB →＝(2，0)，c ＝OC→＝(x ，y )，则a －c ＝(1－x ，3－y )，b －2c ＝(2－2x ，－2y )．由(a －c )·(b －2c )＝1得(x －1)2＋⎝ ⎛⎭⎪⎫y －322＝54，则点C (x ，y )的轨迹是以⎝⎛⎭⎪⎫1，32为圆心，52为半径的圆，则|b －c |＝|CB →|的最小值为（2－1）2＋⎝⎛⎭⎪⎫0－322－52＝7－52，故选A.9．(2021·武汉质检)已知等边△ABC 内接于圆Γ：x 2＋y 2＝1，且P 是圆Γ上一点，则P A →·(PB→＋PC →)的最大值是( )A. 2 B ．1 C. 3 D ．2 答案 D 解析设BC 的中点为E ，连接AE ，向量PO→，OE →的夹角为θ.因为等边△ABC 内接于圆Γ：x 2＋y 2＝1，所以点O 在AE 上，且OA ＝2OE ＝1，所以P A →·(PB →＋PC →)＝P A →·2PE →＝2(PO →＋OA →)·(PO →＋OE →)＝2[PO →2＋PO →·(OA →＋OE →)＋OA →·OE →]＝2[PO →2＋PO →·(－OE →)－2OE →2]＝2⎣⎢⎡⎦⎥⎤1－1×12cos θ－2×⎝ ⎛⎭⎪⎫122＝1－cos θ，所以当cos θ＝－1，∴〈PO→，OE →〉＝π，∴〈OP →，OE →〉＝0，即点P 为AE 的延长线与圆的交点时，P A ·(PB →＋PC →)取最大值2，故选D.10．(2021·名校冲刺卷三)已知|a |＝|b |＝|c |＝2，且a ·b ＝2，(a －c )·(b －c )≤0，则|a ＋b ＋c |( )A ．有最小值23－2，最大值23＋2B ．有最小值23－2，最大值27C ．有最小值27，最大值23＋2D ．有最小值23－2，最大值2 答案 C 解析如图所示，令a ＝OA →，b ＝OB →，c ＝OC →，由a ·b ＝2，|a |＝|b |＝|c |＝2可得∠AOB ＝π3.又(a －c )·(b －c )≤0，所以点C 在以AB 为直径的圆内，|a ＋b ＋c |＝|OD →＋OC →|，所以|a ＋b ＋c |的最大值是OC→，OD →同向为23＋2，最小值是点C 与点A 或点B 重合为27，故选C. 11．已知m ，n 是两个非零向量，且|m |＝1，|m ＋2n |＝3，则|m ＋n|＋|n|的最大值为( )A. 5B.10 C ．4 D ．5答案 B解析因为(m ＋2n )2＝4n 2＋4m ·n ＋1＝9，所以n 2＋m ·n ＝2，所以(m ＋n )2＝m 2＋2m ·n ＋n 2＝5－n 2，所以|m ＋n |＋|n |＝5－|n |2＋|n |.令|n |＝x (0<x ≤5)，f (x )＝5－x 2＋x ，则f ′(x )＝－2x 25－x2＋1.由f ′(x )＝0，得x ＝102，所以当0<x <102时，f ′(x )>0时，当102<x ≤5时，f ′(x )<0，所以函数f (x )在⎝ ⎛⎭⎪⎫0，102上单调递增，在⎝ ⎛⎦⎥⎤102，5上单调递减，所以f (x )max ＝f ⎝ ⎛⎭⎪⎫102＝10，故选B. 12．(2021·北京海淀区检测)已知点M 在圆C 1：(x －1)2＋(y －1)2＝1上，点N 在圆C 2：(x ＋1)2＋(y ＋1)2＝1上，则下列说法错误的是( )A.OM →·ON→的取值范围为[－3－22，0] B ．|OM→＋ON →|的取值范围为[0，22] C ．|OM→－ON →|的取值范围为[22－2，22＋2] D ．若OM→＝λON →，则实数λ的取值范围为[－3－22，－3＋22] 答案 B解析∵M 在圆C 1上，点N 在圆C 2上，∴∠MON ≥90°，∴OM →·ON →≤0，又|OM→|≤2＋1，|ON →|≤2＋1， ∴当|OM→|＝2＋1，|ON →|＝2＋1时， OM →·ON→取得最小值， (2＋1)2cos π＝－3－22，故A 正确；设M (1＋cos α，1＋sin α)，N (－1＋cos β，－1＋sin β)，则OM→＋ON →＝(cos α＋cos β，sin α＋sin β)， ∴|OM→＋ON →|2＝2cos αcos β＋2sin αsin β＋2 ＝2cos (α－β)＋2，∴0≤|OM→＋ON →|≤2，故B 错误； ∵两圆外离，半径为1，|C 1C 2|＝22，∴22－2≤|MN |≤22＋2，即22－2≤|OM→－ON →|≤22＋2，故C 正确； ∵2－1≤|OM→|≤2＋1，2－1≤|ON →|≤2＋1， ∴当OM →＝λON →时，2－12＋1≤－λ≤2＋12－1，解得－3－22≤λ≤－3＋22，故D 正确．13．已知向量OA →，OB →满足|OA →|＝|OB →|＝2，OA →·OB →＝2，若OC →＝λOA →＋μOB →(λ，μ∈R )，且λ＋μ＝1，则|OC→|的最小值为( ) A ．1 B.52 C. 2 D. 3答案 D解析 |OC →|2＝(λOA →＋μOB →)2＝[λOA →＋(1－λ)OB →]2＝4λ2＋4(1－λ)2＋2λ(1－λ)OA →·OB→，因为OA →·OB →＝2，所以|OC →|2＝4λ2＋4(1－λ)2＋2λ(1－λ)·2＝4λ2－4λ＋4＝4⎝ ⎛⎭⎪⎫λ－122＋3，当λ＝12时，|OC →|取得最小值 3.二、填空题14．在△ABC 中，AB ＝6，AC ＝5，A ＝120°，动点P 在以C 为圆心，2为半径的圆上，则P A →·PB→的最小值为________．答案 16解析设AB 的中点为M ，则P A →·PB →＝⎣⎢⎡⎦⎥⎤12（P A →＋PB →）2－⎣⎢⎡⎦⎥⎤12（P A →－PB →）2＝PM →2－MA→2＝PM →2－9，所以要求P A →·PB→的最小值，只需求|PM →|的最小值，显然当点P 为线段MC 与圆的交点时，|PM→|取得最小值，最小值为|MC |－2.在△AMC 中，由余弦定理得|MC |2＝32＋52－2×3×5×cos 120°＝49，所以|MC |＝7，所以|PM →|的最小值为5，则P A →·PB→的最小值为16.15．(2021·宁波适考)在Rt △ABC 中，CA ＝CB ＝2，M ，N 是斜边AB 上的两个动点，且MN ＝2，则CM →·CN →的取值范围是________．答案 ⎣⎢⎡⎦⎥⎤32，2 解析取MN 的中点为P ，由极化恒等式得CM →·CN →＝14[(2CP →)2－MN →2]＝CP →2－12.问题转化为求|CP →|的取值范围，当P 为AB 的中点时，|CP →|取最小值为2，则CM →·CN→的最小值为32；当M 与A (或N 与B )重合时，|CP →|取最大值为102，则CM →·CN →的最大值为2，所以CM →·CN →的取值范围是⎣⎢⎡⎦⎥⎤32，2. 16．(2021·浙江新高考仿真二)若非零向量a 和b 满足|a ＋b |＝|b |＝2，则|a |的取值范围是________，|a －b |的取值范围是________．答案 (0，4] [2，6]解析因为||a ＋b |－|b ||≤|a |＝|a ＋b －b |≤|a ＋b |＋|b |＝4，又a 是非零向量，所以|a |的取值范围是(0，4]，因为|a －b |＋|a ＋b |≥2|b |＝|(a ＋b )－(a －b )|≥||a －b |－|a ＋b ||，所以－4≤|a －b |－|a ＋b |≤4，|a －b |＋|a ＋b |≥4，又|a ＋b |＝2，解得|a －b |的取值范围是[2，6]．17．(2021·稽阳联考)在Rt △ABC 中，∠B ＝90°，BC ＝2，AB ＝1，D 为BC 的中点，E 在斜边AC 上，若AE →＝2EC →，则DE →·AC→＝________．答案 13解析如图，以B 为坐标原点，AB 所在直线为x 轴，BC 所在直线为y 轴，建立平面直角坐标系，则B (0，0)，A (1，0)，C (0，2)，所以AC→＝(－1，2)．因为D 为BC 的中点，所以D (0，1)，因为AE →＝2EC →，所以E ⎝ ⎛⎭⎪⎫13，43，所以DE →＝⎝ ⎛⎭⎪⎫13，13，所以DE →·AC →＝⎝ ⎛⎭⎪⎫13，13·(－1，2)＝－13＋23＝13. 18．(2021·镇海中学检测)已知向量a ，b ，c 满足a ＋b ＋c ＝0，|c |＝23，c 与a －b 所成的角为5π6，若t ∈R ，则|t a ＋(1－t )b |的最小值是________，此时|t a ＋(1－t )b －c |＝________．答案 32 372解析因为a ＋b ＋c ＝0，且|c |＝23，所以|a ＋b |＝2 3.因为c 与a －b 所成的角为5π6，所以a ＋b 与a －b 所成的角为π6.设d ＝t a ＋(1－t )b ，则当三个向量的起点在一起时，终点在a －b 所在直线上，|d |有最小值，所以|t a ＋(1－t )b |min ＝|a ＋b |2·sin 30°＝32，此时|t a ＋(1－t )b －c |＝12＋34＋23×32＝372.。

2021--平面向量--高考极化恒等式在向量问题中的应用

高考极化恒等式在向量问题中的应用大招系列一、秒杀公式的讲解：1.极化恒等式：设a ，b 为两个平面向量，则有恒等式：2214a b a b a b2.极化恒等式几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14，即：2214a b AD AB AD AB 或2214a b AC BD平行四边形模式：2214AB AD和对角线差对角线或2214AB AD AC BD3. 极化恒等式的三角形模式：在ABC 中，记M 为BC 的中点，则2214AB AC AM DB二、以例讲法典型类题 1 〖例1〗(2012浙江文)在ABC 中，M 是BC 的中点，3AM ，10BC ，则AB AC.〖例2〗(2007天津文)在ABC 中，2AB ，3AC ，D 是边BC 的中点，则AD BC.〖例3〗点P 是棱长为1的正方体1111ABCD A B C D 的底面1111A B C D 上一点，则PA PC的取值范围是；〖例4〗(2015新课标1)已知00(,)M x y 是双曲线C ：2212x y 上的一点，1F ，2F 是C 的两个焦点，若120MF MF，则0y 的取值范围是.A ,33 .B ,66 .C ,33 .D ,33〖例5〗(2010福建文数)若点O 和点F 分别为椭圆22143x y 的中心和左焦点，点P 为椭圆上的任意一点，则OP FP的最大值为.A 2 .B 3 .C 6 .D 8〖例6〗已知A ，B 是圆221x y 上的两个点，P 是AB 线段上的动点，当AOB 的面积最大时，则2AO AP AP 的最大值是.A 1 .B 0 .C 18 .D 12〖例7〗(2017新课标Ⅱ理)已知ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC的最小值是.A 2 .B 32 .C 43.D 1〖例8〗(2010全国Ⅰ理)已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为两切点，那么PA PB的最小值为( )．.A 4 .B 3 .C 4 .D 3〖例9〗(2013浙江理)设ABC ，0P 是边AB 上一定点，满足014P B AB，且对于边AB 上任一点P ，恒有00PB PC P B P C，则( )．.A 90BAC .B 90BAC .C AB AC .D AC BC高考数学讲义新华教育张老师：150****2680〖例10〗(2016江苏)如图，在ABC 中，D 是BC 的中点，E ，F 是AD 上的两个三等分点，4BA CA， 1BF CF ，则BE CE的值是 ▲ .〖例11〗(2020天津)如图，在四边形ABCD 中，60B，3AB ，6BC ，且AD BC ，32AD AB ，则实数的值为，若M ，N 是线段BC 上的动点，且1MN ，则DM DN的最小值为 .NMDCBA高考数学讲义新华教育张老师：150****2680『强化练习』在Rt ABC 中，2CA CB ,M ，N 是斜边AB上的两个动点，且MN ，CM CN的取值范围是；正方体1111ABCD A B C D 的棱长为2，MN 是它内切球的一条弦（把球面上任意2个点之间的线段称为球的弦），P 为正方体表面积上的动点，当弦MN 最大时，PM PN的最大值为；(2011上海理)在正三角形ABC 中，D 是BC 上的点，3,1AB BD ，则AB AD；(2010福建理数)若点O 和点(2,0)F 分别为双曲线2221x y a (0a )的中心和左焦点，点P 为双曲线右支上的任意一点，则OP FP的取值范围为( ).A 3 .B3 .C 7,4 .D 7,4(2018天津理数)如图，在平面四边形ABCD 中，AB BC ，AD CD ，120BAD ，1AB AD ．若点E 为边CD 上的动点，则AE BE 的最小值为.A 2116 .B 32 .C 2516.D 3 E DCBA。

“四大妙法”,剖析向量的秒杀体系 (学生版)

“四大妙法”，剖析向量的秒杀体系目录一、重难点题型方法妙法一：奔驰定理与四心问题题型一：奔驰定理题型二：重心问题题型三：内心问题题型四：外心问题题型五：垂心问题妙法二：极化恒等式题型六：极化恒等式的应用妙法三：隐圆题型七：定点定长；定弦定角；对角互补；到两定点数量积(平方和)定值题型八：阿波罗尼斯圆妙法四：等和线题型九：等和线的应用二针对性巩固练习重难点题型方法妙法一：奔驰定理与四心问题题型一：奔驰定理【典例分析】例1.(2023·全国·高三专题练习)“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车(Mercedesbenz )的log o 很相似，故形象地称其为“奔驰定理”．奔驰定理：已知O 是△ABC 内的一点，△BOC ,△AOC ,△AOB 的面积分别为S A ,S B ,S C ，则有S A ⋅OA +S B ⋅OB +S C ⋅OC =0 ．设O 是锐角△ABC 内的一点，∠BAC ,∠ABC ,∠ACB 分别是△ABC 的三个内角，以下命题不正确的有( )A.若OA +OB +OC =0 ，则O 为△ABC 的重心B.若OA +2OB +3OC =0 ，则S A :S B :S C =1:2:3C.若OA =OB =2,∠AOB =5π6，2OA +3OB +4OC =0 ，则S △ABC =92D.若O 为△ABC 的垂心，则tan ∠BAC ⋅OA +tan ∠ABC ⋅OB +tan ∠ACB ⋅OC =0例2.(2023·全国·高三专题练习)奔驰定理：已知O 是△ABC 内的一点，△BOC ，△AOC ，△AOB 的面积分别为S A ，S B ，S C ，则S A ⋅OA +S B ⋅OB +S C ⋅OC =0 .“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车的log o 很相似，故形象地称其为“奔驰定理”.设O 为三角形ABC 内一点，且满足：OA +2OB +3OC =3AB +2BC +CA ，则S △AOB S △ABC=( )A.25B.12C.16D.13【方法技巧总结】1. 奔驰定理：S A ⋅OA +S B ⋅OB +S C ⋅OC =0 ，则△AOB 、△AOC 、△BOC 的面积之比等于λ3:λ2:λ1【变式训练】1.(2023春·湖南常德·高一临澧县第一中学校考阶段练习)如图.P 为△ABC 内任意一点，角A ,B ,C 的对边分别为a ,b ,c ，总有优美等式S △PBC PA +S △PAC PB +S △PAB PC =0 成立，因该图形酯似奔驰汽车车标，故又称为奔驰定理.则以下命题是真命题的有()A.若P 是△ABC 的重心，则有PA +PB +PC =0B.若aPA +bPB +cPC =0 成立，则P 是△ABC 的内心C.若AP =25AB +15AC ，则S △ABP :S △ABC =2:5D.若P 是△ABC 的外心，A =π4，PA =mPB +nPC ，则m +n ∈-2,1 2.(2023春·浙江嘉兴·高一校考阶段练习)“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”(Mercedesbenz )的log o 很相似，故形象地称其为“奔驰定理”.奔驰定理：已知O 是△ABC 内的一点，△BOC ，△AOC ，△AOB 的面积分别为S A ，S B ，S C ，则S A ⋅OA +S B ⋅OB +S C ⋅OC =0 .若O 是锐角△ABC 内的一点，A ，B ，C 是△ABC 的三个内角，且点O 满足OA ⋅OB=OB ⋅OC =OA ⋅OC .则()A.O 为△ABC 的外心B.∠BOC +A =πC.OA :OB :OC =cos A :cos B :cos CD.tan A ⋅OA +tan B ⋅OB +tan C ⋅OC =0题型二：重心问题【典例分析】例1.(四川省达州市2023届高三二模数学(理科))如图，在△ABC 中，AB =3，∠ABC =π4，BA ⋅BC =18，平面ABC 内的点D 、E 在直线AB 两侧，△ABD 与△BCE 都是以B 为直角顶点的等腰直角三角形，O 1、O 2分别是△ABD 、△BCE 的重心.则O 1O 2=( )A.26B.33C.5D.6例2.(2023·全国·高三专题练习)如图所示，已知点G 是△ABC 的重心，过点G 作直线分别与AB ，AC 两边交于M ，N 两点，设xAB =AM ，yAC =AN ，则1x +1y的值为( )A.3B.4C.5D.6【方法技巧总结】1.O 是△ABC 的重心：S △BOC :S △COA :S △A 0B =1:1:1⇔OA +OB +OC =0 ．【变式训练】1.(2022春·浙江·高二统考学业考试)在△ABC 中，设AD =2DB ，BE =2EC ，CF =λFA ，其中λ∈R .若△DEF 和△ABC 的重心重合，则λ=()A.12 B.1 C.32 D.22.(2022春·四川攀枝花·高一攀枝花七中校考阶段练习)已知△ABC 的三个内角分别为A ,B ,C ,O 为平面内任意一点，动点Р满足OP =OA +λAB AB sin B +AC AC sin C,λ∈0,+∞ 则动点P 的轨迹一定经过△ABC 的()A.重心 B.垂心 C.内心 D.外心题型三：内心问题【典例分析】例1.(2003·江苏·高考真题)O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足OP =OA +λAB |AB |+AC |AC |，λ∈[0,+∞)，则P 的轨迹一定通过△ABC 的()A.外心 B.内心 C.重心 D.垂心例2.(2023·全国·高三专题练习)在△ABC 中，cos A =34，O 为△ABC 的内心，若AO =xAB +yAC x ,y ∈R ，则x +y 的最大值为()A.23B.6-65C.7-76D.8-227【方法技巧总结】1.O 是△ABC 的内心：S △B 0C :S △COA :S △AOB =a :b :c ⇔aOA +bOB +cOC =0 ．2.内心在向量AB AB +AC AC所在的直线上；AB ⋅PC +BC ⋅PC +CA ⋅PB =0 ⇔P 为△ABC 的内心.【变式训练】1.(2022·全国·高三专题练习)平面上有△ABC 及其内一点O ，构成如图所示图形，若将△OAB ，△OBC ， △OCA 的面积分别记作S c ，S a ，S b ，则有关系式S a ⋅OA +S b ⋅OB +S c ⋅OC =0 ．因图形和奔驰车的log o 很相似，常把上述结论称为“奔驰定理”．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若满足a ⋅OA +b ⋅OB +c ⋅OC =0 ，则O 为△ABC 的()A.外心B.内心C.重心D.垂心2.(2023·全国·高一专题练习)已知在△ABC 中，AB =BC =3，AC =4，设O 是△ABC 的内心，若AO =mAB +nAC ，则m n=( )A.34 B.916 C.43 D.169题型四：外心问题【典例分析】例1.(2023·全国·高一专题练习)已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP =OB +OC 2+λAB AB cos B +AC ACcos C ，λ∈(0，+∞)，则动点P 的轨迹一定通过△ABC 的()A.重心 B.外心 C.内心 D.垂心例2.(2023·重庆·统考二模)已知点O 是△ABC 的外心，AB =6，BC =8，B =2π3，若BO =xBA +yBC ，则3x +4y =()A.5B.6C.7D.8【方法技巧总结】1.O 是△ABC 的外心：S △B 0C :S △COA :S △AOB =sin2A :sin2B :sin2C ⇔sin2AOA +sin2BOB +sin2COC =0 .2.PA =PB =PC ⇔P 为△ABC 的外心.【变式训练】1.(2022·全国·高三专题练习)如图，△ABC 中，AB =2，AC =3，∠BAC =π3，O 为△ABC 外心，且AO =mAB +nAC ，则m +n 的值为()A.23B.1118C.79D.13182.(2023·北京·北京市八一中学校考模拟预测)已知O 是△ABC 的外心，外接圆半径为2，且满足2AO =AB +AC ，若BA 在BC 上的投影向量为34BC ，则AO ⋅BC =( )A.-4 B.-2 C.0 D.2题型五：垂心问题【典例分析】例1.(2020春·天津和平·高一耀华中学校考阶段练习)已知点O 为△ABC 所在平面内一点，且OA 2+BC 2=OB 2+CA 2=OC 2+AB 2，则O 一定为△ABC 的()A.外心B.内心C.垂心D.重心例2.(2023·全国·高三专题练习)设O 是△ABC 所在平面上一点，点H 是△ABC 的垂心，满足OA +OB +OC =OH ，且3⋅OA +OB +2⋅OC =0 ，则角A 的大小是()A.3π4B.π3C.π2D.π4【方法技巧总结】1.O 是△ABC 的垂心：S △B 0C :S △COA :S △AOB =tan A :tan B :tan C ⇔tan AOA +tan BOB +tan COC =0 ．2.PA ⋅PB =PB ⋅PC =PC ⋅PA ⇔P 为△ABC 的垂心.【变式训练】1.(2023春·重庆南岸·高一重庆市辅仁中学校校考阶段练习)已知O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足OP =OA +λAB AB cos B +AC AC cos C，λ∈0,+∞ ，则动点P 的轨迹一定通过△ABC 的()A.重心 B.外心C.内心D.垂心2.(2023·全国·高三专题练习)已知H 为△ABC 的垂心，若AH =13AB +25AC ，则sin ∠BAC =( )A.155 B.105 C.63 D.33妙法二：极化恒等式题型六：极化恒等式的应用【典例分析】例1.(2023·全国·高三专题练习)已知正方形ABCD 的边长为2,MN 是它的外接圆的一条弦，点P 为正方形四条边上的动点，当弦MN 的长度最大时，PM ⋅PN 的取值范围是()A.-1,0B.0,2C.1,2D.-1,1例2.(2023春·江苏南京·高一校考期中)如图所示，矩形ABCD 的边AB =2，AD =1，以点C 为圆心，CB 为半径的圆与CD 交于点E ，若点P 是圆弧EB (含端点B ､E )上的一点，则PA ⋅PB 的取值范围是()A.0,2-1B.1-2,0C.0,2-22D.2-22,0 【方法技巧总结】1.极化恒等式：14a +b 2-a -b 2 ①平行四边形模式：a ⋅b =14AC 2-DB 2 几何意义：向量的数量积可以表示为以这组向量为邻边平行四边形的“和对角线”与“差对角线”平方差的14.②三角形模式：a ⋅b =AM 2-14DB 2(M 为BD 的中点)【变式训练】1.(2021春·广东东莞·高一东莞市东莞中学松山湖学校校考阶段练习)半径为2的圆O 上有三点A 、B 、C 满足OA +AB +AC =0 ，点P 是圆内一点，则PA ⋅PO +PB ⋅PC 的取值范围为()A.[-4，14)B.[0，4)C.[4，14]D.[4，16]2.(2023·山东潍坊·校考模拟预测)如图所示，△ABC 是边长为8的等边三角形，P 为AC 边上的一个动点，EF 是以B 为圆心，3为半径的圆的直径，则PE ⋅PF 的取值范围是( )A.28,46B.32,58C.39,55D.42,60妙法三：隐圆题型七：定点定长；定弦定角；对角互补；到两定点数量积(平方和)定值【典例分析】例1.(2018秋·江西·高一统考期末)已知向量a ,b 满足a =3, b =2，且a ⊥b ，若向量m 满足a +b -m≤2，则m 的取值范围是A.13-2,13+3B.13-2,13+2C.2,13+3D.2,13+2例2.(2020春·四川成都·高三石室中学校考阶段练习)已知单位向量a ，b 满足2a -b =2，若存在向量c ，使得c -2a ⋅c -b =0，则c 的取值范围是( )A.62,62+1 B.62-1,62 C.62-1,62+1 D.6-1,6+1【方法技巧总结】1.若问题中给出两个运动着向量的夹角为定值，或者间接给出夹角为定值，或某两个向量的和(或差)的模为定值等条件，求有关向量模或夹角的范围等问题可以试着通过寻找向量终点所在的“隐藏圆”来解决问题。

第12讲等和线极化恒等式(学生版)

第12讲等和线、极化恒等式、三角形四心题型一等和线定理应用例1 （2017新课标Ⅲ）在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB ADλμ=+，则λμ+的最大值为（）A ．3B ．22 C ．5 D ．2例2 给定两个长度为1的平面向量OA →和OB →，它们的夹角为2π3.如图所示，点C 在以O 为圆心的AB 上运动．若OC →＝xOA →＋yOB →，其中x ，y ∈R ，求x ＋y 的最大值．例3 (2020·杭州五校联盟一诊)在矩形ABCD 中，AB ＝5，BC ＝3，P 为矩形内一点，且AP ＝52，若AP →＝λAB →＋μAD →(λ，μ∈R )，则5λ＋3μ的最大值为______． [玩转跟踪]1.(2020·菏泽一诊)如图,在扇形OAB 中,60AOB ︒∠=,C 为弧AB 上的一个动点．若OC -→xOA y OB -→-→=+,则y x 4+的取值范围是．2.(2020·合肥一诊)如图,四边形是边长为1的正方形,,点为内（含边界）的动点,设,则的最大值等于题型二极化恒等式的应用例4 如图，在同一平面内，点A 位于两平行直线m ，n 的同侧，且A 到m ，n 的距离分别为1，3，点B ，C 分别在m ，n 上，|AB →＋AC →|＝5，则AB →·AC →的最大值是___．OABC 3=OD P BCD ∆(,)OP OC OD R αβαβ=+∈αβ+例5 （2017新课标Ⅱ）已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是( )A ．2-B ．32-C ．43- D ．1- [玩转跟踪]1.在△ABC 中，点E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则PB →·PC →＋BC →2的最小值是____．2.（2019·苏州模拟）如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，60BCD ∠=︒，CB CD ==若点M 为边BC 上的动点，则AM DM ⋅的最小值为 ▲ ．3.在ABC ∆中，点,E F 分别是线段,AB AC 的中点，点P 在直线EF 上，若ABC ∆的面积为2，则2PB PC BC +的最小值是_____________. 题型三三角形五心设O 为△ABC 所在平面上一点，内角A ，B ，C 所对的边分别为a ，b ，c ，则 (1)O 为△ABC 的外心⇔|OA →|＝|OB →|＝|OC →|＝a 2sin A .(2)O 为△ABC 的重心⇔OA →＋OB →＋OC →＝0. (3)O 为△ABC 的垂心⇔OA →·OB →＝OB →·OC →＝OC →·OA →. (4)O 为△ABC 的内心⇔aOA →＋bOB →＋cOC →＝0. 类型1 平面向量与三角形的“重心”【例6】已知A ，B ，C 是平面上不共线的三点，O 为坐标原点，动点P 满足OP →＝13[(1－λ)OA →＋(1－λ)OB →＋(1＋2λ)·OC →]，λ∈R ，则点P 的轨迹一定经过( ) A.△ABC 的内心B.△ABC 的垂心C.△ABC 的重心D.AB 边的中点类型2 平面向量与三角形的“内心”问题【例7】在△ABC 中，AB ＝5，AC ＝6，cos A ＝15，O 是△ABC 的内心，若OP →＝xOB →＋yOC →，其中x ，y ∈[0，1]，则动点P 的轨迹所覆盖图形的面积为( ) A.1063B.1463C.4 3D.6 2类型3 平面向量与三角形的“垂心”问题【例8】已知O 是平面上的一个定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP →＝OA →＋λ⎝⎛⎭⎪⎫AB →|AB →|cos B + AC →|AC →|cos C ，λ∈(0，＋∞)，则动点P 的轨迹一定通过△ABC 的( ) A.重心B.垂心C.外心D.内心类型4 平面向量与三角形的“外心”问题【例9】已知在△ABC 中，AB ＝1，BC ＝6，AC ＝2，点O 为△ABC 的外心，若AO →＝xAB →＋yAC →，则有序实数对(x ，y )为( )A.()45，35 B.()35，45C.()－45，35D.()－35，45【玩转跟踪】1．O 为三角形内部一点，a ､b ､c 均为大于1的正实数，且满足aOA bOB cOC CB ++=，若OAB S ∆､OAC S ∆､OBCS ∆分别表示OAB ∆､OAC ∆､OBC ∆的面积，则::OAB OAC OBC S S S ∆∆∆为（）A ．(1):(1):c b a +-B ．::c b aC ．111::11a b c -+ D ．222::c b a2．设点A ，B 的坐标分别为()0,1，()1,0，P ，Q 分别是曲线2xy =和2log y x =上的动点，记1I AQ AB =⋅，2I BP BA =⋅.（）A ．若12I I =，则()PQ AB R λλ=∈B ．若12I I =，则AP BQ=C ．若()PQ ABR λλ=∈，则12II =D ．若AP BQ=，则12I I =3．已知P 是ABC ∆所在平面内一点，且满足0AB PC BC PA CA PB ⋅+⋅+⋅=，则点P 是ABC ∆的（） A ．外心B ．内心C ．垂心D ．重心4．已知O 是ABC ∆所在平面上的一点，若aPA bPB cPC PO a b c++=++（其中P 是ABC ∆所在平面内任意一点），则O点是ABC ∆的（） A ．外心B ．内心C ．重心D ．垂心【玩转练习】1．若O 是ABC 垂心，6A π∠=且sin cos sin cos B C AB C BAC+2sin sin m B C AO =，则m =（）A ．12B．2C．3 D2.在ABC ，若0AB AC BC AB AC ⎛⎫ ⎪+⋅= ⎪⎝⎭，且12AB AC AB AC ⋅=，则ABC 的形状为（） A ．直角三角形B ．等腰三角形C ．等边三角形D ．无法判断3．已知P 是ABC ∆内一点，且满足230PA PB PC ++=，记ABP ∆、BCP ∆、ACP ∆的面积依次为1S ，2S ，3S ，则123::S S S 等于（）A ．1:2:3B ．1:4:9C ．2:1:3D ．3:1:24．如图，在平行四边形ABCD 中，M 是BC 的中点，且AD =DM ，N 是线段BD 上的动点，过点N 作AM 的垂线，垂足为H ，当AM MN ⋅最小时，HC =A ．1344AB AD + B ．1142AB AD +C ．1324AB AD + D ．3142AB AD + 5．O 为ABC ∆所在平面上动点，点P 满足AB AC OP OA AB AC λ⎛⎫⎪=++ ⎪⎝⎭,,[)0λ∈+∞ ,则射线AP 过ABC ∆的（）A ．外心B ．内心C ．重心D ．垂心6．在ABC ∆中，6AB =，8BC =，AB BC ⊥，M 是ABC ∆外接圆上一动点，若AM AB AC λμ=+，则λμ+的最大值是（）A ．1B ．54C ．43D ．27．如图所示，设P 为ABC ∆所在平面内的一点，并且1142AP AB AC =+，则BPC ∆与ABC ∆的面积之比等于（）A ．25B ．35C ．34D ．148.在锐角△ABC 中，AC =BC =2，CO =x CA +y CB （其中x +y =1），若函数f （λ）=|CA -λCB ||OC |的最小值为（）A ．1B C ．2D ．9．设非零向量a ，b 夹角为θ，若2a b =，且不等式2a b a bλ+≥+对任意θ恒成立，则实数λ的取值范围为（） A ．[]1,3-B ．[]1,5-C ．[]7,3- D ．[]5,710．已知双曲线C ：22221x y a b-= ()0,0a b >>的左右焦点分别为1F ，2F ， P 为双曲线C 上一点， Q 为双曲线C 渐近线上一点， P ， Q 均位于第一象限，且23QP PF =，120QF QF ⋅=，则双曲线C 的离心率为（）A ．8B ．2C ．2D 211．在等边三角形ABC 中,D 是AC 上一点，2CD DA =,M 是BD 上一点，90AMC ∠=,则tan AMD ∠=( )A ．4B ．3C ．12D ．1312．已知矩形ABCD ，AB 2=，AD=P 为矩形内一点，且AP 1=，则()PC PD AP +⋅的最大值为()A ．0B ．2C ．4D ．613．若平面向量,,a b c 满足2a =，4b =，4a b ⋅=，3c a b -+=，则c b-的最大值为（）A B C ．D ．14．设单位向量1e ，2e 对任意实数λ都有121232e e e e λ+≤+，则向量1e ，2e 的夹角为()A ．3π B ．23πC ．6π D ．56π15．在直角梯形ABCD 中， AB AD ⊥， //AD BC ， 22AB BC AD ===， ,E F 分别为BC ， CD 的中点，以A 为圆心， AD 为半径的圆交AB 于G ，点P 在弧DG 上运动（如图）.若AP AE BF λμ=+，其中λ， R μ∈，则6λμ+的取值范围是（）A ．B ．[1,C ．D ．16．已知点O 是锐角△ABC 的外心，a ，b ，c 分别为内角A 、B 、C 的对边，A=4π ，且cosB cosC AB AC OA sinC sinBλ+=，则λ的值为（）A B C ．D ．﹣。

第九讲平面向量的极化恒等式、等和线

第九讲平面向量的內积、极化恒等式、等和线一、分拆求內积1、（17年联赛真题）在ABC ∆中，M 为边BC 的中点，N 是线段BM 的中点，若3π=∠A ，ABC ∆的面积为3，则⋅的最小值为 ◆答案： 13+ ★解析：由条件知()AC AB AM +=21，AC AB AN 4143+=，则⎪⎭⎫⎝⎛⋅++=⋅AC AB AN AM 481，由A S ABC ⨯=⨯==∆43sin 34=所以2=⋅AC AB ，所以38≥+443232⨯==时取等。

则⎪⎭⎫⎝⎛⋅++=⋅AM 48113+≥。

2、（18年联赛真题）3、（07年联赛真题）二、建系求內积1、（15年联赛真题）在矩形ABCD 中，2=AB ,1=AD ,边DC 上（包含D ,C ）的动点P 与线段CB 延长线上（包含B ）的动点Q =,则向量与向量的数量积⋅的最小值为 ◆答案：34★解析：不妨设 A ( 0 , 0 ) , B ( 2 , 0 ) , D ( 0 , l ) ．设 P 的坐标为（t , l) （其中02t ≤≤），则由||||DP BQ =得Q 的坐标为（2，-t )，故(,1),(2,1)PA t PQ t t =--=---,因此，22133()(2)(1)(1)1()244PA PQ t t t t t t ⋅=-⋅-+-⋅--=-+=-+≥．当12t =时，min 3()4PA PQ ⋅=．2、（15年联赛真题）3、（19年联赛真题）三、极化恒等式极化恒等式：()()[].4122b a b a b a --+=•1、已知ABC ∆是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是2、如图，扇形的圆心角为90°，半径为1，点是圆弧上的动点，作点关于弦的对称点，则的取值范围为____．3 、在等腰直角△ABC 中，∠ABC ＝90°，AB ＝BC ＝2，M ，N 为AC 边上的两个动点(M ，N 不与A ，C 重合)，且满足|MN →|＝2，则BM →·BN →的取值范围为________．4、已知B A 、是单位圆上的两点，O 为圆心，且MN AOB o,120=∠是圆O 的一条直径，点C 在圆内，且满足)10()1(<<-+=λλλOB OA OC ，则CN CM ⋅的取值范围是练习：1、在ABC ∆中，60BAC ∠=若2AB =，BC =，D 在线段AC 上运动，⋅的最小值为2.已知AB 是圆O 的直径,AB 长为2,C 是圆O 上异于,A B 的一点,P 是圆O 所在平面上任意一点,则()PA PB PC +⋅的最小值为____________3．在ABC ∆中，3AB =，4AC =，60BAC ∠=，若P 是ABC ∆所在平面内一点，且2AP =，则PB PC ⋅的最大值为4．若点O 和点(2,0)F -分别是双曲线2221(0)x y a a-=>的中心和左焦点，点P 为双曲线右支上任意一点则OP FP ⋅的取值范围是 .5．在Rt ABC ∆，2AC BC ==，已知点P 是ABC ∆内一点，则(PB +⋅的最小值是 .6. 正ABC ∆边长等于3，点P 在其外接圆上运动，则PB AP ⋅的取值范围是（） A. ⎥⎦⎤⎢⎣⎡-23,23 B. ⎥⎦⎤⎢⎣⎡-21,23 C. ⎥⎦⎤⎢⎣⎡-23,21 D. ⎥⎦⎤⎢⎣⎡-21,21四、等和线1、在矩形ABCD 中，1AB =，2AD =，动点P 在以点C 为圆心且与BD 相切的圆上．若AP AB AD λμ=+，则λμ+的最大值为2、给定两个长度为1的平面向量OA →和OB →，它们的夹角为2π3.如图所示，点C 在以O 为圆心的AB 上运动．若OC →＝xOA →＋yOB →，其中x ，y ∈R ，求x ＋y 的最大值．3、在矩形ABCD 中，AB ＝5，BC ＝3，P 为矩形内一点，且AP ＝52，若AP →＝λAB →＋μAD →(λ，μ∈R )，则5λ＋3μ的最大值为______．4 .如图,在扇形OAB 中,60AOB ︒∠=,C 为弧AB 上的一个动点．若OC -→xOA y OB -→-→=+,则y x 4+的取值范围是．5.如图,四边形是边长为1的正方形,,点为内（含边界）的动点,设,则的最大值等于OABC 3=OD P BCD ∆(,)OP OC OD R αβαβ=+∈αβ+练习：1.如图，在中，是线段上的一点，且，过点的直线分别交直线于点，若，，则的最小值是.2.已知向量OB OA ,满足1=+OB OA ，OB OA ⊥，OB OA OC μλ+=）、（R ∈μλ，若M 为线段AB 的中点，并且1M =C ，则μλ+的最大值是。

极化恒等式(学生版)

课题：极化恒等式在向量问题中的运用之马矢奏春创作时间：二学习目标目标1：经由过程自立进修掌握极化恒等式两种模式,理解其几何意义；目标2-1：经由过程对例1的自立进修掌握用极化恒等式求数量积的值；目标2-2：经由过程对例2的自立进修掌握用极化恒等式求数量积的最值、范围；目标2-3：经由过程小组合作进修掌握极化恒等式解决与数量积有关的分化问题. 重点掌握极化恒等式,运用它解决一类与数量积有关的向量问题难点按照具体的问题情境,灵活运用极化恒等式目标达成途径进修自我评价阅读以下材料： .两倍等于两条邻边平方和的平方和平行四边形的对角线的你能用向量方法证明：何模型。

示向量加法和减法的几引例：平行四边形是表,,b AD a AB ==证明：不妨设，，则b a DB b a A -=+=C ()222222C C b b a a b a A A +⋅+=+== （1）()222222b b a a b a DB DB +⋅-=-== （2）（1）（2）两式相加得：⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+=+22222222C AD AB b a DB A 结论：平行四边形对角线的平方和等于两条邻边平方和的两倍.思虑1：假如将上面（1）（2）两式相减,能得到什么结论呢？b a ⋅＝()()⎥⎦⎤⎢⎣⎡--+2241b a b a ————极化恒等式对于上述恒等式,用向量运算显然随便马虎证实.那么基于上面的引例,你以为极化恒等式的几何意义是什么？几何意义：向量的数量积可以暗示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的41. 即：[]2241DB AC b a -=⋅（平行四边形模式）目标1：阅读材料,理解极化恒等式的由来过程,掌握极化恒等式的两种模式,并理解其几何意义 M图1思虑：在图1的三角形ABD 中（M 为BD 的中点）,此恒等式若何暗示呢？因为AM AC 2=,所以2241DB AMb a -=⋅（三角形模式）例 1.(2012年浙江文15)在ABC ∆中,M 是BC 的中点,3,10AM BC ==,则AB AC ⋅=____.解：因为M 是BC 的中点,由极化恒等式得： 2241BC AM AC AB -=⋅=9-10041⨯= -16 【小结】在运用极化恒等式的三角形模式时,关头在于取第三边的中点,找到三角形的中线,再写出极化恒等式.目标检测.______1)132012(的值为边上的动点，则是点，的边长为已知正方形改编北京文DA DE AB E ABCD ⋅.________O O 2.2的取值范围是则上的一个动点，是圆，点的圆内接于半径为（自编）已知正三角形例PB PA P ABC ⋅解：取AB 的中点D,贯串衔接CD,因为三角形ABC 为正三角形,所以O 为三角形ABC 的重心,O 在CD 上,且22==OD OC ,所以3=CD ,32=AB（也可用正弦定理求AB ）又由极化恒等式得：341222-=-=⋅PD AB PD PB PA 因为P 在圆O 上,所以当P 在点C 处时,3||max =PD 当P 在CO 的延长线与圆O 的交点处时,1||min =PD所以]6,2[-∈⋅PB PA【小结】涉及数量积的范围或最值时,可以运用极化恒等式将多变量改动成单变量,再用数形结合等方法求出单变量的范围、最值即可.目标检测8.6.3.2.)(134)112010(22D C B A FP OP P y x F O 的最大值为则为椭圆上的任意一点，的中心和左焦点，点分别为椭圆和点若点福建文⋅=+问题、迷惑、错解汇集目标2-1：掌握用极化恒等式求数量积的值AB CM 目标2-2：掌握用极化恒等式求数量积的最值、范围才能提升例3.（2013浙江理7）在ABC ∆中,0P 是边AB 上必定点,知足014P B AB =,且对于边AB 上任一点P ,恒有00PB PC P B PC ⋅≥⋅.则( )A. 90ABC ∠=B. 90BAC ∠=C. AB AC =D.AC BC =目标检测22.2.2.1.)(,0)()(2,)92008(D C B A c c b c a c b a 的最大值是则满足，若向量个互相垂直的单位向量是平面内已知浙江理=-⋅- 问题、迷惑汇集常识、方法总结本课的主要进修内容是什么？极化恒等式：平行四边形模型：三角形模型：极化恒等式在处理与_________________有关问题时,显得较有优越性.课后检测1.在ABC ∆中,60BAC ∠=若2AB =,3BC =,D 在线段AC 上运动,DA DB ⋅的最小值为2.已知AB 是圆O 的直径,AB 长为2,C 是圆O 上异于,A B 的一点,P 是圆O 地点平面上随便率性一目标2-3：会用极化恒等式解决与数量积有关的分化问题60,若P⋅的最大值为PB PC4．若点O和点⋅的取值范围是率性一点则OP FP=ABC,AC BCB是单位圆上的两点⋅的取值范围是．-=,则AB ACAB AC2。

微专题06——极化恒等式及其应用(学生版)

讲义：微专题06——极化恒等式及其应用班级：__________________姓名：___________________随着高考对平面向量问题的研究的不断深入，极化恒等式在解决平面向量问题上取得一些进展，随着应用的推进，一些诸如“动点”、“多动动”、“曲线”、“运动动态”、“极限状态”等平面向量复杂问题接踵而至．极化恒等式在2016年江苏高考以后的模拟练习中，经常出现，往往通过极化恒等式能快速地解决一些求数量积问题，在此要注意观察什么样的数量积适用于极化恒等式解决，首先：共起点（或共终点或可化成共起点或终点），其次：有中线（没有自己造）．极化恒等式1．平行四边形中的极化恒等式．设b a ，是平面内的一组基底，如图所示，由恒等式])()[(4122b a b a b a --+=∙可得：2222])()[(41DM AM BD AC -=-=∙b a ．即22||||DM AM AD AB -=∙．此等式称为极化恒等式．其几何意义是向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的41．2．三角形中的极化恒等式．在ABC ∆中，设D 为BC 的中点，2=+，=-，则224)(AD AC AB =+，22)(CB AC AB =-，两式相减可得：2244CB AD AC AB -=∙，化简得极化恒等式2241CB AD AC AB -=∙．说明：1．极化恒等式源于教材又高于教材，在ABC ∆中，)(21AC AB AD +=，)(21AB AC BD -=是教材上出现的两个重要向量三角形关系，而极化恒等式无非就是这两个公式的逆用；2．具有三角几何背景的数学问题利用极化恒等式考虑尤为简单；3．向量与代数的互换运算深入人心，而与几何的运算略显单薄，而极化恒等式恰恰弥补了这个缺憾，可以说极化恒等式把向量的数量积问题用形象的几何图形展示得淋漓尽致．引例：在ABC ∆中，M 是线段BC 的中点，3=AM ，10=BC ，则∙的值为_______．A B C D M B CM A目标一：掌握用极化恒等式求数量积的值例1：如图，在ABC ∆中，D 是BC 的中点，F E ，是AD 上的两个三等分点，4=∙，1-=∙CE BE ，则CF BF ∙的值是__________．训练1：如图，在ABC ∆中，E D ，是BC 上的两个三等分点，2=∙AC AB ，4=∙AE AD ，则BC 的模长的值是__________．B CAE FAB D E C目标二：掌握用极化恒等式求数量积的范围、最值例2：如图，ABC ∆是边长为32的等边三角形，点P 是平面内的任意一点，1||=，则∙的最小值是______________________．训练2：已知正三角形ABC 内接于半径为2的圆O ，点P 是圆O 上的一个动点，则∙的取值范围是______________________．A BCPO BA PC例3：在边长为1的菱形ABCD 中，π32=∠A ，若点P 为对角线AC 上一点，则∙的最大值为______________________．训练3：在菱形ABCD 中，对角线3=AC ，1=BD ，点P 是AD 边上的动点，则PC PB ∙的最小值为______________________．午练：微专题06——极化恒等式及其应用班级：__________________姓名：___________________1．在ABC ∆中，10=BC ，16-=∙AC AB ，D 为边BC 的中点，则AD 的模为__________．2．设P 是ABC ∆的中线AD 的中点，D 为边BC 的中点，且2=AD ，若3-=∙PC PB 则AC AB ∙的值为________________．3．如图，在ABC ∆中，已知4=∙AC AB ，3||=BC ，点N M ，分别为边BC 上的三等分点，则AN AM ∙的值为_________________．4．如图，在ABC ∆中，点F E D ，，依次为边BC 上的四等分点，2=∙AC AB ，5=∙AF AD ，则AE 的长为_____________．5．已知AB 为圆1)1(:22=+-y x C 的直径，点P 为直线01=+-y x 上任意一点，则PB PA ∙的最小值为_________________．AB M NC A BDE CF6．已知圆O 的直径2=AB ，C 为该圆上异于B A 、的一点，P 是圆O 所在平面上任一点，则PC PB PA ∙+)(的最小值为_________________．7．已知点)02( ，A ，)04( ，B ，动点P 在抛物线x y 42-=上运动，则使BP AP ∙取得最小值的点P 的坐标为_________________．8．【选做】已知点B A ，分别在直线31==x x ，上，4||=-OB OA ，则当||+取得最小值时，∙的值为________________．作业：微专题06——极化恒等式及其应用班级：__________________姓名：___________________1．在ABC ∆中，点D 是BC 的中点，若208==BC AD ，，则=∙AC AB _____________．2．在平面直角坐标系中，菱形OABC 的两个顶点为)00( ，O ，)11( ，A ，且1=∙OC OA ，则=∙AC AB ________________．3．已知点M 是边长为2的正方形ABCD 的内切圆内（含边界）一动点，则MB MA ∙的取值范围为_________________．4．在周长为16的PMN ∆中，6=MN ，则PN PM ∙的取值范围为_____________．5．已知D C B A ，，，四点的坐标分别为)01( -，A ，)01( ，B ，)10( ，C ，)02( ，D ，P 是线段CD 上的任意一点，则BP AP ∙的最小值为_________________．6．若等腰ABC ∆底边BC 上的中线长为1，底角︒>60B ，则∙的取值范围为_________________．7．点P 为椭圆1151622=+y x 上的任意一点，EF 为圆4)1(22=+-y x 的一条直径，则PF PE ∙的取值范围为_________________．8．如图，在ABC ∆中，已知︒=∠==12023BAC AC AB ，，，点D 为边BC 的中点，若AD CE ⊥，垂足为E ，则EC EB ∙的值为_________________．AB D EC9．如图，若AB 是圆O 的直径，点M 是弦CD 上的一个动点，68==CD AB ，，则∙的取值范围是______．10．设锐角ABC ∆的面积为1，边AC AB ，的中点分别为F E ，，P 为线段EF 上的动点，则2BC PC PB +∙的最小值是__________________．11．如图，ABC ∆为等腰三角形，4==AC AB ，︒=∠120BAC ，以A 为圆心，1为半径的圆分别交AC AB ，于点F E ，，点P 是劣弧EF 上的一点，则PC PB ∙的取值范围是______．C B AEF PC A BD M O12．【选做】如图，圆O 是ABC Rt ∆的内切圆，已知3=AC ，4=BC ，︒=90C ，过圆心O 的直线l 交圆O 于Q P ，两点，则CQ BP ∙的取值范围为____________．A C BQOPl。

2023高考数学基础知识综合复习专题2平面向量的几何意义极化恒等式等和线课件(共12张PPT)

2
4
a·b=
考点三
等和线
例 6 已知△AOB,点
解由已知 =
P 在直线
||
AB 上,且满足=2t+t(t∈R),求 .
||
2

+
,点
1+2
1+2
P 在直线 AB 上,
2

+
=1,t=1.
1+2 1+2
得
2
3
1
3
可得 = + ,2 = ,
π
2
易得 sin(θ+4)∈[- 2 ,1],
故 ·∈[0,1+ 2].
例2已知单位向量e,平面向量a,b满足a·e=2,b·e=3,a·b=0,求|a-b|的
最小值.
解由题意得,a在e上的投影数量为2,b在e上的投影数量为3,
建系如图:
设 A(2,m),B(3,n),a=(2,m),b=(3,n),m>0,n<0,
例 1 在平面直角坐标系中,已知
A(1,0),B(0,-1),P 是曲线 y= 1- 2 上一
个动点,求 ·的取值范围.
解设 P(cos θ,sin θ),0≤θ≤π,=(1,1),=(cos θ,1+sin θ),
π
∴ ·=cos θ+1+sin θ= 2sin(θ+4)+1,θ∈[中线来表示,即 a·b=||2-|| .它揭
4
示了三角形的中线与边长的关系.
三、等和线
如图,平面内一组基底, 及任一向量 , =x+y .连接

AB,OP 相交于点 Q,则 x+y= ,过 P 作 AB 的平行线分别交

一文搞定极化恒等式和等和线定理

极化恒等式的妙用
向量是高中数学一个非常重要的内容，它集数与形于一身，既有代数的抽象性，又有几何的直观性，是形象思维与抽象思维的有机结合。近几年来，在新课程的引领下，各省市高考试题涌现了一些以向量为背景的好题，有些省市甚至是以向量为突破口来实现高考试题命制的创新。它们以向量的线性运算以及数量积运算为载体，综合考查学生的运算求解能力，推理论证能力，以此做为压轴试题来提高考生的区分度。基于上述原因，除了掌握向量的基本运算之外，还有必要掌握向量中一些常见的解题方法，比如向量的极化恒等式(平面向量的积化和差公式)。本文介绍向量的极化恒等式及其相关应用。
巧用“等和线”解决平面向量问

平面向量等和线与极化恒等式及答案

等和线与极化恒等式知识点1 三点共线结论根据平面向量基本定理，如果P A →，PB →为同一平面内两个不共线的向量，那么这个平面内的任意向量PC →都可以由P A →，PB →唯一线性表示：PC →=xP A →＋yPB →．特殊地，如果点C 正好在直线AB 上，那么x ＋y =1，反之如果x ＋y =1，那么点C 一定在直线AB 上．于是有三点共线结论：已知P A →，PB →为平面内两个不共线的向量，设PC →=xP A →＋yPB →，则A ，B ，C 三点共线的充要条件为x ＋y =1．知识点2 等和线的定义及性质以上讨论了点C 在直线AB 上的特殊情况，得到了平面向量中的三点共线结论．下面讨论点C 不在直线AB 上的情况．如图所示，直线DE ∥AB ，C 为直线DE 上任一点，设PC →=xP A →＋yPB →(x ，y ∈R )．1．平面向量等和线定义(1)当直线DE 经过点P 时，容易得到x ＋y =0．(2)当直线DE 不过点P 时，直线PC 与直线AB 的交点记为F ，因为点F 在直线AB 上，所以由三点共线结论可知，若PF →=λP A →＋μPB →(λ，μ∈R )，则λ＋μ=1．由△P AB 与△PED 相似，知必存在一个常数k ∈R ，使得PC →=kPF →(其中k =|PC ||PF |=|PE ||P A |=|PD ||PB |)，则PC →=kPF →=kλP A →＋kμPB →．又PC →=xP A →＋yPB →(x ，y ∈R )，所以x ＋y =kλ＋kμ=k ．以上过程可逆．在向量起点相同的前提下，所有以与两向量终点所在的直线平行的直线上的点为终点的向量，其基底的系数和为定值，这样的线，我们称之为“等和线”．2．平面向量等和线定理平面内一组基底PA →，PB →及任一向量PF →满足：PF →=λPA →＋μPB →(λ，μ∈R )，若点F 在直线AB 上或在平行于AB 的直线上，则λ＋μ=k （定值），反之也成立，我们把直线AB 以及与直线AB 平行的直线称为等和线．3．平面向量等和线性质(1)当等和线恰为直线AB 时，k =1；(2)当等和线在点P 和直线AB 之间时，k ∈(0，1)； (3)当直线AB 在点P 和等和线之间时，k ∈(1，＋∞)； (4)当等和线过点P 时，k =0；(5)若两等和线关于点P 对称，则定值k 互为相反数．已知点P 是△ABC 所在平面内一点，且AP →=xAB →＋yAC →，则有点P 在直线BC 上⇔x ＋y =1；点P 与点A 在直线BC 异侧⇔x ＋y >1，且x ＋y 的值随点P 到直线BC 的距离越远而越大；点P 与点A 在直线BC 同侧⇔x ＋y < 1，且x ＋y 的值随点P 到直线BC 的距离越远而越小．平面向量共线定理的表达式中的三个向量的起点务必一致，若不一致，本着少数服从多数的原则，优先平移固定的向量；若需要研究两系数的线性关系，则需要通过变换基底向量，使得需要研究的代数式为基底的系数和．考虑到向量可以通过数乘继而将向量进行拉伸压缩反向等操作，那么理论上来说，所有的系数之间的线性关系，我们都可以通过调节基底，使得要求的表达式是两个新基底的系数和．知识点3 极化恒等式a ·b =14[(a ＋b )2－(a －b )2]1.公式推导：()()()()222222222142a b a ab b ab a b a b a b a ab b ⎫+=++⎪⎡⎤⇒=+−−⎬⎢⎥⎣⎦⎪−=−+⎭2.几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14．4.三角形模式：如图，在△ABC 中，设D 为BC 的中点，则AB →·AC →=|AD |2－|BD |2．（1）推导过程：由()()222222111222AB AC AB AC AB AC AD CB AD DB ⎡⎤⎡⎤⎛⎫=+−−=−=− ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭.（2）三角形模式是平面向量极化恒等式的终极模式，几乎所有的问题都是用它解决．（3）记忆规律：向量的数量积等于第三边的中线长与第三边长的一半的平方差．考点一根据等和线求基底系数和的值(1)确定值为1的等和线；A B C图(2)(2)平移(旋转或伸缩)该线，作出满足条件的等和线；(3)从长度比或点的位置两个角度，计算满足条件的等和线的值．例1（2022·河南高三月考）在平行四边形中ABCD 中，E 和F 分别是CD 和BC 边上的中点，且AC AE AF λμ=+,其中λμ∈R ，，则=λμ+___________.例2 （2022·陕西·交大附中模拟预测）在平行四边形ABCD 中，点E 和F 分别是边CD 和BC 的中点．若AC →=λAE →＋μAF →，其中λ，μ∈R ，则λ＋μ=__________．【跟踪精练】1. （2022·山东·山师附中模拟预测）直角梯形中ABCD ,ABD BC AD CD CB ∆⊥，，//是边长为2的正三角形，P 是平面上的动点，1||=CP ，),(R AB AD AP ∈+=μλμλ设，则μλ+的值可以为（）A. 0B.1C.2D.32. （2022·云南玉溪·高三月考）如图，在平行四边形ABCD 中，AC ，BD 相交于点O ，E 为线段AO 的中点．若BE →=λBA →＋μBD →(λ，μ∈R )，则λ＋μ等于( )A ．1B ．34C ．23D ．123. (2013江苏)设D ，E 分别是△ABC 的边AB ，BC 上的点，AD =12AB ，BE =23BC ，若DE →=λ1AB→＋λ2AC →(λ1，λ2∈R )，则λ1＋λ2的值为________．考点二根据等和线求基底的系数和的最值（范围）(1)确定值为1的等和线；(2)平移(旋转或伸缩)该线，结合动点的可行域，分析何处取得最大值和最小值； (3)从长度比或点的位置两个角度，计算最大值和最小值．例3给定两个长度为1的平面向量OA →和OB →，它们的夹角为2π3，如图所示，点C 在以O 为圆心的弧AB 上运动，若OC →=xOA →＋yOB →(x ，y ∈R )，则x ＋y 的最大值是________．例4（2022·福建泉州·模拟预测）在△ABC 中，AC AB ⊥，AB =3，AC =1，点P 是△ABC 所在平面内一点， 2||||AB ACAP AB AC =+，且满足||2PM =，若AM xAB y AC =+，则3x ＋y 的最小值是( )．A ．3+BC ．1D ．3− 【跟踪精练】1.(2017·全国Ⅲ)在矩形ABCD 中，AB =1，AD =2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP →=λAB →＋μAD →，则λ＋μ的最大值为( )A ．3B ．22C ．5D ．22. （2022·苏州中学高三月考）如图所示，A ，B ，C 是圆O 上的三点，线段CO 的延长线与BA 的延长线交于圆O 外的一点D ，若OC →=mOA →＋nOB →，则m ＋n 的取值范围是________．考点三极化恒等式处理数量积的定值问题(1)取第三边的中点，连接向量的起点与中点；(2)利用积化恒等式将数量积转化为中线长与第三边长的一半的平方差；(3)求中线及第三边的长度，从而求出数量积的值．例5（2022·甘肃·高台县第一中学模拟预测）如图，在△ABC 中，D 是BC的中点，E ，F 是AD 上的两个三等分点，BA →·CA →=4，BF →·CF →=－1则BE →·CE →的值是____．例6（2022·山东日照市·高三二模）如图，在平行四边形ABCD 中，已知AB =8，AD =5，CP →=3PD →，AP →·BP →=2，则AB →·AD →的值是( )A ．44B ．22C ．24D ．72 【题型精练】 1．（2022·河北武强中学高三月考）如图，在平面四边形ABCD中，O 为BD 的中点，且OA =3，OC =5，若AB →·AD →=－7，则BC →·DC →的值是________．2. (2022·全国福建省漳州市高三期末) 在△ABC 中，|AB →＋AC →|=|AB →－AC →|，AB =2，AC =1，E ，F 为BC 的三等分点，则AE →·AF →等于( )A ．89B ．109C ．259D ．269考点四极化恒等式处理数量积中的最值范围问题(1)取第三边的中点，连接向量的起点与中点；(2)利用积化恒等式将数量积转化为中线长与第三边长的一半的平方差； (3)求中线长的最值(范围)，从而得到数量的最值(范围)．例7 (全国Ⅱ高考)已知△ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则P A →·(PB →＋PC →)的最小值是( )A ．－2B ．－32C ．－43D ．－1例8 （2022·海南海口·二模）在正三角形ABC 中，点E ，F 是线段AB,AC 的中点，点P 在直线EF 上，若三角形ABC 的面积为2，则2PC PB BC ⋅+的最小值是【题型精练】1. （2022•南通期末）在面积为2的△ABC 中，E ，F 分别是AB ，AC 的中点，点P 在直线EF上，则PC →·PB →＋BC →2的最小值是________．2. (天津高考)如图，在四边形ABCD 中，∠B =60°，AB =3，BC =6，且AD →=λBC →，AD →·AB →=－32，则实数λ的值为________，若M ，N 是线段BC 上的动点，且|MN →|=1，则DM →·DN →的最小值为________．培优专题2 等和线与极化恒等式答案考点一根据等和线求基底系数和的值例1.【答案】43【解析】连接EF ，交AC 于G∵E ，F ，G 共线，则AG xAE y AF =+，且=1x y + 记t AC AG =，则tx ty t λμ+=+=，4t =3AGAC =例2 【答案】43 【解析】如图，EF 为值是1的等和线，过C 作EF 的平行线，设λ＋μ=k ，则k =|AC ||AM |．由图易知，|AC ||AM |=43，故选B ．A【跟踪精练】 1.【答案】BC 【解析】如图 2.【答案】B【解析】如图，AD 为值是1的等和线，过E 作AD 的平行线，设λ＋μ=k ，则k =|BE ||BF |．由图易知，|BE ||BF |=34，故选B ．A3.答案 12解析如图，过点A 作AF →=DE →，设AF 与BC 的延长线交于点H ，易知AF =FH ，∴DF =12BH ，因此λ1＋λ2=12．考点二根据等和线求基底的系数和的最值（范围）例3【答案】2【解析】令x ＋y =k ，所有与直线AB 平行的直线中，切线离圆心最远，即此时k 取得最大值，结合角度，不难得到k =|DO ||OE |=2．1，2），M 在以P 为圆心，半径为2的圆上xAD y AC +，，则有3=x y t +max =111AM MN MG t AN AN AH =+=+≥++min =1113AM MN MG t AN AN AH =−=−≥=−【跟踪精练】1.答案 A 解析建立如图所示的直角坐标系，则C 点坐标为(2，1)．设BD 与圆C 切于点E ，连接CE ，则CE ⊥BD ．因为CD =1，BC =2，所以BD =12＋22=5，EC =BC ·CD BD =25=255，所以P 点的轨迹方程为(x －2)2＋(y －1)2=45．设P (x 0，y 0)，则⎩⎪⎨⎪⎧x 0＝2＋255cos θ，y 0＝1＋255sin θ(θ为参数)，而AP →=(x 0，y 0)，AB →=(0，1)，AD→BB=(2，0)．因为AP →=λAB →＋μAD →=λ(0，1)＋μ(2，0)=(2μ，λ)，所以μ=12x 0=1＋55cos θ，λ=y 0=1＋255 sin θ．两式相加，得λ＋μ=1＋255 sin θ＋1＋55cos θ=2＋sin(θ＋φ)≤3⎝⎛⎭⎫其中sin φ＝55，cos φ＝255，当且仅当θ=π2＋2k π－φ，k ∈Z 时，λ＋μ取得最大值3．故选A ．等和线法过动点P 作等和线，设x ＋y =k ，则k =|AM ||AB |．由图易知，当等和线与EF 重合时，k 取最大值，由EF ∥BD ，可求得|AE ||AB |=3，∴λ＋μ取得最大值3．故选A ．2.【答案】 (－1，0)【解析】如图，作OA →，OB →的相反向量OA 1→，OB 1→，则AB ∥A 1B 1，过O 作直线l ∥AB ，则直线l ，A 1B 1分别为以OA →，OB →为基底的值为0，－1的等和线，由题意线段CO 的延长线与BA 的延长线交于圆O 外的一点D ，所以点C 在直线l 与直线A 1B 1之间，所以m ＋n ∈(－1，0)．考点三极化恒等式处理数量积的定值问题例5【解析】78【解析】极化恒等式法设BD =DC =m ，AE =EF =FD =n ，则AD =3n ．根据向量的极化恒等式，有AB →·AC →=AD →2－DB →2=9n 2－m 2=4，FB →·FC →=FD →2－DB →2=n 2－m 2=－1．联立解得n 2=58，m 2=138．因此EB →·EC →=ED →2－DB →2=4n 2－m 2=78．即BE →·CE →=78．例6【答案】B 【解析】如图，取AB 中点E ，连接EP 并延长，交AD 延长线于F ， AP →·BP →=EP 2－AE 2=EP 2－16=2，∴EP =32，又∵CP →=3PD →，AE →=EB →，AB →=DC →，∴AE =2DP ，即△F AE 中，DP 为中位线，AF =2AD =10，AE =12AB =4，FE =2PE =62，AP 2=40，AD →·AB →=AF →·AE →=AP 2－EP 2=40－(32)2=22．【题型精练】1．【答案】9 【解析】因为AB →·AD →=AO →2－OD →2=9－OD →2=－7⇒OD →2=16，所以BC →·DC →=CO →2－OD →2=25－16=9．2.【答案】B 【解析】取EF 中点M ，连接AM ，则AE →·AF →=|AM |2－|EM |2=54－536=109．考点四极化恒等式处理数量积中的最值范围问题例7 【答案】B【解析】解析法: 建立坐标系如图①所示，则A ，B ，C 三点的坐标分别为A (0，3)，B (－1，0)，C (1，0)．设P 点的坐标为(x ，y )，图①则P A →=(－x ，3－y )，PB →=(－1－x ，－y )，PC →=(1－x ，－y )，∴P A →·(PB →＋PC →)=(－x ，3－y )·(－2x ，－2y )=2(x 2＋y 2－3y )=2⎣⎡⎦⎤x 2＋⎝⎛⎭⎫y －322－34≥2×⎝⎛⎭⎫－34=－32．当且仅当x =0，y=32时，P A →·(PB →＋PC →)取得最小值，最小值为－32．故选B ．极化恒等式法: 设BC 的中点为D ，AD 的中点为M ，连接DP ，PM ，∴P A →·(PB →＋PC →)=2PD →·P A →=2|PM →|2－12|AD →|2=2|PM →|2－32≥－32．当且仅当M 与P 重合时取等号．BC例8 【答案】2【解析】取BC 中点D ，由三角形ABC 的面积为2，所以边长BC 的平方为3 ，PD 的最小值为高的一半，所以22316=PD BC ，所以22222213=44⋅+−+=+PC PB BC PD BC BC PD BC23383158353==16431632=+⨯⨯BC . 【题型精练】 1.【答案】23【解析】取BC 的中点为D ，连接PD ，则由极化恒等式得PC →·PB →＋BC →2=PD →2－BC →24＋BC →2=PD →2＋3BC →24≥AD→24＋3BC →24，此时当且仅当AD →⊥BC →时取等号，PC →·PB →＋BC →2≥AD →24＋3BC→24≥2AD →24·3BC →24=23．2.【答案】16 132【解析】因为AD →=λBC →，所以AD ∥BC ，则∠BAD =120°，所以AD →·AB →=|AD →|·|AB →|·cos 120°=－32，解得|AD →|=1．因为AD →，BC →同向，且BC =6，所以AD →=16BC →，即λ=16．如图，取MN的中点P ，连接PD ，则DM →·DN →=PD →2－MP →2=PD →2－14，当PD →⊥BC →时，|PD →|2取最小值274，所以DM →·DN →的最小值为132．BC。

微专题平面向量(学生版)

微专题平面向量【秒杀总结】结论1：极化恒等式1.平行四边形平行四边形对角线的平方和等于四边的平方和：|a +b |2+|a -b |2=2(|a|2+|b |2)证明：不妨设AB =a ，AD =b ，则AC =a +b ，DB =a -bAC 2=AC 2=a +b 2=a 2+2a ⋅b +b 2(1)DB 2=DB 2=a -b 2=a 2-2a ⋅b +b 2(2)(1)(2)两式相加得：AC 2+DB 2=2a 2+b 2=2AB 2+AD 2 2.极化恒等式：上面两式相减，得：14a +b 2-a -b 2 ----极化恒等式(1)平行四边形模式：a ⋅b =14AC 2-DB 2几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14．(2)三角形模式：a ⋅b =AM 2-14DB 2(M 为BD 的中点)结论2：矩形大法：矩形所在平面内任一点到其对角线端点距离的平方和相等．已知点O 是矩形ABCD 与所在平面内任一点，证明：OA 2+OC 2=OB 2+OD 2．【证明】(坐标法)设AB =a ,AD =b ，以AB 所在直线为轴建立平面直角坐标系xoy ，则B (a ,0),D (0,b ),C (a ,b )，设O (x ,y )，则OA 2+OC 2=(x 2+y 2)+[(x -a )2+(y -b )2]OB 2+OD 2=[(x -a )2+y 2]+[x 2+(y -b )2]∴OA 2+OC 2=OB 2+OD 2结论3：三点共线的充要条件设OA 、OB 、OP 是三个不共线向量，则A 、B 、P 共线⇔存在λ∈R 使OP =(1-λ)OA +λOB ．特别地，当P 为线段AB 的中点时，OP =12OA+12OB ．结论4：等和线【基本定理】(一)平面向量共线定理已知OA =λOB +μOC ，若λ+μ=1，则A ,B ,C 三点共线；反之亦然．(二)等和线平面内一组基底OA ,OB 及任一向量OP ，OP =λOA +μOB (λ,μ∈R )，若点P 在直线AB 上或者在平行于AB 的直线上，则λ+μ=k (定值)，反之也成立，我们把直线AB 以及与直线AB 平行的直线称为等和线．(1)当等和线恰为直线AB 时，k =1；(2)当等和线在O 点和直线AB 之间时，k ∈(0,1)；(3)当直线AB 在点O 和等和线之间时，k ∈(1,+∞)；(4)当等和线过O 点时，k =0；(5)若两等和线关于O 点对称，则定值k 互为相反数；结论5：奔驰定理【奔驰定理】若O 为ΔABC 内任一点，且αOA +βOB +γOC =0 ，则S ΔBOC :S ΔAOC :S ΔAOB =α:β:γ【典型例题】例1.在ΔABC 中，M 是BC 的中点，AM =3,BC =10，则AB ⋅AC =____．例2.正三角形内接于半径为2的圆O ，点P 是圆O 上的一个动点，则PA ⋅PB 的取值范围是．例3.已知圆C 1:x 2+y 2=9与C 2:x 2+y 2=36，定点P (2,0)，A 、B 分别在圆C 1和圆C 2上，满足PA ⊥PB ，则线段AB 的取值范围是．例4.在平面内，已知AB 1 ⊥AB 2 ，OB 1 =OB 2 =1，AP =AB 1 +AB 2 ，若|OP |<12，则|OA |的取值范围是()A.0,52B.52,72 C.52,2D.72,2例5.在△ABC 中，已知D 是AB 边上一点，若AD =2DB ,CD =13CA+λCB ，则λ=()A.13B.23C.-13D.-23例6.给定两个长度为1的平面向量OA 和OB，它们的夹角为1200，点C 在以O 为圆心的圆弧AB 上变动．若OC =xOA +yOB，其中x ,y ∈R ，则x +y 的最大值是__________．【过关测试】一、单选题1.(2023·北京西城·高三统考期末)在△ABC 中，AC =BC =1,∠C =90°．P 为AB 边上的动点，则PB ⋅PC的取值范围是( )A.-14,1B.-18,1C.-14,2D.-18,22.(2023·北京昌平·高三统考期末)已知向量a ,b ,c 满足a =2,b =1,a ,b =π4,c -a⋅c -b =0，则c的最大值是( )A.2-1B.5-12C.5+12D.2+13.(2023·广西桂林·统考一模)如图，在△ABC 中，M 为线段BC 的中点，G 为线段AM 上一点且AG=2GM ，过点G 的直线分别交直线AB 、AC 于P 、Q 两点，AB =xAP (x >0)，AC =yAQ (y >0)，则1x+1y +1的最小值为( )A.34B.1C.43D.44.(2023·全国·高三专题练习)如图，在半径为4的扇形AOB 中，∠AOB =120∘，点P 是AB上的一点，则AP ·BP的最小值为( )A.-8B.-3C.-2D.-45.(2023·全国·高三专题练习)在平面内，定点A ,B ,C ,D 满足|DA |=|DB|=|DC |，DA ⋅DB =DB ⋅DC =DC ⋅DA =-2，动点P ，M 满足|AP |=1，PM =MC ，则|BM |2的最大值是( )A.434B.494C.47+634D.37+23346.(2023·全国·高三专题练习)△ABC 中，AB =2，∠ACB =π4，O 是△ABC 外接圆圆心，是OC ⋅AB +CA ⋅CB的最大值为( )A.0B.1C.3D.57.(2023·全国·高三专题练习)AB 为⊙C ：(x -2)2+(y -4)2=25的一条弦，AB =6，若点P 为⊙C 上一动点，则PA ⋅PB的取值范围是( )A.[0，100]B.[-12，48]C.[-9，64]D.[-8，72]8.(2023·全国·高三专题练习)在△ABC 中，D 为三角形所在平面内一点，且AD =13AB +12AC ，则S △BCDS △ACD =( )A.16B.12C.13D.239.(2023·全国·高三专题练习)已知向量a ，b ，c 满足a =4，a 在b 方向上的投影为2，c ⋅c -a=-3，则|b -c|的最小值为( )A.3-1B.3+1C.23-2D.23+210.(2023·全国·高三专题练习)已知边长为2的菱形ABCD 中，点F 为BD 上一动点，点E 满足BE=2EC ，AE ⋅BD =-23，则AF ⋅EF 的最小值为( )A.-23B.-43C.-15275D.-733611.(2023·全国·高三专题练习)P 是ΔABC 所在平面上的一点,满足PA +PB +PC =2AB,若S ΔABC =6,则ΔPAB 的面积为( )A.2B.3C.4D.812.(2023·全国·高三专题练习)在矩形ABCD 中，AB =1，AD =2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP =λAB +μAD，则λ+μ的最大值为A.3B.22C.5D.2二、多选题13.(2023·全国·高三专题练习)在△ABC 中，AB =AC =3，BC =4，O 为△ABC 内的一点，设AO =λAB +μAC ，则下列说法正确的是( )A.若O 为△ABC 的重心，则λ+μ=23 B.若O 为△ABC 的内心，则λ+μ==25C.若O 为△ABC 的外心，则λ+μ=910 D.若O 为△ABC 的垂心，则λ+μ=1514.(2023·全国·模拟预测)已知a ，b ，c 是互不相等的非零向量，其中a ，b 是互相垂直的单位向量，c =xa+ybx ,y ∈R ，记OA =a ，OB =b ，OC =c ，则下列说法正确的是( )A.若a -c⋅b -c =0，则O ，A ，B ，C 四点在同一个圆上B.若a -c ⋅b -c =0，则c的最大值为2C.若c =1，则a -c ⋅b -c 的最大值为22+1D.若c=1，则x +y 的最小值为-215.(2023·全国·高三专题练习)“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车，(Mercedesbenz )的log o 很相似，故形象地称其为“奔驰定理”，奔驰定理：已知O 是△ABC内一点，△BOC ，△AOC ，△AOB 的面积分别为S A ，S B ，S C ，且S A ⋅OA +S B ⋅OB +S C ⋅OC =0．设O 是锐角△ABC 内的一点，∠BAC ，∠ABC ，∠ACB 分别是的△ABC 三个内角，以下命题正确的有( )A.若OA +2OB +3OC =0，则S A :S B :S C =1:2:3B.若OA =OB =2，∠AOB =5π6，2OA +3OB +4OC =0 ，则S △ABC =92C.若O 为△ABC 的内心，3OA +4OB +5OC =0 ，则∠C =π2D.若O 为△ABC 的垂心，3OA +4OB +5OC =0 ，则cos ∠AOB =-6616.(2023·全国·高三专题练习)重庆荣昌折扇是中国四大名扇之一，始于1551年明代嘉靖年间，明末已成为贡品人朝，产品以其精湛的工业制作而闻名于海内外．经历代艺人刻苦钻研、精工创制，荣昌折扇逐步发展成为具有独特风格的中国传统工艺品，其精雅宜士人，其华灿宜艳女，深受各阶层人民喜爱．古人曾有诗赞曰：“开合清风纸半张，随机舒卷岂寻常；金环并束龙腰细，玉栅齐编凤翅长，偏称游人携袖里，不劳侍女执花傍；宫罗旧赐休相妒，还汝团圆共夜凉”图1为荣昌折扇，其平面图为图2的扇形COD ，其中∠COD=2π3,OC =3OA =3，动点P 在CD 上(含端点)，连接OP 交扇形OAB 的弧AB 于点Q ，且OQ =xOC +yOD ，则下列说法正确的是( )图1 图2A.若y =x ，则x +y =23B.若y =2x ，则OA ⋅OP=0C.AB ⋅PQ≥-2D.PA ⋅PB ≥11217.(2023·全国·高三专题练习)如图，圆О是边长为23的等边三角形ABC 的内切圆，其与BC 边相切于点D ，点M 为圆上任意一点，BM =xBA +yBD(x ，y ∈R )，则2x +y 可以取值为( )A.16B.13C.23D.118.(2023·全国·高三专题练习)“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车(Mercedesbenz )的log o 很相似，故形象地称其为“奔驰定理”.奔驰定理：已知O 是△ABC内的一点，△BOC 、△AOC 、△AOB 的面积分别为S A 、S B 、S C ，则S A ⋅OA +S B ⋅OB +S C ⋅OC =0.若O 是锐角△ABC 内的一点，∠BAC 、∠ABC 、∠ACB 是△ABC 的三个内角，且点O 满足OA ⋅OB =OB ⋅OC=OC ⋅OA，则( )A.O 为△ABC 的垂心B.∠AOB =π-∠ACBC.OA :OB :OC=sin ∠BAC :sin ∠ABC :sin ∠ACBD.tan ∠BAC ⋅OA +tan ∠ABC ⋅OB +tan ∠ACB ⋅OC =0三、填空题19.(2023·全国·高三专题练习)在△ABC 中，点E ，F 分别是线段AB ，AC 的中点，点P 在直线EF 上，若△ABC 的面积为2，则PB ⋅PC +BC 2的最小值是_____________.20.(2023·四川南充·统考一模)已知向量a 与b 夹角为锐角，且a =b =2，任意λ∈R ，a -λ⋅b 的最小值为3，若向量c 满足c -a ⋅c -b =0，则c的取值范围为______．21.(2023·上海徐汇·位育中学校考模拟预测)已知圆O 半径为1，P 、A 、B 是圆O 上不重合的点，则PA ⋅PB的最小值为_____.22.(2023·全国·高三专题练习)已知平面向量a ,b ,c 满足|b |⋅|c |=1，若|3a -(b +c )|=|a ⋅b |⋅|c |，则-a2+2b 2+c2的最小值是_____________．23.(2023·全国·高三专题练习)已知平面向量a 、b 、c 满足：a 与b 的夹角为2π3,c -a⋅c -b =0,a + b =2，记M 是c -a -b的最大值，则M 的最小值是__________．24.(2023·全国·高三专题练习)点M 在△ABC 内部，满足2MA +3MB +4MC =0 ，则S △MAC :S △MAB =____________．。

培优点05极化恒等式、奔驰定理与等和线定理(3大考点+强化训练)(习题版)

培优点05极化恒等式、奔驰定理与等和线定理（3大考点+强化训练）平面向量基本定理及数量积是高考考查的重点，很多时候需要用基底代换，运算量大且复杂，用向量极化恒等式、奔驰定理、等和(高)线求解，能简化向量代换，减少运算量，使题目更加清晰简单．知识导图考点分类讲解考点一：向量极化恒等式极化恒等式：a ·b .变式：(1)a ·b ＝a ＋b24－a －b24，a ·b ＝|a ＋b |24－|a －b |24.(2)如图，在△ABC 中，设M 为BC 的中点，则AB →·AC →＝AM →2－14CB →2＝AM →2－MB →2.规律方法利用向量的极化恒等式可以对数量积进行转化，体现了向量的几何属性，特别适合于以三角形为载体，含有线段中点的向量问题．【例1】(2023·郑州模拟)如图所示，△ABC 是边长为8的等边三角形，点P 为AC 边上的一个动点，长度为6的线段EF 的中点为B ，则PE →·PF →的取值范围是________．【变式】．（2022·北京·高考真题）在ABC 中，3,4,90AC BC C ==∠=︒．P 为ABC 所在平面内的动点，且1PC =，则PA PB ⋅的取值范围是（）A ．[5,3]-B ．[3,5]-C ．[6,4]-D ．[4,6]-考点二:平面向量“奔驰定理”定理：如图，已知P 为△ABC 内一点，则有S △PBC ·PA →＋S △PAC ·PB →＋S △PAB ·PC →＝0.易错提醒利用平面向量“奔驰定理”解题时，要严格按照定理的格式，注意定理中的点P 为△ABC 内一点；定理中等式左边三个向量的系数之比对应三个三角形的面积之比．【例2】（2022·安徽·三模）平面上有ABC 及其内一点O ，构成如图所示图形，若将OAB ，OBC △，OCA 的面积分别记作c S ，a S ，b S ，则有关系式0a b c S OA S OB S OC ⋅+⋅+⋅=uu r uu u r uuu r r．因图形和奔驰车的logo 很相似，常把上述结论称为“奔驰定理”．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若满足0a OA b OB c OC ⋅+⋅+⋅=，则O 为ABC 的（）A ．外心B ．内心C ．重心D ．垂心【变式1】(2023·重庆模拟)△ABC 内一点O 满足关系式S △OBC ·OA →＋S △OAC ·OB →＋S △OAB ·OC →＝0，即称为经典的“奔驰定理”，若△ABC 的三边为a ，b ，c ，现有a ·OA →＋b ·OB →＋c ·OC →＝0，则O 为△ABC 的()A．外心B．内心C．重心D．垂心【变式2】(2023·安阳模拟)如图，已知O 是△ABC 的垂心，且OA →＋2OB →＋3OC →＝0，则tan∠BAC ∶tan∠ABC ∶tan∠ACB 等于()A．1∶2∶3B．1∶2∶4C．2∶3∶4D．2∶3∶6考点三:等和(高)线定理等和(高)线平面内一组基底OA →，OB →及任一向量OP ′——→，OP ′——→＝λOA →＋μOB →(λ，μ∈R )，若点P ′在直线AB 上或在平行于AB 的直线上，则λ＋μ＝k (定值)；反之也成立，我们把直线AB 以及与直线AB 平行的直线称为等和(高)线．(1)当等和线恰为直线AB 时，k ＝1；(2)当等和线在O 点和直线AB 之间时，k ∈(0,1)；(3)当直线AB 在O 点和等和线之间时，k ∈(1，＋∞)；(4)当等和线过O 点时，k ＝0；(5)若两等和线关于O 点对称，则定值k 1，k 2互为相反数；(6)定值k 的变化与等和线到O 点的距离成正比．规律方法要注意等和(高)线定理的形式，解题时一般要先找到k ＝1时的等和(高)线，利用比例求其他的等和(高)线．【例3】．（2022·山东烟台·三模）如图，边长为2的等边三角形的外接圆为圆O ，P 为圆O 上任一点，若AP xAB yAC =+，则22x y +的最大值为（）A ．83B ．2C ．43D ．1【变式3】已知O 是ABC ∆内一点，且0OA OB OC ++=，点M 在OBC ∆内（不含边界），若AM AB AC λμ=+ ，则2λμ+的取值范围是A ．51,2⎛⎫ ⎪⎝⎭B ．()1,2C ．2,13⎛⎫ ⎪⎝⎭D ．1,12⎛⎫ ⎪⎝⎭强化训练一、单选题1．如图，AB 是圆O 的直径，P 是圆弧 AB 上的点，M 、N 是直径AB 上关于O 对称的两点，且6,4AB MN ==，则PM PN ⋅（）A ．13B ．7C ．5D ．32．已知ABC 是边长为2的等边三角形，P 为平面ABC 内一点，则()PA PB PC +的最小值是()A ．2-B ．32-C ．43-D ．1-3．设向量,a b 满足10a b += 6a b -=r r a b ⋅ =A ．1B ．2C ．3D ．54．已知圆C 的半径为2，点A 满足||3AC =uuu r，E ，F 分别是C 上两个动点，且||3EF =AE AF ⋅的取值范围是（）A ．[]416，B ．[]26，C ．[]622，D ．[]113，5．在ABC 中，点D 是线段BC 上任意一点，点P 满足3AD AP =，若存在实数m 和n ，使得BP m AB n AC =+ ，则m n +=（）A ．23B ．13C ．13-D ．23-6．在△ABC 中，M 为边BC 上任意一点，N 为AM 中点，且满足AN AB AC λμ=+，则22λμ+的最小值为（）A ．116B ．14C ．18D ．17．在ABC ∆中，点D 满足34BD BC = ，当E 点在线段AD （不包含端点）上移动时，若AE AB AC λμ=+，则3λμ+的取值范围是A．)+∞B ．[2,)+∞C ．17(,)4+∞D ．(2,)+∞8．在ABC 中，点O 是线段BC 上的点，且满足||3||OC OB =，过点O 的直线分别交直线AB 、AC 于点E 、F ，且AB mAE = ，AC nAF = ，其中0m >且0n >，若1tm n+的最小值为3，则正数t 的值为()A ．2B ．3C ．83D ．1139．如图，在直角梯形ABCD 中，AB AD ⊥，AB ∥DC ，2AB =，1AD DC ==，图中圆弧所在圆的圆心为点C ，半径为12，且点P 在图中阴影部分（包括边界）运动．若AP xAB yAC =+，其中x y R ∈，，则4x y -的取值范围是（）A．234⎡+⎢⎥⎣⎦，B．232⎡+⎢⎥⎣⎦，C．3342⎡-+⎢⎣⎦D．3322⎡-+⎢⎥⎣⎦10．在矩形ABCD 中，AB=1，AD=2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP =λAB +μAD，则λ+μ的最大值为A ．3B ．CD ．211．奔驰定理：已知O 是ABC 内的一点，BOC ，AOC ，AOB 的面积分别为A S ，B S ，C S ，则0A B C S OA S OB S OC ⋅+⋅+⋅=.“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车的log o 很相似，故形象地称其为“奔驰定理”.设O 为三角形ABC 内一点，且满足：2332OA OB OC AB BC CA ++=++，则AOB ABCS S=△△（）A ．25B ．12C ．16D ．1312．已知O 是ABC 内的一点，若,,BOC AOC AOB 的面积分别记为123,,S S S ，则1230S OA S OB S OC ⋅+⋅+⋅=.这个定理对应的图形与“奔驰”轿车的log o 很相似，故形象地称其为“奔驰定理”.如图，已知O 是ABC 的垂心，且230OA OB OC ++=，则tan :tan :tan BAC ABC ACB ∠∠∠=（）A ．1:2:3B ．1:2:4C ．2:3:4D ．2:3:613．已知点P 是ABC 所在平面内一点，若2133AP AB AC =+，则ABP 与ACP 的面积之比是（）A ．3:1B ．2:1C ．1:3D ．1:214．已知点P 为ABC 内一点，230PA PB PC ++=，则△APB ，△APC ，△BPC 的面积之比为（）A ．9:4:1B ．1:4:9C ．1:2:3D ．3:2:1二、多选题15．如图.P 为ABC 内任意一点，角,,A B C 的对边分别为,,a b c ，总有优美等式0PBC PAC PAB S PA S PB S PC ++=成立，因该图形酯似奔驰汽车车标，故又称为奔驰定理.则以下命题是真命题的有（）A ．若P 是ABC 的重心，则有0PA PB PC ++=B ．若0aPA bPB cPC ++=成立，则P 是ABC 的内心C ．若2155AP AB AC =+，则:2:5ABP ABC S S =△△D ．若P 是ABC 的外心，π4A =，PA mPB nPC =+ ，则)m n ⎡+∈⎣16．“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”（Mercedesbenz ）的log o 很相似，故形象地称其为“奔驰定理”.奔驰定理：已知O 是ABC 内的一点，BOC ，AOC ，AOB 的面积分别为A S ，B S ，C S ，则0A B C S OA S OB S OC ⋅+⋅+⋅=.若O 是锐角ABC 内的一点，A ，B ，C 是ABC的三个内角，且点O 满足OA OB OB OC OA OC ⋅=⋅=⋅.则（）A ．O 为ABC 的外心B ．BOC A π∠+=C ．::cos :cos :cos OA OB OC A B C =D ．tan tan tan 0⋅+⋅+⋅=A OAB OBC OC 17．“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车，（Mercedesbenz ）的logo 很相似，故形象地称其为“奔驰定理”，奔驰定理：已知O 是△ABC 内一点，△BOC ，△AOC ，△AOB的面积分别为A S ，B S ，C S ，且0A B C S OA S OB S OC ⋅+⋅+⋅=．设O 是锐角△ABC 内的一点，∠BAC ，∠ABC ，∠ACB 分别是的△ABC 三个内角，以下命题正确的有（）A ．若230OA OB OC ++=，则::1:2:3A B C S S S =B ．若2OA OB == ，5π6AOB ∠=，2340OA OB OC ++= ，则92ABC S =C ．若O 为△ABC 的内心，3450OA OB OC ++= ，则π2C ∠=D ．若O 为△ABC 的垂心，3450OA OB OC ++= ，则cos 6AOB ∠=-18．在平行四边形ABCD 中，AB AC ⊥，1AB AC ==，点P 是ABC 的三边上的任意一点，设AP AB AD λμ=+，().R λμ∈，则下列结论正确的是（）A ．0λ≥，0μ≥B ．当点P 为AC 中点时，1λμ+=C ．AP AD ⋅的最大值为1D ．满足32λμ+=的点P 有且只有一个三、填空题19．在扇形OAB 中，60AOB ∠=，C 为弧AB 上的一动点，若OC xOA yOB =+，则3x y +的取值范围是．20．在ABC 中，点O 是线段BC 上的点，且满足3OC OB =，过点O 的直线分别交直线,AB AC 于点,E F ，且AB m AE = ，AC nAF = ，其中0m >且0n >，若12m n+的最小值为.21．如图，平面内有三个向量OA 、OB 、OC ,其中与OA 与OB的夹角为120 ，OA 与OC 的夹角为30 ,且|||1OA OB ==，||OC =()，OC λOA μOB λμ=+∈R ,则λμ+的值为.22．（22-23高三上·江苏南通·期中）如图，已知M ，N 是ABC 边BC 上的两个三等分点，若6BC =，4AM AN ⋅=，则AB AC ⋅uu u r uuu r =．23．已知线段AB 是圆22:(1)(1)4C x y -+-=上的一条动弦，且3AB =设点O 为坐标原点，则+OA OB的最大值为；如果直线1:310l x my m --+=与2:310l mx y m +++=相交于点M ，则MA MB ⋅的最小值为.24．在锐角三角形ABC 中，已知,23B AB AC π=-= ，则AB AC ⋅的取值范围是．25．四边形ABCD 中，点,E F 分别是,AB CD 的中点，2AB =，22CD =，1EF =，点P 满足0PA PB ⋅=，则PC PD ⋅的最大值为.26．点P 为ABC 内一点，340PA PB PC →→→→++=，则,,APB APC BPC 的面积之比是.。