初等矩阵的性质
初等矩阵及其性质

证明二:初等矩阵不改变向量间的线性关系
要点一
总结词
要点二
详细描述
初等矩阵不会改变向量间的线性关系,即对于任意向量组 ,经过初等变换后,向量间的线性关系不变。
初等矩阵由单位矩阵通过行变换或列变换得到,这些变换 都不会改变向量间的线性关系。因此,对于任意向量组, 经过初等变换后,向量间的线性关系不变。
证明三:初等矩阵的行列式值不为零
总结词
初等矩阵的行列式值不为零,即对于任意一 个初等矩阵,其行列式值不为零。
详细描述
初等矩阵由单位矩阵通过行变换或列变换得 到,这些变换都不会改变矩阵的行列式值。 因此,对于任意一个初等矩阵,其行列式值
用
矩阵的逆
通过初等矩阵的变换,可以求得一个可逆矩阵的逆矩阵,从而进行矩阵运算。
线性变换
在研究线性变换时,可以利用初等矩阵的变换,将线性变换表示为矩阵的形式,便于分析和理解。
04
初等矩阵的实例分析
实例一:求解线性方程组
总结词
通过初等矩阵的行变换,将线性方程组的增广矩阵化为阶梯形矩阵,从而求解线性方程 组。
证明一:初等矩阵是可逆的
总结词
详细描述
初等矩阵是可逆矩阵,即存在一个可逆矩阵, 使得初等矩阵与单位矩阵通过一系列的行变 换或列变换相互转化。
初等矩阵由单位矩阵通过互换两行或两列、 将某一行或某一列乘以非零常数以及将某一 行或某一列乘以另一行或另一列的非零倍数 得到。由于这些变换都是可逆的,因此初等 矩阵也是可逆的。
实例三:求矩阵的逆矩阵
总结词
利用初等矩阵的行变换性质,通过行变 换将可逆矩阵化为单位矩阵,从而求出 其逆矩阵。
VS
详细描述
对于可逆矩阵,可以通过初等矩阵的行变 换将其化为单位矩阵。在行变换过程中, 原矩阵左边的矩阵即为所求的逆矩阵。这 种方法称为高斯消元法,适用于求解可逆 矩阵的逆矩阵。
1-6-2 初等矩阵和初等变换求逆矩阵
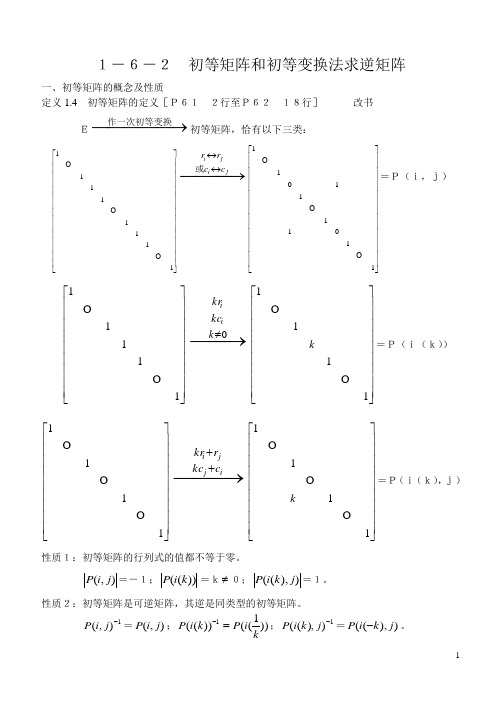
1-6-2 初等矩阵和初等变换法求逆矩阵一、初等矩阵的概念及性质定义1.4 初等矩阵的定义[P61 2行至P62 18行] 改书E−−−−→−作一次初等变换初等矩阵,恰有以下三类:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡11111111 −−−→−↔↔ji ji cc r r 或⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1101111011 =P(i,j) ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡11111 −→−≠0k kc kr i i ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1111 k =P(i(k)) ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1111 −−→−++ij ji c kc r kr ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1111 k =P(i(k),j) 性质1:初等矩阵的行列式的值都不等于零。
),(j i P =-1;))((k i P =k≠0;)),((j k i P =1。
性质2:初等矩阵是可逆矩阵,其逆是同类型的初等矩阵。
1),(-j i P =),(j i P ;))1(())((1ki P k i P =-;1)),((-j k i P =)),((j k i P -。
性质3——定理1.7[P63 牢记]用初等矩阵左乘A,相当于对A作一个初等行变换;验证定理1.7:P62 -4行至P63 16行。
二、可逆矩阵与初等矩阵的关系 定理1.8 任一可逆矩阵−−−−→−行的初等变换E。
证明:P64:2至19行。
[相当于用高斯—若当消元法解有唯一解的线性方程组]如:[复习]P77 3(1)求解线性方程组),(b A A ==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--311222101321→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---555022101321→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--550022103101→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--110022103101→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-110000102001,⎪⎩⎪⎨⎧==-=102321x x x 。
4.6初等矩阵

●初等矩阵的定义 自行列三阶单位矩阵得到的三类初等矩阵!
●初等矩阵的性质
1、初等矩阵是可逆的,并且其逆矩阵也是同一类型的 初等矩阵。
P(i, j)1 P(i, j)
Pi
(k )1
Pi
(
1 k
)
P(i, j(k))-1 P(i, j(k))
2.有限个初等矩阵的乘积仍然可逆.
●初等矩阵的作用(P188引理)
1 1
2 4
1 0
0 1
0 0
r3 r2
r1 r2
1 0
1 1
4 0 1 0 2 1 0 0
1 1 0 0 0 1
0 2 4 0 1 0
r1 r2
r3 2r2
1 0
0 1
2 2
1 1
1 0
0 0 从而知,A不可逆。
0 0 0 2 1 1
思考题
将矩阵A
1 2
0 0
01表示成有限个初等方阵
0 1 0
的乘积.
思考题解答
1 A 2
0 0
0 1
0 1 0
解 A可以看成是由3阶单位矩阵 I 经4次初等变换,
r23, c31(2), r3(1), c3 1
0 0 0 2 1 1
此处不可能化成单位矩阵
1 2 3
(1)
A
2
2
1
3 4 3
1 2 0
(2)
B
1
2
1
0 0 2
3 6 1
0
3
4
2
§5-初等矩阵

与A等价的矩阵有许许多多,那么能否挑出一种简单矩 阵,把它作为A的代表呢?
10
定理5.2 任意一个 s n 矩阵A都与一形如
1
00
Er 0
0
0
0
00
0
r 的矩阵等价,且主对角线上1的个数 等于A的
秩.称这个矩阵为A的标准形.
2、用非零数c乘E的第i 行,得到初等矩阵
1
p(i(c))
c
i
1
称为第二类初等矩阵(又称倍法矩阵).
注 倍法矩阵的特点是:(i, i)元=c ;其它元素与单位
矩阵相同.
3
3、把E的第j 行的k倍加到第i行上,得到初等矩阵
1
1
k
i行
p(i,
(j k))
.
1
j行
1
称为第三类初等矩阵(又称消法矩阵).
1
A1 A1
2)
P(i(c))A
c
Ai
cAi
,
1 As As
这相当于把A的第i 行乘以c.
1
A1 A1
3)
P(i,
j(k)) A
1
k
1
Ai
Ai
kAj
,
Aj
Aj
1 As As
这个定理可以用八个字概括:“左行右列,首尾为主”9 .
因此我们有
PsQ1Q2
Qt ,
定理5.3 n级方阵A可逆 A能表成初等矩阵的乘积
13
推论1: 两个 s n矩阵A、B等价 存在s级可逆矩
阵P和n级可逆矩阵Q,使B=PAQ. 推论2:可逆矩阵可经一系列初等行变换化成单位矩阵E
第三讲 矩阵的初等变换及其性质资料

例2 阶梯形,行简化阶梯形,标准形
1 A 0
0
0 1 0
8 1 0
0 0 1
1
B
0 0 0
0 1 0 0
2 0 0 0
1 0 0 0
0 0 10
0 1 1 0 C 0 0 0 1
0 0 0 0
0 1 2 0 3 D 0 0 0 1 2
0 0 0 0 0
例 3 阶梯形,标准阶梯形,标准形
1 0 0 0 0 1 0 0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0
0 0
1 0
0 0
00
1 0 0 0 0 1 0 0 0 0 1 0
1 0 0 0 0 0 1 0 0 0 0 0 0 0 0
将矩阵用初等行变换化为行简化阶梯形的步骤: 第一步 (1) 在第一列中选一个非0元作为首元
(2) 把某个方程乘以一个非零数
(3) 某个方程的非零倍加到另一个方程上
例1
2x1 x2 x3 x4 2
43xxx111
x2 6x2 6x2
2x3 2x3 9x3
x4 2x4 7 x4
4 4 9
①②
①②
x1 x2 2x3 x4 4
423xxx111
x2 6x2 6x2
第一行乘 -2 加到第二行, 第一行乘-3 加到第三行
1 0 -4 5 1 0 1 -7 6 0 00001
1 0 -4 5 0 0 1 -7 6 0 00001
第二行乘 加到第一行 第二行乘-1 加到第三行
例 5 用初等行变换化为行简化阶梯形
11 1 1 1 1
111111
A= 3 2 1 0 -3 6 r2 3r1 0 -1 -2 -3 -6 3
2.5矩阵的初等变换(重庆工商大学-钟润华老师所编)

1 0 A2 0 0
4 1 1 0 3 0 0 1 3 0 0 0 0
0 1 0
c3 c4 c4 c1 c2 c5 4c1 3c2 3c
1 1 0 0 0 0 3 0 0 0
0 0 1 0 00 00 0 1 0 1 11 00 0 0
i列
j列
1 1 k i行 E ( i , j ( k )) 1 j行 1
消去阵
12
注: (1)
| E(i, j ) | 1,| E(i(k ) | k ,| E(i, j (k )) | 1.
Or ( n r ) O( m r )( n r )
9
二、初等矩阵及其性质
定义2.15 n 阶单位矩阵 E,经过一次初等变换所得
到的矩阵,称为 n 阶初等矩阵.
(1) 交换E的 i, j 两行或两列:
1 0 1 1 1 1 0 1
若 A 可逆,则 X A1 B.
2 3 2 5 2 1 3 1 4 3 4 3 2 3 2
5 2 5 1 9 2 6 2 12
24
3 2 5 1 2 r2 2r1 0 2 5 1 9 r3 3r1 0 2 6 2 12
r2 2 r3 5 r2 r4 3r2
4 1 1 1 1 0 r 1 r 0 4 3 2 0 0 2 6 0 0 0 1 3 0
4 1 1 1 0 A1 0 0 2 6 0 0 0 0 1
2-5初等矩阵及其性质
使 A1 P1P2 Ps
由 A-1A=E; A-1E= A-1;
得 : P1P2…PsA=E
P1P2…PsE=A-1
结论: 若经过一系列初等行变换将A化成单位矩阵
E时,则施行同样的一系列的初等行变换就把单位矩阵
E化成了逆矩阵A-1
用初等变换求逆矩阵的方法:
1)构造矩:(A E);
2)做初等行变换 A E行 E A1
Ei (k )
1 Ei (k )
Eij (k) Eij (k)
3) 初等矩阵的转置还是初等矩阵,即:
EijT Eij ; EiT (k) Ei (k); EijT (k) E ji (k)
二、用初等变换求逆矩阵
【定理2.4】矩阵A可逆的充要条件是:存在有
限个初等阵P1,P2,…,Pk,使 A=P1P2…Pk.
3
4 1
1 2 1
1
4 1
2
2
0
0
1
1 4
1 2
3 4
所以:
3 A1 41
1 2
1
1
4 1
2
2
1 4
1 2
3 4
2.用初等变换解矩阵方程 (1)设矩阵方程为:AX=B,其中A可逆,则矩阵X=A-1B
设:A-1 =P1P2…Ps (Pi为初等矩阵) 由 A-1A=E; A-1B= X;
3
1
2
3
7
2
4 3 3 4 11 3
3
2
1
3
4
1
1 3 2 1 5 2
例四66页 6 1 1 -1
设矩阵
A -1 1
1
1 -1 1
矩阵X 满足 AX A1 2X ,其中 X 是 A的伴随矩阵,求 X.
3.5(2)初等矩阵
2、以数 k ≠ 0 乘某行或某列
以数k≠0乘单位矩阵 的第 行(列), 得到初等矩阵 乘单位矩阵E的第 以数 乘单位矩阵 的第i行 列 得到初等矩阵E(i(k))
3、以数k ≠ 0乘某行(列)加到另一行(列)上去 以 k 乘 E 的第 j 行加到第 i 行上 ,或以 k 乘 E 的第 i 列
加到第 j 列上 , 得到初等矩阵E(i, j(k)) 得到初等矩阵
−1
作业: 作业:P135 45(3)(4), 46(2)(4), 48, 50
0 1 0 将矩阵 A = 2 0 − 1 表示成有限个初等方阵 0 −1 0 的乘积. 解法1 解法 A可以看成是由 阶单位矩阵 E 经4次初等变换 可以看成是由3阶单位矩阵 次初等变换, 次初等变换 r2 ↔ r3 , c1 + 2c3 , (− 1)r3 , (− 1)c3 而得.而这4次初等变换所对应的初等方阵为 次初等变换所对应的初等方阵为: 而得.而这 次初等变换所对应的初等方阵为 1 0 0 1 0 0 1 0 0 P1 = 0 0 1 , P2 = 0 1 0 , P3 = 0 1 0 , 0 0 − 1 0 1 0 2 0 1 1 0 0 由初等方阵的性质得 P4 = 0 1 0 . A = P3 P1 EP2 P4 = P3 P1 P2 P4 . 0 0 − 1
初等矩阵
§6初等矩阵这一节我们来建立矩阵的初等变换与矩阵乘法的联系,并在这个基础上,给出用初等变换求逆矩阵的方法。
一、初等矩阵1.定义:由单位矩阵经过一次初等变换得到的矩阵,称为初等矩阵.显然,初等矩阵都是方阵,每个初等变换都有一个与之相应的初等矩阵。
对应三种初等行、列变换,有三种类型的初等矩阵:101(,)11i j i jr r E p i j Ec c ⎛⎫ ⎪ ⎪↔ ⎪⎪=⎪ ⎪↔ ⎪ ⎪ ⎪⎝⎭或1(())1i ikr E k p i k kEkc ⎛⎫ ⎪⎪≠⎪= ⎪ ⎪ ⎪⎝⎭或1()1(,)()11i j j ir kr E i k p i j k Ej c rc ⎛⎫⎪ ⎪+ ⎪⎪= ⎪ ⎪+ ⎪ ⎪ ⎪⎝⎭()或2.初等矩阵的性质 1)初等矩阵皆可逆,且1111(,)(,),(())(()),(,())(,()).p i j p i j p i k p i p i j k p i j k k ---===-2)对任一s n ⨯矩阵A ,左(右)乘一个s s ⨯初等矩阵相当于对A 作一初等行(列)变换.(,)p i j A : 对换A 的i ,j 两行; A (,)p i j : 对换A 的i ,j 两列.(())p i k A :用非零数k 乘A 的第i 列; A (())p i k :用非零数k乘A 的第i 列.(,())p i j k A :A 的第j 行乘以k 加到第i 行;A (,())p i j k :A 的第i 列乘以k 加到第j 列.证明2) 我们只证行变换的情形,列变换的情形可同样证明。
令()ij b B = 为任意一个s×s 矩阵,12,,,s A A A 为A 的行向量。
则111122121122221122s s s s s s ss s b A b A b A b A b A b A BA b A b A b A +++⎡⎤⎢⎥+++⎢⎥=⎢⎥⎢⎥+++⎣⎦特别,令()j i P B ,=,得()行,行j i A A A A A j i P S i j ⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡= 1,这就相当于把A 的i 行与j 行互换。
第三章5初等矩阵
1 0 0 0 6 3 1 2 0 0 0 1 0 4 1 0 1 1 2 0 1 0 1 / 2 1 / 6 1 / 3 0 1 0 1 1 2 0 1 0 1 / 2 1 / 6 1 / 3 0 1 2 / 3 1 / 3 1 0 4/ 3 1/ 3 2 0 1 / 6 1 / 6 1 / 2 1 2 / 3 1 / 3 1
2 3 1 0. 2 3 2 3 1 0 2 1
14
2 2 3 4 2 1 1 0 1 1 1 2 1 1 2 1 1 0 1 2 2 3 4 1 2 1 1 1 1 0 1 1 0 4 3 2 0 0 1 1 0 3
8
充分性.如果A可以表示为初等矩阵的乘积,由 于初等矩阵可逆,而可逆矩阵的乘积仍然可逆, 故A可逆.
9
二、用初等变换求逆矩阵
设方阵A可逆,其逆为A-1根据前面的定理,存 在初等矩阵 G1 ,, Gk ,使得
A Gk G1 Gk G1 E , A A Gk G1 A E , Gk G1 ( A, E ) (Gk G1 A, Gk G1 E ) ( E , A1 ).
7
定理 方阵A可逆的充要条件是它可以表示为 初等矩阵的乘积. 证明必要性.设A可逆,则其秩为r,根据上一个 定理,存在存在初等矩阵 P1 ,, Ps 和初等矩 阵 Q1 , , Qt ,使得
Ps P1 AQ1 Qt E .
于是
A P11 Ps1Qs1 Q11 .
而初等矩阵的逆仍是初等矩阵,上式表明 A 可以表示为初等矩阵的乘积.
13
求An的逆矩阵,相当解方程AX=E,把E换成 矩 阵B n×m,可以用类似的初等行变换解矩阵方程 AX=B.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性代数
思考 三种类型的初等矩阵是否可逆?
1
O
0L 1
i
P(i,
j)
MO M
1L 0
j
O
1
线性代数
1
O
0L 1
i
P(i,
j)
MO M
1L 0
j
O
1
线性代数
思考 三种类型的初等(i(k))
k
i
O
1
线性代数
1
O
P(i(k))
k
i
O
1
线性代数
思考
三种类型的初等矩阵是否可逆?
1
深圳大学 数学与统计学院
线性代数
第二章 矩阵的代数运算
2.6.3 初等矩阵的性质
初等矩阵
定理 1) P(i, j)左乘一矩阵,相当于对该矩阵施行了同样的初等行变换 ri rj;
P(i, j)右乘一矩阵,相当于对该矩阵施行了同样的初等列变换 ci cj;
2) P(i(k))左乘一矩阵,相当于对该矩阵施行第 i 行乘以数 k 的初等行变换 kri ; P(i(k)) 右乘一矩阵,相当于对该矩阵施行第 i 列乘以数 k 的初等列变换 kci .
O
1
i
P
(i (k ),
j)
MO
kL 1
j
O
1
线性代数
1
O
1
i
P
(i(k
),
j)
MO
kL 1
j
O
1
线性代数
(i)
性质 初等矩阵P可逆,并且其逆矩阵P-1与P是同型 的初等矩阵.
1) P(i, j)1 P(i, j); 2) P(i(c))1 P(i(c1)); 3) P(i(c), j)1 P(i(c), j).
线性代数
1 0 2
思考
0 0
0 1
1 0
是否可逆,若可逆可以用类似的办法求逆?
线性代数
1 0 2
0 0
0 1
1 0
线性代数
思考
1
3
2
4
是否可逆,若可逆如何求逆?
线性代数
