氢原子电子云初步探究
氢原子光谱的研究

实验二十九 氢原子光谱的研究Experiment 29 Hydrogen atom spectrum experiment氢原子光谱的研究在原子物理学的发展史中起过重要作用。
由于它是最简单、最典型、规律性最明显的一种光谱,因此最早为人们所注意,研究的也最为透彻。
实验方面进行了精细结构的探测,数据越来越精确。
理论方面则相当完满地解释了这些谱线的成因,发展了电子与电磁场相互作用的理论(量子电动力学)。
因此,本实验的操作过程对学生能力的培养无疑有较大的意义。
实验目的Experimental purpose1.测量氢光谱巴尔末线系在可见光区域的几条谱线的波长、验证巴尔末规律的正确性。
2.验算里德堡常数。
3.熟悉棱镜摄谱仪、光谱投影仪、阿贝比长仪的使用方法,并了解棱镜摄谱仪的工作原理。
实验原理Experimental principle1885年巴尔末根据实验数据发现了氢原子光谱在可见光区域内的各条谱线波长遵循下述规律4220-=n n λλ (1) 式中λ0为恒量。
当n =3,4,5,6,…时,则对应谱线分别称为H α、H β、H γ、H δ、…谱线。
继巴尔末之后,里德堡又把(1)式改写为⎪⎭⎫ ⎝⎛-=221211n R H λ (2) 式中n =3,4,5,6,…,R H =(10967758.1±0.8)m -1,称为里德堡常数。
通常取R H =1.097×107m -1即可。
氢原子光谱线中遵循上述两式规律的许多谱线组成氢光谱的巴尔末线系。
对于巴尔末线系来说,谱线的间隔和强度由长波向短波方向,以一种十分规则的方式递减,间隔越来越小。
强度越来越弱。
在巴尔末和里德堡经验公式的基础上,玻尔建立起原子模型理论,该理论能较好地解释气体放电时的发光现象。
玻尔理论认为:原子由原子核及核外电子组成,核外电子围绕原子核运动,它们可以有许多分立的运动轨道(见图1所示)。
电子在不同的轨道上运动时具有不同的能量,能量值是不连续的,是量子化的,只能取由量子数决定的各个分立的能量值。
14.10量子物理之氢原子的电子云图和概率密度等值面图

对于4d态电子,当m = 0时, 概率密度分为上下双峰,上下 还有两包,左右还有四双包。 彩色电子云图分上下左右八片, 上下的中间两片比较鲜艳。 概率密度的等值面是六个曲面,上下 四个是封闭曲面,中间两个是环面。
对于4d态电子,当m = ±1时,概 率密度分为对称的四峰和四包。 彩色电子云图分为四角对称的八片。 概率密度的等值面是 上下四个分立的环面。
对于4f态电子,当m =±2时,概率 密度分为上下左右四峰和左右两包。 彩色电子云图分上下左右 六片,上下四片比较鲜艳。 概率密度的等值面是三个曲面,上下 两个是封闭曲面,中间一个是环面。
对于4f态电子,当m = ±2时, 概率密度分为对称的四峰,与m = ±1的3d态电子类似。 彩色电子云图分为四角对称的四片。 概率密度的等值面是上下两个分 立的环面,其形状与3d态(m = ±1)电子的概率密度形状相似。
MATLAB可视化 大学物理学
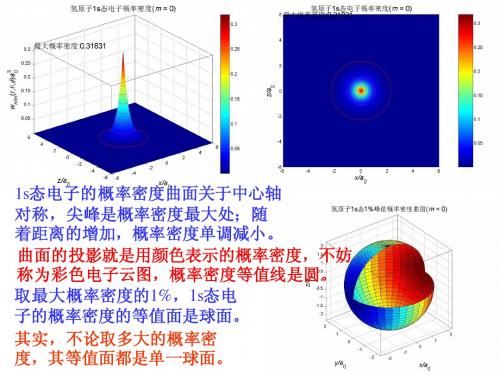
第十四章结束 湖南大学物电院 子,当磁量子数m = 0时,概 率密度曲面形成上下双峰,峰顶比较圆。 上下两片电子云是双峰的投影, 等值线分别围绕着两个峰。 概率密度的等值面是两个分立的闭合曲 面,由此可知:上下两片电子云是分立。
对于2p态电子,当m = ±1时,概 率密度曲面分为左右双峰。 在彩色电子云图中,左右 两片电子云是双峰的投影。 概率密度的等值面是中间空心的环面, 左右两片电子云是绕z轴联成一体的。
对于4p态电子,当m = 0时,概率密度 除了上下双峰之外,还有四个波包, 比m = 0的3p态电子多两个波包。 彩色电子云图分为上下六片,相 邻的波峰和波包是分开的,等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上 下六个分立的闭合曲面。
对于4p态电子,当m = ±1时,概 率密度分为左右双峰和四个波包, 比m = ±1的4p态电子多一对波包。 彩色电子云图分为左右对称的六片。 概率密度的等值面是三个 空心的环面,环面层层相 套,三个环面是相似的。
量子物理之氢原子的电子云图和概率密度等值面图2
概率密度的等值面是三个曲面,上下 两个是封闭曲面,中间一个是环面。
对于4f态电子,当m = ±2时, 概率密度分为对称的四峰,与m = ±1的3d态电子类似。 彩色电子云图分为四角对称的四片。 概率密度的等值面是上下两个分 立的环面,其形状与3d态(m = ±1)电子的概率密度形状相似。
对于4f态电子,当m = ±3时, 概率密度分为左右双峰。 彩色电子云图分为左右两片。 概率密度的等值面是一个环 面,其形状与2p态(m = ±1) 电子的概率密度形状相似。
彩色电子云图分为左右对称的四片。
概率密度的等值面是两个空 心的环面,并且外环面套着 内环面,两个环面是相似的。
对于3d态电子,当m = 0时,概率 密度分为上下双峰和左右双包。
彩色电子云图分上下左右 四片,上下两片比较鲜艳。 概率密度的等值面是三个曲面,上下 两个是封闭曲面,中间一个是环面。
对于3d态电子,当m = ±1时, 概率密度分为对称的四峰。 彩色电子云图分为四角对称的四片。 概率密度的等值面是 上下两个分立的环面。
对于4p态电子,当m = 0时,概率密度 除了上下双峰之外,还有四个波包, 比m = 0的3p态电子多两个波包。 彩色电子云图分为上下六片,相 邻的波峰和波包是分开的,等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上 下六个分立的闭合曲面。
对于4p态电子,当m = ±1时,概 率密度分为左右双峰和四个波包, 比m = ±1的4p态电子多一对波包。
对于3p态电子,当m = 0时,概率密度 除了上下双峰之外,还有两个波包。 由于波包的概率密度相对于 波峰较小,所以颜色较暗。 彩色电子云图分为上下四片,相 邻的波峰和波包是分开的,等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上下四个分立的闭合曲面。
氢原子电子云的计算和可视化分析(PDF)

-
Zr na0
2Z na0
r
L l 2l+ 1 n+ l
2Z na0
r
( 2)
其中, Z 为原子序数 ( 氢原子的 Z = 1) , a0 是第一玻 尔半径; N n l是归一化常数,
Nnl = -
2Z 3 ( n - l- 1)! na0 2n [ ( n + l) ! ] 3
( 3)
L2l+ 1 n+ l
52
大学物 理
第 28卷
概率密度 W n lm是 r 和 的函数 , 某点的 r 和 是一定的, 概率密度也是一定的. 应用递推算法 可计算缔 合 拉 盖尔 多 项 式和 缔 合 勒让 德 函 数的 值, 因此, 根据上述公式就能计算任何一点的概 率密度.
2 蒙特卡罗方法
假设用 1 000个均匀分布在 0和 1之间的随机 数表示电子, 那么 0. 2以下的随机数就表示出现在 该点的电 子. 对于任意一个 随机数来说, 如果它 小 于 0. 2, 就表 示一个 电子出现 在该点. 用计 算机 模 拟时, 如果某随机数小于 (很难等于 )该点的概率 密度, 就在该点画一个点. 这种用随机数模拟电子 概率密度的方法称为蒙特卡罗方法. 假设某点的概 率密度为 0. 2, 如果 1 000个电子 都有相同的机 会 先后出现在该 点, 就会 有 200 个电子出现在 该点, 只是无法断定哪些电子出现在该点. 或者说, 如果 一个电子先后有 1 000次机会出现在该点, 那么 就 有 200次出现在该点, 只是无法预测哪一次出现在 该点.
其中
M lm =
( 2l + 1) ( l - |m | ) ! 4∀( l + |m | ) !
氢原子的能级结构与光谱线的解析

氢原子的能级结构与光谱线的解析氢原子是最简单的原子之一,由一个质子和一个电子组成。
它的能级结构和光谱线的解析对于理解原子结构和光谱学有着重要的意义。
本文将探讨氢原子的能级结构以及与之相关的光谱线的解析。
一、氢原子的能级结构氢原子的能级结构是由其电子的能量水平所决定的。
根据量子力学理论,氢原子的电子存在于不同的能级上,每个能级都对应着不同的能量。
这些能级按照能量的高低被编号为1, 2, 3...,其中1级能级具有最低的能量,被称为基态。
氢原子的能级结构可以通过求解薛定谔方程来获得。
薛定谔方程描述了系统的波函数和能量。
通过求解薛定谔方程,可以得到氢原子的波函数和能量本征值,即能级。
氢原子的能级结构可以用能级图表示。
能级图通常以基态能级为起点,向上依次排列其他能级。
不同能级之间的跃迁会伴随着能量的吸收或释放,产生光谱线。
二、光谱线的解析光谱线是指物质在吸收或发射光时产生的特定波长的光线。
氢原子的光谱线是由电子在不同能级之间跃迁所产生的。
氢原子的光谱线可以分为吸收光谱和发射光谱。
当氢原子吸收能量时,电子从低能级跃迁到高能级,产生吸收光谱。
吸收光谱是连续的,呈现出一条宽带。
当电子从高能级跃迁回低能级时,会发射出光子,产生发射光谱。
发射光谱是分立的,呈现出一系列锐利的谱线。
氢原子的光谱线可以用波长或频率来描述。
根据氢原子的能级结构,可以计算出各个能级之间的跃迁所对应的光谱线的波长或频率。
这些光谱线的波长或频率可以通过实验进行观测,从而验证理论计算的结果。
光谱线的解析对于研究物质的组成和性质具有重要意义。
通过分析光谱线的特征,可以确定物质的化学成分和结构。
光谱学在天文学、化学、物理学等领域都有广泛的应用。
三、氢原子的光谱线系列氢原子的光谱线系列是指在氢原子的能级结构中,特定能级之间跃迁所产生的光谱线的集合。
氢原子的光谱线系列主要包括巴尔末系列、帕舍尼系列、布拉开特系列等。
巴尔末系列是指电子从高能级跃迁到第二能级(巴尔末系列基态)所产生的光谱线。
氢原子光谱实验报告

氢原子光谱实验报告氢原子光谱实验报告引言在物理学中,光谱分析是非常重要的一种实验手段。
通过光谱分析,可以清楚地看到物质的组成和性质。
作为最简单的原子,氢原子的光谱密切相关,因此它一直是原子光谱实验中最经典的案例之一。
在本次实验中,我们将收集氢原子的光谱数据,并分析其中的特征。
实验方法为了收集氢原子的光谱数据,我们需要使用光谱仪。
我们选择了一个封闭式光谱仪,它能够对光进行有效地控制和过滤。
实验前,我们对仪器进行了校准,并准备好了用于产生氢原子的气体。
实验过程中,我们通过管道将氢气引入到可控沸腾器储罐中,并使氢气沸腾。
然后,我们将光谱仪和氢气沸腾器连接起来,将光线通过气体,捕获光谱数据。
结果在实验过程中,我们采集了大量的光谱数据。
通过对这些数据的分析,我们得到了如下的结果:1.氢原子的吸收光谱分布于紫外线和可见光区域。
主要的发射线在红色、青色和紫色光谱区域出现。
2.对氢原子进行分析后,我们发现它在这三个光谱区域中分别有四条、两条和一条发射线。
我们将其编号为Hα, Hβ, Hγ, Hδ, Hε, Hζ和Hη线。
3.每条氢原子发射线的波长都具有独特的值。
通过使用Balmer公式,我们得到平均波长:Hα为656.3nm,Hβ为486.1nm,Hγ为434.0nm,Hδ为410.2nm,Hε为397.0nm和Hζ为388.9nm。
讨论通过实验结果,我们可以得出以下结论:1.氢原子发射线的波长与所远离原子核的能级之差呈线性关系。
因此,当氢原子从高能级跃迁到低能级时,必须以某一个波长的光子将能量释放出来。
2.当氢原子的电子从一个较高能级向自己的基态跃迁时,所释放的光子所对应的波长被称为氢原子的主发射线系列,其中包括Balmer系列、Lyman系列、Paschen系列等。
3.通过测量氢原子辐射的波长和频率,可以确定氢原子的各个能级。
这对于理解氢原子的物理性质非常重要。
结论本实验说明了如何收集氢原子光谱数据,包括使用光谱仪、气体储罐和校准设备等。
武汉理工氢原子电子云可视化

在编辑框中输入数字,若满足取值条件,如n=2,l=1,m=0,左击氢原子径向几率密度按钮,得到如图5所示图形。左击角向几率密度平面图按钮,得到平面图;左击角向几率密度立体图,得到立体图,如图6所示。
图5 n=2,l=1,m=0时氢原子径向几率密度
(a)(b)
图6 n=2,l=1,m=0时角向几率密度平面图和立体图
用它来供用户进行编辑,对各个不同对象输入操作指令,用户可以单击右下方的这个指令区,进入程序代码窗口,编辑回调函数。
3.排列工具(alignment tool)
它用来安排图形对象的位置。排列工作包括三个区域:align(方向排列)、distribute(分布)和set spacing(设定间距),设定完成后,单击apply按钮,即可完成排列工作。
它与 角无关,即对绕z轴旋转是对称的。
2.2.
要想掌握matlab图形用户界面技术,首先需要了解图形对象的概念。图形对象指图形系统中的基本图元。matlab定义了10种图形对象:根对象(root)、图形窗口对象(figure)、轴对象(axes)、线对象(line)、块区域对象(patch)、面对象(surface)、图像对象(image)、文字对象(text)、菜单对象(menu)、控件对象(control)。matlab创建这些图形对象时,会给出每个图形对象一个句柄(handle),用来标识该图形的对象。
if n>=1&l>=0&m>=-l&m<=l&n>=l+1 %判断量子数是否输入错误,若没错,画图
syms r a nn x;%自定义变量,完成符号运算
Nnl=-sqrt((2/n)^3*factorial(n-l-1)/(2*n*(factorial(n+l))^3));%归一化常数Nln
氢原子的电子云

氢原子的电子云
• 给氢原子拍照,并将100张 照片叠加
电子运动特性
电子的质量很小,只有9.11×10-31千 克; 核外电子的运动范围很小(相对于宏 观物体而言); 电子的运动速度很大;
测不准
课堂练习
步骤2:开启电源(包括传感器的 发射器电源)运行DIS应用软件。De
热门是
步骤3:点击DIS“实验条目”中的 “练习使用DIS”
电子云图
小黑点的疏密表示电子在核外空间 单位体积内出现的概率的大小。
谢谢!
• 下次再见!
氢原子的电子云
电子云
当原子处在不同的状态时,电子 在 各处出现的概率不是一样的。如果 用疏密不同的点表示电子在各个位置 出现的频率,画出图来,就想云雾一 样,就可以
氢原子的电子云
• 再给氢原子拍摄一张照片
氢原子的电子云
• 再给氢原子拍摄一张照片
氢原子的电子云
• 再给氢原子拍摄一张照片
氢原子的电子云
• 给氢原子拍照,并将2张照片叠 加
氢原子的电子云
• 给氢原子拍照,并将3张照片 叠加
氢原子的电子云
• 给氢原子拍照,并将4张照片 叠加
氢原子的电子云
• 给氢原子拍照,并将5张照片 叠加
氢原子的电子云
• 给氢原子拍照,并将20张照 片叠加
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4. • •
•
自旋角动量量子数(spin angular momentum quantum number) 符号 s ,取+1/2和-1/2两个值,表示电子自 旋的两种相反方向,也可用箭头符号↑和 ↓表示。 两个电子自旋方向相同称为平行自旋, 方向相反称反平行自旋。 原子轨道由 n、l 和 m 决定,电子运动状 态由 n、l、m、s 确定。一个原子轨道最 多容纳两个自旋相反的电子,每电子层 最多容纳的电子总数应为2n2。
有关氢电子云的探究学习
主讲人:
1、波函数及其意义
2、波函数与电子云
3、氢电ቤተ መጻሕፍቲ ባይዱ云
4、氢电子云画法初步
波函数及其意义
波函数及其意义
经典的波与波函数 机械波:
电磁波:
经典的波为实函数:
波函数及其意义 量子力学的波函数(复函数)
波函数及其意义
1、波函数ψ (wave function) 原子中电子具有波动性,波函数ψ 是薛定谔方程的 解,用来描述电子的运动状态。 若粒子为三维自由运动,波函数可以表示为:
前面形象的介绍电子云(电子 概率密度), 现在再次回到波函数,进行简 单的抽象了解
用Matlab画氢原子的电子概率密度图 —— 是理解氢原子波函数的很好方法
1、求解氢原子核外电子概率密度函数:
氢原子薛定谔方程: 其解为: 则氢原子核外电子的概率密度函数:
①主量子数,决定轨道的能量,既能层,n=0、1、 2、„, ②L为角量子数,决定轨道角动量大小,即能级,l=0、 1、2、„、n-1, ③M为磁量子数,决定轨道角动量在磁场上方向的分量, 即轨道在空间分布上的方向,m=0、±1,、±2、„±1。
一. 测不准原理(uncertainty principle)
Heisenberg指出,无法同时确定微观粒子 的位置和动量: △x· △px≥h/4π △x为粒子在x方向的位置误差,△px为动量 在x方向的误差。由于h是极小的量,所以 △x越小,△px越大,反之亦然。测不准原理 是粒子波动性的结果,意味着微观粒子运动 不存在既确定位置又有确定速度的运动轨迹。
a
b
波函数与电子云
原子轨道(atomic orbital)
描述原子中单个电子运动状态的波函数ψ常称 作原子轨道。原子轨道仅仅是波函数的代名 词,绝无经典力学中的轨道含义。严格地说 原子轨道在空间是无限扩展的,但一般把电 子出现概率在99%的空间区域的界面作为原子 轨道的大小。
波函数与电子云
量子数
波函数与电子云
电子云
电子在原子核外很小的空间内作高速运动,其运动规律跟一般物体 不同,它没有明确的轨道。根据量子力学中的测不准原理,我们不 可能同时准确地测定出电子在某一时刻所处的位置和运动速度,也 不能描画出它的运动轨迹。因此,人们常用一种能够表示电子在一 定时间内在核外空间各处出现机会的模型来描述电子在核外的运动。 在这个模型里,某个点附近的密度表示电子在该处出现的机会的大 小。密度大的地方,表明电子在核外空间单位体积内出现的机会多; 反之,则表明电子出现的机会少。由于这个模型很像在原子核外有 一层疏密不等的“云”,所以,人们形象地称之为“电子云”。
例:
2S能级
2Px能级 最大概率密度:
即:第一波尔轨道半径
1、计算机在一定的范围内随机地选取坐标点( 计算概率密度函数ρ(r )在点( 度函数ρ(r )的最大值,并计算
),并 )是概率密
2.计算机产生一个0至1之间均匀分布的随机数M。 3.将Y与M进行比较若Y≥M,则选取该点( )若Y<M, 则舍去该点( )。重复1至3重新选取坐标点,即可 得到一个按ρ(r )分布的随机函数序列。
能级符号 l s p d f · · ·
0
1
2
3
· · ·
3. •
•
•
磁量子数(magnetic quantum number) 符号 m ,可以取 –l 到 +l 的 2l+1个值, 即 m = 0、±1、±2,…,±l 它决定原子轨道的空间取向。L 亚层共有 2l+1个不同空间伸展方向的原子轨道。 例如 l =1时,m = 0、±1,p轨道有三种 取向,或 l 亚层有3个p轨道。 相同能级的轨道能量相等,称为简并轨 道或等价轨道(equivalent orbital)。
2、ψ的意义 ψ本身物理意义并不明确,但ψ2却有明确的物 理意义。表示在原子核外空间某点处电子出现的概 率密度(probability density),即在该点处单位体 积中电子出现的概率。
波函数及其意义
波函数与电子云
电子云(electron cloud) 图形a是基态氢原子ψ2(概率密度)的立体 图,b是剖面图。黑色深的地方概率密度大, 浅的地方概率密度小。概率密度的几何图形 俗称电子云。
总结
电子云对应的是原子电子轨道,是解薛定 谔方程的结果。 薛定谔方程的解称为“波 函数”,又称“轨道”,表示的是电子在 该空间范围出现的概率,而不应该理解为 电子在空间中的运动轨迹。 其中有四个量子数: 主量子数n(能层), 角量子数l(能级), 磁量子数m (电子云伸展方向),自旋量 子数s
氢原子的电子云的概率密度图:从上向 下为主量子数n=1,2,3,从左向右为方位 角量子数l=s,p,d
电子层n 符号 1 K 2 L 3 M 4 N · · · · · ·
2.
•
• •
轨道角动量量子数(orbital angular momentum quantum number) 符号 l ,它只能取小于 n 的正整数和零 l = 0、1、2、3 … (n – 1),共可取n个值 它决定原子轨道的形状(n 种)。 在多电子原子中 l 还和 n共同决定电子能量高 低。当 n 给定,l 愈大,原子轨道能量越高。 l 称为能级或电子亚层(subshell 或sublevel)。 电子亚层用下列符号表示:
• 合理的波函数ψ必须满足一些整数条件, 否则将为零, ψ2也为零,即空间没有电子 出现。
这些整数是n、l、m,称为量子数 (quantum number) 。 n、l 和 m 这三个量子数的取值一定时, 就确定了一个原子轨道,即波函数ψn,l,m。
• •
波函数与电子云
1. • • • 主量子数(principal quantum number) 符号 n,可以取任意正整数值,即 n = 1 ,2 ,3 ,… 它是决定电子能量的主要因素。氢原子只有一 个电子,能量只由n决定 n 还决定电子离核的平均距离,或者说原子轨 道的大小,n 也称为电子层(shell)。n 愈大, 电子离核距离愈远,原子轨道也愈大。电子层 用下列符号表示:
