北邮数字信号处理第四章附加习题答案
数字信号处理-第4章习题

习题四4.1 用窗函数法设计一线性相位FIR 高通滤波器,通带边界频率为0.6π,阻带边界频率为0.4π,要求阻带衰减不小于40dB ,窗函数从矩形窗、汉宁窗、海明窗和布莱克曼窗中选取,且要求滤波器的阶数最小。
求出该滤波器的单位脉冲响应h (n )的解析式。
解 求理想高通滤波器的边界频率n ω和过渡带宽ω∆:0.60.40.522c rn ωωππωπ++≈== 0.60.40.2c r ωωωπππ∆=-=-=选择窗函数和窗口长度。
阻带衰减不小于40dB ,因此选择汉宁窗。
根据过渡带宽求窗口长度N 和线性相位延迟常数α:6.20.231N Nππ=⇒= 1152N α-== 根据理想边界频率n ω和线性相位延迟常数α,求理想单位脉冲响应d ()h n :[][]()()d sin ()sin ()1()()d d 21n n n j n j n n n n n n h n e e n ωπωαωαπωαπαωαπαωωπωαπ----⎧---≠⎪⎪-⎡⎤=+=⎨⎢⎥⎣⎦⎪-=⎪⎩⎰⎰ 窗函数与理想单位脉冲响应相乘,即可得到线性相位FIR 高通滤波器的单位脉冲响应:[][]sin (15)sin (15)0.50.50.5cos ()15()15(15)0.515N n n n R n n h n n n ππππ⎧---⎡⎤⎛⎫-⋅⋅≠⎪ ⎪⎢⎥=-⎝⎭⎨⎣⎦⎪=⎩0,1,2,,30n =⋅⋅⋅6kHz ,阻带边界频率为2kHz 和8kHz ,采样频率为20kHz ,要求阻带衰减不小于50dB ,窗函数从矩形窗、汉宁窗、海明窗和布莱克曼窗中选取,且要求滤波器的阶数最小。
求出该滤波器的单位脉冲响应h (n )的解析式。
解 求理想带通滤波器的边界频率1ω、2ω和过渡带宽ω∆:12121212112212221120.4 , 20.620.2 , 20.80.3 , 0.7220.2c c c c s s r r r r s sc r c r r c c r f ff f f ff f ωππωππωππωππωωωωωπωπωωωωωπ========++≈=≈=∆=-=-= 选择窗函数和窗口长度。
北邮版通信原理课后习题的答案第四章-精品
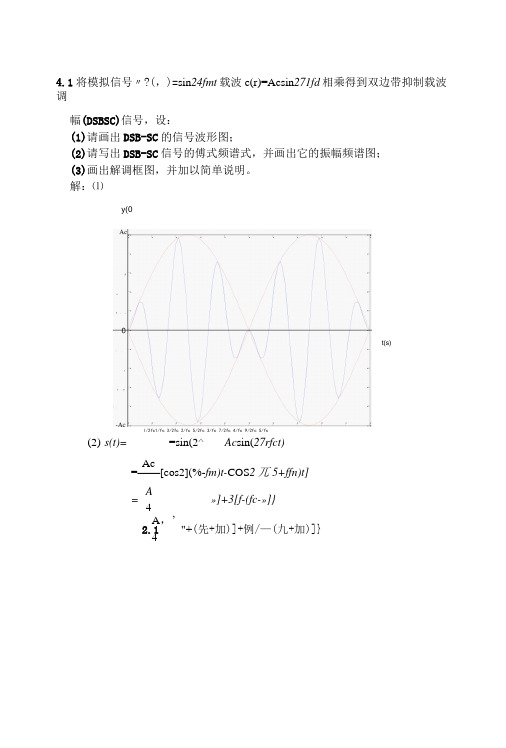
4.1将模拟信号〃?(,)=sin 24fmt 载波c(r)=Acsin 271fd 相乘得到双边带抑制载波调幅(DSBSC)信号,设:(1)请画出DSB-SC 的信号波形图;(2)请写出DSB-SC 信号的傅式频谱式,并画出它的振幅频谱图; (3)画出解调框图,并加以简单说明。
解:⑴(2) s(t)= =sin(2^ Ac sin(27rfct)Ac=——[cos2](%-fm)t-COS 2兀5+ffn)t] A = »]+3[f-(fc-»]} 4A ,’ 2.1 "+(先+加)]+例/—(九+加)]} 4y(0l/2fc1/fc 3/2fc 2/fc 5/2fc 3/fc 7/2fc 4/fc 9/2fc 5/fct(s)S ⑴八3Ac/4- Ac/2.Ac/4(3)相干解调Cos(Wct)与发端相干偏调相干解调:将接收信号与载波信号sin(2乙加)相乘,得至U A cr(t)sin(2^fct)=Acm(t)sin(2^fct)sin(2^fit)=--cos(44fct)]通过低通滤波器抑制载频的二倍频分量,得到解调信号为刈⑺=与机⑺ 2.2 已知某调幅波的展开式为:s(t)=cos(2/rxl()4r)+4COS (2TT xl.lxl040+cos(2万xl.2xl04r) (1)求调幅系数和调制信号频率;(2)写出该信号的傅式频谱式,画出它的振幅频谱图; (3)画出该信号的解调框图。
解:⑴sQ)=cos(24xl04r)+4cos(2乃xl.lxl04r)+cos(2万xl.2xl04r)=4cos(2%xl.lxl04r)[l+0.5cos(2万x0.1xl04r)] 调制系数是a=0.5;信号频率是f=1000Hz(2)S(/)=;U(/+104)+演f —i04)]+2[Mf+l.lxl()4)+5(/—1.1X104)]+-W+1.2X 104)+^(/-1.2X 104)]-fm-fc ・fc -fc+fm。
数字信号处理课后答案

k = n0
∑
n
x[ k ]
(B) T {x[n]} =
∑
x[k ]
(C) T {x[ n]} = 0.5
x[ n ]
(D) T {x[n]} = x[− n]
1-5 有一系统输入为 x[n] ,输出为 y[n] ,满足关系 y[n] = ( x[n] ∗ u[n + 2])u[n] ,则系统是(A) (A)线性的 (B)时不变的 (C)因果的 (D)稳定的 解:
(a) T { x[ n ]} = h[ n] + x[ n ], (c) T {x[ n]} = ∑ x[ n − k ]
δ [n] + aδ [n − n0 ] ,单位阶跃响应 s[n] = u[n] + au[n − n0 ] 。
1-15 线性常系数差分方程为 y[n] − y[n − 1] +
y[n] = 0 , n < 0 , 则 y[3] = 0.5 。 解: y[0] = y[ −1] − 0.25 y[ −2] + x[0] = 1 y[1] = y[0] − 0.25 y[ −1] + x[1] = 1 y[2] = y[1] − 0.25 y[0] + x[2] = 0.75 y[3] = y[2] − 0.25 y[1] + x[3] = 0.5
∞ ∞ k =−∞ n '=−∞
解: (a)
n =−∞
∑ y[n] = ∑ ∑ x[k ]h[n − k ] = ∑ x[k ] ∑ h[n − k ] = ∑ x[k ] ∑ h[n ']
n =−∞ k =−∞ k =−∞ n =−∞
∞
∞
∞
数字信号处理第四章答案
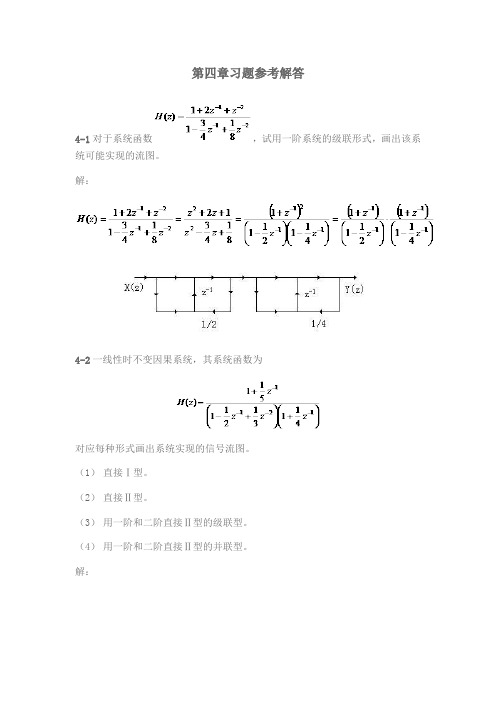
第四章习题参考解答4-1对于系统函数,试用一阶系统的级联形式,画出该系统可能实现的流图。
解:4-2一线性时不变因果系统,其系统函数为对应每种形式画出系统实现的信号流图。
(1)直接Ⅰ型。
(2)直接Ⅱ型。
(3)用一阶和二阶直接Ⅱ型的级联型。
(4)用一阶和二阶直接Ⅱ型的并联型。
解:直接Ⅰ型直接Ⅱ型用一阶和二阶直接Ⅱ型的级联型用一阶和二阶直接Ⅱ型的并联型4-3已知模拟滤波器的传输函数,试用脉冲响应不变法将转换成数字传输函数。
(设采样周期T=0.5)解:4-4若模拟滤波器的传输函数为,试用脉冲响应不变法将转换成数字传输函数。
(设采样周期T=1)解:4-5用双线性变换法设计一个三阶的巴特沃滋数字低通滤波器,采样频率,截至频率。
解:,4-6用双线性变换法设计一个三阶的巴特沃滋数字高通滤波器,采样频率,截至频率。
解:,,归一化,4-7用双线性变换法设计一个三阶的巴特沃滋数字带通滤波器,采样频率,上下边带截至频率分别为,。
解:,,,4-8设计一个一阶数字低通滤波器,3dB截至频率为,将双线性变换应用于模拟巴特沃滋滤波器。
解:一阶巴特沃滋,4-9试用双线性变换法设计一低通数字滤波器,并满足:通带和阻带都是频率的单调下降函数,而且无起伏;频率在处的衰减为-3.01dB;在处的幅度衰减至少为15dB。
解:设,则:,通带:,即阻带:,即阶数:,查表得二阶巴特沃滋滤波器得系统函数为双线性变换实现数字低通滤波器4-10一个数字系统的采样频率,已知该系统收到频率为100Hz的噪声干扰,试设计一个陷波滤波器去除该噪声,要求3dB的边带频率为95Hz和105Hz,阻带衰减不小于14dB。
解:,令,,,,设N=2,则。
数字信号处理课后习题答案(全)1-7章

x(n)=-δ(n+2)+δ(n-1)+2δ(n-3)
h(n)=2δ(n)+δ(n-1)+ δ(n-2)
由于
x(n)*δ(n)=x(n)
1
x(n)*Aδ(n-k)=Ax(n-k)
2
故
第 1 章 时域离散信号和时域离散系统
y(n)=x(n)*h(n)
=x(n)*[2δ(n)+δ(n-1)+ δ(n-2) 1 2
(5) 系统是因果系统, 因为系统的输出不取决于x(n)的未来值。 如果
|x(n)|≤M, 则|y(n)|=|ex(n)|≤e|x(n)|≤eM,
7. 设线性时不变系统的单位脉冲响应h(n)和输入序列x(n)如题7图所示,
要求画出y(n)输出的波形。
解: 解法(一)采用列表法。
y(n)=x(n)*h(n)=
0≤m≤3
-4≤m≤n
非零区间如下:
第 1 章 时域离散信号和时域离散系统
根据非零区间, 将n分成四种情况求解: ① n<0时, y(n)=0
② 0≤n≤3时, y(n)= ③ 4≤n≤7时, y(n)= ④ n>7时, y(n)=0
1=n+1
n
1=8-m n0
3
mn4
第 1 章 时域离散信号和时域离散系统
第 1 章 时域离散信号和时域离散系统
(3) 这是一个延时器, 延时器是线性非时变系统, 下面证明。 令输入为
输出为
x(n-n1)
y′(n)=x(n-n1-n0) y(n-n1)=x(n-n1-n0)=y′(n) 故延时器是非时变系统。 由于
T[ax1(n)+bx2(n)]=ax1(n-n0)+bx2(n-n0) =aT[x1(n)]+bT[x2(n)]
数字信号处理课后答案+第4章(高西全丁美玉第三版)

令 y(n)=x1(n)+jx2(n) Y(k)=DFT[y(n)] 则
这样, 通过一次N点IFFT计算就完成了计算2N点DFT。 当然还要进行由Y(k)求X1(k)、 X2(k)和X(k)的运算(运算量相对
k=0, 1, …, N-1
⎧ ⎛n⎞ ⎪ x1 ⎜ 2 ⎟ ⎪ ⎝ ⎠ x (n) = ⎨ ⎪x ⎛ n −1 ⎞ ⎪ 2⎜ 2 ⎟ ⎠ ⎩ ⎝
n = 偶数 n = 奇数
在编程序实现时, 只要将存放x1(n)和x2(n)的两个数组的元 素分别依次放入存放x(n)的数组的偶数和奇数数组元素中 即可。
运算流图。 但画图占篇幅较大, 这里省略本题解答, 请 读者自己完成。
很少)。 (2) 与(1)相同, 设 x1(n)=x(2n) n=0, 1, …, N-1 x2(n)=x(2n+1) n=0, 1, …, N-1 X1(k)=DFT[x1(n)] X2(k)=DFT[x2(n)] 则应满足关系式
1 X 1 ( k ) = DFT[ x1 ( n)] = Yep ( k ) = [Y ( k ) + Y * ( N − k )] 2 1 jX 2 (k ) = DFT[ jx2 (n)] = Yep (k ) = [Y ( k ) − Y * ( N − k )] 2
4. 设x(n)是长度为2N的有限长实序列, X(k)为x(n)的 2N点DFT。 (1) 试设计用一次N点FFT完成计算X(k)的高效算法。 (2) 若已知X(k) ,试设计用一次N点IFFT实现求X(k)的 2N点IDFT运算。
x1(n)和x2(n)均为实序列, 所以根据DFT的共轭对称性, 可用
② 由X1(k)和X2(k)构成N点频域序列Y(k): Y(k)=X1(k)+jX2(k)=Yep(k)+Yop(k)
北京邮电大学数字信号处理第4章答案

习题解答4.1 根据给定的模拟滤波器的幅度响应平方,确定模拟滤波器的系统函数 H(s)。
(1) 261|()|164H j Ω=+Ω(2) 2222216(25)|()|(49)(36)H j -ΩΩ=+Ω+Ω分析:在模拟滤波器设计中,由各种逼近方法确定了幅度响应,通过下列步骤求出滤波器的系统函数H(s)。
更进一步,通过脉冲响应不变法或双线性变换法,可以得到数字滤波器的传输函数 H(z)。
(1)考虑s j =Ω,将幅度响应表达式整理为s 为变量的表达式,求 ()()a a H s H s - 表达式的零极点;(2)为了系统稳定,选择左半平面的极点构成 H(s);(3)如果没有特殊要求,可以选择取 ()()a a H s H s -以虚轴为对称轴的对称零点的任意一半(应是共轭对)作为 H a (s) 的零点。
但如果要求是最小相位延时滤波器,则应取左半平面零点作为 H a (s) 的零点。
(4)对比()a H s 和()a H j Ω 的低频特性或高频特性,从而确定增益常数K 0。
解:(1)由于2)(Ωj H a 是非负有理函数,它在Ωj 轴上的零点是偶次的,所以满足幅度平方函数的条件,先求2321()()()164()22H s H s H j a a as s -=Ω=+-Ω=-其极点为0.50.250.4330.50.250.433j j --±±我们选出左半平面极点s=0.5和 0.250.433j -± 为)(s H a 的极点,并设增益常数为0K ,则得)(s H a 为:002()(0.5)(0.250.433)(0.250.433)(0.5)(0.50.25)K K H s a s s j s j s s s ==++-+++++ 按着()a H s 和()a H j Ω的低频特性或高频特性的对比可以确定增益常数。
在这里我们采用低频特性,即由00()|()|a s a H s H j =Ω==Ω的条件可得增益常数0K 为:018K =最后得到)(s H a 为:21()8(0.5)(0.50.25)H s a s s s =+++(2)由于2)(Ωj H a 是非负有理函数,它在Ωj 轴上的零点是偶次的,所以满足幅度平方函数的条件,得)36)(49()25(16222)()()(222s s s s j aH s a H s a H --+=-=ΩΩ=- 其极点为:6,7±=±=s s其零点为:5j s ±=(皆为二阶,位于虚轴上)j Ω虚轴上的零点或极点一定是二阶的,其中一半(应为共轭对)属于 H a (s)。
数字信号处理 答案 第四章

z −1
r sin θ
− r sin θ r cos θ
y ( n)
z −1
网络Ⅱ 解 网络Ⅰ:根据信号流程图写出差分方程
y (n) = 2r cos θ y (n − 1) − r 2 y (n − 2) + x(n)
由差分方程得系统函数
H1 ( z ) =
Y ( z) 1 = X ( z ) 1 − 2r cos θ z −1 + r 2 z −1 1 )(rz −1 − e jθ )
(4)并联型
x ( n)
z −1
1/4 10/3
-7/3
y ( n)
z −1
1/2 将系统函数写成部分分式形式
H ( z) =
−7 / 3 10 / 3 + 1 −1 1 1− z 1 − z −1 4 2
4.4 用直接Ⅰ型和直接Ⅱ型结构实现以下系统函数; (1)
H(z)=
−5 + 2 z −1 − 0.5 z −2 1 + 3z −1 + 3z −2 + z −3
3z 3 + 2 z 2 + 2 z + 5 (2) H(x)=0.8 3 z + 4 z 2 + 3z + 2
解 (1)根据系统函数写出差分方程
y (n) + 3 y (n − 1) + 3 y (n − 2) + y (n − 3) = −5 x(n) + 2 x(n − 1) − 0.5 x(n − 2)
可见网络Ⅰ和网络Ⅱ具有相同极点。 4.3 一个因果线性离散系统由下列差分方程描述:
3 1 1 y(n)- y(n-1)+ y(n-2)=x(n)+ x(n-1) 4 8 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 在冲激响应不变法中,数字滤波器的单位采样相应由对连续时间滤波器的冲 激响应采样组成
h n ha nTs
另一种方法是用阶跃响应不变法, 数字滤波器的阶跃响应由对连续时间滤波器阶 跃响应的采样组成。 (1)利用连续时间滤波器原型,用阶跃响应不变法设计一个数字滤波器。
4.若 ua (t ) 是模拟网络 H a ( s) 的阶跃响应,即输入 xa (t ) u(t ) ,则响应 ya (t ) sa (t ) ;s(n)
是数字网络 H ( z ) 的阶跃响应,即输入 x(n) u (n) ,则响应 y(n) s(n) 。如果已知 H a ( s) 以及 s (t ) ,令 s( n) sa ( nT ) 这样来设计 H ( z ) 就称为阶跃不变法。试用阶跃不变法确定
由此得到已知 H a ( s) 以及 ua (t ) 用阶跃不变法求 H ( z ) 的步骤为: (1) (2) 先将 Sa ( s) H a (s) / s 部分分式展开; 展开的分式 z 变换之和为 Sa ( z ) ;
H ( z)
z 1 Sa ( z ) 。 z
s z 1 z 1
Ha s
sa
s a
2
b2
(2)确定设计出来的滤波器是否与用冲激响应不变法设计出来的相同。 解: (1)如果连续时间滤波器的脉冲响应是 ha t ,它的阶跃响应为
sa t ha d
t
阶跃响应的拉普拉斯变换与系统函数 H a s 的关系为
Ha s
极点 sk 为
sk c e
j
Ak k 1 s sk
N
N 1 2 k
2N
k 0,1,
N
, N 1
对于冲激响应不变法,离散时间滤波器的系统函数变成
H z Ak sk Ts 1 z k 1 1 e
这样 H z 的极点位于
ze
T
1 e aT z 1 cos(bT ) 1 2e aT z 1 cos(bT ) e2 aT z 2
,可得:
(2) 先引用拉氏变换的结论
ha (t )
按 Z 变换 a u (k )
k
Aes0t t n 1 u (k ) (n 1)!
1 dX ( z ) ,且 kx(k ) z 1 1 az dz
,数字
H z Ha s
s
z 1 z 1
故
z 1 s j z 1
z e j
cos e j 1 2 j cot j j e 1 2 sin 2
5
即
cot 2
原模拟低通滤波器以 0 为通带中心,由上式可知, 0 时,对应于 。 ,故答案为(2) 方法 2 找出对应于 0 的数字频率 的对应值即可。 令 z 1 ,对应于 e j 1 ,应有 0 ,则 H 1 H a s 不是模拟低通滤波器; 令 z 1 , 对应 e j 1 , 应有 , 则 H 1 H a 0 , 即 0 对应 , 将模拟低通中心频率 0 映射到 处,所以答案为(2) 。 方法 3 直接根据双线性变换法设计公式及模拟域低通到高通频率变换公式 求解。 双线性变换设计公式为
4
H ( z ) 与 H a ( s) 的关系,并与脉冲不变法比较。
解:阶跃不变法就是使 s(n) sa (nT ) 因为 sa (t )
1 ha ( )d Sa ( s) H a ( s) ; s
t
阶跃响应的 变换为
1 S ( z ) F L1 H a ( s) s
sk Ts
e
cTs j
N 1 2 k
2N
k 1, 2,
, N 1
a a cos bTs b sin bTs e aTs z 1 a 1 1 2 a b 2 1 z 1 a 2 b 2 1 2 cos bTs e aTs z 1 e 2 aTs z 2
数字滤波器的系统函数为 H z 1 z 1 S z
1 e
a jb Ts
1 2
z 1
a jb T
1 2
虽然 H z 的极点与用阶跃响应不变法设计的滤波器的极点相同,但系统函 数不同,所以两种方法不等价。 2.设 ha t 表示一模拟滤波器的单位冲激响应,
e0.9t , t 0 ha t 0, t 0
1 Sa s H a s s
这样
1 sa Sa s s s a 2 b 2
用阶跃响应不变法设计数字滤波器时, 我们要先对 H a s 进行部分分式展开
Sa s
其中
A0 A1 A2 s s a jb s a jb
H z 满足稳定条件。 所以, 对 T 1 和 T 0.5 , 画出 H e j T 0 时,z1 1 ,
曲线如题 6 解图实线和虚线所示。
题 2 解图 由图可见,该数字滤波器近似为低通滤波器。且 T 越小,滤波器频率混叠越 小,滤波特性越好(即选择性越好) 。反之, T 越大,极点 z1 e0.9T 离单位圆越 远, 附近衰减越小,而且频率混叠越严重,使数字滤波器频响特性不能模 拟原模拟滤波器的频响特性。
因为 (n) u(n) u(n 1) 所以 h(n) s(n) s(n 1) 对应的 z 变换为
t nT
H ( z ) (1 z 1 ) S ( z )
z 1 1 1 F L H a (s) z s
t nT
用冲激响应不变法,将此模拟滤波器转化成数字滤波器( h n 表示单位取 样响应,即 h n ha nT ) 。确定系统函数 H z ,并把 T 作为参数,T 为任何值 时, 数字滤波器是稳定的, 并说明数字滤波器近似为低通滤波器还是高通滤波器。 解:模拟滤波器系统函数为
h(n) Tha (nT )
T ( a jb ) nT [e e ( a jb ) nT ]u (n) 2
H ( z ) h(n)z n
n 0
T 1 1 [ ] aT jbT 1 aT jbT 1 2 1 e e z 1 e e z
所以阶跃响应的 z 变换为
1
S z
a 1 a jb 1 2 1 2 2 a jb Ts 1 a b 1 z 2a b 1 e z
2
a jb 1 2 2 a jb Ts 1 s a b 1 e z
6
1 p H e j 1
0 p
H e j s
s
假设没有混叠, 问冲激响应不变法中所用的采样周期值对设计结果是否有影 响,并说明理由。 解: 冲激响应不变法是在 内由 H a j 到 H e j 的线性映射,该映射 为
H e j H a j
Ts
1
若没有混叠,所需的滤波器阶数为
1 lg
p
2
N
2 s
2 lg
其中
1 p s
p s
p Ts p 。 s Ts s
很显然,所需的滤波器阶数与 Ts 无关。 将巴特沃斯滤波器的系统函数进行部分分式展开,就有
s z 1 z 1
H a 对应的
H z Ha s
2 1 z 1 2 z 1 s T 1 z 1 T z 1
z 1 当 T 2 时, H z H a ,这时,如果 H a s 为低通,则 H z 亦为低 z 1
z 1 这正是题中所给变换关系,所以数字滤波器 H a 通带中心位于 , z 1
故答案(2)正确。 6. 用冲激响应不变法设计一个离散时间低通滤波器,连续时间巴特沃斯滤波器 的幅度平方函数为
H a j
2
1 1 j / j c
2N
滤波器的技术指标为
2
H a s e0.9t e st dt
0
1 s 0.9
H a s 的极点 s1 0.9 ,数字滤波器系统函数应为
H z 1 1 s1T 1 0.9T 1 1 e z 1 e z
H z 的极点为
z1 e0.9T , z1 e0.9T
通。 如果将 H a s 变换为高通滤波器
1 H ah s H a s
则可将 H ah s 用双线性变换法变成数字高通
H h z H ah s
z 1 s z 1
1 Ha s
z 1 s z 1
z 1 Ha z 1
3.用冲激响应不变法将以下 (1) (2) 分析 (1)冲激响应不变法满足 须让 先用部分分式展开。 ,T 为抽样间隔。这种变换法必 变换为 ,抽样周期为 T。 。 ,n 为任意正整数。
(2)第(2)小题要使用拉普拉斯变换公式 ,
3
可求出 解 (1) 由
又
,则可递推求解。
推出 由冲激响应不变法可得:
Ha s
其中
sa
s a
2
b
2
A1 A2 s a jb s a jb
1 2
A1 A2
所以系统函数为
H z
s 1 1 e z aTs 1 1 e cos bTs z 1 2 cos bTs e aTs z 1 e 2 aTs z 2
