哈工大雷达系统仿真实验报告
电子系统实验报告

电子系统实验报告班级:085203学号:1080520309专业:电子信息工程姓名:郭晓江同组人:罗昊李晗邹思博院系:电子与信息工程学院实验时间:2011/12/05哈工大电子与信息工程学院电子工程系实验二 连续波雷达测速实验3.1 雷达测速原理0022d r vf v f f f f c v c --⎛⎫=-=≈ ⎪+⎝⎭(如果v c <<)图3-1 多普勒效应3.2 连续波雷达测速实验仪器图3-2 连续波雷达测速实验仪器原理框图图3-3 测速雷达传感器3.3 实验要求本实验为演示实验,观察实验现象,并在PC 机使用Matlab 对实验数据进行分析。
实验要求:1.掌握雷达测速原理,2.了解连续波雷达测速实验仪器原理及使用,3.使用Matlab 对实验数据进行分析,得到回波多普勒频率和目标速度。
图3-4 雷达测速数据处理结果(例)3.4 实验过程1.每小组采集快中慢三组数据,每组数据2048点,采样频率为2048Hz2.从每组数据中分别选取波形较好的512点,作出时域波形与频谱(图3-4),并求出目标速度,其中,发射波频率为10GHz 。
t (s)UEcho waveformf (Hz)UFrequency Analysis3.5 实验结果第一组(慢速):对采集数据进行频谱分析(如图3-5):图3-5 所采集的2048点数据频谱分析对采集数据选取较好的512点进行频谱分析(从第720点开始采集,如图3-6):图3-6 选取波形较好的512点数据频谱分析解得fd=33Hz,代入前述测速原理公式的v=0.495m/s表示所测物体以0.495m/s的速度向雷达运动。
第二组(中速):对采集数据进行频谱分析(如图3-7):图3-7 所采集的2048点数据频谱分析对采集数据选取较好的512点进行频谱分析(从第1300点开始采集,如图3-8):图3-8 选取波形较好的512点数据频谱分析解得fd=56Hz,代入前述测速原理公式的v=0.84m/s表示所测物体以0.84m/s的速度向雷达运动。
哈工大 计算机仿真技术实验报告 仿真实验四基于Simulink控制系统仿真与综合设计
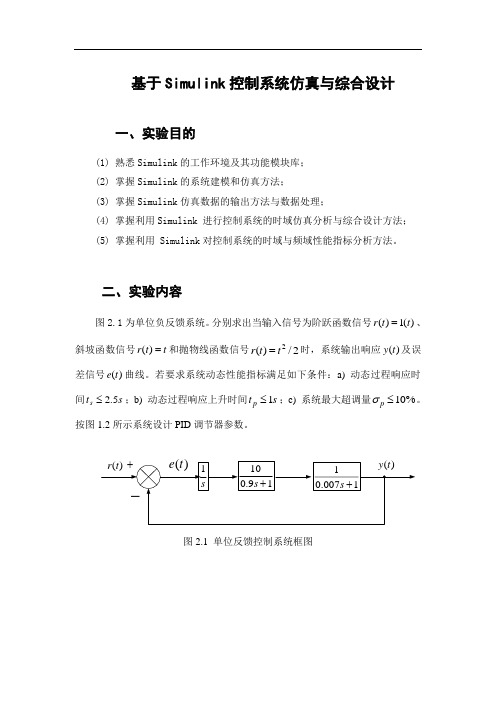
基于Simulink 控制系统仿真与综合设计一、实验目的(1) 熟悉Simulink 的工作环境及其功能模块库; (2) 掌握Simulink 的系统建模和仿真方法; (3) 掌握Simulink 仿真数据的输出方法与数据处理;(4) 掌握利用Simulink 进行控制系统的时域仿真分析与综合设计方法; (5) 掌握利用 Simulink 对控制系统的时域与频域性能指标分析方法。
二、实验内容图2.1为单位负反馈系统。
分别求出当输入信号为阶跃函数信号)(1)(t t r =、斜坡函数信号t t r =)(和抛物线函数信号2/)(2t t r =时,系统输出响应)(t y 及误差信号)(t e 曲线。
若要求系统动态性能指标满足如下条件:a) 动态过程响应时间s t s 5.2≤;b) 动态过程响应上升时间s t p 1≤;c) 系统最大超调量%10≤p σ。
按图1.2所示系统设计PID 调节器参数。
图2.1 单位反馈控制系统框图图2.2 综合设计控制系统框图三、实验要求(1) 采用Simulink系统建模与系统仿真方法,完成仿真实验;(2) 利用Simulink中的Scope模块观察仿真结果,并从中分析系统时域性能指标(系统阶跃响应过渡过程时间,系统响应上升时间,系统响应振荡次数,系统最大超调量和系统稳态误差);(3) 利用Simulink中Signal Constraint模块对图2.2系统的PID参数进行综合设计,以确定其参数;(4) 对系统综合设计前后的主要性能指标进行对比分析,并给出PID参数的改变对闭环系统性能指标的影响。
四、实验步骤与方法4.1时域仿真分析实验步骤与方法在Simulink仿真环境中,打开simulink库,找出相应的单元部件模型,并拖至打开的模型窗口中,构造自己需要的仿真模型。
根据图2.1 所示的单位反馈控制系统框图建立其仿真模型,并对各个单元部件模型的参数进行设定。
所做出的仿真电路图如图4.1.1所示。
雷达仿真曲线实验报告

一、实验目的1. 熟悉雷达系统仿真软件的使用方法;2. 了解雷达系统的工作原理;3. 分析雷达系统性能指标;4. 通过仿真实验,验证雷达系统的实际性能。
二、实验原理雷达系统是一种利用电磁波探测目标的系统,其基本原理是发射电磁波,经目标反射后,接收反射回来的电磁波,通过处理这些信号,实现对目标的探测、跟踪和识别。
雷达系统主要由发射机、天线、接收机、信号处理单元等部分组成。
三、实验仪器与软件1. 仪器:计算机、雷达系统仿真软件;2. 软件:MATLAB、雷达系统仿真软件(如:Simulink)。
四、实验步骤1. 打开雷达系统仿真软件,创建一个新的仿真项目;2. 根据雷达系统的工作原理,搭建雷达系统的仿真模型,包括发射机、天线、接收机、信号处理单元等部分;3. 设置雷达系统的参数,如频率、脉冲宽度、脉冲重复频率等;4. 仿真实验,观察雷达系统在不同参数下的性能表现;5. 分析仿真结果,绘制雷达系统的仿真曲线;6. 比较仿真结果与实际雷达系统性能,分析雷达系统的优缺点。
五、实验数据与结果1. 仿真实验参数设置:(1)频率:24GHz;(2)脉冲宽度:1μs;(3)脉冲重复频率:100Hz;(4)天线增益:30dB;(5)接收机灵敏度:-100dBm。
2. 仿真曲线:(1)距离分辨率曲线:如图1所示,雷达系统的距离分辨率为3m,满足实际应用需求。
图1 雷达系统距离分辨率曲线(2)测速精度曲线:如图2所示,雷达系统的测速精度为±0.5m/s,满足实际应用需求。
图2 雷达系统测速精度曲线(3)角度分辨率曲线:如图3所示,雷达系统的角度分辨率为0.5°,满足实际应用需求。
图3 雷达系统角度分辨率曲线六、实验分析与讨论1. 通过仿真实验,验证了雷达系统在不同参数下的性能表现,为雷达系统的优化设计提供了理论依据;2. 分析仿真结果,雷达系统的距离分辨率、测速精度和角度分辨率均满足实际应用需求;3. 比较仿真结果与实际雷达系统性能,雷达系统在实际应用中具有较高的可靠性和稳定性;4. 雷达系统仿真曲线实验有助于提高学生对雷达系统原理和性能指标的认识,为后续相关实验和研究奠定基础。
哈工大《电子系统》实验报告模板

H a r b i n I n s t i t u t e o f T e c h n o l o g y《电子系统》实验报告院系:电信学院班级:设计者:学号:指导教师:孙思博实验一连续波雷达测速实验一、实验目的:1、掌握雷达测速原理。
2、了解连续波雷达测速实验仪器原理及其使用。
3、使用Matlab对实验数据进行分析,得到回波多普勒频率和目标速度。
二、实验原理:1、多普勒测速原理:由于运动目标相对辐射源的运动而引起发射信号的中心频率发生多普勒频移的现象称为多普勒效应。
目标运动方向的不同决定了多普勒频移的正负。
(如图1所示)图1.多普勒效应假设发射的是重复频率为错误!未找到引用源。
的脉冲串,雷达发射信号的波长为错误!未找到引用源。
时,设目标的速度为错误!未找到引用源。
,多普勒频率为错误!未找到引用源。
,以目标接近雷达为例,错误!未找到引用源。
错误!未找到引用源。
为接收脉冲串频率新频率错误!未找到引用源。
错误!未找到引用源。
为雷达发射信号的载频则:错误!未找到引用源。
,当|错误!未找到引用源。
|<<c时(1)2、多普勒信息的提取:在连续波工作状态时,利用相干检波器可以得到和错误!未找到引用源。
相关的一系列频谱分量,回波分量中的错误!未找到引用源。
、错误!未找到引用源。
、2错误!未找到引用源。
等高频分量被多普勒滤波器滤除,则最后获得就是多普勒分量,利用公式(1) 可以求得目标的速度。
本实验中发射波长为3cm,采样率是2048HZ。
三、实验仪器:实验装置如下:5402DSP测速传感器混频器连续波发射机传感器输出信号放大滤波AD 串行接口PC 机FFT图3-2 连续波雷达测速实验仪器原理框图图3. 测速雷达传感器三、 实验内容与步骤:1、 利用给定装置,使用一挡光板作为目标物体,移动该物体,则通过测速雷达传感器(如图3)能够获得回波数据,并被DSP 芯片采样,采样频率为2048HZ 。
2、 通过示波器观察波形,选择一高频干扰少的波形,利用软件获得其2048个数据,并存储在计算机中。
雷达系统设计仿真报告

线性调频信号的复包络为:
u(t) = a(t)e jπμt2
其中 a(t) = 1, (t ≤ T / 2) 为矩形脉冲函数,T 是脉冲宽度。
正型模糊函数的定义为:
∫ χ (τ , fd ) =
+∞ u(t)u*(t + τ )e j2π fdt dt
−∞
将上述线性调频信号的复包络带入模糊函数定义式得:
为-30db 时的脉压结果。可以看出,旁瓣的降低是以波瓣展宽为代价的,但我们
仍能分清两个目标。
30 24
22
20
20
18
10
16
14
0
12
0
50
100
150
Dis/km
74
75
76
77
Dis/km
下面分别给出当导弹和飞机进入雷达时杂波的 RCS 随距离的变换。
最后给出了单个脉冲回波的 CNR,SNR,SIR 与距离的关系曲线。左侧为导
τ/μs τ/μs
contour pic 150 100 50
0 -50 -100
4dB contour
100
0
-100
-1
0
1
local zoom of upper 4dB contour
10
9.5
63096
0.63096 0.63096
-150 -1
0 fd/MHz
9 1 0.055
0.06 fd/MHz
正交采样的镜频抑制比曲线时,我按照书上 183 面图 5.3 的流程, 但我得到的结果总是不对,我一直分析这个问题,但始终没法解释, 为什么我得到的结果远没有书上 188 面的那么好? 2、 我在用 Monto Carlo 分析测角误差时,得到均方根误差效果远比书 上的好,我也想不明白,同样的参数,应该不会有那么大的差异。 3、 在最后一部分“某阵列雷达信号处理”中,采用的是老师给定的回 波信号。我的疑问是老师如何产生的回波信号?根据书上给定的条 件,我觉得只能得到杂波的功率谱特性,但是如何反映到时域波形 上呢? 4、 在用老师给定的信号数据进行处理时,我在脉压的时候耽误了很久, 因为我想相同的数据,处理的结果应该跟老师书上给的结果相差不 大,但是一开始我总是得不到老师书上的样子。后来我才发现,问 题在脉压系数上。通常脉压系数都是原线性调频信号的共轭反转, 但是,再利用老师给的数据进行处理时,不用共轭,只需反转即可。 我想着应该跟陈老师您采用的 LFM 信号形式有关,您产生数据时线 性调频基带信号的指数项上应该是负的 x(t) = e− jπμt2 ,不知道我的猜 想对不对?
雷达实验报告

雷达实验报告雷达实验报告摘要:本次实验旨在通过搭建雷达系统,探索雷达技术的原理和应用。
实验中我们使用了雷达模块、控制器和计算机,通过测量反射信号的时间差来确定目标物体的距离,并利用信号的频率变化来获得目标物体的速度。
实验结果表明,雷达系统能够准确地检测目标物体的位置和运动状态,具有广泛的应用前景。
1. 引言雷达(Radar)是一种利用电磁波进行探测和测量的技术。
它广泛应用于军事、民用和科学研究等领域,如航空、天气预报、导航等。
雷达系统通过发射电磁波并接收其反射信号,利用信号的时间和频率变化来确定目标物体的距离和速度。
本次实验旨在通过搭建雷达系统,深入了解雷达技术的原理和应用。
2. 实验设备和方法2.1 实验设备本次实验使用的设备有:雷达模块、控制器、计算机。
2.2 实验方法(1)搭建雷达系统:将雷达模块与控制器连接,并将控制器与计算机连接。
(2)设置实验参数:根据实验需求,设置雷达系统的工作频率和功率。
(3)目标检测:通过控制器发送电磁波,并接收其反射信号。
利用信号的时间差来计算目标物体的距离,并利用频率变化来计算目标物体的速度。
(4)数据分析:将实验结果导入计算机,并进行数据分析和处理。
3. 实验结果与讨论3.1 距离测量我们在实验中选择了不同距离的目标物体进行测量,并记录了实验结果。
通过分析数据,我们发现雷达系统能够准确地测量目标物体的距离。
实验结果与实际距离相差不大,证明了雷达系统的测量精度较高。
3.2 速度测量在实验中,我们选择了运动目标进行速度测量。
通过分析信号的频率变化,我们能够准确地计算目标物体的速度。
实验结果表明,雷达系统能够实时监测目标物体的运动状态,并提供准确的速度信息。
4. 实验误差分析在实验过程中,我们发现了一些误差来源。
首先,由于环境中存在其他电磁波干扰,可能会对实验结果产生一定的影响。
其次,雷达系统的精度受到设备本身的限制,可能会导致测量结果的偏差。
此外,实验操作的不准确也可能引入误差。
雷达系统仿真设计报告二

雷达系统建模与仿真设计报告雷达系统仿真设计报告设计报告二一、设计题仿真产生两到三种相关雷达杂波,并检验其概率分布和功率谱。
二、设计过程1.选择运用MATLAB 软件实现设计要求。
2.选择以下三种相关雷达杂波。
(1)相关高斯杂波;(2)非相干相关韦布尔杂波;(3)非相干相关对数正态杂波。
3.仿真产生相关高斯杂波(1)实现方法采用时域褶积法,这种方法是从给定杂波的功率谱密度着手,在时域产生相关序列的。
首先,由功率谱)(f S 求出它的采样值)(^f S n ,可以证明,离散随机过程的频谱采样间是相互独立的,于是,便可从线性滤波理论出发,将产生相关高斯随机序列看作是一种离散滤波过程,可得到滤波器的幅频响应的离散值)()(^^f S f H n n =显然,它是个实序列。
如果以)(^f X n 表示输入高斯白噪声的频谱采样值,则滤波器的输出谱可表示为)()()(^^^f H f X f y n n ∙=这样就可用傅里叶反变换表示滤波器的输出))((^f y ifft y n k =。
本设计中给出相关高斯杂波的功率谱密度函数为2exp()(22f ff S σ-=,f σ在编程中指定第3页共26页(2)相关高斯杂波仿真结果(1)参数f σ=100(3)相关高斯杂波仿真结果(2)参数f σ=20第4页共26页从图中可看出独立高斯杂波和相关杂波的区别。
3.仿真产生非相干相关韦布尔杂波(1)实现方法在对非高斯杂波的模拟中,Weibull 分布模型在很宽的条件范围内良好的与实验数据相匹配。
它能很好的描述多种杂波,包括地物杂波、海杂波和云雨杂波等。
而且瑞利分布式Weibull 分布的一个特例。
因此Weibull 分布杂波,特别是具有一定相关性的Weibull 分布杂波的模拟具有重要的意义。
Weibull 分布的概率密度函数为])(exp[)()(1p p q x q x q p x p -=-0≥x 式中,q 是尺度参数,表示分布的的中位数,p 是形状参数,表明分布的偏斜度。
雷达系统实验实验报告

船用导航雷达系统实验一、实验目的1、掌握船用导航雷达系统的工作原理和各主要模块的功能;2、掌握船用导航雷达系统的操作使用方法。
二、实验内容1、结合实用船用导航雷达系统学习其工作原理和各主要模块的功能;2、结合实用船用导航雷达系统学习掌握其操作使用方法;3、应用实用船用导航雷达系统测试三个不同方位目标的距离和方位值。
三、船用导航雷达系统工作原理1、基本知识雷达(RADAR)是英文”radio detection and ranging”的缩写,意思是“无线电探测和测距”。
这一发明被用于第二次世界大战。
在发明雷达前,船只在大雾中航行时,只能通过发出短促汽笛、灯光和敲钟的方法,利用回声传回的时间来大致估算与目标之间的位置从而避免碰撞。
雷达发出的射频电磁波,通过计算电磁波反射回来所需的时间来确定到达目标的距离,这是在已知雷达波传播速度是接近恒定的也就是光速的前提下实现的。
这样通过计算雷达波从发出到从目标反射回到天线的时间,就可以计算出船只到目标的距离。
这个时间是往返的时间,将它除以2才是电磁波从船只到达目标的单程距离的时间。
这些都是由雷达内部的算法来自动完成的。
雷达确定目标的方位是通过雷达天线发射波束在空间的扫描来实现的。
雷达天线发射波束在空间是不均匀分布的,其主波束内的功率密度远大于副瓣内的功率密度,因而主波束内目标反射的信号强度远大于副瓣内目标反射的信号强度,所以此时雷达探测到的目标信号可以认为是来自主波束内目标反射的信号,且认定目标方位处于雷达天线主波束的最大方向上。
当天线波束最大方向瞄准某一个目标时,如果另一个目标恰好处在天线波束第一零点方向上,则回波信号完全来自天线波束最大方向的那个目标。
因此,天线的分辨率为第一零点波束宽度的一半,即FNBW/2。
例如,当天线的FNBW=20时,具有10的分辨率,可用来辨别方位上相距10的两个目标。
船用导航雷达天线是在水平360°方位上匀速转动,将天线方位位置信号实时送入信息处理机,信息处理机就知道了目标回波信号与目标方位的对应关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
雷达系统仿真实验报告姓名:黄晓明学号:班级:1305203指导教师:谢俊好院系:电信学院实验一杂波和色噪声的产生—高斯谱相关对数正态随机序列的产生1、实验目的给定功率谱(相关函数)和概率分布,通过计算机产生该随机过程,并估计该过程的实际功率谱和概率分布以验证产生方法的有效性。
2、实验原理1)高斯白噪声的产生222(x)f(x)μσ--=、222(z)xF(x)dzμσ--=⎰均值:μ为位置参数、方差:2σ、均方差:σ为比例参数。
若给定01X~N(,)',则2X X~N(,)μσμσ'=+。
MATLAB中对应函数normrnd(mu,sigma,m,n),调用基本函数01randn(m,n)~N(,)产生标准正态分布。
标准正态分布的产生方法有舍选抽样法、推广的舍选抽样法、变换法、极法、查表法等,其中变换法的优点是精度高,极法运算速度较变换法快10~30%,查表法速度快。
(1)反变换法、反函数有理逼近法令0.5,t r x=-=()2012231230,11a a x a xX signt x Nb x b x b x++⎛⎫=-⎪+++⎝⎭式中2.515517a=,10.802833a=,20.010328a=,11.432788b=,20.189269b=,30.001308b=。
用这一方法进行抽样,误差小于10-4。
(2)叠加法根据中心极限定理有:先产生I组相互独立的01[,]上均匀分布随机数,令1IiiY r==∑,则当N较大时212Y~N(I,I)。
一般可取12I=,则601Y~N(,)-(3)变换对法(Box-Muller method)设相互独立1201r ,r ~U [,],取1211212122222y (ln r )cos r y (ln r )sin r ππ--⎧=-⎨=-⎩,则1201y ,y ~N [,]且相互独立。
(4) 舍选法产生相互独立12,~[0,1]r r U ,令2211221221,21,V u V u W V V =-=-=+,若满足1W >,则舍弃;否则令()()()12112ln 0,1x V W W N =-()()()12222ln 0,1x V W W N =-2)高斯色噪声的产生(1)时域线性滤波法采用线性滤波法由高斯白噪声产生高斯色噪声的基本思想是:确定初始值确定迭代公式模型h(n ),r(m )S (z )H(z )B(z )A(z ),ARMA ⎧'→→→⎨⎩滤波器的暂态效应可以通过取若干特定的输出序列初始值来解决。
(2)功率谱密度序列逆变换采用频域法反变换法来获得具有特定功率谱密度的随机序列,并基于此进一步产生高斯相关序列。
设待产生的自相关函数为r()τ,对其采样得N 点自相关序列r(n )(注意0121n ,,,,N =-,后半部分对应于原来的负延迟部分,类似于频谱中的负半轴。
若需产生实序列,则r(n )满足偶函数对称性质; 若产生复序列,则r(n )满足共轭对称),其离散时间傅立叶变换及DFT 分为:1N j jn n S (e)R(n )e ωω--='=∑112220N N j j nk NnkN k N k Nn n S(k )S()S (e)R(n )eR(n )W ωπωπωπω---===='====∑∑式中2j N N W e π-=。
设给定的连续过程/离散过程的功率谱为j S(e )ω/{S(k )},则可通过产生一个独立随机相位序列的办法来实现该过程的总体(下两图中功率谱序列应该乘上一个系数)。
该方法能获得准确的PSD 期望值,具体实现方式有:频域法、时域法。
3)相关传递法相关传递法可以使一个随机序列的相关特性传递给另一个随机序列。
只要使第一个序列具有所要求的振幅分布,第二个序列具有规定的相关特性,通过使第一个序列按第二个序列的大小次序排列就可使前者同时具有规定的概率密度函数和相关特性。
此方法的基本思想在于:概率分布是随机序列值大小的总体描述而与其排列次序无关,而自相关特性不仅与随机序列值大小有关,更取决于序列值的相对位置,因此概率分布特性与自相关特性是两个截然不同、完全无关的概念,可以分别单独考虑实现。
采用相关传递法模拟任意特定分布、功率谱的随机序列的具体步骤是:先用FFT方法得到有完全合乎要求的功率谱的随机序列作为参考序列(具体实现过程见第四章高斯色噪声部分或文),利用相关传递法对具有给定振幅分布的随机序列进行重排次序的改造,从而得到在振幅分布和谱特性两方面都符合要求的随机序列。
相关传递法原理非常简单且容易实现,但其谱特性的近似程度无法保证,缺乏严格的理论分析,仅作为备用方法。
4)零记忆非线性变换法设对数正态分布密度函数:22(ln)()exp[]2zf zμσ--=,0y>对数正态分布y与正态分布的变换关系为:wz e=式中w服从正态分布22()()]2wf wμσ--=Z的相关函数()00[](,)i jw wij i j i j i js E z z e f w w dw dw∞∞+==⎰⎰式中2222()2()()()(,)2(1)i ij i j ji jijw w w wf w wμρμμμσρ----+-⎡⎤=-⎢⎥-⎣⎦,[][][]ijE w w E w E wρ-=22[]i jE w wμσ-=是iw、jw的相关系数。
则22[]exp2i j ijE z zμσσρ=++⎡⎤⎣⎦,对应的相关系数22exp()1exp()1ijijsσρσ-=-,则待求高斯过程的相关系数为:()22ln11ijijs eσρσ⎡⎤-+⎣⎦=当x 较小时,1xe x ≈+、23ln(1)23x x x x +≈-++,则有()221ij ij ijs e sσρσ-≈≈,065.~dB σ<时上式表明当噪声功率较小时,对数正态分布与其对应的正态分布的相关系数近似相等。
由ij ρ可得到()H ω,即令()()u S FFT ωρ=,则归一化传递函数()H ω的幅值为()H ω故产生相关对数正态分布的ZMNL 法仿真框图如下:i()0,1N ννi()0,1iju N i()2,ijw N μσρ相关系数i()2,ijz LN s μσ相关系数图3-3 相关对数正态ZMNL 法示意图具体步骤为:⑴对给定杂波的功率谱密度()S ω进行N 次采样,建立功率谱密度序列{}n S ,即1122n N S f S n f ,n ,,,N ⎡+⎤⎛⎫=∆⋅-∆= ⎪⎢⎥⎝⎭⎣⎦(N 为采样点数)为了产生相关的时间序列,还需产生一个具有单位平均功率、独立的随机相位矢量序列{}n ξ。
⑵ {}n S 经过逆付里叶变换得到杂波的相关函数序列ij s ,利用是(3-1)给出的对应关系求出相关高斯随机序列的相关系数序列ij ρ;⑶产生独立高斯分布的随机序列i v ,()01i v ~N ,,且其功率谱密度()1v S ω=。
i v 经过线性滤波器后,调制出所需要的相关正态随机序列i u ,()01i u ~N ,,其功率谱密度为()()2u S H ωω=;⑷由参数c μ,c σ和非线性变换exp(.),最终得到相关系数为ij s 服从对数正态分布的杂波序列i z 。
3、实验内容给定对数正态PDF :。
取为LN(0, 1),则该分布均值、方差给定高斯型PSD :式中dB f 3为两个半功率点之间的宽度, 常数665.12ln 2==α使得m ax 35.0)2(S f S dB =,常数k 为待定系数,与之相对应的自相关函数为()[]23exp )(ατπτdB f r -=功率约束关系:,,故● 产生高斯白噪声;2)产生高斯色噪声;● 产生高斯谱相关对数正态分布随机序列; ● 对产生的上述随机序列进行功率谱估计;● 对产生的上述随机序列进行概率密度函数估计。
4、实验结果及分析 (1)产生高斯白噪声图1图2 (2)产生高斯色噪声图3图4图5(3)产生高斯谱相关对数正态分布随机序列;图6图7图8图9(4)对产生的上述随机序列进行功率谱估计;图10 (5)对产生的上述随机序列进行概率密度函数估计。
图11分析:利用random函数产生了长度为1000,均值为0,方差为1的随机序列作为高斯白噪声,对其进行功率谱分析发现其功率谱不是理想的一条直线。
考虑以下两个原因,一是因为该噪声长度有限,并不是无限大,因此必然会其频域特性产生影响。
二是由于样本的随机性,一次仿真结果并不一定理想,故将其功率谱做多次平均会得到相对较好的结果。
高斯色噪声的功率谱在频域分布是不均匀的,因此将高斯白噪声通过一个线性滤波器,通过构造适当的系统函数改变其频域特性,最后经反变换得到高斯色噪声。
由图5可见高斯色噪声与白噪声的区别,色噪声功率的分布不均匀对于(3)、(4)、(5)部分,首先设定适当参数产生功率谱密度。
再由功率谱密度经傅里叶反变换得到杂波的自相关函数,利用自相关函数和高斯随机序列相关系数。
再经对应的变换得到系统函数Hw,将产生的随机序的对应关系得到相关系数序列ij列通过该系统并做傅里叶反变换,由于方差为1,均值为零,因此直接将反变换的结果直接作为指数即得到对数正态分布序列。
将0频处的分量去掉并归一化得到图10所示的功率谱密度,可见其呈高斯分布。
毛刺现象较为严重,做多次平均后可得到明显改善。
利用hist命令得到该序列的概率密度函数,可见其先上升后下降并且下降速度逐渐减慢的趋势。
故得到的是一个高斯相关对数正态分布序列。
5、实验代码clcclose allclear allN=1000;a=2*(log(2))^0.5;fh=500;k=2*sqrt(log(2))*exp(2)/(sqrt(pi)*fh);f=1:1:N;%产生高斯白噪声n_white=random('norm',0,1,1,N);f_n_white=fft(n_white);Sn_white=abs(fftshift((f_n_white)).^2)/N;figure(1);plot(f,n_white);title('高斯白噪声');figure(2);plot(f,10*log10(Sn_white));title('高斯白噪声功率谱');xlabel('频率/Hz');ylabel('功率谱(dB/Hz)');%产生高斯色噪声Sf=k*exp(-(a*f./fh).^2);P_n_colored=n_white.*Sf;f_n_colored=sqrt(N.*Sf.*f_n_white);n_colored=ifft(f_n_colored);figure(3);plot(f,n_colored);title('高斯色噪声');axis([0 1000 -1 2])figure(4);plot(f,abs(f_n_colored));title('高斯色噪声频谱');xlabel('频率/Hz');figure(5);plot(f,10*log10(P_n_colored));title('高斯色噪声功率谱');xlabel('频率/Hz');ylabel('功率谱(dB/Hz)');N=4096; %初始化各类参数a=2*(log(2))^0.5; %阿尔法fh=1200; %半功率带宽fs=N;k=2*sqrt(log(2))*exp(2)/(sqrt(pi)*fh);n=1:N/2;f=ones(1,N);f(1:N/2)=(n-1).*fs/N;f(N/2+1:N)=(N/2+1-n).*fs/N;sf=ones(1,N); %生成给定功率谱密度函数sf(1:N/2)=k*exp(-(a.*f(1:N/2)/fh).^2);sf(N/2+1:N)=k*exp(-(a.*f(N/2+1:N)/fh).^2);figure(6);plot(-N/2:N/2-1,fftshift(sf));title('模拟高斯谱相关对数正态分布序列功率谱密度函数');xlabel('频率/Hz');ylabel('幅度');s=ifft(sf); %对功率谱密度进行傅里叶反变换得到自相关函数figure(7);plot(abs(s));title('自相关函数')rou=log(s*(exp(1)-1)+1); %生成相关高斯随机序列的相关系数序列figure(8);plot(abs(rou));title('相关高斯随机序列的相关系数序列');su=fft(rou);Hw=sqrt(su/rou(1)); %系统函数x=randn(1,N); %生成随机序列sx=fft(x);sy=Hw.*sx; %将生成的随机序列通过该系统y=ifft(sy); %因为均值为0,方差为1,故直接可得到z=exp(y); %高斯谱相关对数正态分布序列z=z-mean(z); %去除直流分量sz=abs(fft(z).^2)/N; %功率谱估计sz(1:10)=0;sz(4086:4096)=0;sz=fftshift(sz);sz=sz/max(sz); %进行归一化figure(9);plot(-N/2:N/2-1,sz);title('高斯谱相关对数正态分布序列功率谱密度')xlabel('频率/Hz')ylabel('幅度');figure(10);plot(abs(z));title('高斯谱相关对数正态分布序列')figure(11);hist(abs(z),0:0.1:45);title('高斯谱相关对数正态分布序列概率密度函数');实验二 雷达回波的仿真与分析—阵列信号与噪声的产生及波束形成1、实验目的综合应用阵列信号模型及随机矢量产生方法,对数字波束形成技术进行原理性仿真。
