两道大题
高考解三角形大题(30道)

高考解三角形大题(30道)1.已知在三角形ABC中,内角A,B,C的对边分别为a,b,c,且有 $\frac{\cos A - 2\cos C}{2c-a}=\frac{\cos B b}{\sin C}$。
求该三角形的 $\sin A$ 值和面积 $S$,已知 $\cosB=\frac{1}{4}。
b=2$。
2.已知在三角形ABC中,角A,B,C的对边分别为a,b,c,且有 $\sin C+\cos C=1$。
求 $\sin C$ 值和边c的值,已知$a+b=4(a+b)-8$。
3.已知在三角形ABC中,角A,B,C的对边分别为a,b,c。
求 $\sin(A+\frac{C}{2})=\frac{1}{2}\cos A$,并求角A的值;已知 $\cos A=\frac{1}{3}。
b=3c$,求 $\sin C$ 值。
4.在三角形ABC中,D为边BC上的一点,且有$BD=\frac{3}{3},\sin B=\frac{5}{3},\cos\angle ADC=-\frac{1}{\sqrt{3}}$。
求AD的值。
5.已知在三角形ABC中,角A,B,C的对边分别为a,b,c,且有 $a=1,b=2,\cos C=\frac{1}{4}$。
求该三角形的周长和$\cos(A-C)$ 值。
6.已知在三角形ABC中,角A,B,C的对边分别为a,b,c,且有$\sin A+\sin C=\frac{1}{2}\sin B$,且$ac=\frac{1}{2}b$。
已知 $p=\frac{1}{5},b=1$,求 $a,c$ 的值;若角B为锐角,求p的取值范围。
7.已知在三角形ABC中,角A,B,C的对边分别为a,b,c,且有 $2a\sin A=(2b+c)\sin B+(2c+b)\sin C$。
求角A的值和$\sin B+\sin C$ 的最大值。
8.已知在三角形ABC中,角A,B,C的对边分别为a,b,c,且有 $\cos 2C=-\frac{1}{4}$。
高中数学经典大题150道

高中数学经典大题150道在高中数学学习过程中,经典大题是不可避免的重要内容。
这些经典大题既考察了学生对知识点的掌握程度,又锻炼了他们的思维能力和解题技巧。
下面将列举150道高中数学经典大题,供同学们复习和练习。
1. 一元二次方程求解:求方程$2x^2 - 5x + 3 = 0$的解;2. 直角三角形斜边求长:已知直角三角形的一个锐角为$30^\circ$,斜边长为10,求另外两边的长度;3. 函数求极值:已知函数$f(x) = x^2 - 4x$,求$f(x)$的最小值;4. 三角函数化简:化简$\sin^2x - \cos^2x$;5. 平面向量运算:已知向量$\vec{a} = 2\vec{i} - 3\vec{j}$,$\vec{b} = \vec{i} + \vec{j}$,求$3\vec{a} - 2\vec{b}$的模;6. 不等式求解:解不等式$2x - 5 > 3$;7. 集合运算:已知集合$A = \{1, 2, 3\}$,$B = \{2, 3, 4\}$,求$A\cap B$;8. 对数方程求解:求解方程$\log_x 32 = 5$;9. 三视图绘制:根据给定的正方体的三个视图绘制其立体图形;10. 空间向量垂直判定:已知向量$\vec{a} = 2\vec{i} - 3\vec{j} +\vec{k}$,$\vec{b} = 3\vec{i} + 2\vec{j} - 4\vec{k}$,判断$\vec{a}$和$\vec{b}$是否垂直。
11. 二次函数图象:画出函数$f(x) = x^2 - 4x + 3$的图象;12. 三角函数图象:画出函数$y = \sin x$和$y = \cos x$在同一坐标系内的图像;13. 集合的运算:已知集合$A = \{1, 2, 3\}$,$B = \{3, 4, 5\}$,$C = \{2, 4, 6\}$,求$(A \cup B) \cap C$;14. 对数幂运算:计算$\log_2 8^3$的值;15. 消元解方程组:解方程组$\begin{cases} 2x - 3y = 7 \\ 4x + y = 1 \end{cases}$;16. 平面几何证明:证明过直径的正圆周角是直角;17. 空间几何证明:证明立体对顶点所在直线上的中位线相等;18. 三角函数证明:证明$\sin^2x + \cos^2x = 1$;19. 向量证明:证明向量的模长公式;20. 立体几何体积计算:计算正方体的体积。
三角函数10道大题(带答案)

三角函数10道大题(带答案)三角函数1.已知函数$f(x)=4\cos x\sin(x+\frac{\pi}{6})+\sin(2x-\frac{\pi}{4})+2\cos2x-1,x\in R$。
Ⅰ)求$f(x)$的最小正周期;Ⅱ)求$f(x)$在区间$[-\frac{\pi}{4},\frac{\pi}{4}]$上的最大值和最小值。
2.已知函数$f(x)=\tan(2x+\frac{\pi}{4}),x\in R$。
Ⅰ)求$f(x)$的定义域与最小正周期;II)设$\alpha\in(\frac{\pi}{4},\frac{\pi}{2})$,若$f(\alpha+\frac{\pi}{4})=2\cos2\alpha$,求$\alpha$的大小。
3.已知函数$f(x)=\frac{(sinx-cosx)\sin2x}{\sin x}$。
1)求$f(x)$的定义域及最小正周期;2)求$f(x)$的单调递减区间。
4.设函数$f(x)=\frac{2\pi\cos(2x+\frac{\pi}{4})+\sin2x}{24}$。
Ⅰ)求函数$f(x)$的最小正周期;II)设函数$g(x)$对任意$x\in R$,有$g(x+\pi)=g(x)$,且当$x\in[0,\frac{\pi}{2}]$时,$2\pi g(x)=1-f(x)$,求函数$g(x)$在$[-\pi,0]$上的解析式。
5.函数$f(x)=A\sin(\omega x-\frac{\pi}{6})+1(A>0,\omega>\frac{\pi}{6})$的最大值为3,其图像相邻两条对称轴之间的距离为$\frac{\pi}{2}$。
1)求函数$f(x)$的解析式;2)设$\alpha\in(0,\frac{\pi}{2})$,则$f(\alpha)=2$,求$\alpha$的值。
6.设$f(x)=4\cos(\omega x-\frac{\pi}{6})\sin\omegax+\cos2\omega x$,其中$\omega>0$。
南昌中考数学最后两道大题具体分值

南昌中考数学最后两道大题具体分值中考数学测试卷的最后两题一般都会是综合应用题,一般会分步求解,要求学生不仅要具备一定的阅读能力,还要有一定数学知识点的综合应用能力!也是拉开分差很关键的题!每一年的中考数学最后一题的分数应该都是12分,它是有三个小题的,每个小题的分值不一样,如果第一个小七它简单的话,那么它的分词是差不多是在一到两分,大部分的第一小题的那个都是填空题,几乎都是一分到俩分的,那每一小题的分值按它的难度来算,一般分值在30分左右。
根据上面分数相信大家也可以看出,基础题和较难题占数学的60%多,所以在学习中应该扎实好基础不要会了就不去思考。
只要基础扎实在数学中可以称之为优等生,但是想要从优等生进化为尖子生难题这30分十分关键。
最后两道是压轴题,有一定难度,做中考题时需要沉着冷静,先以后难,不会做的先放下,先把有把握的做完,做完后回过头来在做不怎么会做的,全部做完有时间的话还可以再检查检查。
(完整版)全国卷第二道大题化学平衡试题分类
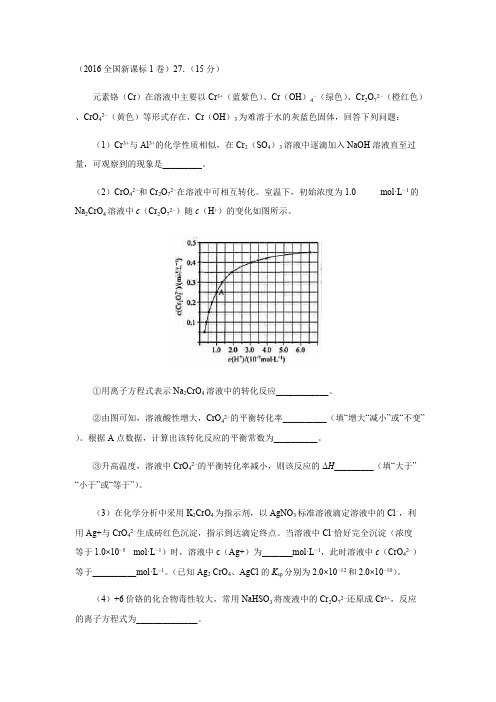
元素铬(Cr)在溶液中主要以Cr3+(蓝紫色)、Cr(OH)4−(绿色)、Cr2O72−(橙红色)、CrO42−(黄色)等形式存在,Cr(OH)3为难溶于水的灰蓝色固体,回答下列问题:(1)Cr3+与Al3+的化学性质相似,在Cr2(SO4)3溶液中逐滴加入NaOH溶液直至过量,可观察到的现象是_________。
(2)CrO42−和Cr2O72−在溶液中可相互转化。
室温下,初始浓度为1.0 mol·L−1的Na2CrO4溶液中c(Cr2O72−)随c(H+)的变化如图所示。
①用离子方程式表示Na2CrO4溶液中的转化反应____________。
②由图可知,溶液酸性增大,CrO42−的平衡转化率__________(填“增大“减小”或“不变”)。
根据A点数据,计算出该转化反应的平衡常数为__________。
③升高温度,溶液中CrO42−的平衡转化率减小,则该反应的ΔH_________(填“大于”“小于”或“等于”)。
(3)在化学分析中采用K2CrO4为指示剂,以AgNO3标准溶液滴定溶液中的Cl−,利用Ag+与CrO42−生成砖红色沉淀,指示到达滴定终点。
当溶液中Cl−恰好完全沉淀(浓度等于1.0×10−5mol·L−1)时,溶液中c(Ag+)为_______mol·L−1,此时溶液中c(CrO42−)等于__________mol·L−1。
(已知Ag2 CrO4、AgCl的K sp分别为2.0×10−12和2.0×10−10)。
(4)+6价铬的化合物毒性较大,常用NaHSO3将废液中的Cr2O72−还原成Cr3+,反应的离子方程式为______________。
丙烯腈(CH 2=CHCN)是一种重要的化工原料,工业上可用“丙烯氨氧化法”生产。
主要副产物有丙烯醛(CH 2=CHCHO)和乙腈(CH 3CN)等。
回答下列问题:(1) 以丙烯、氨、氧气为原料,在催化剂存在下生成丙烯晴(C3H3N)和副产物丙烯醛(C3H 4O)的热化学方程式如下:①C 3H 6(g)+NH 3(g)+O 2(g)=C 3H 3N(g)+3H 2O(g)ΔH =−515 kJ·mol −132②C 3H 6(g)+O 2(g)=C 3H 4O(g)+H 2O(g)ΔH =−353 kJ·mol −1两个反应在热力学上趋势均很大,其原因是 __________ ;有利于提高丙烯腈平衡产率的反应条件是 __________ ;提高丙烯腈反应选择性的关键因素是 __________ 。
中国特色社会主义两道题

1.谈谈如何在全面推进社会建设中统筹协调社会利益关系?答:为了有效地推进和谐社会建设,就必须协调和理顺社会利益关系。
一、 当前社会中利益关系的新特点(一) 利益主体趋于多样化。
当前,我国社会利益主体呈现出多样化趋势。
一是原有工人、农民和知识分子群体内部发生了变化。
(2) 利益差距有所扩大。
a随着社会的变革和体制的转型,当前我国社会关系中出现了利益失衡和不公平现象。
(3) 矛盾对抗程度有所增强。
当前我国社会总体上是和谐稳定的,但随着利益主体分化、利益差距扩大等多方面因素的影响,人民群众内部的利益矛盾日渐凸显。
2、 统筹协调好各方面的利益关系的重要性和紧迫性和谐社会的“真谛”就在于不同领域的统筹兼顾、多种利益的协调统一、人民内部矛盾的化解和各种冲突的妥善处理。
构建和谐社会的过程,就是不断协调利益关系、不断化解社会矛盾的过程。
因此,统筹协调好各方面利益关系,对于经济社会的协调稳定健康发展具有极为重要的意义。
1.有利于推动经济又好又快发展。
2.有利于保持社会稳定、促进社会和谐。
3.有利于实现社会公平正义。
三、统筹协调当前社会各方面的利益关系的方法和途径“统筹协调各方面利益关系,妥善处理社会矛盾。
适应我国社会结构和利益格局的发展变化,形成科学有效的利益协调机制、诉求表达机制、矛盾调处机制、权益保障机制”。
当前,要特别重视加强制度建设,通过创新体制机制,建立一套能够不断解决利益矛盾、妥善化解利益冲突、有效促进和谐的利益调节机制。
(一)顺畅的社会流动机制。
(2) 健全的诉求表达机制。
(3) 公平的利益协调机制。
(4) 完善的矛盾调处机制。
(5) 安全的社会保障机制。
要始终把实现好、维护好、发展好最广大人民的根本利益作为党和国家一切工作的出发点和落脚点,尊重人民主体地位,发挥人民首创精神,保障人民各项权益,走共同富裕道路,促进人的全面发展,做到发展为了人民、发展依靠人民、发展成果由人民共享。
”建设中国特色社会主义,归根到底是为了最广大人民的根本利益,发展的目的是为了不断满足人民群众的物质文化需要。
一次函数练习题(大题30道)
----1.已知一次函数y=ax+b 的图象经过点A(2,0)与B(0,4).(1)求一次函数的解析式,并在直角坐标系内画出这个函数的图象;(2)如果(1)中所求的函数y 的值在-4 ≤y≤4 范围内,求相应的y 的值在什么范围内.2.已知y=p+z,这里p 是一个常数,z 与x 成正比例,且x=2 时,y=1;x=3 时,y=-1 .与x 之间的函数关系式;(1)写出y(2)如果x 的取值范围是1≤x≤4,求y 的取值范围.3. 一次函数的图象经过点(2,1)和(-1 ,-3 )(1)求此一次函数表达式;(2)求此一次函数与x 轴、y 轴的交点坐标;(3)求此一次函数的图象与两坐标轴所围成的三角形的面积。
y=kx+b(-1, -5),(2,a),y= x知一次函数4. 的图象相交于点且与正比例函数的图象经过点求(1)a的值(2)k,b的值(3)这两个函数图象与x 轴所围成的三角形面积 .B?,且点在第三),交正比例函数的图象于点B 0 A5.已知一次函数的图象,交x 轴于(-6 ,求正比例函数和一次函数的 6 平方单位,?的面积为,△象限,它的横坐标为-2 AOB解析式.---------6.如图,一束光线从y 轴上的点A(0,1)出发,经过x 轴上点 C 反射后经过点B(3,3),求光线从A 点到B 点经过的路线的长.7.由方程│x-1 │+│y-1 │=1 确定的曲线围成的图形是什么图形,其面积是多少?22 x+x0yy=的图象与A、B 8.直角坐标系两轴,分别交于y x 轴,中,一次函数3x BCD=∠ABD,求图象经过),点1,0BD 在、D?两点的一次坐标为( C 点,?点轴上,且∠函数的解析式.1x 轴、y 轴分别交于A、y= x-3 的图象与9.已知:如图一次函数 B 两点,过点C(4,0)2作AB的垂线交AB E于点,交y 轴于点D,求点D、E 的坐标.4y=x+4P(?0,.又、BA轴的交点分别为.已知直线轴、y 10两点的坐标分别、与xQP为3Q?),其中,k),-1 Q(0长为半径作圆,则当PQ取何值时,⊙,点,再以Q为圆心k 0<k<4AB相切?与直线---------11.(2005 年宁波市蛟川杯初二数学竞赛)某租赁公司共有50 台联合收割机,其中甲型20 台,乙型30 台.现将这50 台联合收割机派往A、B 两地收割小麦,其中30?台派往A地,20 台派往 B 地.两地区与该租赁公司商定的每天的租赁价格如下:甲型收割机的租金乙型收割机的租金16001800元地/台A台元/1600元1200/台B地台/元(1)设派往A 地x 台乙型联合收割机,租赁公司这50 台联合收割机一天获得的租金为y(元),请用x 表示y,并注明x 的范围.(2)若使租赁公司这50 台联合收割机一天获得的租金总额不低于79600 元,?说明有多少种分派方案,并将各种方案写出.12.已知写文章、出版图书所获得稿费的纳税计算方法是( x400800) 20% (1 30%), x其中x 元应缴纳的=)f (x)表示稿费为f (x20%) 20% (1 30%), xx (1 4007104 元,?问张三的这笔稿费是多缴纳个人所得税后,得到税额.假如张三取得一笔稿费,少元?13.某中学预计用1500 元购买甲商品x 个,乙商品y 个,不料甲商品每个涨价1.5 元,29 元.?又若个,总金额多用元,尽管购买甲商品的个数比预定减少1 10 乙商品每个涨价1 元,并且购买甲商品的数量只比预定数少5 个,那么买甲、乙两商品支甲商品每个只涨价付的总金额是1563.5 元.(1)求x、y 的关系式;(2)若预计购买甲商品的个数的2 倍与预计购买乙商品的个数的和大于205,但小于210,求x,y 的值.---------1l l l y 4x 5 lyx 4 的交点坐标,:和直线并判14. 已知直线和:,求两条直线22112断该交点落在平面直角坐标系的哪一个象限上.15.已知正比例函数y=kx 经过点P(1,2),如图所示.(1)求这个正比例函数的解析式;P 、的像个单位,写出在这个平移下,点P、原点O (2)将这个正比例函数的图像向右平移 4O 的坐标,并求出平移后的直线的解析式.yP(1, 2 )P'O'OxOABC AC2)B(3,A(3,0) 16.如图,在直角坐标系中,已知矩形,的两个顶点坐标,对角线l l 对应的函数解析式.所在直线为,求直线yB Cx O A17. “一方有难,八方支援”.在抗击“5.12”汶川特大地震灾害中,某市组织20 辆汽车100 吨到灾民安置点.按计划20 辆汽车都要装装运食品、药品、生活用品三种救灾物资共运,每辆汽车只能装运同一种救灾物资且必须装满.根据右表提供的信息,解答下列问题:y1y x x 的函数关系式;,装运药品的车辆数为与)设装运食品的车辆数为.求((2)如果装运食品的车辆数不少于那么车辆的5 辆,装运药品的车辆数不少于4 辆,安排有几种方案?并写出每种安排方案;(3)在(2)的条件下,若要求总运费最少,应采用哪种安排方案?并求出最少总运费.物资种类食品药品生活用品每辆汽车运载量(吨)465吨)/每吨所需运费(元100160120---------3 x y (天)之间的函数关系式)与种植时间(米某农户种植一种经济作物,总用水量18.所示.如图1020)第(1天的总用水量为多少米?320 xyx之间的函数关系式.时,求与2)当(33?7000米)种植时间为多少天时,总用水量达到(3)y 米(40001000x O ( )天3020C A B 地营救受困群众,途经19. 武警战士乘一冲锋舟从地逆流而上,前往地时,由所携C A B A 地接到群众后立刻返回到地受困群众运回带的救生艇将地,冲锋舟继续前进,地,xA y 和冲锋舟出发后所用时间地的距离冲锋舟和救生艇距途中曾与救生艇相遇.(千米)假设营救群众的时间忽略不计,(分)之间的函数图象如图所示.水流速度和冲锋舟在静水中的速度不变. C A )请直接写出冲锋舟从(1地所用的时间.地到)求水流的速度.(2C A A 已知救生艇与地群众安全送到又立即去接应救生艇.地后,(3)冲锋舟将地的距离 1x 11 y yx (千米)和冲锋舟出发后所用时间(分)之间的函数关系式为,假设群12A 地多远处与救生艇第二次相遇?众上下船的时间不计,求冲锋舟在距离(千米)y2010x(分)O1244---------x y (分)之间的函(米)与登山时间甲乙两人同时登西山,甲、乙两人距地面的高度20. 数图象如图所示,根据图象所提供的信息解答下列问题:(1)甲登山的速度是每分钟米, b A 为地提速时距地面的高度乙在米.(2)若乙提速后,乙的速度是甲登山速度的3 倍,请分别求出甲、乙二人登山全过程中,y x (米)与登山时间登山时距地面的高度(分)之间的函数关系式. A )登山多长时间时,乙追上了甲?此时乙距(3地的高度为多少米?21.我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10 吨以内(包括10 吨)的用户,每吨收 a a 吨水仍按每吨10 10 水费吨的用户,元;一月用水超过元收费,超过10 吨的部分,按 b ba x y y x 与元(吨,应收水费元,每吨)收费.设一户居民月用水之间的函数关系如图所示.a的值;某户居民上月用水)求(18 吨,应收水费多少元?x 10 b xy之间的函数关系式;时,的值,并写出当)求(2 与(3)已知居民甲上月比居民乙多用水 4 吨,两家共收水费46 元,求他们上月分别用水多少吨?---------22. 我市花石镇组织10 辆汽车装运完A、B、C 三种不同品质的湘莲共100 吨到外地销售,按计划10 辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,解答以下问题:AB C湘莲品种81012每辆汽车运载量(吨)342每吨湘莲获利(万元)(1)设装运 A 种湘莲的车辆数为x,装运B 种湘莲的车辆数为y,求y 与x 之间的函数关系式;(2)如果装运每种湘莲的车辆数都不少于2 辆,那么车辆的安排方案有几种?并写出每种安排方案;(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.23.某电脑公司经销甲种型号电脑,受经济危机影响,电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000 元,如果卖出相同数量的电脑,去年销售额为10 万元,今年销售额只有8 万元.(1)今年三月份甲种电脑每台售价多少元?(2)为了增加收入,电脑公司决定再经销乙种型号电脑,已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000 元,公司预计用不多于5 万元且不少于 4.8 万元的资金购进这两种电脑共15 台,有几种进货方案?(3)如果乙种电脑每台售价为3800 元,为打开乙种电脑的销路,公司决定每售出一台乙种 a a )中所有方案获利相同,2电脑,返还顾客现金元,要使(值应是多少?此时,哪种方案对公司更有利24. 五月份,某品牌衬衣正式上市销售,5 月1 日的销售量为10 件,5 月2 日的销售量为3525 件,直到日销售量达到最大后,销售量开始逐日下降,件,以后每天的销售量比前一天多15 件,直到5 月31 日销售量为0.设该品牌衬衣的日销售量至此,每天的销售量比前一天少为P(件),销售日期为n(日),P 与n 之间的关系如图所示.(1)写出P 关于n 的函数关系式(注明n 的取值范围);P=(2)经研究表明,该品牌衬衣的日销售量超过150 件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?(3)该品牌衬衣本月共销售了P(件)件.10131n(日)(图)---------3时,只付基本费8元和某市为了节约用水,规定:每户每月用水量不超过最低限量am25.3时若用水量超过, am除了付同上的基本费和损耗费外,超过部分每定额损耗费 c 元(c ≤5);3付b 元的超额费.1m某市一家庭今年一月份、二月份和三月份的用水量和支付费用如下表所示:3用水量(m )交水费( 元)一月份99二月份1915三月3322.、 c ba、根据上表的表格中的数据,求、26 .A 市、B 市和C 市有某种机器10台、10 台、8 台,?现在决定把这些机器支援给D 市18 台,E 市10.已知:从 A 市调运一台机器到 D 市、E 市的运费为200 元和800 元;从B?市调运一台机器到 D 市、E 市的运费为300 元和700 元;从 C 市调运一台机器到D市、 E 市元.元和500 的运费为400(1)设从 A 市、B 市各调x 台到 D 市,当28 台机器调运完毕后,求总运费W(元)关于x(台)的函数关系式,并求W的最大值和最小值.(2)设从 A 市调x 台到 D 市, B 市调y 台到 D 市,当28 台机器调运完毕后,用yx、表示总运费W(元),并求W的最大值和最小值.---------27 了学生的身体健康,?小明对学凳的高度都是按一定的关系科学设计的.学校课桌、校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身高调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:第一档第二档第三档第四档凳高x(42.0 cm)40.037.045.070.074.8桌高y(78.0 cm)82.8(1)小明经过对数据探究,发现:桌高y 是凳高x 的一次函数,请你求出这个一次函数的关系式;(不要求写出x 的取值范围);(2)小明回家后,?测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm ,请你判断它们是否配套?说明理由.x小明同学骑自行车去郊外春游,下图表示他离家的距离28. (千米)与所用的时间y(小时)之间关系的函数图象.(1)根据图象回答:小明到达离家最远的地方需几小时?此12)求小明出发两个半小时离家多远?(2 时离家多远?(求小明出发多长时间距家?3)千米?---------29.(50 台联合收割机,其中甲型20 台,某租赁公司共有宁波市蛟川杯初二数学竞赛)30?台派往A、B 两地收割小麦,其中台联合收割机派往30 台.现将这50 A地,乙型台20 B 地.两地区与该租赁公司商定的每天的租赁价格如下:派往甲型收割机的租金乙型收割机的租金18001600地A 元/台台元/16001200地B 台元/元/台(1)设派往A 地x 台乙型联合收割机,50 台联合收割机一天获得的租金为租赁公司这y(元),请用x 表示y,并注明x 的范围.(2)若使租赁公司这50 台联合收割机一天获得的租金总额不低于79600 元,?说明有多少种分派方案,并将各种方案写出.30. 某土产公司组织20 辆汽车装运甲、乙、丙三种土特产共120 吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:土特产种类甲乙丙每辆汽车运载量(吨)865(百元)每吨土特产获利101216y y xx 之间的函与,求,装运乙种土特产的车辆数为(1)设装运甲种土特产的车辆数为数关系式.(2)如果装运每辆土特产的车辆都不少于3 辆,那么车辆的安排方案有几种?并写出每种安排方案.(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.-----。
一次函数练习题(大题30道)
一次函数检测题满分:100分 时长:60分钟1.知一次函数y=kx+b 的图象经过点(-1, -5),且与正比例函数y= x 的图象相交于点(2,a),求(1)a 的值 (2)k,b 的值(3)这两个函数图象与x 轴所围成的三角形面积.2.已知一次函数的图象,交x 轴于A (-6,0),交正比例函数的图象于点B ,且点B•在第三象限,它的横坐标为-2,△AOB 的面积为6平方单位,•求正比例函数和一次函数的解析式.3. 已知直线1l :45y x =-+和直线2l :142y x =-,求两条直线1l 和2l 的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上.4. 我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按>)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系每吨b元(b a如图所示.(1)求a的值;某户居民上月用水8吨,应收水费多少元?x>时,y与x之间的函数关系式;(2)求b的值,并写出当10(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?5. 我市花石镇组织10辆汽车装运完A、B、C三种不同品质的湘莲共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种湘莲,根据下表提供的信息,解答以下问题:(1)设装运A x之间的函数关系式;(2)如果装运每种湘莲的车辆数都不少于2辆,那么车辆的安排方案有几种?并写出每种安排方案;(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.。
高三数学 导数大题20道训练
高三数学导数大题20道训练II)若函数f(x)在[0,1]上单调递增,求a的取值范围;III)若函数f(x)的最小值为-2,求a的取值范围.10.已知函数f(x)=x3-3x2+2x+1.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[0,1]上单调递增,求函数在[0,1]上的最小值.11.已知函数f(x)=x2e-x.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[0,1]上单调递减,求函数在[0,1]上的最大值.12.已知函数f(x)=x3-3x2+3x-1.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[0,2]上单调递增,求函数在[0,2]上的最小值.13.已知函数f(x)=x3-6x2+9x-2.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[1,3]上单调递减,求函数在[1,3]上的最大值.14.已知函数f(x)=x3-3x+2.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[0,2]上单调递增,求函数在[0,2]上的最小值.15.已知函数f(x)=x3-3x2+4.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[0,2]上单调递减,求函数在[0,2]上的最大值.16.已知函数f(x)=x3-6x2+12x-8.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[1,3]上单调递增,求函数在[1,3]上的最小值.17.已知函数f(x)=x3-9x2+24x-16.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[2,4]上单调递减,求函数在[2,4]上的最大值.18.已知函数f(x)=x3-2x2-5x+6.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[1,3]上单调递增,求函数在[1,3]上的最小值.19.已知函数f(x)=x3-3x2+3.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[0,2]上单调递减,求函数在[0,2]上的最大值.20.已知函数f(x)=x3-3x+1.I)求函数f(x)的单调区间;II)求函数f(x)的极值;III)若函数f(x)在[0,2]上单调递增,求函数在[0,2]上的最小值.Ⅱ) 当 $a>0$ 时,若过原点与函数 $f(x)$ 的图像相切的直线恰有三条,求实数 $a$ 的取值范围。
苏格拉底的两道大题-议论文1800字
苏格拉底的两道大题-议论文1800字现代社会,每个人都在追求着自己梦想的生活,都希望自己的人生充满鲜花和阳光,都希望自己能够处在一片梦想的田野之中仰望星空,可是又有多少人真正的明白梦想的路上应该付出多大的困难才能成功呢?有多少人明白,如何努力才是真正的努力呢?大部分人的努力只是假装努力,甚至于根本就没有迈出努力那一步,但是由于潜意识里面告诉自己,自己这就是努力,所以,很多人总是认为自己努力之后没有效果,这就是因为他们找不到真正努力的方向,更不知道自己要怎么做才是正确的选择,而苏格拉底了两道题无疑为我们解开了人生谜题,他不仅告诉我们应该如何努力,如何奋斗,告诉我们应该做选择,更告诉我们生活的意义远不止奋斗这个含义,它包含的是奋斗的过程中那些令人流连忘返的景色,我们应该欣赏的就是这些景色而不是奋斗的过程,奋斗的过程是由这些景色构建而成的。
如果我们实现梦想是为了梦想最后一刻,那么这种想法是大错特错的,因为梦想的之所以珍贵,是因为路途遥远,我们最终到达,所以才觉得它珍贵,而如果露出了那些景色,我们能够欣赏起来,那么实现梦想的过程就是愉快的,而且我们实现梦想的动力也能源源不断的产生,这就是苏格拉底为我们提供的理想希望方式到底是什么?我们首先要知道苏格拉底的两道题是什么以及它背后的含义。
苏格拉底第1道题,苏格拉底第1天上课的时候,跟学生们提了一个要求,就是每天甩手臂甩三下,看看有多少人能够坚持下来,学生们觉得这简直太简单了,因为拜苏格拉底为师的学生都是可以说非常优秀的学生了,他们对此很不屑认为自己肯定能够做到第2天上课,苏格拉底说谁坚持下去了,举个手,所有的学生都举起了手,苏格拉底满意的说非常好,坚持下去,一个星期后苏格拉底再次问谁坚持下去了,举个手,这一次全班有三分之二的学生坚持了下来,另外三分之一的学生早已经把这件事情忘得一干二净了,苏格拉底说已经有三分之一人放弃了,看看剩下的三分之二能否坚持下去,随后苏格拉底继续讲课,但是这一次苏格拉底脸上没有了往常的笑容,真心有些严肃,一个月后苏格拉底问还有谁坚持下去了,举个手,这一次全班只有一半的人坚持下去,另外一半的人通通都放弃了,苏格拉底不满的摇了摇头,然后说要坚持一瞬间的努力,并不值得大肆称赞,只有坚持才能走到最后,才能取得常人难以得到的成功,半年后苏格拉底再次问,还有谁坚持下去了,这一次全班只有一个人坚持下去,这个人叫柏拉图,是苏格拉底最有名的学生,而柏拉图,苏格拉底还有亚里士多德被称为西方哲学三杰,柏拉图之所以能够和苏格拉底还有亚里士多德并列与他的这一种坚持的毅力是密不可分的,这也是苏格拉底想要告诉自己的学生的,当你能够对一件很简单的事情保持坚持并坚持不懈的去做,他认真的去完成它,那么你仍然可以取得比常人难以想象的成功,因为即使是再简单的一件事情,也仍然会有人去放弃,因为它过于简单,所以有人感到特别无趣,然后从心里面漠视他,最后你可以打败他,因为你坚持下去了。
