2014《名师伴你行》系列高考数学(文)一轮复习配套精练考案:第五、六编复习检测题
名师伴你行高考一轮总复习新高考版[数学] 2-5
![名师伴你行高考一轮总复习新高考版[数学] 2-5](https://img.taocdn.com/s3/m/dea3412680eb6294dc886ca3.png)
重
1
1
点
(2)解析:[(-2)6]2-(-1)0=(26)2-1=8-1=7.
突
破
•
第11页
•
•
高考一轮总复习 • 新高考版[数学]
理
清
教
材
巩
2.指数函数常见误区:系数为1.
固 基
函数y=(a2-3a+3)ax是指数函数,则有a=___2_____.
础
解析:根据定义有a2-3a+3=1,解得a=2或a=1(舍去).
题
型 研
当n为奇数时,正数的n次方根是一个__正__数_____,
究 负数的n次方根是一个_负__数_____
符号表示
备注
限
n>1且
时 跟
n∈N*
踪 检
测
na
零的n次方根是零
重 点 突 破
当n为偶数时,正数的n次方根有__两__个____,它们互 为_相__反__数___
±n a(a>0) 负数没有偶次方根
究 性质来解答.
重
点
[易错警示] 运算结果不能同时含有根号和分数指数,也不能既有分母又含有
突
破 负指数,形式力求统一.
•
第15页
•
高考一轮总复习 • 新高考版[数学]
理 清 教 材
巩
角度Ⅱ.“整体代换法”化简求值
固
基
试/题/调/研(题题精选,每题都代表一个方向)
重 点 突 破
•
第3页
•
•
高考一轮总复习 • 新高考版[数学]
理 清 教 材
巩
固
基
础
理清教材•巩固基础
题 型 研 究
重 点 பைடு நூலகம் 破
2014高考数学(文)一轮复习用书配套精练(广东专用)第2课命题与简易逻辑

第2课 命题与简易逻辑1.(2012湛江二模)命题“若a b >,则22(1)(1)a m b m +>+”的逆否命题是( )A .若“a b >,则22(1)(1)a m b m +≤+B .若a b ≤,则22(1)(1)a m b m +>+C .若22(1)(1)a m b m +≤+,则a b ≤D .若22(1)(1)a m b m +≤+,则a b >【答案】C2.(2012湖北高考)命题“0R x Q ∃∈ð,30x Q ∈”的否定是( )A .0R x Q ∃∉ð,30x Q ∈B .0R x Q ∃∈ð,30x Q ∉ C .0R x Q ∀∉ð,30x Q ∈ D .0R x Q ∀∈ð,30x Q ∉ 【答案】D3.(2012辽宁高考)已知命题p :12,x x R ∀∈,1221(()())()0f x f x x x --≥,则p ⌝是( )A .12,x x R ∃∈,1221(()())()0f x f x x x --≤B .12,x x R ∀∈,1221(()())()0f x f x x x --≤C .12,x x R ∃∈,1221(()())()0f x f x x x --<D .12,x x R ∀∈,1221(()())()0f x f x x x --<【答案】C【解析】全称命题的否定形式为将“∀”改为“∃”,后面的加以否定.4.(2012江门一模)下列结论,不正确...的是( ) A .若命题p :R x ∈∀,1≥x ,则命题p ⌝:x R ∀∈,1<x .B .若p 是假命题,q 是真命题,则命题p ⌝与命题q p ∨均为真命题.C .方程122=+ny mx (m ,n 是常数)表示双曲线的充要条件是0<⋅n m .D .若角α的终边在直线x y =上,且00360360<≤-α,则这样的角α有4个.【答案】A【解析】命题p ⌝:x R ∃∈,1<x .5.(2012东莞二模)对于函数①()|2|f x x =+,②2()(2)f x x =-,③()cos(2)f x x =-,判断如下两个命题的真假:命题甲:(2)f x +是偶函数;命题乙:()f x 在(,2)-∞上是减函数,在(2,)+∞上是增函数;能使命题甲、乙均为真的所有函数的序号是( )A .①②B .①③C .②D .③【答案】C【解析】对于①,(2)4f x x +=+不是偶函数,故命题甲假,对于③,()f x 在(,2)-∞上不是减函数,故命题乙假.6.(2012房山二模)有下列命题:①在函数cos()cos()44y x x ππ=-+的图象中,相邻两个对称中心的距离为π; ②函数31x y x +=-的图象关于点(1,1)-对称; ③关于x 的方程2210ax ax --=有且仅有一个实数根,则实数1a =-;④已知命题p :∀R x ∈,都有1sin ≤x ,则p ⌝是:∃x R ∈,使得sin 1x >. 其中真命题的序号是_______.【答案】③ ④7.已知函数()f x 是(,)-∞+∞上的增函数,,a b R ∈,对命题“若0a b +≥,则()()()()f a f b f a f b +≥-+-”.(1)写出否命题,判断其真假,并证明你的结论;(2)写出逆否命题,判断其真假,并证明你的结论.【解析】(1))否命题:已知函数()f x 是(,)-∞+∞上的增函数,,a b R ∈,对命题“若0a b +<,则()()()()f a f b f a f b +<-+-”.该命题是真命题,证明如下:∵0a b +<,∴,a b b a <-<-.又∵()f x 在(,)-∞+∞上是增函数.∴()(),()()f a f b f b f a <-<-,∴()()()()f a f b f a f b +<-+-,∴否命题为真命题.(2)逆否命题:已知函已知函数()f x 是(,)-∞+∞上的增函数,,a b R ∈,若()()()()f a f b f a f b +<-+-,则0a b +<.真命题,可证明原命题为真来证明它.∵0a b +≥,∴,a b b a ≥-≥-,∵()f x 在(,)-∞+∞上是增函数.∴()(),()()f a f b f b f a ≥-≥-,∴()()()()f a f b f a f b +≥-+-,故原命题为真命题,所以逆否命题为真命题.8.已知函数2()21()f x ax x a R =++∈.(1)若()f x 的图象与x 轴恰有一个公共点,求a 的值;(2)若方程()0f x =至少有一正根,求a 的范围.【解析】(1)当0a =时,()f x 图象与x 轴恰有一个公共点1(,0)2-,满足题意. 当0a ≠时,440a ∆=-=,即1a =.∴0a =或1.(2)由(1)可知0a ≠.当方程有实根时,01440a a a ≠⎧⇒≤⎨∆=-≥⎩且0a ≠.若0a <,则由1210x x a =<, 可知方程()0f x =有一正一负两根,此时满足题意.若01a <≤,则12122010x x a x x a ⎧+=-<⎪⎪⎨⎪=>⎪⎩时, 方程()0f x =有两负根,不满足题意.∴a 的范围是0a <.。
2014《名师伴你行》系列高考地理一轮复习配套考案部分:复习质量综合检测题(共25张PPT)
本考案共4页,共16题,满分为100分,考试时间45分钟。 第Ⅰ卷(选择题,共44分)
本卷共11小题,每小题4分,共44分;在每小题给出的四个选项中, 只有一项是符合题目要求的。
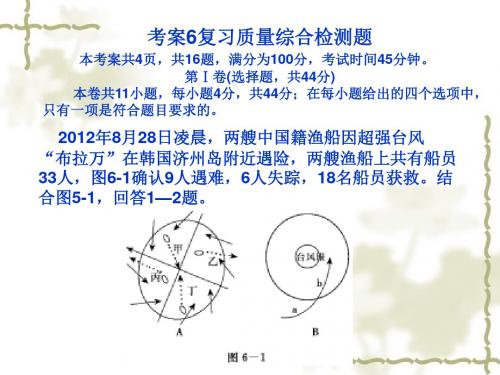
2012年8月28日凌晨,两艘中国籍渔船因超强台风 “布拉万”在韩国济州岛附近遇险,两艘渔船上共有船员 33人,图6-1确认9人遇难,6人失踪,18名船员获救。结 合图5-1,回答1—2题。
1.图6-1中A图所示圆圈为台风系统,该系统分成四个区域, 短箭头表示风向,长箭头表示台风整体移动方向,图中四 艘船的逃生路线(虚线箭头)正确的是( ) A.甲路线 B.乙路线 C.丙路线 D.丁路线 2.图6-1中B图所示箭头为台风系统中风的运动路线图,圆 圈为等压线,据图叙述正确的是( ) A.该台风在北半球,受地转偏向力影响风向左偏 B.a点气压小于b点 C.在台风系统中,风沿ab路线运动,最后做旋转上升运动 D.台风登陆后势力继续加强
1—2.BC(从A图中可以看出,台风向西北方向 移动,乙路线的逃生方向与台风运动方向相反,并驶离台 风中心比较安全。台风中心气压低,四周气压高,在北半 球台风呈逆时针方向旋转,气流由四周气流向中心汇聚, 中心气流辐合上升;当台风登陆后由于受地面摩擦力以及 地形等影响,风力逐渐减小,最后消失。)
页岩气是从页岩层中开采出来的天然气,是一种重要的 非常规天然气资源,它往往以吸附或游离状态分布在古盆地 内,厚度较大、分布广的页岩烃源岩地层中,储量初步估 计是天然气储量的4倍。读各钻井某页岩层顶部高程分布 图6-2,回答3-5题。
③促进产业结构的调整 ④摆脱目前对石油的依赖
A.①②
B.②③
C.①②③ D.②③④
3—5.ACC(根据等高线中部高,四周低的特 点可知,图示区域的地形是山地,由于该地有页岩气分布, 因此图示构造为背斜山。背斜是良好的储油气构造,顶部 易被侵蚀,所以页岩顶部高程小。页岩气属于沉积矿床, 是不可再生的新能源,黄土高原是沉积作用形成的。所以 该地区有页岩气分布。页岩气大规模开发利用有利于改变 能源消费结构,改善大气环境质量,促进产业结构的调 整。)
2014高考数学总复习一轮用书与名师对话5-3

课前自主回顾
课堂互动探究
课时作业
与名师对话
高考总复习 ·课标版 ·数学(理)
建立坐标系,将平面向量的线性运算转化为坐标运算, 便于理解和计算.
课前自主回顾
课堂互动探究
课时作业
与名师对话
高考总复习 ·课标版 ·数学(理)
2π (1)(2011 年江苏)已知 e1,2 是夹角为 的两个单位向量, e 3 a=e1-2e2,b=ke1+e2,若 a· b=0,则 k 的值为________. (2)(2011 年湖南)在边长为 1 的正三角形 ABC 中, → = 设BC → → → → BE → 2BD,CA=3CE,则AD· =________.
【答案】 (1)3 2
π 5 (2)6,6π
课前自主回顾
课堂互动探究
课时作业
与名师对话
高考总复习 ·课标版 ·数学(理)
在数量积的基本运算中,经常用到数量积的定义、模、 夹角等公式,尤其对|a|= a· a要引起足够重视,是求距离常 用的公式.
课前自主回顾
课堂互动探究
课时作业
与名师对话
1.求向量的长度(模)时通常遵循以下规则: “要求向量的 长度,先求向量长度的平方”,其依据是 a· a=|a|2,这样就 把向量长度的平方转化为向量的平方,进而转化为已知向量 的数量积问题. a· b 2.一般由公式 cos θ= 求向量的夹角.若给出向量 |a||b| x1x2+y1y2 的坐标形式,则可根据公式 cos θ= 2 2 2 2求两个向 x1+y1 x2+y2 量的夹角.
与名师对话
高考总复习 ·课标版 ·数学(理)
课前自主回顾
课堂互动探究
课时作业
2014高考数学(文)一轮复习用书配套精练(广东专用)第57课空间直角坐标系

第57课空间直角坐标系
1.已知空间直角坐标系中,A(1,1,1),,则()
A.B.C.D.
【答案】A
2.到的距离除以到的距离的值为的点的坐标满足()
A.B.
C.D.
【答案】A
【解析】,
化简得.
3.正方形、的边长都是,而且平面和平面互相垂直,点在上移动,点在上移动,若.
(1)求的长;
(2)为何值时,的长最小?
【解析】(1)∵平面⊥平面,
平面平面,,
∴平面,则两两垂直,
以为坐标原点,以分别为轴建立空间直角坐标系,
则,,
.
(2)由(1)知,当时,||最短,为.
此时,恰好为,的中点.
4.已知三棱锥中,平面,,,为上一点,,、分别为、的中点.
(1)求,,;
(2)判断的形状.
【解析】以为原点,射线分别为轴建立空间直角坐标系,如图.
则.
(1),
,
.
(2),
∴,
∴,
∴为钝角三角形.。
《名师伴你行》系列高考数学(文)一轮复习配套精练考案:第三、四编复习检测题

❖
返回
返回
返回
返回
返回
返回
返回
返回
返回
ห้องสมุดไป่ตู้ 返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
返回
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/182021/9/182021/9/182021/9/189/18/2021 ❖14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月18日星期六2021/9/182021/9/182021/9/18 ❖15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/182021/9/182021/9/189/18/2021 ❖16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/182021/9/18September 18, 2021 ❖17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/182021/9/182021/9/182021/9/18
返回
返回
返回
返回
返回
返回
❖9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/182021/9/18Saturday, September 18, 2021 ❖10、阅读一切好书如同和过去最杰出的人谈话。2021/9/182021/9/182021/9/189/18/2021 4:36:24 AM ❖11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/182021/9/182021/9/18Sep-2118-Sep-21 ❖12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/182021/9/182021/9/18Saturday, September 18, 2021
2014届高考数学文一轮复习方案人教A版课程标准卷:滚动基础训练卷63页15套附详细解析
2014届高考数学文一轮复习方案人教A版课程标准卷:滚动基础训练卷63页15套附详细解析45分钟滚动基础训练卷(一) (考查范围:第1讲~第3讲分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.[2013·惠州调研] 集合M={4,5,-3m},N={-9,3},若M∩N≠∅,则实数m的值为()A.3或-1 B.3C.3或-3 D.-12.[2013·哈尔滨三中月考] 已知集合A={3,a2},集合B={0,b,1-a},且A∩B={1},则A∪B=()A.{0,1,3}B.{1,2,4}C.{0,1,2,3}D.{0,1,2,3,4}3.[2012·开封二模] 下列命题中的真命题是()A.∃x0∈R,使得sin x0+cos x0=3 2B.∀x∈(0,+∞),e x>x+1C .∃x 0∈(-∞,0),2x 0<3x 0D .∀x ∈(0,π),sin x >cos x4.[2012·东北四校一模] 集合⎩⎪⎨⎪⎧x ∈N *⎪⎪⎪⎪⎭⎪⎬⎪⎫12x ∈Z 中含有的元素个数为( )A .4B .6C .8D .125.[2012·银川一中一模] 有下列命题: ①设集合M ={x |0<x ≤3},N ={x |0<x ≤2},则“a ∈M ”是“a ∈N ”的充分不必要条件;②命题“若a ∈M ,则b ∉M ”的逆否命题是:“若b ∈M ,则a ∉M ”;③若p ∧q 是假命题,则p ,q 都是假命题; ④命题p :“∃x 0∈R ,x 20-x 0-1>0”的否定綈p :“∀x ∈R ,x 2-x -1≤0”.则上述命题中为真命题的是( )A .①②③④B .①③④C .②④D .②③④6.[2012·河北名校俱乐部模拟] “k =1”是“函数y =sin 2kx -cos 2kx +1的最小正周期为π”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.[2012·鹰潭一模] 关于x 的不等式ax 2-2x+1<0的解集非空的一个必要不充分条件是()A.a<1 B.a≤1C.0<a<1 D.a<08.[2012·豫南九校四联] 在下列四个命题中,其中为真命题的是()A.命题“若x2=4,则x=2或x=-2”的逆否命题是“若x≠2或x≠-2,则x2≠4”B.若命题p:所有幂函数的图象不过第四象限,命题q:所有抛物线的离心率为1,则命题p 且q为真C.若命题p:∀x∈R,x2-2x+3>0,则綈p:∃x0∈R,x20-2x0+3<0D.若a>b,则a n>b n(n∈N*)二、填空题(本大题共3小题,每小题6分,共18分)9.命题:“若x2<1,则-1<x<1”的逆否命题是________.10.设全集U=R,M={x|x2>4},N={x|x2+3≤4x},则图中阴影部分所表示的集合是________.图G1-111.[2012·泉州四校二联] 下列“若p,则q”形式的命题中,p是q的充分不必要条件的有________个.①若x ∈E 或x ∈F ,则x ∈E ∪F ;②若关于x 的不等式ax 2-2ax +a +3>0的解集为R ,则a >0; ③若2x 是有理数,则x 是无理数.三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.[2012·荆州中学月考] 已知集合A =x ∈R ⎪⎪⎪3x +1≥1,集合B ={x ∈R |y =-x 2+x -m +m 2}.若A ∪B =A ,求实数m 的取值范围.13.命题p :方程x 2+mx +1=0有两个不等的正实数根,命题q :方程4x 2+4(m +2)x +1=0无实数根.若“p 或q ”为真命题,求m 的取值范围.14.已知集合A={x∈R|log2(6x+12)≥log2(x2+3x+2)},B={x|2x2-3<4x,x∈R}.求A∩(∁R B).45分钟滚动基础训练卷(二) (考查范围:第4讲~第7讲分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.[2012·吉林质检] 下列函数中,在区间(0,1)上为增函数的是()A.y=log 12x B.y=1xC.y=sinx D.y=x2-x2.函数y=x+1-x-1的最大值为()A.2 2 B. 2 C.1 D.43.[2012·吉林一中二模] 已知定义在R上的函数f(x)关于直线x=1对称,若f(x)=x(1-x)(x≥1),则f(-2)=()A.0 B.-2 C.-6 D.-124.[2012·银川一中月考] 已知定义域为R的函数f(x)在区间(4,+∞)上为减函数,且函数y =f(x+4)为偶函数,则()A.f(2)>f(3) B.f(2)>f(5)C .f (3)>f (5)D .f (3)>f (6)5.函数y =2x -5x -3的值域是{y |y ≤0或y ≥4},则此函数的定义域为( )A.⎩⎪⎨⎪⎧x ⎪⎪⎪⎪⎭⎪⎬⎪⎫52<x ≤72 B.⎩⎪⎨⎪⎧x ⎪⎪⎪⎪⎭⎪⎬⎪⎫52≤x ≤72 C.⎩⎪⎨⎪⎧x ⎪⎪⎪⎪⎭⎪⎬⎪⎫x ≤52或x ≥72 D.⎩⎪⎨⎪⎧x ⎪⎪⎪⎪⎭⎪⎬⎪⎫52≤x <3或3<x ≤72 6.[2012·昆明二模] 已知函数f (x )=x 2-|x |,则{x |f (x -1)>0}等于( )A .{x |x >1或x <-1}B .{x |x >0或x <-2}C .{x |x >2或x <0}D .{x |x >2或x <-2}7.[2012·武昌调研] 函数y =f (x )的图象如图G2-1 图G2-1①函数y =f (x )的定义域是[-1,5];②函数y =f (x )的值域是(-∞,0]∪[2,4]; ③函数y =f (x )在定义域内是增函数; ④函数y =f (x )在定义域内的导数f ′(x )>0. 其中正确的是( )A.①②B.①③C.②③D.②④8.[2012·信阳二调] 已知定义在R上的奇函数f(x),满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则()A.f(-25)<f(11)<f(80)B.f(80)<f(11)<f(-25)C.f(11)<f(80)<f(-25)D.f(-25)<f(80)<f(11)二、填空题(本大题共3小题,每小题6分,共18分)9.[2012·哈尔滨三中月考] 函数f(x)=tan x-1+1-x2的定义域为________.10.已知函数f(x)为R上的偶函数,当x>0时,f(x)=1x,设a=f⎝⎛⎭⎪⎪⎫32,b=f⎝⎛⎭⎪⎪⎫log212,c=f(32),则a,b,c的大小关系为________.11.[2013·保定摸底] 已知f(x)是定义在R上的奇函数,且当x>0时f(x)=e x+a,若f(x)在R 上是单调函数,则实数a的最小值是________.三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.已知二次函数f(x)的二次项系数为a,满足不等式f(x)>-2x的解集为(1,3),且方程f(x)+6a=0有两个相等的实根,求f(x)的解析式.13.[2013·珠海模拟] 对于函数f(x)=a-2(a∈R,b>0且b≠1).b x+1(1)判断函数f(x)的单调性并证明;(2)是否存在实数a使函数f(x)为奇函数?并说明理由.14.已知函数f(x)=ax2-2x+1.(1)试讨论函数f(x)的单调性;(2)若13≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式.45分钟滚动基础训练卷(三)(考查范围:第4讲~第12讲,以第8讲~第12讲内容为主 分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数f(x)=3x +12x -2的零点所在的一个区间是( )A .(-2,-1)B .(-1,0)C .(0,1)D .(1,2)2.log 318+log 132=( )A .1B .2C .4D .53.[2012·天津卷] 已知a =21.2,b =⎝ ⎛⎭⎪⎪⎫12-0.8,c =2log 52,则a ,b ,c 的大小关系为( )A .c <b <aB .c <a <bC .b <a <cD .b <c <a4.[2012·正定中学月考] 函数f(x)=log a |x|+1(0<a<1)的图象大致为()图G3-15.某商店按每件80元的成本购进某种商品,根据市场预测,销售价为每件100元时可售出1 000件,定价每提高1元时销售量就减少5件,若要获得最大利润,销售价应定为每件() A.100元B.110元C.150元D.190元6.有以下程序,若函数g(x)=f(x)-m在R 上有且只有两个零点,则实数m的取值范围是()IF x<=-1THENf(x)=x+2ELSEIF x>-1AND x<=1THENf(x)=x∧2ELSE f(x)=-x+2END IFEND IFPRINT f(x)A.m>1 B.0<m<1C.m<0或m=1 D.m<07.[2012·哈尔滨师大附中期中] 函数y=log a(2-ax)在[0,1]上是减函数,则实数a的取值范围是()A.(0,1) B.(1,2)C.(1,2] D.[2,+∞)8.[2012·山东卷] 设函数f(x)=1x,g(x)=-x2+bx.若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是()A.x1+x2>0,y1+y2>0B.x1+x2>0,y1+y2<0C.x1+x2<0,y1+y2>0D.x1+x2<0,y1+y2<0二、填空题(本大题共3小题,每小题6分,共18分)9.[2012·江苏卷] 函数f(x)=1-2log6x的定义域为________.10.[2012·银川一中月考] 函数f(x)在R上是奇函数,当x∈(-∞,0]时,f(x)=2x(x-1),则f(x)=__________________.11.已知函数f(x)=4cosπx(4x2+4x+5)(4x2-4x+5),对于下列命题:①函数f(x)不是周期函数;②函数f(x)是偶函数;③对任意x∈R,f(x)满足|f(x)|<14.其中真命题是________.三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.已知关于x 的二次函数f (x )=x 2+(2t -1)x +1-2t .(1)求证:对于任意t ∈R ,方程f (x )=1必有实数根;(2)若12<t <34,求证:方程f (x )=0在区间(-1,0)及⎝ ⎛⎭⎪⎪⎫0,12内各有一个实数根.13.若f (x )=x 2-x +b ,且f (log 2a )=b ,log 2f (a )=2(a >0且a ≠1).(1)求f (log 2x )的最小值及相应x 的值;(2)若f (log 2x )>f (1)且log 2f (x )<f (1),求x 的取值范围.14.[2012·上海闵行区三模] 某药厂在动物体内进行新药试验,已知每投放剂量为m 的药剂后,经过x h 该药剂在动物体内释放的浓度y (mg/L)满足函数y =mf (x ),其中f (x )=⎩⎨⎧-12x 2+2x +5(0<x ≤4),-x -lg x +10(x >4).当药剂在动物体内中释放的浓度不低于4(mg/L)时,称为该药剂达到有效.(1)若m =2,试问该药达到有效时,一共可持续多长时间(取整数小时)?(2)为了使在8 h 之内(从投放药剂算起包括8 h)达到有效,求应该投放的药剂量m 的最小值(取整数).45分钟滚动基础训练卷(四) (考查范围:第4讲~第15讲,以第13讲~第15讲内容为主分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知函数f(x)=ax2+c,且f′(1)=2,则a的值为()A. 2 B.1C.-1 D.02.曲线y=x3-2x+1在点(1,0)处的切线方程为()A.y=x-1 B.y=-x+1C.y=2x-2 D.y=-2x+23.[2012·哈尔滨附中月考] 若函数f(x)的定义域为[a,b],且b>-a>0,则函数g(x)=f(x)+f(-x)的定义域为()A.[a,b] B.[-b,-a]C.[-b,b] D.[a,-a]4.[2012·银川一中月考] 过点(0,1)且与曲线y =x +1x -1在点(3,2)处的切线垂直的直线的方程为( )A .2x -y +1=0B .2x +y -1=0C .x +2y -2=0D .x -2y +2=05.设函数f(x)=⎩⎪⎨⎪⎧1,x>0,0,x =0,-1,x<0,g(x)=x 2f(x -1),则函数g(x)的递减区间是( )A .(0,1)B .(1,+∞)C .(-∞,0)D .(0,+∞)6.[2012·乌鲁木齐押题卷] 设f(x)为可导函数,且满足 f (1)-f (1-2x )2x=-1,则过曲线y =f(x)上点(1,f(1))处的切线斜率为( )A .2B .-1C .1D .-27.设f(x)=x(ax 2+bx +c)(a≠0)在x =1和x =-1处有极值,则下列点中一定在x 轴上的是( )A .(a ,b)B .(a ,c)C .(b ,c)D .(a +b ,c)8.[2012·山西四校联考] 设曲线y =x n +1(n∈N *)在点(1,1)处的切线与x 轴的交点横坐标为x n,则log2 012x1+log2 012x2+…+log2 012x2011的值为()A.-log2 0122 011 B.-1C.-1+log2 0122 011 D.1二、填空题(本大题共3小题,每小题6分,共18分)9.[2012·福州质检] 函数f(x)=x3+ax(x∈R)在x=1处有极值,则曲线y=f(x)在原点处的切线方程是________.10.[2012·课程标准卷] 曲线y=x(3ln x+1)在点(1,1)处的切线方程为________.11.设f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0且g(-3)=0,则不等式f(x)g(x)<0的解集为________.三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.[2012·双鸭山一中期中] 某商品进货价每件50元,据市场调查,当销售价格(每件x元)为50<x≤80时,每天售出的件数为P=105,若要使每天获得的利润最多,销售(x-40)2价格每件应定为多少元?13.已知函数f(x)=e x(ax2+x+1).(1)设a>0,讨论f(x)的单调性;(2)设a=-1,证明:对∀x1,x2∈[0,1],都有|f(x1)-f(x2)|<2.14.已知函数f(x)=e x+1x-a.(1)当a=12时,求函数f(x)在x=0处的切线方程;(2)当a>1时,判断方程f(x)=0实根的个数.45分钟滚动基础训练卷(五)(考查范围:第16讲~第19讲 分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.cos -20π3的值等于( ) A.12 B.32 C .-12 D .-322.[2012·昆明一中一模] 设α是第二象限角,P (x ,4)为其终边上的一点,且cos α=15x ,则tan α=( )A.43B.34 C .-34 D .-433.[2012·济南三模] 如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:①f (x )=sin x cos x ;②f (x )=2sin x +π4;③f (x )=sin x +3cos x ;④f (x )=2sin2x +1.其中“同簇函数”的是( )A .①②B .①④C .②③D .③④4.将函数f (x )=2cos2x 的图象向右平移π4个单位,再向下平移2个单位,则平移后得到图象的解析式是( )A .y =2sin2x -2B .y =2cos2x -2C .y =2cos2x +2D .y =2sin2x +25.[2012·吉林模拟] 为了得到函数y =3sin x cos x +12cos2x 的图象,只需将函数y =sin2x 的图象( )A .向左平移π12个长度单位 B .向右平移π12个长度单位 C .向左平移π6个长度单位 D .向右平移π6个长度单位 6.函数f (x )=|sin πx -cos πx |对任意的x ∈R 都有f (x 1)≤f (x )≤f (x 2)成立,则|x 2-x 1|的最小值为( )A.34B .1C .2 D.127.[2012·商丘三模] 已知函数f (x )=3sin ωx +cos ωx (ω>0)的最小正周期为4π,则对该函数的图象与性质判断错误的是( )A .关于点-π3,0对称 B .在0,2π3上递增 C .关于直线x =5π3对称 D .在-4π3,0上递增 8.函数f (x )=A sin(ωx +φ)ω>0,|φ|<π2,x ∈R 的部分图象如图G5-1,则( )图G5-1A .f (x )=-4sin π8x +π4B .f (x )=4sin π8x -π4C .f (x )=-4sin π8x -π4D .f (x )=4sin π8x +π4二、填空题(本大题共3小题,每小题6分,共18分)9.[2012·沈阳二模] 已知tan α=2,则sin (π+α)-sin π2+αcos 3π2+α+cos (π-α)的值为________. 10.若g (x )=2sin2x +π6+a 在0,π3上的最大值与最小值之和为7,则a =________.11.电流强度I (A)随时间t (s)变化的函数I=A sin ωt +π6(A >0,ω≠0)的部分图象如图G5-2所示,则当t =150s 时,电流强度是________A.图G5-2 三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.已知函数f(x)=3sin2x-2sin2x.(1)若点P(1,-3)在角α的终边上,求f(α)的值;(2)若x∈-π6,π3,求f(x)的值域.13.[2012·沈阳四校联考] 已知函数f(x)=2cos x·cos x-π6-3sin2x+sin x cos x.(1)求f(x)的最小正周期;(2)把f(x)的图象向右平移m个单位后,在0,π2上是增函数,当|m|最小时,求m的值.14.已知函数f (x )=2sin 2π4-x -23cos 2x +3.(1)求f (x )的最小正周期和单调递减区间;(2)若f (x )<m +2在x ∈0,π6上恒成立,求实数m 的取值范围.45分钟滚动基础训练卷(六)(考查范围:第16讲~第23讲,以第20讲~第23讲内容为主 分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.[2013·河北五校联盟调研] 已知sin(α+45°)=45,45°<α<135°,则sin α=( ) A.25 B .-25C.7210 D .-72102.在△ABC 中,a =4,b =52,5cos(B +C )+3=0,则角B 的大小为( )A.π6B.π4C.π3D.5π63.[2012·银川一中月考] 已知△ABC 的三边长成公差为2的等差数列,且最大角的正弦值为32,则这个三角形的周长是( ) A .18 B .21 C .24 D .154.在△ABC 中,AC =7,BC =2,B =60°,则BC 边上的高等于( ) A.32 B.332C.3+62D.3+3945.[2012·汕头测评] 已知△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,a =4,b =43,A =30°,则B 等于( )A .60°B .60°或120°C .30°D .30°或150°6.[2012·江西师大附中模拟] 下列函数中,周期为π,且在0,π2上为减函数的是( ) A .y =sin ⎝⎛⎭⎪⎫2x +π2 B .y =cos ⎝⎛⎭⎪⎫2x +π2 C .y =sin ⎝⎛⎭⎪⎫x +π2 D .y =cos ⎝ ⎛⎭⎪⎫x +π27.为了得到函数y =sin2x -π6的图象,可以将函数y =cos x 3的图象( )A .横坐标缩短为原来的16(纵坐标保持不变),再向右平移π3个单位 B .横坐标缩短为原来的16(纵坐标保持不变),再向右平移2π3个单位 C .横坐标伸长为原来的6倍(纵坐标保持不变),再向左平移2π个单位D .横坐标伸长为原来的6倍(纵坐标保持不变),再向左平移2π3个单位 8.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .若sin 2B +sin 2C -sin 2A +sin B sin C =0,则tan A 的值是( ) A.33 B .-33C. 3 D .- 3 二、填空题(本大题共3小题,每小题6分,共18分)9.已知tan α=2,计算1cos2α+tan2α的值为________.10.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若a =2,b =2,sin B +cos B =2,则角A 的大小为________.11.在△ABC 中,B =60°,AC =3,则AB +2BC 的最大值为________.三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.在△ABC 中,内角A ,B ,C 所对应的边分别为a ,b ,c ,且满足b sin A =3a cos B .(1)求角B 的值;(2)若cos A 2=255,求sin C 的值.13.已知△ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,设向量m =(a ,b ),n =(sin B ,sin A ),p =(b -2,a -2).(1)若m ∥n ,求证:△ABC 为等腰三角形;(2)若m ⊥p ,C =π3,c =2,求△ABC 的面积.14.在锐角△ABC 中,A ,B ,C 三内角所对的边分别为a ,b ,c .设m =(cos A ,sin A ),n =(cos A ,-sin A ),a =7,且m·n =-12. (1)b =3,求△ABC 的面积;(2)求b +c 的最大值.45分钟滚动基础训练卷(七) (考查范围:第24讲~第27讲分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知向量a=(1,2),b=(0,1),设u=a +k b,v=2a-b,若u∥v,则实数k的值是()A.-72B.-12C.-43D.-832.已知向量a=(n,4),b=(n,-1),则n =2是a⊥b的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件3.已知e1,e2是两夹角为120°的单位向量,a=3e1+2e2,则|a|等于()A.4 B.114.已知非零向量a ,b ,若a +2b 与a -2b互相垂直,则|a ||b |等于( ) A.14B .4 C.12D .2 5.已知向量OA→=(1,-3),OB →=(2,-1),OC→=(k +1,k -2),若A ,B ,C 三点不能构成三角形,则实数k 应满足的条件是( )A .k =-2B .k =12C .k =1D .k =-16.已知圆O 的半径为3,直径AB 上一点D 使AB→=3AD →,E ,F 为另一直径的两个端点,则DE→·DF →=( ) A .-3 B .-4 C .-8 D .-67.已知向量a =(1,2),b =(x ,4),若|b|=2|a |,则x 的值为( )A .2B .4C .±2D .±48.已知菱形ABCD 的边长为2,∠A =60°,M 为DC 的中点,若N 为菱形内任意一点(含边界),则AM→·AN →的最大值为( ) A .3 B .2 3二、填空题(本大题共3小题,每小题6分,共18分)9.已知D ,E ,F 分别为△ABC 的边BC ,CA ,AB 上的中点,且BC→=a ,CA →=b ,下列结论中正确的是________.①AD →=12a -b ;②BE →=a +12b ; ③CF →=-12a +12b ;④AD →+BE →+CF →=0. 10.若|a |=2,|b |=4,且(a +b )⊥a ,则a 与b 的夹角是________.11.在△ABC 中,已知D 是AB 边上的一点,若AD →=2DB →,CD →=13CA →+λCB →,则λ=________. 三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.已知向量a =e 1-e 2,b =4e 1+3e 2,其中e 1=(1,0),e 2=(0,1).(1)试计算a·b 及|a +b |的值.(2)求向量a 与b 的夹角的正弦值.13.已知向量a=(1,2),b=(-2,m),x=a+(t2+1)b,y=-k a+1t b,m∈R,k,t为正实数.(1)若a∥b,求m的值;(2)若a⊥b,求m的值;(3)当m=1时,若x⊥y,求k的最小值.14.[2012·沈阳二模] 已知向量m=sin2x+1+cos2x2,sin x,n=12cos2x-32sin2x,2sin x,设函数f(x)=m·n,x∈R.(1)求函数f(x)的最小正周期;(2)若x∈0,π2,求函数f(x)的值域.45分钟滚动基础训练卷(八) (考查范围:第28讲~第30讲分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.等差数列{a n}共有10项,公差为2,奇数项的和为80,则偶数项的和为()A.90 B.95C.98 D.1002.在等比数列{a n }中,若a 3a 5a 7a 9a 11=32,则a 7=( )A .9B .1C .2D .33.已知数列{a n }是等差数列,若a 1+a 5+a 9=2π,则cos(a 2+a 8)=( )A .-12B .-32 C.12 D.324.[2012·黄冈中学二联] 已知{a n }是等比数列,a 2=4,a 5=32,则a 1a 2+a 2a 3+…+a n a n +1=( )A .8(2n -1) B.83(4n -1) C.163(2n -1) D.23(4n -1)5.[2012·唐山三模] 等差数列{a n }的前n 项和为S n ,已知S 7=21,S 11=121,则该数列的公差d =( )A .5B .4C .3D .26.[2012·衡阳八中月考] 已知各项均为正数的等比数列{a n },a 1a 2a 3=5,a 4a 5a 6=52,则a 7a 8a 9=( )A .10B .2 2C .8 D.27.[2012·合肥一中质检] 设等比数列{a n }的前n 项和为S n ,若8a 2+a 5=0,则下列式子中数值不能确定的是( )A.a 5a 3B.S 5S 3C.a n +1a nD.S n +1S n8.[2012·珠海一中模拟] 设正项等比数列{a n },若等差数列{lga n }的公差d =lg3,且{lga n }的前三项和为6lg3,则{a n }的通项为( )A .a n =nlg3B .a n =3nC .a n =3nD .a n =3n -1二、填空题(本大题共3小题,每小题6分,共18分)9.若S n =1-2+3-4+…+(-1)n -1·n ,则S 50=________.10.等差数列{a n }中,S n 为其前n 项和,若S 2∶S 5=1∶4,则a 5∶a 9=________.11.[2012·包头一模] 已知数列{a n }满足a 1=1,a 2=1,a n +1=|a n -a n -1|(n ≥2),则该数列前2 013项和等于________.三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.已知数列{a n }是首项a 1=4,公比q≠1的等比数列,S n 是其前n 项和,且4a 1,a 5,-2a3成等差数列.(1)求公比q的值;(2)求T n=a2+a4+a6+…+a2n的值.13.[2012·河北名校俱乐部模拟] 已知等差数列{a n}满足a4=6,a6=10.(1)求数列{a n}的通项公式;(2)设公比大于1的等比数列{b n}的各项均为正数,其前n项和为T n,若a3=b2+2,T3=7,求T n.14.[2012·长春二调] 在等差数列{a n}中,2a1+3a2=11,2a3=a2+a6-4,其前n项和为S n.(1)求数列{a n}的通项公式;(2)设数列{b n}满足b n=1S n+n,求数列{b n}的前n项和T n.45分钟滚动基础训练卷(九) (考查范围:第28讲~第32讲,以第31讲~第32讲内容为主分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.在等比数列{a n}中,已知a1a3a11=8,则a2a8=()A.4 B.6C.12 D.162.[2012·朝阳一模] 已知数列{a n}的前n项和为S n,且S n=2a n-1(n∈N*),则a5=() A.-16 B.16C.31 D.323.[2012·豫东、豫北十校联考] 已知S n是数列{a n}的前n项和,则“S n是关于n的二次函数”是“数列{a n}为等差数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.[2012·惠州三调] 公差不为零的等差数列{a n }中,a 1+a 2+a 3=9,且a 1,a 2,a 5成等比数列,则数列{a n }的公差为( )A .1B .2C .3D .45.已知等差数列{a n }的前n 项和为S n ,若OB →=a 1OA→+a 2 012OC →,且A ,B ,C 三点共线(该直线不过原点O ),则S 2 012=( )A .1 000B .2 001C .2 010D .1 006 6.[2012·东北三校一模] 等差数列{a n }中,a 5+a 6=4,则log 2(2a 1·2a 2·…·2a 10)=( )A .10B .20C .40D .2+log 257.[2012·陕西师大附中三联] 一个蜂巢里有1只蜜蜂,第一天,它飞出去带回了5个伙伴;第二天,6只蜜蜂飞出去各自带回了5个伙伴……,如果这个过程继续下去,那么第6天所有蜜蜂归巢后,蜂巢中共有蜜蜂( )A.6(66-1)6-1只 B .66只C .63只D .62只 8.[2012·南阳联考] 已知数列{a n },{b n }满足a 1=b 1=1,a n +1-a n =b n +1b n=2,n ∈N +,则数列{ba n }的前10项的和为( )A.43(49-1)B.43(410-1) C.13(49-1) D.13(410-1) 二、填空题(本大题共3小题,每小题6分,共18分)9.{a n }为等比数列,公比q =-2,S n 为其前n 项和.若S 10=S 11-29,则a 1=________.10.{a n }是首项a 1=-3,公差d =3的等差数列,如果a n =2 013,则n =________.11.如果-1,a ,b ,c ,-9成等比数列,那么ac =________,b =________.三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.[2013·唐山模拟] 已知数列{a n }的前n 项和S n =27(8n-1).(1)求数列{a n }的通项公式a n ;(2)设b n =log 2a n ,求1b 1b 2+1b 2b 3+…+1b n b n +1.13.[2012·济南模拟] 在数列{a n }中,a 1=1,并且对于任意n ∈N *,都有a n +1=a n 2a n +1.(1)证明数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 为等差数列,并求{a n }的通项公式;(2)设数列{a n a n +1}的前n 项和为T n ,求使得T n >1 0002 011的最小正整数n .14.[2012·黄冈模拟] 已知数列{a n }中,a 1=1,前n 项和为S n 且S n +1=32S n +1(n ∈N *).(1)求数列{a n }的通项公式;(2)设数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 的前n 项和为T n ,求满足不等式T n<12S n+2的n值.45分钟滚动基础训练卷(十) (考查范围:第33讲~第36讲分值:100分)一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.在平面直角坐标系中,若点(-2,t)在直线x-2y+4=0的上方,则t的取值范围是() A.(-∞,1) B.(1,+∞)C.(-1,+∞) D.(0,1)2.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x ≥-1,y ≥x ,3x +2y ≤5,则z =2x +y 的最大值为( )A .1B .2C .3D .43.已知命题p :m<0,命题q :对任意x ∈R ,x 2+mx +1>0成立.若p 且q 为真命题,则实数m 的取值范围是( )A .m <-2B .m >2C .m <-2或m >2D .-2<m <04.已知a >0,b >0,A 为a ,b 的等差中项,正数G 为a ,b 的等比中项,则ab 与AG 的大小关系是( )A .ab =AGB .ab ≥AGC .ab ≤AGD .不能确定 5.[2012·广东卷] 已知变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤1,x -y ≤1,x +1≥0,则z =x +2y 的最小值为( )A .3B .1C .-5D .-66.[2012·金山一中考前测试] 若“p :x -32-x≥0”,“p 成立”是“q 成立”的充要条件,则满足条件的q 是( )A .q :(x -3)(x -2)≤0B .q :x -2x -3≤0C .q :lg(x -2)≤0D .q :|5-2x |≤17.[2012·合肥质检] 已知函数f (x )=x +ax -2(x >2)的图象过点A (3,7),则此函数的最小值是( )A .2B .4C .6D .8 8.[2012·东北师大附中月考] 已知O 是坐标原点,点A (-1,-2),若点M (x ,y )是平面区域⎩⎪⎨⎪⎧x +y ≥2,x ≤1,y ≤2上的任意一点,且使OA →·(OA →-MA →)+1m≤0恒成立,则实数m 的取值范围为( ) A .(-∞,0)∪⎣⎢⎢⎡⎭⎪⎪⎫13,+∞B .(-∞,0]∪⎝ ⎛⎭⎪⎪⎫13,+∞ C .(-∞,0)∪[3,+∞) D .(-∞,0]∪[3,+∞)二、填空题(本大题共3小题,每小题6分,共18分)9.[2012·湖南卷] 不等式x 2-5x +6≤0的解集为________.10.[2012·湖北卷] 若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥-1,x +y ≥1,3x -y ≤3,则目标函数z =2x +3y 的最小值是________.11.[2012·长春三调] 如果直线2ax -by +14=0(a >0,b >0)和函数f (x )=m x +1+1(m >0,m ≠1)的图象恒过同一个定点,且该定点始终落在圆(x-a +1)2+(y +b -2)2=25的内部或圆上,那么b a的取值范围是________.三、解答题(本大题共3小题,每小题14分,共42分,解答应写出文字说明,证明过程或演算步骤)12.已知关于x 的不等式ax -5x 2-a<0的解集为M ,当3∈M 且5∉M 时,求实数a 的取值范围.。
