理论力学--第2章 平面任意力系分解

FR' Fi Fxi Fy j
M O M O ( Fi )
3. 平面任意力系的简化结果 （1）FR´= 0，Mo ≠ 0, （2）FR´ ≠ 0，Mo = 0, （3）FR´≠ 0，Mo ≠ 0, （4）FR´= 0，Mo = 0, 合力偶，合力偶矩， M O M O ( Fi ) 合力，合力作用线通过简化中心O。 合力，合力作用线到简化中心O的距离为 平衡。
FAx
解方程得
FAx
1 Fcos30 q 3a 316.4kN 2

FAy P Fsin30 300kN
1 M A M q 3l l Fsin30 l Fcos30 3l 1188kN 22 2
4. 平面平行力系的平衡条件和平衡方程
B A d
F
B
d
F
A
F´
B
M
F´ F = F´ = －F´´
其中
´
M = Fd = MB ( F )
1
2 .平面任意力系向作用面内一点简化 • 主矢和主矩
F2 F1
F2´
M2
F1´
M1 M
FR
´
o
Mn
o Fn Fn´
o
任意点O 为简化中心 F1´ = F1 ， F2´ = F2 ，… ，Fn´ = Fn Mi = Mo ( Fi ) (i = 1，2，…，n)
（2）列静力平衡方程
Fx 0 : X A P 0
Fy 0:
C
a B
M=Pa P
a
Y A RB 0
RB
MA( F ) 0 :
联解上各式得：
RB 2P
X A P YA 2 P
a XA A
RB a P a M 0
YA
18
解法二：（1）选AB为研究对象，画受力图 （2）列静力平衡方程
3 1 FB p q a 4 2
FAx 0
1 3 FAy p q a 4 2 16
例13 如图所示平面刚架AB，其上作用有力P 和力 偶M，力偶矩等于Pa，若P、a均为已知，求A、B两处 的约束反力。
C
a a M=Pa B
P
a A
17
解法一：（1）选AB为研究对象，画受力图
q
A 2a
P
M
B
4a
15
解：（1）取AB梁为研究对象，画受力图 FAy q （2）列静力平衡方程
A
P
M
FB
B
FAx
2a
4a
Fx 0 Fy 0
MA( F ) 0
联解上各式得
FAx 0 FAy q 2a p FB 0
FB 4a M p 2a - q 2a a 0

1 10
y
F
1 3 j
F3
2 5
F
´
x
1 2
437.6 N

F2
F3
O i 200
Fy F1sin45 F2
3 10
F1
1
1
100
F3
1 5
161.6 N
9
FR′ 437.6i 161.6 j
M O M O ( F ) F1 0.1 .sin45 1 F3 0.2 0.08F 21.44 N m 5
7
平面任意力系的合力矩定理
Mo
FR´ o´ o
FR´
d
FR o´
FR
o
o
d
o´
FR´ ´
(a) (b)
(c)
由图(b), 合力 FR 对点O的矩为
由式（3—2） 得
n i 1
MO ( FR )=FRd = MO
M O M O (Fi )
M O ( FR ) M O ( Fi )
y
F
1 3 j
F
´
x
1 2
得力系向点O的简化结果如图（b);
FR ′ ( Fx ) ( Fy )
2 2 2 2
F2
F3
O i
200
(437.6) (161.6) 466.5N
F1
1
1
100
M O 21.44 N m
合力及其与原点O的距离如图(c) 。
MO
y
y
x
O
d
A
D
YA
19
解法三：（1）选AB为研究对象，画受力图
（2）列静力平衡方程
M A (F ) 0 :
C
a B M=Pa RB
RB a P a M 0
M D (F ) 0 :
P
YA a P a M 0
a A D
M B (F ) 0 : X A 2a YA a P a M 0
平面任意力系等效为两个简单力系：平面汇交力系 和平面力偶系。
2
F2
F1
F2´
M2
F1´
M1
FR
MO
´
o
Mn
o Fn
o
Fn´
平面汇交力系可合成为作用线通过点O的一个力FR´ FR´ = F1´+ F2´+…+ Fn´ =
Fi
i 1
n
(3—1)
平面力偶系可合成为一个力偶，这个力偶的矩Mo等于各附加力 偶矩的代数和，又等于原来各力对点O的矩的代数和。 n (3—2) M = M +M +…+M = MO( Fi)
如图：物体受平面平行力系F1 ， F2 ， …， Fn的作用。
y F1 F3 Fn
如取 x 轴与各力垂直，不论力系是否 平衡，恒有 Fx 0 则平行力系的独立平衡方程为 ：
O
F2
x
Fy 0 M A (F ) 0
M A (F ) 0
M B (F ) 0
平行力系平衡方程的二力矩式：
Mo
FR´ o´
FR´ o
d
FR o´ o
d
FR o´
o
FR´ ´
FR´ = FR =－FR´´
原力系简化为一个力，合力矢等于主矢；合力的作用线在 点O的哪一侧，根据主矢和主矩的方向确定；合力作用线到点O 的距离为d。 （3）平面任意力系平衡的情形
MO d FR '
FR´= 0，Mo = 0
平面任意力系平衡。
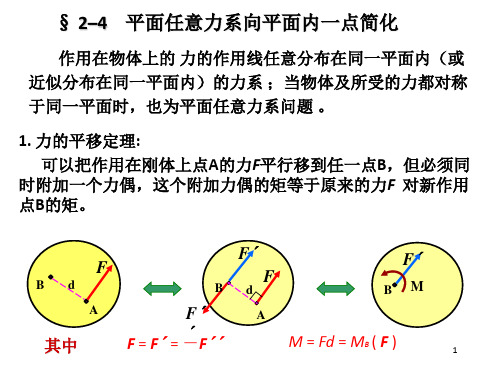
§ 2–4 平面任意力系向平面内一点简化
作用在物体上的 力的作用线任意分布在同一平面内（或 近似分布在同一平面内）的力系 ；当物体及所受的力都对称 于同一平面时，也为平面任意力系问题 。 1. 力的平移定理: 可以把作用在刚体上点A的力F平行移到任一点B，但必须 同时附加一个力偶，这个附加力偶的矩等于原来的力F 对新 作用点B的矩。 F´
条件是：A、B两点 的连线不能与 x 轴 或 y 轴垂直 条件是：A、B、C 三点不能共线
23
14
3. 三力矩式
M B (F ) 0
M C (F ) 0
例12 图示水平梁AB，A端为固定铰链支座，B端为 一滚动支座。梁长为4a，梁重P，作用在梁的中点C。在 梁的AC段上受均布载荷q作用，在梁的BC段上受力偶作 用，力偶矩M = Pa。求A和B处的支座约束力。
x O
FR FR ′ 466.5N
MO d 45.96mm FR
FR´
FR
(b)
(c)
10
例11 水平梁AB受按三角形分布的载荷作用，如图示。载荷 的最大值为q，梁长l，求合力作用线的位置。
解: 在梁上距A端为 x 处的载荷集度为 q(x) = qx/l。在此处
取的一微段dx，梁在微段d x 受的力近似为 F(x) = qxdx/l。 梁由 x=0 到 x=l 的分布载荷合力为 F
Fx 0 : X A P 0
C
a B
RB a P a M 0
M D (F ) 0 :
P
YA a P a M 0
联解上各式得：
X A P
a
a
M A (F ) 0 :
M=Pa
RB
RB 2P
YA 2 P
二力矩 式
17
XA
MB 0:
Q W 6m 12m P
Q(6 2) W 2 P(12 2) R A 4 0
解方程得:
o 1 2 n
FR´——主矢
i 1
Mo ——主矩
平面任意力系向作用面内任一点O简化，可得一个力和一 个力偶。这个力等于该力系的主矢，作用线通过简化中心O。 3 这个力偶的矩等于该力系的主矩。
F2
F1
F2´
M2
y j
F1´
M1 x
y MO j
FR
´
o
Mn
o Fn
i
o
i
x
Fn´
取坐标系Oxy，i，j为沿x，y轴的单位矢量，则力系主矢 的解析表达式为
q
F
l 0 q( x)dx
ql 2
q(x)dx A x dx l xc
B
设合力作用线到A端的 距离为 xC ， 根据合力矩定理
l F xc 0 q( x) xdx
xC
1 l qx 2 ql 2 dx 0 3 F l
2 ql l 2 3
11Βιβλιοθήκη 小结1. 力的平移定理:平移一力的同时必须附加一个力偶，附加力偶 的矩等于原来的力 对新作用点的矩。 2. 平面任意力系向平面内任选一点O简化:可得一个力和一个力 偶。这个力等于该力系的主矢，作用线通过简化中心O。这个力 偶的矩等于该力系的主矩。