第四章2根轨迹分析
合集下载
第四章根轨迹法4-2

P( s )Q( s ) P( s )Q( s ) 0
即 其中
P( s ) Q( s ) P( s ) Q( s )
d [ln P(s)] d [ln Q(s)]
ds
ds
P(s) (s z1 )(s z2 ) (s zm )
Q(s)- (s p1 )(s p2 ) (s pn )
的 j 值。工作在此点时,系统处于临界稳定状态。
介绍二种常用的求交点的方法。 (1) 利用特征方程求取。用 j 替代s,令虚部、实部分别等
于 零,求得 和对应的K1。 (2) 利用劳斯表求取。将劳斯表中s2行系数构造的辅助方程
求得。若根轨迹与虚轴的交点多于两个,则应取劳斯 阵列中大于2的偶次方行的系数构造的辅助方程求得。
i1
ib
8 虚轴交点 (1)满足特征方程 1 G( j)H( j) 0 的 j 值;
(2)由劳斯判据求临界稳定时的特征根;
9
根之和与 根之积
n
pcj
n
p
j
j 1
j 1
n
j 1
pcj
1
n
n
j 1
pj
K1
m
i 1
zi
19
例1: 系统的开环传递函数 试画根轨迹。
G(s)H(s)
K1
s(s 4)(s 6)
ω4 -36ω2 K0 jω80 - 8ω2 0
ω4 -36ω2 K0 0
jω80 - 8ω2 0
求得 ω 10 , K0 260
( (4)出射角
极点-p3的出射角 : 3 180 (2k 1) (2 90 180 2 ) 90
同理不难求得极点-p4处的出射角: 4 90
第4章_线性系统的根轨迹法(2)

3 0.82 2 0.91 1 Imag Axis 0.975 3 2.5 2 1.5 1 0.5
root locus plot of G(s)=K/[s(s+2)(s +s+2)]
0.7 0.56 0.42 0.28 0.14
2
0
-1
0.975 0.91
-2 0.82 -3 -3.5 0.7 -3 -2.5 0.56 -2 0.42 -1.5 0.28 0.14 -1 -0.5 0 0.5 1 1.5
∏ (s − p )
i =1
21
n
例4-7参数 不以乘法因子出现情况的处理方法
1)画零极点分布 2)实轴上的根轨迹 3)根轨迹的渐近线
(2 k + 1)π ϕa = n−m =π/2,3π/2 (k=0,1)
σa =
5 5 4 4 3 3 2 2 Imag Axis Imag Axis 1 1 0 0 -1 -2
2
2
0.91
1 0.975 Imag Axis 3.5 3 2.5 2 1.5 1 0.5
0
-1 0.975 0.91
-2
-3 -4
0.82 -3.5
0.7 -3 -2.5
0.56 -2
0.42 -1.5
0.28 0.14 -1 -0.5 0 0.5 1
11
Real Axis
开环零极点分布及相应的根轨迹图
0.72 0.58 0.44 0.32 0.22 0.1 0.96
1 2 3 4
-4
-3
-2 Real Axis
-1
0
1
7
Open-Loop Pole-Zero Configuration and Corresponding Root Locus
root locus plot of G(s)=K/[s(s+2)(s +s+2)]
0.7 0.56 0.42 0.28 0.14
2
0
-1
0.975 0.91
-2 0.82 -3 -3.5 0.7 -3 -2.5 0.56 -2 0.42 -1.5 0.28 0.14 -1 -0.5 0 0.5 1 1.5
∏ (s − p )
i =1
21
n
例4-7参数 不以乘法因子出现情况的处理方法
1)画零极点分布 2)实轴上的根轨迹 3)根轨迹的渐近线
(2 k + 1)π ϕa = n−m =π/2,3π/2 (k=0,1)
σa =
5 5 4 4 3 3 2 2 Imag Axis Imag Axis 1 1 0 0 -1 -2
2
2
0.91
1 0.975 Imag Axis 3.5 3 2.5 2 1.5 1 0.5
0
-1 0.975 0.91
-2
-3 -4
0.82 -3.5
0.7 -3 -2.5
0.56 -2
0.42 -1.5
0.28 0.14 -1 -0.5 0 0.5 1
11
Real Axis
开环零极点分布及相应的根轨迹图
0.72 0.58 0.44 0.32 0.22 0.1 0.96
1 2 3 4
-4
-3
-2 Real Axis
-1
0
1
7
Open-Loop Pole-Zero Configuration and Corresponding Root Locus
第四章 控制系统根轨迹分析法
i j 1 j
4.1 根轨迹的概念
模条件与角条件的作用: 1、角条件与k无关,即s平面上所有满足角条件的 点都属于根轨迹。(所以绘制根轨迹只要依据角条 件就足够了)。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k
j 1 m
n
s p
j
s Zi
args Z i
1
所以结论:实轴上线段右侧的零、极点数目之和为奇 数时,此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j
1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
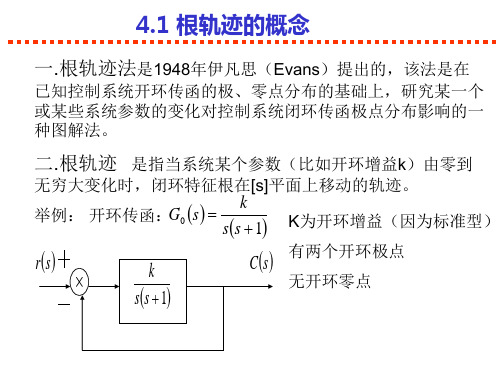
k G0 s 举例: 开环传函: ss 1
K为开环增益(因为标准型) 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函: s sk
2 D s s sk 0 则闭环特征方程为:
1 1 闭环特征根(即闭环传函的极点): s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2
-0.5 0
4.2 根轨迹的绘制规则
规则四:根轨迹的渐近线: (1)条数: (n-m)条 (2)与实轴所成角度 当
m n 2k 1
n m
s 时,认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点
4.1 根轨迹的概念
模条件与角条件的作用: 1、角条件与k无关,即s平面上所有满足角条件的 点都属于根轨迹。(所以绘制根轨迹只要依据角条 件就足够了)。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k
j 1 m
n
s p
j
s Zi
args Z i
1
所以结论:实轴上线段右侧的零、极点数目之和为奇 数时,此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j
1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
k G0 s 举例: 开环传函: ss 1
K为开环增益(因为标准型) 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函: s sk
2 D s s sk 0 则闭环特征方程为:
1 1 闭环特征根(即闭环传函的极点): s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2
-0.5 0
4.2 根轨迹的绘制规则
规则四:根轨迹的渐近线: (1)条数: (n-m)条 (2)与实轴所成角度 当
m n 2k 1
n m
s 时,认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点
(自动控制)第四章:根轨迹法

动态性能:从根轨迹图可以分析出系统的工作状态,
如过阻尼状态、欠阻尼状态……
根轨迹增益、闭环零极点与开环零极点的关系 l f
* G(s)= KG
∏( s-p ) i i=1
f i i 1 H q
q
∏( s-z ) i i=1
;
l
j=1 * H (s)= KH h
f l m
∏(s-zj )
C(s)
C ( s) 2k 2 R ( s ) S 2 S 2k
特征方程(闭环):
S2+2s+2k=0
k s(0.5s+1)
特征根:s1,2= -1±√1-2k k=0时, s1=0, s2=-2
K:0 ~ ∞
0<k<0.5 时,两个负实根 ;若s1=-0.25, s2=? k=0.5 时,s1=s2=-1 0.5<k<∞时,s1,2=-1±j√2k-1 j
注意:一组根对应同一个K;
K一变,一组根变; K一停,一组根停;
-2
-1
0
由以上分析,s1、s2两条根轨迹反映了系统特征根随参 数k变化的规律,组成了系统的根轨迹。 1.二阶系统有两个特征根,它的根轨迹有两条分支; 一个n阶系统的根轨迹则应有n条分支。 2.k=0时的闭环极点,s1=0、s2=-2正好是开环传递函 数的两个极点,因此说,系统开环极点就是它各条根轨 迹的起点。 3. k=∞时的闭环极点,是根轨迹的终点。 4.特征方程的重根点是根轨迹的分支离开负实轴进入复 数平面的分支点。
a.系统响应单调上升(ξ>1)系统具有两个不相等的负实根┈ 过阻尼响应。 b.系统响应衰减振荡(0<ξ<1)系统具有一对负实部的共 轭复根┈欠阻尼响应。
第四章 根轨迹分析法 2

4. 牛顿余数定理
(1)求出表达式 Ps D(s)N(s) N(s)D(s)
(2)分析根轨迹,估计在其分离点(或会合点)可能出现的实轴 坐标附件找一个试探点 s1。
(3)用 s s1 去除 Ps ,得出商多项式 Qs 及余数,该余数记
为 R1 ;
(4)再用 s s1 去除商多项式 Qs,得第二个余数,定义为 R2 ;
s2 3
k gp
s1 6-kgp 3
s0 kgp
令 6-kgp 3
0 kgp
6
由辅助方程求交点坐标:
3s2 Hale Waihona Puke 6 0s1,2 2 j
法则10 闭环极点的和与积
若n-m>=2,则有
n
n
(sj ) ( pj ) const
j1
j1
证明:
开环传递函数:
m
根轨迹的入射角:终止于开环零点的根轨迹在终点出的切线同正 实轴的夹角。
j
[s]
p1 p1 z1
z1
0 z2
z2 p2 p2
m
n
先求出射角: (s zi ) (s pj ) 180o (2k 1)
i 1
j 1
• s1 →-p1则 0, (s1 pa ) a
1802k 1 (180 arctan1) arctan 1 90 71.6
j
2
p4 p3 71.6
7) 根轨迹同虚轴的交点:
-p3
1.1j
p3
j
特征方程 s4 5s3 8s2 6s kg 0
令s j
-p2 s1
-3
4第四章__根轨迹法(2)

3
2
1
Imag Axis
0
-1
-2
-3 -2
-1.5
-1
-0.5 Real Axis
0
0.5
1
第四章 线性系统的根轨迹分析
2)确定内环的闭环极点 要求内环的反馈系数 内环的特征方程 3.2<Kf<3.5
( s 0.6)(s2 2s 4) K f 0
在实轴上选取试验点进行试探,P1=-1.6时,Kf =3.36 可求得内环的另外两个闭环极点为 p2 0.5 j1.83 p3 0.5 j1.83 3)绘制外环的根轨迹图 外环的开环传递函数
(2)根轨迹的起点 (3)实轴上的根轨迹
0,-1,-3
终点 均为∞
[0 , ] [3 , 1]
第四章 线性系统的根轨迹分析
(4)根轨迹的渐近线
a
n
2k 180 0 ,120 nm
m j i 1 i
k 0、 1
a=
( p ) ( z )
i 1 j与虚轴的交点 (相同) (9)闭环极点的和 (相同)
第四章 线性系统的根轨迹分析
例:控制系统方框图如下所示
R(s )
Kc s2
K0 s( s 1)
C (s )
1 s3
系统的内环为正反馈,绘制内环根轨迹图。 解: (1)内环的开环传递函数
G1 ( s ) H1 ( s ) K0 s( s 1)(s 3)
第四章 线性系统的根轨迹分析
4-3
广义根轨迹
其它种类的根轨迹: 1.参数根轨迹
2.多回路系统的根轨迹 3.正反馈回路和零度根轨迹
2
1
Imag Axis
0
-1
-2
-3 -2
-1.5
-1
-0.5 Real Axis
0
0.5
1
第四章 线性系统的根轨迹分析
2)确定内环的闭环极点 要求内环的反馈系数 内环的特征方程 3.2<Kf<3.5
( s 0.6)(s2 2s 4) K f 0
在实轴上选取试验点进行试探,P1=-1.6时,Kf =3.36 可求得内环的另外两个闭环极点为 p2 0.5 j1.83 p3 0.5 j1.83 3)绘制外环的根轨迹图 外环的开环传递函数
(2)根轨迹的起点 (3)实轴上的根轨迹
0,-1,-3
终点 均为∞
[0 , ] [3 , 1]
第四章 线性系统的根轨迹分析
(4)根轨迹的渐近线
a
n
2k 180 0 ,120 nm
m j i 1 i
k 0、 1
a=
( p ) ( z )
i 1 j与虚轴的交点 (相同) (9)闭环极点的和 (相同)
第四章 线性系统的根轨迹分析
例:控制系统方框图如下所示
R(s )
Kc s2
K0 s( s 1)
C (s )
1 s3
系统的内环为正反馈,绘制内环根轨迹图。 解: (1)内环的开环传递函数
G1 ( s ) H1 ( s ) K0 s( s 1)(s 3)
第四章 线性系统的根轨迹分析
4-3
广义根轨迹
其它种类的根轨迹: 1.参数根轨迹
2.多回路系统的根轨迹 3.正反馈回路和零度根轨迹
《自动控制原理》第4章_根轨迹分析法

一般有两个解,从中
因此求分离点和会合点公式: 可以判断是分离点或
N(s)D '(s) N '(s)D(s) 0 会合点,只有满足条
Kg 0
件Kg≥0的是有用解。
例4-1.设系统结构如图, 试绘制其概略根轨迹。
R(s)
k(s 1) c(s)
s(s 2)(s 3)
解:画出 s 平面上的开环零点(-1),开环极点(0, -2,-3)。
逆时针为正。(- , )
m
n
pj (2k 1) ( z j pi ) pj pi
j 1
j 1
ji
m
n
zi (2k 1) ( z j zi ) p j zi
j 1
j 1
j i
k 0,1,
k 0, 1,
例3.设系统开环传递函数为: G(s) Kg(s 1.5)(s 2 j)(s 2 j) s(s 2.5)(s 0.5 j1.5)(s 0.5 j1.5)
K
s1
00
0.5 1
1 1 j1
s2
K
K 2.5
2
K 1
1 K 0
1 j1
2 1
2 1 j 3 1 j 3
1 j 1 j
j
2
1
0
K 0.5
1
2
一、根轨迹的一般概念
开环系统(传递函数)的某一个参数从零变化到 无穷大时,闭环系统特征方程根在 s 平面上的轨迹 称为根轨迹。
根轨迹法:图解法求根轨迹。 借助开环传递函数来求闭环系统根轨迹。
nm
独立的渐近线只有(n-m)条 u=0,1…,(n-m-1)
(2)渐近线与实轴的交点
分子除以分母
因此求分离点和会合点公式: 可以判断是分离点或
N(s)D '(s) N '(s)D(s) 0 会合点,只有满足条
Kg 0
件Kg≥0的是有用解。
例4-1.设系统结构如图, 试绘制其概略根轨迹。
R(s)
k(s 1) c(s)
s(s 2)(s 3)
解:画出 s 平面上的开环零点(-1),开环极点(0, -2,-3)。
逆时针为正。(- , )
m
n
pj (2k 1) ( z j pi ) pj pi
j 1
j 1
ji
m
n
zi (2k 1) ( z j zi ) p j zi
j 1
j 1
j i
k 0,1,
k 0, 1,
例3.设系统开环传递函数为: G(s) Kg(s 1.5)(s 2 j)(s 2 j) s(s 2.5)(s 0.5 j1.5)(s 0.5 j1.5)
K
s1
00
0.5 1
1 1 j1
s2
K
K 2.5
2
K 1
1 K 0
1 j1
2 1
2 1 j 3 1 j 3
1 j 1 j
j
2
1
0
K 0.5
1
2
一、根轨迹的一般概念
开环系统(传递函数)的某一个参数从零变化到 无穷大时,闭环系统特征方程根在 s 平面上的轨迹 称为根轨迹。
根轨迹法:图解法求根轨迹。 借助开环传递函数来求闭环系统根轨迹。
nm
独立的渐近线只有(n-m)条 u=0,1…,(n-m-1)
(2)渐近线与实轴的交点
分子除以分母
4-2根轨迹的基本规律及绘制-353

1
s 1
a1
b1 s
nm
K*
1
j2k 1
nm nm K*e nm
08:03
1
s
1
a1
s
b1
nm
的化简
由二项式定理
a b
n
n
Cni aibni
i0
n
i0
n! aibni i!(n i)!
1
a1
b1 s
1
nm
1
1 nm
a1
b1 s
11 2! n m
n
1 m
1
a1
渐近线与实轴的交点:
n
m
pi z j
a
i1
j 1
nm
渐近线与实轴正方向的夹角:
a
2k1
n m
k 0,1, 2, , n m1
08:03
思路:研究s值很大时根轨迹(近似直线)的表达方
式(通过列写直线的方程)。
m
(s zj )
证明:
GsH s K*
j 1 n
(s pi )
i 1
K * (sm b1sm1 sn a1sn1
j1
K* = sj = z j(j = 1,2, ,m) 根轨迹终止于开环零点。
08:03
讨论:
1.当m=n时,即开环零点数与极点数相同时,根轨迹 的起点与终点均为有限的值。
2.当m<n时,即开环零点数小于开环极点数时,除有 m条根轨迹终止于开环零点(称为有限零点)外,还有nm条根轨迹终止于无穷远点(称为无限零点)。
只有s0点右侧实轴上的开环极点和开环零点的个数之 和为奇数时,才满足相角条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K G ( s ) H ( s ) ,试绘制 s ( s 1 )( s )
α =0
1 K 0 2 s (s 1)
以α为参变量的根轨迹方程
s2(s1)K (s1 )s (s1 )s
s (s1 )K
2
- 1
将特征方程进行数学处理,把待定 参数放到增益K的位置
以α为参变量的根轨迹方程 不同K值,可得到系统不 同根轨迹图,即根轨迹簇 根轨迹与虚轴交点
提高系统开环增益10倍
参数变化对闭环极点的影响 控制系统开环传递函数 以α为参变量的根轨迹以及同时变化K时的根轨迹。 闭环控制系统的特征方程
K 1 G ( s ) H ( s ) 1 0 s ( s 1 )( s )
2 s ( s 1 ) ( s 1 ) s K 0
(b)为加入比例微分(PD)校正后的系统
0 . 8 s 1 0 . 8 s 1 5 ( 1 0 . 8 s ) ( s ) G ( s ) H ( s ) b 2 b b s 0 . 5 j 0 . 866 )( s 0 . 5 j 0 . 866 ) s s 1( s ( 5 s 1 )
增加开环极点的影响 增加开环零点的影响
s pc ) 增加一个惯性环节 1/(
加入一阶微分环节(s-zc)
( s z ) /( s p ) c c
增加一对开环零极点的影响 加入环节 |zc|<|pc| |zc|>|pc|
开环偶极子
参数变化对闭环极点的影响 (广义根轨迹、根轨迹簇) 比例微分控制作用与微分反馈对系统性能的影响
(b)为加入比例微分(PD)校正后的系统
控制理论基础(I)
课程负责人:丁 汉 教授
顾问:王显正 教授
交通大学精品课程系列
2004.4.30
第八章 根轨迹法
8.1 根轨迹法基本概念 8.2 绘制根轨迹图的基本规则 8.3 控制系统的根轨迹分析 8.4 根轨迹法设计与校正控制系统
8.3 控制系统的根轨迹分析 根轨迹图上希望闭环极点的位置 开环零点和极点对根轨迹的影响
根轨迹图上希望闭环极点的位置
二阶系统的等Mp线(即等ζ线) 二阶系统的等ts线
闭环传递函数特征根的分布与动态性能指标的关系
s j j 1 , 2 n d d
ts 3 3
Mp增大
n
0 . 05
由实部决定
等Mp线 Mp减小
β
Tp减小
等tp线
s s s s
3 2 1 0
(s 1 )s
s2(s 1 ) K
- 1
1 a 1 a (a 1) K a ! K
a K 0
1 ( 1 ) K 0
14K 2
比例微分控制作用与微分反馈对系统性能的影响 (a)为无校正的位置伺服系统
5 1 G ( s ) H ( s ) a a s ( 5 s 1 ) s ( s 0 . m )
a i i
渐近线与实轴倾角随着 n数增大而减小 根轨迹向右方向弯曲
渐近线与实轴交点随着pc增 大(pc点在实轴上向右移) 而右移,故更靠近原点 。 向右弯曲趋势随着所增加 的极点移近原点而加剧
降低了系统的相对稳定性
增加开环极点的影响
pc 2
增加一个极点的情况
右移极点
pc 1
开环传递函数上增加零点
( 2 k 1 ) 180 ( n m )
a
( p z ) ( n m )
a i i
渐近线与实轴倾角随着 m数增大而增加 根轨迹向左方向弯曲
渐近线与实轴交点随着 Zc增大(Zc点在实轴上 向右移)而左移
tp 2 1 d n
M e p e
σ
Ts减小 等ts线
1 2
由实部决定
100 % e
n
2 n 1
100 %
d
100 % tg d
由实部虚部比 值决定
开环传递函数上增加极点
( 2 k 1 ) 180 ( n m )
开环偶极子位于原点附近
零点zc和极点pc到主导极点的矢 量也基本相等;幅角条件和幅值 条件中作用也基本抵消。
不影响主导极点附近的 根轨迹及根轨迹增益K’ 零极点自身比值zc /pc- 较大 影响系统的开环增益、改变稳态误差。
K K'
i 1 i 1 n
m
zi pi
zc pc
p 0 .01 c zc 0 .1
“超前校正”
|zc|>|pc| 增加的极点相对靠近虚轴而起主导作用
c c
c) 附加提供一个滞后角 ( c
( s z ) ( s p ) c c
相当于附加极点的作用 (使根轨迹向右弯曲)
开环偶极子 开环偶极子距离原点较远 极点pc ’和零点zc ’到较远的s 点的矢量基本相等;幅值条件和 幅角条件中的作用相互抵消; 对离其较远的近虚轴区域的根轨 迹形状和开环增益几乎没有影响, 基本上不影响系统静动态性能。
(a)为无校正的位置伺服系统
5 1 G ( s ) H ( s ) a a s ( 5 s 1 ) s ( s 0 . 2 )
(c)为加入速度内反馈校正后的系统
0 . 8 ( s 1 . 25 ) G ( s ) H ( s ) c c s ( s 0 . 2 )
1 1 ( s ) c 2 s 0 . 5 j 0 . 866 )( s 0 . 5 j 0 . 866 ) s s 1(
提高了系统的相对稳定性
增加一个零点的情况
Zc 3
右移零点
Zc 2
|zc|<|pc| 增加的零点相对靠近虚轴而起主导作用
零极点对应的矢量幅角
c c
( s z ) ( s p ) c c
c) 附加提供一个超前角 ( c
相当于附加零点的作用
(使根轨迹向左弯曲, 改善了系统动态性能。)
