边界条件
边界条件的类型

边界条件的类型一、边界条件的类型嘿,小伙伴们!今天咱们来唠唠边界条件的类型这个事儿哈。
那啥是边界条件呢?简单来说,就是在解决一些物理、数学或者工程问题的时候,在研究区域的边界上所需要满足的一些条件啦。
咱先说说第一类边界条件,这也叫狄利克雷边界条件哦。
想象一下,就像是在一个大的区域里面,边界上的值是给定好的。
比如说,在研究热传导问题的时候,在物体的边界上,温度是已经知道的数值,这个数值就像是一个固定的标准,不管里面怎么变,边界上就是这个数,是不是很神奇呢?接着呢,就是第二类边界条件啦,也被称为诺伊曼边界条件。
这个条件就有点不同咯,它规定的不是边界上的值,而是边界上值的变化率。
就好比在流体流动的问题里,在边界上流体的流速的变化率是给定的。
这就像是在一个游戏里,不是告诉你边界上的具体状态,而是告诉你这个状态的变化速度呢。
还有第三类边界条件,这可就更有趣了。
它是前两种边界条件的一种混合形式呢。
比如说在一些热交换的问题里,边界上的热量交换既和边界上的温度有关,也和温度的变化率有关。
这就像是把两个规则混合起来玩一个更复杂的游戏。
然后呢,还有周期性边界条件。
这个在研究一些具有周期性结构的问题里特别有用。
比如说晶体结构,它的边界就像是循环的一样,一边的边界和另一边的边界在某种意义上是一样的。
就像一个无限循环的图案,这边的边界和那边的边界就像双胞胎一样有着相同的性质。
最后呀,还有混合边界条件。
这个就比较复杂啦,它是把好几种不同的规则组合在一起,根据具体的问题来设定边界上的各种条件。
就像是一个超级复杂的拼图,每一块都有自己的规则,但是组合起来就能解决那些特别难搞的问题。
哈哈,边界条件的类型是不是很有趣呢?它们就像是一把把钥匙,能帮我们打开解决各种问题的大门哦。
边界条件的定义

边界条件的定义
边界条件是指在计算机程序、数学模型或系统设计中,定义问题的输入、输出或操作所必须满足的条件。
这些条件是问题解决的关键因素,因为如果边界条件不正确或不完整,那么计算机程序或解决方案将无
法正确工作。
边界条件通常可分为两类:输入边界条件和输出边界条件。
输入边界
条件是指在程序中需要接收的输入信息,而输出边界条件是指在程序
运行完毕后需要输出的结果。
以下是边界条件的几个基本定义:
1. 最小值和最大值- 最小值和最大值是边界条件的基本概念。
在很多
问题中,最小和最大值是非常重要的因素。
例如,在一些排序算法中,最小和最大值可能直接影响算法的效率。
2. 边界顺序- 当问题有多个边界情况的时候,它们的顺序也非常的重要。
例如,在一些搜索算法中,问题的解可能受限于某个边界情况。
如果这个边界情况与其他条件冲突,那么这个算法将无法产生有效的
解决方案。
3. 特定的值- 在一些特定的问题中,特定的值可能会与边界条件有关。
例如,在寻找图像的边缘时,边缘的像素通常被视为边界条件。
除了输入和输出边界条件,还有一些其他的边界条件需要考虑。
例如,在计算机程序中,内存和时间通常是有限的资源。
因此,程序设计者
需要考虑程序可能需要运行的时间和内存使用量。
正如你所看到的,边界条件对于任何问题的解决方案都是至关重要的。
只有当问题的输入和输出的边界清晰明确时,我们才能保证程序的正
确性和解决方案的有效性。
因此,在分析问题时,我们应该非常注意问题的边界条件,并且确保它们被正确地定义和实现。
有限元边界条件定义

有限元边界条件定义有限元方法是一种常用的数值分析方法,用于解决工程和科学领域中的各种物理问题。
在使用有限元方法进行计算之前,需要定义适当的边界条件。
边界条件是指在计算区域的边界上所施加的约束条件,用于模拟真实世界中的物理现象。
本文将详细介绍有限元边界条件的定义和应用。
1. 强制边界条件强制边界条件是指在计算区域的边界上施加的已知值或已知函数。
这些边界条件通常是由实验数据、分析解或其他先验知识提供的。
强制边界条件可以是以下几种类型:1.1 固定边界条件固定边界条件是指在计算区域的边界上施加的位移或变形的已知值。
例如,当我们研究一个悬臂梁的弯曲问题时,可以将梁的一端固定在原点,这样就施加了一个固定边界条件。
1.2 力边界条件力边界条件是指在计算区域的边界上施加的外力或力密度的已知值。
例如,当我们研究一个杆件的拉伸问题时,可以在杆件的一端施加一个已知的拉力,这样就施加了一个力边界条件。
1.3 热边界条件热边界条件是指在计算区域的边界上施加的温度或热流的已知值。
例如,当我们研究一个热传导问题时,可以在物体的表面上施加一个已知的温度,这样就施加了一个热边界条件。
2. 自然边界条件自然边界条件是指在计算区域的边界上施加的无约束条件。
这些边界条件通常是由物理现象本身决定的,不需要额外的输入。
自然边界条件可以是以下几种类型:2.1 自由边界条件自由边界条件是指在计算区域的边界上不施加任何约束条件。
例如,当我们研究一个流体力学问题时,可以将流体的边界设置为自由边界,这样流体可以自由地进出计算区域。
2.2 绝缘边界条件绝缘边界条件是指在计算区域的边界上施加的无热流或无质量流的条件。
例如,当我们研究一个热传导问题时,可以将物体的边界设置为绝缘边界,这样热量不能通过边界传递。
2.3 对称边界条件对称边界条件是指在计算区域的边界上施加的关于某个轴对称的条件。
例如,当我们研究一个结构的弯曲问题时,可以将结构的边界设置为对称边界,这样只需要计算一半的结构即可。
边界条件 写法

边界条件是在数值模拟中经常需要处理的一个重要问题,它指的是模拟区域的边界上需要满足的限制条件。
边界条件的正确设置对于数值模拟结果的准确性和稳定性都有着重要的影响。
下面介绍一些常见的边界条件的写法:
1. Dirichlet边界条件
Dirichlet边界条件是最常见的边界条件之一,它要求在边界上给定一个具体的值,例如:
u(0,t) = 0
u(1,t) = 1
这表示在x=0处,函数值为0;在x=1处,函数值为1。
2. Neumann边界条件
Neumann边界条件是另一种常见的边界条件,它要求在边界上给定一个导数值,例如:
u_x(0,t) = 0
u_x(1,t) = 0
这表示在x=0处,函数的斜率为0;在x=1处,函数的斜率也为0。
3. Robin边界条件
Robin边界条件是Dirichlet和Neumann边界条件的结合,它要求在边界上同时给定一个函数值和导数值,例如:
u(0,t) + ku_x(0,t) = 0
u(1,t) + ku_x(1,t) = 0
这表示在x=0和x=1处,函数值和导数值的线性组合等于0。
4. 周期性边界条件
周期性边界条件是指在模拟区域的一个边界处,将函数值赋为另一个边界处的函数值。
例如:
u(0,t) = u(L,t)
这表示在x=0处的函数值等于x=L处的函数值,其中L为模拟区域的长度。
以上是一些常见的边界条件的写法,不同的边界条件适用于不同的模拟问题,需要根据具体问题选择合适的边界条件。
材料力学边界条件

材料力学边界条件边界条件在材料力学中起到非常重要的作用,它们是物理现象或力学问题的解决方案的关键要素之一、边界条件确定了在研究区域边界上发生的物理过程和影响。
在材料力学中,常见的边界条件包括:1.位移边界条件:位移边界条件是指物体在边界上的位移情况。
常见的位移边界条件有固定边界条件、自由边界条件和摩擦边界条件等。
固定边界条件是指物体在其中一边界上的位移被限制为零,即该边界上的点不能发生位移。
自由边界条件是指物体在其中一边界上的位移没有任何限制,即该边界上的点可以自由运动。
摩擦边界条件是指物体在其中一边界上的位移受到边界面上的摩擦力所限制。
2.力边界条件:力边界条件是指物体在边界上受到的外力情况。
常见的力边界条件有固定力边界条件和自由力边界条件等。
固定力边界条件是指物体在其中一边界上受到的外力为零,即该边界上没有外力作用。
自由力边界条件是指物体在其中一边界上受到的外力没有任何限制,即该边界上的外力可以自由作用。
3.应力边界条件:应力边界条件是指物体在边界上的应力情况。
常见的应力边界条件有固定应力边界条件和自由应力边界条件等。
固定应力边界条件是指物体在其中一边界上的应力被固定为其中一个值,即该边界上的应力受到限制。
自由应力边界条件是指物体在其中一边界上的应力没有任何限制,即该边界上的应力可以自由变化。
边界条件的选择需要根据具体问题的要求和实际情况进行确定。
通常情况下,边界条件需要满足力学平衡条件、位移连续条件和应力连续条件等。
同时,边界条件的选择也需要考虑到物体的边界特性,比如是否有固定边界、自由边界或者摩擦边界等。
边界条件的正确选择对于力学问题的解决至关重要。
不恰当的边界条件会导致计算结果的不准确甚至错误。
因此,在进行模拟和计算时,需要仔细分析和确定边界条件,并考虑到实际问题的特点和要求。
总之,材料力学边界条件是研究区域边界上发生的物理过程和影响的要素,其正确选择对于解决力学问题具有重要作用。
在选择边界条件时,需要考虑到力学平衡、位移连续和应力连续等方面,以获得准确的计算结果。
数学物理方法三类边界条件

数学物理方法三类边界条件
在数学物理中,常常会遇到需要考虑边界条件的问题。
根据不同的情况,可以将数学物理方法中的边界条件分为三类,第一类边界条件、第二类边界条件和第三类边界条件。
1. 第一类边界条件(Dirichlet边界条件):
第一类边界条件是指在边界上给定了物理量的具体值。
例如,在一个热传导问题中,可以给定边界上的温度值。
在一个波动方程中,可以给定边界上的振幅值。
这类边界条件可以用数学上的等式或函数来表示。
2. 第二类边界条件(Neumann边界条件):
第二类边界条件是指在边界上给定了物理量的导数。
例如,在一个热传导问题中,可以给定边界上的热流密度(即温度梯度)。
在一个波动方程中,可以给定边界上的振幅的导数。
这类边界条件可以用数学上的导数来表示。
3. 第三类边界条件(Robin边界条件):
第三类边界条件是指在边界上给定了物理量的线性组合,其中既包括物理量的值,也包括物理量的导数。
例如,在一个热传导问题中,可以给定边界上的热流密度和温度的线性组合。
这类边界条件可以用数学上的线性组合来表示。
需要注意的是,以上分类只是一种常见的方式,具体问题中的边界条件可能会有其他形式。
此外,边界条件的选择和应用也取决于所研究的具体物理问题和数学模型。
在实际问题中,根据边界条件的具体形式,可以选择合适的数学方法和技巧来求解。
边界条件定义

边界条件定义边界条件在计算机科学和工程中扮演着至关重要的角色。
它们定义了系统或算法的输入、输出和行为的范围,保证了系统的正确性和可靠性。
本文将探讨边界条件的重要性、应用场景以及如何正确处理边界条件。
边界条件的定义对于系统设计和实现至关重要。
它们定义了系统的输入和输出的限制,可以帮助开发人员避免输入错误或输出错误。
例如,在一个银行系统中,边界条件可以限制存款金额的范围,确保用户输入的金额在合理的范围内,从而避免了可能的错误或风险。
边界条件在算法设计和优化中起着关键的作用。
通过定义算法的输入和输出的边界,可以确保算法在各种情况下的正确性和可靠性。
例如,在排序算法中,边界条件可以定义输入数据的最大和最小值,以确保算法可以正确地处理这些边界情况。
边界条件的处理还可以提高系统的性能和效率。
通过正确处理边界条件,可以避免系统因为无效或异常的输入而崩溃或降低性能。
例如,在一个网络服务器中,正确处理边界条件可以防止恶意用户发送恶意请求,提高系统的安全性和稳定性。
在实际的软件开发过程中,边界条件的处理通常包括以下几个步骤。
首先,需要仔细分析系统或算法的需求和约束,确定可能的边界条件。
然后,对于每个边界条件,需要定义相应的处理逻辑,以确保系统的正确性和可靠性。
在编码过程中,需要对边界条件进行验证和测试,以确保系统在各种情况下的正确性和稳定性。
在处理边界条件时,还需要注意一些常见的问题。
首先,边界条件应该尽可能地详细和全面,以覆盖各种可能的情况。
其次,在处理边界条件时,需要考虑到不同的场景和用户的需求,以保证系统的灵活性和可扩展性。
此外,还需要注意边界条件的变化和更新,及时调整系统的设计和实现。
边界条件在计算机科学和工程中起着至关重要的作用。
它们定义了系统或算法的输入、输出和行为的范围,保证了系统的正确性和可靠性。
正确处理边界条件可以提高系统的性能和效率,避免系统崩溃和错误。
因此,在软件开发和系统设计中,我们应该重视边界条件的定义和处理,确保系统的正确性和可靠性。
三类边界条件推导
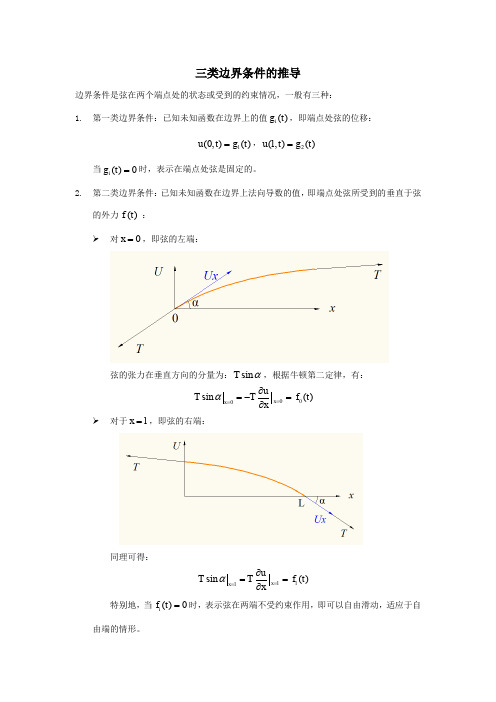
边界条件是弦在两个端点处的状态或受到的约束情况,一般有三种: 1. 一类边界条件:已知未知函数在边界上的值 gi (t ) ,即端点处弦的位移:
u(0, t ) g1 (t ) , u(l , t ) g2 (t )
当 gi (t ) 0 时,表示在端点处弦是固定的。 2. 第二类边界条件: 已知未知函数在边界上法向导数的值, 即端点处弦所受到的垂直于弦 的外力 f (t ) : 对 x 0 ,即弦的左端:
弦的张力在垂直方向的分量为: T sin ,根据牛顿第二定律,有:
T sin x0 T
对于 x l ,即弦的右端:
u x
x 0
f 0 (t )
同理可得:
T sin xl T
u x
x l
fl (t )
特别地,当 fi (t ) 0 时,表示弦在两端不受约束作用,即可以自由滑动,适应于自 由端的情形。
设
k f (t ) , v(t ) ,可以得到,弹性支撑条件下,弦振动的边界条件为: T T u ( u ) x0 v(t ) x
对于 x l ,即弦的右端:
弦对支撑外力的垂直分量为: T 此时得到的弦振动的边界条件为:
u u ,由胡克定律知 T x x
x l
ku
x l
fl (t)
(
u u) x
x l
v(t )
对于外力 fi (t ) 0 的特殊情况,即 v(t ) 0 ,边界条件在弦的两端可统一简化为:
(
u u) x
x a
0 (a 0, a l )
3. 第三类边界条件: 又称混合边界条件, 它给出了未知函数和它的法线方向上的导数的线 性组合在边界上的值。 对弦的一维振动问题,即已知端点处弦的位移(引起弹性支撑的力)和所受的垂直于弦 线的外力。 对 x 0 ,即弦的左端:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网格化分:
机体网格划分采用四面体网格。
上部采用6mm网格,下部采用8mm网格,与缸套接触部分采用2mm网格,共有382111个单元,网格模型如图3和图4所示。
缸套网格划分主要采用六面体2mm网格,4个缸套共有309472个单元,网格模型如图5所示。
缸盖螺栓网格划分采用六面体4mm网格,18个螺栓共有13896个单元,网格模型如图6所示。
缸垫网格划分采用六面体4mm网格,共有4075个单元,网格模型如图7所示。
等效缸盖网格划分采用四面体7mm网格,共有186582个单元,网格模型如图8所示。
总体计算网格模型如图9所示,共有896136个单元。
边界条件:
1 位移边界条件
机体底部约束为零
2 力边界条件
气缸套受力主要有装配应力、燃气压力、热应力和活塞侧向力。
2.1螺栓预紧力
螺栓预紧力通过拧紧力矩获得。
根据YN33柴油机的螺栓拧紧力矩和螺栓结构尺寸计算得到螺栓预紧力为62490N。
2.2活塞对缸套的侧向力
活塞对缸套侧向力采用曲轴转角81°时的工况。
假定力边界条件为:载荷沿缸套轴线方向按二次抛物线规律分布;沿缸套圆周120°角范围内按余弦规律分布。
选择侧击力影响最大位置进行研究,经过分析,选定1缸曲轴转角24°(活塞位于最大爆发压力处)、81°(活塞位于行程中间位置)时的工况进行研究,此时活塞对缸套的侧向力和侧向压力幅值如表1所示。
加载边界条件时取L=43.5,x=0的位置为活塞销的位置。
表1 气缸套壁面加载的活塞侧向力
注:正值表示活塞侧向力作用在主推力侧,负值表示活塞侧向力作用在次推力侧。
2.3 缸套壁面的气体作用力
表2 一缸气缸套壁面加载的气体压力
热应力由温度边界条件计算得到温度场后施加到机械应力分析中进行热力耦合计算。
3 接触边界条件
主要接触对有:气缸盖与气缸垫、气缸盖与气缸套、气缸垫与机体、气缸垫与缸套、气缸套与机体、气缸盖与预紧螺栓下端面、预紧螺栓螺纹与机体螺栓孔螺纹。
4 温度边界条件
常见的导热特征边界条件有:第1类边界条件——恒定温度;第2类边界条件——热流密度;第3类边界条件——对流。
本文研究机型选用采用第三类边界条件。
4.1气缸套温度边界条件
表3 AB段加载的热边界条件
表4 其他段加载的热边界条件
缸盖温度边界条件
缸盖暴露于大气环境中,其表面与周围环境换热极为微弱,因此换热系数不大,本次计算取23 W/m2·℃,环境温度取25℃。
4.2机体温度边界条件
机体外表面暴露于大气环境中,本次计算取23 W/m2·℃,环境温度取25℃。
机体水套部分换热系数取1524 W/m2·℃,介质温度为85℃
5.材料属性
YN33柴油机缸盖和机体材料均为灰铸铁HT250,气缸套材料为钒钛铸铁。
对于气缸垫,其力学特性是非线性的,但其非线性区域为变形量大于0.35mm,本计算变形量不会超过该区域,所以气缸垫的性能参数取为常数。
本文采用mm-N-s单位制。
由于缺少钒钛铸铁资料,当前计算中,气缸套和气缸垫按照HT250的材料属性进行计算。
缸盖螺栓材料为40Cr。
各部分材料属性表5所示。
表5 各部件材料属性。
