《电动力学(第三版)》chapter1_4
郭硕鸿《电动力学》第三版 课后解答详细解释
电动力学答案
第一章 电磁现象的普遍规律
1. 根据算符 的微分性与向量性，推导下列公式： ( A B) B ( A) (B ) A A ( B) ( A )B
A (
A)
1 2
A2
(A )A
解：（1） ( A B) ( A Bc ) (B Ac )
Bc ( A) (Bc ) A Ac ( B) ( Ac )B
可见 r 'r
○2
1 r
d dr
1 r
r
1 r2
r
r r3
'
1 r
d dr
1 ' r r
1 r2
' r
r r3
可见 1/ r '1/ r
○3 (r / r 3 ) [(1/ r 3 )r] (1/ r 3 ) r (1/ r 3 ) r
d dr
1 r3
r r
第1页
电动力学习题解答
从源点指向场点。 （1）证明下列结果，并体会对源变量求微商与对场变量求微商的关系：
r ' r r / r ； (1/ r) '(1/ r) r / r 3 ； (r / r 3 ) 0 ； (r / r 3 ) '(r / r 3 ) 0 ， (r 0) 。 （2）求 r ， r ， (a )r ， (a r) ， [E0 sin(k r)] 及 [E0 sin(k r)] ，其中 a 、 k 及 E0 均为常向量。
M
1 2r1
M dl 0
在 r r2 处，磁化面电流密度为
M
0 1 2r2
M
dl
( 0
1) (r22 r12 ) 2r22
电动力学第三版课后答案
ε
0
)∇
⋅
[
(r
3− 3εr
r13
3
)
ρf
rr] =
−ε
−ε0 3ε
ρ f ∇ ⋅ (rr
−
r13 r3
rr)
=
−ε
−ε0 3ε
ρ
f
(3 − 0)
=
−(ε
− ε
ε
0
)
ρ
f
σ P = P1n − P2n
考虑外球壳时 r r2 n 从介质 1 指向介质 2 介质指向真空 P2n = 0
-5-
电动力学习题解答
4π 3ε 0
(r23
−
r13 )ρ
f
, (r
>
r2 )
∴
Er
=
(r23 − r13 ) 3ε 0r 3
ρ
f
rr, (r
>
r2 )
r < r1时 Er 0
2) Pr
ε 0 χ e Er
= ε0
ε
−ε0 ε0
Er
=
(ε
− ε 0 )Er
∴ρP
=
−∇ ⋅ Pr
=
−(ε
− ε 0 )∇ ⋅ Er
=
−(ε
−
源点指向场点
1
证明下列结果
并体会对源变数求微商 (∇'
=
erx
∂ ∂x '
+ ery
∂ ∂y '
+ erz
∂ ∂z
'
)
与对场变数求
微商 (∇
=
erx
∂ ∂x
+
电动力学课件1-4
JP
=
∂P ∂t
(极化电流体密度 )
∇×B
=
µ0J总
=
µ0J + µ0JM
+ µ0JP
+ µ0ε0
∂E ∂t
H=
B
−M
µ0
∴∇×
H
=
J
+
∂D
∂t
各向同性介质 M = χ m H ⇒ B = µH
Maxwell equations (介质中)
∇×E =
∇ × H=
− ∂B
J
∂t + ∂D
第一章 总结
电磁现象的基本规律，从库仑定律及电荷守恒定律，毕奥—沙伐
尔定律出发，研究了静电场、静磁场的基本规律以及电磁场所满
足的基本方程—Maxwell equations.并研究了非连续介质分界面处
所满足的边值关系。
库仑定律：
F
=
Q1Q2
4πε 0r 3
r ，
r
场强：
E=
Q
r
4πε 0r 3
的方向由源点到场点
D = ε0E + P
qp = −∫∫ S P ⋅ dS =∫∫∫ V ρPdV
σP
=−(P2
−
P1
)
⋅
n
∇⋅D = ρf
各向同性介质 P = ε0χeE
D=ε E
2、磁性质
∑
mi
M= i ∆V
IM= ∫ L M ⋅ d=l ∫∫ S JM ⋅ dS
J M = ∇ × M (磁化电流体密度 )
能量密度 δ w = E ⋅δ D + H ⋅δ B
能量变化率
∂w
电动力学第三版答案
电动力学第三版答案第一章：静电学1.1 静电场静电场是由电荷所产生的场，它是一种无时间变化的电磁场。
静电场的性质可以通过电场强度、电势和电荷分布来描述。
电场强度表示单位正电荷所受到的力，并且是一个向量量。
在任意一点的电场强度可以通过库仑定律计算。
电势是单位正电荷所具有的势能，它是一个标量量。
电势可以通过电势差来定义，电势差是两点之间的电势差别。
1.2 电场的高斯定律电场的高斯定律是描述电场在闭合曲面上的通量与该闭合曲面内的电荷有关系的定律。
它可以通过以下公式表示：\[ \oint \mathbf{E} \cdot \mathbf{n} \, ds =\frac{Q_{\text{enc}}}{\varepsilon_0} \]其中，\(\mathbf{E}\) 是电场强度，\(\mathbf{n}\) 是曲面上的单位法向量，\(ds\) 是曲面上的微元面积，\(Q_{\text{enc}}\) 是闭合曲面内的总电荷，\(\varepsilon_0\) 是真空电容率。
1.3 电势电势是单位正电荷所具有的势能，它是一个标量量。
它可以通过电势差来定义，电势差是两点之间的电势差别。
电势可以通过以下公式计算：\[ V = - \int \mathbf{E} \cdot d\mathbf{l} \]其中，\(V\) 是电势，\(\mathbf{E}\) 是电场强度，\(d\mathbf{l}\) 是路径上的微元长度。
1.4 静电场中的导体在静电场中，导体内部的电场强度为零。
当导体受到外部电场作用时，其表面会产生等效于外部电场的电荷分布，这种现象被称为静电感应。
静电感应可以通过以下公式来计算表面电荷密度：\[ \sigma = \mathbf{n} \cdot \mathbf{E} \]其中，\(\sigma\) 是表面电荷密度，\(\mathbf{n}\) 是表面法向量，\(\mathbf{E}\) 是外部电场强度。
《电动力学》(郭硕鸿第三版)答案
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
批注本地保存成功开通会员云端永久保存去开通
Waylen
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
郭硕鸿《电动力学》第三版 课后答案详细解释
证明： （1） f (u )
f (u ) f (u ) f (u ) df u df u df u ex ey ez ex ey ez x y z du x du y du z df u u u df ( ex ey ez ) u du x y z du Ax (u ) Ay (u ) Az (u ) dAx u dAy u dAz u （2） A(u ) x y z du x du y du z d Ay dA dA u u u dA ( x ex e y z ez ) ( ex ey e z ) u du du du x y z du
（2）在（1）中令 A B 得：
( A A) 2 A ( A) 2( A ) A ， 所以 A ( A) 1 2 ( A A) ( A ) A
即
2 A ( A ) 1 2 A ( A ) A 2. 设 u 是空间坐标 x, y, z 的函数，证明： df dA dA f (u ) u ， A(u ) u ， A(u ) u du du du
方向由原点指向场点。 证明： （ 1 / r ) r / r
3
方法（II）
mr 1 1 ) [m ( )] [( ) m ] 3 r r r 1 1 1 1 ( m ) (m ) [ ( )]m [( ) ]m r r r r 1 1 (m ) [ 2 ]m r r 2 其中 (1 / r ) 0 ， （r 0） 1 A (m ) ， （ r 0 ） r mr 1 又 ( 3 ) [ m ( )] r r 1 1 1 1 m [ ( )] ( ) ( m ) (m )( ) [( ) ]m r r r r 1 (m )( ) r 所以，当 r 0 时， A 7. 有一内外半径分别为 r1 和 r2 的空心介质球，介质的电容率为 ，使介质球内均匀带静 A (
电动力学郭硕鸿(第三版)第一章习题答案
U
U U (
3 H (
(
3
3 (
(
> U
U U
I U@
I
U
U U
U
I
I
3 3Q 3Q
U U Q
3Q
3 3Q
U
U U
I U U U
3
W
W U
U
-
- I
U
G9 O UGU
3
E
I O UGU
D U
O
I
OQ
E D
:
E ' (G9
E
O
I
GU
O
I
OQ E
D
D U
D
: W
O I OQ E D
I
W
O
I
OQ E D
O
O
GO GO
U U
U U
GO
GO
GO GO
O O
U U
GO
O
GO
U U
O
GO
O
GU U
GO
O
U
GO GO
O O
U U
) )
,,
O O
X G$ GX
H[
H\
$ X
[
\
H]
$]
]
\
$[ X $\ X $] X
《电动力学》第一章
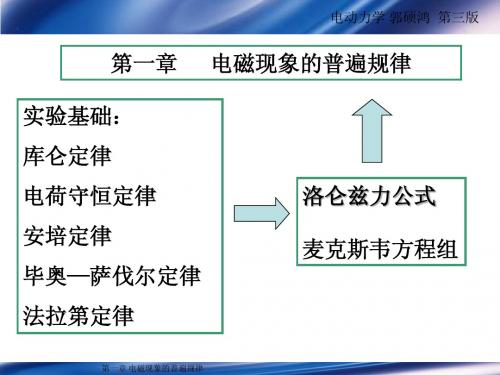
第一章 电磁现象的普遍规律
电动力学 郭硕鸿 第三版
2.高斯(Gauss)定理和电场的散度
设S表示包围着电荷Q的一个闭合曲面， dS 为S上的定向面元，以外法线方向为正 E 向。通过闭合曲面S的电场 的通量定 义为面积分 E dS ，由库仑定律可以 推出关于电场强度通量的高斯定理： Q (1.6) E dS S 0 如空间中有多个电荷 Q 1 i (1.7) E dS Qi
所以：
J v
第一章 电磁现象的普遍规律
§2 电流和磁场 1． 电荷守恒定律 (1)描述电流的物理量 A.电流强度 I 通过截面S 的电荷 随时间的变化率.
电动力学 郭硕鸿 第三版
S
+ + + + + +
I
dq I dt
I envd S
单位: A
dq envddtS
第一章 电磁现象的普遍规律
由库仑定律导出了关于静电场的方程！
第一章 电磁现象的普遍规律
E dl 0
电动力学 郭硕鸿 第三版
例 Q均匀分布于半径为a的球体内，求各 点的电场强度，并由此直接计算电场 的散度。（P7） 解： 作半径为r的球（与电荷 球体同心）。由对称性， 在球面上各点的电场强度 有相同的数值E，并沿径 向。
1 er dV 2 4π 0 r
点 P处电场强度
dq dV E
V
第一章 电磁现象的普遍规律
电动力学 郭硕鸿 第三版
dq 电荷面密度 ds 1 σ er E ds 2 4π 0 r S
ds
q
《电动力学(第三版)》chapter1s
4. 磁场的旋度和散度
(1) 安培环路定理和磁场的旋度
Bdl
L
0I
0
J
S
dS
B 0J
(2) 磁场的散度
因为电流激发的磁 场磁感应线是闭 合的,所以
SB dS 0 B 0
注意旋度概念的局域性,即某点邻域上的磁感应强度的旋度只 和该点上的电流密度有关.虽对包围电流的回路都有磁场环量， 但是磁场的旋度只存在于有电流分布的区域,而在周围空间中的 磁场是无旋的.
• 环路定理说明电场力对电荷做功与路径无关，静 电场是保守力场. 由此可知，无旋场是保守力场.
• 静电场是无旋场，表明电场线不能闭合.
• 积分形式和微分形式均对于变化的电场不成立.
E
0
E 0
电荷是电场的源 静电场是有源无旋场
§1.2 电流和磁场
1. 电流的描述 电流密度矢量
I lim Q dQ
束缚电荷面密度
P en P2 P1
en 为分界面上由介质1指向2的法线方向
(3) 束缚电荷对电场的影响
介质内的电现象: ①电场使介质极化产生束缚电荷;
②束缚电荷反过来激发电场.
0 E f P 0E P f
电位移矢量
D 0E P D f
• 自由电荷决定电位移矢量；
一个电 流元 Idl 在磁场中受力可以表为 dF Idl B,
矢量 B是电流元所在点上磁场的性质,称为磁感应强度.
恒定电流激发的磁场：
B(x)
0
4π
J (x') r
r3 dV'
细导线(闭合回路)激发的磁场：
B(x)
0
4π
Idl r
r3
V
J (x')
电动力学第一章PPT
1
A
ez
Special Orthogonal Coordinate II
(r , ,)
A Ar e r A e A e
Chapter 1 Introduction to Electrostatics
Introduction to Electrostatics
Wave Frequency
1019Hz 1018Hz 1017Hz 1016Hz
300 pm
30 nm
1015Hz
1014Hz 1013Hz 1012Hz 1011Hz 3 µm 30 µm 300 µm 3 mm
333 cm-1 33.3 cm-1 3.3 cm-1
109Hz 30 cm
108Hz 3m
Velocity Acceleration
d er dt
d
dt
e
d e dt
d
dt
er
Vector Differential Operator
Scalar Vector Gradient Divergence
Curl
Laplacian Operator
Two Important Conclusions
Reference Books: 1) John David Jackson, 《Classical Electrodynamics》, Third Edition,
John Wiley and Sons Inc. 2) D. J. Griffiths, 《Introduction to Electrodynamics》, Prentice Hall 3) 郭硕鸿,《电动力学》第三版，高等教育出版社 4) 虞福春、邓春开，《电动力学》，北京大学出版社 5) 梁昆淼，《数学物理方法》第四版，高等教育出版社
电动力学 郭硕鸿 第三版
27
（3）无旋场必可表示为标量场的梯度
f 0
f
（4）无源场必可表示为另一矢量的旋度
f 0
f A
28
4.
算符运算公式
f f f f f f f g f g f g
7
3. 学生必修课程
物理学专业所有学生都 必须修读 《电动力学》。
8
4. 本课程主要内容
静电场、静磁场
（1）麦克斯韦方程 及其应用 平面电磁波的传播 电磁波的辐射 带电粒子和电磁 场相互作用
9
（2）狭义相对论
4. 本课程特点
(1) 数学运算形式相对较复杂， 尤其是矢量运算多，同时运用数 学物理方程
f
ex
x
ey
y
ez
z
fx
fy
fz
f dL ( f ) dS
S
24
3.关于散度和旋度的一些定理
（1）标量场的梯度必为无旋场
0
25
令
f
x
f z f y f x y z y 0 y z z
ab平行四边形面积 c a b cd平行四边形面积
a b d , d a, b c a b f , f c , d
x分量
c2 a1b2 a 2 b1 c3 a 3 b1 a1b3 f1 c2d 3 c3 d 2
《电动力学第三版郭硕鸿》第1-5章练习题答案
10. 变化磁场激发电场
11. 电场强度随时间的变化率
∇
×
G E
=
−
G ∂B
12.
∂t
G ∇×H
=
G J+
G ∂D
13.
∂t
G 14. ∇ ⋅ D = ρ
G
15. ∇ ⋅ B = 0 16. 稳恒电流
G
G GG
17. f = ρ E + J × B (适用于电荷分布情况)
G
GG
18. e E + e v × B
0
Pn (cos
θ
)]
=
Q
⇒
b0
=
Q 4πε 0
, b1
=
−
E 0 R03 2
,bn
=
0(n
≠
0 ,1)
⇒
ϕ
=
− E 0 R cos θ
+
Q 4πε 0 R
−
E 0 R03 2R 3
cos
θ
-8-
《电动力学》各章练习题参考答案（2014） __________________________________________________________________________________
（三）证明题： 1. 书上内容P112-113。 2．书上内容P115。 3. 书上内容P115。 4. 书上内容P122。 5. 书上内容P126。
（四）计算、推导题：
1.解： G
GGG
(1)k G ek =
= G k
k
−3ex
+ G
ey
+ G
ez
《电动力学第三版》电动力学总结
q'q,x'ak
4π 1
q
q
x2y2(za)2 x2y2(za)2
(2) 接地导体球外点电荷
b R02 a
Q' R0 Q a
(P) 1 4π0
Qr Ra0rQ'
(3) 接地导体球内点电荷
b R12 a
Q' R1 Q a
(P) 1 4π0
Qr Ra1rQ'
4 拉普拉斯方程的解 分离变量法
其中
Ex
A1 cos kx x sin k y yeikzz
Ey A2 sin kx x cos k y yeikzz
Ez A3 sin kx x sin k y yeikzz
kxA 1kyA 2ikzA 30
kx
m,
a
ky
n,
b
为求三角形波导的E, 只需从上述解中选出满足最后一个边
界条件的即可
面电荷 0 R|RR 00 R 0 l0n R 02E 0co s
第一项是均匀面电荷,它在柱体内激发的电场为零.第二项是非 均匀分布,它贡献的总电量是零,它在柱体内激发的电场正好与 均匀电场抵消.
例3 试用格林函数证明:在无电荷空间任—点的电势恒等于以该 点为球心的任一球面的电势的平均值.
E
B
H
t D
J
t
D
B 0
电荷守恒定律
J
t
罗伦兹力公式
FQ (EvB )
欧姆定律
JE
第二、三章：静电场和稳恒磁场
利用电磁场唯一性定理，通过求解拉普拉斯方程（或
者镜像法，格林函数）主要研究电偶极矩、电四极矩
和磁偶极矩产生的稳态场。
电动力学-郭硕鸿-第三版-课后题目整理（复习备考专用）.
电动⼒学-郭硕鸿-第三版-课后题⽬整理（复习备考专⽤）.电动⼒学答案第⼀章电磁现象的普遍规律1. 根据算符的微分性与向量性，推导下列公式：2. 设是空间坐标的函数，证明：，，证明：3. 设为源点到场点的距离，的⽅向规定为从源点指向场点。
（1）证明下列结果，并体会对源变量求微商与对场变量求微商的关系：；；；，。
（2）求，，，，及，其中、及均为常向量。
4. 应⽤⾼斯定理证明，应⽤斯托克斯（Stokes）定理证明5. 已知⼀个电荷系统的偶极矩定义为，利⽤电荷守恒定律证明p的变化率为：6. 若m是常向量，证明除点以外，向量的旋度等于标量的梯度的负值，即，其中R为坐标原点到场点的距离，⽅向由原点指向场点。
7. 有⼀内外半径分别为和的空⼼介质球，介质的电容率为，使介质球内均匀带静⽌⾃由电荷，求：（1）空间各点的电场；（2）极化体电荷和极化⾯电荷分布。
8. 内外半径分别为和的⽆穷长中空导体圆柱，沿轴向流有恒定均匀⾃由电流，导体的磁导率为，求磁感应强度和磁化电流。
9. 证明均匀介质内部的体极化电荷密度总是等于体⾃由电荷密度的倍。
10. 证明两个闭合的恒定电流圈之间的相互作⽤⼒⼤⼩相等⽅向相反(但两个电流元之间的相互作⽤⼒⼀般并不服从⽜顿第三定律11. 平⾏板电容器内有两层介质，它们的厚度分别为和，电容率为和，今在两板接上电动势为E 的电池，求：（1）电容器两极板上的⾃由电荷⾯密度和；（2）介质分界⾯上的⾃由电荷⾯密度。
(若介质是漏电的，电导率分别为和当电流达到恒定时，上述两物体的结果如何？12.证明：（1）当两种绝缘介质的分界⾯上不带⾯⾃由电荷时，电场线的曲折满⾜其中和分别为两种介质的介电常数，和分别为界⾯两侧电场线与法线的夹⾓。
（2）当两种导电介质内流有恒定电流时，分界⾯上电场线的曲折满⾜其中和分别为两种介质的电导率。
13.试⽤边值关系证明：在绝缘介质与导体的分界⾯上，在静电情况下，导体外的电场线总是垂直于导体表⾯；在恒定电流情况下，导体内电场线总是平⾏于导体表⾯。
电动力学第一章 郭硕鸿第三版
第一章一．主要内容：电磁场可用两个矢量—电场强度 ),,,(t z y x 和磁感应强度),,,(t z y x B 来完全描写，这一章的主要任务是：在实验定律的基础上找出 E , B所满足的偏微分方程组—麦克斯韦方程组以及洛仑兹力公式，并讨论介质的电磁性质及电磁场的能量。
在电磁学的基础上从实验定律出发运用矢量分析得出电磁场运动的普遍规律；使学生掌握麦克斯韦方程的微分形式及物理意义；同时体会电动力学研究问题的方法，从特殊到一般，由实验定律加假设总结出麦克斯韦方程。
完成由普通物理到理论物理的自然过渡 知 识 体 系：库仑定律： 30()4V x r E x dV r r r r rDr电磁感应定律：L S ddl dS dtr r r r Ñ t介质极化规律：0D P r rr 毕——萨定律：Lr rdV J B 3040 r 介质磁化规律：0rr rD J tr r r 能量守恒定律能量密度12w D H B r r，能流密度：H S二．内容提要：1．电磁场的基本实验定律： （1）库仑定律： 对静电场：30()4V x rE x dV rr r r r 对n 个点电荷在空间某点的场强等于各点电荷单独存在时在该点场强的矢量 和，即：涡旋电场假设位移电流假设 边值 关 系3110()4n n i ii i i i Q r E x E r r r r r 对于场中的一个点电荷，受力 F Q E r r（2）毕奥——萨伐尔定律（电流决定磁场的实验定律） 闭合线电流 ：Lr r l Id B 304闭合体电流：Lr rdV J B 304（3）电磁感应定律L S i S d dt d l dt①感生电场为有旋场（i E r 又称漩涡场）,与静电场S E r本质不同。
②磁场与它激发的电场间关系是电磁感应定律的微分形式。
（4）电荷守恒的实验定律Vs dV t s d JtJ①反映空间某点 与J r之间的变化关系，非稳恒电流线不闭合。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
D t
H
0
Jf
D t
对于各向同性非铁磁物质,磁化强度M和H之间
是线性关系
M MH
介质磁导率: r0
介质相对磁导率: r 1 M
介质磁化率
B H
电位移矢量与磁场强度
• 极化电荷、极化电流、磁化电流同样可以产生电磁 场，故介质中有
E
1
0
(f
B 0(Jf
P)
JM
JP
薄层内出现的净余电荷为
PdS P2 P1 dS
P en P2 P1
en
ds
介质2 介质1
束缚电荷面密度
PdS P2 P1 dS P en P2 P1
en 为分界面上由介质1指向2的法线
对于表面，介质2为真空
P en P1
H
J
t
D
描述变化的磁场激发电场，相关实验 规律是法拉第“电磁感应定律”；
描述电流和变化的电场激发磁场，相 关实验规律是毕奥-萨伐尔定律”；
t
D
描述电荷激发电场，相关实验规律是
自由! “库伦定律”；
描述磁场是无源场(磁单极子不存在)，
B 0
D 0E P
相关实验H规律B是“M毕 奥-萨伐尔定律”；
若单位体积分子数为n，被边界L
a
链环着的分子电流数目为
Lna dl
dl
穿过(穿出向外)曲面的总(净余)磁化电流
IM
nia dl
L
nm dl
L
M dl
L
磁化电流密度
IM S JM dS
JM M
磁化电流不会出现在均匀介质内部，只可能出现在介质 表面.
介质对磁场的影响 极化电流密度
定义磁化强度
M
mi
V
• 单位体积内的等效磁偶极矩 • 局域量
由图可知，通过S的总磁化电流IM等于边界线L所 链环着的分子数目乘上每个分子的电流i. 因为若分子 电流被边界线L链环着,该分子电流就对S的电流有贡献. 在其他情形下,或者分子电流根本不通过S, 或者从S背 面流出来后再从前面流进,所以对IM没贡献.
没有外场时，介质内部的宏观电磁场为零. 有外 场时，介质中的带电粒子受到场的作用，正负电荷发 生相对位移，有极分子的取向以及分子电流的取向呈 现一定的规则性，这就是介质的极化和磁化现象.
介质的电特性 介质的磁特性
极化 磁化
束缚电荷 磁化电流
束缚电荷和磁化电流反过来又激发起附加的宏 观电磁场，叠加外场后得到介质内的总电磁场.
V
l
en
P, E
(1) 介质的内部
dS
nql dS np dS P dS
由V内通过界面 S穿出去的正电荷为:
P dS S
V内净余的负电荷：
VPdV
P dS
S
P P
束缚电荷
束缚电荷不能自由移动，是电极化强度矢量之源.
束缚电荷讨论
•
对非均匀介质
P
P(x)
一般存在束缚电荷
有外场时
一致极化
pi 0
F- + -+
- - + -+
-
p
+
-
+ +
-
F+
+
- + - + - + - + E0
有无外极场分时子的取pi 向 0极化
取向无规则
pi 0
有外场时
取向趋同＋极化
pi
0
E E0 E
-
E
+
+ +
E0
F
-
+ E0
+
-p
F E0
电极化强度矢量：
P
pi
2. 介质的极化
两大类电介质分子结构： 有极分子：分子的正、负电荷中心在无外场时不 重合，分子存在固有电偶极矩.
O2
O2
=
H
H
H2O
H
无极分子：分子的正、负电荷中心在无外场时重 合，分子没有固有电偶极矩.
H+
H+
C4-
H+
=
±
H+
CH4
=
CH4
无极分子的位移极化
无外场时
pi 0
pi
0
±±±±± ±±±±± ±±±±±
D E
11 12 13 21 22 23
31 32 33
• 各向异性非线性电介质（强场下）：
Di
E (1) ij j
E E (2) ijk j k
j
j,k
• 铁磁介质，B 与 H 一般为
非线性关系，而且非单值，
两者之间的关系与过程相关，
B
O
H
具有记忆效应.
B
a
Br b -Hs Hc
怎样改写麦克斯韦方程组？
E
B
B
t
0 J e
0 0
E t
E
e
0
E Jm
H Je
D e
B
t D t
B 0
B m
( B) 0
Je
e
t
0
( E) 0 ?
Jm
m
t
0
E
Jm
B t
(3) 关于复杂介质
常用描述词：(非)均匀、各向同(异)性、(非)线性.
(x x) (x) C
• 各向同性: 物理 性质 与方向无关
I
• 线性: 物理量之间的关 系是线性函数
D E
• 非均匀、非线性、非各向同性的 “三非”介质
Di
(1) ij
(
x
)E
j
(2) ijk
(
x)E
j
Ek
j
j,k
非均匀 非线性
各向 异性
一般介质电磁性质方程
• 各向异性线性电介质，一般介电常量为张量：
度与传导电流密度的关系.
解：
B H 0 (H M )
M
(
1)H
0
H Jf
JM
(
0
1) J f
M JM
例2 求线性均匀导体内自由电荷密度随时间变化 的规律.
解：
D E
J E
D f
Jf
f
t
0
f
t
Jf
E
f
t
f (x,t) f (x,0)e
例3 若自由磁荷（磁单极）存在，试猜想应当
第一章
电磁现象的普 遍规律
§1.4 介质的电磁性质
内容概要
1. 关于介质的概念 2. 介质的极化 3. 介质的磁化 4. 介质中的麦克斯韦方程组
1. 关于介质的概念 介质由分子组成. 从电磁学观点看来，介质是一
个带电粒子系统，其内部存在着不规则而又迅速变化 的微观电磁场. 电介质的分类： ①介质分子的正、负电荷中心重合，没有电偶极矩. ②介质分子的正、负电荷中心不重合，有分子电偶极 矩，但因分子的无规则热运动，在物理小体积内的平 均电偶极矩为零，故没有宏观上的电偶极矩分布.
0
(2) 辅助方程
• 介质的电磁性质方程（本构方程）
P e0E
M MH
D H
B0EMP 0
对于各向同性介质 D E r0E B H r0H
• 欧姆定律（微分形式） J E 为电导率
• 洛伦兹力密度公式 • 电荷守恒定律
f E J B
ห้องสมุดไป่ตู้
J
0
t
例1 求稳恒条件下，线性均匀介质内磁化电流密
实验表明
P e0E
介质极化率
介质相对电容率: r 1 e 介质电容率: r0
D E
3. 介质的磁化
微观分子中 电子的运动，可以等效成载有电流i，面 积矢量为 a的电流环
每个电流环具有磁偶极矩
m ia
单个分子 微体积元
B 0
mi 0 mi 0
B 0
mi 0 mi 0 取向趋同
E 0 t )
0(Jf
1
0
(f
M
P
t
P)
0
E t
)
• 引入个两辅助场量：
电位移矢量 D 0E P
磁场强度
H
B
M
0
• 整理方程，有
0 E
B
0
P
M
f
Jf
t
0E P
D f
D
H Jf t
4. 介质中的麦克斯韦方程组
(1)
麦E克 斯韦方B程组
(3) 束缚电荷对电场的影响
介质内的电现象: (i)电场使介质极化产生束缚电荷;
(ii)束缚电荷反过来激发电场.
0 E f P 0E P f
定义电位移矢量 D 0E P
D f
• 自由电荷决定电位移矢量； • 宏观总电场决定于自由电荷和极化电荷.
对于线性介质（铁电材料就不是线性介质），
c O f Hs H
e d
作
业
7 8 10 11 12 14
• 对均匀介质
PE
P P E f
均匀介质内部没有束缚电荷，束缚电荷仅出现在 自由电荷附近以及介质界面处.
• 若电场变化束缚电荷密度会变化极化电流
P
t
JP
0
P P
P
JP t
极化电流密度
(2) 介质界面(表面)
介质2通过 薄层右侧进入薄层
的正电荷为 P2dS，由介质1通过薄 层左侧进入薄层的正电荷为 P1dS
J
P
P t