销售额预测分析模板(直线回归法)
销售额预测分析报告

销售额预测分析报告一、模型选择预测是重要的统计技术,对于领导层进行科学决策具有不可替代的支撑作用。
常用的预测方法包括定性预测法、传统时间序列预测(如移动平均预测、指数平滑预测)、现代时间序列预测(如ARIMA模型)、灰色预测(GM)、线性回归预测、非线性曲线预测、马尔可夫预测等方法。
综合考量方法简捷性、科学性原则,我选择ARIMA模型预测、GM(1,1)模型预测两种方法进行预测,并将结果相互比对,权衡取舍,从而选择最佳的预测结果。
二ARIMA模型预测(一)预测软件选择----R软件ARIMA模型预测,可实现的软件较多,如SPSS、SAS、Eviews、R等。
使用R 软件建模预测的优点是:第一,R是世最强大、最有前景的软件,已经成为美国的主流。
第二,R是免费软件。
而SPSS、SAS、Eviews正版软件极为昂贵,盗版存在侵权问题,可以引起法律纠纷。
第三、R软件可以将程序保存为一个程序文件,略加修改便可用于其它数据的建模预测,便于方法的推广。
(二)指标和数据指标是销售量(x),样本区间是1964-2013年,保存文本文件data.txt中。
(三)预测的具体步骤1、准备工作(1)下载安装R软件目前最新版本是R3.1.2,发布日期是2014-10-31,下载地址是/。
我使用的是R3.1.1。
(2)把数据文件data.txt文件复制“我的文档”①。
(3)把data.txt文件读入R软件,并起个名字。
具体操作是:打开R软件,输入(输入每一行后,回车):data=read.table("data.txt",header=T)①我的文档是默认的工作目录,也可以修改自定义工作目录。
data #查看数据①回车表示执行。
完成上面操作后,R窗口会显示:(4)把销售额(x)转化为时间序列格式x=ts(x,start=1964)x结果:2、对x进行平稳性检验ARMA模型的一个前提条件是,要求数列是平稳时间序列。
案例之四回归分析:销售额影响因素--------解答
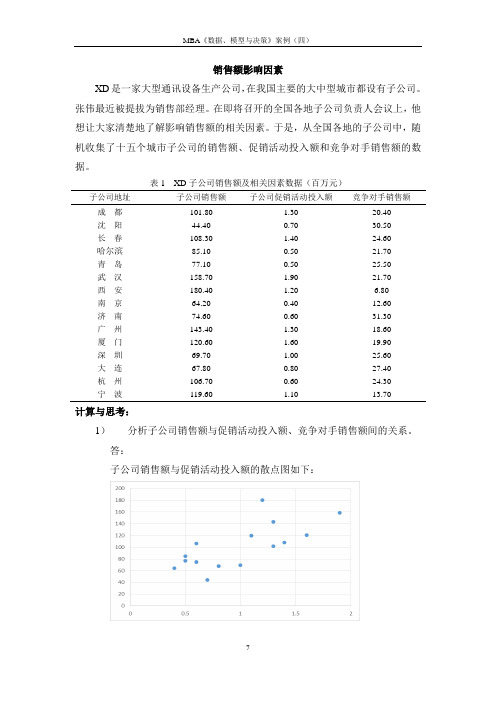
销售额影响因素XD是一家大型通讯设备生产公司,在我国主要的大中型城市都设有子公司。
张伟最近被提拔为销售部经理。
在即将召开的全国各地子公司负责人会议上,他想让大家清楚地了解影响销售额的相关因素。
于是,从全国各地的子公司中,随机收集了十五个城市子公司的销售额、促销活动投入额和竞争对手销售额的数据。
表1 XD子公司销售额及相关因素数据(百万元)子公司地址子公司销售额子公司促销活动投入额竞争对手销售额成都101.80 1.30 20.40沈阳44.40 0.70 30.50长春108.30 1.40 24.60哈尔滨85.10 0.50 21.70青岛77.10 0.50 25.50武汉158.70 1.90 21.70西安180.40 1.20 6.80南京64.20 0.40 12.60济南74.60 0.60 31.30广州143.40 1.30 18.60厦门120.60 1.60 19.90深圳69.70 1.00 25.60大连67.80 0.80 27.40杭州106.70 0.60 24.30宁波119.60 1.10 13.70计算与思考:1)分析子公司销售额与促销活动投入额、竞争对手销售额间的关系。
答:子公司销售额与促销活动投入额的散点图如下:可以看出大致趋势为子公司销售额与促销活动投入额成正比关系子公司销售额与竞争对手销售额间的散点图如下可以看出子公司销售额与竞争对手销售额间成反比关系2)建立子公司促销活动投入额对其销售额的回归方程;解释方程的含义,说明子公司促销活动投入额对其销售额的影响程度;假设某地的子公司促销活动投入额为120万元,预计其销售额及在置信水平95%下的预测区间。
答:设y为销售额,x为促销活动投入额,做回归分析过程如下SUMMARY OUTPUT回归统计Multiple R 0.707693R Square 0.500829Adjusted R Square 0.462431标准误差27.9912观测值15方差分析df SS MS F SignificanceF回归分析 1 10219.42 10219.42 13.04317 0.003161 残差13 10185.59 783.5072总计14 20405.01Coefficients 标准误差t Stat P-value Lower 95% Upper95%下95Intercept 42.21206 17.93509 2.353601 0.03499 3.465645 80.95847 3.46 X Variable 1 59.67914 16.5246 3.611532 0.003161 23.9799 95.37837 23.子公司促销活动投入额对其销售额的回归方程为:y = 59.679x + 42.212 R² = 0.5008子公司促销活动投入额对其销售额的影响程度:从R²= 0.5008,可以看出回归方程拟合优度不高,子公司促销活动投入额对其销售额的影响程度仅为50%。
一元线性回归-商店面积与销售额PPT教学课件
回归 (可解释) df 误差 (残差) df
总计 df
SSR
SST SSE
一元线性回归模型
•
r2
SSR SST
回归平方和 总平方和
• 度量Y 变动可以由X 变动所解释的比例
一元线性回归:分析
n
•
SYX
SSE n2
(Y Yˆi )2
i 1
n2
• 度量围绕回归方程的Y 的标准变动
一元线性回归:分析
第二节 消化腺
15
几个概念
鱼类消化系统的组成:消化管、各种消化腺。 生理机能:直接或间接担任食物的消化和吸
收。 体腔:鱼类和其他脊椎动物一样,具一肌肉
壁包围的体腔,有一横隔将体腔分隔为前 后两个腔:围心腔、腹腔。 背腔:容纳肾脏和鳔的空腔。位于腹腔之外。
16
第一节 消化管
消化管为一肌肉的管子,起自口,最后从泄殖腔 或肛门开口于外,包括口咽腔、食道、胃、肠 等部分。
28
二、食道(esophagus)
鱼类的食道短而宽,管壁较厚。
组织构成:粘膜层、肌肉层及 浆膜层。肌肉层全由横纹肌 组成。
有选择食物的作用。
食道囊:鲳科鱼类的食道呈卵 圆形的球状物,肌肉壁很厚, 粘膜具几丁质,且有许多长 条状乳头状突起,每一突起 上附有许多小齿状突起,29 称
三、胃(Stomach)
少数鱼类舌退化甚至无舌,如海龙科。 一些鱼类的舌上布有味蕾,并有神经支配。 鱼类的味蕾不仅分布于舌上,在口腔、触须及
体侧等处均有分布。 22
(三)鳃耙(gill raker)
鱼类鳃弓朝口腔的一侧 长有鳃耙,一般每一 鳃弓长有内外两行鳃 耙,其中以第一鳃弓 外鳃耙最长。
鳃耙是鱼类的一种滤食 器官,亦有保护鳃丝 的作用。
回归分析法在销售预测中的应用

回归分析法在销售预测中的应用滕宁宇冯润莜赵智钰程慧玲摘要:销售预测是企业经营预测的起点,它对企业成本、利润、资金需求的预测会产生非常深刻地影响,可谓牵一发而动全身。
本文以啤酒行业为例,选取其行业内上市企业197个样本数据,利用回归法对其季度销售收入进行预测,以期帮助行业管理者进行后续有效管理及科学决策。
关键词:回归分析;销售预测;应用一、销售预测的意义销售预测在企业的预测分析中起着举足轻重的作用,它可以帮助管理者做好一系列合理规划,如销售计划、采购计划、生产计划、满足企业长、短期资金需求的融资计划等等,从而有利于管理者对企业的经营管理进行全方位的有效控制及科学决策;与此同时,销售预测又是企业管理中的一大难点,究期原因,影响销售的因素很多,通常可以分为外部因素与内部因素两大类,外部因素有宏观经济环境、行业景气度、竞争对手状况等,而内部因素主要有企业产能、产品生命周期、产品性价比、企业提供的附加服务等,如何在纷繁复杂的影响因素中找到对企业销售产生至关影响的关键性因素是企业管理者进行后续有效管理及科学决策的必要条件。
二、销售预测相关文献回顾(Cravens and Piercy,2006)在《战略营销》中写到:销售预测必需关注目标主体的销售模式,其销量不可能超越市场潜能,它可以用判断方法或高等计量方法来实现。
通常可通过PEST 分析模型,从政治、经济、社会、科技四个方面着手分析其对企业销售的影响,考虑到行业景气度、竞争对手采用的经营策略、企业内部相关条件来对销售进行定性或定量预测。
定性分析法又称非数量分析法,由专业人员根据个人经验和知识,对预测对象的特点进行综合分析,对企业未来经济状况和发展趋势作出研判的一类预测方法。
定量分析法,又称数量分析法,是指在完全掌握与预测对象有关的各种要素资料的基础上,运用现代数学方法进行数据处理,建立有关变量之间的规律性的联系的预测模型的方法体系。
回归分析法是定量分析的一种,是在分析预测对象自变量(如时间t 或其他变量)和因变量(如销量或销售收入)之间的相关关系的基础上,建立变量之间的回归模型,并将回归模型作为预测未来市场状况的一种分析方法,这种分析方法在销售预测中有着广泛的应用,通常又可分为时间序列分析及因果预测分析。
回归分析预测法预测新田公司销售

案例一:回归分析预测法预测新田公司销售一、新田公司的发展现状新田公司全称为新田摩托车制造有限公司,成立于1992年3月,当时的锡山市(那时还叫无锡县)有两个生产摩托车的乡镇企业:查桥镇的捷达摩托车厂和洛社镇的雅西摩托车厂。
在9l、92年这两家厂可以说是如目中天,但这两家厂又各具特点:雅西摩托车厂完全是自主生产,除发动机外其余配件都由本厂生产;捷达摩托车厂则是装配型厂,配件由其他厂家生产,本厂只是组装(后来也发展成了连发动机都生产的综合型企业)。
顾建新当时还只是一家村办企业的供销员,他就瞄准了摩托车行业的发展前景,于是想方设法和捷达厂取得了联系,从1992年3月起为捷达厂生产两种型号的减震器,厂名是无锡减震器厂,由此开始了企业发展的道路。
减震器厂自成立以后,随着捷达摩托车厂摩托车年产量的不断增长而得到了迅速发展。
到了1994年6月,顾建新终于有了一个极好的机会:捷达摩托车厂的销售部门和捷达摩托车的销售商产生了予盾,因此捷达摩托车的销售商答应顾建新,若顾建新也能生产出和捷达差不多质量的摩托车,则他们会在相同条件下优先销售顾建新生产的摩托车。
有了这个承诺,顾建新于94年lO月就成立了新田摩托车制造有限公司,开始生产新田牌摩托车。
新田公司成立以后,在顾总和匡建中总工程师的领导下,开始了艰苦的创业过程,经过六年多的奋斗,薪田公司终于从一个20多人的小厂发展成了如今的工人总数超过400人,日产摩托车超过200辆,年利润超过2000万的集团型企业,新田摩托车的配件包括发动机在内都由本企业自主生产。
新田公司如今已是一个企业集团,除公司本部(总装厂)外,还有减震器厂、发动机厂、塑件厂、车架车间、油箱车间、喷涂车间等独立部门,这些部门除满足新田公司所需配件外,还可以对外供应。
1999年底,由于摩托车市场竞争的日趋激烈,新田公司的销售模式由代理制转向了派员销售制(由公司往各城市直接派出销售人员,负责各城市的销售工作),以减少中间环节,确保公司产品在整个摩托车市场的竞争力。
基于回归分析的销售模型

1.基于回归分析的公司销售额模型摘要本文讨论了利用全行业销售额预测公司销售额的线性回归问题。
对于问题一,根据1977-1981年公司销售额和行业销售额的分季度数据,利用Matlab软件画出散点图,并由此得知他们显然存在正相关,因此可采取线性回归模型进行拟合;对于问题二,首先,由公司销售额和行业销售额之间的正自相关性建立相应的线性回归模型,利用Matlab统计工具箱计算回归方程中的决定系数、F统计量及各级参数和参数置信区间;其次,根据决定系数判断模型计算结果的可信度,并将参数代入回归方程得到相应回归模型;最后,采用WD-检验法检验模型中随机误差的自相关性。
得出结论:该回归模型的随机误差存在正自相关性。
对于问题三,进一步建立消除随机误差自相关性后的回归模型,类比问题二,利用Matlab统计工具箱计算回归方程中的决定系数及各级参数,检验其随机误差的自相关性,代入参数即得到消除自相关性后的回归模型。
考虑到全行业销售额与公司销售额之间的相互关联性,可进一步对模型进行推广,预测下一年和季度的公司销售额。
关键词回归分析法;自相关性;WD-检验一、问题重述某公司欲用全行业销售额作自变量预测该公司销售额,下表为1977-1981年公司销售额和行业销售额的分季度数据(单位:百万元)。
回答如下问题:问题一:根据数据画出公司销售额与全行业销售额的散点图,并观察用线性回归模型拟合是否合适;问题二:建立公司销售额对全行业销售额的回归模型,并用WD-检验诊断随机误差项的自相关性;问题三:建立消除了随机误差项自相关性后的回归模型。
二、问题分析全行业的销售额情况通常情况下能够用来预测公司的销售额。
本文将根据1977-1981年某公司及其全行业销售额数据解决如下问题:对于问题一公司销售额与全行业销售额的散点图,根据所给数据,利用matlab软件画出图像,并判断其自相关性;对于问题二公司及全行业销售额的回归模型,首先,本文将利用matlab统计工具箱分别求解出回归方程中的各级参数及参数置信区间,代入得到线性回归模型;其次,画出其残差散点图,分析随机误差的自相关性;最后,采用WD-检验法通过求解DW统计量并查阅其检验临界值诊断其随机误差项的自相关性([1]);对于问题三消除随机误差自相关项的回归模型,利用matlab统计工具箱分别求解回归方程中的各级参数及其置信区间,进一步利用DW检验确定其自相关性,代入数据得到相应的线性回归模型。
(完整版)销售预测相关计算公式

完整版)销售预测相关计算公式引言销售预测是企业进行销售计划和业务决策的重要依据之一。
通过合理的销售预测,企业能够合理安排生产、采购和库存等资源,有效控制成本,并提升客户满意度。
本文档将介绍一些常用的销售预测相关计算公式,帮助企业进行销售预测分析。
1.简单移动平均法(Simple Moving Average)简单移动平均法是最常用的销售预测方法之一,在一定时间范围内平均销售数据,用于预测未来一段时间内的销售情况。
其计算公式如下:SMA = (D1 + D2 +。
+ Dn) / n其中,SMA为简单移动平均值,D1至Dn为过去n个时期的销售数据。
2.加权移动平均法(___)加权移动平均法适用于过去销售数据的变动幅度不同的情况,通过给不同时期的销售数据赋予不同的权重,得到加权移动平均值。
其计算公式如下:WMA = (w1 * D1 + w2 * D2 +。
+ wn * Dn) / (w1 + w2 +。
+ wn)其中,WMA为加权移动平均值,D1至Dn为过去n个时期的销售数据,w1至wn为对应时期的权重。
3.指数平滑法(___)指数平滑法是一种适用于预测短期销售趋势的方法,它将过去销售数据按照指数权重降低,越近期的销售数据权重越大。
其计算公式如下:ES = α * Yt + (1 - α) * ES(t-1)其中,ES为指数平滑值,Yt为当前时期的销售数据,ES(t-1)为上一个时期的指数平滑值,α为平滑系数,其取值范围在0到1之间。
4.季节性指数法(Seasonal Index)季节性指数法考虑销售数据的季节性变化,将每个季度的销售数据与整体平均销售数据进行比较,得到季节性指数。
其计算公式如下:SI = (D / MA) * 100其中,SI为季节性指数,D为季度的销售数据,MA为整体平均销售数据。
5.线性回归分析(Linear n)线性回归分析根据过去销售数据与其他相关因素的关系,建立销售预测模型,并进行预测。
年销售额的回归模型预测

学号武汉理工大学数学建模与仿真课程设计设计题目专业班级姓名指导老师2011年 1 月16 日附件2:课程设计任务书学生姓名:专业班级:指导教师:工作单位:题目:初始条件:要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)时间安排:指导教师签名:年月日系主任(或责任教师)签名:年月日年销售额的回归模型预测【摘要】本文首先利用题目所给数据做出散点图,分析自变量与因变量之间的线性关系,建立基本的线性回归模型t t t x y εββ++=10[1],对所建立的模型直接用MATLAB 统计工具箱[2]求解,得到的回归系数估计值及其置信区间(置信水平05.0=α)、检验统计量2R ,F ,P [3],将参数估计值代入初始模型得到t t x y 17628.04548.1+-=∧。
但是这个模型没有考虑到题目所给的数据是一个时间序列。
实际上,在对时间序列数据作回归分析时,模型的随机误差项t ε有可能存在相关性。
违背模型关于t ε(对t )相互独立的基本假设。
所以对原模型进行自相关检验,发现其随机误差存在正自相关,故对原模型作变量变换:1'--=t t t y y y ρ ,1'--=t t t x x x ρ得到新的模型:t t t u x y ++=''1'0'ββ,其中,()ρββ-=10'0,1'1ββ=。
对新的模型利用MATLAB 统计工具箱求解,并对新的模型也作一次自相关检验,即诊断随机误差t u 是否还存在自相关,经检验认为新的模型中随机误差不存在自相关。
因此经变换所得到的回归模型t t t u x y ++=''1'0'ββ是适用的。
最后,将模型t t t u x y ++=''1'0'ββ中的't y 和't x 还原为原始变量t y 和t x ,得到结果为:111099.01737.06326.03916.0--∧-++-=t t t t x x y y关键词:时间序列 回归模型 统计检验 D —W 检验一、问题重述与分析1.1、问题提出某公司(记为A)想用全行业的销售额作为自变量来预测公司的销售额,表1给出了2006年~2010年公司销售额和行业销售额的分季度数据(单位:百万元)。
