微积分(第二版吴传生)第二章 第7节 函数的连续性教案

0
f x0
0
f x0
例3
讨论函数
f
(x)
x
x
2, 2,
x 0, x 0,
在 x 0处的
连续性.
解 lim f ( x) lim( x 2) 2 f (0),
x0
x0
lim f ( x) lim( x 2) 2 f (0),
x0
x0
右连续但不左连续 ,
故函数 f ( x)在点x 0处不连续.
3.单侧连续
若函数f ( x)在(a, x0 ]内有定义,且f ( x0 0) f ( x0 ),
则
称f
(
x
)在
点x
处左
0
连续;
若函数f ( x)在[ x0 , b)内有定义,且f ( x0 0) f ( x0 ), 则称f ( x)在点x0处右连续.
定理
lim
xx0
f
x
f
x0
f
x0
由第四节可知，f ( x)为基本初等函数 , 其定义域
为D
,当
x0
D 时， lim x x0
f ( x) f ( x0 ).
所以基本初等函数在其定义域内连续 .
二、函数的间断点(points of discontinuity)
如果点 x0 不是函数 f (x)的连续点 , 则 称点 x0 为 f (x) 的间断点 .
4.连续函数与连续区间
在区间上每一点都连续的函数,叫做在该区间上 的连续函数,或者说函数在该区间上连续.
函数 f (x)在闭区间[a,b]上连续： （1）函数在开区间(a, b)内连续； （2）在左端点x a处右连续； （3）在右端点x b处左连续.
连续函数的图形是一条连续而不间断的曲线.
5.基本初等函数的连续性
如果 f ( x)在点 x0处的极限存在，但
lim
x x0
f (x)
A
f ( x0 ),
或
f ( x)在点 x0处无定
义则称点 x0为函数 f ( x)的可去间断点.
例4 讨论函数
ቤተ መጻሕፍቲ ባይዱ
y y 1 x
f
(
x)
2 1,
x,
0 x 1, x 1
1 x, x 1,
在x 1处的连续性 .
2 y2 x
1
o1
函数 f ( x) 当 x x0 时的极限存在,且等于它在
点 x0 处的函数值 f ( x0 ),即
lim f ( x)
x x0
f ( x0 )
那末就称函数 f ( x)在点x 连续. 0
" "定义 :
0, 0, 使当 x x0 时, 恒有 f ( x) f ( x0 ) .
x0 为 f ( x) 的间断点 ,有以下三种情形：
(1) f ( x)在点x0处没有定义;
(2) lim f ( x) 不存在;
x x0
(3)
f
(
x
)在点x0处有定义
,
lim
x x0
f ( x)存在
但 lim x x0
f (x)
f ( x0 ).
1.可去间断点(a removable discontinuity)
设函数 f ( x) 在 U( x0 , )内有定义, 当 x 在 U( x0 , )
内由 x0 变到 x0 x 时，称 x 为自变量 x 在点 x0 的增量；相应地，函数 y 从 f ( x0 ) 变到 f ( x0 x) ，
y f ( x0 x) f ( x0 ) 称为函数 f ( x)相应于x的增量.
2
1 x, x 1,
1
在x 1处连续.
o1
x
例5
讨论函数
f
(x)
x, 1 x,
x 0,在x 0处的连续性. x 0,
解 f (0 0) 0, f (0 0) 1,
y
f (0 0) f (0 0),
x)
f ( x0 )]
0,那末就称函数f ( x)
在
点 x 0 连续, x 0 称为 f ( x) 的连续点.
设 x x x, 0
y f ( x) f ( x0 ),
x 0 就是 x x0 , y 0 就是 f ( x) f ( x0 ).
定义 2 设函数 f ( x) 在U ( x0 , ) 内有定义,如果
第七节 函数的连续性
一、函数的连续性的概念 二、函数的间断点 三、初等函数的连续性 四、小结 思考题
一、函数的连续性(continuity)
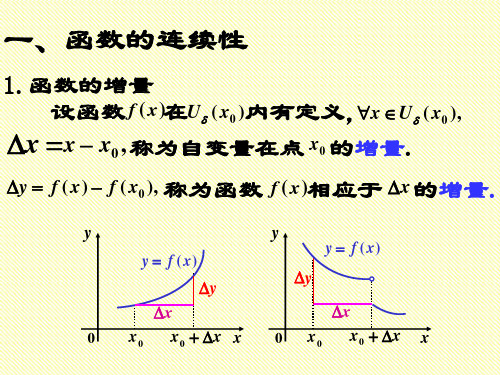
1.函数的增量(increment)
设变量 u 从它的初值 u1 变到终值 u2 则 u u2 u1
称为变量 u 的增量.
注意：(1) u 可正可负；
(2) u 是一个整体，不能看作 与 u 的乘积 .
x
解 f (1) 1,
f (1 0) 2, f (1 0) 2,
lim f (x) 2 f (1), x1
x 0为函数的可去间断点.
注意 可去间断点只要改变或者补充可去间断 处函数的定义, 则可使其变为连续点.
如例4中, 令 f (1) 2,
y
则
f (x)
2
x,
0 x 1,
限存在且等于该点的函数值.
例1
试证函数
f
(x)
x sin
1 x
,
x 0,
在x 0
0, x 0,
处连续.
证 lim x sin 1 0,
x0
x
又 f (0) 0, lim f ( x) f (0), x0
由定义2知
函数 f ( x)在 x 0处连续.
例2 证明函数 y sin x在区间(,)内连续.
从这个定义我们可以看出，函数 f ( x) 在点x0
处连续，必须满足以下三个条件：
（1）函数 f ( x)在点 x 处有定义； 0
（2）极限 lim f ( x)存在，即 x x0
lim f ( x) lim f ( x)
x x0
x x0
（3）lim f ( x) x x0
f (x ) 0
.
即：函数在某点连续等价于函数在该点的极
证 任取 x (,),
y sin( x x) sin x 2 sin x cos( x x )
2
2
cos( x x) 1, 则 y 2 sin x .
2
2
对任意的, 当 0时, 有 sin ,
故 y 2 sin x x , 当x 0时, y 0. 2
即函数 y sin x对任意 x (,)都是连续的.
y
y f (x)
y
y
y f (x)
y
x
x
0 x0 x0 x x 0 x0 x0 x x
2.连续的定义
定义 1 设函数 f ( x) 在U ( x0 , ) 内有定义,如果当
自变量的增量x 趋向于零时,对应的函数的增量
y 也趋向于零,即 lim y 0 或 x 0
lim [
x 0
f (x0