2008年新课标(宁夏海南)卷高考理科数学试卷真题及解析
2008年宁夏高考数学试卷(理)及答案

2008年宁夏高考数学试卷(理)一、选择题(共12小题,每小题5分,满分60分)1.(5分)已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=()A.1 B.2 C.D.2.(5分)已知复数z=1﹣i,则=()A.2i B.﹣2i C.2 D.﹣23.(5分)如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为()A.B.C.D.4.(5分)设等比数列{a n}的公比q=2,前n项和为S n,则=()A.2 B.4 C.D.5.(5分)下面程序框图,如果输入三个实数a、b、c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A.c>x B.x>c C.c>b D.b>c6.(5分)已知a1>a2>a3>0,则使得(1﹣a i x)2<1(i=1,2,3)都成立的x 取值范围是()A.B.C.D.7.(5分)=()A.B.C.2 D.8.(5分)平面向量,共线的充要条件是()A.,方向相同B.,两向量中至少有一个为零向量C.∃λ∈R,D.存在不全为零的实数λ1,λ2,9.(5分)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有()A.20种B.30种C.40种D.60种10.(5分)由直线x=,x=2,曲线y=及x轴所围成的图形的面积是()A.B.C.D.2ln211.(5分)已知点P在抛物线y2=4x上,那么点P到点Q(2,﹣1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.B. C.(1,2) D.(1,﹣2)12.(5分)某几何体中的一条线段长为,在该几何体的正视图中,这条线段的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为()A.B.C.4 D.二、填空题(共4小题,每小题5分,满分20分)13.(5分)已知向量知=(0,﹣1,1),=(4,1,0),|λ+|=,且λ>0,则λ=.14.(5分)设双曲线﹣=1的右顶点为A,右焦点为F.过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为.15.(5分)一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为3,那么这个球的体积为.16.(5分)从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307308 310 314 319 323 325 325 328 331 334 337 352乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318320 322 322 324 327 329 331 333 336 337 343 356由以上数据设计了如下茎叶图:根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:①;②.三、解答题(共8小题,22--24题选做其中一题,满分70分)17.(12分)已知{a n}是一个等差数列,且a2=1,a5=﹣5.(Ⅰ)求{a n}的通项a n;(Ⅱ)求{a n}前n项和S n的最大值.18.(12分)如图,已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上,∠PDA=60°.(Ⅰ)求DP与CC′所成角的大小;(Ⅱ)求DP与平面AA′D′D所成角的大小.19.(12分)A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为X 15%10%X22%8%12%P0. 8 0.2P.2.50.3(Ⅰ)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;(Ⅱ)将x(0≤x≤100)万元投资A项目,100﹣x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.(注:D(aX+b)=a2DX)20.(12分)在直角坐标系xOy中,椭圆C1:=1(a>b>0)的左、右焦点分别为F1,F2.F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=.(Ⅰ)求C1的方程;(Ⅱ)平面上的点N 满足,直线l∥MN,且与C1交于A,B两点,若,求直线l的方程.21.(12分)设函数f(x)=ax +(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程是y=3.(Ⅰ)求y=f(x)的解析式;(Ⅱ)证明:函数y=f(x)的图象是一个中心对称图形,并求其对称中心;(Ⅲ)证明:曲线y=f(x)上任意一点的切线与直线x=1和直线y=x所围成的三角形的面积是定值,并求出这个定值.22.(10分)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.(1)证明:OM•OP=OA2;(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.证明:∠OKM=90°.23.自选题:已知曲线C1:(θ为参数),曲线C2:(t为参数).(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.24.自选题:已知函数f(x)=|x﹣8|﹣|x﹣4|.(Ⅰ)作出函数y=f(x)的图象;(Ⅱ)解不等式|x﹣8|﹣|x﹣4|>2.2008年宁夏高考数学试卷(理)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)(2008•海南)已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=()A.1 B.2 C.D.【分析】由图象确定周期T,进而确定ω.【解答】解:由图象知函数的周期T=π,所以.故选B.2.(5分)(2008•海南)已知复数z=1﹣i,则=()A.2i B.﹣2i C.2 D.﹣2【分析】把z代入分式,然后展开化简,分母实数化,即可.【解答】解:∵z=1﹣i,∴,故选B.3.(5分)(2008•海南)如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为()A.B.C.D.【分析】先得到3边之间的关系,再由余弦定理可得答案.【解答】解:设顶角为C,因为l=5c,∴a=b=2c,由余弦定理得,故选D.4.(5分)(2008•海南)设等比数列{a n}的公比q=2,前n项和为S n,则=()A.2 B.4 C.D.【分析】根据等比数列的性质,借助公比q表示出S4和a1之间的关系,易得a2与a1间的关系,然后二者相除进而求得答案.【解答】解:由于q=2,∴∴;故选:C.5.(5分)(2008•海南)下面程序框图,如果输入三个实数a、b、c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A.c>x B.x>c C.c>b D.b>c【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用,由于该题的目的是选择最大数,因此根据第一个选择框作用是比较x与b的大小,故第二个选择框的作用应该是比较x与c的大小,而且条件成立时,保存最大值的变量X=C.【解答】解:由流程图可知:第一个选择框作用是比较x与b的大小,故第二个选择框的作用应该是比较x与c的大小,∵条件成立时,保存最大值的变量X=C故选A.6.(5分)(2008•海南)已知a1>a2>a3>0,则使得(1﹣a i x)2<1(i=1,2,3)都成立的x取值范围是()A.B.C.D.【分析】先解出不等式(1﹣a i x)2<1的解集,再由a1>a2>a3>0确定x的范围.【解答】解:,所以解集为,又,故选B.7.(5分)(2008•海南)=()A.B.C.2 D.【分析】本题是分式形式的问题,解题思路是约分,把分子正弦化余弦,用二倍角公式,合并同类项,约分即可.【解答】解:原式====2,故选C.8.(5分)(2008•海南)平面向量,共线的充要条件是()A.,方向相同B.,两向量中至少有一个为零向量C.∃λ∈R,D.存在不全为零的实数λ1,λ2,【分析】根据向量共线定理,即非零向量与向量共线的充要条件是必存在唯一实数λ使得成立,即可得到答案.【解答】解:若均为零向量,则显然符合题意,且存在不全为零的实数λ1,λ2,使得;若,则由两向量共线知,存在λ≠0,使得,即,符合题意,故选D.9.(5分)(2008•海南)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有()A.20种B.30种C.40种D.60种【分析】根据题意,分析可得,甲可以被分配在星期一、二、三;据此分3种情况讨论,计算可得其情况数目,进而由加法原理,计算可得答案.【解答】解:根据题意,要求甲安排在另外两位前面,则甲有3种分配方法,即甲在星期一、二、三;分3种情况讨论可得,甲在星期一有A42=12种安排方法,甲在星期二有A32=6种安排方法,甲在星期三有A22=2种安排方法,总共有12+6+2=20种;故选A.10.(5分)(2008•海南)由直线x=,x=2,曲线y=及x轴所围成的图形的面积是()A.B.C.D.2ln2【分析】由题意画出图形,再利用定积分即可求得.【解答】解:如图,面积.故选D.11.(5分)(2008•海南)已知点P在抛物线y2=4x上,那么点P到点Q(2,﹣1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为()A.B. C.(1,2) D.(1,﹣2)【分析】先判断点Q与抛物线的位置,即点Q在抛物线内,再由点P到抛物线焦点距离等于点P到抛物线准线距离,根据图象知最小值在S,P,Q三点共线时取得,可得到答案.【解答】解:点P到抛物线焦点距离等于点P到抛物线准线距离,如图PF+PQ=PS+PQ,故最小值在S,P,Q三点共线时取得,此时P,Q的纵坐标都是﹣1,故选A.12.(5分)(2008•海南)某几何体中的一条线段长为,在该几何体的正视图中,这条线段的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为()A.B.C.4 D.【分析】设棱长最长的线段是长方体的对角线,由题意所成长方体的三度,求出三度与面对角线的关系,利用基本不等式即可求出a+b的最大值【解答】解:结合长方体的对角线在三个面的投影来理解计算.如图设长方体的长宽高分别为m,n,k,由题意得,⇒n=1,所以(a2﹣1)+(b2﹣1)=6⇒a2+b2=8,∴(a+b)2=a2+2ab+b2=8+2ab≤8+a2+b2=16⇒a+b≤4当且仅当a=b=2时取等号.故选C.二、填空题(共4小题,每小题5分,满分20分)13.(5分)(2008•海南)已知向量知=(0,﹣1,1),=(4,1,0),|λ+|=,且λ>0,则λ=3.【分析】根据所给的向量坐标写出要求模的向量坐标,用求模长的公式写出关于变量λ的方程,解方程即可,解题过程中注意对于变量的限制,把不合题意的结果去掉.【解答】解:由题意知λ+=(4,1﹣λ,λ),∴16+(λ﹣1)2+λ2=29(λ>0),∴λ=3,故答案为:3.14.(5分)(2008•海南)设双曲线﹣=1的右顶点为A,右焦点为F.过点F平行于双曲线的一条渐近线的直线与双曲线交于点B,则△AFB的面积为.【分析】根据题意,由双曲线的方程可得a、b的值,进而可得c的值,可以确定A、F的坐标,设BF的方程为y=(x﹣5),代入双曲线方程解得B的坐标,计算可得答案.【解答】解:a2=9,b2=16,故c=5,∴A(3,0),F(5,0),不妨设BF的方程为y=(x﹣5),代入双曲线方程解得:B(,﹣).=|AF|•|y B|=•2•=.∴S△AFB故答案为:.15.(5分)(2008•海南)一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的高为,底面周长为3,那么这个球的体积为.【分析】先求正六棱柱的体对角线,就是外接球的直径,然后求出球的体积.【解答】解:∵正六边形周长为3,得边长为,故其主对角线为1,从而球的直径,∴R=1,∴球的体积故答案为:.16.(5分)(2008•海南)从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:甲品种:271 273 280 285 285 287 292 294 295 301 303 303 307308 310 314 319 323 325 325 328 331 334 337 352乙品种:284 292 295 304 306 307 312 313 315 315 316 318 318320 322 322 324 327 329 331 333 336 337 343 356由以上数据设计了如下茎叶图:根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论:①乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度;②乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度.【分析】利用茎叶图中的数据可以计算乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度;通过观察茎叶图中数据的分布可知甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大.【解答】解:(1)乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度).(2)甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散.(或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大).(3)甲品种棉花的纤维长度的中位数为307mm,乙品种棉花的纤维长度的中位数为318mm.(4)乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近).甲品种棉花的纤维长度除一个特殊值(352)外,也大致对称,其分布较均匀.三、解答题(共8小题,22--24题选做其中一题,满分70分)17.(12分)(2008•海南)已知{a n}是一个等差数列,且a2=1,a5=﹣5.(Ⅰ)求{a n}的通项a n;(Ⅱ)求{a n}前n项和S n的最大值.【分析】(1)用两个基本量a1,d表示a2,a5,再求出a1,d.代入通项公式,即得.(2)将S n的表达式写出,是关于n的二次函数,再由二次函数知识可解决之.【解答】解:(Ⅰ)设{a n}的公差为d,由已知条件,,解出a1=3,d=﹣2,所以a n=a1+(n﹣1)d=﹣2n+5.(Ⅱ)=4﹣(n﹣2)2.所以n=2时,S n取到最大值4.18.(12分)(2008•海南)如图,已知点P在正方体ABCD﹣A′B′C′D′的对角线BD′上,∠PDA=60°.(Ⅰ)求DP与CC′所成角的大小;(Ⅱ)求DP与平面AA′D′D所成角的大小.【分析】方法一:如图,以D为原点,DA为单位长建立空间直角坐标系D﹣xyz.连接BD,B'D'.在平面BB'D'D中,延长DP交B'D'于H.求出.(Ⅰ)利用,求出.即可.(Ⅱ)平面AA'D'D的一个法向量是.通过,得到.即可.方法二:如图,以D为原点,DA为单位长建立空间直角坐标系D﹣xyz.求出解题过程同方法一.【解答】解:方法一:如图,以D为原点,DA为单位长建立空间直角坐标系D ﹣xyz.则,.连接BD,B'D'.在平面BB'D'D中,延长DP交B'D'于H.设,由已知,由可得.解得,所以.(4分)(Ⅰ)因为,所以.即DP与CC'所成的角为45°.(8分)(Ⅱ)平面AA'D'D的一个法向量是.因为,所以.可得DP与平面AA'D'D所成的角为30°.(12分)方法二:如图,以D为原点,DA为单位长建立空间直角坐标系D﹣xyz.则,,.设P(x,y,z)则,∴(x﹣1,y﹣1,z)=(﹣λ,﹣λ,λ)∴,则,由已知,,cos==∴λ2﹣4λ+2=0,解得,∴(4分)(Ⅰ)因为,所以.即DP与CC'所成的角为45°.(8分)(Ⅱ)平面AA'D'D的一个法向量是.因为,所以.可得DP与平面AA'D'D所成的角为30°.(12分)19.(12分)(2008•海南)A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为X 15%10%X22%8%12%P0. 8 0.2P.2.50.3(Ⅰ)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1,DY2;(Ⅱ)将x(0≤x≤100)万元投资A项目,100﹣x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.(注:D(aX+b)=a2DX)【分析】(1)Y1和Y2分别表示投资项目A和B所获得的利润,根据两个投资项目的利润率分别为随机变量X1和X2的分布列,可以得到Y1和Y2的分布列,得到分布列,余下的问题只是运算问题,分别求出变量的方差.(2)由题意知f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和,写出用x表示的方差的解析式,结合二次函数的最值问题,得到结果.【解答】解:(Ⅰ)∵Y1和Y2分别表示投资项目A和B所获得的利润,根据两个投资项目的利润率分别为随机变量X1和X2的分布列可以得到Y1和Y2的分布列分别为Y 151Y22812P0. 8 0.2P0.2.5.3EY1=5×0.8+10×0.2=6,DY1=(5﹣6)2×0.8+(10﹣6)2×0.2=4,EY2=2×0.2+8×0.5+12×0.3=8,DY2=(2﹣8)2×0.2+(8﹣8)2×0.5+(12﹣8)2×0.3=12.(Ⅱ)===,当时,f(x)=3为最小值.20.(12分)(2008•海南)在直角坐标系xOy中,椭圆C1:=1(a>b>0)的左、右焦点分别为F1,F2.F2也是抛物线C2:y2=4x的焦点,点M为C1与C2在第一象限的交点,且|MF2|=.(Ⅰ)求C1的方程;(Ⅱ)平面上的点N满足,直线l∥MN,且与C1交于A,B两点,若,求直线l的方程.【分析】(Ⅰ)先利用F2是抛物线C2:y2=4x的焦点求出F2的坐标,再利用|MF2|=以及抛物线的定义求出点M的坐标,可以得到关于椭圆方程中参数的两个等式联立即可求C1的方程;(Ⅱ)先利用,以及直线l∥MN得出直线l与OM的斜率相同,设出直线l的方程,把直线方程与椭圆方程联立得到关于A,B两点坐标的等式,整理代入,即可求出直线l的方程.【解答】解:(Ⅰ)由C2:y2=4x知F2(1,0).设M(x1,y1),M在C2上,因为,所以,得,.M在C1上,且椭圆C1的半焦距c=1,于是消去b2并整理得9a4﹣37a2+4=0,解得a=2(不合题意,舍去).故椭圆C1的方程为.(Ⅱ)由知四边形MF1NF2是平行四边形,其中心为坐标原点O,因为l∥MN,所以l与OM的斜率相同,故l的斜率.设l的方程为.由消去y并化简得9x2﹣16mx+8m2﹣4=0.设A(x1,y1),B(x2,y2),,.因为,所以x1x2+y1y2=0.x1x2+y1y2=x1x2+6(x1﹣m)(x2﹣m)=7x1x2﹣6m(x1+x2)+6m2==.所以.此时△=(16m)2﹣4×9(8m2﹣4)>0,故所求直线l的方程为,或.21.(12分)(2008•海南)设函数f(x)=ax+(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方程是y=3.(Ⅰ)求y=f(x)的解析式;(Ⅱ)证明:函数y=f(x)的图象是一个中心对称图形,并求其对称中心;(Ⅲ)证明:曲线y=f(x)上任意一点的切线与直线x=1和直线y=x所围成的三角形的面积是定值,并求出这个定值.【分析】(I)欲求在点(2,f(2))处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决.(Ⅱ)由函数y1=x,都是奇函数.可得和函数也是奇函数,其图象是以原点为中心的中心对称图形.再按向量a=(1,1)平移,即得到函数f(x)的图象,故函数f(x)的图象是以点(1,1)为中心的中心对称图形.(Ⅲ)先在曲线上任取一点.利用导数求出过此点的切线方程为,令x=1得切线与直线x=1交点.令y=x得切线与直线y=x交点.从而利用面积公式求得所围三角形的面积为定值.【解答】解:(Ⅰ),于是解得或因a,b∈Z,故.(Ⅱ)证明:已知函数y1=x,都是奇函数.所以函数也是奇函数,其图象是以原点为中心的中心对称图形.而.可知,函数g(x)的图象按向量a=(1,1)平移,即得到函数f(x)的图象,故函数f(x)的图象是以点(1,1)为中心的中心对称图形.(Ⅲ)证明:在曲线上任取一点.由知,过此点的切线方程为.令x=1得,切线与直线x=1交点为.令y=x得y=2x0﹣1,切线与直线y=x交点为(2x0﹣1,2x0﹣1).直线x=1与直线y=x的交点为(1,1).从而所围三角形的面积为.所以,所围三角形的面积为定值2.22.(10分)(2008•海南)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P.(1)证明:OM•OP=OA2;(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.证明:∠OKM=90°.【分析】(1)在三角形OAM中考虑,因为MA是圆O的切线,所以OA⊥AM,从而由射影定理即得;(2)结合(1)问的结论,利用比例线段证明两个三角形△ONP、△OMK相似,通过对应角相等即可得.【解答】证明:(1)因为MA是圆O的切线,所以OA⊥AM,又因为AP⊥OM,在Rt△OAM中,由射影定理知OA2=OM•OP,故OM•OP=OA2得证.(2)因为BK是圆O的切线,BN⊥OK,同(1)有:OB2=ON•OK,又OB=OA,所以OM•OP=ON•OK,即,又∠NOP=∠MOK,所以△ONP~△OMK,故∠OKM=∠OPN=90°.即有:∠OKM=90°.23.(2008•海南)自选题:已知曲线C1:(θ为参数),曲线C2:(t为参数).(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.【分析】(I)先利用公式sin2θ+cos2θ=1将参数θ消去,得到圆的直角坐标方程,利用消元法消去参数t得到直线的普通方程,再根据圆心到直线的距离与半径进行比较,从而得到C1与C2公共点的个数;(II)求出压缩后的参数方程,再将参数方程化为普通方程,联立直线方程与圆的方程,利用判别式进行判定即可.【解答】解:(Ⅰ)C1是圆,C2是直线.C1的普通方程为x2+y2=1,圆心C1(0,0),半径r=1.C2的普通方程为.因为圆心C1到直线的距离为1,所以C2与C1只有一个公共点.(Ⅱ)压缩后的参数方程分别为C1′:(θ为参数);C2′:(t为参数).化为普通方程为:C1′:x2+4y2=1,C2′:,联立消元得,其判别式,所以压缩后的直线C2′与椭圆C1′仍然只有一个公共点,和C1与C2公共点个数相同.24.(2008•海南)自选题:已知函数f(x)=|x﹣8|﹣|x﹣4|.(Ⅰ)作出函数y=f(x)的图象;(Ⅱ)解不等式|x﹣8|﹣|x﹣4|>2.【分析】(I)这是一个绝对值函数,先转化为分段函数,再分段作出其图象;(II)借助(I)的图象,找出函数值为2的点,依据图象找出不等式的解集.【解答】解:(Ⅰ)f(x)=图象如下:(Ⅱ)不等式|x﹣8|﹣|x﹣4|>2,即f(x)>2,观察知当4<x<8时,存在函数值为2的点.由﹣2x+12=2得x=5.由函数f(x)图象可知,原不等式的解集为(﹣∞,5).。
2008年海南高考真题及答案

2008年普通高等学校招生全国统一考试英语注:海南、宁夏使用本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
第一卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一篇。
例:How much is the shirt?A. &19.15B. &9.15C. &9.18答案是B。
1.What is the weather like?A. It's raining.B.It's cloudy.C.It's sunny.2.Who will go to China next month?A.Lucy.B.Alice.C.Richard.3.What are the speakers talking about?A.The man's sister.B.A film.C.An actor.4.Where will the speakers meet?A.In Room 340B.In Room 314.C.In Room 223.5.Where does the conversation most probably take place?A.In a restaurant.B.In an office.C.At home.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
2008年海南高考真题及答案

2008年普通高等学校招生全国统一考试英语注:海南、宁夏使用本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
第一卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一篇。
例:How much is the shirt?A. &19.15B. &9.15C. &9.18答案是B。
1.What is the weather like?A. It's raining.B.It's cloudy.C.It's sunny.2.Who will go to China next month?A.Lucy.B.Alice.C.Richard.3.What are the speakers talking about?A.The man's sister.B.A film.C.An actor.4.Where will the speakers meet?A.In Room 340B.In Room 314.C.In Room 223.5.Where does the conversation most probably take place?A.In a restaurant.B.In an office.C.At home.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
2008年普通高等学校招生全国统一考试(宁夏、海南卷)理科数学

2008年普通高等学校招生全国统一考试(宁夏、海南卷)理科
数学
田彦武
【期刊名称】《上海中学数学》
【年(卷),期】2008(000)007
【摘要】无
【总页数】2页(P29-30)
【作者】田彦武
【作者单位】无
【正文语种】中文
【相关文献】
1.2009年普通高等学校招生全国统一考试宁夏卷(理科数学) [J],
2.2008年普通高等学校招生全国统一考试(湖北卷)理科数学 [J], 王勇
3.2008年普通高等学校招生全国统一考试(北京卷)理科数学 [J], 王芝平
4.2007年普通高等学校招生全国统一考试 (宁夏、海南卷)理科数学 [J], 田彦武
5.2007年普通高等学校招生全国统一考试(宁夏、海南卷)理科数学 [J],
因版权原因,仅展示原文概要,查看原文内容请购买。
2008高考海南宁夏数学理科试卷含答案(全word版)
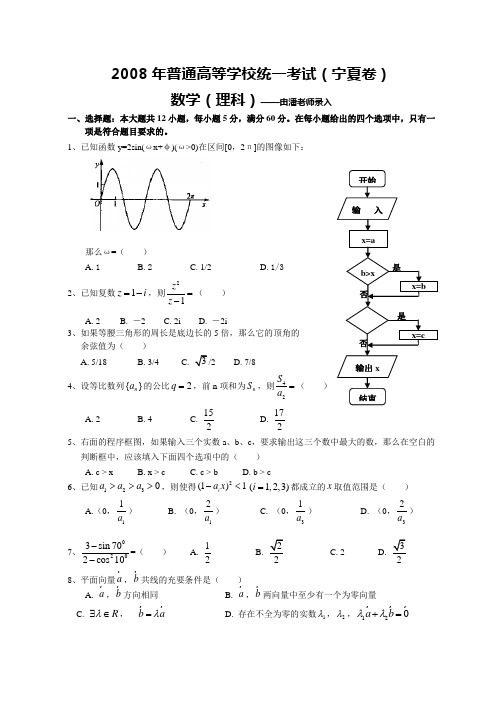
2008年普通高等学校统一考试(宁夏卷)数学(理科)——由潘老师录入一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( ) A. 1B. 2C. 1/2D. 1/32、已知复数1z i =-,则21z z =-( )A. 2B. -2C. 2iD. -2i3、如果等腰三角形的周长是底边长的5倍,那么它的顶角的 余弦值为( ) A. 5/18B. 3/4C.D. 7/84、设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A. 2 B. 4 C.152D.1725、右面的程序框图,如果输入三个实数a 、b 、c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( ) A. c > xB. x > cC. c > bD. b > c6、已知1230a a a >>>,则使得2(1)1i a x -<(1,2,3)i =都成立的x 取值范围是( )A.(0,11a ) B. (0,12a ) C. (0,31a ) D. (0,32a ) 7、0203sin 702cos 10--=( ) A. 12B. 2C. 2D.8、平面向量a ,b共线的充要条件是( )A. a ,b 方向相同B. a ,b 两向量中至少有一个为零向量C. R λ∃∈, b a λ=D. 存在不全为零的实数1λ,2λ,120a b λλ+=9、甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面。
不同的安排方法共有( ) A. 20种B. 30种C. 40种D. 60种10、由直线21=x ,x=2,曲线xy 1=及x 轴所围图形的面积是( ) A. 415 B. 417 C. 2ln 21 D. 2ln 211、已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为( ) A. (41,-1) B. (41,1) C. (1,2) D. (1,-2)12、某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a + b 的最大值为( )A. 22B. 32C. 4D. 52二、填空题:本大题共4小题,每小题5分,满分20分。
2008年全国统一高考数学试卷(理科)(全国卷Ⅰ)(后附答案解析)

2008年全国统一高考数学试卷(理科)(全国卷Ⅰ)一、选择题(共12小题,每小题5分,满分60分) 1.(5分)函数的定义域为( )A .{x |x ≥0}B .{x |x ≥1}C .{x |x ≥1}∪{0}D .{x |0≤x ≤1}2.(5分)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s 看作时间t 的函数,其图象可能是( )A .B .C .D .3.(5分)在△ABC 中,=,=.若点D 满足=2,则=( )A .B .C .D .4.(5分)设a ∈R ,且(a +i )2i 为正实数,则a=( )A .2B .1C .0D .﹣15.(5分)已知等差数列{a n }满足a 2+a 4=4,a 3+a 5=10,则它的前10项的和S 10=() A .138B .135C .95D .236.(5分)若函数y=f (x )的图象与函数y=ln 的图象关于直线y=x 对称,则f (x )=( )A .e 2x ﹣2B .e 2xC .e 2x +1D .e 2x +27.(5分)已知曲线y=在点(3,2)处的切线与直线ax +y +1=0垂直,则a的值为( )A .2B .C .﹣D .﹣28.(5分)为得到函数的图象,只需将函数y=sin2x 的图象( )A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位9.(5分)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为( )A.(﹣1,0)∪(1,+∞)B.(﹣∞,﹣1)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞)D.(﹣1,0)∪(0,1)10.(5分)若直线=1与圆x2+y2=1有公共点,则( )A.a2+b2≤1B.a2+b2≥1C.D.11.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC 内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于( )A.B.C.D.12.(5分)如图,一环形花坛分成A,B,C,D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( )A.96B.84C.60D.48二、填空题(共4小题,每小题5分,满分20分)13.(5分)若x,y满足约束条件,则z=2x﹣y的最大值为 .14.(5分)已知抛物线y=ax2﹣1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .15.(5分)在△ABC中,AB=BC,.若以A,B为焦点的椭圆经过点C ,则该椭圆的离心率e= .16.(5分)等边三角形ABC与正方形ABDE有一公共边AB,二面角C﹣AB﹣D 的余弦值为,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于 .三、解答题(共6小题,满分70分)17.(10分)设△ABC的内角A,B,C所对的边长分别为a,b,c,且acosB﹣bcosA=c.(Ⅰ)求的值;(Ⅱ)求tan(A﹣B)的最大值.18.(12分)四棱锥A﹣BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,,AB=AC.(Ⅰ)证明:AD⊥CE;(Ⅱ)设CE与平面ABE所成的角为45°,求二面角C﹣AD﹣E的大小.19.(12分)已知函数f(x)=﹣x2+ax+1﹣lnx.(Ⅰ)当a=3时,求函数f(x)的单调递增区间;(Ⅱ)若f(x)在区间(0,)上是减函数,求实数a的取值范围.20.(12分)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方法:方案甲:逐个化验,直到能确定患病动物为止.方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;(Ⅱ)ξ表示依方案乙所需化验次数,求ξ的期望.21.(12分)双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.已知||、||、||成等差数列,且与同向.(Ⅰ)求双曲线的离心率;(Ⅱ)设AB被双曲线所截得的线段的长为4,求双曲线的方程.22.(12分)设函数f(x)=x﹣xlnx.数列{a n}满足0<a1<1,a n+1=f(a n).(Ⅰ)证明:函数f(x)在区间(0,1)是增函数;(Ⅱ)证明:a n<a n+1<1;(Ⅲ)设b∈(a1,1),整数.证明:a k+1>b.2008年全国统一高考数学试卷(理科)(全国卷Ⅰ)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)函数的定义域为( )A.{x|x≥0}B.{x|x≥1}C.{x|x≥1}∪{0}D.{x|0≤x≤1}【考点】33:函数的定义域及其求法.【分析】偶次开方的被开方数一定非负.x(x﹣1)≥0,x≥0,解关于x的不等式组,即为函数的定义域.【解答】解:由x(x﹣1)≥0,得x≥1,或x≤0.又因为x≥0,所以x≥1,或x=0;所以函数的定义域为{x|x≥1}∪{0}故选:C.【点评】定义域是高考必考题通常以选择填空的形式出现,通常注意偶次开方一定非负,分式中分母不能为0,对数函数的真数一定要大于0,指数和对数的底数大于0且不等于1.另外还要注意正切函数的定义域.2.(5分)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s看作时间t的函数,其图象可能是( )A.B.C.D.【考点】3A:函数的图象与图象的变换.【专题】16:压轴题;31:数形结合.【分析】由已知中汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,汽车的行驶路程s看作时间t的函数,我们可以根据实际分析函数值S(路程)与自变量t(时间)之间变化趋势,分析四个答案即可得到结论.【解答】解:由汽车经过启动后的加速行驶阶段,路程随时间上升的速度越来越快,故图象的前边部分为凹升的形状;在汽车的匀速行驶阶段,路程随时间上升的速度保持不变故图象的中间部分为平升的形状;在汽车减速行驶之后停车阶段,路程随时间上升的速度越来越慢,故图象的前边部分为凸升的形状;分析四个答案中的图象,只有A答案满足要求,故选:A.【点评】从左向右看图象,如果图象是凸起上升的,表明相应的量增长速度越来越慢;如果图象是凹陷上升的,表明相应的量增长速度越来越快;如果图象是直线上升的,表明相应的量增长速度保持不变;如果图象是水平直线,表明相应的量保持不变,即不增长也不降低;如果图象是凸起下降的,表明相应的量降低速度越来越快;如果图象是凹陷下降的,表明相应的量降低速度越来越慢;如果图象是直线下降的,表明相应的量降低速度保持不变.3.(5分)在△ABC中,=,=.若点D满足=2,则=( )A.B.C.D.【考点】9B:向量加减混合运算.【分析】把向量用一组向量来表示,做法是从要求向量的起点出发,尽量沿着已知向量,走到要求向量的终点,把整个过程写下来,即为所求.本题也可以根据D点把BC分成一比二的两部分入手.【解答】解:∵由,∴,∴.故选:A.【点评】用一组向量来表示一个向量,是以后解题过程中常见到的,向量的加减运算是用向量解决问题的基础,要学好运算,才能用向量解决立体几何问题,三角函数问题,好多问题都是以向量为载体的4.(5分)设a∈R,且(a+i)2i为正实数,则a=( )A.2B.1C.0D.﹣1【考点】A4:复数的代数表示法及其几何意义.【分析】注意到a+bi(a,b∈R)为正实数的充要条件是a>0,b=0【解答】解:(a+i)2i=(a2+2ai﹣1)i=﹣2a+(a2﹣1)i>0,a=﹣1.故选D.【点评】本题的计算中,要注意到相应变量的范围.5.(5分)已知等差数列{a n}满足a2+a4=4,a3+a5=10,则它的前10项的和S10=( )A.138B.135C.95D.23【考点】83:等差数列的性质;85:等差数列的前n项和.【专题】11:计算题.【分析】本题考查的知识点是等差数列的性质,及等差数列前n项和,根据a2+a4=4,a3+a5=10我们构造关于基本量(首项及公差)的方程组,解方程组求出基本量(首项及公差),进而代入前n项和公式,即可求解.【解答】解:∵(a3+a5)﹣(a2+a4)=2d=6,∴d=3,a1=﹣4,∴S10=10a1+=95.故选:C.【点评】在求一个数列的通项公式或前n项和时,如果可以证明这个数列为等差数列,或等比数列,则可以求出其基本项(首项与公差或公比)进而根据等差或等比数列的通项公式,写出该数列的通项公式,如果未知这个数列的类型,则可以判断它是否与某个等差或等比数列有关,间接求其通项公式.6.(5分)若函数y=f(x)的图象与函数y=ln的图象关于直线y=x对称,则f(x)=( )A.e2x﹣2B.e2x C.e2x+1D.e2x+2【考点】4R:反函数.【专题】11:计算题.【分析】由函数y=f(x)的图象与函数y=ln的图象关于直线y=x对称知这两个函数互为反函数,故只要求出函数y=f(x)的反函数即可,欲求原函数的反函数,即从原函数y=ln中反解出x,后再进行x,y互换,即得反函数的解析式.【解答】解:∵,∴,∴x=(e y﹣1)2=e2y﹣2,改写为:y=e2x﹣2∴答案为A.【点评】本题主要考查了互为反函数图象间的关系及反函数的求法.7.(5分)已知曲线y=在点(3,2)处的切线与直线ax+y+1=0垂直,则a 的值为( )A.2B.C.﹣D.﹣2【考点】6H:利用导数研究曲线上某点切线方程.【专题】53:导数的综合应用.【分析】求出函数的导数,切线的斜率,由两直线垂直的条件,即可得到a的值.【解答】解:∵y=,∴y′==,∴曲线y=在点(3,2)处的切线的斜率k=﹣,∵曲线y=在点(3,2)处的切线与直线ax+y+1=0垂直,∴直线ax+y+1=0的斜率k′=﹣a×=﹣1,即a=﹣2.故选:D.【点评】本题考查导数的几何意义的求法,考查导数的运算,解题时要认真审题,仔细解答,注意直线与直线垂直的性质的灵活运用.8.(5分)为得到函数的图象,只需将函数y=sin2x的图象( )A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【专题】11:计算题.【分析】先根据诱导公式将函数化为正弦的形式,再根据左加右减的原则进行平移即可得到答案.【解答】解:∵,只需将函数y=sin2x的图象向左平移个单位得到函数的图象.故选:A.【点评】本题主要考查诱导公式和三角函数的平移.属基础题.9.(5分)设奇函数f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式<0的解集为( )A.(﹣1,0)∪(1,+∞)B.(﹣∞,﹣1)∪(0,1)C.(﹣∞,﹣1)∪(1,+∞)D.(﹣1,0)∪(0,1)【考点】3N:奇偶性与单调性的综合.【专题】16:压轴题.【分析】首先利用奇函数定义与得出x与f(x)异号,然后由奇函数定义求出f(﹣1)=﹣f(1)=0,最后结合f(x)的单调性解出答案.【解答】解:由奇函数f(x)可知,即x与f(x)异号,而f(1)=0,则f(﹣1)=﹣f(1)=0,又f(x)在(0,+∞)上为增函数,则奇函数f(x)在(﹣∞,0)上也为增函数,当0<x<1时,f(x)<f(1)=0,得<0,满足;当x>1时,f(x)>f(1)=0,得>0,不满足,舍去;当﹣1<x<0时,f(x)>f(﹣1)=0,得<0,满足;当x<﹣1时,f(x)<f(﹣1)=0,得>0,不满足,舍去;所以x的取值范围是﹣1<x<0或0<x<1.故选:D.【点评】本题综合考查奇函数定义与它的单调性.10.(5分)若直线=1与圆x2+y2=1有公共点,则( )A.a2+b2≤1B.a2+b2≥1C.D.【考点】J9:直线与圆的位置关系.【分析】用圆心到直线的距离小于或等于半径,可以得到结果.【解答】解:直线与圆有公共点,即直线与圆相切或相交得:d≤r,∴,故选:D.【点评】本题考查点到直线的距离公式,直线和圆的位置关系,是基础题.11.(5分)已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC 内的射影为△ABC的中心,则AB1与底面ABC所成角的正弦值等于( )A.B.C.D.【考点】LP:空间中直线与平面之间的位置关系.【专题】11:计算题;31:数形结合;4R:转化法;5G:空间角.【分析】法一:由题意可知三棱锥A1﹣ABC为正四面体,设棱长为2,求出AB1及三棱锥的高,由线面角的定义可求出答案;法二:先求出点A1到底面的距离A1D的长度,即知点B1到底面的距离B1E的长度,再求出AE的长度,在直角三角形AEB1中求AB1与底面ABC所成角的正切,再由同角三角函数的关系求出其正弦.【解答】解:(法一)因为三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等,A1在底面ABC内的射影为△ABC的中心,设为D,所以三棱锥A1﹣ABC为正四面体,设棱长为2,则△AA1B1是顶角为120°等腰三角形,所以AB1=2×2×sin60°=2,A1D==,所以AB1与底面ABC所成角的正弦值为==;(法二)由题意不妨令棱长为2,点B1到底面的距离是B1E,如图,A1在底面ABC内的射影为△ABC的中心,设为D,故DA=,由勾股定理得A1D==故B1E=,如图作A1S⊥AB于中点S,过B1作AB的垂线段,垂足为F,F=A1S=,AF=3,BF=1,B在直角三角形B1AF中用勾股定理得:AB1=2,所以AB1与底面ABC所成角的正弦值sin∠B1AE==.故选:B.【点评】本题考查了几何体的结构特征及线面角的定义,还有点面距与线面距的转化,考查了转化思想和空间想象能力.12.(5分)如图,一环形花坛分成A,B,C,D四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为( )A.96B.84C.60D.48【考点】C6:等可能事件和等可能事件的概率.【专题】16:压轴题.【分析】这道题比起前几年出的高考题要简单些,只要分类清楚没有问题,分为三类:分别种两种花、三种花、四种花,分这三类来列出结果.【解答】解:分三类:种两种花有A42种种法;种三种花有2A43种种法;种四种花有A44种种法.共有A42+2A43+A44=84.故选:B.【点评】本题也可以这样解:按A﹣B﹣C﹣D顺序种花,可分A、C同色与不同色有4×3×(1×3+2×2)=84.二、填空题(共4小题,每小题5分,满分20分)13.(5分)若x,y满足约束条件,则z=2x﹣y的最大值为 9 .【考点】7C:简单线性规划.【专题】11:计算题;13:作图题.【分析】首先作出可行域,再作出直线l0:y=2x,将l0平移与可行域有公共点,直线y=2x﹣z在y轴上的截距最小时,z有最大值,求出此时直线y=2x﹣z经过的可行域内的点的坐标,代入z=2x﹣y中即可.【解答】解:如图,作出可行域,作出直线l0:y=2x,将l0平移至过点A处时,函数z=2x﹣y有最大值9.【点评】本题考查线性规划问题,考查数形结合思想.14.(5分)已知抛物线y=ax2﹣1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 2 .【考点】K8:抛物线的性质.【专题】11:计算题.【分析】先根据抛物线y=ax2﹣1的焦点坐标为坐标原点,求得a,得到抛物线方程,进而可知与坐标轴的交点的坐标,进而可得答案.【解答】解:由抛物线y=ax2﹣1的焦点坐标为坐标原点得,,则与坐标轴的交点为(0,﹣1),(﹣2,0),(2,0),则以这三点围成的三角形的面积为故答案为2【点评】本题主要考查抛物线的应用.考查了学生综合运用所学知识,解决实际问题的能力.15.(5分)在△ABC中,AB=BC,.若以A,B为焦点的椭圆经过点C ,则该椭圆的离心率e= .【考点】K4:椭圆的性质.【专题】11:计算题;16:压轴题.【分析】设AB=BC=1,,则,由此可知,从而求出该椭圆的离心率.【解答】解:设AB=BC=1,,则,∴,.答案:.【点评】本题考查椭圆的性质及应用,解题时要注意的正确计算.16.(5分)等边三角形ABC与正方形ABDE有一公共边AB,二面角C﹣AB﹣D 的余弦值为,M,N分别是AC,BC的中点,则EM,AN所成角的余弦值等于 .【考点】LM:异面直线及其所成的角;MJ:二面角的平面角及求法.【专题】11:计算题;16:压轴题.【分析】先找出二面角的平面角,建立边之间的等量关系,再利用向量法将所求异面直线用基底表示,然后利用向量的所成角公式求出所成角即可.【解答】解:设AB=2,作CO⊥面ABDE,OH⊥AB,则CH⊥AB,∠CHO为二面角C﹣AB﹣D的平面角,结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,则,=故EM,AN所成角的余弦值故答案为:【点评】本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.三、解答题(共6小题,满分70分)17.(10分)设△ABC的内角A,B,C所对的边长分别为a,b,c,且acosB﹣bcosA=c.(Ⅰ)求的值;(Ⅱ)求tan(A﹣B)的最大值.【考点】GP:两角和与差的三角函数;HP:正弦定理.【分析】本题考查的知识点是正弦定理及两角和与差的正切函数,(Ⅰ)由正弦定理的边角互化,我们可将已知中,进行转化得到sinAcosB=4cosAsinB,再利用弦化切的方法即可求的值.(Ⅱ)由(Ⅰ)的结论,结合角A,B,C为△ABC的内角,我们易得tanA=4tanB>0,则tan(A﹣B)可化为,再结合基本不等式即可得到tan(A﹣B)的最大值.【解答】解:(Ⅰ)在△ABC中,,由正弦定理得即sinAcosB=4cosAsinB,则;(Ⅱ)由得tanA=4tanB>0当且仅当时,等号成立,故当时,tan(A﹣B)的最大值为.【点评】在解三角形时,正弦定理和余弦定理是最常用的方法,正弦定理多用于边角互化,使用时要注意一般是等式两边是关于三边的齐次式.18.(12分)四棱锥A﹣BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,,AB=AC.(Ⅰ)证明:AD⊥CE;(Ⅱ)设CE与平面ABE所成的角为45°,求二面角C﹣AD﹣E的大小.【考点】LY:平面与平面垂直;MJ:二面角的平面角及求法.【专题】5F:空间位置关系与距离.【分析】(1)取BC中点F,证明CE⊥面ADF,通过证明线面垂直来达到证明线线垂直的目的.(2)在面AED内过点E作AD的垂线,垂足为G,由(1)知,CE⊥AD,则∠CGE 即为所求二面角的平面角,△CGE中,使用余弦定理求出此角的大小.【解答】解:(1)取BC中点F,连接DF交CE于点O,∵AB=AC,∴AF⊥BC.又面ABC⊥面BCDE,∴AF⊥面BCDE,∴AF⊥CE.再根据,可得∠CED=∠FDC.又∠CDE=90°,∴∠OED+∠ODE=90°,∴∠DOE=90°,即CE⊥DF,∴CE⊥面ADF,∴CE⊥AD.(2)在面ACD内过C点作AD的垂线,垂足为G.∵CG⊥AD,CE⊥AD,∴AD⊥面CEG,∴EG⊥AD,则∠CGE即为所求二面角的平面角.作CH⊥AB,H为垂足.∵平面ABC⊥平面BCDE,矩形BCDE中,BE⊥BC,故BE⊥平面ABC,CH⊂平面ABC ,故BE⊥CH,而AB∩BE=B,故CH⊥平面ABE,∴∠CEH=45°为CE与平面ABE所成的角.∵CE=,∴CH=EH=.直角三角形CBH中,利用勾股定理求得BH===1,∴AH=AB﹣BH=AC﹣1;直角三角形ACH中,由勾股定理求得AC2=CH2+AH2=3+(AC﹣1)2,∴AB=AC=2.由面ABC⊥面BCDE,矩形BCDE中CD⊥CB,可得CD⊥面ABC,故△ACD为直角三角形,AD===,故CG===,DG==,,又,则,∴,即二面角C﹣AD﹣E的大小.【点评】本题主要考查通过证明线面垂直来证明线线垂直的方法,以及求二面角的大小的方法,属于中档题.19.(12分)已知函数f(x)=﹣x2+ax+1﹣lnx.(Ⅰ)当a=3时,求函数f(x)的单调递增区间;(Ⅱ)若f(x)在区间(0,)上是减函数,求实数a的取值范围.【考点】3D:函数的单调性及单调区间;3E:函数单调性的性质与判断.【专题】16:压轴题.【分析】(1)求单调区间,先求导,令导函数大于等于0即可.(2)已知f(x)在区间(0,)上是减函数,即f′(x)≤0在区间(0,)上恒成立,然后用分离参数求最值即可.【解答】解:(Ⅰ)当a=3时,f(x)=﹣x2+3x+1﹣lnx∴解f′(x)>0,即:2x2﹣3x+1<0函数f(x)的单调递增区间是.(Ⅱ)f′(x)=﹣2x+a﹣,∵f(x)在上为减函数,∴x∈时﹣2x+a﹣≤0恒成立.即a≤2x+恒成立.设,则∵x∈时,>4,∴g′(x)<0,∴g(x)在上递减,∴g(x)>g()=3,∴a≤3.【点评】本题考查函数单调性的判断和已知函数单调性求参数的范围,此类问题一般用导数解决,综合性较强.20.(12分)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方法:方案甲:逐个化验,直到能确定患病动物为止.方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;(Ⅱ)ξ表示依方案乙所需化验次数,求ξ的期望.【考点】C6:等可能事件和等可能事件的概率;CH:离散型随机变量的期望与方差.【分析】(1)由题意得到这两种方案的化验次数,算出在各个次数下的概率,写出化验次数的分布列,求出方案甲所需化验次数不少于依方案乙所需化验次数的概率.(2)根据上一问乙的化验次数的分布列,利用期望计算公式得到结果.【解答】解:(Ⅰ)若乙验两次时,有两种可能:①先验三只结果为阳性,再从中逐个验时,恰好一次验中概率为:②先验三只结果为阴性,再从其它两只中验出阳性(无论第二次试验中有没有,均可以在第二次结束),∴乙只用两次的概率为.若乙验三次时,只有一种可能:先验三只结果为阳性,再从中逐个验时,恰好二次验中概率为在三次验出时概率为∴甲种方案的次数不少于乙种次数的概率为:(Ⅱ)ξ表示依方案乙所需化验次数,∴ξ的期望为Eξ=2×0.6+3×0.4=2.4.【点评】期望是概率论和数理统计的重要概念之一,是反映随机变量取值分布的特征数,学习期望将为今后学习概率统计知识做铺垫.同时,它在市场预测,经济统计,风险与决策等领域有着广泛的应用,为今后学习数学及相关学科产生深远的影响.21.(12分)双曲线的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.已知||、||、||成等差数列,且与同向.(Ⅰ)求双曲线的离心率;(Ⅱ)设AB被双曲线所截得的线段的长为4,求双曲线的方程.【考点】KB:双曲线的标准方程;KC:双曲线的性质.【专题】11:计算题;16:压轴题.【分析】(1)由2个向量同向,得到渐近线的夹角范围,求出离心率的范围,再用勾股定理得出直角三角形的2个直角边的长度比,联想到渐近线的夹角,求出渐近线的斜率,进而求出离心率.(2)利用第(1)的结论,设出双曲线的方程,将AB方程代入,运用根与系数的关系及弦长公式,求出待定系数,即可求出双曲线方程.【解答】解:(1)设双曲线方程为,由,同向,∴渐近线的倾斜角范围为(0,),∴渐近线斜率为:,∴.∵||、||、||成等差数列,∴|OB|+|OA|=2|AB|,∴|AB|2=(|OB|﹣|OA|)(|OB|+|OA|)=(|OB|﹣|OA|)•2|AB|,∴,∴,可得:,而在直角三角形OAB中,注意到三角形OAF也为直角三角形,即tan∠AOB=,而由对称性可知:OA的斜率为k=tan,∴,∴2k2+3k﹣2=0,∴;∴,∴,∴.(2)由第(1)知,a=2b,可设双曲线方程为﹣=1,∴c=b.由于AB的倾斜角为+∠AOB,故AB的斜率为tan(+∠AOB )=﹣cot(∠AOB)=﹣2,∴AB的直线方程为y=﹣2(x﹣b),代入双曲线方程得:15x2﹣32bx+84b2=0,∴x1+x2=,x1•x2=,∴4=•=•,即16=﹣112b2,∴b2=9,所求双曲线方程为:﹣=1.【点评】做到边做边看,从而发现题中的巧妙,如据,联想到对应的是2渐近线的夹角的正切值,属于中档题.22.(12分)设函数f(x)=x﹣xlnx.数列{a n}满足0<a1<1,a n+1=f(a n).(Ⅰ)证明:函数f(x)在区间(0,1)是增函数;(Ⅱ)证明:a n<a n+1<1;(Ⅲ)设b∈(a1,1),整数.证明:a k+1>b.【考点】6B:利用导数研究函数的单调性;RG:数学归纳法.【专题】16:压轴题.【分析】(1)首先求出函数的导数,然后令f′(x)=0,解出函数的极值点,最后根据导数判断函数在区间(0,1)上的单调性,从而进行证明.(2)由题意数列{a n}满足0<a1<1,a n+1=f(a n),求出a n+1=a n﹣a n lna n,然后利用归纳法进行证明;(3)由题意f(x)=x﹣xlnx,a n+1=f(a n)可得a k+1=a k﹣b﹣a k,然后进行讨论求解.【解答】解:(Ⅰ)证明:∵f(x)=x﹣xlnx,∴f′(x)=﹣lnx,当x∈(0,1)时,f′(x)=﹣lnx>0故函数f(x)在区间(0,1)上是增函数;(Ⅱ)证明:(用数学归纳法)(i)当n=1时,0<a1<1,a1lna1<0,a2=f(a1)=a1﹣a1lna1>a1,∵函数f(x)在区间(0,1)是增函数且函数f(x)在x=1处连续,∴f(x)在区间(0,1]是增函数,a2=f(a1)=a1﹣a1lna1<1,即a1<a2<1成立,(ⅱ)假设当x=k(k∈N+)时,a k<a k+1<1成立,即0<a1≤a k<a k+1<1,那么当n=k+1时,由f(x)在区间(0,1]是增函数,0<a1≤a k<a k+1<1,得f(a k)<f(a k+1)<f(1),而a n+1=f(a n),则a k+1=f(a k),a k+2=f(a k+1),a k+1<a k+2<1,也就是说当n=k+1时,a n<a n+1<1也成立,根据(ⅰ)、(ⅱ)可得对任意的正整数n,a n<a n+1<1恒成立.(Ⅲ)证明:由f(x)=x﹣xlnx,a n+1=f(a n)可得a k+1=a k﹣a k lna k=,1)若存在某i≤k,满足a i≤b,则由(Ⅱ)知:a k+1﹣b>a i﹣b≥0,2)若对任意i≤k,都有a i>b,则a k+1=a k﹣a k lna k==≥a1﹣b1﹣ka1lnb=0,即a k+1>b成立.【点评】此题主要考查多项式函数的导数,函数单调性的判定,函数最值,函数、方程与不等式等基础知识及数学归纳法的应用,一般出题者喜欢考查学生的运算求解能力、推理论证能力及分析与解决问题的能力,要出学生会用数形结合的思想、分类与整合思想,化归与转化思想、有限与无限的思想来解决问题.。
2008年全国高考理科数学试题及答案-宁夏卷
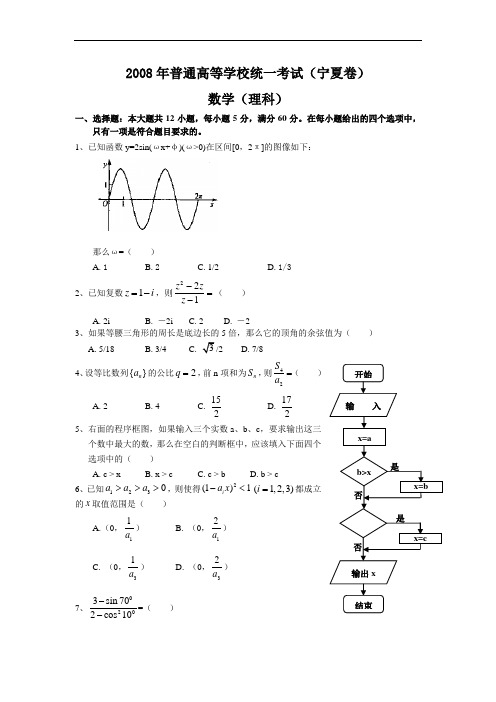
2008年普通高等学校统一考试(宁夏卷)数学(理科)一、选择题:本大题共12小题,每小题5分,满分60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知函数y=2sin(ωx+φ)(ω>0)在区间[0,2π]的图像如下:那么ω=( ) A. 1B. 2C. 1/2D. 1/32、已知复数1z i =-,则221z zz -=-( ) A. 2i B. -2i C. 2 D. -23、如果等腰三角形的周长是底边长的5倍,那么它的顶角的余弦值为( ) A. 5/18B. 3/4C.3/2 D. 7/84、设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A. 2 B. 4 C.152D.1725、右面的程序框图,如果输入三个实数a 、b 、c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( ) A. c > xB. x > cC. c > bD. b > c6、已知1230a a a >>>,则使得2(1)1i a x -<(1,2,3)i =都成立的x 取值范围是( )A.(0,11a )B. (0,12a )C. (0,31a ) D. (0,32a ) 7、0203sin 702cos 10--=( )是否 开始输入x=ab>x 输出x结束x=bx=c否是A.12B.2C. 2D.28、平面向量a ,b 共线的充要条件是( )A. a ,b 方向相同B. a ,b 两向量中至少有一个为零向量C. R λ∃∈, b a λ=D. 存在不全为零的实数1λ,2λ,120a b λλ+=9、甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面。
不同的安排方法共有( ) A. 20种B. 30种C. 40种D. 60种10、由直线21=x ,x=2,曲线xy 1=及x 轴所围图形的面积为( ) A. 415 B. 417 C. 2ln 21 D. 2ln 211、已知点P 在抛物线y 2 = 4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为( ) A. (41,-1) B. (41,1) C. (1,2) D. (1,-2)12、某几何体的一条棱长为7,在该几何体的正视图中,这条棱的投影是长为6的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a 和b 的线段,则a + b 的最大值为( )A. 22B. 32C. 4D. 52二、填空题:本大题共4小题,每小题5分,满分20分。
一校版2008全国新课标卷(宁夏卷)文理合卷

离的取值范围是(
B
)
5 A. 0,
10 B. 0,
10 C. 5,
15 D. 5,
(理 11)已知点 P 在抛物线 y 2 4 x 上,那么点 P 到点 Q(2, 1) 的距离与点 P 到抛物线焦点距 离之和取得最小值时,点 P 的坐标为(
1 A. , 1 4
A ) D. (1, 2) C )
1 B. , 1 4
C. (1, 2)
(文 11)函数 f ( x) cos 2 x 2sin x 的最小值和最大值分别为( A.-1, 1 B.-2, 2 C.-3,
3 2
D.-2,
3 2
(理 12)某几何体的一条棱长为 7 ,在该几何体的正视图中,这条棱的投影是长为 6 的线 段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为 a 和 b 的线段,则 a+b 的最大 值为( C ) A. 2 2 B. 2 3 C. 4 D. 2 5
第 4 页 共 6 页
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (Ⅱ)按照给出的尺寸,求该多面体的体积; (Ⅲ)在所给直观图中连结 BC ,证明: BC ∥面 EFG .
G
D
F
C
2
6 4
2 2 4
B
C B
E D A
(理 19) (本小题满分 12 分) A,B 两个投资项目的利润率分别为随机变量 X1 和 X2.根据市场分析,X1 和 X2 的分布列 分别为 X1 5% 10% X2 2% 8% 12% P 0.8 0.2 P 0.2 0.5 0.3 (Ⅰ)在 A,B 两个项目上各投资 100 万元,Y1 和 Y2 分别表示投资项目 A 和 B 所获得的利润, 求方差 DY1,DY2; (Ⅱ)将 x(0≤x≤100)万元投资 A 项目,100-x 万元投资 B 项目,f(x)表示投资 A 项目所得利润 的方差与投资 B 项目所得利润的方差的和.求 f(x)的最小值,并指出 x 为何值时,f(x)取到最小 值. (注:D(aX+b)=a2D(X)) (文 19)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某 校 6 名学生进行问卷调查.6 人得分情况如下:5,6,7,8,9,10. 把这 6 名学生的得分看成一个总体. (Ⅰ)求该总体的平均数; (Ⅱ)用简单随机抽样方法从这 6 名学生中抽取 2 名,他们的得分组成一个样本.求该样本平 均数与总体平均数之差的绝对值不超过 0.5 的概率. (理 20) (本小题满分 12 分) 在直角坐标系 xOy 中,椭圆 C1:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. 2 2
B. 2 3
C. 4
结合长方体的对角线在三个面的投
影来理解计算. 如图设长方体的 高宽高分别为 m, n, k
D. 2 5
则 m2 n2 k2 7, m2 k 2 6, n 1
kn
m
12. 某几何体的一条棱长为 7, 在该几何体的正视图中,
这条棱的投影是长为 6的线段, 在该几何体的侧视图 与俯视图中, 这条棱的投影分别是长为a和b的线段, 则 a b的最大值为( C )
10
15
5
O
A 5F
2
B
4
15. 一个六棱柱的底面是正六边形,其侧棱垂直底面.
已知该六棱柱的顶点都在同一个球面上, 且该六棱柱
A. 2 2
B. 2 3
C. 4
D. 2 5
1 k2 a, 1 m2 b,
m2 k 2 (a2 1) (b2 1) 6, a2 b2 8
(a b)2 a2 2ab b2 8 2ab 8 a2 b2 16 a b 4,当且仅当a b 2时取等号
二、填空题:本大题共4小题,每小题5分。
13.已知向量a (0, 1,1), b (4,1, 0), a b 29且 0, 则 3 . 根据题意, a b = (4,1 , ), 16 ( 1)2 2 29( 0) 3
14. 设双曲线 x2 y2 1的右顶点为A, 右焦点为F . 过点 9 16
如下,那么 ( B )
A. 1
B. 2
C. 1
D. 1
2
3
y
1 O1
2 x 由周期知函数的周期T , 所以 2 2 T
2.已知复数z 1 i, 则 z2 2z ( B ) z1
A. 2i
B. 2i
C. 2
2
z2 2z (1 i)2 2(1 i) 2
z 1 i,
1, 4
1
66
B.
44
1 4
,1
22
11
F
22
C. (1, 2)
D. (1, 2)
S
11
Q
P
22
如图, PF PQ PS PQ , 最小S 值在 P
33
S, P,Q三点共线时取得,此时P,Q的纵
坐标都是 1.
44
12. 某几何体的一条棱长为 7, 在该几何体的正视图中,
这条棱的投影是长为 6的线段, 在该几何体的侧视图 与俯视图中, 这条棱的投影分别是长为a和b的线段, 则 a b的最大值为( )
A.
0,1 a1
B.
0,2 a1
C
.
0,1 a3
D.
0,2 a3
(1
ai
x)2
1
ai2
x2
2ai
x
0
ai2
x(
x
2 ai
)
0,
所以解集为
0,
2 ai
又2 a1
2 a2
2 a3
,
所以x
0,
2 a1
3 sin 70 7. 2 cos2 10 ( C )
B. 17 4
C. 1 ln 2 2
D. 2 ln 2
如图, 面积
S
21
1 2
x
ln x
2 1 2
ln 2 ln 1 2 ln 2 2
11.已知点P在抛物线y2 4x上,那么点33P到点Q(2, 1)的
距离与点P到抛物线焦点距离之和取得最小值时, 点P 22
的坐标为( A )
A.
88
2,
前n项和为Sn
,
则
S4 a2
(
C)
15
17
A. 2
B. 4
C.
D.
2
2
S4 a1 a2 a3 a4 1 2 4 8 15
a2
a2
2
2
5. 右面的程序框图,如果输 入三个实数a,b,c,要求 输出这三个数中最大的数, 那么在空白的判断框中, 应该填入下面四个选项中 的( ) A
2008年普通高等学校招生全国统一考试
理科数学
新课标卷:使用地区:宁夏,海南
1234 5678
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
一、选择题:本大题共12小题,每小题5分,在每小题给 出的四个选项中,只有一项是符合题目要求的。
1.已知函数y 2sin( x )( 0)在区间[0, 2 ]的图像
A. 1
B. 2
C. 2
2
2
D. 3 2
3 sin 70 3 cos 20 3 (2cos2 20 1) 2 cos2 10 2 cos2 10 2 cos2 10 2
8. 平面向量a, b共线的充要条件是( D ) A. a, b方向相同 B. a, b两向量中至少有一个为零向量
A.c>x B.x>c C.c>b D.b>c
变量x的作用是保留3个数中的最大 值,所以第二个条件结构的判断 框内语句为“c>x”,满足“是” 则交换两个变量的数值后输出的 值结束程序,满足“否”直接输 出的值结束程序。
6.已知a1 a2 a3 0, 则使得(1 ai x)2 1(i 1,2,3)都 成立的x的取值范围是( B )
A.20种
B.30种
C.40种
D.60种
分类计数:
甲在星期一有A42 12种安排方法, 甲在星期二有A32 6种安排方法, 甲在星期三有A22 2种安排方法, 总共有12 6 2 20种
10.由直线x 1 , x 2,曲线y 1 及x轴所围图形的面积
2
x
为( D )
A. 15 4
2i
z1
1 i 1
i
3. 如果等腰三角形的周长是底边长的5倍,那么它的 顶角的余弦值为(D )
A. 5
B. 3
C. 3
D. 7
18
4
2
8
设顶角为C,因为l 5c,a b 2c,由余弦定理
cos C a2 b2 c2 4c2 4c2 c2 7
2ab
2 2c 2c 8
4. 设等比数列{an }的公比q
C. R, b a D. 存在不全为零的实数1, 2 , 1a 2 b 0
① 方向相同或相反的非零向量共线 ② 零向量与任何向量共线
9. 甲、乙、丙3位志愿者安排在周一至周五的5天中参
加某项志愿者活动,要求每人参加一天且每天至多
安排一人,并要求甲安排在另外两位前面.不同的
安排方法共有( A )
F 平行双曲线的一条渐近线的直线与双曲线交于点B,
则△AFB的面积为
.
由题意A(3, 0), F (5, 0), 一条渐近线方程为10 y 4 x
3
由
y 4(x 3
x2 y2
9 16
5) 1
,
得交点的纵坐标y
32 15
8 6 4 2
1 32 32
S 20 △AFB
2 15 2 15
